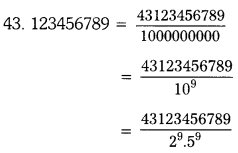Students can practice TS 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 1 Real Numbers Exercise 1.3
Question 1.
Write the following rational numbers in their decimal form and also state which are terminating and which are non-terminating repeating decimal form.
(i) \(\frac{3}{8}\)
Solution:
\(\frac{3}{8}\) = \(\frac{3}{2.2 .2}\) = \(\frac{3}{2^3}\) (∵ Denominator consists of only 2’s. terminating decimal)
\(\frac{3 \times 5^3}{2^3 \times 5^3}\) = \(\frac{3 \times 125}{10^3}\) = \(\frac{375}{1000}\) = 0.375
(ii) \(\frac{229}{400}\)
Solution:
\(\frac{229}{400}\) = \(\frac{229}{2.2 .2 .2 \times 5 \times 5}\) (∵ Denominator consists of only 2 ‘s.)
= \(\frac{229}{2^4 \cdot 5^2}\) (terminating decimal)
= \(\frac{229 \times 5^2}{2^4 \times 5^2 \times 5^2}\) = \(\frac{229 \times 5^2}{2^4 \times 5^4}\)
= \(\frac{229 \times 25}{(2 \times 5)^4}\) = \(\frac{5725}{10^4}\)
= \(\frac{5725}{10000}\) = 0.5725 (∵ Denominator consists of only 2’s. terminating decimal)

(iii) 4\(\frac{1}{5}\)
Solution:
4\(\frac{1}{5}\) = \(\frac{21}{5}\) (terminating decimal)
\(\frac{21}{5}\) = 4.2 (∵ Denominator consists of only 2’s.)
(iv) \(\frac{2}{11}\)
Solution:
\(\frac{2}{11}\) (∵ Denominator doesn’t contain 2s or 5’s or both. Hence it is an non-terminating, repeating decimal) (non-terminating, re-peating decimal because the denomination does not contain power of 2 or power of 5 of both 2 and 5)
\(\frac{2}{11}\) = 0.181818……..
= \(0 . \overline{18}\)
(v) \(\frac{8}{125}\)
Solution:
\(\frac{8}{125}\) = \(\frac{8}{5^3}\) (∵ Denominator does not consists of only 2’s.) (terminating decimal)
= \(\frac{8}{5^3}\) × \(\frac{2^3}{2^3}\) = \(\frac{8 \times 8}{(5 \times 2)^3}\) = \(\frac{64}{1000}\) = 0.064
Question 2.
Without performing division, state whether the following rational numbers will have a terminating decimal form or a non-terminating repeating decimal form.
(i) \(\frac{13}{3125}\)
Solution:
\(\frac{13}{3125}\). It is of the form \(\frac{p}{q}\)
\(\frac{13}{3125}\) = \(\frac{13}{5 \times 5 \times 5 \times 5 \times 5}\) = \(\frac{13}{5^5}\)
∵ q = 55 which is of the form 2n5m (n = 0; m = 5)
Given rational number has a terminating decimal expansion.
(ii) \(\frac{11}{12}\)
Solution:
\(\frac{11}{12}\) it is of the form \(\frac{p}{q}\).
\(\frac{11}{12}\) = \(\frac{11}{2 \times 2 \times 3}\) = \(\frac{11}{2^2 \times 3}\) = 0.916666.
∵ Here q = 22 × 3 which is not of the form 2n × 5m.
∴ Given rational number has a non-termi-nating repeating decimal expansion.

(iii) \(\frac{64}{455}\)
Solution:
\(\frac{64}{455}\) It is of the form \(\frac{p}{q}\).
\(\frac{64}{455}\) = \(\frac{64}{5 \times 7 \times 13}\)
∵ q = 5 × 7 × 13 which is not of the form 2n.5m.
∵ Given rational number has a non-terminating, repeating decimal expansion.
(iv) \(\frac{15}{1600}\)
Solution:
\(\frac{15}{1600}\) It is of the form \(\frac{p}{q}\).
\(\frac{15}{1600}\) = \(\frac{3}{320}\) = \(\frac{3}{2^6 \times 5}\)
∵ Here q = 26 × 51 which is of the form 2n.5m (m = 1, n = 6)
∴ Given rational number has a terminating decimal expansion.
(v) \(\frac{29}{343}\)
Solution:
\(\frac{29}{343}\) It is of the form \(\frac{p}{q}\).
\(\frac{29}{343}\) = \(\frac{29}{7 \times 7 \times 7}\) = \(\frac{29}{7^3}\)
∵ Here q = 73 which is not of the form 2n5m.
∴ Given rational number has a non-terminating, repeating decimal expansion.
(vi) \(\frac{23}{2^3 \cdot 5^2}\)
Solution:
\(\frac{23}{2^3 \times 5^2}\) It is of the form \(\frac{p}{q}\).
∵ Here q = 23 × 52 which is of the form of 2n5m (n = 3, m = 2).
∴ Given rational number has a terminating decimal expansion.
(vii) \(\frac{129}{2^2 \cdot 5^7 \cdot 7^5}\)
Solution:
\(\frac{129}{2^2 \times 5^7 \times 7^5}\) It is of the form \(\frac{p}{q}\).
∵ Here q = 22 × 57 × 75 which is not of the form 2n5m.
∴ Given rational number has a non-terminating, repeating decimal expansion.
(viii) \(\frac{9}{15}\) = \(\frac{3}{5}\) It is of the form \(\frac{p}{q}\).
Solution:
\(\frac{9}{15}\) = \(\frac{3}{5}\) It is of the form \(\frac{p}{q}\).
Here q = 51 which is of the form 2n5m (n = 0; m = 1). .
∴ Given rational number has a terminating decimal expansion.
(ix) \(\frac{36}{100}\)
Solution:
\(\frac{36}{100}\) It is of the form \(\frac{p}{q}\).
\(\frac{36}{100}\) = \(\frac{36}{2 \times 2 \times 5 \times 5}\) = \(\frac{36}{2^2 5^2}\)
∵ Here q = 22. 52 which is of the form 2n5m (n = 2, m = 2).
∴ Given rational number has a terminating decimal expansion.
(x) \(\frac{77}{210}\)
Solution:
\(\frac{77}{210}\) it is of the form \(\frac{p}{q}\).
\(\frac{77}{210}\) = \(\frac{11}{30}\) = \(\frac{11}{2 \times 3 \times 5}\)
∵ q = 2 × 3 × 5 which is not of the form 2n5m
∴ Given rational number has non-terminating, repeating decimal expansion.
Question 3.
Write the following rational numbers in decimal form using Theorem 1.4.
(i) \(\frac{13}{25}\)
Solution:
\(\frac{13}{25}\) = \(\frac{13}{5 \times 5}\) = \(\frac{13 \times 2^2}{5^2 \times 2^2}\)
= \(\frac{13 \quad 4}{10^2}\) = \(\frac{52}{100}\) = 0.52
(ii) \(\frac{15}{16}\)
Solution:
\(\frac{15}{16}\) = \(\frac{15}{2 \times 2 \times 2 \times 2}\) = \(\frac{15 \times 5^4}{2^4 \times 5^4}\)
= \(\frac{15 \quad 5^4}{10^4}\) = \(\frac{9375}{10000}\) = 0.9375

(iii) \(\frac{23}{2^3 \cdot 5^2}\)
Solution:
\(\frac{23}{2^3 \times 5^2}\) = \(\frac{23 \times 5}{2^3 \times 5^2 \times 5}\)
= \(\frac{115}{10^3}\) = \(\frac{115}{1000}\) = 0.115
(iv) \(\frac{7218}{3^2 .5^2}\)
Solution:
\(\frac{7218}{3^2 \times 5^2}\) = \(\frac{3 \times 3 \times 802}{3^2 \times 5^2}\)
= \(\frac{802 \times 2^2}{5^2 \times 2^2}\) = \(\frac{3208}{100}\) = 32.08
(v) \(\frac{143}{110}\)
Solution:
\(\frac{143}{110}\) = \(\frac{11 \times 13}{11 \times 10}\) = \(\frac{13}{10}\) = 1.3
Question 4.
Express the following decimal numbers in the form of q and write the prime factors of q. What do you observe?
(i) 43.123
Solution:
43.123456789
Given decimal expansion terminates. Hence given real number is a rational.
It is in the form of \(\frac{p}{q}\)
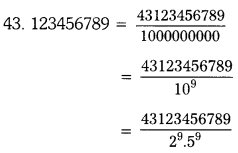
∵ Here q = 29.59 ; q is of the form 2n5m (n = 9; m = 9)

(ii) 0.120112001120001…
Solution:
0.120120012000120000 …………
Given decimal expansion is not either ter-minating or non-terminating repeating.
∵ Hence given real number is not rational.
(iii) \(43 . \overline{12}\)
Solution:
\(43 . \overline{123456789}\)
Given decimal expansion is non-terminating, repeating.
Given real number is rational and so of the \(\frac{p}{q}\)
Let x = \(43 . \overline{123456789}\)
x = \(43 . \overline{123456789}\) …… (2)
Multiplying both sides of (1) by 1000000000, we get
x = 43123456789.123456789 ……. (2)
Substracting (1) from (2) we get
999999999 x = 43123456746
x = \(\frac{43123456746}{999999999}\)
x = \(\frac{14374485582}{333333333}\)
q = 333333333 which is not of the form 2n5m.
![]()

![]()