Telangana SCERT 9th Class Telugu Guide Telangana 4th Lesson రంగాచార్యతో ముఖాముఖి Textbook Questions and Answers.
TS 9th Class Telugu 4th Lesson Questions and Answers Telangana రంగాచార్యతో ముఖాముఖి
చదువండి – ఆలోచించి చెప్పండి (Textbook Page No. 34)
తెలంగాణకు చెందిన ప్రముఖ భాషాశాస్త్రవేత్త డా॥ చేకూరి రామారావుతో పత్రికా విలేఖరి ముఖాముఖి.
పత్రికా విలేఖరి : మీ వ్యక్తిగత వివరాలు చెప్పండి.
చేకూరి రామారావు : మాది ఇల్లిందలపాడు గ్రామం, ఖమ్మం జిల్లా. తల్లి భారతమ్మ, తండ్రి లింగయ్య. భాషాశాస్త్రంలో ఉపన్యాసకుడిగా ఉద్యోగం ప్రారంభించి, హైదరాబాదు కేంద్రీయ విశ్వవిద్యాలయంలో డీన్ గా పదవీ విరమణ చేశాను.
పత్రికా విలేఖరి : మీకు కేంద్ర సాహిత్య అకాడమీ అవార్డు ఎప్పుడు, ఏ రచనకు వచ్చింది ?
చేకూరి రామారావు : నేను రాసిన “స్మృతి కిణాంకం” అనే వ్యాస సంకలనానికి 2002 సంవత్సరంలో ఉత్తమమైన విమర్శ గ్రంథంగా కేంద్ర సాహిత్య అకాడమీ అవార్డు వచ్చింది.
పత్రికా విలేఖరి : వాడుకభాష గురించి చెప్పండి.
చేకూరి రామారావు : వ్యావహారిక భాషావాదమంటే మాట్లాడినట్లు రాయడం కాదు. మాట్లాడే భాషకు, రాసే భాషకు పరిమితులు వేరు. ప్రయోజనం వేరు. రచనా వ్యవస్థకు కొన్ని నియమాలు అవసరం.
పత్రికా విలేఖరి : తెలుగు కనుమరుగు అవుతుందేమోనన్న ఆందోళన గురించి మీ అభిప్రాయం.
చేకూరి రామారావు : ఇన్ని కోట్లమంది మాట్లాడే భాష కనుమరుగుకాదు. కాకపోతే మన తెలుగులో ఇతర భాషల మిశ్రమం ఎక్కువగా కనిపిస్తున్నది.
ప్రశ్నలు
ప్రశ్న 1.
పై పేరాలో ఎవరు ఎవరిని ప్రశ్నలడుగుతున్నారు?
జవాబు:
పై పేరాలో ప్రముఖ భాషాశాస్త్రవేత్త అయిన డా॥ చేకూరి రామారావుగారిని, పత్రికా విలేఖరి ప్రశ్నలు అడుగుతున్నాడు.
ప్రశ్న 2.
పై సమాధానాల ద్వారా మీకు తెలిసిన సాహితీ విశేషాలేమిటి?
జవాబు:
వ్యవహారిక భాషావాదము అంటే, మాట్లాడినట్లు రాయడం కాదనీ, మాట్లాడే భాషకూ, రాసే భాషకూ పరిమితులు వేరనీ, ప్రయోజనం వేరనీ, రచనా వ్యవస్థకు కొన్ని నియమాలు అవసరమనీ తెలిసింది. నేటి తెలుగుభాషను కోట్లాదిమంది మాట్లాడుతున్నారు కాబట్టి తెలుగు ఎప్పటికీ కనుమరుగు కాదనీ, నేటి తెలుగులో ఇతర భాషల మిశ్రమం ఎక్కువగా ఉందనీ తెలిసింది.

ప్రశ్న 3.
ఈ విధంగా ప్రశ్నలడిగే విధానాన్ని ఏమంటారు?
జవాబు:
ఈ విధంగా ప్రశ్నలడిగే విధానాన్ని ఇంగ్లీషు భాషలో ‘ఇంటర్వ్యూ’ అంటారు. తెలుగులో “ముఖాముఖి” అని, ‘పరిపృచ్ఛ’ అని పిలుస్తారు.
ఆలోచించండి – చెప్పండి (Textbook Page No. 37)
ప్రశ్న 1.
“తెలంగాణ సాయుధపోరాటం” గురించి విన్నారా ? మీకు తెలిసింది చెప్పండి.
జవాబు:
తెలంగాణ ప్రాంతంలో భూస్వాముల నుండి, దొరల నుండి, నిజాం ప్రభుత్వం నుండి, వెట్టిచాకిరి నుండి, విముక్తి కోసం, రైతులూ, రైతుకూలీలూ, కార్మికులూ స్త్రీలూ, పిల్లలూ కమ్యూనిస్టు పార్టీ ఆధ్వర్యంలో జరిపిన పోరాటమే, “తెలంగాణ సాయుధపోరాటం”.
ఈ పోరాటం, 1946 నుండి 1951 వరకు కొనసాగింది. వందలాది ఎగరాలు కలిగిన భూస్వాములపై, వారికి అండదండలు అందించిన నిజాం ప్రభుత్వంపై, రైతులు చేసిన పోరాటం ఇది. భూమి కోసం, భుక్తి కోసం, బానిసత్వ విముక్తి కోసం, పేద రైతులు చేసిన ఈ సాయుధ పోరాటం, ఎంతో మందికి స్ఫూర్తిని ఇచ్చింది.
ప్రశ్న 2.
“వారసత్వం” అనే మాటను ఏ విధంగా గ్రహించాలి ?
జవాబు:
‘వారసత్వం’ అనే పదానికి, ఒకతరం నుండి మరో తరానికి వచ్చే సంప్రదాయ హక్కు అని అర్థము. తాత ఆస్తి తండ్రికి, తండ్రి ఆస్తి కొడుకుకి వారసత్వంగా సంక్రమిస్తుంది. అలాగే తెలంగాణ సాయుధపోరాట స్ఫూర్తి, ఒక తరం నుండి వారి తరువాత తరానికి సంక్రమించాలి.
తెలంగాణ సాయుధపోరాటంలో ఆనాటి రైతులూ వగైరా ప్రజలు, ఎలా ప్రభుత్వంపై, భూస్వాములపై, తమ హక్కుల కోసం పోరాడారో, అలాగే భావితరాల వారు కూడా, తమ న్యాయమైన హక్కుల కోసం పోరాటం చేసే పట్టుదల, దీక్ష, వారసత్వంగా వారికి రావాలని ఆ మనం ఈ మాటనుబట్టి గ్రహించాలి.
ఆలోచించండి – చెప్పండి (Textbook Page No. 38)
ప్రశ్న 1.
“జనపదం” నవల ఇతివృత్తమేమిటి ?
జవాబు:
తెలంగాణలో పోలీసు యాక్షన్ తరువాత రైతుల భూములను దొరలు కాజేశారు. దానితో ‘జనపదం’ కథ మొదలవుతుంది. తరువాత వచ్చిన ఉద్యమాల గురించి, ఉద్యమాల పేరున జరిగిన మోసాల గురించి, ఆనాడు రాజకీయాలు భ్రష్టు పట్టడం గురించి, ఈ “జనపదం” నవలలో వివరంగా చెప్పబడింది. ఇది ఒక్క తెలంగాణ కాక, భారతదేశానికి చెందిన నవల. ఈ నవలలో నిజం చెప్పబడింది.
ప్రశ్న 2.
రంగాచార్య నవలల్లో ప్రధాన విషయం ఏమిటి ?
జవాబు:
రంగాచార్య నవలల్లో ప్రధాన విషయం, “తెలంగాణ సాయుధపోరాటం”. రంగాచార్య నవలలు, తెలంగాణ సాయుధ పోరాటం నేపథ్యంగా రాయబడ్డాయి. ‘మోదుగు పూలు’ అనే నవల ఆయన జీవిత చరిత్ర ప్రధానంగా రాయబడింది.

ప్రశ్న 3.
తన ఆత్మకథగా వర్ణించిన పుస్తకమేది ?
జవాబు:
రంగాచార్య రాసిన ‘మోదుగుపూలు’ అనే నవల సుమారుగా ఆయన ‘ఆత్మకథ’ వంటిది. రంగాచార్య తన జీవన యానాన్ని ఈ నవలా రూపంలో రాశాడు. ఈ నవల పర్ఫెక్షన్ సాగింది. ఈ నవలలో ఒక్క లోపాన్ని కూడా చూపించలేరని రంగాచార్య చెప్పారు. ఈ నవలలో సిద్ధాంతం కన్నా, విశ్వాసం కన్నా, కర్తవ్యం గొప్పది అని రంగాచార్య చెప్పాడు.
ఆలోచించండి – చెప్పండి (Textbook Page No. 39)
ప్రశ్న 1.
‘మాండలికమే ప్రజల భాష !’ నిజమేనా ?
జవాబు:
మాండలిక భాష అంటే ఆ మండలంలో లేక ఆ ప్రాంతంలో సామాన్య ప్రజలు వారి నిత్య వ్యవహారాలలో ఒకరితో ఒకరు మాట్లాడుకొనే భాష, మాండలిక భాష, ప్రజల హృదయాల్లోంచి అప్రయత్నంగా వచ్చిన భాష, అది కావ్య భాషవలె కృత్రిమం కాదు. కాబట్టి మాండలిక భాషను నిజమైన ప్రజల భాష అని చెప్పవచ్చు.
ప్రశ్న 2.
‘వసుధైక కుటుంబం’ అంటే మీరు ఏమనుకుంటున్నారు?
జవాబు:
కుటుంబము అంటే మనకు తెలుసు. మన తల్లిదండ్రులు, అన్నదమ్ములు, అప్పాచెల్లెండు, తాతామామ్మలు మన కుటుంబము. మన కుటుంబ సభ్యులపట్ల, మనం ప్రేమాదరాలతో ఉంటాము. మన కుటుంబ సభ్యుల కష్టసుఖాల్లో మనం పాలుపంచుకుంటాము.
వసుధైక కుటుంబం, అంటే ప్రపంచంలోని భూమండలంపై ఉండే ప్రజలందరూ ఒకే కుటుంబం అని అర్థం. అంటే ప్రపంచ ప్రజలంతా కులమత భేదాలు విడిచి, ఒకే తల్లిదండ్రుల పిల్లల్లా కలసిమెలసి, కష్టసుఖాల్లో పాలుపంచుకోడాన్ని ‘వసుధైక కుటుంబం’ అనవచ్చు.
ఆలోచించండి – చెప్పండి (Textbook Page No. 39)
ప్రశ్న 1.
కృషి – గుర్తింపు వీటి మధ్య సంబంధాన్ని చెప్పండి.
జవాబు:
కొందరు వ్యక్తులు సంఘం కోసం తమ జీవితాన్ని కూడా త్యాగం చేసి ఎంతో ‘కృషి’ అనగా ప్రయత్నం చేస్తారు. కొందరు సంఘసంస్కర్తలు, సాంఘిక సంస్కరణల కోసం గొప్ప కృషి చేస్తారు. కొందరు శాస్త్రవేత్తలు, శాస్త్రాభివృద్ధికై కృషి చేస్తారు. కొందరు డాక్టర్లు, ఎన్నో పరిశోధనలు చేసి గొప్ప విజయాలు సాధిస్తారు. కొందరు రాజకీయ వేత్తలు దేశం కోసం కృషి చేస్తారు.
అందులో కొందరిని సంఘం గుర్తించి వారిని గౌరవిస్తుంది. వారికి సన్మానాలు చేస్తుంది. అందులో కొందరి కృషికి, గుర్తింపు ఉండదు. ఎవరూ వారి కృషిని మెచ్చుకోరు. కాబట్టి కృషికీ, గుర్తింపుకూ మధ్య సంబంధం ఉండదు.
ప్రశ్న 2.
సందేశమిచ్చే అవకాశం ఎవరికి ఉంటుందని మీరు అనుకుంటున్నారు ?
జవాబు:
కొందరు వ్యక్తులు దేశం కోసం, శాస్త్రాభివృద్ధి కోసం, జనం కోసం, ఎంతో కృషి చేసి తమ సర్వస్వాన్ని త్యాగం చేస్తారు. వారు ప్రజలకు చెప్పిన మాటలను తాము కూడా ఆచరిస్తారు. అటువంటి మహాత్ములకు, ఆదర్శ జీవనం కలవారికి, ఇతరులకు సందేశం ఇచ్చే అవకాశం ఉంటుంది.

ప్రశ్న 3.
‘సాంస్కృతిక వైభవం’ అంటే ఏమని అర్థం చేసుకోవచ్చు?
జవాబు:
‘సంస్కృతి’ అంటే నాగరికత. ఒక్కొక్క ప్రాంతంలో కొన్ని కళలు, కొన్ని ఆచార వ్యవహారాలు, కొన్ని పండుగలు, కొన్ని ఉత్సవాలు సంప్రదాయబద్ధంగా జరుపుకుంటారు. తెలంగాణలో బతుకమ్మ పండుగ చేసుకుంటారు. గణేశ్ ఉత్సవాలు చేస్తారు. మహంకాళి అమ్మవార్ని ఆరాధిస్తారు. దీనినే సాంస్కృతిక వైభవం అని చెప్పవచ్చు.
ఇవి చేయండి
I. అవగాహన-ప్రతిస్పందన
ప్రశ్న 1.
దాశరథి రంగాచార్యతో ఇంటర్వ్యూ ఎట్లా అనిపించింది ? మీ అభిప్రాయం చెప్పండి.
జవాబు:
దాశరథి రంగాచార్యగారితో ఇంటర్వ్యూ మంచి ఆనందాన్ని కల్గించింది. తెలంగాణ ముద్దుబిడ్డ అయిన రంగాచార్యగార్కి తెలంగాణ సాయుధపోరాటంతో గల సంబంధం, మాకు మంచి స్ఫూర్తినిచ్చింది. రంగాచార్య రచించిన చిల్లర దేవుళ్ళు, జనపదం, మోదుగుపూలు వంటి నవలలు కొని, తప్పక చదవాలనిపించింది. ఆ నవలలు ప్రతి పాఠశాల, గ్రంథాలయంలోనూ ఉండేలా, ప్రభుత్వం శ్రద్ధ తీసుకుంటే బాగుంటుదనిపించింది.
నాలుగు వేదాలనూ, 10 ఉపనిషత్తులనూ తెనిగించిన ఆ మహాపండితుడిని, ఒక్కసారి కన్నులారా చూడాలనిపించింది. రంగాచార్య వంటి పండితునిపై కమ్యూనిస్టుల ప్రభావం ఉందని తెలిసి, ఆశ్చర్యం అనిపించింది. రంగాచార్యగారు ఉత్తమ మనీషి అని, మంచి మనిషి అని నాకు అనిపించింది. రంగాచార్య ఉద్యమజీవి అనిపించింది. రంగాచార్య తెలంగాణ ముద్దుబిడ్డ అనిపించింది.
ప్రశ్న 2.
ఈ మధ్యకాలంలో టి.వి.లో లేదా ఇంకెక్కడైన మీరు చూసిన ఇంటర్వ్యూ గురించి మాట్లాడండి.
జవాబు:
అఖిల భారత, భారతీయ జనతాపార్టీ అధ్యక్షడు ‘అమిత్’తో, ఈనాడు పత్రిక వారు చేసిన ఇంటర్వ్యూ వివరాలను దిగువ ఇస్తున్నాం.
ఈనాడు ప్రతినిధి : మోదీ ప్రభుత్వం, మొదటి సంవత్సరం పాలనలో సాధించిన అతిపెద్ద విజయం ఏమిటి ?
అమిత్ షా : మేము 2014 మే 26న అధికారానికి వచ్చాం. ఈ ఏడాది పాలనలో మాపై ఒక్క అవినీతి మచ్చ కూడా లేదు. అదే యూ.పీ. ఏ – 10 ఏళ్ళ పాలనలో 12 లక్షల కోట్ల కుంభకోణాలు వెలుగులోకి వచ్చాయి. ఇది మేము సాధించిన మొదటి పెద్ద విజయం.
ఈనాడు ప్రతినిధి : ఇవి కాకుండా, ఇంకా ఏమి సాధించారు ?
అమిత్ షా : గాడి తప్పిన ఆర్థిక రంగాన్ని పట్టాలపైకి ఎక్కించాం. ద్రవ్యలోటు దిగి వస్తోంది. కాశ్మీర్ వరదలు, నేపాల్ భూకంపం, వంటి ఉపద్రవాలలో, వేగంగా బాధితులను మేము ఆదుకున్నాం. ఏడాది కాలంలో 14 కోట్ల (జన్ ధన్) బ్యాంకు ఖాతాలు ప్రారంభించాం. మూడు సామాజిక భద్రతా పథకాలు, పేదవారి కోసం తీసుకువచ్చాం.
ఈనాడు ప్రతినిధి : మోదీ సర్కారు కార్పొరేట్లకు వత్తాసు పలుకుతోందని ప్రతిపక్షాలు అంటున్నాయి కదా!
అమిత్ షా : అదంతా వట్టి అబద్దం. గత ప్రభుత్వం, బొగ్గు, ఖనిజ నిక్షేపాలను, కార్పొరేట్లకు దాదాపు ఉచితంగా ఇచ్చింది. మేము మొత్తం గనుల్లో 10 శాతం వేలం వేస్తే, 2 లక్షల కోట్లు ప్రభుత్వానికి వచ్చింది. అలాగే స్పెక్ట్రమ్ వేలంలో 1.08 లక్షల కోట్లు ప్రభుత్వానికి వచ్చాయి. మీరే గమనించండి. ఎవరు ఎవరికి వత్తాసో !
ఈనాడు ప్రతినిధి : ఆంధ్ర రాష్ట్రానికి ప్రత్యేక హోదా ఇవ్వడంలో మీరు ఎందుకు ఆలస్యం చేస్తున్నారు ?
అమిత్ షా : ఈ సమస్యను త్వరలో ఆర్థిక మంత్రి పరిష్కరిస్తారు.
ఈనాడు ప్రతినిధి : భూసేకరణ బిల్లును మీరు రాజ్యసభలో పాస్ చేయించుకోలేకపోతున్నారు కదా !
అమిత్ షా : అవును. ప్రతిపక్షాలు అనవసరంగా అడ్డు వస్తున్నాయి. ఆ బిల్లు త్వరలోనే పార్లమెంట్లో పాసవుతుంది.
ఈనాడు ప్రతినిధి : ధన్యవాదాలు, సెలవు.
ప్రశ్న 3.
పాఠం ఆధారంగా దాశరథి రంగాచార్య నవలలు, వాటిలోని ఇతివృత్తాలను తెలుపుతూ ఒక జాబితా రాయండి.

జవాబు:
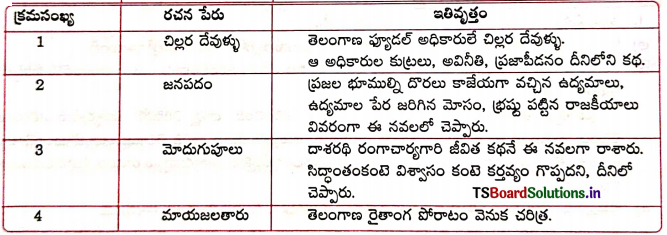
ప్రశ్న 4.
ఇంటర్వ్యూకు సంబంధించిన కింది పేరా చదువండి. ప్రశ్నలకు జవాబులు రాయండి.
పత్రికల్లో, టి.వి.లో రకరకాల ఇంటర్వ్యూలను చూస్తుంటాం. ఇంటర్వ్యూలు రెండు రకాలని తెలుసుకదా ! ఉద్యోగాల ఎంపికకై అభ్యర్థి ప్రతిభను పరీక్షించటానికి చేసేది ఒకరకం. ఉద్యోగాన్ని సంపాదించటానికి అభ్యర్థులు పూర్తి సంసిద్ధతతో ఇంటర్వ్యూకు పోతారు. దీనిలో ఇంటర్వ్యూ చేసే వ్యక్తులు ముఖ్యపాత్ర పోషిస్తారు. ఇది మొదటిది. ప్రముఖుల జీవిత విశేషాలను తెలుసుకోవటానికి చేసేది మరోరకం. ప్రముఖుల, గొప్పవాళ్ళ నుండి వారి వివరాలను విశేషాలను తెలుసుకోవడానికి చేసేది రెండవది. దీనిలో ఇంటర్వ్యూ చేయబడే వ్యక్తే కీలకం.
రెండవ రకం ఇంటర్వ్యూలో ఇంటర్వ్యూ చేసే వ్యక్తులు ముందుగా కొన్ని అంశాలపై ప్రశ్నలు తయారుచేసుకుంటారు. మొదట వారిని పరిచయం చేసుకొని వారి వ్యక్తిగత వివరాల నుండి మొదలై వారి జీవితంలోని ముఖ్య సన్నివేశాలు, ఘట్టాలు, వారందించిన సేవలు, ఆశయాలు, సమాజానికి వారిచ్చే సందేశంతో ముగ్గుస్తుంది.
ఇట్లా చేసే ఇంటర్వ్యూల వివరాలను పత్రికల్లో, ప్రసార మాధ్యమాల్లో ప్రజలు చూస్తుంటారు. ఆదర్శవంతులు, సంఘసంస్కర్తలు, కవులు, రచయితలు, ఉద్యమకారులు, శాస్త్రవేత్తలు, రాజకీయనాయకులు మొదలగు వారే కాకుండా మరే ఇతర రంగంలోనైనా ‘ఉత్తమ’ సేవలందించిన వాళ్ళందరిని ఇంటర్వ్యూ చేయడం మనం చూస్తుంటాం. వీళ్ళ జీవితాలు ఎందరికో స్పూర్తిని కలిగిస్తాయి. దారిని చూపుతాయి.
ప్రశ్నలు
అ) ఇంటర్వ్యూ అంటే ఏమిటి ?
జవాబు:
ఉద్యోగాల కొరకై అభ్యర్థుల ప్రతిభను పరీక్షించడానికి చేసే ఒక ప్రక్రియను ఇంటర్వ్యూ అంటారు.
ఆ) ప్రముఖులను ఇంటర్వ్యూ ఎందుకు చేస్తారు ?
జవాబు:
ప్రముఖుల జీవిత విశేషాలు, వారి అనుభవాలు, వారు అందించిన సేవలు, ఎందరికో స్ఫూర్తినిస్తాయి. మరెందరికో దారిని చూపుతాయి. అందుకోసం ప్రముఖులను ఇంటర్వ్యూ చేస్తారు.
ఇ) మొదటిరకం ఇంటర్వ్యూ దేనికి సంబంధించినది ?
జవాబు:
ఉద్యోగాల ఎంపికకై అభ్యర్థుల ప్రతిభను పరీక్షించడానికి చేసే ఇంటర్వ్యూ మొదటి రకం. దీనిలో ఇంటర్వ్యూ చేసే వ్యక్తులు ప్రముఖపాత్ర వహిస్తారు.

ఈ) ప్రముఖులను ఇంటర్వ్యూ చేయడానికి ఎట్లా సిద్ధం కావాలి ?
జవాబు:
ఇంటర్వ్యూ చేసే వ్యక్తులు ముందుగా కొన్ని అంశాలపై ప్రశ్నలు తయారుచేసుకుంటారు. మొదట ప్రముఖులను పరిచయం చేసుకొని, వారి వ్యక్తిగత వివరాలను అడిగి, తరువాత వారి జీవితంలోని ముఖ్య సన్నివేశాలు, వారందించిన సేవలు, వారి ఆశయాలు, సమాజానికి వారిచ్చే సందేశంతో ఇంటర్వ్యూ ముగుస్తుంది.
ఉ) ప్రముఖుల నుండి ఇంటర్వ్యూలో సాధారణంగా రాబట్టే విషయాలు ఏవి ?
జవాబు:
- వ్యక్తిగత వివరములు,
- వారి జీవితంలోని ముఖ్య సన్నివేశాలు, ఘట్టాలు, వారందించిన సేవలు, వారి ఆశయాలు, సమాజానికి వారిచ్చే సందేశం మొదలయిన విషయాలు ప్రముఖుల నుండి రాబడతారు.
II. వ్యక్తీకరణ-సృజనాత్మకత
1. కింది ప్రశ్నలకు ఐదేసి వాక్యాల్లో జవాబులు రాయండి.
అ) దాశరథి రంగాచార్య తాను రచనలు ఎందుకు చేయాలనుకున్నారో సొంతమాటల్లో రాయండి.
జవాబు:
రంగాచార్య ఆంధ్ర మహాసభ ఉద్యమాల ప్రభావంతో మొదట రచన ప్రారంభించారు. నిజాం రాజ్యంలోని పరిస్థితులను గురించి, పత్రికలకు లేఖలూ, వ్యాసాలూ రాశారు.
ప్రభుత్వం, తెలంగాణ సాయుధపోరాట చరిత్రను వక్రీకరించింది. దాన్ని చెరిపివేసి విద్యార్థులకు తెలియకుండా చేసింది. అందువల్ల తెలంగాణ మహోజ్జ్వల వారసత్వం, తరువాతి తరాల వారికి తెలియకుండా పోతుందనే బాధతో, ఆందోళనతో, రంగాచార్య, తెలంగాణ సాయుధపోరాట గాథలో వట్టికోట ఆళ్వారుస్వామి రాయగా మిగిలిన విషయాలను నవలలుగా రచించారు.

ఆ) “తెలంగాణ ఏర్పాటు సంతోషాన్ని”చ్చిందని రచయిత అనటంపై మీ అభిప్రాయాన్ని రాయండి.
జవాబు:
తెలంగాణ రాష్ట్రం 2014లో ఆవిర్భవించింది. అలా రాష్ట్రం ఏర్పాటు కావడం తనకు సంతోషాన్ని కలుగజేసిందని రంగాచార్యగారు చెప్పారు. అదే సందర్భంలో రంగాచార్యగారు తెలంగాణ వచ్చిందనుకుంటే లాభం లేదని, వచ్చిన తెలంగాణను కాపాడుకోవాలని, అభివృద్ధి చేసుకోవాలని చెప్పారు.
దీనినిబట్టి దాశరథి రంగాచార్యగారికి, తెలంగాణ రాష్ట్రం పట్ల ఎంతో ప్రేమ ఉందని అర్ధం అవుతోంది. తెలంగాణ రాష్ట్రం వచ్చిందన్న విషయంలో తెలంగాణలో పుట్టినవారందరూ సంతోషిస్తారని నా అభిప్రాయం.
ఇ) “ప్రజల భాష” అంటే మీరేమి అర్థం చేసుకున్నారో రాయండి.
జవాబు:
రంగాచార్య తన నవలలను ప్రజల భాషలో వ్రాశానని చెప్పారు. ప్రజల భాష అంటే ప్రజలు మాట్లాడుకొనే మాండలిక భాష, నవలల్లో పాత్రలకు వారు పాత్రోచితమైన తెలంగాణలోని మాండలిక భాష వాడారు. రంగాచార్య గారికి తెలంగాణ అంటే అభిమానం. తెలంగాణ యాస సొగసులు అంటే ఇష్టం. అందుకే వారు నవలలలోని పాత్రలను బట్టి, పాత్రలు మాట్లాడేటప్పుడు ప్రజల భాషయైన మాండలికాన్ని వాడారు.
ఇక కథను చెప్పేటప్పుడు సాధారణ భాషనే వాడారు. ఆయన ప్రజాజీవితాన్ని చిత్రించడానికి, ప్రజల కోసం రచనలు చేశారు. అందుకే ప్రజల భాషయైన తెలంగాణ యాసతో ప్రజలు మాట్లాడే భాషను, తమ నవలల్లో ఉపయోగించారని గ్రహించాను.
ఈ) రంగాచార్య తన రచనలకు “తెలంగాణ ప్రజల జీవితాన్ని” నేపథ్యంగా ఎందుకు తీసుకున్నాడు ?
జవాబు:
దాశరథి రంగాచార్య తెలంగాణ సాయుధపోరాటంలో ప్రత్యక్షంగా పాల్గొన్నారు. ఆయనను ఆ ఉద్యమం ఎక్కువగా ప్రభావితం చేసింది. ఆయన ఉద్యమ జీవి. ముఖ్యంగా కమ్యూనిష్టు ఉద్యమం, ఆయనకు జీవితాన్ని నేర్పి’ మనిషిని చేసింది.
ప్రభుత్వం తెలంగాణ సాయుధపోరాట చరిత్రను వక్రీకరించింది. దాన్ని చరిత్ర నుండి చెరిపేయడానికి ప్రయత్నించింది. రైతులూ, కూలీలూ, కార్మికులూ, స్త్రీలూ, పిల్లలూ చేసిన చారిత్రాత్మక పోరాటం భావితరాలకు తెలియకుండా పోతుందనే బాధతో, ఆవేదనతో రంగాచార్య తెలంగాణ ప్రజల జీవితాన్ని నేపథ్యంగా తీసుకొని, తన రచనలను సాగించారు. తెలంగాణ ప్రజా జీవితాలు, ప్రజల ఆశలు పోరాటాలు, శాశ్వతంగా భావితరాలకు స్ఫూర్తినియ్యాలని, రంగాచార్య తన రచనలను తెలంగాణ ప్రజల జీవితాలు నేపథ్యంగా రచించారు.
2. కింది ప్రశ్నకు పది వాక్యాల్లో జవాబు రాయండి.
అ) డా॥ దాశరథి రంగాచార్య చేసిన సాహిత్యసేవను వివరించండి.
జవాబు:
మహాకవి దాశరథి రంగాచార్యగారు తెలంగాణ సాయుధపోరాటం నేపథ్యంగా చిల్లర దేవుళ్ళు, జనపదం, మోదుగుపూలు, మాయజలతారు వంటి అద్భుతమైన నవలలు రాశారు. చారిత్రాత్మకమైన తెలంగాణ పోరాట చరిత్రను తన రచనల ద్వారా భావితరాలకు వారు అందజేశారు.
ఇంతేకాక, నాలుగు వేదాలనూ, పది ఉపనిషత్తులనూ తెలుగులోకి అనువదించారు. రామాయణ, భారత, భాగవతాలను సరళవచనంలో రాశారు. తెలంగాణ జనజీవనం, రైతాంగ పోరాటం, వంటి అంశాలు నేపథ్యంగా ఈయన విశిష్టమైన నవలలు రచించి, తెలుగు సాహిత్యాన్ని సుసంపన్నం చేశారు. తెలుగు నవలలో పాత్రోచిత యాసను మొదటగా ప్రవేశపెట్టారు. వీరి రచనలు ఇతర భారతీయ భాషలలోకి కూడా అనువదింపబడ్డాయి.
ఈయన నవలలు చలన చిత్రాలుగా వచ్చాయి. ఈయన రచనాశైలి, పాఠకుడిని ఆకట్టుకొంటుంది. ఈయన రాసిన “చిల్లర దేవుళ్ళు” నవలకు, రాష్ట్ర సాహిత్య అకాడమీ పురస్కారం లభించింది. ఈయనను ‘గద్య దాశరథి’ అనేవారు. ఈయన సంస్కృతాంధ్ర భాషల్లో మహాపండితుడు. ఈయన జీవిత చరిత్రను ‘మోదుగుపూలు’ నవలలో చిత్రించారు. రంగాచార్య గొప్ప రచయిత.

3. కింది అంశాల గురించి సృజనాత్మకంగా / ప్రశంసాత్మకంగా రాయండి.
అ) మీ పాఠశాలకు ఒక క్రీడాకారుడు, కళాకారుడు లేదా నాయకుడు వచ్చాడనుకోండి. వారిని ఇంటర్వ్యూ చేయడానికి కావలసిన ప్రశ్నావళిని తయారు చేయండి.
జవాబు:
మా పాఠశాలకు క్రికెట్ దిగ్గజం సచిన్ టెండూల్కర్ వస్తే, నేను ఈ కింది ప్రశ్నలతో ఆయనను ఇంటర్వ్యూ చేస్తాను.
- భారతరత్న మహాశయా ! మీకు క్రికెట్ ఆట కాకుండా, ఇంకా ఇష్టమైన ఇతర ఆటలేవో చెప్పండి.
- మీరు ఎన్నో సంవత్సరంలో క్రికెట్ ఆడుగు పెట్టారు ?
- క్రికెట్లో మీరు సాధించిన విజయాలు మీకు పూర్తి సంతృప్తినిచ్చాయా ?
- క్రికెట్, పాఠశాలల్లో, కళాశాలల్లో బాగా వ్యాప్తి చెందడానికి ప్రభుత్వం ఏ చర్యలు చేపట్టాలి ?
- నేడు భారత క్రికెట్ రంగంలో, రాజకీయాలు ప్రవేశించాయి కదా ! దానిపై మీ అభిప్రాయం ఏమిటి ?
- మీరు అభిమానించే క్రికెట్ క్రీడాకారుడు ఎవరు ?
- మీకు క్రికెట్ నేర్పిన గురువు ఎవరు ?
- భారత్లో క్రికెట్ అభివృద్ధికి మీరిచ్చే సూచనలు ఏమిటి ?
- క్రికెట్ నేర్చుకొనే యువతకు మీరిచ్చే సలహాలు ఏమిటి ?
- మొత్తంపై క్రీడాకారులకు మీరిచ్చే సందేశం ఏమిటి ?
(లేదా)
ఆ) డా॥ దాశరథి రంగాచార్య వ్యక్తిత్వాన్ని లేదా సాహిత్యసేవను ప్రశంసిస్తూ వార్తా పత్రికకు ఒక లేఖ రాయండి.
జవాబు:
నమస్తే తెలంగాణ పత్రిక ప్రధాన సంపాదకులకు లేఖ
నల్గొండ,
X X X X X.
ప్రధాన సంపాదకులు,
నమస్తే తెలంగాణ దినపత్రిక,
హైదరాబాదు.
ఆర్యా,
నమస్కారాలు. నేను నల్గొండ ప్రభుత్వ పాఠశాలలో తొమ్మిదవ తరగతి చదువుతున్నాను. మాకు దాశరథి రంగాచార్య గారితో ఇంటర్వ్యూ పాఠం ఉంది. శ్రీ రంగాచార్య మహా మనీషి, వారిని గూర్చి ప్రతి తెలంగాణబిడ్డ తెలుసుకోవాలి. వారిని గూర్చి తెలిసిన విషయాలు రాస్తున్నా. మీ పత్రిక ద్వారా ప్రజలకు అందించకోరుచున్నాను.
“దాశరథి రంగాచార్య తెలంగాణ సాయుధపోరాటంలో పాల్గొన్న ఉద్యమ శీలి. వీరు తెలంగాణ ప్రజాజీవితం నేపథ్యంగా ఎన్నో నవలలు రాశారు. వీరి నవలల్లో ‘చిల్లర దేవుళ్ళు’ నవలకు రాష్ట్ర సాహిత్య అకాడమీ పురస్కారం లభించింది. ‘జనపదం’ అనే నవలలో మొత్తం సమాజాన్ని మైక్రోస్కోపిక్ గా చూపించారు. ఇది తెలంగాణకి సంబంధించిన నవల కాదు. ఇది భారతదేశానికి చెందిన నవల. ‘మోదుగుపూలు’ నవలలో వీరి జీవిత చరిత్రను రాశారు.
దాశరథి రంగాచార్య గారిపై కమ్యూనిస్టు ఉద్యమ ప్రభావం ఉంది. ఆ ఉద్యమం వీరికి జీవితాన్ని నేర్పింది. వీరిని మనిషిని చేసింది. ప్రభుత్వం, తెలంగాణ సాయుధపోరాటాన్ని వక్రీకరించింది. చరిత్ర నుండి చెరిపివేయడానికి ప్రయత్నించింది. ఎందరో రైతులు, కూలీలు, స్త్రీలు, కార్మికులు, పిల్లలు చేసిన ఆ చారిత్రక పోరాటం వివరాలు, భావితరాలకు అందజేయాలని వీరు తెలంగాణ ప్రజల నేపథ్యంలో నవలలు రాశారు.
ఈయనకు తెలంగాణ అంటే గొప్ప ప్రేమ. ఈయన నేపథ్యంలో మహాపండితుడు. నాలుగు వేదాలను, పది ఉపనిషత్తులను, తెలుగులోకి అనువదించారు. భారత, భాగవత, రామాయణములను సరళ వచనంలో రాశారు.
రంగాచార్య చరిత్రను మీ పత్రికలో తప్పక అచ్చువేయండి. నమస్తే కృతజ్ఞతలతో
ఇట్లు,
మీ విశ్వసనీయుడు,
పి. రామకృష్ణ,
9వ తరగతి, ప్రభుత్వ పాఠశాల,
నల్గొండ.
చిరునామా :
ప్రధాన సంపాదకుడు,
నమస్తే తెలంగాణ,
దినపత్రిక, హైదరాబాదు.
III. భాషాంశాలు
పదజాలం
1. కింది వాక్యాల్లో గీత గీసిన పదాలకు అర్థాలు రాయండి.
ఉదా : విలువలతో కూడిన విద్య మానవ జీవన వికాసానికి దోహదం చేస్తుంది.
జవాబు:
వికాసం = వికసించడం, విప్పారడం
అ) రామప్పగుడి శిల్పకళ సొగసును వర్ణించ శక్యమా ?
జవాబు:
సొగసు = అందము, సౌందర్యము
ఆ) వట్టికోట ఆళ్వారుస్వామి రచనల్లో ప్రజల మనిషి ఉత్కృష్టమైన రచన.
జవాబు:
ఉత్కృష్టం = శ్రేష్ఠము, గొప్పది

ఇ) భాగవతంలో కృష్ణలీలలు సమగ్రం గా రాశారు.
జవాబు:
సమగ్రం = సంపూర్ణంగా, సమస్తమూ
ఈ) నానాటికి మానవ సంబంధాలు క్షీణించి పోతున్నాయి.
జవాబు:
క్షీణించు = తరుగు, నశించు
2. కింది వాక్యాల్లో గల ప్రకృతి – వికృతులను గుర్తించి రాయండి.
అ) కథలంటే నాకిష్టమని మా నాయినమ్మ నాకు రోజూ కతలు చెప్పింది.
జవాబు:
కథ (ప్రకృతి) – కత (వికృతి)
ఆ) స్వచ్ఛభారతం కోసం ప్రతిజ్ఞ చేద్దాం. ప్రతిన చేయడమే కాదు పనిచేసి చూపుదాం.
జవాబు:
ప్రతిజ్ఞ (ప్రకృతి) – ప్రతిన (వికృతి)
ఇ) ప్రజలకోసం కవిత్వం రాశాడు. ఆ కైత ప్రజలను చైతన్యపరిచింది.
జవాబు:
కవిత్వం (ప్రకృతి) – కైతం (వికృతి)
ఈ) ఆశ ఉండవచ్చు. మితమీరిన ఆస ఉండరాదు.
జవాబు:
ఆశ (ప్రకృతి) – ఆస (వికృతి)
వ్యాకరణాంశాలు
ప్రశ్న 1.
కింది పదాలను విడదీయండి. సంధిపేరు రాయండి.
జవాబు:
సంధి పదం – విడదీసిన రూపం – సంధిపేరు
ఉదా :
పోయినాడంటే – పోయినాడు + అంటే -ఉత్వసంధి
అ) ఏమని – ఏమి + అని – ఇత్వసంధి
ఆ) కాదనుకున్నాడు – కాదు + అనుకున్నాడు – ఉత్వసంధి
ఇ) పిల్లలందరూ – పిల్లలు + అందరూ – ఉత్వసంధి

ప్రశ్న 2.
కింది విగ్రహ వాక్యాలను సమాస పదాలుగా మార్చండి. సమాసం పేరు రాయండి.
ఉదా : మూడు సంఖ్యగల రోజులు మూడురోజులు – ద్విగు సమాసం
అ) రెండు సంఖ్యగల రోజులు = రెండురోజులు – ద్విగు సమాసం
ఆ) వజ్రమూ, వైడూర్యము = వజ్రవైడూర్యములు – ద్వంద్వ సమాసం (లేదా) ఉభయ పద విశేషణ కర్మధారయ సమాసం)
ఇ) తల్లియూ, బిడ్డయూ = తల్లీబిడ్డలు – ద్వంద్వ సమాసం
కర్తరి, కర్మణి వాక్యాలు
కింది వాక్యాలు పరిశీలించండి.
- ఆళ్వారుస్వామి “చిన్నప్పుడే” అనే కథ రాశాడు. (కర్తరి)
- ‘చిన్నప్పుడే అనే కథ ఆళ్వారుస్వామిచే రచింపబడింది. (కర్మణి)
పై రెండింటిలో మొదటివాక్యం కర్తరి వాక్యం. భావం సూటిగా ఉంది కదా ! అది కర్త ప్రధానంగా కలిగిన వాక్యం. అంటే ‘రాశాడు’ అనే క్రియ, ‘ఆళ్వారుస్వామి’ అనే కర్తను సూచిస్తోంది. ఇటువంటి వాక్యాలను ‘కర్తరి వాక్యాలు’ అంటారు. రెండవ వాక్యం ‘కర్మణి వాక్యం’. ఇది కర్మ ప్రధానంగా కలిగిన వాక్యం. అంటే ‘రాయబడింది’ అనే క్రియ, ‘చిన్నప్పుడే అనే కథ’ అనే కర్మను సూచిస్తోంది.
ఈ వాక్యంలో రెండు మార్పులు స్పష్టంగా కనిపిస్తున్నాయి.
- ‘బడు’ అనే ధాతువు చేరడం
- ‘చే’ అనే విభక్తి చేరడం.
కర్తరి వాక్యం : కర్త ప్రధానంగా రూపొందుతుంది.
కర్మణి వాక్యం : కర్మ ప్రధానంగా రూపొందుతుంది. క్రియ మీద ‘బడు’ ధాతువు, కర్తమీద ‘చే / చేత’ విభక్తి చేరుతుంది.
ప్రశ్న 3.
కింది వాక్యాలను కర్మణి వాక్యాలుగా మార్చి రాయండి.
అ) లింగయ్య మా నాయకునికి ఉసిరికాయ ఇచ్చాడు. (కర్తరి వాక్యం)
జవాబు:
లింగయ్య చేత మా నాయకునికి ఉసిరికాయ ఇవ్వబడింది. (కర్మణి వాక్యం)
ఆ) బాలు ఇసుకతో ఇల్లు కట్టాడు. (కర్తరి వాక్యం)
జవాబు:
బాలుచే ఇసుకతో ఇల్లు కట్టబడింది. (కర్మణి వాక్యం)
ఇ) అక్క ఇంటి ముందు ముగ్గు వేసింది. (కర్తరి వాక్యం)
జవాబు:
అక్కచే ఇంటి ముందు ముగ్గు వేయబడింది. (కర్మణి వాక్యం)
ప్రశ్న 4.
కింది వాక్యాలను కర్తరి వాక్యాలుగా రాయండి.
అ) గ్రామీణులచే నాయకులు ఎదుర్కొని పోబడ్డారు. (కర్మణి వాక్యం)
జవాబు:
గ్రామీణులు నాయకులను ఎదుర్కొని పోయారు. (కర్తరి వాక్యం)
ఆ) కాయలన్నీ అతని చేత ముందర పోయబడ్డాయి. (కర్మణి వాక్యం)
జవాబు:
కాయలన్నీ అతని ముందర పోశారు. (కర్తరి వాక్యం)
ఇ) బాలురచే సెలవు తీసుకోబడింది. (కర్మణి వాక్యం)
జవాబు:
బాలురు సెలవు తీసుకున్నారు. (కర్తరి వాక్యం)

ప్రశ్న 5.
మీరు తత్పురుష సమాసం గురించి తెలుసుకున్నారు కదా ! కింది విగ్రహవాక్యాల్లో గీత గీసిన విభక్తి ప్రత్యాయాల ఆధారంగా ఆయా తత్పురుష సమాసాల పేర్లు రాయండి.
అ) విద్యను అర్థించువారు
జవాబు:
(ద్వితీయా తత్పురుష సమాసం)
ఆ) గుణాలచేత< హీనుడు
జవాబు:
(తృతీయా తత్పురుష సమాసం)
ఇ) సభ కొరకు భవనం
జవాబు:
(చతుర్థీ తత్పురుష సమాసం)
ఈ) దొంగల వల్ల భయం
జవాబు:
(పంచమీ తత్పురుష సమాసం)
ఉ) రాముని యొక్క బాణం
జవాబు:
(షష్ఠీ తత్పురుష సమాసం)
ఊ) గురువు నందు భక్తి
జవాబు:
(సప్తమీ తత్పురుష సమాసం)
ప్రాజెక్టు పని
మీ గ్రామంలోని వేరు వేరు రంగాలకు చెందిన ప్రముఖులను ఇంటర్వ్యూ చేసేందుకు ప్రశ్నావళి రూపొందించుకుని ముఖాముఖి నిర్వహించండి. నివేదిక రాయండి.
జవాబు:
విద్యారంగం :
- మీరు ఎంత కాలంనుండి విద్యాబోధన చేస్తున్నారు ?
- విద్యా ప్రణాళికలో నైతిక విలువల ప్రాధాన్యత ఎంతవరకు ఉంది ?
- ప్రాథమిక స్థాయిలో యోగా విద్యకు ప్రాధాన్యతను ఇవ్వాలా ?
- ప్రస్తుత విద్యా విధానంలో పరీక్షల సంస్కరణలు ఎలా ఉండాలి ?
- పనిబాట పట్టిన పిల్లలను బడిబాట పట్టడానికి మనం ఎలాంటి చర్యలు తీసుకోవాలి ?
- పాఠశాల వాతావరణం ఎలా ఉండాలి ? లోపాలను ఎలా సరిదిద్దాలి ?
వ్యాపార రంగం :
- వ్యాపారంలో నైతికత అవసరం ఎంతవరకు ఉంది ?
- పెట్టుబడులకు బ్యాంకుల సహకారం ఎంతవరకు ఉండాలి?
- వినియోగదారుల మన్ననను వ్యాపారులు ఎట్లా పొందాలి ?
- వ్యాపారుల మధ్య పోటీ ఎలా ఉండాలి ?
- వ్యాపారస్థులు సమాజం పట్ల బాధ్యతను ఎలా గుర్తించాలి ?
వైద్యరంగం :
- గ్రామాలలో ప్రాథమిక ఆరోగ్య కేంద్రాల ఆవశ్యకత ఎంతవరకు ఉంది ?
- గ్రామస్థులకు వైద్యులు ఎలాంటి ఆరోగ్య సూత్రాలను అందించాలి ?
- వర్షాకాలంలోనూ, ఎండాకాలంలోనూ, ప్రజలకు ఎలాంటి సూచనలను వైద్యులు అందించాలి ?
- అంటురోగాలు ప్రబలకుండా ప్రజలు ఎలాంటి జాగ్రత్తలు తీసుకోవాలి ?
వ్యవసాయరంగం :
- పంటలో సేంద్రియ ఎరువుల ఆవశ్యకత ఎంతవరకు ఉంది ?
- రైతులకు గిట్టుబాటు ధరలు కావాలంటే ప్రభుత్వం ఏం చేయాలి ?
- ప్రస్తుత తరుణంలో సమష్టి వ్యవసాయం అవసరం ఉందా ? లేదా ?
- రైతుల ఆత్మహత్యలను ఎలా నివారించాలి ?
- ఆధునిక వ్యవసాయంలో ఎలాంటి మెలకువలు పాటించాలి ?
కఠిన పదాలకు అర్థాలు
I
36వ పేజి
సాహితీ రంగ ప్రవేశం = సాహిత్య రంగములో ప్రవేశించడం
ఆంధ్రమహాసభ = ఆంధ్రులు పెట్టుకున్న మహాసభ;
మహోద్యమం (మహా + ఉద్యమం) = గొప్ప పోరాటం ;
ప్రభావితుణ్ణయి = ప్రభావం పొందినవాడినయి
పూనుకున్నాను = సిద్ధపడ్డాను
ఉద్యమం = పోరాటం
ప్రజాజీవితం = ప్రజల యొక్క జీవితం
నేపథ్యంగా = పూర్వరంగంగా
వక్రీకరించింది = తప్పుదారి పట్టించింది ;
సాయుధపోరాటం = ఆయుధములతో పోరాటం ;
జడుసుకుంది = భయపడింది
బుగులుపడింది = కలతపడింది (కలత చెందింది)
చారిత్రాత్మక పోరాటం = చరిత్ర ప్రసిద్ధమైన పోరాటం
ప్రతిన = ప్రతిజ్ఞ
రక్తా రుణ సమరాలు
(రక్త + అరుణ, సమరాలు) = రక్తంతో ఎరుపెక్కిన యుద్ధాలు;
మహోజ్జ్వల వారసత్వం
(మహా + ఉజ్జ్వల, వారసత్వం) = గొప్పగా ప్రకాశించే వారసత్వం
వ్యథ = దుఃఖము
ఆవేదన = బాధ
ఆవిర్భవించినవి = పుట్టాయి
ఉత్కృష్టమైన = శ్రేష్ఠమైన
పోరాటగాథ = పోరాటానికి సంబంధించిన కథ;
37వ పేజి
ఆందోళన = ఊగిసలాట (కంగారు)
బృహత్ కార్యము = పెద్దపని
ఉపక్రమించినాను = మొదలుపెట్టినాను

II
37వ పేజి
అగ్రజులు = అన్నగారు
తొలుత = మొదట
ప్రక్రియలో = రచనా పద్ధతిలో
ఉభయులు = ఇద్దరూ
ప్రభావాత్మకము = ప్రభావం కల్గించేది
దృక్పథాన్ని = దృష్టి మార్గాన్ని
విస్తృతమయిన = విశాలమైన
సమాజాన్ని = సంఘాన్ని
మైక్రోస్కోపిక్ (Microscopic) = అత్యంత సూక్ష్మంగా ;
పోలీస్ యాక్షన్ (Police Action) = (1948లో నిజాం నుండి రాజ్యాన్ని స్వాధీనం చేసుకోడాన్ని భారత యూనియన్ వారు, చేపట్టిన పోలీసు చర్య)
కాజేయడం = ఆక్రమించడం;
ఉద్యమాలొచ్చినయి = ఉద్యమాలు (పోరాటాలు) వచ్చాయి
భ్రష్టుపట్టడం = చెడిపోవడం
వ్యాఖ్య చెయ్యడం = వివరంగా వ్యాఖ్యానించి చెప్పడం ;
గర్వకారణం = గర్వపడడానికి కారణం
38వ పేజి
ప్రియమయిన = ఇష్టమైన
ఆత్మకథ = తన జీవిత కథ
జీవనయానం = జీవన ప్రయాణం (ఆత్మ జీవిత కథ)
ఇవాల్టికీ = నేటికీ
పర్ఫెక్షన్ (Perfection) = సంపూర్ణత (లోపం లేకపోడం)
కర్తవ్యం = చేయదగిన పని
డూ ఆర్ డై (Do or die) = చేయడం లేకపోతే చావడం ;
సిద్ధాంతం = స్థిరమైన నిరూపిత సారాంశము
III
38వ పేజి
కృషి = ప్రయత్నం
భగవదనుగ్రహం
(భగవత్ + అనుగ్రహం) = భగవంతుడి దయ
విశ్వాసం = నమ్మకం
అసాధ్యమైన = సాధ్యముకాని
సంప్రదాయ సిద్ధము = గురుపరంపరగా వచ్చినట్టిది
చదువుల రాణి = సరస్వతి
కీర్తించు = పొగడను
శ్లాఘించను = కొనియాడను
మాండలికం = మండలములోని భాష (ప్రాంతీయమైన యాస పలుకుబడి)
తెలంగాణేతర
(తెలంగాణ + ఇతర) = తెలంగాణ కంటే ఇతరమైన
దురభిమానం = చెడ్డ అభిమానం
యాససొగసులు = మాట్లాడే తీరులోని అందాలు
నివేదనకు = వెల్లడించడానికి
సంక్షిప్తంగా = కొద్దిగా
వాల్మీకి = సంస్కృత రామాయణ కర్త
వ్యాసుడు = అష్టాదశపురాణాలు, భారత భాగవతాలు సంస్కృతంలో వ్రాసిన మునీశ్వరుడు
కాళిదాసు = అభిజ్ఞాన శాకుంతలం వంటి సంస్కృత నాటకాలు వ్రాసిన సంస్కృత మహాకవి
గోర్కీ = మాక్సింగోర్కి (రష్యన్ రచయిత ఈయన రాసిన ‘అమ్మ’ నవల ప్రసిద్ధము.)
చెఖోవ్ = రష్యాదేశ ప్రసిద్ధ కథా రచయిత;
డికెన్స్ = ఫ్రాన్సు దేశ రచయిత (A Tale of two cities) రెండు మహా నగరాల కథా రచయిత
ప్రేంచంద్ = హిందీ నవలా రచయిత (గోదాన్ నవలా కర్త)
ఉన్నవ = ఉన్నవ లక్ష్మీనారాయణ గారు (మాలపల్లి నవలా రచయిత)
విశ్వనాథ = వేయిపడగలు నవలా కర్త (విశ్వనాథ సత్యనారాయణగారు)
అల్లం రాజయ్య = నవలా రచయిత, కథా రచయిత
పరిధులు = సరిహద్దులు
వసుధైక కుటుంబం = ప్రపంచం అంతా ఒకే కుటుంబంగా భావించడం
39వ పేజి
ప్రభావితం చేసిన = ప్రభావం కలుగజేసిన
వ్యక్తులుగా = మనుషులుగా
ఉద్యమజీవిని = ఉద్యమమే ఊపిరిగా జీవించినవాడిని
సమాజం = సంఘము

IV
39వ పేజి
అధ్యయన దశ = గురుముఖంగా చదివి నేర్చుకోవలసిన, స్థితి
అధ్యయనం = చదవడం
ఆచరణ దశ = పనిచేయవలసిన, స్థితి
సాహిత్య సాంస్కృతిక జీవనవైభవానికి = సాహిత్యము, సంస్కృతికి సంబంధించిన, జీవితంలోని గొప్పదనానికి
జీవగడ్డ = జీవనాధారమైన నేల ;
వారసత్వ సంపద = పూర్వీకుల నుండి వచ్చే సంపద
పునరుజ్జీవనానికి (పునః + ఉజ్జీవనానికి) = తిరిగి, బ్రతికించడానికి
ప్రణాళిక = పథకము
మేనిఫెస్టోలు = ప్రకటన కాగితము
రూపొందించుకోవచ్చు = తయారుచేసికోవచ్చు
నిర్వర్తించాను = నెరవేరతాయి
సందేశం = చెప్పవలసి మాట
సిద్ధిస్తాయి = నెరవేర్చాను
పాఠం ఉద్దేశం
తెలంగాణకు ఒక విశిష్టమైన చరిత్ర ఉన్నది. నాటి నుండి నేటి వరకు ఈ గడ్డపై పోరాడిన వీరులు, కవులు, రచయితలు, కళాకారులు ఎంతోమంది ఉన్నారు. నాటి తెలంగాణ పోరాటాన్ని కళ్ళార చూసిన సాహితీయోధుడు డా॥ దాశరథి రంగాచార్య. తెలంగాణ ప్రజల జీవనాన్ని, అస్తిత్వాన్ని, పోరాటాలను తన రచనల ద్వారా ప్రతిఫలింప చేశాడు. అలాంటి ప్రముఖ రచయిత వ్యక్తిత్వస్ఫూర్తిని, రచనల గొప్పదనాన్ని ఇంటర్వ్యూ ప్రక్రియ ద్వారా విద్యార్థులకు తెలియజేయటమే పాఠ్యాంశ ముఖ్య ఉద్దేశం.
పాఠ్యభాగ వివరాలు
ఈ పాఠ్యభాగం ఇంటర్వ్యూ (పరిపృచ్చ) ప్రక్రియకు చెందినది. ఇంటర్వ్యూ (Interview)నే, పరిపృచ్ఛ, లేక ‘ముఖాముఖి’ అని కూడా అంటారు. ఈ ఇంటర్వ్యూ రెండు రకాలుగా ఉంటుంది.
ఉద్యోగాలకు అభ్యర్థులను ఎంపికచేసే ప్రక్రియలో ఉద్యోగార్థుల ప్రతిభను పరీక్షించడం కోసం చేసే ఇంటర్వ్యూ మొదటిరకం. ఇక నిర్దిష్ట రంగంలో సేవలందించిన మహాత్ముల అనుభవాలను, అంతరంగాన్ని తెలిసికోడానికి చేసే ఇంటర్వ్యూ రెండవది.
డా॥ దాశరథి రంగాచార్య, వేరువేరు సందర్భములలో వివిధ పత్రికలకు ఇచ్చిన ఇంటర్వ్యూలలోని ముఖ్యాంశాలే ఈ పాఠ్యభాగం.
డా॥ దాశరథి రంగాచార్య కవి పరిచయం

పాఠము పేరు : “రంగాచార్యతో ముఖాముఖి”
ఇంటర్వ్యూలో జవాబులు చెప్పినవారు : దాశరథి రంగాచార్య
రంగాచార్య జననం : 24-08-1928
రంగాచార్య మరణం : 07-06-2015
జన్మస్థలం : మహబూబాబాద్ జిల్లాలోని చిన్న గూడూరులో జన్మించారు.
సోదరుడు : ప్రముఖ కవి డా|| దాశరథి కృష్ణమాచార్య వీరి సోదరుడు.
ఉద్యోగము : ఈయన ఉపాధ్యాయుడిగా, గ్రంథాలయ నిర్వాహకుడిగా, సికింద్రాబాద్ పురపాలకశాఖలో పనిచేశారు. తెలంగాణ సాయుధ పోరాటంలో పాల్గొన్నారు.
నవలా రచన : ఈయన విశిష్టమైన తెలుగు నవలలు రచించి, తెలుగు సాహిత్యాన్ని సుసంపన్నం చేశారు.
అనువాదము :
- నాలుగు వేదములను, పది ఉపనిషత్తులను, సంస్కృతం నుండి తెలుగులోకి అనువాదం చేశారు.
- రామాయణ, భారత, భాగవతాలను సరళమైన తెలుగు వచనంలో రాశారు.
రచనలలోని విషయము : తెలంగాణ జనజీవనము, రైతాంగ పోరాటం వంటి విషయాలు పూర్వరంగంగా, (నేపథ్యంగా) ఈయన రచనలు సాగాయి. వీరు తెలుగు నవలలో ‘పాత్రోచితయాస’ను ప్రవేశపెట్టారు. ఈయన రచనలు, ఇతర భాషల్లోకి అనువదింపబడ్డాయి. సినిమాలుగా వచ్చాయి.
పురస్కారం : వీరి “చిల్లర దేవుళ్ళు” నవలకు, రాష్ట్ర సాహిత్య అకాడమీ పురస్కారం లభించింది.
శైలి : వీరి రచనాశైలి పాఠకులను ఆకట్టుకొంటుంది.

ప్రవేశిక
తెలుగు సాహిత్యంలో దాశరథి రంగాచార్యులుగారికి విశిష్టస్థానము ఉంది. ఈయన తెలంగాణ పోరాటం పూర్వరంగాన్ని, తన జీవశక్తిగా మార్చుకొని, తెలుగువారి సాంస్కృతిక జీవనాన్ని అద్భుతంగా చిత్రించారు. అటువంటి రంగాచార్యగారి అంతరంగాన్ని మరింత దగ్గరగా తెలుసుకోవాలనే ఆసక్తి, ఉత్సాహం పాఠకులకు సహజంగానే ఉంటుంది. అలా తెలుసుకోడానికి ఈ ముఖాముఖి (Interview) ప్రక్రియ తోడ్పడుతుంది.
రచయితతో పరిచయం వల్ల, ఆయన రచనల్లో తెలియని కొత్త కోణాలు సాహితీలోకానికి పరిచయం అవుతాయి. అందుకోసం డా॥ దాశరథి రంగాచార్యగారితో ముఖాముఖిని చదువుదాం.








