TS 10th Class Maths Bits Chapter 11 Trigonometry

Solving these TS 10th Class Maths Bits with Answers Chapter 11 Trigonometry Bits for 10th Class will help students to build their problem-solving skills.

Trigonometry Bits for 10th Class

Question 1.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\) then tan θ =

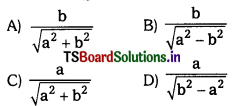
Answer:
(D)

Question 2.
cos² θ + sin² θ is
A) 0
B) 1
C) \(\frac{1}{2}\)
D) θ²
Answer:
B) 1

Question 3.
If sin θ = cos θ, then the value of 2 tan θ + cos²θ
A) 1
B) \(\frac{1}{2}\)
C) \(\frac{5}{2}\)
D) \(\frac{2}{5}\)
Answer:
C) \(\frac{5}{2}\)

Question 4.
If tan θ + sec θ = 8, then sec θ – tan θ is
A) 8
B) \(\frac{1}{8}\)
C) 6
D) 64
Answer:
B) \(\frac{1}{8}\)

Question 5.
The maximum value of sin θ is
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{2}\)
C) 1
D) \(\frac{1}{\sqrt{2}}\)
Answer:
C) 1

Question 6.
If tan θ = \(\frac{7}{8}\) then the value of \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
A) \(\frac{7}{8}\)
B) \(\frac{8}{9}\)
C) \(\frac{64}{49}\)
D) \(\frac{49}{64}\)
Answer:
C) \(\frac{64}{49}\)

Question 7.
If 5 tan θ = 4, then the value of \(\frac{5 \sin \theta-3 \cos \theta}{5 \sin \theta+3 \cos \theta}\) is
A) 0
B) 1
C) \(\frac{1}{7}\)
D) \(\frac{2}{7}\)
Answer:
C) \(\frac{1}{7}\)

Question 8.
\(\frac{\sin \theta}{1+\cos \theta}\) is

Answer:
(C)

Question 9.
The value of \(\frac{2 \tan 30}{1+\tan ^2 30}\) =
A) sin 60°
B) cos 60°
C) tan 60°
D) sin 30°
Answer:
A) sin 60°

Question 10.
The value of sin 45° + cos 45° is
A) \(\frac{1}{\sqrt{2}}\)
B) \(\sqrt{2}\)
C) \(\frac{\sqrt{3}}{2}\)
D) 1
Answer:
B) \(\sqrt{2}\)

Question 11.
If tan θ = 1, the value of \(\frac{5 \sin \theta+4 \cos \theta}{5 \sin \theta-4 \cos \theta}\) is
A) 9
B) 46°
C) 1
D) 0
Answer:
A) 9

Question 12.
tan θ is not defined when θ is
A) 90°
B) 60°
C) 30°
D) 0°
Answer:
A) 90°

Question 13.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\) then cos θ =
A) \(\frac{\sqrt{a^2-b^2}}{b}\)
B) \(\frac{b}{a}\)
C) \(\frac{\sqrt{b^2-a^2}}{b}\)
D) \(\frac{b-a}{b}\)
Answer:
C) \(\frac{\sqrt{b^2-a^2}}{b}\)

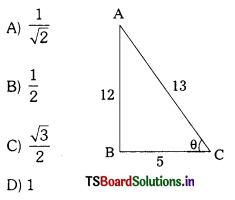
Question 14.
If sin θ = \(\frac{12}{13}\) then tan θ =
A) \(\frac{13}{5}\)
B) \(\frac{5}{12}\)
C) \(\frac{13}{12}\)
D) \(\frac{12}{5}\)
Answer:
D) \(\frac{12}{5}\)

Question 15.
sin θ . sec θ =
A) tan θ
B) cosec θ
C) cot θ
D) sin θ . cos θ
Answer:
A) tan θ

Question 16.
\(\sqrt{1+\cot ^2 \theta}\) =
A) cosec² θ
B) 1 + cot θ
C) sec θ
D) cosec θ
Answer:
D) cosec θ

Question 17.
tan 135° =
A) \(\frac{1}{\sqrt{3}}\)
B) \(\sqrt{3}\)
C) – \(\sqrt{3}\)
D) -1
Answer:
D) -1

Question 18.
\(\sqrt{1+\sin A} \cdot \sqrt{1-\sin A}\) =
A) sin A
B) 1 – sin² A
C) cos A
D) 1
Answer:
C) cos A

Question 19.
sin (90 + θ) =
A) cos θ
B) – cos θ
C) sin θ
D) – sin θ
Answer:
A) cos θ

Question 20.
If tan θ = \(\frac{1}{\sqrt{3}}\), then cos θ =
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{2}{\sqrt{3}}\)
D) \(\sqrt{3}\)
Answer:
B) \(\frac{\sqrt{3}}{2}\)

Question 21.
If cos θ = \(\frac{\sqrt{3}}{2}\) and ‘θ’ is acute, then the value of 4 sin² θ + tan² θ =
A) \(\frac{3}{4}\)
B) 1
C) \(\frac{4}{3}\)
D) \(\frac{5}{3}\)
Answer:
C) \(\frac{4}{3}\)

Question 22.
sin (A – B) = \(\frac{1}{2}\); cos (A + B) = \(\frac{1}{2}\). So, A =
A) 60°
B) 15°
C) 30°
D) 45°
Answer:
D) 45°

Question 23.
sin (-θ) =
A) sin θ
B) cos θ
C) – cos θ
D) – sin θ
Answer:
D) – sin θ

Question 24.
If sin (A – B) = \(\frac{1}{2}\); cos (A + B) = \(\frac{1}{2}\) then B =
A) 15°
B) – sin θ
C) sin θ
D) cos θ
Answer:
A) 15°

Question 25.
If α + β = 90° and α = 2β, then cos² β + sin² β =
A) 1
B) 0
C) \(\frac{1}{2}\)
D) 2
Answer:
A) 1

Question 26.
If tan θ = \(\frac{1}{\sqrt{3}}\) then 7 sin² θ + 3 cos² θ =
A) 1
B) 2
C) 3
D) 4
Answer:
D) 4

Question 27.
cos² 0° + cos² 60° =
A) \(\frac{5}{4}\)
B) \(\frac{2}{\sqrt{3}}\)
C) \(\frac{1}{\sqrt{2}}\)
D) \(\frac{\sqrt{3}}{2}\)
Answer:
A) \(\frac{5}{4}\)

Question 28.
cot (270° – θ) =
A) -tan θ
B) tan θ
C) cot θ
D) – cot θ
Answer:
B) tan θ

Question 29.
sin 240° =
A) \(\frac{1}{\sqrt{2}}\)
B) \(\frac{2}{\sqrt{3}}\)
C) – \(\frac{\sqrt{3}}{2}\)
D) \(\frac{\sqrt{3}}{2}\)
Answer:
C) – \(\frac{\sqrt{3}}{2}\)

Question 30.
\(\frac{1-\tan ^2 30}{1+\tan ^2 30}\) =
A) \(\frac{1}{2}\)
B) 1
C) 0
D) 2
Answer:
A) \(\frac{1}{2}\)

Question 31.
If sin (A + B) = \(\frac{\sqrt{3}}{2}\) ; cos B = \(\frac{\sqrt{3}}{2}\) value of A is
A) 45°
B) 60°
C) 30°
D) 90°
Answer:
C) 30°

Question 32.
cos (A – B) = \(\frac{1}{2}\); sin B = \(\frac{1}{\sqrt{2}}\) measure of A =
A) 15°
B) 105°
C) 90°
D) 60°
Answer:
B) 105°

Question 33.
sin² 45° + cos² 45° + tan² 45° =
A) 2
B) 1
C) 3
D) \(\frac{3}{\sqrt{2}}\)
Answer:
A) 2

Question 34.
sin \(\frac{\pi}{6}\) + cos \(\frac{\pi}{3}\) =
A) \(\frac{2}{\sqrt{3}}\)
B) 2
C) \(\frac{1}{2}\)
D) 1
Answer:
D) 1

Question 35.
If sec θ + tan θ = 4; then cos θ =
A) \(\frac{8}{17}\)
B) \(\frac{4}{17}\)
C) \(\frac{15}{17}\)
D) \(\frac{17}{8}\)
Answer:
A) \(\frac{8}{17}\)

Question 36.
tan 0° =
A) 1
Β) α
C) \(\frac{1}{\sqrt{3}}\)
D) 0
Answer:
D) 0

Question 37.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\); cos θ = \(\frac{\mathrm{c}}{\mathrm{d}}\) then cot θ =
A) \(\frac{\mathrm{ab}}{\mathrm{cd}}\)
B) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)
C) \(\frac{\mathrm{ca}}{\mathrm{bd}}\)
D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)
Answer:
B) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)

Question 38.
cos(xy) =
A) cos x sin x + cos y sin
B) cos x sin y + cos y sin y
C) sin x cos y + cos x sin y
D) cos x cos y + sin x sin y
Answer:
D) cos x cos y + sin x sin y

Question 39.
\(\frac{\tan \theta}{\sqrt{1+\tan ^2 \theta}}\) =
A) \(\frac{\tan \theta}{1+\tan \theta}\)
B) \(\frac{1}{\tan \theta}\)
C) cot θ
D) sin θ
Answer:
D) sin θ

Question 40.
cos θ:
A) 1 – sin² θ
B) sin² θ + 1
C) \(\frac{\cot \theta}{\ cosec \theta}\)
D) \(\frac{\ cosec \theta}{\ cot \theta}\)
Answer:
C) \(\frac{\cot \theta}{\ cosec \theta}\)

Question 41.
Value of cos 0° + sin 90° + \(\sqrt{3}\) cosec 60° =
A) 2
B) 3
C) 4
D) 1
Answer:
C) 4

Question 42.
π radians =
A) 90°
B) 60°
C) 180°
D) 45°
Answer:
C) 180°

Question 43.
cos⁶θ + sin⁶ θ =
A) 1 + sin³θ cos³ θ
B) 1 – 3sin²θ cos² θ
C) 1 – 3sin³θ cos³ θ
D) 45°
Answer:
C) 1 – 3sin³θ cos³ θ

Question 44.
cos 12 – sin 78 = …………. (A.P. Mar. ’15)
A) 1
B) \(\frac{1}{2}\)
C) 0
D) – 1
Answer:
C) 0

Question 45.
If x = cosec θ + cot θ and y = cosec θ – cot θ, then which of the following is true ………… (A.P Mar.’15)
A) x + y = 0
B) x – y = 0
C) \(\frac{x}{y}\) = 1
D) xy = 1
Answer:
D) xy = 1

Question 46.
cos (A – B) = …… (A.P. Mar.’15)
A) cos A cos B + sin A sin B
B) cos A sin A + cos B sin B
C) sin A sin B – cos A cos B
D) cos A cos B – sin A sin B
Answer:
A) cos A cos B + sin A sin B

Question 47.
cos (90 – θ) = ………….. (A.P. Mar.’15)
A) cos θ
B) sin θ
C) cosec θ
D) tan θ
Answer:
B) sin θ

Question 48.
In ∆ ABC, sin C = \(\frac{3}{5}\) then cos A = (A.P. June’15_
A) \(\frac{3}{5}\)
B) \(\frac{4}{5}\)
C) \(\frac{5}{4}\)
D) \(\frac{5}{3}\)
Answer:
A) \(\frac{3}{5}\)

Question 49.
tan² θ – sec² θ = ………. (A.P. June ’15)
A) 1
B) -1
C) 0
D) α
Answer:
B) -1

Question 50.
sec (90 – A) = …………… (A.P. June
A) cos A
B) cosec A
C) sin A
D) tan A
Answer:
B) cosec A

Question 51.
If cosec θ + cot θ = 5 then cosec θ – cot θ = ………….. (A.P. June ’15)
A) \(\frac{1}{5}\)
B) 5
C) -5
D) – \(\frac{1}{5}\)
Answer:
A) \(\frac{1}{5}\)

Question 52.
If x = 2 sec θ; y = 2 tan θ then x² – y² = ………………. (A.P. June ’15)
A) 0
B) -2
C) 4
D) 2
Answer:
C) 4

Question 53.
If \(\sqrt{3}\) tan θ = 1 then θ = ………. (A.P. June’15)
A) 60°
B) 90°
C) 45°
D) 30°
Answer:
D) 30°

Question 54.
(sec 60) (cos 60) = …………… (A.P. June’15)
A) 1
B) \(\frac{1}{2}\)
C) – 1
D) – \(\frac{1}{2}\)
Answer:
A) 1

Question 55.
sin (60 + 30) = ………………. (A.P. Mar. ’16)
A) 2
B) -2
C) 1
D) 1
Answer:
D) 1

Question 56.
If sin θ + tan θ = \(\frac{1}{2}\), then sin θ – tan θ = …………… (A.P. Mar.’16)
A) 1
B) – 1
C) 2
D) \(\frac{1}{2}\)
Answer:
C) 2

Question 57.
cos (90 – θ) = …………….. (A.P. Mar. ’16)
A) cos θ
B) tan θ
C) cosec θ
D) sin θ
Answer:
D) sin θ

Question 58.
If cot A = \(\frac{5}{12}\) then sin A + cos A = ………… (T.S. Mar. ’15)
A) \(\frac{17}{13}\)
B) \(\frac{12}{13}\)
C) \(\frac{5}{13}\)
D) \(\frac{20}{13}\)
Answer:
A) \(\frac{17}{13}\)

Question 59.
Which of the following is not possible value for sin x ………. (T.S. Mar. ’15)
A) \(\frac{3}{4}\)
B) \(\frac{3}{5}\)
C) \(\frac{4}{5}\)
D) \(\frac{5}{4}\)
Answer:
D) \(\frac{5}{4}\)

Question 60.
If sin cos θ (0 < θ < 90) then tan θ + cot θ = ………….. (T.S Mar. ’16)
A) 2\(\sqrt{3}\)
B) \(\frac{2}{\sqrt{3}}\)
C) 2
D) 1
Answer:
C) 2

Question 61.
If sec θ + tan θ = 3 then sec θ – tan θ = ……………. (T.S. Mar. ’16)
A) \(\frac{1}{3}\)
B) \(\frac{2}{3}\)
C) \(\frac{4}{3}\)
D) \(\frac{5}{3}\)
Answer:
A) \(\frac{1}{3}\)

Question 62.
In ∆ABC, AB = c, BC = a, AC = b and ∠BAC = θ then area of ∆ABC is …………… (θ is acute) (T.S. Mar.’16)
A) \(\frac{1}{2}\) ab sin θ
B) \(\frac{1}{2}\) ca sin θ
C) \(\frac{1}{2}\) bc sin θ
D) \(\frac{1}{2}\) b² sin θ
Answer:
C) \(\frac{1}{2}\) bc sin θ

Question 63.
The value of sin² 60° – sin²30° is ………………..
A) \(\frac{1}{4}\)
B) \(\frac{1}{2}\)
C) \(\frac{3}{4}\)
D) –\(\frac{1}{2}\)
Answer:
B) \(\frac{1}{2}\)

Question 64.
If cosec θ = 2 and cot θ = \(\sqrt{3}\) p, where θ is an acute angle, then the value of ‘p’ is
A) 2
B) 1
C) 0
D) \(\sqrt{3}\)
Answer:
B) 1

Question 65.
The value of \(\left(\frac{11}{\cot ^2 \theta}-\frac{11}{\cos ^2 \theta}\right)\) is
A) 11
B) 0
C) \(\frac{1}{11}\)
D) -11
Answer:
D) -11

Question 66.
If sec 2A = cosec (A – 27°), where 2A is an acute angle, then the measure of ∠A is
A) 35°
B) 37°
C) 39°
D) 21°
Answer:
C) 39°

Question 67.
\(\frac{1-\sec ^2 A}{{cosec}^2-1}\) = ………………….
A) -tan² A
B) -tan⁴ A
C) 1
D) -sec² A
Answer:
B) -tan⁴ A

Question 68.
If sec θ = 3k and tan θ = \(\frac{3}{\mathrm{k}}\) then (k² – \(\frac{1}{\mathrm{k}^2}\)) = …………….
A) 9
B) 3
C) \(\frac{1}{9}\)
D) 1
Answer:
C) \(\frac{1}{9}\)

Question 69.
If P, Q and R are interior angles of a ∆PQR, then tan \(\left(\frac{P+Q}{2}\right)\) equals.
A) sin \(\left(\frac{\mathrm{R}}{2}\right)\)
B) cos \(\left(\frac{\mathrm{R}}{2}\right)\)
C) cot \(\left(\frac{\mathrm{R}}{2}\right)\)
D) \(\left(\frac{\mathrm{R}}{2}\right)\)
Answer:
C) cot \(\left(\frac{\mathrm{R}}{2}\right)\)

Question 70.
If sin (x – 20)° = cos (3x – 10)°, then ‘x’ is
A) 60
B) 30
C) 45
D) 35.5
Answer:
B) 30

Question 71.
Maximum value of \(\frac{1}{\sec \theta}\), 0° ≤ θ ≤ 90° is
A) 1
B) 2
C) \(\frac{1}{2}\)
D) \(\frac{1}{\sqrt{2}}\)
Answer:
A) 1

Question 72.
The value of cos² 17° – sin²73° is
A) 1
B) \(\frac{1}{3}\)
C) 0
D) -1
Answer:
C) 0

Question 73.
If A = 30°, then sin 2A equals…………..
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{\sqrt{2}}\)
D) 1
Answer:
B) \(\frac{\sqrt{3}}{2}\)

Question 74.
In a right angled ∆ABC, right angle at ‘C’ if tan A = \(\frac{8}{15}\), then the value of cosec² A – 1 is
A) 0
B) \(\frac{64}{225}\)
C) \(\frac{225}{64}\)
D) \(\frac{289}{64}\)
Answer:
C) \(\frac{225}{64}\)

Question 75.
If \(\frac{1}{2}\) tan² 45° = sin²A and ‘A’, acute, then the value of A is
A) 60°
B) 45°
C) 30°
D) 15°
Answer:
B) 45°

Question 76.
sin (45° + θ) cos (45 – θ) =
A) 2 sin θ
B) 0
C) 1
D) 2 cos θ
Answer:
B) 0

Question 77.
If cos 2θ sin 40; here 2θ and 4θ are acute angles, then the value of ‘θ’ is
A) 60°
B) 45°
C) 15°
D) 30°
Answer:
C) 15°

Question 78.
If sin x = cos x, 0 ≤ x ≤ 90°, then x =
A) 30°
B) 90°
C) 0°
D) 45°
Answer:
D) 45°

Question 79.
2 sin θ = sin²θ is true for the value of θ is ………….
A) 0°
B) 45°
C) 30°
D) 60°
Answer:
A) 0°

Question 80.
If sin 45°.cos 45° + cos 60° = tan θ, then the value of θ is
A) 0°
B) 30°
C) 45°
D) 60°
Answer:
C) 45°

Question 81.
From the below figure ON= x; PN = y and Op = r; ∆PON = θ and ∆PON = 90°; sin θ =

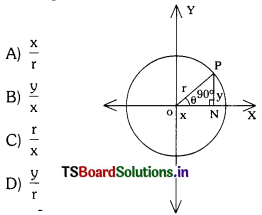
Answer:
(D)

Question 82.
cos θ = …………………..
A) \(\frac{x}{r}\)
B) \(\frac{y}{r}\)
C) \(\frac{r}{x}\)
D) \(\frac{y}{x}\)
Answer:
A) \(\frac{x}{r}\)

Question 83.
tan θ =
A) \(\frac{x}{y}\)
B) \(\frac{y}{x}\)
C) \(\frac{r}{x}\)
D) \(\frac{r}{y}\)
Answer:
B) \(\frac{y}{x}\)

Question 84.
sin θ . cosec θ + cos θ . sec θ + tan θ . cot θ =
A) 3
B) 1
C) sinθ.cosθ.tanθ
D) none
Answer:
A) 3

Question 85.
If sinθ. cosec θ = x; then x =
A) 0
B) 1
C) \(\frac{1}{\sin \theta}\)
D) \(\frac{1}{\ cosec \theta}\)
Answer:
B) 1

Question 86.
If sec θ = \(\frac{13}{12}\), then sin θ =
A) \(\frac{5}{13}\)
B) \(\frac{5}{12}\)
C) \(\frac{12}{5}\)
D) \(\frac{12}{13}\)
Answer:
A) \(\frac{5}{13}\)

Question 87.
sin (90 + θ) =
A) cos θ
B) – cos θ
C) sin θ
D) – sin θ
Answer:
A) cos θ

Question 88.
Value of tan² 30° + 2 cot² 60° =
A) \(\frac{2}{3}\)
B) 2
C) 1
D) \(\frac{4}{3}\)
Answer:
C) 1

Question 89.
sin² 75° + cos² 75° =
A) 75
B) 150
C) tan² 75°
D) 1
Answer:
D) 1

Question 90.
sin⁴θ – cos⁴θ =
A) 1
B) cos²θ – sin²θ
C) 2 sin² θ – 1
D) 2 sin²θ
Answer:
C) 2 sin² θ – 1

Question 91.
(1 + tan θ)² =
A) sec² θ
B) sec²θ + 2 tan θ
C) sec²θ + tan²θ
D) sec²θ + tan θ
Answer:
B) sec²θ + 2 tan θ

Question 92.
Expressing tan θ, interms of sec θ.

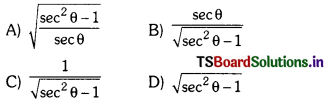
Answer:
(D)

Question 93.
If 5 sin A = 3; then sec² A – tan² A =
A) \(\frac{9}{25}\)
B) 0
C) \(\frac{25}{9}\)
D) 1
Answer:
D) 1

Question 94.
(sin θ + cos θ)² + (sin θ – cos θ)² =
A) 2 sin²θ+ cos²θ
B) 2
C) 2 sin²θ + 4 cos²θ
D) 2 sin²θ
Answer:
B) 2

Question 95.

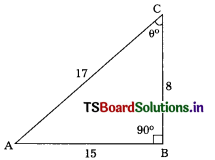
In ∆ABC, ∠B = 90°; ∠C = 0. From the figure, tan θ =
A) \(\frac{8}{17}\)
B) \(\frac{15}{8}\)
C) \(\frac{8}{15}\)
D) \(\frac{17}{15}\)
Answer:
B) \(\frac{15}{8}\)

Question 96.
Value of cos 0° + sin 90° + \(\sqrt{2}\) sin 45°
A) 0
B) 2 + \(\sqrt{2}\)
C) 4
D) 3
Answer:
D) 3

Question 97.
Value of 3 sin² 45° + 2cos² 60° =
A) 2
B) 4
C) 32
D) 1 1/2
Answer:
A) 2

Question 98.
Value of cos 240° =
A) \(\frac{1}{2}\)
B) –\(\frac{\sqrt{3}}{2}\)
C) – \(\frac{1}{2}\)
D) none
Answer:
C) – \(\frac{1}{2}\)

Question 99.
If tan θ + cot θ = 2; then tan²θ + cot²θ =
A) 4
B) 2
C) 6
D) 1
Answer:
B) 2

Question 100.
Value of tan 60° – tan 30°
A) \(\frac{1}{\sqrt{3}}-\sqrt{3}\)
B) \(\frac{1}{\sqrt{3}}\)
C) \(\frac{2 \sqrt{3}}{3}\)
D) \(\frac{\sqrt{3}}{3}\)
Answer:
C) \(\frac{2 \sqrt{3}}{3}\)

Question 101.
If sin θ = cos θ, then θ =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
B) 45°

Question 102.
(1 + tan² 60°)² =
A) 1
B) 2
C) 4
D) 16
Answer:
D) 16

Question 103.
cos (270° – θ)
A) – cos θ
B) – sin θ
C) sin θ
D) cos θ
Answer:
B) – sin θ

Question 104.
When 0° ≤ θ ≤ 90°; the maximum value of sin θ + cos θ is
A) \(\sqrt{2}\)
B) \(\frac{1}{\sqrt{2}}\)
C) 1
D) 2
Answer:
A) \(\sqrt{2}\)

Question 105.
In right angle ∆ABC; ∠B = 90°; tan C = \(\frac{5}{12}\) then the length of hypotenuse is
A) 16
B) 13
C) 21
D) 17
Answer:
B) 13

Question 106.
If A, B are acute angles; sin (A – B) = \(\frac{1}{2}\) sin A = \(\frac{1}{2}\) then B =
A) \(\frac{\pi}{3}\)
B) \(\frac{\pi}{5}\)
C) \(\frac{\pi}{6}\)
D) \(\frac{\pi}{12}\)
Answer:
D) \(\frac{\pi}{12}\)

Question 107.
In ∆ABC, a = 3; b = 4; c = 5 then cos A =
A) \(\frac{3}{5}\)
B) \(\frac{3}{4}\)
C) \(\frac{5}{3}\)
D) \(\frac{4}{5}\)
Answer:
D) \(\frac{4}{5}\)

Question 108.

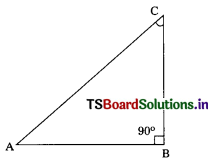
If sin C = \(\frac{3}{5}\) then cos A =
A) \(\frac{3}{5}\)
B) \(\frac{4}{5}\)
C) \(\frac{5}{4}\)
D) \(\frac{5}{3}\)
Answer:
A) \(\frac{3}{5}\)

Question 109.
sec A. \(\sqrt{1-\sin ^2 A}\) =
A) cos A
B) sec A
C) 0
D) 1
Answer:
D) 1

Question 110.
cot(270° – θ) =
A) -tan θ
B) tan θ
C) cot θ
D) – cot θ
Answer:
B) tan θ

Question 111.
\(\frac{\sin 18^{\prime \prime}}{\cos 72^{\prime \prime}}\) =
A) 1
B) \(\frac{1}{4}\)
C) 0
D) ∞
Answer:
A) 1

Question 112.
If π < θ < \(\frac{3 \pi}{2}\) then θ lies in
A) first quadrant
B) second quadrant
C) third quadrant
D) fourth quadrant
Answer:
C) third quadrant

Question 113.
If sinθ . cosθ = k; then sin θ + cos θ =
A) K²
B) K² – 1
C) \(\sqrt{2 K^2-1}\)
D) \(\sqrt{1+2 \mathrm{~K}}\)
Answer:
D) \(\sqrt{1+2 \mathrm{~K}}\)

Question 114.
If tan² 60° + 2 tan² 45° = x tan 45°; then x =
A) 0
B) 5
C) 1
D) 2
Answer:
B) 5

Question 115.
sin³θ cos θ . cos³ θ . sin θ =
A) sin θ + cos θ
B) sin θ cos θ
C) sin θ
D) cos θ
Answer:
B) sin θ cos θ

Question 116.
\(\frac{\sqrt{1+\tan ^2 \theta}}{\sqrt{1+\cot ^2 \theta}}\) =
A) sin θ
B) cos θ
C) tan θ
D) cot θ
Answer:
C) tan θ

Question 117.
sin² 47° + sin² 43° =
A) 0
B) ∞
C) 1
D) can not be determined
Answer:
C) 1

Question 118.
sec (360° – θ) =
A) cos θ
B) sec θ
C) cosec θ
D) cot θ
Answer:
B) sec θ

Question 119.
If sin θ + cos θ = \(\sqrt{2}\); then value of θ =
A) 0°
B) 30°
C) 45°
D) 60°
Answer:
C) 45°

Question 120.
(1 + cot²45°)²: =
A) 4
B) 2
C) 1
D) \(\sqrt{2}\)
Answer:
A) 4

Question 121.
\(\frac{{\ cosec}^2 \theta}{\cot \theta}\) – cot θ =
A) cot θ
B) cosec θ
C) sec θ
D) tan θ
Answer:
D) tan θ

Question 122.
If the following, which are in geometric progression ?
A) sin 30°, sin 45°, sin 60°
B) sec 30°, sec 45°, sec 60°
C) tan 30°, tan 45°, tan 60°
D) cos 45°, cos 60°, cos 90°
Answer:
C) tan 30°, tan 45°, tan 60°

Question 123.
\(\sqrt{\frac{\sec x+\tan x}{\sec x-\tan x}}\) =
A) sec x + tan x
B) sec x- tan x
C) 2 tan x
D) 2 sec x
Answer:
A) sec x + tan x

Question 124.
\(\frac{1}{\sec ^2 A}+\frac{1}{{cosec}^2 A}\) =
A) 2
B) 1
C) tan2A + cos2A
D) 0
Answer:
B) 1

Question 125.
If 4 sin 30° . sec 60° = x tan 4°; then x =
A) 0
B) 1
C) 3
D) 4
Answer:
D) 4

Question 126.
Value of sin 60° cos 30° + cos 60°. sin 30°
A) \(\frac{1}{2}\)
B) 1
C) \(\frac{\sqrt{3}}{2}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
B) 1

Question 127.
Value of cos 60°. cos 30° + sin 60°. sin 30°
A) \(\frac{\sqrt{3}}{2}\)
B) \(\frac{1}{\sqrt{2}}\)
C) 1
D) \(\frac{2}{\sqrt{3}}\)
Answer:
A) \(\frac{\sqrt{3}}{2}\)

Question 128.
\(\frac{\tan 45^{\prime \prime}}{\ cosec 30^{\prime \prime}}+\frac{\sec 60^{\prime \prime}}{\cot 45^{\prime \prime}}\) =
A) 1 1/2
B) 1
C) 2
D) 2 1/2
Answer:
D) 2 1/2

Question 129.
Value of cos 75° =
A) sin 15°
B) – sin 15°
C) cos 15°
D) \(\frac{\sqrt{3}}{2}\)
Answer:
A) sin 15°

Question 130.
tan θ . cot θ = sec θ . x; then x =
A) cos θ
B) sec θ
C) tan θ
D) cot θ
Answer:
A) cos θ

Question 131.
(1 + tan²A) (1 – sin² A) =
A) sec²A
B) cos²A
C) 1
D) 1 – sin²A + tan²A
Answer:
C) 1

Question 132.
tan 240° =
A) \(\frac{1}{\sqrt{3}}\)
B) \(\sqrt{3}\)
C) –\(\sqrt{3}\)
D) –\(\frac{1}{\sqrt{3}}\)
Answer:
B) \(\sqrt{3}\)

Question 133.
\(\frac{\sin ^4 A-\cos ^4 A}{\sin ^2 A-\cos ^2 A}\) =
A) sin² A – cos² A
B) 1
C) sin² A
D) cos²
Answer:
B) 1

Question 134.
If sin θ = \(\frac{1}{2}\); then cos \(\frac{3 \theta}{2}\)
A) \(\frac{1}{\sqrt{2}}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{2}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
A) \(\frac{1}{\sqrt{2}}\)

Question 135.
cos \(\left(\frac{3}{2}+\theta\right)\) =
A) cos θ
B) sin θ
C) – sin θ
D) sec θ
Answer:
B) sin θ

Question 136.
\(\frac{\tan \theta \cdot \sqrt{1-\sin ^2 \theta}}{\sqrt{1-\cos ^2 \theta}}\)
A) sin θ
B) cos θ
C) sec θ
D) 1
Answer:
D) 1

Question 137.
If sec θ + tan θ = \(\frac{1}{5}\), then sin θ =
A) \(\frac{5}{13}\)
B) \(\frac{12}{13}\)
C) \(\frac{13}{12}\)
D) \(\frac{5}{13}\)
Answer:
B) \(\frac{12}{13}\)

Question 138.
(sec 45° + tan 45°) (sec 45° – tan 45°) =
A) 1
B) 0
C) 2
D) 2\(\sqrt{2}\)
Answer:
A) 1

Question 139.
If the angle in a triangle are in the ratio of 1 : 2 : 3 then the smallest angle in radius is
A) \(\frac{\pi}{3}\)
B) \(\frac{\pi}{6}\)
C) \(\frac{2\pi}{3}\)
D) \(\frac{\pi}{2}\)
Answer:
B) \(\frac{\pi}{6}\)

Question 140.
\(\sqrt{{\ cosec}^2 \theta-\cot ^2 \theta}\) =
A) cosec θ – cot θ
B) cosec θ + cot θ
C) 1
D) 0
Answer:
C) 1

Question 141.
tan A, in terms of sin A is

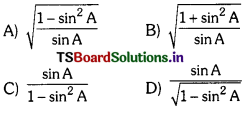
Answer:
(D)

Question 142.
\(\frac{1}{1-\sin \theta}\) + \(\frac{1}{1+\sin \theta}\) =
A) 2 tan² θ
B) 2 sec² θ
C) 2 cosec² θ
D) 2 cot² θ
Answer:
B) 2 sec² θ

Question 143.
If cot² θ = 3; then cosec θ =
A) 4
B) 2
C) 3
D) 1
Answer:
B) 2

Question 144.
If cos θ = – cos θ, then θ is
A) 60°
B) 45°
C) 30°
D) 90°
Answer:
B) 45°

Question 145.
If A is acute and tan A = \(\frac{1}{\sqrt{3}}\); then sin A = ……………….
A) \(\frac{1}{2}\)
B) 1
C) \(\sqrt{2}\)
D) \(\frac{\sqrt{3}}{2}\)
Answer:
A) \(\frac{1}{2}\)

Question 146.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\); cos θ = \(\frac{\mathrm{c}}{\mathrm{d}}\) ;then tan θ =
A) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)
b) \(\frac{\mathrm{ac}}{\mathrm{bd}}\)
C) \(\frac{\mathrm{ab}}{\mathrm{cd}}\)
D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)
Answer:
D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)

Question 147.
If sin A = \(\frac{1}{\sqrt{2}}\) ; then tan A =
A) 3
B) 4
C) 1
D) \(\sqrt{2}\)
Answer:
C) 1

Question 148.
If sec θ = cosec θ; then value of θ =
A) \(\frac{\pi}{2}\)
B) \(\frac{\pi}{4}\)
C) \(\frac{\pi}{6}\)
D) \(\frac{\pi}{3}\)
Answer:
B) \(\frac{\pi}{4}\)

Question 149.
The radius of a circle is ‘r’; an arc of length ‘l’ is making an angle θ, at the centre of the circle, then θ =
A) \(\frac{\mathrm{l}}{\mathrm{r}}\)
B) \(\frac{\mathrm{r}}{\mathrm{l}}\)
C) lr
D) l + r
Answer:
A) \(\frac{\mathrm{l}}{\mathrm{r}}\)

Question 150.
tan (A + B) =

Answer:
(B)

Question 151.
tan(A – B) =

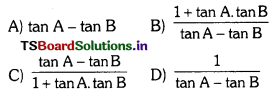
Answer:
(C)

Question 152.
\(\frac{\sqrt{\ cosec^2 \theta-1}}{\ cosec \theta}\) =
A) 1+ sec θ
B) cosec θ + cot θ
C) cos θ
D) tan θ
Answer:
C) cos θ

Question 153.
\(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\) =
A) tan θ
B) cosec θ
C) cot θ
D) sec θ
Answer:
A) tan θ

Question 154.
\(\frac{\sqrt{\sec ^2 \theta-1}}{\sec \theta}\) =
A) cosec θ
B) sin θ
C) cosec θ – cot θ
D) 2 sec θ
Answer:
B) sin θ

Question 155.
If x = 2 cosec θ; y = 2 cot θ; then x² – y² =
A) 4
B) 0
C) 1
D) 2
Answer:
A) 4

Question 156.
If cos(A + B) = θ, cos B = \(\frac{\sqrt{3}}{2}\); then A is
A) 60°
B) 180°
C) 15°
D) 115°
Answer:
A) 60°

Question 157.
\(\frac{\sqrt{1-\cos ^2 \theta}}{\cos \theta}\) =
A) tan θ
B) cos θ
C) sec θ
D) cot θ
Answer:
A) tan θ

Question 158.
\(\frac{1}{\sqrt{1+\tan ^2 \theta}}\) =
A) sin θ
B) cos θ
C) sec θ
D) cosec θ
Answer:
B) cos θ

Question 159.
cos θ . tan θ =
A) cos θ
B) cot θ
C) sin θ
D) cos² θ
Answer:
C) sin θ

Question 160.
sin 225° =
A) \(\frac{1}{\sqrt{2}}\)
B) –\(\frac{1}{\sqrt{2}}\)
C) \(\frac{\sqrt{3}}{2}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
B) –\(\frac{1}{\sqrt{2}}\)

Question 161.
sec² 33° – cot² 57° =
A) 0
B) 1
C) -1
D) \(\frac{1}{2}\)
Answer:
B) 1

Question 162.
sin 180° =
A) 0
B) 1
C) -1
D) ∞
Answer:
A) 0

Question 163.
If cos θ = \(\frac{1}{2}\) ; then cos \(\frac{\theta}{2}\) =
A) \(\frac{1}{4}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{2}\)
D) 1
Answer:
B) \(\frac{\sqrt{3}}{2}\)

Question 164.
sin (A + B).cos (A – B) + sin (A – B). cos (A + B) =
A) cos 2A
C) sin 2A
B) cos 2B
D) sin 2B
Answer:
B) cos 2B

Question 165.
Value of cos 60° . cos30° – sin 60° . sin 30° =
A) 1
B) 0
C) \(\frac{1}{4}\)
D) \(\frac{1}{2}\)
Answer:
B) 0

Question 166.
cos 300° =
A) \(\frac{\sqrt{3}}{2}\)
B) 1
C) 0
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 167.
If sin (A + B) = 1; sin B = \(\frac{1}{2}\) ; then A =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
C) 60°

Question 168.
\(\sqrt{\sec ^2 A+\ cosec^2 A}\) =
A) cos A + sin A
B) sec A + cosec A
C) tan A+ cot A
D) 1
Answer:
C) tan A+ cot A

Question 169.
If \(\sqrt{3}\) tan θ = 1; then θ =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
A) 30°

Question 170.
\(\sqrt{\ cosec ^2 \theta-\sin ^2 \theta-\cos ^2 \theta}\) =
A) cot θ
B) tan θ
C) sec θ
D) cosec θ
Answer:
A) cot θ

Question 171.
sin 750° =
A) \(\frac{1}{\sqrt{2}}\)
B) \(\frac{1}{2}\)
C) 1
D) \(\frac{\sqrt{3}}{2}\)
Answer:
B) \(\frac{1}{2}\)

Question 172.
Cosec 60° × cos 90° =
A) ∞
B) \(\frac{2}{\sqrt{3}}\)
C) 0
D) 3
Answer:
C) 0

Question 173.
sin 81° = ………………
A) cos 9°
B) cos 81°
C) – cos 9°
D) can not be possible to determine without tables
Answer:
A) cos 9°

Question 174.
If sin θ = \(\frac{11}{15}\) ; then cos θ =
A) \(\frac{\sqrt{26}}{7}\)
B) \(\frac{2 \sqrt{26}}{3}\)
C) \(\frac{2 \sqrt{26}}{15}\)
D) none
Answer:
C) \(\frac{2 \sqrt{26}}{15}\)

Question 175.
If tan θ = \(\sqrt{3}\), then sec θ = ……………….
A) 2
B) -2
C) 4
D) 5
Answer:
A) 2

Question 176.
If 3 cot θ = 5, then \(\frac{5 \sin \theta-3 \cos \theta}{5 \sin \theta+3 \cos \theta}\) = ………………..
A) -1
B) 1
C) 7
D) 0
Answer:
D) 0

Question 177.
(1 + tan²θ) cos²θ = …………….
A) 1
B) 0
C) 8
D) 14
Answer:
A) 1

Question 178.
(sec²θ – 1) (1 – cosec²θ) = ………………
A) 2
B) -1
C) 3
D) -4
Answer:
B) -1

Question 179.
cot²θ – \(\frac{1}{\sin ^2 \theta}\)
A) 4
B) -3
C) 2
D) -1
Answer:
D) -1

Question 180.
If cos θ . sin θ = \(\frac{1}{2}\) ; then θ = …………….
A) 1
B) -1
C) 3
D) 4
Answer:
A) 1

Question 181.
If cos θ = -cos θ; then θ in radian measure is ………….
A) π^c
B) \(\frac{\pi^c}{2}\)
C) \(\frac{\pi^c}{3}\)
D) \(\frac{\pi^c}{7}\)
Answer:
C) \(\frac{\pi^c}{3}\)

Question 182.
If sin A = \(\frac{3}{5}\) ; then sin (90 + A) = ………….
A) \(\frac{4}{5}\)
B) \(\frac{5}{4}\)
C) \(\frac{1}{3}\)
D) \(\frac{2}{3}\)
Answer:
A) \(\frac{4}{5}\)

Question 183.
\(\sqrt{(\sec \theta+1)(\sec \theta-1)}\) = ……………..
A) cot θ
B) tan θ
C) cos θ
D) sin θ
Answer:
B) tan θ

Question 184.
\(\sqrt{\sec ^2 \theta-\tan ^2 \theta+\cot ^2 \theta}\) = …………………..
A) -cos θ
B) 1
C) sec θ
D) cosec θ
Answer:
D) cosec θ

Question 185.
cos 150° = …………….
A) –\(\frac{\sqrt{3}}{2}\)
B) – \(\sqrt{3}\)
C) –\(\frac{1}{2}\)
D) none
Answer:
A) –\(\frac{\sqrt{3}}{2}\)

Question 186.
sin² 75° + cos² 75° = ………………..
A) 3
B) 2
C) 4
D) 1
Answer:
D) 1

Question 187.
sin 240° + sin 120° = …………..
A) 0
B) -1
C) 3
D) none
Answer:
A) 0

Question 188.
If cosec θ + cot θ = 2; then cosec θ – cot θ = ………………
A) -1
B) 2
C) \(\frac{1}{2}\)
D) 3
Answer:
C) \(\frac{1}{2}\)

Question 189.
If sec A + tan A = \(\frac{1}{3}\); then sec A – tan A = ……………
A) 4
B) 1
C) -3
D) 3
Answer:
D) 3

Question 190.
sin 30° + cos 60° = ………………
A) 1
B) 4
C) 3
D) none
Answer:
A) 1

Question 191.
(cos A + sin A)² + (cos A – sin A)² = ………………..
A) 1
B) 2
C) 4
D) none
Answer:
B) 2

Question 192.
sin 450° = ……………….
A) 4
B) 2
C) -1
D) none
Answer:
D) none

Question 193.
cos(A + B) = ……………..
A) cos A cos B – sin A sin B
B) cos A sec B – sin A sin B
C) cos A cos B + sin A sec B
D) none
Answer:
A) cos A cos B – sin A sin B

Question 194.
tan(A – B) = ………….
A) tan A – cos B
B) tan B – tan A
C) \(\frac{\tan B-\tan A}{1+\tan A+\tan B}\)
D) none
Answer:
C) \(\frac{\tan B-\tan A}{1+\tan A+\tan B}\)

Question 195.
tan (360 – θ) = ……………….
A) sin θ
B) sec θ
C) tan θ
D) -tan θ
Answer:
D) -tan θ

Question 196.
The value of tan 75° = …………..
A) 2 + \(\sqrt{3}\)
B) 2 – \(\sqrt{3}\)
C) \(\sqrt{3}\) – 1
D) none
Answer:
A) 2 + \(\sqrt{3}\)

Question 197.
cos 110°. cos 70° – sin 110°.sin 70° = ……………..
A) 4
B) 1
C) -1
D) 3
Answer:
C) -1

Question 198.
Express tan θ, interms of sin θ = ………………
A) \(\frac{\cos \theta}{1-\sin \theta}\)
B) \(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\)
C) \(\frac{\sin \theta}{1+\cos \theta}\)
D) none
Answer:
B) \(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\)

Question 199.
cosec 60° . sec 60° = ……………….
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{4}\)
C) \(\frac{4}{3}\)
D) \(\frac{4}{\sqrt{3}}\)
Answer:
D) \(\frac{4}{\sqrt{3}}\)

Question 200.
sin(A + B) =
A) sin A cos B + cos A sin B
B) sin A – cos B sin B
C) sin A cos B – sin A sin B
D) none
Answer:
A) sin A cos B + cos A sin B

Question 201.
cos (180 – θ) = ……………..
A) – cos θ
B) cos θ
C) sec θ
D) none
Answer:
A) – cos θ

Question 202.
sin 2A = ………………
A) 2 sin A cos A
B) cos A sin A
C) sin² A
D) cos² A
Answer:
A) 2 sin A cos A

Question 203.
\(\sqrt{\ cosec ^2 \theta-\sin ^2 \theta-\cos ^2 \theta}\) = ……………….
A) -tan θ
B) -sin θ
C) sec θ
D) cot θ
Answer:
D) cot θ

Question 204.
(1 – sec²θ) (1 – cosec²θ) = ……………….
A) 3
B) -1
C) 4
D) 1
Answer:
D) 1

Question 205.
If cos θ = \(\frac{3}{5}\); then cos (-θ) = …………….
A) \(\frac{-3}{5}\)
B) \(\frac{3}{5}\)
C) \(\frac{1}{5}\)
D) \(\frac{1}{4}\)
Answer:
B) \(\frac{3}{5}\)

Question 206.
2 sin 45°. cos 45° = …………….
A) 1
B) 4
C) -1
D) none
Answer:
A) 1

Question 207.
If cot = x; then cosec θ = ………….
A) \(\sqrt{2 x+1}\)
B) \(\sqrt{1+x}\)
C) \(\sqrt{x^2+1}\)
D) none
Answer:
C) \(\sqrt{x^2+1}\)

Question 208.
In the figure, AB = ………………

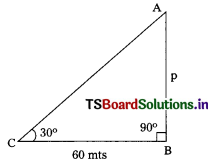
A) 16 \(\sqrt{3}\)
B) 10 \(\sqrt{3}\)
C) 9\(\sqrt{3}\)
D) 20\(\sqrt{3}\)
Answer:
D) 20\(\sqrt{3}\)

Question 209.
sin 45°.cos 45° + \(\sqrt{3}\) sin 60° = ………..
A) 2
B) -2
C) 3
D) none
Answer:
A) 2

Question 210.
\(\frac{\sqrt{\sec ^2 A-1}}{\sec A}\) = ………………
A) sec A
B)-cos A
C) cos A
D) sin A
Answer:
D) sin A

Question 211.
\(\frac{\sqrt{\ cosec ^2 \theta-1}}{\ cosec \theta}\) = …………..
A) -sin θ
B)-cos θ
C) cos θ
D) none
Answer:
C) cos θ

Question 212.
If α + β = 90° and α = 2β; then cos² α + sin² β = ………………
A) \(\frac{-1}{2}\)
B) -1
C) 2
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 213.
tan 30° + cot 30° = ………….
A) \(\frac{4}{\sqrt{3}}\)
B) \(\frac{4}{3}\)
C) \(\frac{\sqrt{3}}{4}\)
D) none
Answer:
A) \(\frac{4}{\sqrt{3}}\)

Question 214.
\(\sqrt{\tan ^2 \theta+\cot ^2 \theta+2}\) = ………………..
A) tan θ – cos θ
B) tan θ
C) tan θ + cot θ
D) tan θ – cot θ
Answer:
C) tan θ + cot θ

Question 215.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\); then tan θ = …………….

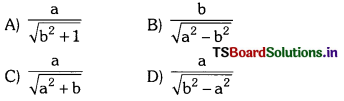
Answer:
(D)

Question 216.
tan θ = \(\frac{1}{\sqrt{3}}\) ; cos θ = ……………
A) \(\frac{\sqrt{3}}{2}\)
B) \(\sqrt{3}\)
C) \(\frac{2}{\sqrt{3}}\)
D) \(\frac{1}{2}\)
Answer:
A) \(\frac{\sqrt{3}}{2}\)

Question 217.
If 5 sin A = 3; sec²A – tan²A = ……………..
A) 3
B) -1
C) 4
D) 1
Answer:
D) 1

Question 218.
sin (-θ) = …………………..
A) cos θ
B) -tan θ
C) sec θ
D) -sin θ
Answer:
D) -sin θ

Question 219.
cos (-θ) = ………………..
A) sec θ
B) -cos θ
C) cos θ
D) 1
Answer:
C) cos θ

Question 220.
sin (180 – θ) = ………………
A) cos θ
B) sin θ
C) tan θ
D) 0
Answer:
B) sin θ

Question 221.
cos (270 – θ)
A) cos θ
B) sin θ
C) – sin θ
D) none
Answer:
C) – sin θ

Question 222.
tan (360 – θ) = ……………
A) -tan θ
B) tan θ
C) sec θ
D) cos θ
Answer:
A) -tan θ

Question 223.
cosec (270 – θ) = ……………..
A) sec θ
B) -sec θ
C) tan θ
D) none
Answer:
C) tan θ

Question 224.
sec (90 + θ) = …….
A) tan θ
B) cosec θ
C) – cos θ
D) – cosec θ
Answer:
D) – cosec θ

Question 225.
cos 240° = ……………..
A) \(\frac{-1}{2}\)
B) -1
C) \(\frac{2}{3}\)
D) -3
Answer:
A) \(\frac{-1}{2}\)

Question 226.
sin 420° = ………….
A) – \(\frac{\sqrt{3}}{2}\)
B) 1
C) \(\frac{\sqrt{3}}{2}\)
D) \(\frac{2}{\sqrt{2}}\)
Answer:
C) \(\frac{\sqrt{3}}{2}\)

Question 227.
tan 750° = ……………..
A) \(\frac{-1}{\sqrt{3}}\)
B) \(\sqrt{3}\)
C) -1
D) \(\frac{1}{\sqrt{3}}\)
Answer:
D) \(\frac{1}{\sqrt{3}}\)

Question 228.
cosec 300° = ………………
A) \(\frac{-2}{\sqrt{3}}\)
B) \(\frac{1}{\sqrt{3}}\)
C) \(\frac{-1}{2}\)
D) –\(\frac{1}{\sqrt{3}}\)
Answer:
A) \(\frac{-2}{\sqrt{3}}\)

Question 229.
sec 240° = …………..
A) 3
B) -1
C) 2
D) -2
Answer:
D) -2

Question 230.
sin² 47° + sin² 43° = ……………
A) 1
B) -1
C) 3
D) none
Answer:
A) 1

Question 231.
If cosec θ – cot θ = 4, then cosec θ + cot θ = ……………….
A) 1
B) \(\frac{1}{2}\)
C) \(\frac{-1}{4}\)
D) \(\frac{1}{4}\)
Answer:
D) \(\frac{1}{4}\)

Question 232.
tan θ in terms of cosec θ = ………………….
A) \(\frac{1}{\sqrt{\ cosec ^2 \theta-1}}\)
B) \(\frac{1}{\sqrt{1+\ cosec \theta}}\)
C) \(\frac{1}{1+\tan ^2 \theta}\)
D) none
Answer:
A) \(\frac{1}{\sqrt{\ cosec ^2 \theta-1}}\)

Question 233.
\(\frac{\ cosec ^2 \theta}{\cot \theta}\) – cot θ = …………………
A) cot θ
B) sec θ
C) tan θ
D) none
Answer:
C) tan θ

Question 234.
\(\frac{1-\tan ^2 30^{\prime \prime}}{1+\tan ^2 30^{\prime \prime}}\) = ………………
A) -2
B) \(\frac{-1}{2}\)
C) 1
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 235.
\(\frac{1}{\sec ^2 A}+\frac{1}{\ cosec ^2 A}\) = ………………
A) -1
B) 1
C) 3
D) 4
Answer:
B) 1

Question 236.
tan θ. cot θ = sec θ. x; then x = …………………….
A) cos θ
B) – cos θ
C) tan θ
D) none
Answer:
A) cos θ

Question 237.
If sin (A + B) = \(\frac{\sqrt{3}}{2}\) ; cos B = \(\frac{\sqrt{3}}{2}\) then A = ……………….
A) 70°
B) 45°
C) 60°
D) 30°
Answer:
D) 30°

Question 238.
cos \(\left(\frac{3 \pi}{2}+\theta\right)\) = …………….
A) tan θ
B) cos θ
C) -sin θ
D) sin θ
Answer:
D) sin θ

Question 239.
sec θ + tan θ = \(\frac{1}{2}\); then sin θ = …………….
A) \(\frac{2}{13}\)
B) \(\frac{1}{13}\)
C) \(\frac{12}{13}\)
D) \(\frac{13}{2}\)
Answer:
C) \(\frac{12}{13}\)

Question 240.
If sec = cosec θ; then the value of θ in radians = …………………
A) \(\frac{\pi^c}{2}\)
B) \(\frac{\pi^c}{4}\)
C) \(\frac{\pi^c}{3}\)
D) \(\frac{\pi^c}{12}\)
Answer:
B) \(\frac{\pi^c}{4}\)

Question 241.
Maximum value of sin θ + cos θ = ……………..
A) 3
B) \(\sqrt{3}\)
C) 2
D) \(\sqrt{2}\)
Answer:
D) \(\sqrt{2}\)

Question 242.
Maximum value of cos θ = …………………
A) 1
B) -1
C) 2
D) 0
Answer:
A) 1

Question 243.
Minimum and maximum value of tan θ = ……………
A) (-∞, ∞)
B) (- ∞, 0)
C) (3, 2)
D) (1, -1)
Answer:
A) (-∞, ∞)

Question 244.
\(\frac{\sin ^4 \theta-\cos ^4 \theta}{\sin ^2 \theta-\cos ^2 \theta}\) = ……………….
A) 2
B) -1
C) 1
D) none
Answer:
C) 1

Question 245.
cos 0° + sin 90° + \(\sqrt{3}\) cosec 60° = ………………
A) 0
B) -1
C) 3
D) 4
Answer:
D) 4

Question 246.
\(\left|\begin{array}{l}
\tan \theta \sec \theta \\
\sec \theta \tan \theta
\end{array}\right|\) = …………………
A) -1
B) -4
C) 1
D) none
Answer:
C) 1

Question 247.
If cosec θ + cot θ = 3, then cosec θ – cot θ = …………….
A) \(\frac{1}{2}\)
B) \(\frac{1}{3}\)
C) \(\frac{-1}{3}\)
D) none
Answer:
B) \(\frac{1}{3}\)

Question 248.
\(\frac{\tan \theta}{\sqrt{1+\tan ^2 \theta}}\) = ……………..
A) -cos θ
B) -sin θ
C) sin θ
D) sin² θ
Answer:
C) sin θ

Question 249.
\(\frac{\sqrt{1-\cos ^2 \theta}}{\cos \theta}\) = ……………
A) -cot θ
B) tan θ
C) sec θ
D) none
Answer:
B) tan θ

Question 250.
x = 2 cosec θ; y = 2 cot θ; x² – y² = …………….
A) 4
B) -1
C) -3
D) 2
Answer:
A) 4

Question 251.
\(\sqrt{\sec ^2 A+\ cosec ^2 A}\) = ……………….
A) tan A – cos A
B) tan A + cos A
C) 1
D) tan A + cot A
Answer:
D) tan A + cot A

Question 252.
sin 81° = ……………….
A) cos 9°
B) cos 20°
C) tan 9°
D) none
Answer:
A) cos 9°

Question 253.
\(\frac{\sqrt{\sec ^2 \theta-1}}{\sec \theta}\) = ………………
A) – tan θ
B) cos θ
C) sin θ
D) none
Answer:
C) sin θ

Question 254.
If sin A = \(\frac{1}{\sqrt{2}}\); then tan A = ……………
A) 4
B) 3
C) -1
D) 1
Answer:
D) 1

Question 255.
sin 225° = ………………
A) \(\frac{-1}{\sqrt{2}}\)
B) \(\sqrt{2}\)
C) \(\frac{-1}{2}\)
D) 1
Answer:
A) \(\frac{-1}{\sqrt{2}}\)

Question 256.
cos (x – y) = ………………
A) cos x cos y + sin x sin y
B) cos x – sin x sin y
C) cos x cos y – 1
D) all
Answer:
A) cos x cos y + sin x sin y

Question 257.
\(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = ………………..
A) sec⁴ θ
B) sec θ
C) \(\frac{\sec ^2 \theta}{2}\)
D) 2 sec² θ
Answer:
D) 2 sec² θ

Question 258.
sin⁴ θ – cos⁴ θ = ………………..
A) 2 sec² θ – 1
B) sec² θ + 1
C) sec² θ – 3
D) none
Answer:
A) 2 sec² θ – 1

Question 259.
tan θ is not defined if θ = ……………..
A) 0°
B) 70°
C) 90°
D) 20°
Answer:
C) 90°

Question 260.
If cosec θ = \(\frac{25}{7}\) ; then cot θ = …………….
A) \(\frac{4}{7}\)
B) \(\frac{7}{24}\)
C) \(\frac{4}{23}\)
D) \(\frac{24}{7}\)
Answer:
D) \(\frac{24}{7}\)

Question 261.
tan 26°. tan 64° = …………..
A) 1
B) -1
C) 3
D) 7
Answer:
A) 1

Question 262.
If tan 2A = cot (A – 18°) where 2A is an acute angle then A = ……………
A) 116°
B) 20°
C) 16°
D) 36°
Answer:
D) 36°

Question 263.
sin(90 – Φ) = ……………
A) cos Φ
B) sin Φ
C) – cos Φ
D) 0
Answer:
A) cos Φ

Question 264.
In ∆ABC, sin \(\left(\frac{B+C}{2}\right)\) = ………………
A) cos \(\frac{A}{2}\)
B) cos \(\frac{C}{2}\)
C) tan \(\frac{A}{2}\)
D) 1
Answer:
A) cos \(\frac{A}{2}\)

Question 265.
\(\frac{\sec 35^{\prime}}{\ cosec 55^{\prime \prime}}\) = …………………
A) -3
B) 8
C) 4
D) 1
Answer:
D) 1

Question 266.
sin \(\frac{\pi^c}{4}\) + cos 45° = ……………….
A) 2
B) \(\sqrt{2}\)
C) -1
D) 0
Answer:
B) \(\sqrt{2}\)

Question 267.
sec 0° = ………………..
A) -1
B) 1
C) 0
D) 7
Answer:
B) 1

Question 268.
sec θ – tan θ = \(\frac{1}{n}\) then sec θ + tan θ = ………………
A) -n
B) -1
C) n
D) none
Answer:
C) n

Question 269.
If 3 tan A = 4 then cos A = ……………..
A) \(\frac{1}{2}\)
B) \(\frac{1}{3}\)
C) \(\frac{1}{7}\)
D) none
Answer:
D) none

Question 270.
From the figure, sin C = …………..

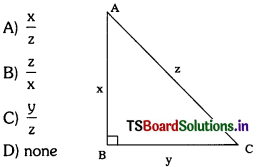
Answer:
(A)

Question 271.
cos² θ = ……………….
A) 1 + sin² θ
B) 1 – sin² θ
C) 1 – sin θ
D) 1 + cos θ
Answer:
B) 1 – sin² θ

Question 272.
sec θ is not defined if θ = …………………
A) 0°
B) 90°
C) 30°
D) 45°
Answer:
B) 90°

Question 273.
(1 + tan² 60)² = ………………..
A) 1
C) 16
B) 10
D) 12
Answer:
B) 10

Question 274.
Reciprocal of cot A = ……………..
A) sin A
B) sin² A
C) sec² A
D) tan A
Answer:
D) tan A

Question 275.
sin A = cos B then A + B = …………….
A) 20°
B) 70°
C) 90°
D) none
Answer:
C) 90°

Question 276.
Trigonometry was introduced by ……………….
A) Cantor
B) Cayley
C) Hipparchus
D) none
Answer:
C) Hipparchus

Question 277.
If tan A = \(\frac{3}{4}\) then sec² A – tan² A = ………………..
A) 4
B) 3
C) -1
D) 1
Answer:
D) 1

Question 278.
tan² Φ sec² Φ = ………………..
A) -1
B) 1
C) 3
D) 0
Answer:
A) -1

Question 279.
In the figure, tan X = ……………..

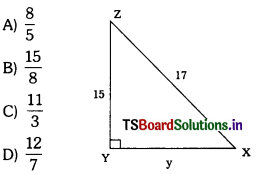
Answer:
(B)

Question 280.
If sin θ = cos 66° then θ = ………………
A) 30°
B) 24°
C) 36°
D) 48°
Answer:
B) 24°

Question 281.
If sec = \(\frac{\mathrm{X}}{\cos \theta}\) then X = ……………….
A) \(\frac{1}{2}\)
B) 0
C) -1
D) 1
Answer:
D) 1

Question 282.
Which of the following is not the value of sin θ ?
A) 1
B) \(\frac{3}{4}\)
C) \(\frac{4}{3}\)
D) \(\frac{1}{2}\)
Answer:
B) \(\frac{3}{4}\), C) \(\frac{4}{3}\)

Question 283.
Which of the following is not correct?
A) cos 0°
B) sin 90° = 0
C) tan 45° = cot 45°
D) both A and B
Answer:
D) both A and B

Question 284.
(sec A + tan A) (1 = sin A) = ……………….
A) sec A
B) sin A
C) cosec A
D) cos A
Answer:
D) cos A

Question 285.
If sec θ + tan θ = X then cosec θ = ……………..

Answer:
(C)

Question 286.
From the adjacent figure, \(\frac{c}{a}=\frac{29}{21}\) represents

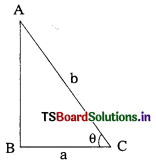
A) cos θ
B) cosec θ
C) cot θ
D) sin θ
Answer:
B) cosec θ

Question 287.
From the adjacent figure, value of ‘sin²A + cos²A’

Answer:
(D)