TS 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.2

Students can practice TS 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 1 Real Numbers Exercise 1.2

Question 1.
Express each of the following numbers as a product of its prime factors.

(i) 140
Answer:
140

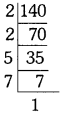
∴ 140 = 2 × 2 × 5 × 7 = 2² × 5 × 7

(ii) 156
Answer:
156

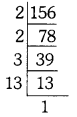
∴ 156 = 2 × 2 × 3 × 13 = 2² × 3 × 13

(iii) 3825
Answer:
3825

∴ 3825 = 3 × 3 × 5 × 5 × 17
= 3² × 5² × 17

(iv) 5005
Answer:
5005

∴ 5005 = 5 × 7 × 11 × 13

(v) 7429
Answer:
7429

∴ 7429 = 17 × 19 × 23

Question 2.
Find the LCM and HCF of the following integers by the prime factorization method.
(i) 12, 15 and 21
Answer:
12, 15, 21
12 = 2 × 2 × 3, 15 = 3 × 5
21 = 3 × 7
H.C.F of 12, 15, 21 is 3.
L.C.M of 12, 15, 21 = 2 × 2 × 3 × 5 × 7 = 420

(ii) 17, 23, and 29
Answer:
17, 23, 29
17 = 1 × 17, 23 = 1 × 23
29 = 1 × 29
H.C.F of 17, 23 and 29 is 1.
L.C.M of 17, 23, 29 is 17 × 23 × 29 = 11339

(iii) 8, 9 and 25
Answer:
8, 9, 25
8 = 1 × 2 × 2 × 2, 9 = 1 × 3 × 3
25 = 1 × 5 × 5
H.C.F. = 1
L.C.M = 2 × 2 × 2 × 3 × 3 × 5 × 5
= 1800

(iv) 72 and 108
Answer:
72, 108

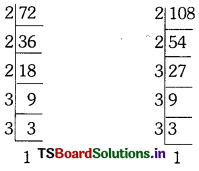
72 = 2 × 36
= 2 × 2 × 18
= 2 × 2 × 2 × 9
= 2 × 2 × 2 × 3 × 3

108 = 2 × 54
= 2 × 2 × 27
= 2 × 2 × 3 × 9
= 2 × 2 × 3 × 3 × 3
H.C.F. = 2 × 2 × 3 × 3 = 36
L.C.M. = 2 × 2 × 2 × 3 × 3 × 3 = 216

(v) 306 and 657
Answer:
306, 657

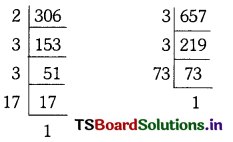
H.C.F. = 9
L.C.M. = 9 × 34 × 73
= 22338

Question 3.
Check whether 6″ can end with the digit 0 for any natural number n.
Answer:
If the number 6ⁿ for any n, were to end with digit ‘0’ then it would be divisible by 5.
The prime factorisation of 6n would contain the prime 5.
6ⁿ = (2 × 3)ⁿ
Prime factorisation of 6ⁿ does not contain 5 as a factor, so 6ⁿ can never end with the digit 0 for any natural number.

Question 4.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Answer:
Given number is 7 × 11 × 13 + 13
= 13 (7 × 11 + 1)
= (7 × 11 + 1) × 13 distributive law
= (77 + 1) × 13
= 78 × 13
= (2 × 3 × 13) × 13
= 2 × 3 × 13²
= Product of prime factors
Hence the given number is a composite number.
Given number is
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5(7 × 6 × 4 × 3 × 2 × 1 + 1)
= 5 (1008 + 1)
= 5 × 1009
= Product of prime numbers
Hence the given number is a composite number.

Question 5.
How will you show that (17 × 11 × 2)+ (17 × 11 × 5) is a composite number? Explain.
Answer:
Given number is
(17 × 11 × 2) + (17 × 11 × 5)
= 17 × 11 × (2 + 5)
= 17 × 11 × 7 = Product of primes
We know that every composite number can be expressed as a product of primes.

Question 6.
Which digit would occupy the units place of 6¹⁰⁰.
Answer:
6¹⁰⁰ = (2 × 3)¹⁰⁰
So the last digit of 6¹⁰⁰ is 6.