TS 10th Class Maths Bits Chapter 3 Polynomials

Solving these TS 10th Class Maths Bits with Answers Chapter 3 Polynomials Bits for 10th Class will help students to build their problem-solving skills.

Polynomials Bits for 10th Class

Question 1.
The coefficient of ‘z’ in the polynomial
z⁵ – 3z² + 4 is
A) 1
B) -3
C) 4
D) 0
Answer:
D) 0

Question 2.
If p(x) = 3x² – x – 4, then p(-1) =
A) 2
B) 0
C) -2
D) 1
Answer:
B) 0

Question 3.
If p(x) = 4x² – 4x + 1; then p(0) =
A) 1
B) -1
C) 4
D) -4
Answer:
A) 1

Question 4.
The remainder when 2x² + 3x + 1 is divided by x + 2 is
A) 15
B) -15
C) 3
D) -3
Answer:
C) 3

Question 5.
The number of zeroes of the polynomial 2x + 1 is
A) 0
B) \(\frac{-1}{2}\)
C) 3
D) 2
Answer:
B) \(\frac{-1}{2}\)

Question 6.
The zeroes of the polynomial p(x) = x² – 3 are
A) 1, 3
B) 1, -3
C) \(\sqrt{3}\), 1
D) \(\sqrt{3}\), –\(\sqrt{3}\)
Answer:
D) \(\sqrt{3}\), –\(\sqrt{3}\)

Question 7.
If α, β are the zeroes of x² + 7x + 10, then αβ =
A) -7
B) 7
C) 10
D) -10
Answer:
C) 10

Question 8.
If α, β are the zeroes of the polynomial f(x) = x² + x + 1, then \(\frac{1}{a}\) + \(\frac{1}{b}\) =
A) -1
B) 1
C) 0
D) none of these
Answer:
A) -1

Question 9.
If α, β are the zeroes of the polynomial f(x) = x² + x + 1, then (α + 1) (β + 1) = ……
A) αβ + α + β
B) α + β + 1
C) 3
D) -1
Answer:
C) 3

Question 10.
If α, β are the zeroes of the quadratic poly-nomial p(t) = t² – 4t + 3, then the value of
A) 4
B) 3
C) 4/3
D) -4/3
Answer:
B) 3

Question 11.
If α, β, γ are the zeroes of 3x³ – 5x² – 11x – 3, then α + β + γ =
A) -5/3
B) 5/3
C) -11/3
D) 1
Answer:
B) 5/3

Question 12.
The degree of the polynomial
\(\sqrt{2}\)x² – 3x + 1 is
A) 2
B) 1
C) 72
D) 3
Answer:
A) 2

Question 13.
The zero of the linear polynomial px + q is
A) \(\frac{-\mathrm{q}}{\mathrm{p}}\)
B) \(\frac{\mathrm{p}}{\mathrm{q}}\)
C) \(\frac{-\mathrm{p}}{\mathrm{q}}\)
D) q
Answer:
A) \(\frac{-\mathrm{q}}{\mathrm{p}}\)

Question 14.
4x – 3 is a
A) linear polynomial
B) cubic polynomial
C) biquadratic polynomial
D) quadratic polynomial
Answer:
A) linear polynomial

Question 15.
The degree of a cubic polynomial is
A) 1
B) 2
C) 3
D) 0
Answer:
C) 3

Question 16.
The zero of p(x) = ax + b is (
A) -a/b
B) a/b
C) -b/a
D) b/a
Answer:
C) -b/a

Question 17.
The degree of the polynomial (x + 1) (x + 2) (x + 3) is
A) 3
B) 4
C) 1
D) 2
Answer:
A) 3

Question 18.
The product of the zeroes of 3x³ – 5x² – 11x – 3 is
A) 3
B) 1
C) -1
D) -3
Answer:
B) 1

Question 19.
The sum of the zeroes of 2x³ – 5x² – 14x + 8 is
A) 5/2
B) -7
C) 4
D) -14
Answer:
A) 5/2

Question 20.
If α, β are the zeroes of the quadratic poly-nomial 4x² – 1, find the value of α² + β²
A) 1/4
B) -1/4
C) 3/4
D) 1/2
Answer:
D) 1/2

Question 21.
If α, β, γ are the zeroes of the polynomial
p(x) = ax³ + bx² + cx + d then \(\frac{1}{a}\) + \(\frac{1}{b}\) + \(\frac{1}{c}\) = r
A) -c/d
B) -b/d
C) c/a
D) -b/a
Answer:
A) -c/d

Question 22.
If α, β are the zeroes of the polynomial x² – 16, find αβ (α + β)
A) -16
B) -8
C) 0
D) -1
Answer:
C) 0

Question 23.
In the following expressions which one is a polynomial ?
A) \(\frac{1}{x+1}\)
B) 2x² – \(\frac{3}{x}\) + 5
C) x² + xy + y²
D) x^1/2 + x + 3
Answer:
B) 2x² – \(\frac{3}{x}\) + 5

Question 24.
The degree of the polynomial
9xy³ + y⁴ + \(\frac{3}{4}\) x⁴ + 7x³y² is
A) 3
B) 4
C) 2
D) 5
Answer:
D) 5

Question 25.
x³ – 3x² + 4x – 5 is divided by (x + 1) then the remainder is
A) 0
B) 13
C) -13
D) none of these
Answer:
C) -13

Question 26.
A polynomial of degree 2 is called ____ poly-nomial.
A) linear
B) quadratic
C) cubic
D) biquadratic
Answer:
B) quadratic

Question 27.
p(x) = 2x + 1 then p(-1/2) =
A) 2
B) -2
C) 0
D) 1
Answer:
C) 0

Question 28.
p(x) = x² – 3x + 2 then p(0) =
A) 0
B) 2
C) -3
D) 1
Answer:
B) 2

Question 29.
The graph of y = ax+b is a straight line which intersects x-axis at
A) (0, -b/a)
B) (0, b)
C) (b, 0)
D) (-b/a, 0)
Answer:
D) (-b/a, 0)

Question 30.
Number of zeroes for any cubic polynomial are ( )
A) 1
B) 3
C) 2
D) 4
Answer:
B) 3

Question 31.
If α, β, γ are the zeroes of the cubic polynomial ax³ + bx² + cx + d = 0 then αβγ
A) -b/a
B) c/a
C) -d/a
D) d/a
Answer:
C) -d/a

Question 32.
Order of the polynomial 5x⁷ – 6x⁵ + 7x – 6 is …….. (T.S.Mar.15)
A) 4
B) 5
C) 6
D) 7
Answer:
D) 7

Question 33.
If the order of ax⁵ + 3x⁴ + 4x³ + 3x² + 2x + 1 is 4 then a = …………
A) 5
B) 4
C) 0
D) not possible
Answer:
C) 0

Question 34.
Sum of zeroes of the polynomial 2x² – 8x + 6 is …… (T.S. Mar.15)
A) 4
B) -4
C) 3
D) -3
Answer:
A) 4

Question 35.
Product fo zeroes of the cubic polynomial 3x³ – 5x² – 11x – 3 is ……….. (T.S. Mar.15)
A) 1
B) -1
C) \(\frac{5}{3}\)
D) \(\frac{-5}{3}\)
Answer:
A) 1

Question 36.
The value of p(x) = 4x² + 3x + 1 at x = -1 is (T.S. Mar.’15)
A) 4
B) 3
C) 2
D) 1
Answer:
C) 2

Question 37.
The zero value of polynomial px + q is ….. (June’15)
A) \(\frac{-\mathrm{q}}{\mathrm{p}}\)
B) \(\frac{\mathrm{p}}{\mathrm{q}}\)
C) \(\frac{-\mathrm{p}}{\mathrm{q}}\)
D) q
Answer:
A) \(\frac{-\mathrm{q}}{\mathrm{p}}\)

Question 38.
4y² – 5y + 1 is a ………. (June’15)
A) linear polynomial
B) cubic polynomial
C) constant polynomial
D) quadratic polynomial
Answer:
D) quadratic polynomial

Question 39.
4x + 6y = 18 doesn’t pass through origin. It indicates a ………. (June’15)
A) curved line
B) straight line
C) parabola
D) None
Answer:
B) straight line

Question 40.
If α, β are the zeroes of the polynomial x² – x – 6 then α²β² = ……… (June ’14)
A) 36
B) 6
C) -6
D) -36
Answer:
A) 36

Question 41.
When p(x) = x² – 8x + k leaves a remainder when it is divided by (x – 1) then k = ………. (A.P. Mar.15)
A) 13
B) 8
C) -5
D) 5
Answer:
A) 13

Question 42.
The zero value of linear polynomial ax – b = ………… (T.S.Mar.16)
A) \(\frac{b}{a}\)
B) \(\frac{a}{b}\)
C) –\(\frac{b}{a}\)
D) –\(\frac{a}{b}\)
Answer:
A) \(\frac{b}{a}\)

Question 43.
The product of zeroes of 2x² – 3x + 6 = …….. (A.P. Mar.’15)
A) 3
B) -3
C) 2
D) -2
Answer:
A) 3

Question 44.
Sum of zeroes of bx² + ax + c = ……… (A.P.Mar. 16)
A) \(\frac{-a}{a}\)
B) \(\frac{a}{b}\)
C) –\(\frac{b}{a}\)
D) \(\frac{b}{a}\)
Answer:
A) \(\frac{-a}{a}\)

Question 45.
If α, β, γ are zeroes of x³ + 3x² – x + 2 then αβγ = ……. (A.P.Mar.16)
A) 2
B) 3
C) 5
D) -2
Answer:
D) -2

Question 46.
The quadratic polynomial having 2, 3 as zeroes is ……. (T.S. Mar.15)
A) x² – 5x – 6
B) x² + 5x + 6
C) x² – 5x + 6
D) x² + 5x – 6
Answer:
C) x² – 5x + 6

Question 47.
Which of the following has only one zero. (T.S.Mar.15)
A) p(x) = 2x² – 3x + 4
B) p(x) = x² – 2x + 1
C) p(x) = 2x + 3
D) p(x) = 5
Answer:
C) p(x) = 2x + 3

Question 48.
Observe the given rectangular figure, then its area in polynomial function is ………. (T.S. Mar.15)

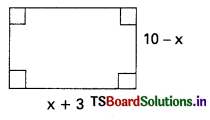
A) A(x) = x² + 7x + 30
B) A(x) = -x² + 7x + 30
C) A(x) = x² – 7x + 30
D) A(x) = -x² – 7x + 30
Answer:
B) A(x) = -x² + 7x + 30

Question 49.
The coefficient of x⁷ in the polynomial 7x⁷ – 17x¹¹ + 27x⁵ – 7 is ……….. (T.S.Mar.16)
A) -1
B) 0
C) 7
D) 17
Answer:
B) 0

Question 50.
A quadratic polynomial whose zeroes are 5 and -2 is
A) x² + 5x – 2
B) x² + 3x – 10
C) x² – 3x – 10
D) x² – 2x + 5
Answer:
C) x² – 3x – 10

Question 51.
If \(\sqrt{3}\) and –\(\sqrt{3}\) are fhe zeroes of a polynomial p(x), then p(x) is
A) x² – 9
B) 3x² – 1
C) x² + 3
D) x² – 3
Answer:
D) x² – 3

Question 52.
The quadratic polynomial whose zeroes are \(\sqrt{15}\) and –\(\sqrt{15}\) is
A) x² – 15
B) x² – 225
C) 15x² – 1
D) x² – \(\sqrt{15}\)
Answer:
A) x² – 15

Question 53.
If one zero of the quadratic polynomial 2x² + kx – 15 is 3, then the other zero is
A) \(\frac{-15}{2}\)
B) k
C) \(\frac{-5}{2}\)
D) -15
Answer:
C) \(\frac{-5}{2}\)

Question 54.
The maximum number of zeroes that a poly-nomial of degree 3 can have is
A) three
B) one
C) two
D) none
Answer:
A) three

Question 55.
The product and sum of the zeroes of the quadratic polynomial ax² + bx + c respectively are
A) \(\frac{c}{b}\), 1
B) \(\frac{-b}{a}\), \(\frac{c}{a}\)
C) \(\frac{c}{a}\), \(\frac{b}{a}\)
D) \(\frac{c}{a}\), \(\frac{-b}{a}\)
Answer:
D) \(\frac{c}{a}\), \(\frac{-b}{a}\)

Question 56.
The number of zeroes of the polynomial function p(x) whose graph is given below is ( )

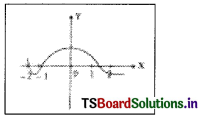
A) 2
B) 2
C) 0
D) 3
Answer:
D) 3

Question 57.
The zeroes of the polynomial p(x) = 4x² – 12x + 9 are
A) \(\frac{-3}{2}\), \(\frac{-3}{2}\)
B) -3, -4
C) \(\frac{3}{2}\), \(\frac{3}{2}\)
D) 3, 4
Answer:
C) \(\frac{3}{2}\), \(\frac{3}{2}\)

Question 58.
If α and β are zeroes of the polynomial p(x) = x² – 5x + 6, then the value of α + β – 3αβ is
A) – 13
B) 6
C) 13
D) -5
Answer:
A) – 13

Question 59.
If 1 is the zero of the quadratic polynomial x² + kx – 5, then the value of k is
A) 0
B) 5
C) -4
D) 4
Answer:
D) 4

Question 60.
The number of zeroes lying between -2 and 2 of the polynomial f(x) whose graph is given below is

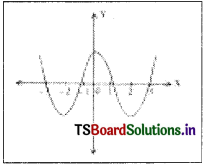
A) 3
B) 4
C) 2
D) 1
Answer:
C) 2

Question 61.
If both the zeroes of a quadratic polynomial ax² + bx + c are equal and opposite in sign, then b is
A) -1
B) 5
C) 1
D) 0
Answer:
D) 0

Question 62.
Sum and product of the zeroes of polynomial x² – 3 are respectively
A) 0, 3
B) 0, -3
C) -3, 0
D) 3, 0
Answer:
B) 0, -3

Question 63.
If the zeroes of a quadratic polynomial are equal in magnitude but opposite in sign, then
A) product of its zeroes is 0
B) sum of its zeroes is 0
C) there are no zeores of the polynomial
D) one of the zero is 0
Answer:
B) sum of its zeroes is 0

Question 64.
If one of the zeroes of the quadratic polynomial ax² + bx + c is 0, thenn the other zero
A) \(\frac{b}{a}\)
B) \(\frac{-c}{a}\)
C) \(\frac{-b}{a}\)
D) 0
Answer:
C) \(\frac{-b}{a}\)

Question 65.
The polynomial whose zeroes are -5 and 4 is
A) x² + x – 20
B) x² + 5x – 4
C) x² – 9x – 20
D) x² – 5x + 4
Answer:
A) x² + x – 20

Question 66.
If – 1 is a zero of the polynomial f(x) = x² – 7x – 8, then the other zero is
A) 8
B) -8
C) 1
D) 6
Answer:
A) 8

Question 67.
If one zero of the quadratic polynomial x² – 5x – 6 is 6, then the other zero is ( )
A) 1
B) – 5
C) -1
D) – 6
Answer:
C) -1

Question 68.
If a and p are the zeros of the polynomial f(x) = x² + px + q, then a polynomial having \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\) as its zeros is ……….
A) qx² + px + 1
B) qx² + px + 10
C) px² + qx + 1
D) none
Answer:
A) qx² + px + 1

Question 69.
If f(x) = ax² + bx + c has no real zeros and a + b + c < 0 then ……….
A) c = 0
B) c < 9
C) c < 0 D) c > 0
Answer:
C) c < 0

Question 70.
If α, β, γ are the zeroes of the polynomial f(x) = ax³ + bx² + cx + d then \(\frac{1}{\alpha}\) + \(\frac{1}{\beta}\) + \(\frac{1}{\gamma}\) = ………..
A) \(\frac{1}{d}\)
B) \(\frac{1}{c}\)
C) \(\frac{c}{d}\)
D) –\(\frac{c}{d}\)
Answer:
D) –\(\frac{c}{d}\)

Question 71.
If the product of zeros of the polynomial f(x) = ax³ – 6x² + 11x – 6 is 4 then a = ……..
A) \(\frac{2}{3}\)
B) \(\frac{3}{2}\)
C) -1
D) 9
Answer:
B) \(\frac{3}{2}\)

Question 72.
If α, β are the zeros of the polynomial f(x) = x² + x + k is reciprocal of the other then k = ……..
A) 5
B) -5
C) 1
D) none
Answer:
D) none

Question 73.
If one root of the polynomial f(x) = 5x² + 13x + k is reciprocal of the other then k = ………..
A) 5
B) – 5
C) 1
D) none
Answer:
A) 5

Question 74.
If α, β are the zeros of polynomial f(x) = x² – p (x + 1) – C then (α + 1) (β + 1) = ……….
A) a
B) 1 + c
C) 1 – c
D) c
Answer:
C) 1 – c

Question 75.
If the sum of the zeros of the polynomial f(x) = 2x³ – 3kx² + 4x – 5 is 6 then k =
A) – 1
B) 9
C) 0
D) 4
Answer:
D) 4

Question 76.
If α, β, γ are the zeros of the polynomial f(x) = ax³ + bx² + cx + d then α² + β² + γ² = ………
A) \(\frac{\mathrm{b}^2+4 \mathrm{ac}}{2}\)
B) \(\frac{b^2-2 a c}{a^2}\)
C) \(\frac{b+2 a c}{a^2}\)
D) none
Answer:
B) \(\frac{b^2-2 a c}{a^2}\)

Question 77.
If the polynomial f(x) = ax³ – bx – a is divisible by the polynomial g(x) = x² + bx + c then ab = ………
A) 1
B) 7
C) -1
D) 0
Answer:
A) 1

Question 78.
The product of the zeros of x³ + 4x² + x – 6 is ……….
A) 8
B) 7
C) 6
D) – 6
Answer:
C) 6

Question 79.
A quadratic polynomial, the sum of whose zeros is 0 and one zero is 3 is
A) x² + 3
B) x – 3
C) x² – 9
D) x² – 3
Answer:
C) x² – 9

Question 80.
If \(\sqrt{5}\) and –\(\sqrt{5}\) are two zeros of the polynomial x³ + 3x² – 5x – 15 then its third zero is ………
A) 7
B) 3
C) -3
D) none
Answer:
C) -3

Question 81.
If α, β, γ are the zeros of the polynomial f(x) = x³ – px² + qx – r then \(\frac{1}{\alpha \beta}+\frac{1}{\beta \gamma}+\frac{1}{\gamma \alpha}\) = …………
A) \(\frac{r}{p}\)
B) \(\frac{p}{r}\)
C) -r
D) none
Answer:
B) \(\frac{p}{r}\)

Question 82.
If x + 2 is a factor of x² + ax + 2b and a + b = 4 then a = ………
A) 3
B) 2
C) -1
D) 4
Answer:
A) 3

Question 83.
In the above problem b = ………
A) 9
B) 0
C) -1
D) 1
Answer:
D) 1

Question 84.
If one zero of the polynomial f(x) = (k² + 4)x² + 13x + 4k is reciprocal of the other then k =
A) -2
B) 2
C) 9
D) 1
Answer:
B) 2

Question 85.
If two zeros of x³ + x² – 5x – 5 are \(\sqrt{5}\) and –\(\sqrt{5}\) then its third zero is …………
A) -3
B) 2
C) -1
D) none
Answer:
C) -1

Question 86.
If zeros of the polynomial f(x) = x³ – 3px² + qx – r are in AP then 2p³ = …………..
A) pq – r
B) p – r
C) pq + 1
D) p + q – r
Answer:
A) pq – r

Question 87.
If α, β are the zeros of the polynomial f(x) = ax² + bx + c then \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}\) = ……….
A) b² – 2ac
B) \(\frac{b+4 a c}{c}\)
C) \(\frac{b+4 a c}{c^2}\)
D) \(\frac{b^2-2 a c}{c^2}\)
Answer:
D) \(\frac{b^2-2 a c}{c^2}\)

Question 88.
What should be subtracted from the polynomial x² – 16x + 30 so that 15 is the zero of the resulting polynomial ?
A) 15
B) -1
C) -15
D) none
Answer:
A) 15

Question 89.
The number of zeros of the polynomial in the graph is …………

A) 2
B) -1
C) 4
D) 1
Answer:
D) 1

Question 90.
The number of zeros of the polynomial in the graph is …….

A) 1
B) -2
C) 0
D) 4
Answer:
C) 0

Question 91.
The below graph represents

A) polynomial
B) not a polynomial
C) two zeros
D) none
Answer:
B) not a polynomial

Question 92.
ax + b represents ………. polynomial.
A) quadratic
B) cubic
C) linear
D) none
Answer:
C) linear

Question 93.
ax² + bx + c is a …… polynomial.
A) quadratic
B) linear
C) cubic
D) fourth
Answer:
A) quadratic

Question 94.
Which of the following is a cubic polyno-mial in general form ?
A) bx² + c³x + x + 1
B) ax³ + bx² + cx + d
C) x² + 2³
D) none
Answer:
B) ax³ + bx² + cx + d

Question 95.
The degree of the polynomial ax⁴ + bx³ + cx² + dx + e is ……..
A) 5
B) 4
C) 6
D) 0
Answer:
B) 4

Question 96.
a₀xⁿ + a₁x^n-1 + a₂x^n-2 + ………. a_nxⁿ is polyno-mial of degree ……….
A) 1
B) n – 2
C) n
D) n²
Answer:
C) n

Question 97.
If a < 0 then the shape of ax² + bx + c = 0 is ……..

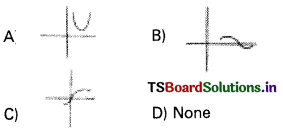
Answer:
D) None

Question 98.
If α, β, γ are roots of a cubic polynomial α + β + γ = ………
A) \(\frac{c}{a}\)
B) \(\frac{b}{a}\)
C) \(\frac{-b}{a}\)
D) none
Answer:
C) \(\frac{-b}{a}\)

Question 99.
If α, β, γ are roots of a cubic polynomial then αβ + βγ + γα = ……
A) \(\frac{-c}{a}\)
B) \(\frac{c}{a}\)
C) \(\frac{-d}{a}\)
D) none
Answer:
B) \(\frac{c}{a}\)

Question 100.
If α, β, γ are roots of a cubic polynomial then αβγ = ……
A) \(\frac{c}{a}\)
B) \(\frac{d}{a}\)
C) \(\frac{-d}{a}\)
D) none
Answer:
C) \(\frac{-d}{a}\)

Question 101.
f(x) = 3x – 2 then zero of f(x) is ………
Answer:
A) \(\frac{1}{2}\)
B) \(\frac{1}{3}\)
C) \(\frac{2}{-3}\)
D) \(\frac{2}{3}\)
Answer:
D) \(\frac{2}{3}\)

Question 102.
p(t) = t³ – 1, p(-2) = ………..
A) -9
B) -4
C) 1
D) 0
Answer:
A) -9

Question 103.
p(x) = x² + 5x + 6 then zeros of p(x) = ……….
A) -2, -3
B) 3, -2
C) 4, 1
D) 1, 8
Answer:
A) -2, -3

Question 104.
p(x) = 4x² + 3x – 1 then p(\(\frac{1}{4}\)) = ……..
A) 1
B) 0
C) -1
D) 12
Answer:
B) 0

Question 105.
x² + 7x + 10 = ……..
A) (x + 3)²
B) (x + 2)²
C) (x – 2) (x – 3)
D) (x + 2) (x + 5)
Answer:
D) (x + 2) (x + 5)

Question 106.
p(x) = x³ + 4x² + 5x – 2 then p(1) = ………
A) 8
B) 7
C) 3
D) none
Answer:
A) 8

Question 107.
p(x) = 3x³ – 2x² + 6x – 5 then p(2) = ……..
A) 19
B) 10
C) 12
D) 23
Answer:
D) 23

Question 108.
If m and n are zeros of the polynomial 3x² + 11x – 4 then the value of \(\frac{m}{n}\) + \(\frac{n}{m}\) = ………..
A) \(\frac{4}{11}\)
B) \(\frac{4}{7}\)
C) \(\frac{11}{4}\)
D) none
Answer:
C) \(\frac{11}{4}\)

Question 109.
Sum of the zeros of x² + 7x + 10 is ……..
A) 7
B) -3
C) 4
D) none
Answer:
D) none

Question 110.
If p and q are the zeros of the polynomial t² – 4t + 3 then \(\frac{1}{p}\) + \(\frac{1}{q}\) – 2pq + \(\frac{14}{3}\) = ……..
A) 0
B) -1
C) 2
D) 3
Answer:
A) 0

Question 111.
A polynomial of degree 3 is called …….. polynomial.
A) zero
B) order
C) qudratic
D) cubic
Answer:
D) cubic

Question 112.
The quotient when x⁴ + x³ + x² – 2x – 3 is divided by x² – 2 is ……..
A) x² + x + 3
B) x – 2
C) x² + 3x + 1
D) none
Answer:
A) x² + x + 3

Question 113.
In the above problem remainder is ……..
A) 1
B) 4
C) 3
D) -3
Answer:
C) 3

Question 114.
One zero of the polynomial 2x² + 3x + k is \(\frac{1}{2}\) then k = ………
A) 4
B) 1
C) 2
D) – 2
Answer:
D) – 2

Question 115.
In the above problem other zero is …….
A) -2
B) 2
C) 3
D) 4
Answer:
A) -2

Question 116.
Sum of the zeros of 6x² = 1 is ……
A) 3
B) 2
C) 0
D) -1
Answer:
C) 0

Question 117.
What must be subtracted or added to p(x) = 8x⁴ + 14x³ – 2x² + 8x – 12 so that 4x² + 3x – 2 is a factor of p(x) ?
A) 5x – 3
B) 15x – 1
C) 5x – 2
D) 15x – 14
Answer:
D) 15x – 14

Question 118.
The quadratic polynomial whose zeros are 4 + \(\sqrt{5}\) and 4 – \(\sqrt{5}\) is ……..
A) x² – 8x + 11
B) x² – 11x + 1
C) x² + 8x + 3
D) none
Answer:
A) x² – 8x + 11

Question 119.
If one of the zeros of the quadratic polyno-mial f(x) = 14x² – 42k²x – 9 is negative of the other then k = ……….
A) 3
B) -1
C) 0
D) none
Answer:
C) 0

Question 120.
If one zero of a polynomial 3x² – 8x + 2k + 1 = 0 is seven times the other then k = ……..
A) \(\frac{2}{3}\)
B) \(\frac{1}{3}\)
C) 1
D) none
Answer:
A) \(\frac{2}{3}\)

Question 121.
If 2x + 3 is a factor of 2x³ – x – b + 9x² then the value of b is
A) 3
B) 7
C) 10
D) 15
Answer:
D) 15

Question 122.
Divide (x³ – 6x² + 11x – 12) by (x² – x + 2) then quotient is …………
A) x + 5
B) x – 5
C) x + 1
D) none
Answer:
A) x + 5

Question 123.
In the above problem remainder is ……….
A) 2x – 1
B) x + 1
C) 4x – 2
D) none
Answer:
C) 4x – 2

Question 124.
Product of zeros of 3x² = 1 is ……….
A) -1
B) -2
C) 3
D) \(-\frac{1}{3}\)
Answer:
D) \(-\frac{1}{3}\)

Question 125.
Degree of 5x⁷ – 6x⁵ + 7x + 1 is …….
A) 4
B) 1
C) 7
D) 3
Answer:
C) 7

Question 126.
(3x – 4) (x + 1) = …….
A) x² – 3x + 1
B) x² – x + 4
C) x² – 3x + 7
D) 3x² – x – 4
Answer:
D) 3x² – x – 4

Question 127.
(x² – 3x – 28) + (x + 4) = ……….
A) x – 7
B) x + 7
C) x + 3
D) x – 1
Answer:
A) x – 7

Question 128.
In the above problem f(\(\frac{1}{2}\)) = ……..
A) 1
B) 7
C) x + 3
D) 0
Answer:
D) 0

Question 129.
(x + \(\sqrt{5}\)) (x – 3\(\sqrt{5}\)) = ………
A) x² – 2\(\sqrt{5}\) x + 15
B) x² – 2\(\sqrt{5}\)x – 15
C) x² – \(\sqrt{5}\)x + 15
D) none
Answer:
B) x² – 2\(\sqrt{5}\)x – 15

Question 130.
The remainder when 3x³ + x² + 2x + 5 is divided by x² + 2x + 1 is ……….
A) 9x + 10
B) x + 10
C) x – 1
D) 9x – 1
Answer:
A) 9x + 10

Question 131.
α = a – b, β = a + b then the quadratic polynomial is ……….
A) x³ – a²x + b²
B) x² – a³x + a²
C) x² – ax + a² + b²
D) x² – 2ax + a² – b²
Answer:
D) x² – 2ax + a² – b²

Question 132.
If the product of zeros of 9x² + 3x + p is 7 then p = ………
A) 14
B) -63
C) 63
D) 70
Answer:
C) 63

Question 133.
Degree of (x – 1) (x – 3) is ……..
A) 3
B) 2
C) 1
D) 7
Answer:
B) 2

Question 134.
The value of x¹⁵ – 1 at x = 0 is ……..
A) 3
B) 9
C) 7
D) -1
Answer:
D) -1

Question 135.
Zeros of the polynomial x² – 4x + 3 are 1 and p then p = ……..
A) 7
B) 3
C) 1
D) none
Answer:
B) 3

Question 136.
Degree of a linear polynomial is ……..
A) 2
B) 3
C) 7
D) 1
Answer:
D) 1

Question 137.
(a + 1)² = ………..
A) a² + 1
B) a² + 2 + a
C) a² + 2a + 1
D) none
Answer:
C) a² + 2a + 1

Question 138.
(x³ – 8) + x⁴ + 2x³ – 8x – 16
A) x
B) x – 1
C) x + 2
D) none
Answer:
C) x + 2

Question 139.
p(x) = \(\frac{x+1}{1-x}\) then P(0) = ………
A) 1
B) -1
C) 2
D) 3
Answer:
A) 1

Question 140.
(x – \(\sqrt{3}\)) (x + \(\sqrt{3}\)) = ……
A) x + 3
B) x² – 3
C) x + 7
D) none
Answer:
B) x² – 3

Question 141.
If one zero of the polynomial is \(\sqrt{2}\) – 1 then other zero may be ……
A) 1 + \(\sqrt{3}\)
B) \(\sqrt{2}\) + 1
C) \(\sqrt{2}\) – 2
D) all
Answer:
B) \(\sqrt{2}\) + 1

Question 142.
Binomial contains almost ….. terms.
A) 5
B) 4
C) 1
D) 2
Answer:
D) 2

Question 143.
p(x) = \(\frac{12}{x-3}\), p(3) = ……..
A) 1
B) 12
C) 0
D) not defined
Answer:
D) not defined

Question 144.
p(-3) = 0 then p(x) = ……
A) x – 7
B) x + 1
C) x – 4
D) x + 3
Answer:
D) x + 3

Question 145.
Number of constant terms in the polynomial x² + 7x – 7 is ……
A) 2
B) 1
C) 3
D) 2
Answer:
B) 1

Question 146.
In the product (x + 4) (x + 2) the constant term is ……..
A) 7
B) -3
C) 6
D) 8
Answer:
D) 8

Question 147.
p(\(\frac{\mathbf{a}}{\mathbf{b}}\)) = 0 then p(x) = ……….
A) ax – b
B) bx – a
C) ax
D) bx
Answer:
B) bx – a

Question 148.
a(a + 1) (a + 2) (a + 3) + a(a + 3) =
A) (a + 1) (a + 2)
B) (a + 1)²
C) (a + 2)²
D) none
Answer:
A) (a + 1) (a + 2)

Question 149.
(x² – 8x + 12) + (x – 6) = ………
A) x + 3
B) x + 1
C) x + 2
D) x – 2
Answer:
D) x – 2

Question 150.
x(3x² – 108) + 3x(x – 6) = …….
A) x + 3
B) x – 6
C) x + 6
D) x – 7
Answer:
C) x + 6

Question 151.
(p + 4) (p – 4) (p² + 16) = ……..
A) p⁴ – 16
B) p⁴ + 256
C) p³ – 100
D) p⁴ – 256
Answer:
D) p⁴ – 256

Question 152.
36(x + 4) (x² + 7x + 10) + 9 (x + 4) = …….
A) 4(x + 5) (x + 2)
B) (x + 5) (x – 7)
C) (x + 5) (3x – 1)
D) none
Answer:
A) 4(x + 5) (x + 2)

Question 153.
The degree of the polynomial 9xy³ + 10y⁴ + \(\frac{5}{4}\) x⁴ + \(\frac{7}{3}\) x³y² is (T.S.Mar.15)
A) 3
B) 2
C) 4
D) 5
Answer:
D) 5

Question 154.
The zero of the linear polynomial 2x + 3 is (T.S.Mar.15)
A) 0
B) \(\frac{-3}{2}\)
C) -1 \(\frac{1}{2}\)
D) B and C
Answer:
B) \(\frac{-3}{2}\)

Question 155.
The product of the zeroes of the polynomial 3x³ – 5x² – 10x + 15 is ……. (T.S. Mar.’15)
A) – 5
B) 5
C) \(\frac{5}{3}\)
D) \(\frac{-10}{3}\)
Answer:
D) \(\frac{-10}{3}\)

Question 156.
The quadratic polynomial with zeros 2 and 3 is (T.S. Mar.’15)
A) x² – 5x + 6
B) (x – 2) (x – 3)
C) 2x² – 10x + 12
D) All the above
Answer:
B) (x – 2) (x – 3)

Question 157.
If a fraction becomes 2 when 9 is added to its numerator and 1 when 2 is substracts from its denominator then the fraction is ………… (AP-SA-I-2016 )
A) 5/8
B) 8/5
C) 5/7
D) 7/9
Answer:
C) 5/7

Question 158.
The graph of y = ax + b is a straight line which intersects X-axis at exactly one point namely, ……
A) (0, \(\frac{b}{a}\))
B) (\(\frac{b}{a}\), 0)
C) (0, \(\frac{-b}{a}\))
D) (\(\frac{-b}{a}\), 0)
Answer:
D) (\(\frac{-b}{a}\), 0)

Question 159.
Coefficient of x in a polynomial ax² + bx + c is ‘0’. Then its zeroes are ………
A) equal
B) additive inverses to one another
C) multiplicative inverses to one another
D) none
Answer:
B) additive inverses to one another