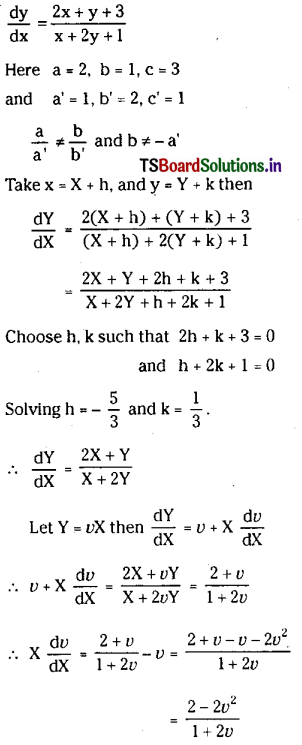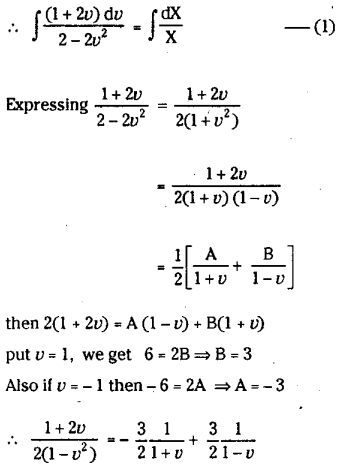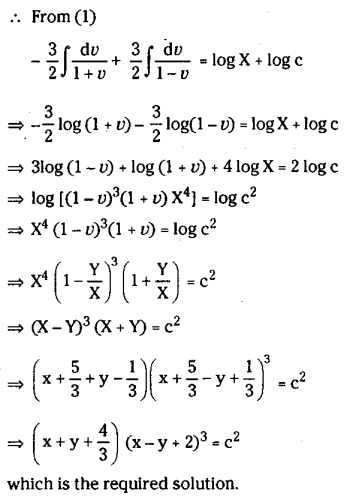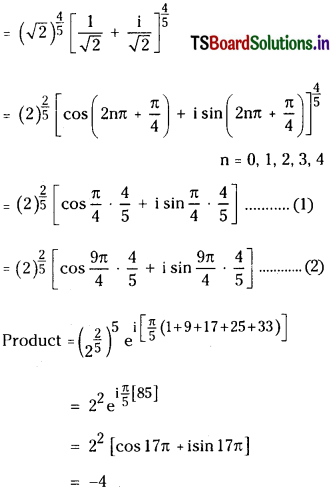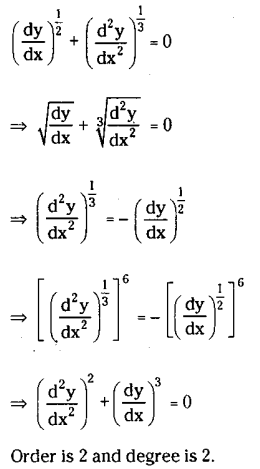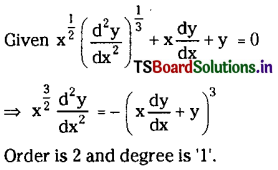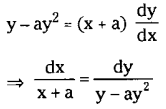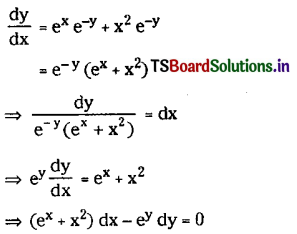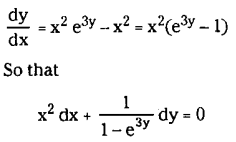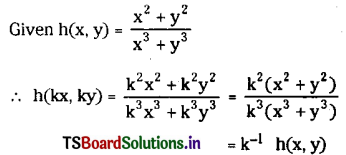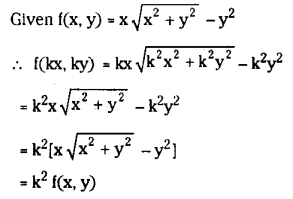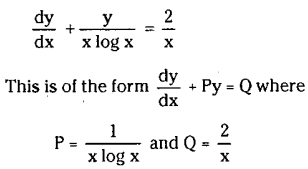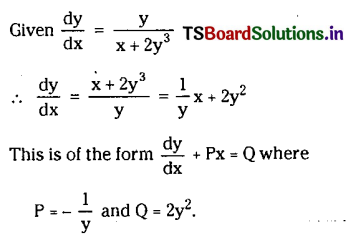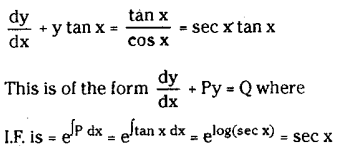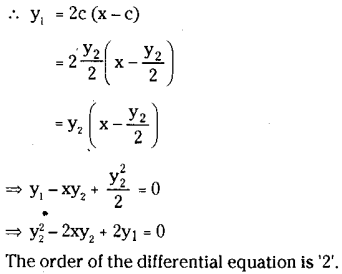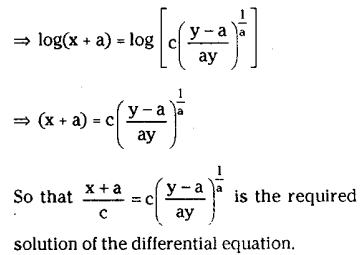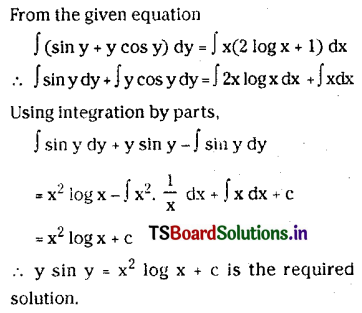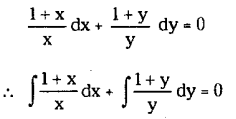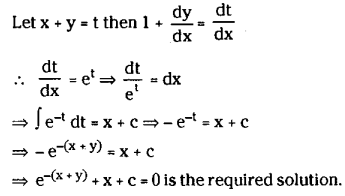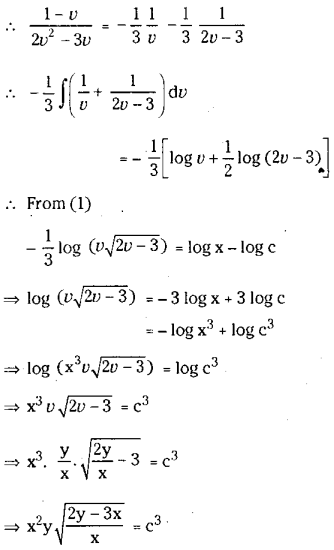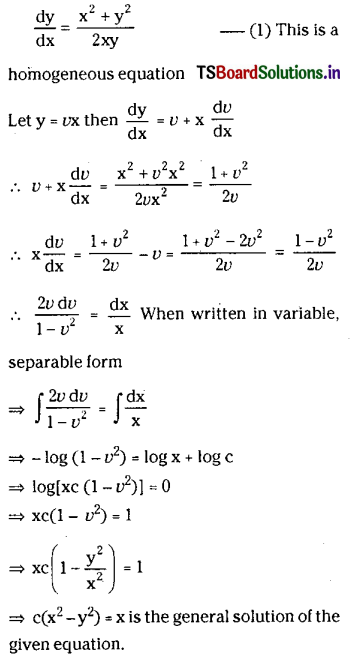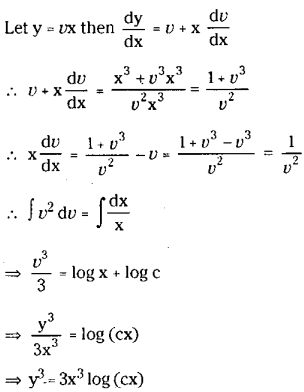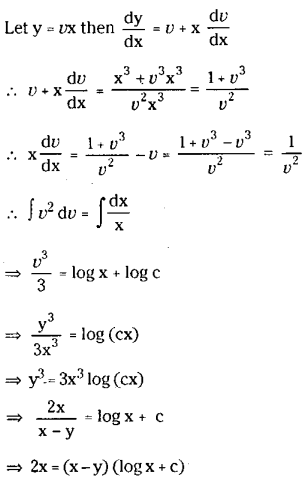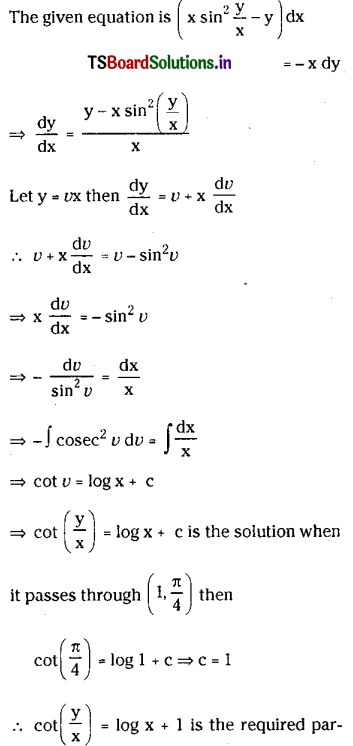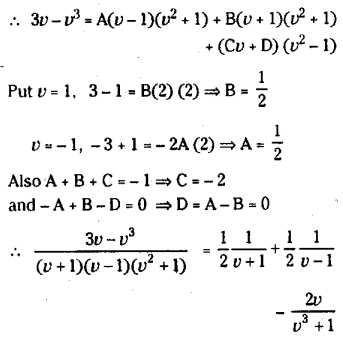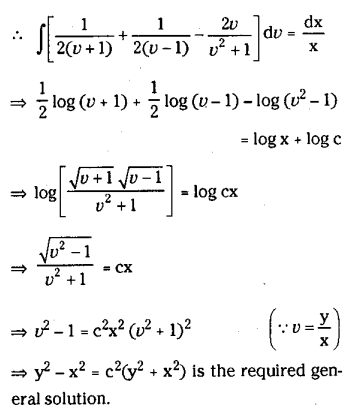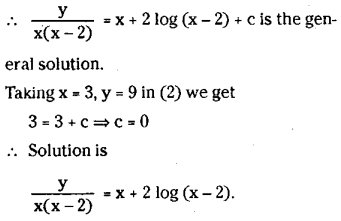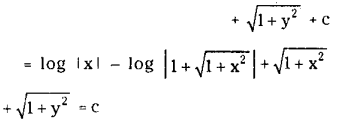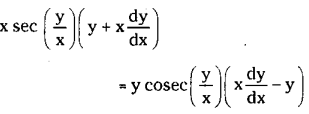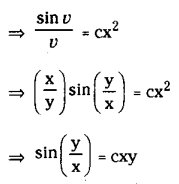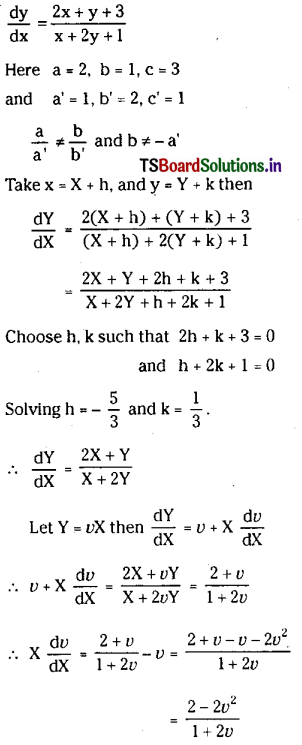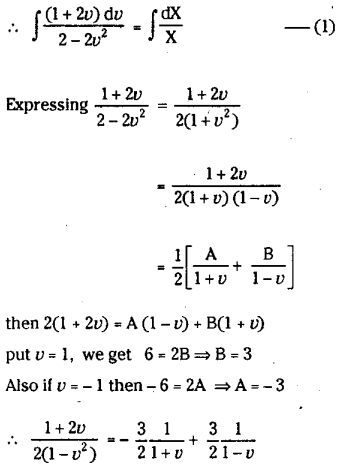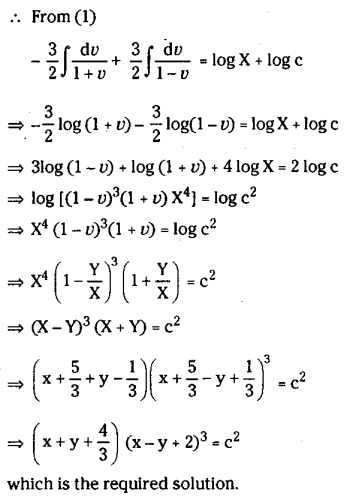Students must practice these TS Inter 2nd Year Maths 2B Important Questions Chapter 8 Differential Equations to help strengthen their preparations for exams.
TS Inter 2nd Year Maths 2B Differential Equations Important Questions
Very Short Answer Type Questions
Question 1.
Find the order and degree of \(\frac{d y}{d x}=\frac{x^{1 / 2}}{y^{1 / 2}\left(1+x^{1 / 2}\right)}\)
Solution:
Order is 1 and Degree is ‘1’
Since there is first order derivative with highest degree is ‘1’.
Question 2.
Find the degree and order of the differential equation \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\)
Solution:
The equation can be written as \(\left(\frac{d^2 y}{d x^2}\right)^3=\left[1+\left(\frac{d y}{d x}\right)^2\right]^5\)
The order is 2 and degree is ‘3’

Question 3.
Find the order and degree of the equation
\(1+\left(\frac{d^2 y}{d x^2}\right)^2=\left[2+\left(\frac{d y}{d x}\right)^2\right]^{3 / 2}\)
Solution:
The equation can be expressible as
\(\left[1+\left(\frac{d^2 y}{d x^2}\right)^2\right]^2=\left[2+\left(\frac{d y}{d x}\right)^2\right]^3\)
Order is 2 and degree is 4.
Question 4.
Find the order and degree of \(\frac{d^2 y}{d x^2}+2 \frac{d y}{d x}+y=\log \left(\frac{d y}{d x}\right)\)
Solution:
Order is 2and degree is not defined since the equation cannot be expressed as a polynomial equation In the derivatives.
Question 5.
Find the order and degree of \(\left[\left(\frac{d y}{d x}\right)^{\frac{1}{2}}+\left(\frac{d^2 y}{d x^2}\right)^{\frac{1}{3}}\right]^{\frac{1}{4}}=0\)
Solution:
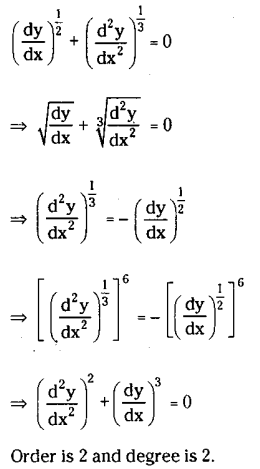
Question 6.
Find the order and degree of = \(\frac{d^2 y}{d x^2}=-p^2 y\)
Solution:
Equation is a polynomial equation in \(\frac{d^2 y}{d x^2}\)
So degree is ‘1′ and order is ‘2’.

Question 7.
Find the order and degree of \(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\)
\(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\)
Solution:
The equation is a polynomial equation in and \(\frac{d y}{d x}\) \(\frac{\mathrm{d}^3 \mathrm{y}}{\mathrm{dx}^3}\)
∴ Order is 3 and degree is 2.
Question 8.
Find the order and degree of \(x^{\frac{1}{2}}\left(\frac{d^2 y}{d x^2}\right)^{\frac{1}{3}}+x \frac{d y}{d x}+y=0\)
Solution:
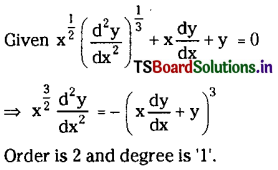
Question 9.
Find the order and degree of \(\left[\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3\right]^{\frac{6}{5}}=6 y\)
Solution:
The given equation can be written as
\(\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3=(6 y)^{5 / 6}\)
order is ‘2’ and degree is ‘1’.
Question 10.
Find the order of the differential equation corresponding to y = Aex + Be3x + Ce5x (A, B, C are parameters) is a solution.
Solution:
Since there are 3 constants in
y = Aex + Be3x + Ce5x we can have a differential equation of third order by eliminating A,B,C.
∴ Order of the differential equation is ‘3’.
Question 11.
Form the differential equation to y = cx – 2c2 where c is a parameter.
Solution:
Given y = cx-2c2 ………….. (1)
we have y1=c ……………….. (2)
∴From(1)
y=xy1 – 2y21 ………………….. (3)
∴ This is a differential equation corresponding to (1).

Question 12.
Form the differential equation corresponding to y = A cos 3x+ B sin 3x where A and B are parameters.
Solution:

Question 13.
Express the following differential equations in the form f(x) dx + g(y) dy = 0
(i) \( \frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
Solution:
\(\frac{d x}{1+x^2}-\frac{d y}{1+y^2}=0\)
(ii) \(y-x \frac{d y}{d x}=a\left(y^2+\frac{d y}{d x}\right)\)
Solution:
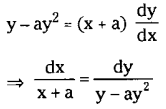
(iii) \(\frac{d y}{d x}=e^{x-y}+x^2 e^{-y}\)
Solution:
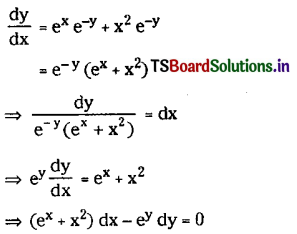
(iv) \(\frac{d y}{d x}+x^2=x^2 e^{3 y}\)
Solution:
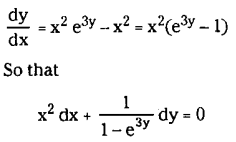
Question 14.
Find the general solution of x + y \(\frac{dy}{dx}\) = 0.
Solution:
The given equation can be written as
x dx + y dy = 0
∴ ∫ xdx+∫ ydy = c
⇒ x2 + y2 = 2c
Question 15.
Find the general solution of \(\frac{d y}{d x}=e^{x+y}\)
Solution:
The given equation can be written as \(\frac{d y}{d x}=e^x \cdot e^y\)
writing in variable separable form ex dx = e-y dy = 0
∴ ex + e-y = c is the required solution.

Question 16.
Find the degree of the following homogeneous functions.
(i) f(x, y) = 4x2y + 2xy2
Solution:
Given f(x, y) = 4x2y+2xy2
we have f(kx, ky) = 4k2x2ky + 2kxk2y2
⇒ 4k3x2y + 2k3xy2
⇒ k3(4x2y + y2)
⇒ k3 f(x, y) ∀ k
and f(x, y), x3 Φ \(\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\) and hence f(x, y) is a homogeneous function of degree ‘3’.
(ii) g(x,y)=xy1/2+yx1/2
Solution:
Given g(x, y) =xy1/2+ yx1/2
g(kx, ky) = kx(ky)1/2 + (ky)(kx)1/2
⇒ k3/2 (xyk1/2 + yx1/2)
⇒ k3/2 g(x, y)
∴ g(x, y) is a homogeneous function of degree ‘3’.
(iii) \(h(x, y)=\frac{x^2+y^2}{x^3+y^3}\)
Solution:
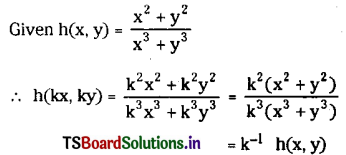
∴ h(x, y) is a homogeneous function of degree – 1.
(iv) Show that f(xy) = I +ex/y is a homogeneous function of x and y.
Solution:

(v) f(x,y) = x \(\sqrt{\mathbf{x}^2+y^2}-y^2\) is a homogeneous function of x and y.
Solution:
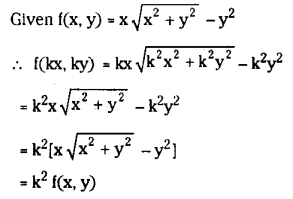
∴f(x, y) is a homogeneous function of degree ‘1’.
(vi) f(x,y) = x – y log y + y log x
Solution:
Givenf(x, y) =x-ylogy+ylogx
∴ f(kx, ky) – kx – ky log (ky) + ky log(kx)
= k[x-y log(ky) + ylog(kx)]
= k[x- y(logk+logy) +y(logk+logx)]
= k[x – y log y + y log x]
= k f(x, y)
∴ f(x, y) is a homogeneous function of degree ‘F.
Question 17.
Express (1+ex/y) dx + ex/y \(\left(1-\frac{x}{y}\right)\) dy = 0 in the form \(\frac{\mathbf{d x}}{\mathbf{d y}}=F\left(\frac{x}{y}\right)\)
Solution:

Question 18.
Express \(\left(x \sqrt{x^2+y^2}-y^2\right)\) dx+xy dx = 0 in the form \(\frac{\mathbf{d y}}{\mathbf{d x}}=F\left(\frac{x}{y}\right)\)
Solution:

Question 19.
Express \(\frac{d y}{d x}=\frac{y}{x+y e^{-\frac{2 x}{y}}}\) in the form \(\frac{d x}{d y}=F\left(\frac{x}{y}\right)\)
Solution:

Question 20.
Transform x logx \(\frac{d y}{d x}\) y into linear form.
Solution:
Dividing both sides by x log x we get
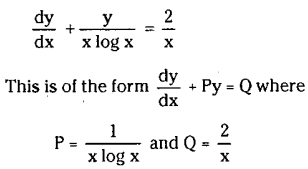

Question 21.
Transform \(\left(x+2 y^3\right) \frac{d y}{d x}=y\) into linear form
Solution:
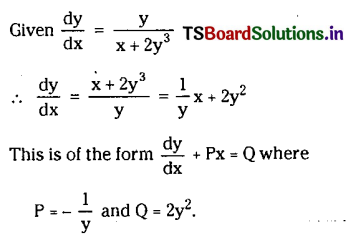
Question 22.
Find I.F. of the following differential equations by converting them into linear form.
(i) cosx\(\frac{d y}{d x}\)+y sinx=tanx
Solution:
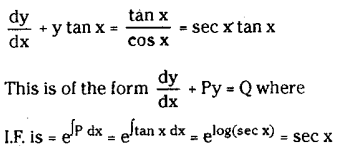
(ii) (2y -10y3) \(\frac{d y}{d x}\) + y = 0
Solution:

Short Answer Type Questions
Question 1.
Find the order of the differential equation corresponding to y = c( x- c)2 where c is an arbitrary constant
Solution:
Given y = c(x – e)2; eliminate ‘c’ and form the differential equation.

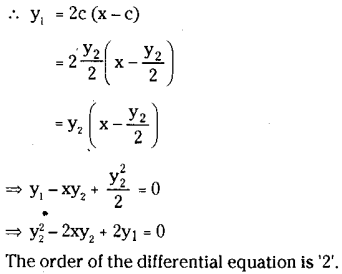
Question 2.
Form the differential equation corresponding to the family of circles of radius ‘r’ given by (x-a)2+(y-b)2=r2 where a and b are parameters.
Solution:


Question 3.
Form the differential equation corresponding to the family of circles passing through the origin and having centres on Y- axis.
Solution:
The equation of family of circles passing through the origin and having centres on Y-axis is
x2+y2-2fy=0 ……………….. (1)
Differentiating w.r.t x, we get

Question 4.
Solve \(y^2-x \frac{d y}{d x}=a\left(y+\frac{d y}{d x}\right)\)
Solution:

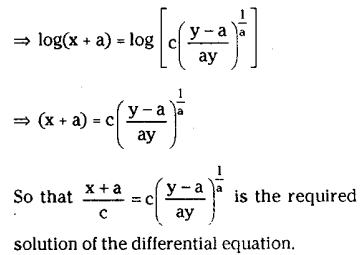
Question 5.
Solve \(\frac{d y}{d x}=\frac{y^2+2 y}{x-1}\)
Solution:
The equation can be written as

Question 6.
Solve \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\)
Solution:
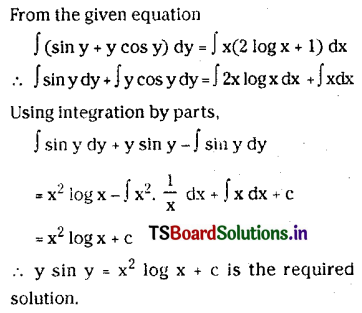

Question 7.
Find the equation of the curve whose slope at any point (x, y) is \(\frac{y}{x^2}\) and which satisfy the condition y = 1 when x =3.
Solution:
We have the slope at any point x, y) on the

Question 8.
Solve y (1+x)dx+x(1+y) dy = 0
Solution:
The given equation can be expressed as
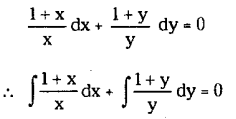
logx+x+logy+y=c
x + y + log (xy) = c which is the required solution.
Question 9.
Solve \(\frac{d y}{d x}\) = sin(x + y) +cos(x + y)
Solution:
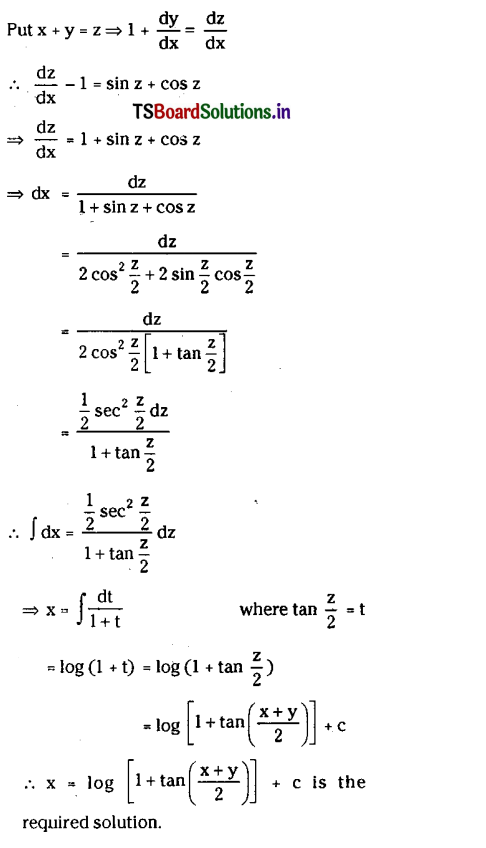
Question 10.
Solve that (x – y)2 \(\frac{d y}{d x}=a^2\)
Solution:

Question 11.
Solve \(\frac{d y}{d x}=\frac{x-2 y+1}{2 x-4 y}\)
Solution:

Question 12.
Solve \(\frac{d y}{d x}=\sqrt{y-x}\)
Solution:


Question 13.
Solve \(\frac{d y}{d x}\) +1 = ex+y
Solution:
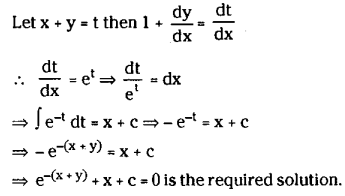
Question 14.
Solve \(\frac{d y}{d x}\) = (3x + y + 4)2
Solution:

Question 15.
Solve \(\frac{d y}{d x}\) – x tan(y-x)= 1
Solution:

Question 16.
Solve \(\frac{d y}{d x}=\frac{y^2-2 x y}{x^2-x y}\)
Solution:
The given equation ¡s a homogeneous equation of degree ‘2’.

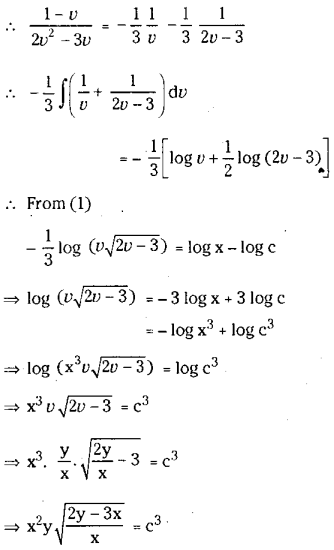
which is athe general solution of the given equation.

Question 17.
Solve(x2+y2)dx=Zxydy
Solution:
The given equation can be written as
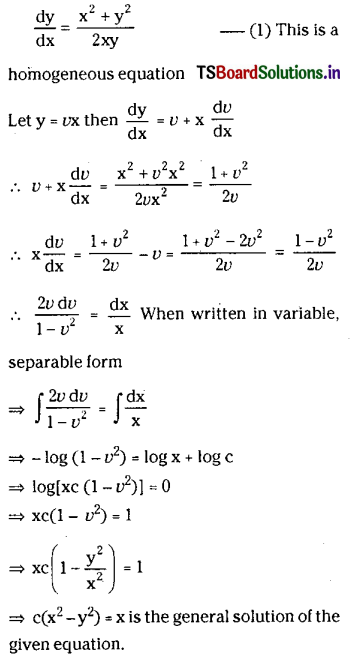
Question 18.
Solve xy2dy – (x3+y)dx=0
Solution:
The given equation can be written as \(\frac{d y}{d x}=\frac{x^3+y^3}{x y^2}\) which is a homogeneous equation.
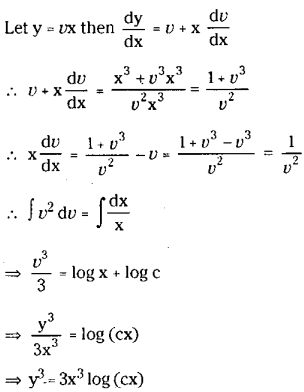
which is the general solution of the given equation.
Question 19.
Solve \(\frac{d y}{d x}=\frac{x^2+y^2}{2 x^2}\)
Solution:
The given equation \(\frac{d y}{d x}=\frac{x^2+y^2}{2 x^2}\) homogeneous equation.
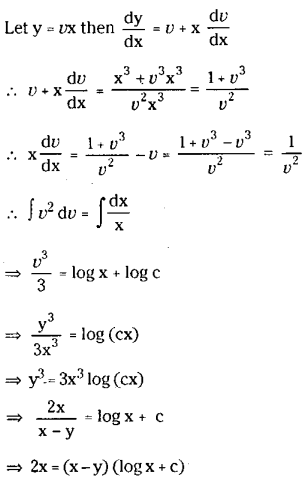
which is the general solution of the given equation.
Question 20.
Give the solution of x sin2 \(\left(\frac{y}{x}\right)\) dx = y dx – x dy which passes through the point \(\left(1, \frac{\pi}{4}\right)\)
Solution:
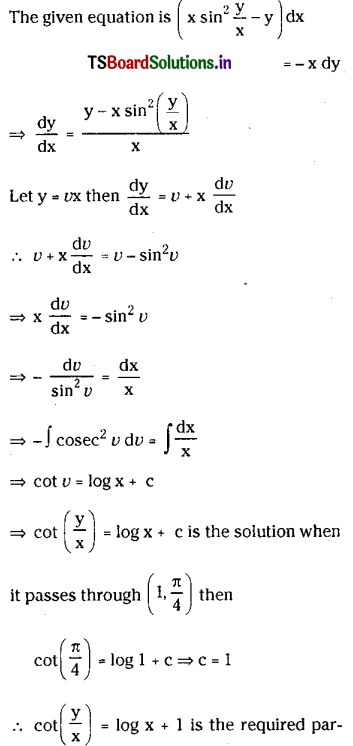
is the required particular solution of the given equation.
Question 21.
Solve(x3-3xy2)dx+(3x2y-y3)dy=0
Solution:
The given equation can be written as

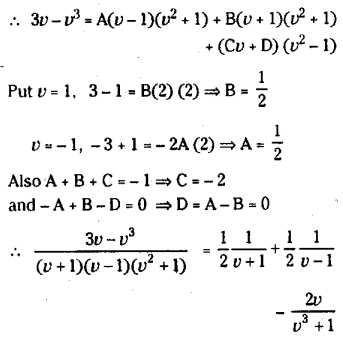
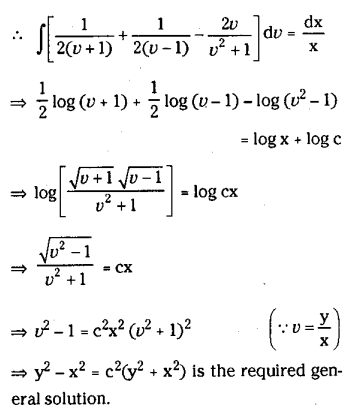

Question 22.
Solve the equation \(\frac{d y}{d x}=\frac{3 x-y+7}{x-7 y-3}\)
Solution:
Here a=3, b =-1,c = 7
a’=1, b’=-7,c’ = -3
and b =- a’. Hence that solution can be obtained by grouping.
∴ From the given equation
3xdx – ydx+7dx = xdy-7ydy – 3dy
= (xdy+ydx) – 7ydy – 7dx – 3xdx – 3dy = 0
= ∫d(xy) -∫7ydy – 7∫dx – 3∫xdx – 3∫dy = 0
= xy – 7\(\frac{y^2}{2}\) – 7x -3 \(\frac{x^2}{2}\) -3y =c
⇒ 2xy – 7y2-14x-3x2– 6y=2c
⇒ 2xy – 7y2 – 14x-3x2 – 6y= c’ where C – 2c
Is the required solution.
Question 23.
Solve (1+x2) \(\frac{\mathrm{dy}}{\mathbf{d x}}\) +2xy = 4x2
Solution:

Question 24.
Solve sin 2 x \(\frac{d y}{d x}\) +y = cot x
Solution:

Question 25.
Find the solution of the equation x(x – 2) \(\frac{d y}{d x}\) (x – 1)y=x3(x-2) which sotisfies the condition that y=9 where x=3.
Solution:
The equation can be written as

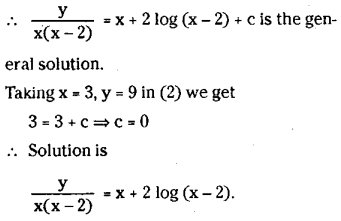
Question 26.
Solve (1+y2)dx = (tan-1 y-x)dy
Solution:
The given equation can be written as

Long Answer Type Questions
Question 1.
Solve \(\sqrt{1+x^2} \sqrt{1+y^2}\)dx + xy dy =0.
Solution:
The given equation can he written as

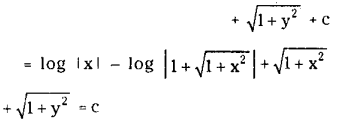
Is the solution of the given differential equation.

Question 2.
Solve x sec \(\left(\frac{\mathbf{y}}{\mathbf{x}}\right)\) (y dx+xdy)=y cosec \(\left(\frac{\mathbf{y}}{\mathbf{x}}\right)\)
Solution:
The given equation can be written as
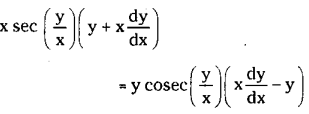


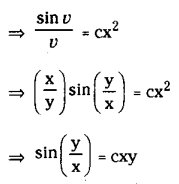
which is the general solution of the given equation.

Question 3.
Solve (2x+y+3)dx=(2y+x+1)dy
Solution: