TS Inter 2nd Year

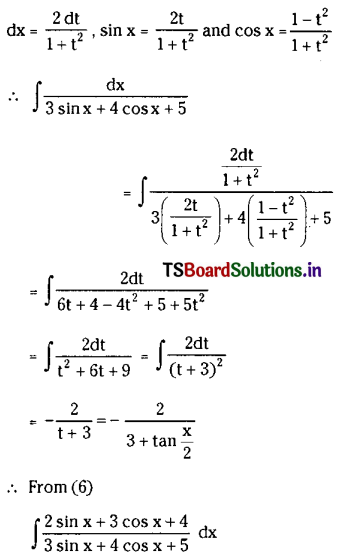
Telangana TSBIE TS Inter 2nd Year Economics Study Material 5th Lesson వ్యవసాయ రంగం Textbook Questions and Answers.

TS Inter 2nd Year Economics Study Material 5th Lesson వ్యవసాయ రంగం

వ్యాసరూప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
భారత ఆర్థిక వ్యవస్థలో వ్యవసాయరంగ ప్రాధాన్యతను వివరించండి.
జవాబు.
1. స్థూలదేశీయ ఉత్పత్తి లేదా జోడించిన స్థూల విలువలో వ్యవసాయ రంగం వాటా :
మొదటి ప్రపంచ యుద్ధ కాలం నాటికి జాతీయాదాయంలో 2/3వ వంతు వ్యవసాయ రంగం నుంచే వచ్చింది. భారతదేశంలో ప్రణాళికలు ప్రారంభమైన తరవాత, ద్వితీయ, తృతీయ రంగాలు అభివృద్ధి చెందడంవల్ల వ్యవసాయ రంగం వాటా తగ్గింది. 1950-51లో స్థూల దేశీయ ఉత్పత్తిలో వ్యవసాయ రంగం, దాని అనుబంధ రంగాల వాటా 56.5 శాతంగా ఉంటే 2000-01 నాటికి ఇది 24.7 శాతానికి తగ్గింది. అలాగే 2012-13 నాటికి బాగా తగ్గి 13.9% కి చేరింది.

వ్యవసాయం మరియు అనుబంధ రంగాలు జోడించిన స్థూల విలువ 2014-15 సం||లో రూ.20.94 లక్షల కోట్లు ఉండగా 2019-20 సం॥ నాటికి రూ.30.47 లక్షల కోట్లకు పెరిగింది. జోడించిన స్థూల విలువలో వ్యవసాయం మరియు అనుబంధ రంగాల వాటా 2014-15 సం॥లో 18.2 శాతం ఉండగా 2019-20 సం॥ నాటికి 16.5 శాతంకు తగ్గినది. జోడించిన స్థూల విలువలో వ్యవసాయ ఉత్పత్తుల వాటా 2014-15 సం॥లో 11.2 శాతం ఉండగా 2017-18 సం॥ నాటికి 10 శాతంకు తగ్గినది.

అదే కాలంలో పశుసంపద వాటా 4.4 శాతం నుండి 4.9 శాతానికి పెరగగా అటవీ ఉత్పత్తుల వాటా 1.5 శాతం నుండి 1.2 శాతంకు తగ్గింది. అయితే మత్స్య సంపద వాటా 1.0 శాతం నుండి 1.1 శాతంకు స్వల్పంగా పెరిగినది. అమెరికా, బ్రిటన్ లాంటి అభివృద్ధి చెందిన దేశాలలో వ్యవసాయ రంగం నుంచి స్థూల దేశీయ ఉత్పత్తికి 2% మాత్రమే వస్తుంది.

2. ఉద్యోగితను కల్పిస్తుంది :
1951లో 98 మిలియన్లు మంది ప్రజలు వ్యవసాయ రంగంలో పనిచేస్తే 2001 నాటికి ఈ సంఖ్య 235 మిలియన్లకు పెరిగింది. శాతం రూపంలో చెప్తే 1951లో 70 శాతం మంది వ్యవసాయ రంగంలో పనిచేస్తే 2001 నాటికి 59 శాతానికి తగ్గింది. 2008-2011 మధ్య కాలంలో వ్యవసాయం 46 శాతం పురుష శ్రామికులకు, 60 శాతం శ్రామికులకు ఉద్యోగితను కల్పించింది.

మొత్తం మీద భారతదేశంలో వ్యవసాయ రంగంపై ఆధారపడిన ప్రజలు 2011 సం॥లో 49 శాతం ఉండగా 2019 సం॥లో 43 శాతం ఉన్నారు. అభివృద్ధి చెందిన దేశాలలో వ్యవసాయ రంగంలో పనిచేస్తున్న శ్రామికులు శాతం చాలా తక్కువ. బ్రిటన్, అమెరికాలో 2 శాతం నుంచి 3 శాతం, ఫ్రాన్స్లో 7 శాతం, ఆస్ట్రేలియాలో 6 శాతం శ్రామికులు వ్యవసాయ రంగం పై ఆధారపడి జీవిస్తున్నారు.

3. పరిశ్రమలకు ముడిపదార్థాలను అందిస్తుంది :
వివిధ ముందంజ పరిశ్రమలకు వ్యవసాయ రంగం ముడిపదార్థాలను అందిస్తుంది. పంచదార, జనపనార, వస్త్ర పరిశ్రమ, వనస్పతి, పిండి మరలు, పండ్ల తోటలు, ఆహార తయారీ పరిశ్రమలు వ్యవసాయ రంగంపై ప్రత్యక్షంగా ఆధారపడ్డాయి. పరోక్షంగా చాలా పరిశ్రమలు వ్యవసాయ రంగంపై ఆధారపడుతున్నాయి. చాలా చిన్న తరహా పరిశ్రమలు, కుటీర పరిశ్రమలు వాటికి కావలసిన ముడి సరుకుల కోసం వ్యవసాయ రంగంపైన ఆధారపడుతున్నాయి.

4. పారిశ్రామిక వస్తువులకు గిరాకీ :
అభివృద్ధి చెందుతున్న ఆర్థిక వ్యవస్థలలో అధిక జనాభా గ్రామీణ ప్రాంతాలలో నివసిస్తున్నందువల్ల పెరిగే గ్రామీణ కొనుగోలు శక్తి పారిశ్రామిక అభివృద్ధికి ప్రేరేపకంగా ఉంటుంది. వ్యవసాయ ఉత్పత్తిని, ఉత్పాదకతను విస్తరించడానికి చర్యలను తీసుకుంటే గ్రామీణ రంగంలో ఆదాయం పెరుగుతుంది.

కాబట్టి పారిశ్రామిక ఉత్పత్తులకు డిమాండు పెరిగి పారిశ్రామిక అభివృద్ధి ప్రక్రియకు మద్దతు లభిస్తుంది. గ్రామీణుల సంపదను పరిశ్రమల సంపదగా పరిగణిస్తారు. అల్ప ధరలు, మధ్య రకం ధరలు ఉన్న వినియోగ వస్తువులకు గ్రామాలు పెద్ద మార్కెట్గా ఉన్నాయి.

5. మూలధన సమీకరణం :
మూలధన సమీకరణ రేటు పెరిగినంత వరకు ఉన్నత స్థాయి ఆర్థికాభివృద్ధిని సాధించే వీలు కాదు. అభివృద్ధి చెందుతున్న దేశాలలో వ్యవసాయం అతి పెద్ద పరిశ్రమ కాబట్టి మూలధన సమీకరణ రేటును పెంచడంలో వ్యవసాయ రంగం ప్రముఖ పాత్రను పోషిస్తుంది. ఇది జరిగినట్లయితే, ఆర్థికాభివృద్ధి ప్రక్రియ పూర్తిగా నష్టపోతుంది. గణనీయంగా వ్యవసాయ ఉత్పాదకత పెరగడంపై వ్యవసాయ రంగంలో మిగులు సృష్టి ఆధారపడుతుంది.

6. ఆహార భద్రతను కల్పించడం, పేదరికాన్ని తగ్గించడం :
శ్రామికులు మిగులు దేశాలలో జనాభా తాకిడి అధికంగా ఉండటమేగాక, ఇది వేగంగా పెరగడం వల్ల ఆహారానికి డిమాండ్ వేగవంతమైన రేటులో పెరుగుతుంది. ఈ దేశాలలో ఉన్న అల్పస్థాయి ఆహార వినియోగం, తలసరి ఆదాయంలోని అల్ప పెరుగుదల వల్ల ఆహారానికి డిమాండ్ వేగంగా పెరుగుతుంది. అందుకే ఆహార ధాన్యాల మిగులు పెరుగుదల తప్పనిసరి అవుతుంది.

7. అంతర్జాతీయ వర్తకంలో వ్యవసాయ రంగం ప్రాధాన్యత :
భారతదేశం ఎగుమతుల్లో టీ, చక్కెర, నూనెగింజలు, పొగాకు, సుగంధ ద్రవ్యాలు మొదలైన వ్యవసాయ ఉత్పత్తులు ప్రధానమైనవి. మొత్తం ఎగుమతుల్లో వ్యవసాయ వస్తువుల ఎగుమతుల అనుపాతం 50%, వ్యవసాయ అంశాలతో కూడుకొన్న ఎగుమతుల అనుపాతం మరొక 20% ఉన్నాయి.

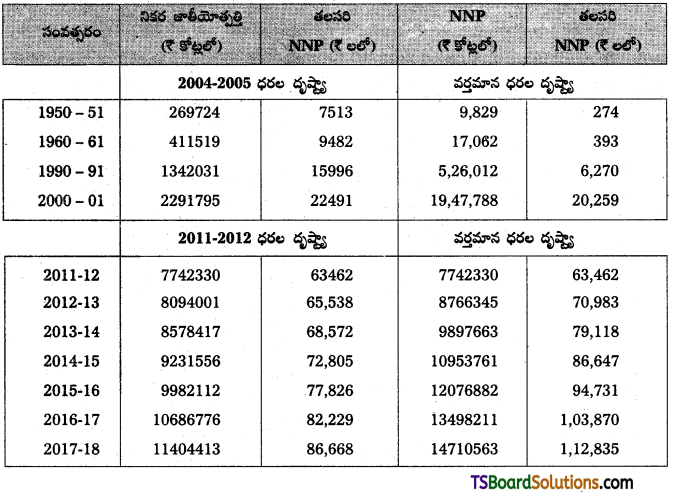
ఈ విధంగా 1950- 51లో మొత్తం ఎగుమతుల్లో 70 శాతం వ్యవసాయ ఎగుమతులుండేవి. 1960-61లో మొత్తం ఎగుమతుల్లో వ్యవసాయ ఎగుమతుల వాటా 44.27% ఉంటే, 2010-11లో ఇది 9.9 శాతానికి పడిపోయినట్లు పట్టిక తెలుపుతుంది. అయితే 2012-13లో ఈ వాటి 13.5 శాతానికి పెరిగింది. కొన్ని సంవత్సరాలలో ఏర్పడిన తీవ్ర కరువు పరిస్థితుల వల్ల ఆహార ధాన్యాలను, పాల ఉత్పత్తులను భారతదేశం దిగుమతి చేసుకుంది.

పట్టిక : మొత్తం ఎగుమతులలో ఎగుమతుల శాతం (రూ.లు కోట్లలో)

ఆధారం : GOI (2009), Economic Survey, 2008-09; Economic Survery, 2011-12

8) ఆర్థిక ప్రణాళికలలో, ఆర్థికాభివృద్ధిలో వ్యవసాయ రంగం పాత్ర :
భారత రవాణా వ్యవస్థకు, బాంకింగ్కు వ్యవసాయ రంగం ముఖ్యంగా మద్దతును ఇస్తుంది. అంతర్గత వర్తకం ముఖ్యంగా వ్యవసాయ ఉత్పత్తుల వల్లనే ఉంది. పంటలు బాగా పండాయా లేదా దెబ్బ తిన్నాయా అనే దాని ప్రభావం ఆర్థిక ప్రణాళికల పైనా, ఆర్థికాభివృద్ధిపైనా ఉంటుంది.

జీవ వైవిధ్య సంతులితను కొనసాగించడానికి, వ్యవసాయ, ఇతర అనుబంధ రంగాలలో సుస్థిర, సంతులిత అభివృద్ధి. ఆవశ్యకత ఉంది. “దేశంలో త్వరిత ఆర్థికాభివృద్ధికి వ్యవసాయ అభివృద్ధి మూలం” అని పదవ పంచవర్ష ప్రణాళిక స్పష్టం చేసింది.

ప్రశ్న 2.
వ్యవసాయ రంగంలో తక్కువ ఉత్పాదకతకు గల కారణాలను విశదీకరించండి.
జవాబు.
మనదేశంలో వ్యవసాయరంగంలో అల్ప ఉత్పాదకతకు అనేక కారణాలున్నాయి. అవి :

1. సాధారణ కారణాలు
2. సంస్థాగత కారణాలు
3. సాంకేతిక కారణాలు.

1. సాధారణ కారణాలు :
i) సాంఘిక వాతావరణం :
వ్యవసాయ అభివృద్ధికి గ్రామీణ ప్రాంతాల్లోని సాంఘిక వాతావరణం అవరోధంగా ఉంది. నూతన వ్యవసాయ పద్ధతులకు రైతులు ప్రత్యుత్తరమివ్వరు. అయినా కూడా భారతీయ రైతులు వారి పరిమితులకు లోబడి వారి వనరులను సమర్థవంతంగా వాడుతున్నారు.

ii) భూమిపైన జనాభా ఒత్తిడి :
భూమిపైన జనాభా ఒత్తిడి అధికంగా వుంది. 2011లో 349 మిలియన్ల గ్రామీణ శ్రామికులలో 263 మిలియన్ల శ్రామికులకు వ్యవసాయ రంగంలోనే పనిని కల్పించడం జరిగింది. భూకమతాల విభజనకు, విఘటనకు భూమిపైన పెరిగే జనాభా ఒత్తిడి కొంతమేరకు కారణమని చెప్పవచ్చు. చిన్న, లాభకరం కాని భూకమతాలలో ఉత్పాదకత తక్కువగా వుంది.

iii) భూమి క్షీణించడం :
దేశంలోని 329 మిలియన్ల హెక్టార్లు భూమిలో సుమారు సగం భూమిలో భూసారం క్షీణించింది. 43% భూమిలో చాలా ఎక్కువగా భూసారం క్షీణించినందువల్ల 33-67 వరకు దిగుబడి నష్టం జరుగుతుంది. 5% భూమి ఉపయోగించే స్థితిలో లేదు. ఈ కారణంగా అంత ఎక్కువగా నష్టం జరిగింది. భారతదేశంలోని అనేక ప్రాంతాలలో వ్యవసాయ దిగుబడి తక్కువగా వుండటానికి ముఖ్యకారణం భూసారం క్షీణించడమే.

iv) అవస్థాపనా సౌకర్యాల కొరత:
రోడ్లు, కమ్యూనికేషన్లు, మార్కెటింగ్, పరపతి, విద్యుచ్ఛక్తి మురుగునీటి పారుదల లాంటి అవస్థాపనా సౌకర్యాలు కొరతగా వున్నందువల్ల వ్యవసాయ ఉత్పాదకత తక్కువగా వుంది.

2. సంస్థాగత కారణాలు :
i) భూమి కౌలు విధానం :
ఉత్పత్తిని, ఉత్పాదకతను పెంచడానికి రైతులకున్న సామార్థ్యాన్ని, ఇష్టతను, ఉత్సాహాన్ని, బాగా దోపిడీ చేసే జమిందారీ వ్యవస్థ తగ్గించింది. కౌలు చట్టం, కౌలు భద్రత,

ii) కమతాల పరిమాణం:
భారతదేశంలో భూకమతాల సగటు పరిమాణం చాలా తక్కువగా ఉంది. 2010-2011లో 85% భూకమతాల పరిమాణం 2 ఎకరాలకంటే తక్కువగా వుంది. లాభకరం కాని భూకమతాలు వుండటం వల్ల వ్యవసాయ దిగుబడి తక్కువగా వుంది.

iii) ఉద్యమిత్వం లేకపోవడం :
వ్యవసాయరంగంలోని వ్యవసాయ కార్యకలాపాలలోని ఉద్యమిత్వం, పోటీతత్వం లేవు. అభివృద్ధి చెందిన దేశాలలో వ్యవసాయ రంగంలో కూడా ఉద్యమిత్వం విధానం వుంది.

iv) పెట్టుబడి తక్కువగా వుండటం :
వ్యవసాయరంగంలో ఇది మరొక సమస్య. గ్రామీణ అవస్థాపనలోని ముఖ్య అంశాలలో పెట్టుబడిని కేంద్ర గణాంక సంస్థ పరిగణలోకి తీసుకోలేదు. విద్యుద్దీకరణ, రోడ్ల అభివృద్ధి, గిడ్డంగులు, టెలికమ్యూనికేషన్లో పెట్టుబడులు మొదలైన వాటిని మినహాయించారు.

3. సాంకేతిక కారణాలు :
i) అల్ప ఉత్పత్తి పద్ధతులు :
భారతీయ రైతులలో ఎక్కువ మంది సంప్రదాయ ఉత్పత్తి పద్ధతులను వాడుతున్నారు. ఎరువులను, నూతన అధిక దిగుబడిని ఇచ్చే రకాల విత్తనాలను ఉపయోగించడం కూడా పరిమితంగానే వుంది. ఆధునిక ఉత్పాదకాల లభ్యత పరిమితంగా వుండటమే కాక వాటి వ్యయం ఎక్కువగా వుంది. అందుకే ఉత్పాదకత తక్కువగా వుంది. కోతల అనంతరం వాడే సాంకేతిక జ్ఞానం కూడా పరిమితంగానే ఉండటమేకాక నాణ్యత లేకపోవడం కూడా సమస్యగానే ఉంది.

ii) నీటిపారుదల సౌకర్యాల కొరత:
ఉత్పాదకాలలో ముఖ్యమైనది నీటిపారుదల సౌకర్యం. భారతదేశంలో 2010-11లో మొత్తం పంటవిస్తీర్ణం 199 మిలియన్ల హెక్టార్లయితే ఇందులో 89 మిలియన్ల హెక్టార్ల భూమికే నీటిపారుదల సౌకర్యం వుంది. అంటే పంట విస్తీర్ణంలో 45% భూమికి నీటిపారుదల సౌకర్యం వుంది. నీటిపారుదల సౌకర్యాలు లేక పూర్తిగా వర్షాలపై ఆధారపడుతున్న అన్ని ప్రాంతాలలో ఉత్పాదకత తక్కువగా వుంది.

iii) పర్యావరణ కారకాలు :
భూసార క్షీణత ఎక్కువగా వుండటం, వర్షపాతం ఎక్కువ కావడం వల్ల భూమికి జరిగే నష్టం, వరదలు, అడవులు క్షీణించడం, అధిక నీటి నిల్వలు, మురుగు నీటి పారుదల సౌకర్యం లేకపోవడం, కరువు ‘మోతాదు’ను మించి రసాయన ఎరువులను వాడటం, గాలి కాలుష్యాలు ఇవన్నీ కూడా వ్యవసాయ రంగాల్లో అల్ప ఉత్పాదకతకు దోహదపడుతున్నాయి.

ప్రశ్న 3.
భారతదేశ భూ సంస్కరణల ప్రధానాంశాలు వ్రాయండి.
జవాబు.
భూ సంస్కరణలు-అర్థం:
భూమిలేని గ్రామీణ కుటుంబాలు చిన్న, సన్నకారు రైతుల ప్రయోజనాలను పరిరక్షించటానికి భూసంస్కరణలు భూపునః పంపిణీకి సహాయపడతాయి. వ్యవసాయ అభివృద్ధితోపాటు ఆర్థిక, ఆర్థికేతర మార్పులను భూ సంస్కరణల ద్వారా ప్రవేశపెడతారు.

ప్రత్యక్షంగా ప్రభుత్వం వ్యవసాయ రంగంలో జోక్యం చేసుకొని వ్యవసాయ నిర్మాణంలో మార్పులను తీసుకొని రావడాన్ని “భూ సంస్కరణలు” అంటారు. సమానత్వం, సామాజిక న్యాయం ప్రాతిపదిక మీద గ్రామీణ ఆర్థిక వ్యవస్థ పునః నిర్మాణం కోసం భారత ప్రభుత్వ స్వాతంత్య్రానంతరం భూ సంస్కరణలను ప్రవేశపెట్టింది.

భూ సంస్కరణలలో ప్రధాన అంతర్భాగాలు.

1. మధ్య వర్తుల తొలగింపు
2. కౌలు సంస్కరణలు.
3. భూ కమతాలపై గరిష్ట పరిమితి విధించడం.

భూ సంస్కరణల అమలుకు ప్రభుత్వ చర్యలు :
1. మధ్యవర్తుల తొలగింపు: ‘శాశ్వత శిస్తు వసూలు చట్టం’ ద్వారా బ్రిటీష్ ప్రభుత్వం జమిందారీ పద్ధతిని ప్రవేశపెట్టింది. జమిందారులు, జాగీర్దారులు, ఇనాందారులు వంటి మధ్యవర్తుల ఆధీనంలో పెద్ద మొత్తంలో భూకమతాలు ఉండేవి. వ్యవసాయదారుల నుంచి భాటకాన్ని (rent) వీరు వసూలు చేసేవారు.

ఈ మధ్యవర్తులు బ్రిటీష్ ప్రభుత్వానికి స్థిరమైన రేటులో భూమి శిస్తును చెల్లించి వ్యవసాయదారుల నుంచి అధిక మొత్తంలో భాటకాన్ని వసూలు చేసేవారు, నిజానికి జమిందారులు లేదా మధ్యవర్తులు అనుపస్థిత భూస్వాములుగా ఉంటూ, భూమిని అభివృద్ధి చేయడం వల్ల విముఖంగా ఉండేవారు.

2. కౌలు సంస్కరణలు :
కౌలుదారు కౌలు చెల్లించే షరతుపై భూ యజమాని నుంచి భూమిని నిర్ణీత కాలానికి లీజుకు తీసుకొని సేద్యం చేస్తాడు. కౌలుదారుని భూ యజమాన్యం హక్కులేని వాస్తవ వ్యవసాయదారునిగా చెప్పవచ్చు. ఒప్పందం ప్రకారం నిర్దిష్ట పద్ధతిలో భాటకాన్ని చెల్లిస్తాడు.

కౌలుదారులను భూస్వాముల నుంచి రక్షించడానికి ప్రభుత్వం కింది చర్యలను ప్రవేశపెట్టింది.

ఎ) కౌలు పరిమాణాన్ని క్రమబద్దం చేయడం :
కౌలుదారులపై ఆర్థిక భారాన్ని తగ్గించడం కోసం కౌలు పరిమాణాన్ని ప్రభుత్వం క్రమబద్ధీకరించింది. మొదటి పంచవర్ష ప్రణాళికలో గరిష్ఠకౌలు పరిమాణం మొత్తం ఉత్పత్తిలో 1/4 లేదా 1/5వ వంతు మాత్రమే ఉండాలని నిర్ణయించబడింది. ఈ విధంగా ఎప్పటికప్పుడు కౌలు పరిమాణాన్ని పెంచే అవకాశం తొలగించబడి కౌలుదారులకు రక్షణ కల్పించబడింది.

హైదరాబాదు రాష్ట్రంలో అమలులో ఉన్న ‘కౌలుదారు రక్షణ చట్టం’ కౌలుదారులను తొలగించడానికి గల అవకాశాలను రద్దు చేయడంతోపాటు యజమాని నుంచి భూమి కొనుగోలు చేయగల హక్కులను వారికి కల్పించింది. ఈ చట్టం దేశవ్యాప్తంగా అమలులో ఉన్న ప్రగతిశీల చట్టాలలో ఒకటిగా కొనియాడబడింది.

బి) కౌలుదారులకు భద్రతను కల్పించడం :
వివిధ రాష్ట్ర ప్రభుత్వాలు కౌలుదారులను తరుచుగా తొలగించకుండా చట్టం ద్వారా భద్రతను కల్పించింది.

• భూస్వాములు తమ ఇష్టానుసారంగా కౌలుదారులను తొలగించలేదు.
• స్వంత వ్యవసాయం కోసం మాత్రమే భూస్వాములు కౌలుదారు నుంచి భూమిని తీసుకోవచ్చు.
• భూస్వామి స్వంత వ్యవసాయానికి భూమి తీసుకొనే సమయంలో భూమిలో కొంత భాగాన్ని కౌలుదారు ఆధీనంలో ఉంచవలసి ఉంటుంది.

సి) యాజమాన్యపు హక్కులు:
కొన్ని రాష్ట్ర ప్రభుత్వాలు కౌలుదారులకు హక్కులను కల్పించడానికి చట్టాలను రూపొందించాయి. ఈ చర్య ఎంతో ప్రశంసనీయమైనదైనా దీని ద్వారా సాధించిన ఫలితాలు అంత సంతృప్తికరంగా లేవు.

3. భూకమతాలపై గరిష్ఠ పరిమితి :

1. కమతాల సమీకరణ :
భారతదేశంలో చిన్న కమతాలు, కమతాలు విఘటన (Fragmentation of land holdings) సర్వసాధారణం, ఈ విధమైన లాభసాటికాని కమతాలు (Uneconomic holdings) మెరుగైన వ్యవసాయ పద్ధతులకు అనువుగా ఉండవు. చిన్న కమతాలు, కమతాల విఘటన సమస్యను పరిష్కరించడానికి ప్రభుత్వం కమతాల సమీకరణను ప్రోత్సహించింది.

ఈ సంస్కరణలో భాగంగా పంజాబ్, హర్యానా, మహారాష్ట్రలలో లాభసాటి కమతాలు గణనీయమైన సంఖ్యలో చిన్న, విఘటన చెందిన కమతాలు యజమానులకు అందించబడ్డాయి. 2001 సెప్టెంబరు నాటికి 1,633 లక్షల ఎకరాల భూమి మాత్రమే సమీకరించబడింది. చాలా రాష్ట్రలలో వ్యవసాయదారులు సమీకరణ కార్యక్రమానికి సహకరించకపోవడం వల్ల సమీకరణ మందకొడిగా సాగింది.

2. సహకార వ్యవసాయం :
ఇది ఒక సంస్కరణ కాదు. ఐచ్ఛిక స్ఫూర్తిపై ఈ విధానం ఆధారపడుతుంది. ఒక ప్రాంతంలోని వ్యవసాయదారులు తమ చిన్న చిన్న కమతాలను ఏక కమతంగా కలిపి సహకార వ్యవసాయ క్షేత్రంగా రూపొందిస్తారు. ఎంపిక కాబడిన సభ్యులచే సహకార వ్యవసాయ క్షేత్రం నిర్వహించబడుతుంది.

ప్రశ్న 4.
భారతదేశంలో ఆహార ధాన్యాలు స్వయం సమృద్ధిని, ఆహార భద్రతను గురించి వివరించండి.
జవాబు.
ప్రపంచ ఆహార భద్రతపై నివేదికను అందజేసిన ఐక్యరాజ్య సమితి కమిటీ ప్రకారం, ప్రజలందరికి అన్ని కాలాలలో చురుకైన, ఆరోగ్యవంతమైన జీవనానికి తమ అభిరుచి మరియు ఆహారపు అలవాట్ల ప్రకారం తగినంత సురక్షితమైన, పౌష్టికాహారం భౌతికంగా, సామాజికంగా, ఆర్థికంగా అందుబాటులో ఉండటాన్ని ఆహార భద్రత అంటారు.

భారతదేశంలో ఆహార స్వయం – సమృద్ధి, ఆహార భద్రత :
ప్రణాళికా కాలం ప్రారంభమైనప్పటి నుంచి భారతదేశపు ప్రణాళికావేత్తలు ప్రణాళికీకరణలో ఆహార ధాన్యాలలో స్వయం సమృద్ధిని సాధించాలనేది అన్ని లక్ష్యాలలో ఒక ముఖ్యమైన లక్ష్యంగా ఉంటుందని తెలుసుకున్నారు.

1965, 1966 సంవత్సరాలలో భారతదేశం తీవ్రమైన కరువు పరిస్థితులను చవిచూచినప్పుడు అమెరికా అధ్యక్షుడు Lyndon Johnson, P.L. 480 పథకంలో నెలవారి ప్రాతిపదికన ఆహార సహాయాన్ని పరిమితం చేశాడు. ఆ తదుపరి కాలంలో ప్రధాన మంత్రి ఇందిరాగాంధీ నేతృత్వంలో భారత ప్రభుత్వం “విత్తనం – నీరు-ఎరువు” (seed-water-fertilizer) విధానాన్ని అవలంబించింది. ఈ విధానాన్నే “హరిత విప్లవం” అని అంటారు.

ఈ విధానం అవలంబించడం వల్ల భారతదేశ ఆహారోత్పత్తిలో విప్లవాన్ని సాధించడమే కాకుండా దాదాపుగా ఆహారోత్పత్తుల దిగుమతులకు స్వస్తి పలికింది. 1976 వ సంవత్సరం నాటికి భారతదేశం ఆహారోత్పత్తుల విషయంలో స్వయం సమృద్ధిని సాధించింది. అప్పటి నుండి భారతదేశ ఆహార పదార్థాల దిగుమతులు ఉపేక్షింపదగినవిగా ఉన్నాయి. 1950-51 సం॥లో 30 మిలియన్ టన్నులున్న ఆహార ధాన్యాల ఉత్పత్తి 2018 19 సం॥నాటికి 285 మిలియన్ టన్నులకు చేరింది.

భారతదేశం ఆహార ధాన్యాల విషయంలో స్వయం సమృద్ధిని సాధించినప్పటికీ, సురేశ్ డి. టెండూల్కర్ అధ్యక్షతన ఎక్స్పర్ట్ గ్రూప్ చేసిన అధ్యయనం ప్రకారం భారతదేశంలో 2011-12 సం॥లో మొత్తం మీద 21.9 శాతం, గ్రామాలలో 25.7 శాతం, పట్టణాలలో 13.7 శాతం ప్రజలు పేదరికం రేఖకు దిగువన నివసిస్తుంటే, 2014 సం||లో డాక్టర్ సి. రంగరాజన్ అధ్యక్షతన నియమింపబడిన ఎక్స్పర్ట్ గ్రూప్ ప్రకారం 2009-10 సం॥లో 38.2 శాతం ప్రజలు (454 మిలియన్లు), 2011-12 సం|| లో 29.5 శాతం ప్రజలు (363 మిలియన్లు) పేదరికం రేఖకు దిగువన నివసించారు.

అంటే ఆహార ధాన్యాలు భౌతికంగా దేశంలో అందుబాటులో ఉన్నా ప్రజలు వాటిని కొనగలిగే ఆర్థిక స్తోమతను కల్గిలేరు. ఎందుకంటే ప్రజలకున్న అల్ప ఆదాయాల వల్ల వారికి అల్ప కొనుగోలు శక్తి ఉండటమే కారణం.

ప్రశ్న 5.
భారతదేశంలో నూతన వ్యవసాయక వ్యూహం ప్రభావాన్ని అంచనా వేయండి.
జవాబు.
భారతదేశంలో హరిత విప్లవం, ఆర్థిక వ్యవస్థపై దాని ప్రభావం :
అధిక దిగుబడినిచ్చే వంగడాలు, రసాయన ఎరువులు లాంటి ఆధునిక ఉత్పాదకాల సహాయంతో 1960-1970 మధ్యలో వ్యవసాయ ఉత్పాదకత, ఉత్పత్తిలో సాధించిన పెరుగుదలను హరిత విప్లవం అన్నారు. వ్యవసాయ రంగంలో వచ్చిన నూతన సాంకేతిక మార్పులను సూచిస్తూ విలియం ఎస్. గౌడ్ (william S.Gaud) మొదటిసారిగా ‘హరిత విప్లవం’ అనే పదంను 1968లో ఉపయోగించారు.

నూతన వంగడాల ఉత్పత్తిలో చేసిన కృషి వలన ప్రఖ్యాత అమెరికన్ వ్యవసాయ ఆర్థిక వేత్త మరియు నోబెల్ శాంతి బహుమతి గ్రహీత అయిన నార్మన్ ఎర్నెస్ట్ బోర్లాగ్ను ఈ రంగంలో ముందుగా కృషి చేసిన వ్యక్తిగా, ‘హరిత విప్లవ పితామహుడు’ గా గుర్తించడం జరిగింది.

భారతదేశ ఆర్థిక వ్యవస్థపై నూతన వ్యవసాయిక వ్యూహం / అధిక దిగుబడినిచ్చే వంగడాల కార్యక్రమం ప్రభావం :
నూతన వ్యవసాయిక వ్యూహం లేదా అధిక దిగుబడి నిచ్చే వంగడాల కార్యక్రమం అంతిమ ఫలితం హరిత విప్లవం. అయితే ఈ ప్రక్రియ ఇతర ప్రభావాలను కూడా క్రింది విధంగా విశ్లేషించవచ్చు.

i) వ్యవసాయ ఉత్పాదకత మరియు ఉత్పత్తిలో పెరుగుదల :
నూతన వ్యవసాయిక వ్యూహంలో భాగంగా ఆధునిక వ్యవసాయ ఉత్పాదకాలను వాడడం వల్ల భారతదేశంలో వ్యవసాయ ఉత్పాదకత, ఉత్పత్తిలో గణనీయమైన పెరుగుదల వచ్చింది.

దీనినే హరిత విప్లవం అంటాం. వివిధ ప్రధాన పంటల ఉత్పాదకత, ఉత్పత్తిలో వచ్చిన మార్పును మనం పట్టిక 5.3లో చూశాము. 1966-67 సం||లో నూతన వ్యవసాయిక వ్యూహం ఆరంభం కాగా పది సం॥రాల కాలంలో అంటే 1976 సం॥ నాటికి భారతదేశం ఆహార ధాన్యాల ఉత్పత్తిలో స్వయం సమృద్ధిని సాధించింది.

ii) ఉద్యోగిత :
నూతన వ్యవసాయ వ్యూహం అమలు పంట భూముల విస్తీర్ణంలో, ఆహార పదార్థాల ఉత్పత్తిలో, వ్యవసాయ ఉత్పాదకతలో చెప్పుకోదగ్గ పెరుగుదలకు దారితీసింది. హరిత విప్లవం వ్యవసాయ రంగంలో బహుళ పంటలను ప్రోత్సహించడం ద్వారా ఉద్యోగ అవకాశాలను విస్తరింపజేసింది.

అధిక శ్రమ సాంద్రతతో కూడుకొన్న పంటలైన వరి, చెరకు, బంగాళాదుంపలు, కూరగాయలు, పండ్లు వంటివి వ్యవసాయ రంగంలో ఉద్యోగ అవకాశాలను పెంచాయి. వ్యవసాయ ఉత్పత్తుల చిల్లర వర్తకం ఒక పెద్ద వ్యాపారంగా రూపుదాల్చింది.

iii) రైతుల ఆదాయాల్లో పెరుగుదల :
ప్రత్యేకించి కేరళ, మధ్యప్రదేశ్, ఆంధ్రప్రదేశ్, తమిళనాడు, గుజరాత్, పంజాబ్, హర్యానా, హిమాచల్ ప్రదేశ్ రాష్ట్రాల్లోని రైతుల ఆదాయాలు పెరగడానికి మంచి అవకాశాలు ఏర్పడ్డాయి. హరిత విప్లవం పొలాలలోనే పంటలను నాణ్యతా పరంగా క్రమబద్ధీకరించడం లాంటి శాస్త్రీయ, సాంకేతిక పరమైన సామాన్య పద్ధతులను రైతులు అనుసరించడానికి అవకాశాలను కల్పించింది.

మధ్యలో దళారీల ప్రమేయం లేకుండా నేరుగా రిటైల్ కంపెనీలకు అమ్ముకోవడం వల్ల కూడా రైతుల ఆదాయంలో పెరుగుదల ఏర్పడింది. ఎందుకంటే సంఘటిత రిటేలర్స్ మంచి గిట్టుబాటు ధరను రైతులకు ఇవ్వడం జరిగింది.

iv) ఎగుమతుల్లో పెరుగుదల :
భారతదేశం హరిత విప్లవంకు పూర్వం ఆహార ధాన్యాలను అధికంగా దిగుమతి చేసుకునేది. కాని హరిత విప్లవం తరువాత ఈ పరిస్థితి అరుదుగా ఉండటమే గాక వ్యవసాయ ఎగుమతులు బాగా పెరిగాయి. 1960-61 సం||లో వ్యవసాయ మరియు దాని సంబంధిత ఎగుమతులు విలువ రూ. 284 కోట్లు ఉండగా ఇది 2018-19 సం॥ నాటికి రూ.2.7 లక్షల కోట్లకు పెరిగింది.

ప్రశ్న 6.
భారతదేశంలో వ్యవసాయ పరపతికి గల ఆధారాలను పరిశీలించండి.
జవాబు.
మనదేశంలో వ్యవసాయదారులకు అవసరమయ్యే వ్యవసాయ పరపతిని ఉత్పాదక, అనుత్పాదక రుణాల రూపంగా విభజించవచ్చు. విత్తనాలు, ఎరువులు, పశువులు, వ్యవసాయ పనిముట్ల కొనుగోలు, బావులు లేదా గొట్టపు బావుల త్రవ్వకం వంటి వాటి కోసం ఉత్పాదక రుణాలు అయితే, పెళ్ళిళ్ళు, సామాజిక వేడుకలు, మతపరమైన వేడుకలు, పండుగలు వంటి వాటిపై ఖర్చు చేసే అవసరాల కోసం అనుత్పాదక రుణాలు.

భారతదేశంలో వ్యవసాయదారులకు అందుబాటులో ఉన్న వ్యవసాయపరపతి ఆధారాలను రెండు రకాలుగా విభజించవచ్చు.

ఎ) సంస్థాపూర్వకం కాని ఆధారాలు :
సంస్థాపూర్వకం కాని ఆధారాల్లో వడ్డీ వ్యాపారులు, భూస్వాములు, వ్యాపారస్థులు, కమీషన్ ఏంజెట్లు, బంధువులు, మిత్రులు మొదలైనవారు వ్యవసాయ పరపతి కల్పనలో ప్రధాన భూమికను నిర్వహిస్తారు. 1951-52లో వ్యవసాయ పరపతి కల్పనలో సంస్థాపూర్వకం కాని మార్గంలో వ్యవసాయదారులు 93 శాతం రుణాన్ని పొందితే ప్రభుత్వం కేవలం 7 శాతం పరపతిని సమకూర్చింది.

బి) సంస్థాపూర్వకమైన ఆధారాలు :
సంస్థాగతం కాని వ్యవసాయపరపతి కల్పనలో అనేక లోపాలుండటం వల్ల వ్యవసాయదారులు దోపిడికి గురవుతున్నందువల్ల ప్రభుత్వ పరంగా సహకార సంఘాలు, వాణిజ్య బ్యాంకులు, ప్రాంతీయ గ్రామీణ బ్యాంకులు వంటి బహుళ ఏజెన్సీలను ప్రోత్సహించింది. వీటి ద్వారా రైతులకు పరపతిని చౌకగా అందుబాటులో ఉంచాలని ప్రభుత్వం తలపెట్టింది.

i) సహకార సంఘాలు :
గ్రామీణ ప్రాంతాల్లో ప్రజలను రుణగ్రస్థత నుంచి విముక్తి చేసే లక్ష్యంతో 1904 సంవత్సరంలోనే ప్రభుత్వం సహకార ఉద్యమాన్ని ప్రోత్సహించింది. ఈ లక్ష్య సాధన దిశగా సహకార సంఘాలు స్థాపించబడ్డాయి. భారతదేశంలో స్వల్పకాల, మధ్య, దీర్ఘకాల రుణ కల్పన దృష్టా వివిధ స్థాయిల్లో స్థాపించబడ్డాయి.

రైతులకు స్వల్పకాలిక రుణాలను అందించే సంస్థలు మూడు స్థాయిల్లో ప్రవేశపెట్టబడ్డాయి. మొదటిస్థాయిలో ప్రాథమిక వ్యవసాయ పరపతి సంఘాలు (PACS) గ్రామ స్థాయిలో ప్రవేశపెట్టబడ్డాయి. రెండవ స్థాయి అయిన జిల్లా స్థాయిలో జిల్లా కేంద్ర సహకార బ్యాంకులు (DCCB) స్థాపించబడ్డాయి. మూడవ స్థాయి అయిన రాష్ట్ర స్థాయిలో రాష్ట్ర సహకార బ్యాంకులు (SCB) నెలకొల్పబడ్డాయి. స్వల్ప, మధ్యకాలిక రుణాల కల్పనలో PACs, DCCB లను సమన్వయ పరచడంలో SCB ప్రధాన పాత్రను పోషిస్తుంది.

ii) వాణిజ్య బ్యాంకులు :
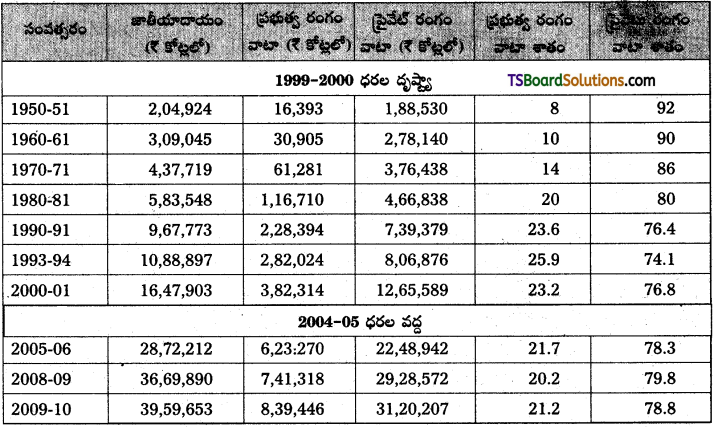
1950లో వాణిజ్య బ్యాంకులు అందించిన వ్యవసాయ పరపతి నామమాత్రమేనని చెప్పాలి. 1951-52లో వాణిజ్య బ్యాంకులు అందించిన పరపతి మొత్తం వ్యవసాయ పరపతిలో 0.9 శాతం అయితే, అది 1960-61లో 0.7 శాతం మాత్రమే. 1969లో ఇవి అందజేసిన రుణాలు 162 కోట్ల, రుపాయలు, జాతీయీకరణ అనంతరం 1969 నుంచి 1980 మధ్య కాలంలో గ్రామీణ ప్రాంతాల్లో వాణిజ్య బ్యాంకుల శాఖలు పెద్ద మొత్తంలో పెరగడమే కాకుండా అవి అందజేసిన రుణాలు కూడా గణనీయంగా పెరిగాయి.

మార్చి 31,2013 నాటికి ఇవి అందజేసిన రుణాలు 5,30,600 కోట్ల రూపాయలు. అయితే, మార్చి 31,2013 నాటికి ప్రైవేటు బ్యాంకులు అందించిన రుణం 1,11,900 కోట్ల రూపాయలు. ప్రభుత్వరంగ ప్రైవేట్ రంగ బ్యాంకులు కలిపి మొత్తం వ్యవసాయ పరపతిలో 71.2 శాతం సంస్థాగత రుణాలను అందించాయి.

iii) ప్రాంతీయ గ్రామీణ బ్యాంకులు :
గ్రామీణ ప్రాంతాల్లో వ్యవసాయ పరపతి డిమాండ్, సప్లయ్ గల వ్యత్యాసాన్ని సహకార సంఘాలు సర్దుబాటు చేయలేకపోవడం వల్ల దీని నివారణ కోసం శ్రీ ఎం. నరసింహం అధ్యక్షతన నియమించిన గ్రామీణ బ్యాంకుల వర్కింగ్ గ్రూప్ ప్రాంతీయ గ్రామీణ బ్యాంకుల స్థాపనను సిఫారసు చేసింది.

చిన్న, ఉపాంత రైతులు, భూమిలేని శ్రామికులు, కుల వృత్తులు, చిల్లర వ్యాపారం చేసే ఉద్యమదారులకు అవసరమయ్యే గ్రామీణ పరపతికి సహకార సంఘాలు, వాణిజ్య బ్యాంకులు అందించే పరపతికి మధ్యగల వ్యత్యాసాన్ని తగ్గించే లక్ష్యంగా RRB లను స్థాపించాలని ఈ గ్రూప్ పేర్కొన్నది. ఈ సిఫారసులకు అనుగుణంగా అక్టోబర్ 2, 1975లో మొదటి 5 ప్రాంతీయ గ్రామీణ బ్యాంకులు స్థాపించబడ్డాయి. 2012-13 సంవత్సరం నాటికి ఈ బ్యాంకులు సంస్థాగత వ్యవసాయ పరపతిలో 10.5 శాతం రుణ సదుపాయం కల్పించాయి.

ప్రశ్న 7.
వ్యవసాయ మార్కెటింగ్ లోపాలు ఏమిటి ? వ్యవసాయ మార్కెటింగ్ లోపాలను అధిగమించేందుకు ప్రభుత్వం తీసుకున్న చర్యలను వివరించండి.
జవాబు.
భారత దేశంలో వ్యవసాయ మార్కెటింగ్ :
జాతీయ వ్యవసాయ కమీషన్ ప్రకారం “అమ్ముడుపోదగిన వ్యవసాయ సరుకులను . ఉత్పత్తి చేయాలనే నిర్ణయం తీసుకోవడంతో ప్రారంభమయి వ్యవస్థలోని మార్కెట్ నిర్మితికి చెందిన అన్ని అంశాలను కలుపుకొని పోయే ప్రక్రియనే వ్యవసాయ మార్కెటింగ్గా చెప్పవచ్చు.”

పంట కోతకు ముందు, తరువాత జరిగే కార్యకలాపాలన్నీ ఇందులోకి వస్తాయి. ఉత్పత్తులను కూడదీయడం, నాణ్యతను అనుసరించి విడదీయడం (గేడింగ్), నిలువ చేయడం, రవాణా చేయడం, పంపిణీ చేయడం లాంటి పనులన్నీ వ్యవసాయ మార్కెటింగ్ పరిధిలోకే వస్తాయి.

భారతదేశ వ్యవసాయ మార్కెటింగ్ లోని లోపాలు :
నిలువ సౌకర్యాలు తగినంత స్థాయిలో లేనందువల్ల, మార్కెట్లోని సప్లయి, డిమాండ్ పరిస్థితులతో నిమిత్తం లేకుండానే, పంటకోతల తర్వాత వెంటనే రైతులు తమ వ్యవసాయ మిగులును బలవంతంగా అమ్మవలసి వస్తుంది.

తగిన రవాణా సౌకర్యాలు లేక రైతులు వారి ఉత్పత్తిని స్థానిక వర్తకులకు, వడ్డీ వ్యాపారస్తులకు, కమీషన్ ఏజంట్లకు, మార్కెట్ ధరల కంటే తక్కువకే అమ్మవలసిన తప్పనిసరి పరిస్థితి ఉంది. స్థానిక సంతల్లో సరైన తూనికలు, కొలతలు ఉండనందువల్ల రైతులు మోసపోతున్నారు.

రైతులు బ్రోకర్ల, వ్యాపారుల మోసాలకు కూడా గురవుతున్నారు. రైతులు తూకపు చార్జీలు, సరుకు దించినందుకు చార్జీలు, ఉత్పత్తులను శుద్ధి చేసే ఖర్చులు, ఇతర అనేక నిర్వచించని, నిర్ణయింపబడని చార్జీలను చెల్లించాల్సి వస్తుంది. సరైన గ్రేడింగ్ వ్యవస్థ లేకపోవడం వల్ల రైతు తగిన ధరను పొందడం లేదు.

1. క్రమబద్ధమైన మార్కెట్లు:
వ్యవసాయ మార్కెటింగ్లో ఉన్న అనారోగ్య పరిస్థితులను తొలగించి రైతులకు లాభదాయకమయ్యే ధరలు పొందటానికి వీలుగా క్రమబద్ధ మార్కెట్ల స్థాపనకు ప్రభుత్వం రాష్ట్ర వ్యవసాయ ఉత్పత్తుల చట్టాన్ని రూపొందించింది. తదనుగుణంగా 1951లో దేశంలో 200 క్రమబద్ధ మార్కెట్లు నెలకొల్పబడ్డాయి. ప్రస్తుతం మనదేశంలో 7,246 క్రమబద్ధమైన మార్కెట్లు పనిచేస్తున్నాయి.

మార్కెట్ వ్యవస్థ నిర్మాణపు అభివృద్ధిలో క్రమబద్ధమైన మార్కెట్లను క్రింద పేర్కొన్న ఆశయాలతో రూపొందించడమైనది.

• వ్యవసాయదారుల ఉత్పత్తులకు లాభదాయక ధరలు వచ్చేటట్లు చూడటం.
• ఉత్పత్తిదారుడి నుంచి వినియోగదారుడి వరకు వస్తువుల ధరల్లో తేడాను తగ్గించటం.
• వ్యాపారస్థులు, మధ్య దళారీల మోసపూరిత చర్యలను అరికట్టడం.

2. శ్రేణీకరణ, ప్రామాణీకరణ (Grading and Standardisation) :
వ్యవసాయ ఉత్పత్తులకు సంబంధించి శ్రేణీకరణ, ప్రామాణీకరణ సౌకర్యాలను కల్పించనంతవరకు, వ్యవసాయ మార్కెటింగ్ వ్యవస్థను మెరుగుపరచడానికి వీలుకాదు. అయితే, వ్యవసాయ ఉత్పత్తుల శ్రేణీకరణ, ప్రామాణీకరణ కోసం ప్రభుత్వం అనేక చర్యలు చేపట్టింది.

వ్యవసాయ ఉత్పత్తుల చట్టం 1937 ప్రకారం ప్రభుత్వం అనేక గ్రేడింగ్ స్టేషన్లను ఏర్పాటు చేసింది. వస్తువుల కన్నా మార్కెట్ను మరింత విస్తృత పరచడానికి వ్యవసాయ మార్కెటింగ్ విభాగం ద్వారా శ్రేణీకరణ చేసిన వస్తువులపైన AGMARK ను ముద్రిస్తున్నారు.

3. గిడ్డంగి సౌకర్యాలు :
రైతులు వారి వస్తూత్పత్తిని నిలువ ఉంచుకొని లాభదాయక ధరను పొందటానికి వీలుగా గ్రామాలు పట్టణాల్లో గిడ్డంగి సౌకర్యాలు విస్తరించబడ్డాయి. ఇందులో భాగంగా 1957లో కేంద్ర గిడ్డంగి కార్పోరేషన్ CWC స్థాపించబడింది. అలాగే వివిధ రాష్ట్రాల్లో రాష్ట్ర గిడ్డంగి కార్పోరేషన్లను SWC ఏర్పాటు చేయడమైంది. ఇంతేగాక జాతీయ స్థాయిలో భారత ఆహార సంస్థ (FCI) స్థాపించబడింది. జూన్, 2013 నాటికి భారతదేశంలో FCI లో 355 లక్షల టన్నులు నిలువ చేసుకొనే శక్తి ఉంది.

4. మార్కెట్ సమాచారం :
వివిధ మార్కెట్లలో వ్యవసాయ వస్తువులకు పలికిన ధరల సమాచారాన్ని రైతులకు చేరవేసేందుకు ప్రభుత్వం పలు చర్యలు చేపట్టింది. ఆకాశవాణి ప్రసారాల ద్వారా ఈ ధరలకు సంబంధించిన సమాచారాన్ని ప్రతిరోజు రైతులకు చేరవేస్తోంది. ఆకాశవాణి, దూరదర్శన్ లు ప్రతి వారం మార్కెట్ ధరలపై సమీక్షలు నిర్వహిస్తున్నాయి. కేంద్ర ప్రభుత్వం 26-5- 2015న కిసాన్ ఛానల్ను ప్రారంభించింది.

5. మద్దతు ధరలు :
వ్యవసాయ మార్కెటింగ్లో రైతులు లాభదాయకమైన ధరలు పొందడానికి వీలుగా ప్రభుత్వం వివిధ వస్తువులకు సంబంధించి ‘కనీస మద్ధతు ధరల’ను ప్రకటిస్తుంది. వ్యవసాయ వస్తువుల వ్యయాలు, ధరల కమీషన్ Commis- sion for Agricultural Costs and Prices – CACP సిఫారసుల మేరకు ప్రభుత్వం ఈ ధరలను ప్రకటిస్తుంది.

6. ఇతర చర్యలు :
పై ప్రయత్నాలతోపాటు కింద వివరించిన చర్యలు చేపడితే వ్యవసాయ మార్కెటింగ్లోని లోపాలను తొలగించవచ్చు. అవి :

1. రోడ్లు-సమాచార సంబంధాలను పెంచడం-అన్ని పల్లెలకు వీటిని అనుసంధానం చేయడం.
2. బాంకులతోనూ-విత్తసంస్థలతోనూ అనుసంధానం చేయడం.
3. ఫోన్లు, ఇంటర్ నెట్ కేబుల్ వగైరా ఎలక్ట్రానిక్ సదుపాయాలను అనుసంధానం చేయడం.
4. క్రమబద్ధమైన మార్కెట్లు బయట వ్యవసాయ వస్తువుల అమ్మకాలను నిషేధించడం..
5. రవాణా ఖర్చులను తగ్గించడం.
6. రైతు బజార్లును ప్రోత్సహించడం.
7. మార్కెట్లలో ప్రమాణీకరించిన తూనికలు, కొలతలు ఉపయోగించే విధంగా చర్యలు చేపట్టడం.
8. గ్రామాలు, గ్రామీణ ప్రాంతాల్లో గిడ్డంగి. సౌకర్యాలను పెంచడం.

ప్రశ్న 8.
భారతదేశంలో గ్రామీణ రుణగ్రస్తతకు గల కారణాలను, వాటిని సరిదిద్దేందుకు తీసుకొనే చర్యలను పరిశీలించండి.
జవాబు.
గ్రామీణ ఋణగ్రస్తత :
భారతదేశంలో జనాభాలో 70 శాతంపైగా ప్రజలు గ్రామాల్లో నివసిస్తున్నారు. అయితే ఈ ప్రాంతాల్లోని పేద ప్రజలు తాము పొందిన రుణాల్లో ఎక్కువ మొత్తం ఏ రకమైన ఆదాయం ఇవ్వని అనుత్పాదక అవసరాలపై ఖర్చు చేస్తారు. అందువల్ల వీరు పాత ఋణాలను తీర్చలేక రుణగ్రస్తులవుతున్నారు. ఎప్పుడైతే వారికి సంస్థాపరమైన ఋణం తక్కువగా లభిస్తుందో లేదా పూర్తిగా లభించకపోతుందో అప్పుడు వారు దురాశాపరులైన వడ్డీ వ్యాపారుల వద్ద రుణం తీసుకొంటారు.

ఎందుకంటే వీరు అడిగిన వెంటనే అందుబాటులో ఉంటారు. పేదవారు వారి అవసరాల ఒత్తిడి దృష్ట్యా అధిక వడ్డీ రేట్లకు రుణం తీసుకొంటూ వడ్డీ వ్యాపారుల కంబంధ హస్తాల్లో వారి ఆస్తులను తాకట్టు పెట్టి వాటిని పోగొట్టుకొంటున్నారు. ఈ కారణాల వల్ల వారి ఋణగ్రస్తత రానురాను పెరిగిపోతూ శాశ్వతంగా వారు రుణగ్రస్తులుగా మారిపోతున్నారు.

రుణగ్రస్తతకు గల కారణాలు :
గ్రామీణ ప్రాంతాల్లో ఋణం పెరగడానికి కింది విషయాలు కారణభూతం అవుతున్నాయని చెప్పవచ్చు. అవి :

1. గ్రామ ప్రాంతాల్లో రైతులు రుణగ్రస్తులుగా మారడానికి ప్రధాన కారణం వారి పేదరికం, తక్కువ స్థాయి పొదుపులు, పంట నష్టపోవడం.
2. అప్పులు చేసి పొలాలను బాగుపరచి అభివృద్ధి చేయాలనే తపన.
3. అనుత్పాదక పనులపై ఖర్చు పెట్టడం.
4. తల్లిదండ్రుల నుంచి వారసత్వంగా అప్పులు సంక్రమించడం.
5. సంస్థాగతం కాని ఋణాలపైన ఎక్కువగా ఆధారపడటం.
6. పంటలకు మద్ధతు ధరలు తగినంతగా లేకపోవడం.
7. సేద్యపు ఖర్చులు బాగా పెరిగిపోవడం.

గ్రామీణ ఋణగ్రస్తత తగ్గడానికి తీసుకోవలసిన చర్యలు :
గ్రామీణ ఋణగ్రస్తత, దానికున్న వివిధ రూపాలతోనూ, పరిమాణంతోనూ గ్రామీణ ప్రాంతాల్లో రకరకాల సమస్యలను సృష్టిస్తుంది. దారిద్ర్యాన్ని పెంచుతూ రైతులు దుర్భర జీవితం గడపడానికి కారణమవుతూ ఉంది. ఈ రుణగ్రస్తత వల్ల రైతులు తమ ఉత్పత్తులకు సరసమైన ధరలను పొందక ఆహార భద్రతను కోల్పోతున్నారు. కాబట్టి దీన్ని తగ్గించడానికి తగిన చర్యలు తీసుకోవల్సిన అవసరం ఉంది.

కింద సూచించిన చర్యలు అమలు పరచగలిగితే ఋణగ్రస్తత తగ్గడానికి అవకాశం ఉంటుంది.

1. చట్టాలను అమలుపరిచి పూర్వీకుల నుంచి వారసత్వంగా వచ్చిన ఋణాలను వీలయినంత వరకు తగ్గించడం.
2. గ్రామాల్లో వడ్డీ వ్యాపారుల ప్రాధాన్యత తగ్గించే దిశగా సహకార సంఘాలు, వాణిజ్య బ్యాంకులు, ప్రాంతీయ గ్రామీణ బ్యాంకుల నెట్వర్క్స్ ను వేగవంతం చేయడం.
3. సన్న, చిన్నకారు రైతులకు, గ్రామీణ వృత్తి కళాకారులకు తగిన సమయంలో తగినంత పరపతి మొత్తాన్ని అందించడం.
4. గ్రామీణ పరపతి అవసరాలను గమనించి, వాటికి తగిన ప్రాధాన్యతను ఇచ్చి “ప్రాధాన్యతా రంగాల”కు (Priority sector) ఇచ్చే పరపతిని పెంచడం..
5. బలహీన వర్గాలకు వాణిజ్య బ్యాంకులు వినియోగ వస్తువుల కొనుగోలుకు రుణం ఇచ్చేటట్లు చూడటం.
6. పొలాలను సంస్థాగతం కాని వడ్డీ వ్యాపారులకు అమ్మడాన్ని, కుదువ పెట్టడాన్ని నిషేధించడం.
7. అప్పులను ఒకే విడతలో చెల్లిస్తే ఇచ్చే తగ్గింపును పెంచడం.
8. సూక్ష్మ రుణాల పథకం కింద మహిళా రైతులకు రుణాలను ఇవ్వడం, పెంచడం.

ప్రశ్న 9.
వ్యవసాయ ధరల విధాన ప్రధాన లక్షణాలను వ్రాయండి.
జవాబు.
జాతీయ ఆర్థిక వ్యవస్థలో వ్యవసాయపు సాపేక్ష ప్రాముఖ్యతను బట్టి, ఒక దేశానికి, మరొక దేశానికి వ్యవసాయ ధరల విధానపు లక్ష్యాలు మారుతుంటాయి. సాధారణంగా అభివృద్ధి చెందిన దేశాలలో ధర విధానం ప్రధాన లక్ష్యం వ్యవసాయ ఆదాయం అనూహ్యంగా తగ్గకుండా నిరోధించడం.
వ్యవసాయ ధరల విధానం లక్షణాలు :
ఈ విధానపు ప్రధాన లక్షణాలను కింది విధంగా పేర్కొనవచ్చు. అవి :

1. సంస్థలు :
ధరల విధానాల అమలుకై ప్రభుత్వం రెండు సంస్థలను నెలకొల్పింది. అవి :

i. వ్యవసాయ ధరల సంఘం (1965) :
వ్యావసాయిక ధరల విధానం, కనీస మద్ధతు ధరలను నిర్ధారించడంలోనూ, వ్యావసాయిక ఉత్పత్తుల సేకరణ ధరలకు సంబంధించి ఈ సంఘం ప్రభుత్వానికి సలహాలనిస్తుంది.

ii. భారతదేశ ఆహార కార్పోరేషన్ (Food Corporation of India-1985) :
ప్రభుత్వంచే నిర్ధారించబడిన ధరల వద్ద ఆహారధాన్యాల సేకరణను వ్యవస్థీకరించడం, ప్రజా పంపిణీ వ్యవస్థ ద్వారా వాటి అమ్మకాలను కొనసాగించడం ఈ కార్పోరేషన్ పరిధిలోకి వస్తాయి.

2. కనీస మద్ధతు ధరలను (Minimum Support Price) లేదా సేకరణ ధరలను నిర్ణయించడం :
ప్రతి సంవత్సరం వ్యావసాయిక వ్యయాల ధరల సంఘం (CACP) చేసిన సూచనల ప్రాతిపదికన గోధుమ, బియ్యం, మొక్కజొన్న లాంటి ప్రధాన వ్యావసాయిక ఉత్పత్తుల కనిష్ట మద్దతు ధరలను ప్రభుత్వం నిర్ణయిస్తుంది.

3. గరిష్ఠ ధర నిర్ణయం :
కొన్ని నిర్ధిష్ట వ్యావసాయిక వస్తువులకు ప్రభుత్వం గరిష్ఠ ధరలను నిర్ధారిస్తుంది. ప్రజా పంపిణీ వ్యవస్థ కింద ఫల వ్యవసాయిక ఉత్పత్తులైన ధాన్యాలు, చక్కెర, బియ్యం మొదలైన వాటిని సరసమైన ధరలకు ప్రభుత్వం అమ్మకాలను ఛేపట్టడం జరుగుతుంది.

ప్రజాపంపిణీ వ్యవస్థ అనేది ధరల విధానపు మరొక ముఖ్య లక్ష్యం. ఇది రెండు రకాలైన రేషనింగ్ను కలిగి ఉంటుంది. అవి : శాసనపరమైన రేషనింగ్, అనియత రేషనింగ్ (informal rationing). శాసనపరమైన నియంత్రిత (rationed) ప్రాంతాలలో బహిరంగ మార్కెట్ పనితీరును చట్టాన్ని అనుసరించి నిరోధించబడుతుంది.

4. బఫర్ నిల్వలు :
ధర చాంచల్యాలు లేకుండా చేసే ఏకైక ఉద్దేశ నిమిత్తమై నిల్వల, అమ్మకాల, కొనుగోళ్ళను బఫర్ నిల్వలు సూచిస్తాయి. దీనిని FCI చేపడుతుంది. అహార ధాన్యాల ధర పెరగడం ప్రారంభమైనపుడు, నిర్ధిష్ట ధరల వద్ద బఫర్ నిల్వల నుంచి ఆహార ధాన్యాల అమ్మకాలను ప్రభుత్వం ప్రారంభిస్తుంది. తత్ఫలితంగా ఆహార ధాన్యాల ధరలలోని పెరుగుదల నియంత్రించ
బడుతుంది.

ప్రశ్న 10.
భారతదేశంలో ఆహార భద్రత కల్పనకు చర్యలు వ్రాయండి.
జవాబు.
ఆహార భద్రత భావన :
ప్రపంచ ఆరోగ్య భద్రతపై నివేదికను అందజేసిన ఐక్యరాజ్య సమితి కమిటీ ప్రకారం “ప్రజలందరికి అన్ని కాలాలలో చురుకైన, ఆరోగ్యవంతమైన జీవనానికి తమ అభిరుచి మరియు ఆహారపు అలవాట్ల ప్రకారం తగినంత సురక్షితమైన, * పౌష్టికాహారం భౌతికంగా, సామాజికంగా, ఆర్థికంగా అందుబాటులో ఉండటం”ను ఆహార భద్రత అంటాం.

ప్రపంచ అభివృద్ధి నివేదిక (World Development Report, 1986) ప్రకారం, “చురుకైన, ఆరోగ్యవంతమైన జీవనాని కోసం అన్ని సమయాలలో చాలినంత ఆహారం ప్రజలందరికీ అందుబాటులో ఉండటమే ఆహార భద్రత”. ఆహార వ్యవసాయ సంస్థ (Food and Agriculture Organisation, 1983) ప్రకారం “ప్రజలందరికీ అన్ని సమయాలలో అవసరమైన ప్రాథమిక ఆహారాన్ని భౌతికంగా, ఆర్థికంగా అందుబాటులోకి తేవడమే ఆహార భద్రత” గా చెప్పవచ్చు.

భారతదేశంలో ఆహార భద్రత ఏర్పాటుకు చర్యలు :
ఆహార భద్రత సమస్యకు చెందిన పరిమాణాత్మక, గుణాత్మక అంశాలను పరిష్కరించేందుకు భారత ప్రభుత్వం క్రింది మూడు ఆహార ఆధారిత భద్రతా వలలపై ఆధారపడింది.

• ప్రజా పంపిణీ వ్యవస్థ ఆర్యా
• సమగ్ర శిశు అభివృద్ధి సేవలు.
• మధ్యాహ్న భోజన పథకం.

i) ప్రజా పంపిణీ వ్యవస్థ :
ప్రజా పంపిణీ వ్యవస్థ క్రింద ఆహార ధాన్యాలను చౌకధరలకు చౌకధరల దుకాణాల ద్వారా అందించడం జరుగుతుంది. ఇది ఇప్పుడు లక్షిత ప్రజా పంపిణీ వ్యవస్థగా పనిచేస్తుంది. దీని కింద పేదలలోని లక్షిత నిరుపేదలకు ముందుగా సేవలను అందిస్తారు.

ii) సమగ్ర శిశు అభివృద్ధి సేవలు :
ఈ పధకం క్రింద ప్రిస్కూల్ కేంద్రాల (అంగన్ వాడీ కేంద్రాలు) ద్వారా ఇంకా పాఠశాలకు వెళ్ళని బాల, బాలికలకు ఉచిత ఆహారం పంపిణీ జరుగుతుంది.

iii) ‘మధ్యాహ్న భోజన పధకం :
పాఠశాలకు వెళ్ళే బాల, బాలికలకు ఈ పధకం క్రింద మధ్యాహ్నం ఉచితంగా భోజన -సౌకర్యం కల్పిస్తున్నారు.

ఆహారభద్రత చట్టం :
భారతదేశంలో ఆహార భద్రతను కల్పించడం కోసం సమగ్ర విధానంగా భారత ప్రభుత్వం 2013 సం. జూలైలో జాతీయ ఆహార భద్రతా చట్టంను ఆమోదించారు. ఈ చట్టం ప్రకారం దేశంలోని 67 శాతం ప్రజలకు (గ్రామాలలో 75 శాతం, పట్టణాలలో 50 శాతం) న్యాయమైన హక్కుగా అధిక సబ్సిడీతో కూడిన ఆహార ధాన్యాల పంపిణీ ఉంటుంది. ప్రతి వ్యక్తికి, ప్రతి నెల అయిదు కిలోల చొప్పున ప్రాధాన్యతా కుటుంబాలకు ఆహార ధాన్యాల సరఫరా ఉంటుంది. అంత్యోదయ అన్న

యోజన కుటుంబాలకు చెందిన ప్రతి కుటుంబంకు ప్రతి నెల 35 కిలోల ఆహార ధాన్యాలను అధిక సబ్సిడీతో కూడిన ధరలకు ప్రతి కిలోకు న్యూట్రీసిరల్స్ అయితే రూ.1, గోధుమలు అయితే రూ. 2, బియ్యం అయితే రూ.3కి అందిస్తారు. 2011 జనాభా లెక్కల ప్రకారం లబ్ధిదారుల సంఖ్యను నిర్ణయిస్తారు.

ఆ ప్రకారం దేశంలోని 36 రాష్ట్రాలు మరియు కేంద్రపాలిత ప్రాంతాలలోని 81.35 కోట్ల ప్రజలు ఈ పథకం క్రిందికి వస్తారు. ఈ చట్టం క్రింద మరియు ఇతర సంక్షేమ పథకాల క్రింద కలిపి మొత్తం 610 లక్షల మెట్రిక్ టన్నుల ఆహార ధాన్యాలను ఒక సంవత్సరానికి కేటాయిస్తారు.

గర్భవతులు గర్భవతులుగా ఉన్న కాలంలోనూ, మరియు ప్రసవం తరువాత ఆరునెలల వరకు అంగన్ వాడీల ద్వారా ఉచితంగా ఆహారం పొందుతారు మరియు ప్రసవం తరువాత ప్రసూతి ప్రయోజనంగా రూ. 6,000 పొందుతారు. ఆరునెలల నుండి 6సం॥ల వయస్సు గల బాల బాలికలకు అంగన్ వాడీల ద్వారా ఉచితంగా ఆహారం అందిస్తారు.

పాఠశాలకు వెళ్ళే 6 నుండి 14 సం॥ ల బాల బాలికలకు మాధ్యమిక తరగతుల వరకు ఉచితంగా మధ్యాహ్నం భోజనం ఇస్తారు. ఒకవేళ ప్రభుత్వం అర్హులకు ఆహార ధాన్యాలను పంపిణీ చేయకపోతే ఆహార భద్రత భత్యంను ఇవ్వవలసి ఉంటుంది.

స్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
వ్యవసాయ రంగం వృద్ధి తీరును వివరించండి.
జవాబు.
వ్యవసాయ వృద్ధి : ఈ భావనను క్రింది రెండు అంశాల దృష్ట్యా చర్చించవచ్చు.

i) వ్యవసాయ వృద్ధి ధోరణులు :
స్వాతంత్ర్యం వచ్చేనాటికి భారత వ్యవసాయం వెనుకబడిన స్థితిలో ఉంది. రైతులు ఎక్కువగా అప్పుల పాలవడమే కాకుండా, సరైన యంత్రాలను, మంచి విత్తనాలను, రసాయన ఎరువులను వాడటానికి కావలసిన పరిజ్ఞానం వారికి లేదు. నీటి పారుదల సౌకర్యాలున్న కొన్ని ప్రాంతాలు తప్ప మిగతా అన్ని చోట్ల రైతులు వర్షపాతం, వర్షాకాలం పైన ఆధారపడ్డారు. హెక్టారుకు శ్రామికుని ఉత్పాదకశక్తి చాలా అల్పంగా ఉండేది. ఆహార ధాన్యాల విషయంలో స్వయం సమృద్ధి లేకపోవడం వల్ల దేశం ఆహార ధాన్యాల దిగుమతుల పైన ఆధారపడింది.

70 శాతం వ్యవసాయ రంగం పైన ఆధారపడ్డారు. భారతదేశం తన ఆర్థికాభివృద్ధి కోసం అమలు పరిచిన ప్రణాళికా ప్రక్రియలో మొదటి (1951-56), మూడవ (1961-66) మరియు నాల్గవ (1969-74) పంచవర్ష ప్రణాళికలు. వ్యవసాయ రంగంకు అధిక శాతం నిధులను కేటాయించడం వల్ల ఈ రంగానికి ప్రాధాన్యతను ఇచ్చాయి. వ్యవసాయ అభివృద్ధి కొరకు భారతదేశం భూసంస్కరణలను కూడా అమలు పరిచింది.

1966-67 సం||లో ఆధునిక వ్యవసాయ ఉత్పాదకాలయిన అధిక దిగుబడి వంగడాల విత్తనాలు, రసాయనిక ఎరువులు, తెగుళ్ళ నివారణ మందులు మొదలగు వాటిని సరఫరా చేయడం ద్వారా నూతన వ్యవసాయక వ్యూహంను భారతదేశం అనుసరించింది. ఫలితంగా భారతదేశం 1976 సం॥ నాటికి ఆహార ధాన్యాల ఉత్పత్తిలో స్వయం సమృద్ధిని సాధించింది.

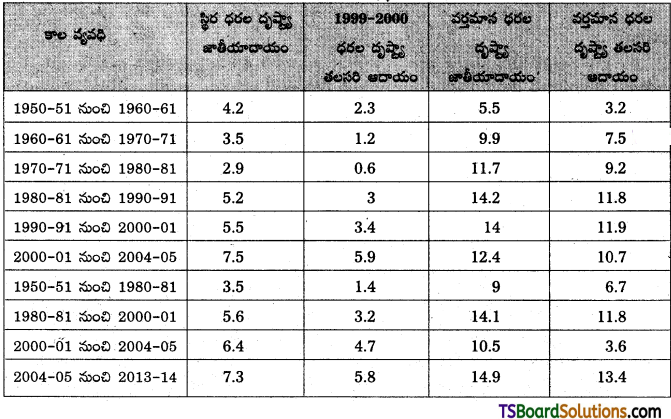
1950-51 నుండి 2019-20 మధ్యకాలంలో భారతదేశ వ్యవసాయ రంగ సగటు వార్షిక వృద్ధి దాదాపు 3 శాతంగా ఉంది. భారతదేశ ఆర్థిక వ్యవస్థ తక్కువ వృద్ధి రేటు (హిందూ వృద్ధి రేటు)ను సాధించిన దశ (సగటు వార్షిక వృద్ధి 3.5 శాతం 1950-51 నుండి 1969 – 70 వరకు) లోనూ, మాధ్యమిక వృద్ధి రేటును సాధించిన దశ (దాదాపు 5 శాతం వార్షిక ఆర్థిక వృద్ధి 1970-71 నుండి 1990-91 వరకు) లోనూ, అధిక వృద్ధిని సాధించిన కాలం (1991-92 నుండి 2019-20 వరకు దాదాపు 7 శాతం సగటు వార్షిక ఆర్థిక వృద్ధి) లోనూ వ్యవసాయ రంగం వృద్ధి రేటు వరుసగా 3.5 శాతం, 5 శాతం, 7 శాతంగా ఉంది. ఆర్థిక సంస్కరణల కాలంలో భారతదేశం సాధించిన అధిక వృద్ధిరేటు సేవల రంగం ప్రత్యేకించి సమాచార, సాంకేతిక రంగం సాధించిన వృద్ధితోనే ప్రభావితం అయింది.

ii) ప్రధాన పంటల ఉత్పాదకత, ఉత్పత్తిలో పెరుగుదల :
భారతదేశానికి స్వాతంత్య్రం వచ్చిన ప్రారంభంలో ప్రధాన పంటల ఉత్పాదకత, ఉత్పత్తి చాలా తక్కువగా ఉన్నప్పటికీ భారతదేశం 60వ దశకం రెండవ భాగంలో అనుసరించిన నూతన వ్యవసాయిక వ్యూహం వలన 70వ దశకంలో పెరిగింది. వ్యవసాయ ఉత్పాదకత, ఉత్పత్తిలో వచ్చిన గణనీయమైన పెరుగుదలనే హరిత విప్లవం అన్నారు.

1) ఆహారధాన్యాల ఉత్పత్తి 50.8 మిలియన్ టన్నుల (మి.ట) నుండి 285 మిలియన్ టన్నులకు పెరిగింది. అదే కాలంలో బియ్యం ఉత్పత్తి 20.5 మి.ట నుండి 116.4 మి.టలకు, గోధుమల ఉత్పతి 6.4 మి.ట నుండి 102.2 మి.టలకు, మొక్కజొన్నల ఉత్పత్తి 1.7 మి.ట నుండి 27.2 మి. టలకు, పప్పుధాన్యాల ఉత్పత్తి 8.4 మి.ట నుండి 23.4 మి.ట లకు, నూనె గింజల ఉత్పత్తి 5.1 మి.ట నుండి 23.4 మి.టలకు పెరిగింది. ప్రధాన పంటల ఉత్పత్తి విషయంలో కూడా ఎక్కువ పెరుగుదల గోధుమల ఉత్పత్తిలో ఉండగా తక్కువ పెరుగుదల పప్పు ధాన్యాల ఉత్పత్తిలో ఉంది.

2) ఆహార ధాన్యాల ఉత్పాదకత 1950-51 సం॥లో సగటున ఒక హెక్టారుకు 522 కిలోలుగా ఉండి 2018-19 సం॥ నాటికి 2299 కిలోలకు పెరిగింది. అదే కాలంలో బియ్యం ఉత్పాదకత 688 కిలోల నుండి 2,659 కిలాలకు, గోధుమ ఉత్పాదకత 663 కిలోల నుండి 3,507 కిలోలకు, మొక్కజొన్నల ఉత్పాదకత 547 కిలోల నుండి 2,966 కిలోలకు, పప్పుధాన్యాల ఉత్పాదకత 441 కిలోల నుండి 806 కిలోలకు, నూనెగింజల ఉత్పాదకత 481 కిలోల నుండి 1265 కిలోలకు పెరిగింది. మొత్తం మీద 1950-51 నుండి 2018-19 సం॥ల మధ్యకాలంలో గోధుమల ఉత్పాదకత ఆరు రెట్లు పెరగగా, పప్పుధాన్యాల ఉత్పాదకత రెండింతలు పెరిగింది.

ప్రశ్న 2.
భారతదేశ ప్రధాన వ్యవసాయ పంటల ఉత్పత్తిలో గల ధోరణులను వ్రాయండి.
జవాబు.
ప్రధాన పంటల ఉత్పత్తిలో గల పెరుగుదల :
భారతదేశం 60వ దశకం రెండవ భాగంలో అనుసరించిన నూతన వ్యవసాయిక వ్యూహం వలన 70వ దశకంలో పెరిగింది. వ్యవసాయ ఉత్పాదకత, ఉత్పత్తిలో వచ్చిన గణనీయమైన పెరుగుదలనే హరిత విప్లవం అని అంటాము. ప్రధాన పంటల ఉత్పత్తిలో గల పెరుగుదలను క్రింది పట్టిక ద్వారా వివరించవచ్చును.

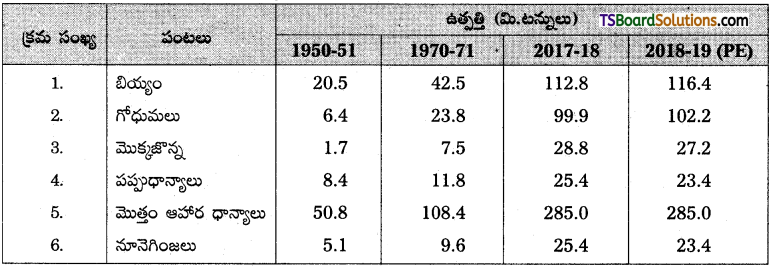
పట్టిక ప్రకారం ఉత్పత్తి ధోరణి పరిశీలిస్తే 1950 – 51 సం॥ నుండి 2018-19 సం॥ల మధ్య కాలంలో ఆహారధాన్యాల ఉత్పత్తి 50.8 మిలియన్ టన్నుల (మి.ట) నుండి 285 మిలియన్ టన్నులకు పెరిగింది. అదే కాలంలో బియ్యం ఉత్పత్తి 20.5 మి.ట నుండి 116.4 మి.టలకు, గోధుమల ఉత్పతి 6.4 మి.ట నుండి 102.2 మి.టలకు, మొక్కజొన్నల ఉత్పత్తి 1.7 మి.ట నుండి 27.2 మి.టలకు, పప్పుధాన్యాల ఉత్పత్తి 8.4 మి.ట నుండి 23.4 మి.ట లకు, నూనె గింజల ఉత్పత్తి 5.1 మి.ట నుండి 23.4 మి.టలకు పెరిగింది. ప్రధాన పంటల ఉత్పత్తి విషయంలో కూడా ఎక్కువ పెరుగుదల గోధుమల ఉత్పత్తిలో ఉండగా తక్కువ పెరుగుదల పప్పు ధాన్యాల ఉత్పత్తిలో ఉంది.

ప్రశ్న 3.
భారతదేశంలో వ్యవసాయోత్పాదకత ధోరణులేవి ? వివరించండి.
జవాబు.
వ్యవసాయ ఉత్పత్తి అంటే సాగు చేస్తున్న మొత్తం నుంచి లభించిన మొత్తం ఉత్పత్తి. అదే వ్యవసాయ ఉత్పాదకత అనగా సగటున ఒక హెక్టారు నుండి లభించిన దిగుబడి. భారతదేశంలో వ్యవసాయోత్పాదకతలో వివిధ పంటల ధోరణులను క్రింది పట్టిక ద్వారా వివరించవచ్చు.

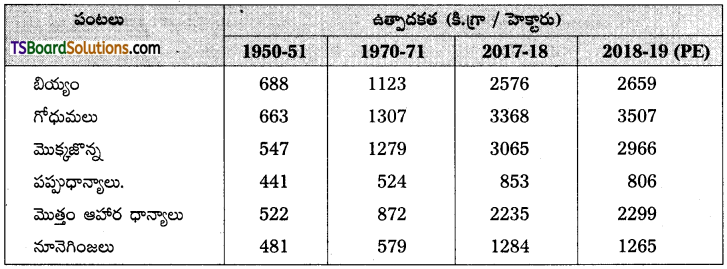
ప్రధాన పంటల ఉత్పత్తి ధోరణిని పరిశీలిస్తే 1950-51 సంవత్సరం నుండి 2018-19 సం॥ల మధ్యకాలంలోమొత్తం ఆహార ధాన్యాల ఉత్పాదకత 1950-51 సం॥లో సగటున ఒక హెక్టారుకు 522 కిలోలుగా ఉండి 2018-19 సం॥ నాటికి 2299 కిలోలకు పెరిగింది.

అదే కాలంలో బియ్యం ఉత్పాదకత 688 కిలోల నుండి 2,659 కిలాలకు, గోధుమ ఉత్పాదకత 663 కిలోల నుండి 3,507 కిలోలకు, మొక్కజొన్నల ఉత్పాదకత 547 కిలోల నుండి 2, 966 కిలోలకు, పప్పుధాన్యాల ఉత్పాదకత 441 కిలోల నుండి 806 కిలోలకు, నూనెగింజల ఉత్పాదకత 481 కిలోల నుండి 1265 కిలోలకు పెరిగింది. మొత్తం మీద 1950-51 నుండి 2018-19 సం॥ల మధ్యకాలంలో గోధుమల ఉత్పాదకత ఆరు రెట్లు పెరగగా, పప్పుధాన్యాల ఉత్పాదకత రెండింతలు పెరిగింది.

ప్రశ్న 4.
భారతదేశంలో భూ సంస్కరణల అమలు సరిగా లేకపోవడానికి కారణాలు ఏమిటి ?
జవాబు.
భూ సంస్కరణల అమలు విమర్శనాత్మక పరిశీలన :
భారతదేశంలో భూసంస్కరణ కార్యక్రమాలు ఎంతో ఉత్సాహంగా ప్రారంభించబడ్డాయి. సమ సమాజ ఆవిర్భావానికి భూసంస్కరణలు సాధనాలుగా ప్రశంసించబడ్డాయి. సిద్ధాంతపరంగా వ్యవసాయ రంగంలో వ్యవస్థాపూర్వక మార్పులను తేవడంతో పాటు వ్యవసాయ ఉత్పత్తుల పెరుగుదలకు ఈ సంస్కరణలు దోహదపడతాయి. అయితే, అమలు ఏమాత్రం సంతృప్తికరంగా లేదు. భూసంస్కరణల అమలులో వైఫల్యాలకు కింది కారణాలు ప్రధానమైనవి.

1. చట్టాలలో లొసుగులు :
భూ సంస్కరణల చట్టాలలో లొసుగులు (loopholes in the acts) ఉన్నాయి. ఈ లొసుగులను ఉపయోగించుకొని పెద్ద భూస్వాములు తమ ఆర్థిక, రాజకీయ బలంతో భూమిపై తమ యాజమాన్యాన్ని నిలుపుకోగలిగారు.

2. రాజకీయ నిబద్ధత లేకపోవడం :
అధికారంలో ఉన్న రాజకీయ పార్టీలు పెద్ద భూస్వాములకు ఎటువంటి ఉపద్రవాన్ని కల్గించకుండా ఉండటానికి చట్టాల అమలులో నిజమైన శ్రద్ధను కనబరచలేదు. అందువల్ల చట్టాలను నిర్వీర్యపరిచారు.

3. లబ్ధిదారుల నిశ్చేష్ట స్వభావం :
సన్నకారు, చిన్న రైతులు, భూమిలేని శ్రామికులు వారి హక్కులకు, జరుగుతున్న ప్రక్రియకు సంబంధించిన పరిజ్ఞానంను కలిగిలేరు. వీరిలో అధిక సంఖ్యాకులు నిరక్షరాస్యతతో, అమాయకంగా ఉంటారు. తమకు ప్రయోజనం కలిగించే సంస్కరణల పట్ల వీరికి చైతన్యం తక్కువ.

4. పాలనా యంత్రాంగం :
భారతదేశంలో ప్రభుత్వ యంత్రాంగం వలస పాలనలో శిక్షణ పొంది ఆ పద్ధతులకు అలవాటు పడింది. అందువల్ల భూసంస్కరణల పట్ల, గ్రామీణ ప్రజల సమస్యల పట్ల ఉదాసీన వైఖరిని ప్రదర్శించడం జరిగింది. · సంస్కరణల అమలులో తగినంత శ్రద్ధను ప్రభుత్వ యంత్రాంగం కనబరచలేదు.

5. న్యాయపరమైన అవరోధాలు :
చట్టంలోని లొసుగులను అనుకూలంగా చేసుకొని ఇంతమంది పెద్ద భూస్వాములు న్యాయ స్థానాలలో కేసులు వేశారు.

6. భూమి రికార్డులు అందుబాటులో లేకపోవడం :
దశాబ్దాల తరబడి భారతదేశంలో భూమికి సంబంధించిన రికార్డులు సరైన తీరులో నిర్వహించబడలేదు. సరైన రికార్డులు లేకపోవడం వల్ల సంస్కరణల అమలు కష్టతరమైన కార్యక్రమంగా మారింది.

7. రాష్ట్ర జాబితా :
వ్యవసాయం రాష్ట్ర ప్రభుత్వ జాబితాలోని అంశం. వివిధ రాష్ట్రాలు చట్టాలను వివిధ స్థాయిలలో అమలు పరిచాయి. భూసంస్కరణల చట్టాల అమలులో రాష్ట్రాల చర్యలకు ఏకీకృత స్వభావం లేదు. జాతీయ భూసంస్కరణల మండలి (National Council for Land Reforms) 2008లో స్థాపించబడినా ఫలితం శూన్యంగా ఉంది.

8. తదుపరి చర్యలలో జాప్యం :
తదుపరి చర్యలను (follow up actions) తీసుకోవడంలో పాలనా యంత్రాంగం అసాధారణ జాప్యాన్ని ప్రదర్శించింది. ప్రకటిత మిగులు భూమి మొత్తం ప్రభుత్వ స్వాధీనంలోకి తీసుకోబడలేదు. స్వాధీనం చేసుకొన్న మొత్తం భూమి పంపిణీ చేయబడలేదు. పరపతి, ఇతర ఉత్పాదకాలు లాంటి అనుషంగిక సహాయాన్ని లబ్దిదారులకు అందజేయలేదు. భూమిపై యాజమాన్య హక్కులు మాత్రమే లబ్దిదారులకు కల్పించబడ్డాయి.

ప్రశ్న 5.
సంస్థాపరంకాని వ్యవసాయ పరపతి మూలాధార లోపాలు ఏమిటి ?
జవాబు.
కాలాన్ని, పరపతి ఉద్దేశాన్ని అనుసరించి మన దేశంలో వ్యవసాయదారులు కోరుకొనే పరపతి మూడు రకాలుగా ఉంటుంది. అవి :

1. వ్యవసాయ సాగుకు 15 నెలల లోపు అవసరమయ్యే స్వల్పకాలిక రుణం. ఇది విత్తనాలు, ఎరువులు, పశుగ్రాసం వంటి కొనుగోళ్ల రూపంలో ఉంటుంది.
2. వ్యవసాయ భూమిని బాగు చేయడానికి పశువులు, వ్యవసాయ పనిముట్లు వంటి వాటి కొనుగోలు కోసం వ్యవసాయదారులకు 15 నెలల నుంచి 5 సంవత్సరాల కాల పరిమితి ఉండే మధ్య కాలిక పరపతి అవసరమవుతుంది.
3. భూమిని అభివృద్ధి చేయడానికి, నీటి సౌకర్య ఏర్పాటుకు, భారీ యంత్రాల కొనుగోలు మొదలైన వాటి కోసం వీరికి 5 సంవత్సరాల పైబడిన దీర్ఘకాలిక అవసరం ఉంటుంది.

మనదేశంలో వ్యవసాయదారులకు అవసరం అయ్యే పరపతిని ఉత్పాదక, అనుత్పాదక రుణాల రూపంగా విభజించవచ్చు. విత్తనాలు, ఎరువులు, పశువులు, వ్యవసాయ పనిముట్ల కొనుగోలు, బావులు లేదా గొట్టపు బావులు త్రవ్వకం వంటి వాటి కోసం ఉత్పాదక రుణాలు అయితే పెళ్ళిళ్ళు, సామాజిక వేడుకలు, మతపరమైన వేడుకలు, పండుగలు వంటి వాటిపై చేసే ఖర్చు అవసరాల కోసం అనుత్పాదక ఋణాలు.

సంస్థాపూర్వకం కాని ఆధారాలు :
సంస్థాపూర్వకం కాని ఆధారాల్లో వడ్డీ వ్యాపారులు, భూస్వాములు, వ్యాపారస్థులు, కమీషన్ ఏజెంట్లు, బంధువులు, మిత్రులు మొదలైనవారు ఉంటారు. 1951-52 లో వ్యవసాయ పరపతికి సంబంధించి సంస్థాపూర్వకం కాని మార్గంలో వ్యవసాయదారులు 93 శాతం రుణాన్ని పొందితే ప్రభుత్వం కేవలం 7 శాతం పరపతిని సమకూర్చింది. వడ్డీ వ్యాపారులు, భూస్వాములు ఉత్పాదక, అనుత్పాదక రుణాలను కల్పిస్తారు.

వీరు ఏ సమయంలోనైనా వ్యవసాయదారులకు సులభంగా అందుబాటులో ఉంటారు.

1. ఈ రకమైన వ్యవస్థ వడ్డీ వసూళ్ళలో ఏకరూపత ఉండదు.
2. అత్యధిక వడ్డీ 18 నుంచి 50 శాతం వరకు కూడా ఉంటుంది.
3. చిన్న రైతులను మోసం చేయడమే కాకుండా వారి వ్యవసాయ భూమిని కూడా స్వాధీనం చేసుకొంటారు.
4. భూమి లేని శ్రామికులు బలవంతంగా బానిసలుగా మారే అవకాశం ఈ వ్యవస్థలో ఉంటుంది.

ప్రశ్న 6.
గ్రామీణ ఋణగ్రస్తతకు గల కారణాలు ఏవి ?
జవాబు.
గ్రామీణ ఋణగ్రస్తతకు గల కారణాలు : గ్రామీణ ప్రాంతాల్లో ఋణం పెరగడానికి కింది విషయాలు కారణభూతం అవుతున్నాయని చెప్పవచ్చు. అవి :

1. గ్రామ ప్రాంతాల్లో రైతులు రుణగ్రస్తులుగా మారడానికి ప్రధాన కారణం వారి పేదరికం, తక్కువ స్థాయి పొదుపులు, పంట నష్టపోవడం.
2. అప్పులు చేసి పొలాలను బాగుపరచి అభివృద్ధి చేయాలనే తపన.
3. అనుత్పాదక పనులపై ఖర్చు పెట్టడం.
4. తల్లిదండ్రుల నుంచి వారసత్వంగా అప్పులు సంక్రమించడం.
5. సంస్థాగతం కాని ఋణాలపైన ఎక్కువగా ఆధారపడటం.
6. పంటలకు మద్ధతు ధరలు తగినంతగా లేకపోవడం.
7. సేద్యపు ఖర్చులు బాగా పెరిగిపోవడం.

ప్రశ్న 7.
నాబార్డు విధులను వివరించండి.
జవాబు.
వ్యవసాయ రంగ అభివృద్ధికి ఉన్నత స్థితిని కల్పించడానికి, బ్యాంకులకు పునర్ విత్త సౌకర్యం కల్పించడం కోసం రిజర్వు బ్యాంకు వ్యవసాయ పునర్ విత్త అభివృద్ధి కార్పోరేషన్ (ARDC) ని నెలకొల్పింది. బ్యాంకు పరపతి పాత్ర వ్యవసాయ రంగ అభివృద్ధికే పరిమితం కాక గ్రామీణ అభివృద్ధికి కూడా విస్తరించడంతో పరపతి సంస్థలకు ఊతాన్ని, మార్గదర్శనాన్ని ఇవ్వడానికి శిఖరాగ్ర స్థాయిలో విస్తృత వ్యవస్థను ప్రభుత్వం ప్రతిపాదించింది. తదనుగుణంగా (ARDC) స్థానంలో జులై 1982వ సం||లో జాతీయ వ్యవసాయ గ్రామీణ అభివృద్ధి బ్యాంకు (నాబార్డు NABARD) ను స్థాపించారు.

సాధారణంగా నాబార్డ్ ఈ క్రింది విధులను నిర్వహిస్తుంది :

1. గ్రామీణ ప్రాంతాల్లో పెట్టుబడి, ఉత్పత్తి పనులకు పరపతిని అందించేందుకు గాను అన్ని రకాల సంస్థలకు ఋణాలను అందిస్తుంది.
2. గ్రామీణ అవస్థావనా సౌకర్యాలను అభివృద్ధి చేసేందుకుగాను రాష్ట్ర ప్రభుత్వాలకు, ప్రభుత్వేతర సంస్థలకు (NGO) పంచాయితీ రాజ్ సంస్థలకు రుణాలను అందిస్తుంది.
3. ప్రభుత్వేతర సంస్థలు, ఇతర సంస్థాగతంగాని ఏజెన్సీల నవకల్పనలకు దోహదం చేస్తుంది.
4. స్వయం సహాయక బృందాలను (SHGs) ప్రోత్సహిస్తూ వ్యవస్థీకృత బ్యాంకుల సేవలను గ్రామీణ పేదలకు అందేలా చూస్తుంది.
5. వర్షాధార వ్యవసాయం ఉత్పాదకత లాభదాయకతలు మనగలిగే విధంగా ప్రజల భాగస్వామ్యంతో వాటర్ షెడ్లను అభివృద్ధి చేస్తుంది.
6. అభివృద్ధి పరచడానికి అనుకూలంగా ఉండే వ్యవసాయ, వ్యవసాయేతర అవకాశాలను గుర్తించి, బ్యాంకుల రుణాల ద్వారా వాటిని అభివృద్ధి చేసేందుకు వీలుగా పరపతి ప్రణాళికలను తయారు చేస్తుంది.
7. ప్రాంతీయ గ్రామీణ బాంకుల, సహకార బాంకుల కార్యకలాపాలను తనిఖీ చేస్తుంది.
8. అభివృద్ధి చర్యల్లో అన్నిసంస్థలు చేస్తున్న విత్త సహాయక పనులను సమన్వయ పరుస్తుంది.
9. రైతుల క్లబ్బుల ద్వారా సాంకేతిక విజ్ఞానాన్ని బదిలీచేసే పనులకు సహాయాన్ని అందిస్తుంది.
10. గ్రామీణ ప్రాంతాల్లో వ్యవసాయేతర రంగాలైన చిన్న తరహా పరిశ్రమలు, చిన్న మధ్య తరహా వ్యాపార సంస్థలు, కుటీర, గ్రామీణ పరిశ్రమలు, హస్తకళలు, ఇతర గ్రామీణ వృత్తులకు పునర్విత్త సహాయాన్ని అందించి అభివృద్ధి పరుస్తుంది.

ప్రశ్న 8.
భారతదేశ వ్యవసాయ మార్కెటింగ్లో గల లోపాలు ఏవి ?
జవాబు.
జాతీయ వ్యవసాయ కమీషన్ అభిప్రాయంలో, “వ్యవసాయ మార్కెటింగ్లోని వివిధ దశలను కలుపుకొని ప్రస్తుత ధరల వద్ద రైతులు తమ ఉత్పత్తులకు విక్రయించే ప్రక్రియే వ్యవసాయ మార్కెటింగ్”.
పై నిర్వచనం ప్రకారం వ్యవసాయ మార్కెటింగ్ అంటే మార్కెట్ ధరల వద్ద వ్యవసాయదారులు తమ ఉత్పత్తిని అంతిమ వినియోగదారులకు చేర్చే ప్రక్రియను వ్యవసాయ మార్కెటింగ్ అని చెప్పవచ్చు. పంట పండించడానికి ముందు పండించిన తరువాత జరిగే కార్యకలాపాలన్నీ వ్యవసాయ ఉత్పత్తి కిందకు వస్తాయి.

భారత వ్యవసాయ మార్కెటింగ్లో లోపాలు:
భారత వ్యవసాయ మార్కెటింగ్ దోపిడీ అధికంగా ఉంది.. అందువల్ల రైతులు తమ ఉత్పత్తులకు గిట్టుబాటు ధరలను పొందలేకపోతున్నారు. వ్యవసాయ మార్యెటింగ్ లోని ముఖ్యమైన లోపాలను కింద వివరించడం జరిగింది.

1. మధ్యవర్తుల జోక్యం :
దళారీలు వ్యాపారులతో రహస్య మంతనాలు జరిపి ఉత్పత్తులకు తక్కువ ధర చెల్లించి రైతులను మోసగిస్తున్నారు. రకరకాల మోసపూరిత పద్ధతుల ద్వారా వీరు రైతులను దోపిడికి గురి చేస్తున్నారు. కొన్ని అధ్యయనాల ప్రకారం ఉత్పత్తి యొక్క మార్కెట్ ధరల్లో 60 నుంచి 70 శాతం వరకు మధ్య దళారీలే దోచుకుంటున్నారన్నది ఒక అంచనా.

2. మార్కెట్ లోని మోసపూరిత విధానాలు:
వ్యాపారస్తులు ఉపయోగించే తూనికలు, కొలతలు ప్రామాణికమైనవికావు. వీరు నాణ్యతా పరీక్షలు, ధర్మాలు, మాముళ్ల పేరిట ఉత్పత్తుల్లో కొంత భాగాన్ని కాజేస్తుంటారు. అంతేగాక వ్యాపారస్తులు రైతులకు ఉత్పత్తుల ప్రతిఫలాలను వాయిదా పద్ధతుల్లో చెల్లిస్తుంటారు. మార్కెట్లో రైతులకు, వ్యాపారులకు మధ్య వచ్చే వివాదాలను పరిష్కరించడం కోసం ఎలాంటి వివాద పరిష్కార – యంత్రాంగం ఏర్పాటు చేయబడలేదు.

`3. రవాణా సౌకర్యాల కొరత :
ఎక్కువ భాగం గ్రామీణ రహదారులు రైలు మార్గాలతోను, పక్కా రోడ్డు మార్గాలతో అనుసంధానం చేయబడలేదు. నేటికి మనదేశంలో రైతులు రవాణాకు ఎడ్లబండ్లను ఉపయోగిస్తున్నారు. అందువల్ల మనదేశంలోని అధిక భాగం రైతులు తమ ఉత్పత్తులను స్థానిక సంతలలో లేదా మండీలలో గిట్టుబాటు కాని ధరలకు అమ్ముకోవడం తప్పనిసరైంది.

4. గిడ్డంగి సౌకర్యాల కొరత :
గిడ్డంగి సౌకర్యాల కొరత వలన రైతులు తమ ఉత్పత్తులను పాతర్లలోను, మట్టికుండల్లోను అశాస్త్రీయ పద్ధతుల్లో నిల్వ చేస్తారు. ఈ అశాస్త్రీయ పద్ధతుల వల్ల తేమ తగిలి పంట నాణ్యత తగ్గుతుంది. అంతేకాక 10 నుంచి 20 శాతం వరకు పంటను చీమలు, ఎలుకలు, పందికొక్కులు తింటున్నాయి. రైతులు గిట్టుబాటు ధర వచ్చేంతవరకు ధాన్యాన్ని దాచుకోలేక తక్కువ ధరలకు నిర్బంధంగా అమ్ముకోవలసి వస్తుంది.

5. మార్కెట్ సమాచార లోపం :
మనదేశంలోని రైతులు గ్రామీణ ప్రాంతాల్లో నివసించడంవల్ల వీరికి మార్కెట్ సమాచారం తెలియదు. నిరక్షరాస్యులైన వీరికి డిమాండ్, సప్లయ్, ధరల్లో మార్పులు, ప్రభుత్వ ధరల విధానం, మొదలైన విషయ పరిజ్ఞానం ఉండదు. సమాచార లోపం కారణంగా రైతులు తమ ఉత్పత్తులకు గిట్టుబాటు ధరలను పొందడంలో విఫలమవుతున్నారు.

6. శ్రేణీకరణ, ప్రామాణికీకరణ సదుపాయాల కొరత:
వ్యవసాయ ఉత్పత్తులను మనదేశంలో తగిన రీతిలో శ్రేణీకరణ చేయడం లేదు. సాధారణంగా రైతులు తమ ఉత్పత్తులను నాణ్యతాపరంగా శ్రేణీకరణ, ప్రామాణికీకరణ చేయకుండా మొత్తం ఉత్పత్తినంతటిని ఒకే ధరకు అమ్ముతున్నారు. శ్రేణీకరణ చేయకపోవడం వల్ల రైతులు తమ నాణ్యమైన ఉత్పత్తులను సైతం తక్కువ ధరలకు అమ్ముకొని నష్టపోతున్నారు.

7. పరపతి సౌకర్యాల కొరత :
సంస్థాగత పరపతి సౌకర్యాల కొరతవల్ల మనదేశంలోని పేద రైతులు గ్రామీణ ప్రాంతాలలో పరపతి కోసం వడ్డీవ్యాపారులపై ఆధారపడుతారు. రైతులు పంట చేతికొచ్చిన తక్షణమే మార్కెట్ ధరలు ఎంత తక్కువగా ఉన్నప్పటికి అమ్మి వడ్డీ వ్యాపారులకు చెల్లించవలసి ఉంటుంది. అందువల్ల గిట్టుబాటు ధరలు వచ్చేంతవరకు వేచి ఉండలేక రైతులు నష్టపోతున్నారు.

8. రైతులు అసంఘటితంగా ఉండటం :
మనదేశంలోని రైతులు వేర్వేరు ప్రాంతాలలో నివసించడంవల్ల సంఘటితం కాలేకపోతున్నారు. కాని వ్యాపారస్తులు మాత్రం సంఘటితంగా ఉండి రైతులను గిట్టుబాటు ధరలు పొందకుండా అడ్డుకుంటున్నారు. ఫలితంగా అసంఘటితమైన రైతులు సంఘటితమై సమిష్టిగా బేరమాడుతున్న వ్యాపారస్తులను ఎదుర్కొని గిట్టుబాటు ధరలు పొందలేక నష్టపోతున్నారు.

ప్రశ్న 9.
వ్యవసాయ ధరల విధానపు లక్ష్యాలను పేర్కొనండి.
జవాబు.
వ్యవసాయ ధరల విధానపు లక్ష్యాలు :
జాతీయ ఆర్థిక వ్యవస్థలో వ్యవసాయపు సాపేక్ష ప్రాముఖ్యతపై ఆధారపడి, ఒకదేశం నుంచి మరొక దేశానికి గల వ్యావసాయిక ధరల విధానపు లక్ష్యాలు మారుతుంటాయి. సాధారణంగా, అభివృద్ధి చెందిన దేశాలలో ధర విధానం ప్రధాన లక్ష్యం వ్యావసాయక ఆదాయం అనూహ్యంగా తగ్గకుండా నిరోధించడం, ఏది ఏమైనప్పటికీ, వ్యావసాయక ధరల విధాన లక్ష్యాలను ఈ క్రింది విధంగా పేర్కొనవచ్చు. అవి :

1. దేశీయ వినియోగ అవసరాలను తీర్చడం.
2. వ్యావసాయిక ఉత్పత్తుల ధరలలో స్థిరీకరణను సాధించడం.
3. ఆహార ధాన్యాల, ఆహారేతర ధాన్యాల ధరల మధ్య సహేతుక సంబంధాన్ని ఆపాదించడం.
4. వ్యావసాయక పరమైన ఉత్పత్తుల ధరల యొక్క ఋణపరమైన, చక్రీయపరమైన చాంచల్యాలు లేకుండా చేయడం.
5. రెండు ప్రాంతాల మధ్యగల ధరల వ్యత్యాసాలను తొలగించడం.
6. కొరతలున్న సమయాలలో వినియోగ ఆహారం అందుబాటులోనికి తేవడం.
7. వ్యావసాయక ఉత్పత్తుల ఉత్పత్తి, ఎగుమతులను పెంచడం.
8. సహేతుకమైన ధరలవద్ద పరిశ్రమలకు ముడిసరుకులను కల్పించడం.
9. వ్యవసాయంలో ఆధునిక ఉత్పాదకాల స్థిర ఉపయోగితను కొనసాగించేందుకు రైతులు ఉత్పత్తి చేసిన ఉత్పత్తికిగాను వారికి కనీస గిట్టుబాటుధరను కల్పించడం ఆవశ్యకం. వ్యావసాయక ఉత్పత్తుల నిర్దిష్ట స్వభావం వల్ల నశ్వరత్వం, నిల్వ సమస్యల లాంటి వ్యావసాయక మార్కెటింగ్ లోని పలు ఇబ్బందులను అధిగమించడం కోసం సరైనపంట ప్రణాళికీకరణ కోసం ధరల విధానం ముఖ్యమైంది.
10. ధరల విధానంలేని సందర్భాలలో జమీందార్లు, ఇతర మధ్య దళారులు రైతుల నుంచి వారి ఉత్పత్తిని అతి తక్కువ ధరలకు కొనుగోలు చేస్తూ వారిని దోపిడీకి గురిచేసే క్రమాన్ని నిరోధించేందుకు ధరల విధానం ఆవశ్యకం.

అతిస్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
జాతీయాదాయంలో వ్యవసాయం వాటా.
జవాబు.
భారతదేశంలో ప్రణాళికలు ప్రారంభమైన తర: ఐ క, ద్వితీయ, తృతీయ గంగాలు అభివృద్ధి చెందడం వల్ల జాతీయాదాయంలో వ్యవసాయ రంగం వాటా తగ్గింది. 1950-51లో స్థూల దేశీయ ఉత్పత్తిలో వ్యవసాయ రంగం, దాని అనుబంధ రంగాల వాటా 56.5%. ఉంటే 2000-2001 నాటికి అవి 24.7% తగ్గింది. 2013-14 నాటికి 13.9% కి చేరింది. ఇది 2019 – 20 సం॥ నాటికి 16.5 శాతంగా అంచనా వేయబడింది.

ప్రశ్న 2.
ఉద్యోగితలో వ్యవసాయ వాటా.
జవాబు.
భారతదేశంలో చాలా అధిక శాతం. (శ్రామికులు వ్యవసాయ రంగంలో పనిచేస్తున్నారు. 1951లో 98 మిలియన్లు వ్యవసాయ రంగంలో పనిచేస్తే 2001 నాటికి ఈ సంఖ్య 235 మిలియన్లకు పెరిగింది. మొత్తం మీద వ్యవసాయ రంగంపై ఆధారపడిన ప్రజలు 2011వ సంవత్సరంలో 49 శాతం ఉండగా అది 201వ సం॥లో 43 శాతానికి తగ్గింది.

ప్రశ్న 3.
వ్యవసాయ పారిశ్రామిక సంబంధం
జవాబు.
వివిధ ముందంజ పరిశ్రమలకు వ్యవసాయ రంగం ముడిపదార్థాలను అందిస్తుంది. పంచదార, జనపనార, వస్త్ర పరిశ్రమ, వనస్పతి, పిండి మరలు, పండ్ల తోటలు, ఆహార తయారీ పరిశ్రమలు వ్యవసాయ రంగంపై ప్రత్యక్షంగా ఆధారపడ్డాయి. పరోక్షంగా చాలా పరిశ్రమలు వ్యవసాయ రంగంపై ఆధారపడుతున్నాయి. చాలా చిన్న తరహా పరిశ్రమలు, కుటీర పరిశ్రమలు వాటికి కావలసిన ముడి సరుకుల కోసం వ్యవసాయ రంగంపైన ఆధారపడుతున్నాయి.

ప్రశ్న 4.
నీటిపారుదల.
జవాబు.
భారతదేశ జనాభాకు కావలసిన ఆహార పదార్థాలను సరఫరా చేయడానికి వ్యవసాయ ఉత్పత్తులను పెంపొందించాలంటే నీటి పారుదల సౌకర్యం అవసరం. మన దేశంలో నీటి పారుదల సామర్థ్యం ప్రణాళికలకు ముందుకాలంలో 23 మిలియన్ల హెక్టారులుంటే, 2006-2007 నాటికి మొత్తం నీటిపారుదల సామర్థ్యం 103 మిలియన్ల హెక్టార్లకు పెరిగింది. భారతదేశంలో 2019-20 సం॥ నాటికి మొత్తం సాగు విస్తీర్ణంలో 45 శాతం భూమికి మాత్రమే నీటిపారుదల సౌకర్యాలు కల్పించగలిగాము.

ప్రశ్న 5.
వ్యవసాయ ఉత్పాదకత.
జవాబు.
ఒక హెక్టారులో పండించిన పంట సగటు ఉత్పత్తి ద్వారా ఆ పంట ఉత్పాదకత గణిస్తారు. 1965 సం॥ తరువాత హరిత విప్లవం ప్రభావం వలన సాగులో ఉన్న భూ విస్తీర్ణం, నీటి పారుదల సౌకర్యాలు ఉన్న భూమి పరిమాణం, అధిక దిగుబడి విత్తనాలను ఉపయోగిస్తున్న భూమి పరిమాణం మొదలగునవి స్థిరంగా పెరిగాయి. అదే విధంగా ఉత్పత్తి ఉత్పాదకతలలో స్థిరమైన పెరుగుదల నమోదైంది.

ప్రశ్న 6.
భూసార క్షీణత.
జవాబు.
దేశంలోని 329 మిలియన్ల హెక్టార్ల భూమిలో సుమారు సగం భూమిలో భూసారం క్షీణించింది. 43% భూమిలో చాలా ఎక్కువగా భూసారం క్షీణించినందువల్ల 33.67% వరకు దిగుబడి నష్టం జరుగుతుంది. 5% భూమి ఉపయోగించే స్థితిలో లేదు.

ప్రశ్న 7.
మధ్యవర్తుల తొలగింపు (Abolition of Intermediaries).
జవాబు.
శాశ్వత శిస్తు వసూలు చట్టం ద్వారా బ్రిటీష్ ప్రభుత్వం జమిందారీ పద్ధతిని ప్రవేశపెట్టింది. జమిందారులు, జాగీర్దారులు, ఇనాందారులు వంటి మధ్యవర్తుల ఆధీనంలో పెద్ద మొత్తంలో భూకమతాలు ఉండేవి. వ్యవసాయదారుల నుంచి భాటకాన్ని (rent) వీరు వసూలు చేసేవారు.

ఈ మద్యవర్తులు బ్రిటీష్ ప్రభుత్వానికి స్థిరమైన రేటులో భూమి శిస్తును చెల్లించి వ్యవసాయదారుల నుంచి అధిక ‘మొత్తంలో భాటకాన్ని వసూలు చేసేవారు, నిజానికి జమిందారులు లేదా మధ్యవర్తులు అనుపస్థిత భూస్వాములుగా ఉంటూ, ” భూమిని అభివృద్ధి చేయడం వల్ల విముఖంగా ఉండేవారు.

ప్రశ్న 8.
సాంధ్ర వ్యవసాయ అభివృద్ధి పథకం.
జవాబు.
1960 61 సం॥లో భారతదేశంలోని ఏడు జిల్లాలలో సాంద్ర వ్యవసాయ అభివృద్ధి పధకంగా పైలెట్ ప్రాజెక్టు రూపంలో దీనిని అమలు చేశారు. తరువాత ఈ కార్యక్రమాన్ని సాంద్ర వ్యవసాయ ప్రాంతాల కార్యక్రమం పేరిట ఎంపిక చేసిన 114 జిల్లాలలో అమలు చేశారు. 1966-67 సం॥లో అధిక దిగుబడినిచ్చే వంగడాల కార్యక్రమంను అమలు పరిచారు. దీని ఆశయం దిగుబడినిచ్చే వంగడాలు, రసాయనిక ఎరువుల వాడకాన్ని బాగా పెంచి వ్యవసాయ ఉత్పాదకతను పెంచడం.

ప్రశ్న 9.
హరిత విప్లవం.
జవాబు.
అధిక దిగుబడినిచ్చే వంగడాలు, రసాయన ఎరువులు లాంటి ఆధునిక ఉత్పాదకాల సహాయంతో 1960-70 మధ్యలో వ్యవసాయ ఉత్పాదకత, ఉత్పత్తిలో సాధించిన పెరుగుదలను హరిత విప్లవం అన్నారు. వ్యవసాయ రంగంలో వచ్చిన నూతన సాంకేతిక మార్పులను సూచిస్తూ విలియం S. గాండ్ మొదటిసారిగా హరిత విప్లవం అనే పదాన్ని ఉపయోగించినాడు. అమెరికన్ వ్యవసాయ ఆర్థికవేత్త నార్మన్ బోర్లాగ్ను హరిత విప్లవ పితామహునిగా చెబుతారు.

ప్రశ్న 10.
ప్రాథమిక వ్యవసాయ పరపతి సంఘాలు.
జవాబు.
సహకార సంఘ వ్యవస్థలో ప్రాథమిక వ్యవసాయ పరపతి సంఘాలు గ్రామస్థాయిలో ఉండి వ్యవసాయదారులకు స్వల్పకాలిక, మధ్యకాలిక, రుణాలను కల్పిస్తాయి. 2012 మార్చి 31 నాటికి భారతదేశంలో 92,432 ప్రాథమిక, వ్యవసాయ, సహకార పరపతి సంఘాలు స్వల్పకాలిక పరపతిని అందచేస్తున్నాయి. ఈ సంఘాలను గ్రామస్థాయిలో 10 లేదా అంతకంటే ఎక్కువ మంది సభ్యుల చేత ప్రారంభించబడతాయి.

ప్రశ్న 11.
ప్రాంతీయ గ్రామీణ బ్యాంకులు.
జవాబు.
1975 సంవత్సరంలో ప్రాంతీయ గ్రామీణ బ్యాంకులు ఏర్పాటు చేసారు. చిన్న, ఉపాంత రైతులు, భూమిలోని శ్రామికులు, కులవృత్తులు చేసే ఉద్యమదారులకు అవసరమయ్యే గ్రామీణ పరపతికి సహకార సంఘాలు, వాణిజ్య బ్యాంకులు అందించే పరపతికి మధ్యగల వ్యత్యాసాన్ని తగ్గించే లక్ష్యంగా వీటిని స్థాపించారు.

ప్రశ్న 12.
సూక్ష్మ విత్తం.
జవాబు.
గ్రామాలలో, పట్టణాలలో, నగరాలలో పేద ప్రజల ఆదాయ, జీవన ప్రమాణ స్థాయిని పెంపొందించటానికి, తక్కువ పరిమాణంలో ఋణం, పొదుపు, విత్తపరమైన సేవలను కల్పించే విధానాన్ని సూక్ష్మ విత్తం అంటారు. వీటిని ఎక్కువగా మహిళలు ఉపయోగించుకుంటున్నారు. పేదరిక నిర్మూలన సూక్ష్మ విత్తం వల్ల సాధ్యపడుతుంది.

ప్రశ్న 13.
స్వయం సహాయక బృందాలు.
జవాబు.
ఈ భావనను బంగ్లాదేశ్ గ్రామీణ బ్యాంకు ద్వారా మహ్మద్ యూనస్ 1975వ సంవత్సరంలో కనుగొన్నారు. అయితే భారతదేశంలో నాబార్డ్ ద్వారా 1986-87వ సం॥లో ఈ భావనను ఉపయోగించడం జరిగింది. సాధారణంగా 10 నుంచి 15 మంది సభ్యులచే స్త్రీలు ఒక స్వయం సహాయంగా ఏర్పడుట, బృందంలోని సభ్యులంతా తరచూ కొంత మొత్తాన్ని పొదుపుచేసి దాని నుంచి అవసర నిమిత్తం ఋణాలు పొందుట.

ప్రశ్న 14.
శ్రేణీకరణ, ప్రామాణికీకరణ.
జవాబు.
వ్యవసాయ ఉత్పత్తుల శ్రేణీకరణ ప్రమాణీకరణ కోసం ప్రభుత్వం అనేక చర్యలు చేపట్టింది. వ్యవసాయ ఉత్పత్తుల చట్టం 1937 ప్రకారం ప్రభుత్వం అనేక చర్యలు చేపట్టింది. వస్తువులకున్న మార్కెట్ను మరింత విస్తృతపరచడానికి వ్యవసాయ మార్కెటింగ్ విభాగం ద్వారా శ్రేణీకరణ చేసిన వస్తువులపైన AGMARK ను ముద్రిస్తున్నారు.

ప్రశ్న 15.
గిడ్డంగి సౌకర్యాలు.
జవాబు.
రైతులు వారి వస్తూత్పత్తిని నిలువ ఉంచుకొని లాభదాయక ధరను పొందటానికి వీలుగా గ్రామాలు పట్టణాల్లో గిడ్డంగి సౌకర్యాలు విస్తరించబడ్డాయి. ఇందులో భాగంగా 1957లో కేంద్ర గిడ్డంగి కార్పోరేషన్ CWC స్థాపించబడింది. అలాగే వివిధ రాష్ట్రాల్లో రాష్ట్ర గిడ్డంగి కార్పోరేషన్లను SWC ఏర్పాటు చేయడమైంది. ఇంతేగాక జాతీయ స్థాయిలో భారత ఆహార సంస్థ (FCI) స్థాపించబడింది. జూన్, 2013 నాటికి భారతదేశంలో FCI లో 355 లక్షల టన్నులు నిలువ చేసుకొనే శక్తి ఉంది.

ప్రశ్న 16.
వ్యవసాయ వ్యయాలు మరియు ధరల సంఘం.
జవాబు.
(CACP) వ్యవసాయ ధరల విధానం గూర్చి ప్రభుత్వానికి ఈ సంఘం సలహాలనిస్తుంది. ఇది కనీస మద్ధతు ధరలను మరియు వ్యవసాయిక వ్యయాలను తెలియజేయును. దీనిని 1965లో వ్యవసాయక ధరల సంఘాన్ని 1985 నుంచి ఈ సంఘాన్ని “వ్యవసాయ వ్యయాల మరియు ధరల సంఘం” అంటారు.

ప్రశ్న 17.
కనీస మద్దతు ధరలు (MSP).
జవాబు.
కనీస మద్ధతు ధరలను (Minimum Support Price) లేదా సేకరణ ధరలను నిర్ణయించడం :
ప్రతి సంవత్సరం వ్యావసాయిక వ్యయాల ధరల సంఘం (CACP) చేసిన సూచనల ప్రాతిపదికన గోధుమ, బియ్యం, మొక్కజొన్న లాంటి ప్రధాన వ్యావసాయిక ఉత్పత్తుల కనిష్ట మద్దతు ధరలను ప్రభుత్వం నిర్ణయిస్తుంది.

ప్రశ్న 18.
గరిష్ఠ ధర నిర్ణయం.
జవాబు.
కొన్ని నిర్ధిష్ట వ్యావసాయిక వస్తువులకు ప్రభుత్వం గరిష్ఠ ధరలను నిర్ధారిస్తుంది. ప్రజా పంపిణీ వ్యవస్థ కింద ఫల వ్యవసాయిక ఉత్పత్తులైన ధాన్యాలు, చక్కెర, బియ్యం మొదలైన వాటిని సరసమైన ధరలకు ప్రభుత్వం అమ్మకాలను చేపట్టడం జరుగుతుంది.

ప్రజాపంపిణీ వ్యవస్థ అనేది ధరల విధానపు మరొక ముఖ్య లక్ష్యం. ఇది రెండు రకాలైన రేషనింగ్ను కలిగి ఉంటుంది. అవి : శాసనపరమైన రేషనింగ్, అనియత రేషనింగ్ (informal rationing). శాసనపరమైన నియంత్రిత (rationed) ప్రాంతాలలో బహిరంగ మార్కెట్ పనితీరును చట్టాన్ని అనుసరించి నిరోధించబడుతుంది.

ప్రశ్న 19.
బఫర్ నిల్వ.
జవాబు.
ధర చాంచల్యాలు లేకుండా చేసే ఏకైక ఉద్దేశ నిమిత్తమై నిల్వల, అమ్మకాల, కొనుగోళ్ళను బఫర్ నిల్వలు సూచిస్తాయి. దీనిని FCI చేపడుతుంది. అహార ధాన్యాల ధర పెరగడం ప్రారంభమైనపుడు, నిర్ధిష్ట ధరల వద్ద బఫర్ నిల్వల నుంచి ఆహార దాన్యాల అమ్మకాలను ప్రభుత్వం ప్రారంభిస్తుంది. తత్ఫలితంగా ఆహార ధాన్యాల ధరలలోని పెరుగుదల నియంత్రించ బడుతుంది.

ప్రశ్న 20.
ఆహార భద్రత.
జవాబు.
ప్రపంచ ఆహార భద్రతపై నివేదికను అందజేసిన ఐక్యరాజ్య సమితి కమిటీ ప్రకారం, ప్రజలందరికి అన్ని కాలాలలో చురుకైన, ఆరోగ్యవంతమైన జీవనానికి తమ అభిరుచి మరియు ఆహారపు అలవాట్ల ప్రకారం తగినంత సురక్షితమైన, పౌష్టికాహారం భౌతికంగా, సామాజికంగా, ఆర్థికంగా అందుబాటులో ఉండటాన్ని ఆహార భద్రత అంటారు.

ప్రశ్న 21.
ఆహార భద్రత చట్టం.
జవాబు.
6 నుంచి 14 సంవత్సరముల వయస్సు గల పిల్లలు మాధ్యమిక తరగతి వరకు చదువుతున్నట్లయితే ఉచిత మధ్యాహ్న భోజనం ఈ చట్టం ద్వారా లభ్యమవుతుంది. ఒకవేళ అర్హులైన ప్రజలకు ఆహారధాన్యాలు పొందడంలో ప్రభుత్వం విఫలమైనట్లయితే వారికి ఆహార భద్రత అలవెన్స్లను కల్పించడమనే అంశం కూడా ఈ చట్టంలో ఇమిడి ఉంది. దీనిని జూలై 5, 2013న భారత ప్రభుత్వం ఆర్డినెన్స్ జారీచేసింది.

ప్రశ్న 22.
భారత ఆహార సంస్థ.
జవాబు.
ప్రభుత్వం నిర్ధారించిన ధరలకే ఆహార ధాన్యాలను భారత ఆహార సంస్థ సేకరించి ప్రజా పంపిణీ వ్యవస్థ ద్వారా అమ్ముతుంది. భారత ఆహార సంస్థను 1965వ సం॥లో భారత ప్రభుత్వం’ ప్రారంభించింది. ప్రభుత్వం నిర్దేశించిన ధరలకే ఆహార ధాన్యాలను ఈ సంస్థ సేకరిస్తుంది.

Telangana TSBIE TS Inter 2nd Year Economics Study Material 4th Lesson ప్రణాళికలు, నీతి ఆయోగ్ Textbook Questions and Answers.

TS Inter 2nd Year Economics Study Material 4th Lesson ప్రణాళికలు, నీతి ఆయోగ్

వ్యాసరూప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
భారతదేశంలో పంచవర్ష ప్రణాళికల లక్ష్యాలు ఏవి ? ఆ లక్ష్యాలను సమీక్షించండి
జవాబు.
భారత రాజ్యాంగంలో పొందుపరచిన ఆదేశ సూత్రాలు సామాజిక ఆర్థిక విధాన స్థూల లక్ష్యాలను నిర్వచించాయి. పర్యవసానంగా భారత ప్రభుత్వం ఆర్థికాభివృద్ధి ప్రణాళికా బద్ధంగా ఉండాలని నిర్ణయించి 1950 మార్చి నెలలో ప్రణాళికా సంఘాన్ని నియమించింది. ఈ విధంగా భారతదేశంలో ప్రణాళికా యుగం 1951 నుంచి ఆరంభమైంది.

పంచవర్ష ప్రణాళికల అమలు :
ప్రణాళికాబద్ధమైన ఆర్థికాభివృద్ధికి భారతదేశంలో మొదటి పంచవర్ష ప్రణాళిక శ్రీకారం చుట్టింది. 1951-56లో మొదటి ప్రణాళికను 1956-61లో రెండవ ప్రణాళికను, 1961-65లో మూడవ ప్రణాళికను అమలు. చేయడమైంది. పాకిస్తాన్తో వైషమ్యాలు, బహిర్గత సంక్షోభాల కారణంగా 1966-67, 1967-68; 1968-69 సంవత్సరాలకు గాను వార్షిక ప్రణాళికలు (annual plans) రూపొందించబడ్డాయి.

కొందరు ఈ విరామ కాలాన్ని ప్రణాళికా విరామంగా (plan holiday) తెలియజేసారు. 1969లో తిరిగి ప్రణాళికలు ప్రారంభమై 1969-74 మధ్య కాలంలో నాలుగవ ప్రణాళిక అమలు చేయబడింది. అయితే 5వ ప్రణాళిక కాలం (1974-79) పూర్తి కాకుండా కేంద్రంలో రాజకీయ మార్పు వల్ల 1978-83 సంవత్సరాలకు జనతా ప్రభుత్వం 6వ ప్రణాళికను ప్రవేశపెట్టింది. 1980లో తిరిగి రాజకీయ మార్పుల కారణంగా 1980-85 సంవత్సరాలకు గాను 6వ ప్రణాళిక అమలు చేయబడింది.

1985-90 సంవత్సరాలకు 7వ ప్రణాళిక అమలు చేయబడినా, 1990లో 8వ ప్రణాళిక అమలు కాలేదు. తిరిగి రెండు వార్షిక ప్రణాళికల తరువాత 1992-97 కాలానికి 8వ పంచవర్ష ప్రణాళిక, 1997-2002 సంవత్సరాలకు 9వ ప్రణాళిక, 2002-07 సంవత్సరాలకు 10వ ప్రణాళిక, 2007-12 సంవత్సరాలకు 11వ ప్రణాళిక మరియు 2012-17 సంవత్సరాలకు 12వ పంచవర్ష ప్రణాళిక అమలు చేయబడినవి. అంటే ఇప్పటికి 12 పంచవర్ష ప్రణాళికలు మన దేశంలో అమలు చేయబడ్డాయి.

పంచవర్ష ప్రణాళికల ప్రధాన లక్ష్యాలు :
ఇప్పటి వరకు అమలు చేసిన వివిధ ప్రణాళికల లక్ష్యాలు భిన్నంగా ఉన్నప్పటికీ కొన్ని సాంఘిక, ఆర్థిక లక్ష్యాలు అన్ని ప్రణాళికలలోనూ పునఃప్రస్తావించబడ్డాయి.
వీటిలో ముఖ్యమైనవి :

1. ఆర్థిక వృద్ధి
2. స్వావలంబన
3. సంతులిత ప్రాంతీయాభివృద్ధి
4. ఉపాధి అవకాశాల విస్తరణ
5. ఆదాయ వ్యత్యాసాల తొలగింపు
6. పేదరిక నిర్మూలన
7. ఆధునికీకరణ
8. సమ్మిళిత – సుస్థిర వృద్ధి.

12వ పంచవర్ష ప్రణాళికలో కూడా సమ్మిళిత ఆర్థిక వృద్ధి ముఖ్య లక్ష్యంగా ఉంది. ఈ ప్రణాళిక స్థూల జాతీయోత్పత్తిలో సాలీనా 8 శాతం పెరుగుదల లక్ష్యంగా నిర్ణయించింది. వివిధ ప్రణాళికలలో ప్రాధాన్యతలు వివిధ రకాలుగా నిర్ణయించబడ్డాయి.

మొదటి పంచవర్ష ప్రణాళిక వ్యవసాయానికి, రెండవ ప్రణాళిక పారిశ్రామికీకరణకు ప్రాధాన్యత ఇస్తే ఆరవ ప్రణాళిక నిరుద్యోగ నిర్మూలన, ఏడవ ప్రణాళిక అధిక వృద్ధి రేటుకు ప్రాధాన్యతలను కల్పించాయి. 10వ పంచవర్ష ప్రణాళిక రోడ్లు, అవస్థాపనా సౌకర్యాల విస్తరణకు ప్రాధాన్యతను ఇస్తే, 11, 12 ప్రణాళికలు అధిక స్థాయిలో సమ్మిళిత-సుస్థిర వృద్ధిని (inclusive and sustainable growth) ప్రాధాన్యతగా గుర్తించాయి.

భారతదేశంలో ఇంతవరకు పూర్తిగా అమలు చేసిన 11 పంచవర్ష ప్రణాళికల (1951-2012) ప్రధాన లక్ష్యాలను కింది పట్టికలో సంక్షిప్తంగా పొందుపరచడమైంది.

వివిధ ప్రణాళికల ప్రధాన లక్ష్యాలు (1951-2012):

వివిధ ప్రణాళికలలో విధుల కేటాయింపు సమీక్షిస్తే, వ్యవసాయం, నీటి పారుదల మొదటి ప్రణాళికలో అత్యధికంగా 31 శాతం కేటాయించబడి క్రమంగా 18-24 శాతం మధ్య ఇతర ప్రణాళికలలో కేటాయించబడింది. విద్యుత్ రంగానికి 7-11 ప్రణాళికల మధ్య 20 శాతం వరకు నిధుల కేటాయింపు జరిగింది. పారిశ్రామిక రంగానికి అత్యధికంగా 24 శాతం నిధులు రెండవ ప్రణాళికలో కేటాయించబడి, ఆరవ ప్రణాళికలో 26 శాతానికి పెరిగి తదుపరి తగ్గుతూ వస్తున్నాయి.

రవాణా, కమ్యూనికేషన్ల రంగాలకు కేటాయింపులు మొదటి మూడు ప్రణాళికలలో 25 నుంచి 28 శాతం వరకు ఉండగా, ఏడవ ప్రణాళికలో 19 శాతానికి తగ్గి, 10వ ప్రణాళికలో 21 శాతానికి పెరిగాయి. మొత్తం ప్రణాళికా కాలంలో రవాణా, కమ్యూనికేషన్ రంగాలకు 18-27 శాతం మధ్య వనరుల కేటాయింపు జరిగింది. సామాజిక సేవా రంగానికి 22 శాతం నిధులు మొదటి ప్రణాళికలో కేటాయించబడి క్రమంగా 7వ ప్రణాళిక వరకు కేటాయింపు శాతం తగ్గుతూ వచ్చింది.

అయితే, ఈ రంగానికి 8వ ప్రణాళికలోని 22 శాతం కేటాయింపులు 11వ ప్రణాళిక నాటికి 35.5శాతానికి పెరిగింది. సామాజిక సంక్షేమానికి 8వ ప్రణాళికలోని 22 శాతం కేటాయింపులు 11వ ప్రణాళిక నాటికి 35.5 శాతానికి పెరిగింది. సామాజిక సంక్షేమానికి 8వ ప్రణాళిక నుంచి 11వ ప్రణాళిక వరకు నిధుల కేటాయింపు క్రమంగా పెరుగుతూ వచ్చింది.

ప్రశ్న 2.
భారతదేశంలో పంచవర్ష ప్రణాళికలను దృష్టిలో ఉంచుకుని ప్రణాళికల అమలు తీరును వివరించండి. జవాబు. భారతదేశ ఆర్థిక వ్యవస్థలో ప్రణాళికల అమలు తీరును క్రింది విధంగా వివరించవచ్చు.
జవాబు.
1. ఆర్థిక వృద్ధి (Economic Growth) :
స్వాతంత్ర్యానికి పూర్వం 20వ శతాబ్దం మొదటి అర్థభాగంలో జాతీయాదాయంలో పెరుగుదల అతిస్వల్పంగా ఉండి తలసరి ఆదాయంలో పెరుగుదల ఇంచుమించు స్తబ్ధంగా ఉండేవి. 20వ శతాబ్దం రెండవ అర్థ భాగంలో ప్రణాళికల అమలుతో స్థూల జాతీయోత్పత్తి, స్థూల తలసరి ఉత్పత్తులు నిలకడ వృద్ధిని సాధించాయి.

2. ఆర్థిక స్వావలంబన (Economic Self-Reliance) :
నాలగవ పంచవర్ష ప్రణాళిక (1969-74) స్థిరత్వంతో కూడిన వృద్ధి, ‘స్వావలంబన సాధనలో పురోగమనం’ అనే రెండూ ప్రధాన లక్ష్యాలకు ప్రాధాన్యత ఇచ్చింది. అయిదవ ప్రణాళిక నుంచి ప్రధాన రంగాలలో, ఉత్పత్తి కార్యకలాపాల్లో స్వావలంబన సాధించడానికి ప్రపంచంలోని 115 అభివృద్ధి చెందుతున్న దేశాలలో ఒక్క భారతదేశమే స్వావలంబనతో కూడిన వృద్ధిని చెప్పుకోదగ్గ స్థాయిలో సాధించడం చిన్న విషయం కాదు.

ఆహార రంగంలో దిగుమతులపై ఆధారపడటం తగ్గి స్వయం సమృద్ధిని సాధించింది. ఇనుము, ఉక్కు, యంత్ర నిర్మాణం, భారీ ఇంజనీరింగ్ వంటి పరిశ్రమల స్థాపన ద్వారా మూలధన పరికరాల ఉత్పత్తిలో స్వాలంబన విషయంలో ఈ రెండు అంశాలను ప్రగతి పరమైన అంశాలుగా చెప్పవచ్చు.

3. సంతులిత ప్రాంతీయ అభివృద్ధి (Balanced Regional Development) :
ప్రణాళికా కాలంలో ప్రాంతీయ అసమానతలు ఒక ముఖ్యమైన సవాలుగా గుర్తించబడ్డాయి. ప్రాంతీయ అసమానతలను అధిగమించడానికి ప్రణాళికా సంఘం కింది సూచనలను చేసింది.
(a) కేంద్రం నుంచి రాష్ట్రాలకు విత్త వనరుల బదిలీ ప్రక్రియలో వెనుకబాటుతనాన్ని ఒక ముఖ్య కారకంగా గుర్తించడం.
(b) వెనుకబడిన ప్రాంతాల అభివృద్ధికి ఉద్దేశించిన ప్రత్యేక ప్రాంతాల అభివృద్ధి కార్యక్రమాలను అమలుచేయడం.
(c) వెనకబడిన ప్రాంతాలలో ప్రైవేటు పెట్టుబడులను ప్రోత్సహించే చర్యలను చేపట్టడం.

4. ఉపాధి అవకాశాల పెంపు (Enhancement of Employment opportunities) :
భారతదేశంలో నిరుద్యోగం ఒక ప్రత్యేక రూపంలో ఉంది. గ్రామీణ ప్రాంతాలలో ఋతుపరమైన నిరుద్యోగిత, ప్రచ్ఛన్న నిరుద్యోగిత అధికం, పట్టణ ప్రాంతాలలో కూడా అసంఘటిత రంగంలో నిరుద్యోగిత ఎక్కువగానే ఉంది. విద్యావంతులలో కూడా నిరుద్యోగిత పెరుగుతున్నది.

NSSO 68వ రౌండ్ సమాచారం ప్రకారం 2011-12 సంవత్సరాల మధ్య సాధారణ ప్రధాన స్థాయి ప్రకారం 2.7 శాతం, వారాంతపు స్థాయి ప్రకారం 3.7 శాతం, ప్రస్తుత రోజూవారీ స్థాయి ప్రకారం 5.6 శాతంగా ఉంది. ప్రభుత్వం నిరుద్యోగ నిర్మూలనకు వివిధ కార్యక్రమాలను ఎప్పటికప్పుడు అమలుచేస్తున్న, ‘నిరుద్యోగిత’ ఒక సమస్యగానే మిగిలింది.

5. ఆదాయ అసమానతలను తగ్గించడం (Reduction in Income Inequalities) :
ప్రణాళికా కాలంలో భారతదేశంలో ఆదాయ పంపిణీ అగ్రశ్రేణిలో ఉన్న 20 శాతం ప్రజానీకానికే అనుకూలంగా ఉంది. 1990వ దశకంలో ఉన్నత వర్గాలు, అట్టడుగు వర్గాల మధ్య ఆదాయ వ్యత్యాసాలు 5 రెట్లుగా ఉన్నట్లు గుర్తించారు. 2013 ప్రపంచ అభివృద్ధి సూచికల ప్రకారం భారతదేశపు స్థూల జాతీయోత్పత్తిలో 1/6వ వంతు 100 మంది సంపన్నవంతుల చేతిలో ఉన్నట్లు తెలియజేయబడుతుంది. ప్రణాళికా కాలంలో ఆదాయ అసమానతలు తొలగిపోలేదు.

6. పేదరిక నిర్మూలన (Elimination of Poverty) :
ప్రణాళికల ద్వారా పేదరికాన్ని నిర్మూలించడానికి ప్రభుత్వం ఎన్నో కార్యక్రమాలను అమలుచేస్తోంది. ప్రజా పంపిణీ వ్యవస్థ నుంచి నిత్యావసర ఆహార వస్తువులు, కిరోసిన్ వంటి ఇతర వస్తువులను సబ్సిడీ ద్వారా గ్రామీణ, పట్టణ పేద ప్రజలకు అందజేయడం, ఆదాయాలను పెంచడానికి ఉపాధి కార్యక్రమాలను అమలుచేయడం, ఉచిత విద్య, ఆరోగ్యం, గృహ నిర్మాణంవంటి సౌకర్యాలను కల్పించడం వంటివి ప్రభుత్వ కార్యక్రమాలలో ముఖ్యమైనవిగా చెప్పవచ్చు.

7. ఆధునికీకరణ (Modernisation) :
సంస్థాగతమైన వ్యవస్థాపూర్వక మార్పులను ప్రవేశపెట్టడం ఆధునికీకరణగా చెప్పవచ్చు. ప్రణాళికా కాలంలో వివిధ రంగాలలో ఉత్పాదకతలను పెంపొందించడానికి శాస్త్రసాంకేతిక విజ్ఞానానికి, హేతుబద్ధ నిర్వహణకు ప్రాధాన్యత కల్పించడమైనది. మూడవ పంచవర్ష ప్రణాళికలో నూతన వ్యవసాయ వ్యూహం హరిత విప్లవంగా ప్రవేశపెట్టడం జరిగింది. వ్యవసాయ ఉత్పాదకతను పెంచడానికి హరిత విప్లవం ఎంతో దోహదపడింది. సాంకేతిక పరిజ్ఞానాన్ని పెంపొందించు కోవడానికి ఏడవ ప్రణాళిక ఎంతో కృషి జరుగుతోంది.

8. సమ్మిళిత, సుస్థిర వృద్ధి (Inclusive and Sustainability of Growth) :
స్థూల ఆర్థిక అంశాలలో సంతృప్తికరమైన ప్రగతి సాధించినా, సంస్కరణల కాలంలో పేదరిక నిర్మూలన, ఉపాధి కల్పన, గ్రామీణ-పట్టణ వ్యత్యాసాలు, ఆదాయ అసమానతలు, ప్రాంతీయ అసమానతలు అంతగా తగ్గలేదు. వ్యవసాయ రంగంలో వృద్ధిరేటు స్వల్పంగా ఉండి, రైతుల ఆత్మహత్యలు పెరుగుతున్నాయి.

ఈ అంశాలను దృష్టిలో ఉంచుకొని 11వ ప్రణాళికలో ‘సమ్మిళిత మరియు సుస్థిర వృద్ధి లక్ష్యానికి ప్రాధాన్యత ఇవ్వడమైంది. సమ్మిళిత వృద్ధి అనేది ఒక విస్తృత భావన. ఆర్థిక, సామాజిక, సాంస్కృతిక అంశాలు ఇందులో అంతర్భాగాలు.

1. వ్యవసాయ రంగంలో వృద్ధి,
2. ఉపాధి కల్పన, పేదరిక నిర్మూలన
3. ప్రాంతీయ అసమానతల తగ్గింపు,
4. న్యాయబద్ధమైన వృద్ధి మొదలైన అంశాలు భారతదేశ సమ్మిళిత వృద్ధిలో ప్రధాన భాగాలుగా ఉన్నాయి.

ప్రశ్న 3.
పంచవర్ష ప్రణాళికల కాలంలో సాధించిన ఆర్థిక వృద్ధిని వివరించండి.
జవాబు.
పంచవర్ష ప్రణాళికలలో నిర్దేశించిన ప్రధాన లక్ష్యాల ఆధారంగా స్వతంత్ర భారతదేశంలో ప్రణాళికా కాలంలో సాధించిన ఆర్థిక ప్రగతిని క్రింది విధంగా సమీక్షించవచ్చు.

ఆర్థిక వృద్ధి (Economic Growth) : స్వాతంత్ర్యానికి పూర్వం 20వ శతాబ్దం మొదటి అర్థ భాగంలో జాతీయాదాయంలో పెరుగుదల అతి స్వల్పంగా ఉండి తలసరి ఆదాయంలో పెరుగుదల ఇంచుమించు స్తబ్ధంగా (near stagnation) ఉండేది. 20వ శతాబ్దం రెండవ అర్థ భాగంలో ప్రణాళికల అమలలో స్థూల జాతీయోత్పత్తి, స్థూల తలసరి ఉత్పత్తుల నిలకడ వృద్ధిని (steady growth) సాధించాయి.

ప్రణాళికా కాలంలో జాతీయాదాయంలో పెరుగుదల సగటున సాలీనా 1 శాతం నమోదు కాబడింది. వ్యవసాయ రంగ వృద్ధి రేటు 0.3 శాతం కాగా పారిశ్రామిక రంగ వృద్ధి రేటు కేవలం 2 శాతంగా నమోదయ్యింది. ప్రణాళికా కాలంలో తలసరి ఆదాయంలో వార్షిక పెరుగుదల 0.2 శాతం. 1900-01 నుంచి 1946-47 సంవత్సరాల మధ్య అవిభాజ్య భారతదేశంలో 1938-39 స్థిరమైన ధరలలో జాతీయాదాయంలో పెరుగుదల 11 శాతంగా లెక్కించబడింది.

ఒక అధ్యయనం ప్రకారం 1950-51 నుంచి 2004-05 మధ్య కాలంలో స్థిరమైన ధరలలో స్థూల జాతీయోత్పత్తి 1,000 శాతం, తలసరి జాతీయోత్పత్తి 250 శాతం పెరిగాయి. ఈ వివరాల నేపథ్యంలో 1951-2017 మధ్య పంచవర్ష ప్రణాళికల కాలంలో ఆర్థిక వృద్ధి పనితీరును క్రింది పట్టిక ద్వారా తెలుసుకోవచ్చు.

పంచవర్ష ప్రణాళికలలో వృద్ధి పనితీరు (1993-94 ధరలలో):
(నికర జాతీయోత్పత్తిలో వార్షిక పెరుగుదల (శాతంలో) ఉత్పత్తి కారకాల ధరలలో):

ప్రణాళికా కాలంలో సాధించిన వృద్ధిరేట్ల ధోరణులు, స్థూల జాతీయోత్పత్తిలో (GDP) వివిధ రంగాల వాటాలలో వచ్చిన మార్పులను సంక్షిప్తంగా క్రింద వివరించడమైనది.

1. మొదటి పంచవర్ష ప్రణాళిక నుంచి 11వ ప్రణాళికా కాలం వరకు వృద్ధిరేటు సగటున 4.5 శాతంగా లెక్కించారు. ఇది వాస్తవంగా గణనీయమైన ప్రగతిగా చెప్పవచ్చు.
2. స్వాతంత్ర్యానికి ముందు కాలంలో వ్యవసాయ రంగంలో వార్షిక వృద్ధిరేటు కేవలం 0.3 శాతం మాత్రమే కాని, ప్రణాళిక కాలంలో వృద్ధిరేటు సగటున సంవత్సరానికి 2 నుంచి 3 శాతం చొప్పున పెరుగుతూ ఉంది.
3. ప్రణాళికా కాలంలో అద్భుతమైన పారిశ్రామిక ప్రగతి సాధించబడింది. 6-8 శాతంగా నమోదు అయిన పారిశ్రామిక వృద్ధిరేటు స్వాతంత్ర్యానికి ముందు ఉన్న పారిశ్రామిక వృద్ధిరేటుతో పోలిస్తే 3 నుంచి 4 రెట్లు అధికంగా ఉంది.
4. వృద్ధిరేటు ధోరణి మొదటి మూడు దశాబ్దాల ప్రణాళికా కాలంలో స్వల్పంగా 3.5 శాతం మాత్రమే ఉండేది. కాని 1981-2013 సంవత్సరాల మధ్య సాలీనా 5.9 శాతం వృద్ధిరేటు నమోదయ్యింది.
5. 1980 తరువాత వృద్ధిరేటులో పెరుగుదల స్పష్టంగా కనిపిస్తోంది. కొంత కాలం పాటు ఈ వృద్ధిరేటును ప్రణాళికా సంఘం అంతగా గమనించలేదు. 2000 సంవత్సరం నుంచి పెరిగిన ఈ వృద్ధిరేటును గుర్తించారు. చాలామంది ఆర్థిక నిపుణుల అభిప్రాయంలో 1980 ప్రాంతంలో ఆర్థిక వ్యవస్థ పనితీరులో సంస్థాగత మార్పులు (structural break) చోటు చేసుకున్నాయి.
6. గణాంక మరియు కార్యక్రమాల అమలు మంత్రిత్వశాఖ (Ministry of statistics and programme imple- mentation) వివరాల ప్రకారం భారతదేశంలో 2016-19 సంవత్సరంలో 2011-12 ధరల ననుసరించి వ్యవసాయం, (అనుబంధ కార్యక్రమాలు), పరిశ్రమలు, సేవారంగం వాటాలు వరుసగా స్థూల జాతీయోత్పత్తిలో 14.39, 31.46, 54,15 శాతాలుగా ఉన్నాయి.
7. స్థూల దేశీయోత్పత్తిలో వ్యవసాయ రంగం వాటా క్రమంగా తగ్గుతూ, 2013-2014 నాటికి 13.9 శాతానికి దిగజారింది. భారత వ్యవసాయ రంగం సంక్షోభంలో చిక్కుకొని వ్యవసాయ కార్యకలాపాలకు విరామం (crop holiday) ప్రకటించడంతో పాటు రైతుల ఆత్మహత్యలు పెరుగుతున్నాయి. ఆహార భద్రత దృష్ట్యా ఈ పరిణామం ఆందోళనను కలిగిస్తుంది.
8. భారత్లో స్థూల దేశీయోత్పత్తికి అత్యధిక వాటాను సమకూర్చే సేవా రంగం ఎంతో ప్రధానమైనది. 2018-19 సంవత్సరంలో 2011-12 ధరలననుసరించి సేవారంగం సమకూర్చిన స్థూల జోడింపబడిన విలువలో (GVA) 54.15 శాతం. ఈ పెరుగుదల అభివృద్ధిలో మనం సాధించిన ప్రగతికి వ్యవస్థాపూర్వకమైన పరివర్తనకు సంకేతం (structural trans- formation). అయితే, ఈ పెరుగుదల సుస్థిరంగా (sustainable) కొంతకాలం పాటు కొనసాగవలసి ఉంది. అభివృద్ధి జీవన ప్రమాణాలను పెంచి, సామాన్య ప్రజల స్థితిగతులను మెరుగుపరుస్తుంది.

ప్రశ్న 4.
ప్రాంతీయ అసమానతలకు గల కారణాలను, వాటిని తగ్గించడానికి అవసరమైన చర్యలను సూచించండి.
జవాబు.
భారతదేశంలో ప్రాంతీయ అసమానతలకు గల కారణాలు :
జాతీయ సమైక్యతకు, ఆర్థిక వృద్ధికి, సర్వతోముఖ అభివృద్ధికి ప్రాంతీయ అసమానతలు ప్రతిబంధకాలు. వెనుకబడిన రాష్ట్రాలు లేదా ప్రాంతాలు అసంతృప్తితో ఉండటం వల్ల ఆర్థికాభివృద్ధి ఏకపక్ష స్వభావాన్ని కలిగి ఉంటుంది.

చారిత్రాత్మకంగా బ్రిటిష్ పాలన మన దేశంలో కొన్ని ప్రాంతాలు వెనకబడటానికి ఒక కారణం. కలకత్తా, బొంబాయి, మద్రాస్ నగరాలు ప్రెసిడెన్సీ నగరాలుగా ఎన్నో పరిశ్రమలను, అవస్థాపనా సౌకర్యాలను ఆకర్షించగలిగాయి. బ్రిటిష్ ప్రభుత్వం అనుసరించిన భూమి శిస్తు విధానం గ్రామీణ ప్రజలను పేదరికంలోకి నెట్టింది.

ఆర్థికాభివృద్ధిని భూమి, భూసారం, నదులు, పర్వతాలు వంటి భౌగోళిక అంశాలు ప్రభావితం చేస్తాయి. ఈ రోజుకు కూడా ఉత్తరప్రదేశ్, హిమాచల్ ప్రదేశ్, జమ్ము కాశ్మీర్ రాష్ట్రాలలోని కొండ, పర్వత ప్రాంతాలు వెనుకబడి ఉంటాయి. ప్రతికూల వాతావరణ పరిస్థితులు ఉన్న ప్రాంతాలలో వ్యవసాయ కార్యకలాపాలు, పారిశ్రామిక ఉత్పత్తులు తక్కువగా ఉంటాయి.

అభివృద్ధి చెందిన ప్రాంతాలు, రాష్ట్రాలలో లాభాల స్థాయి అధికంగా ఉండటంవల్ల ప్రైవేటు రంగంలో అత్యధిక పెట్టుబడులను ఆకర్షించగలుగుతాయి. ప్రాంతీయ అసమానతలకు సహజ వనరుల లభ్యత ప్రధాన కారణం. కొన్ని ప్రాంతాలు నాణ్యమైన, అవసరమైనన్ని సహజ వనరులను కలిగి ఉంటాయి. ఇలాంటి ప్రాంతాలు వేగంగా అభివృద్ధిచెంది అభివృద్ధిపరమైన ప్రభావాలను ఏర్పాటు చేసుకోగలుగుతాయి. రవాణా సౌకర్యాలు, టెలీకమ్యూనికేషన్లు, విద్యుచ్ఛక్తి, నీటిపారుదల వసతులు వంటి అవస్థాపనా సౌకర్యాలు ఎక్కువగా ఉన్న రాష్ట్రాలు లేదా ప్రాంతాలు అత్యధిక రేటులో అభివృద్ధిని సాధించగలుగుతాయి.

ప్రాంతీయ అసమానతలు తగ్గించడానికి సూచనలు :

1. వెనుకబడిన ప్రాంతాల్లో పెట్టుబడులను పెంచడం ద్వారా అభివృద్ధిని సాధించి పేదరిక భారాన్ని తగ్గించవచ్చు. ఇందుకోసం ప్రైవేట్ పెట్టుబడులు వెనకబడిన ప్రాంతాలకు తరలించాలి. ఈ పెట్టుబడులను తరలించడానికి కేంద్ర, రాష్ట్రాలు, ప్రభుత్వాలు వెనకబడిన ప్రాంతాల్లో అవస్థాపనా సౌకర్యాలు, సాంకేతిక పరిజ్ఞానం, నైపుణ్యంగల శ్రామికులను అభివృద్ధి పరచాలి.
2. ఆర్థికంగా వెనకబడిన రాష్ట్రాలు ఆరోగ్య, విద్య, శిక్షణా సౌకర్యాలు ఇతర భౌతిక అవస్థాపన సౌకర్యాల కల్పనపై దృష్టిని కేంద్రీకరించాలి.
3. వెనుకబడిన రాష్ట్రాలు జనాభా పెరుగుదలను తగ్గించడానికి విధానాలను రూపొందించాలి. ఆర్థిక వృద్ధి పెరుగుదలకు జనాభాను అదుపుచేయడం అవసరమని గుర్తించాలి.
4. చాలా వెనుకబడిన రాష్ట్రాలలో వ్యవసాయ రంగం సంక్షోభంలో ఉంది. వ్యవసాయ ఉత్పత్తులను పెంపొందించడానికి ఈ రాష్ట్రాలు పరపతి సౌకర్యాలు, నీటి పారుదలపై పెట్టుబడులు పెంచడం, వ్యవసాయ ఉత్పత్తులకు మార్కెట్లో లాభసాటి ధరలను కల్పించడంవంటి చర్యలు చేపట్టాలి. ఇందుకు ఉద్యానవన పంటలు, నూనె గింజలు, పప్పు ధాన్యాలువంటి పంటలను ఆహార ధాన్యాలతోపాటు ఉత్పత్తి చేయాలి.
5. వ్యవసాయ, పారిశ్రామిక రంగాలకు సంబంధించిన అసమానతలను తగ్గించడానికి సాంకేతిక విజ్ఞానం ఎంతో సహాయ పడుతుంది. వెనకబడిన ప్రాంతాల అవసరాలను తీర్చేవిధంగా సాంకేతిక విజ్ఞానాన్ని రూపొందించాలి.
6. వెనకబడిన ప్రాంతాలలో పేదరికాన్ని తగ్గించడానికి ఉద్యోగ అవకాశాలు విస్తరించబడాలి. ఈ సందర్భంగా జాతీయ ఉపాధి హామీ పథకం (NREGA)లో పనిదినాలను పెంచవలసిన అవసరం ఉంది. ఈ పెరుగుదల ముఖ్యంగా బాగా వెనుకబడిన ప్రాంతాల్లో ప్రజలకు, ఏజెన్సీ ప్రాంతాలలో నివసించే గిరిజనులకు ఎంతో ప్రయోజనము చేకూరుస్తుంది.
7. వెనుకబడిన ప్రాంతాలలో సామాజిక రంగం కేటాయింపులు పెంచడం, దాని పనితీరును మెరుగుపరచడం అవసరం. విద్య, ఆరోగ్య రంగాలలో అధిక పెట్టుబడులు, ఆర్థిక వృద్ధి, మానవ నైపుణ్యతను మెరుగుపరుస్తాయి.
8. అభివృద్ధి ప్రక్రియలో వెనకబడిన రాష్ట్రాలలో ఎస్.సి., ఎస్.టి., విస్మరించబడిన వర్గాలకు భాగస్వామ్యాన్ని కల్పించాలి.
9. వెనుకబడిన ప్రాంతాలలో పాలనా విధానం సమర్థవంతంగా ఉండి పారదర్శక స్వభావాన్ని కలిగి ఉండాలి. అభివృద్ధి ప్రక్రియలో పంచాయితీరాజ్ సంస్థలకు వికేంద్రీకరణ ద్వారా నిధులు, విధులు, అధికారాలు బదిలీచేయాలి.
10. పన్ను రాయితీలు, సబ్సిడీలు, నిర్వహణపరమైన శిక్షణ, పర్యవేక్షణ ద్వారా వెనుకబడిన ప్రాంతాలలో లభించే వనరులను వినియోగిస్తూ కుటీర, కుటుంబ, చిన్నతరహా పరిశ్రమలను అభివృద్ధి పరచాలి.
    ఆర్థికాభివృద్ధి ఫలాలు అన్ని రాష్ట్రాలకు అందుతున్నాయి. అనే భావన జాతీయ సమైక్యతకు ఎంతో దోహదపడుతుంది. ఇందుకుగాను ప్రాంతీయ అసమానతలను తగ్గించడం భారతదేశంలో తప్పనిసరి.

ప్రశ్న 5.
నీతి ఆయోగ్ స్వభావం, లక్ష్యాలు మరియు నిర్మాణంలను విశ్లేషించుము.
జవాబు.
భారతదేశ పరివర్తన కోసం జాతీయ సంస్థ (నీతి ఆయోగ్) (National Institution for Transforming India – NITI Aayog) :
ప్రణాళికా సంఘం స్థానంలో ‘నీతి ఆయోగ్’ సంస్థను భారతదేశ కేంద్ర ప్రభుత్వం జనవరి 1, 2015 నాడు స్థాపించింది. రాష్ట్ర ప్రభుత్వాలతో, ప్రధాన సంస్థలతో, నిపుణులతో, మేధావులతో విస్తృతంగా చర్చించి ఈ సంస్థను ఏర్పాటు చేశారు. ఈ సంస్థ అకస్మాత్తుగా ప్రభుత్వ మార్పిడి వల్ల స్థాపించబడలేదు. ఎనిమిదవ ప్రణాళికా డాక్యుమెంట్లో ఆర్థిక విధానాలపై ఏర్పాటు చేసిన కమిటీ (2011-12) ప్రణాళికా సంఘంలో మార్పులను సూచించాయి.

డా॥ మన్మోహన్ సింగ్ 2014 వ సంవత్సరంలో ప్రధానమంత్రిగా తన చివరి ప్రసంగంలో ప్రణాళికా సంఘాన్ని ఉద్దేశిస్తూ మారుతున్న పరిస్థితులలో ప్రణాళికా సంఘంలో కూడా మార్పులు అవసరమని సూచించాడు. పర్యవసానంగా విమర్శనాత్మక, దిశాత్మక (directional), వ్యూహాత్మక మౌళిక సలహాలను (strategical inputs) ఆర్థిక ప్రక్రియకు అందించడానికి నీతి ఆయోగ్ను ఏర్పాటు చేశారు.

భారత్లో కేంద్ర – రాష్ట్ర ప్రభుత్వాలు భాగస్వామ్యం ద్వారా సహకార సమాఖ్యగా (co-operative federation) వ్యవహరించడంపై నీతి ఆయోగ్ తన దృష్టిని కేంద్రీకరిస్తుంది. కేంద్ర ప్రభుత్వం రాష్ట్ర ప్రభుత్వాలను ఏకపక్షంగా నిర్ణయాలను నిర్దేశించకుండా చూస్తుంది.

నీతి ఆయోగ్ వివిధ అంశాలపై విధానాలను సూచిస్తుంది. అమలు చేయడం మాత్రం ప్రభుత్వాలపై ఆధారపడి ఉంటుంది. గతంలోని ప్రణాళిక సంఘం మాదిరిగా కేంద్ర నిధులను రాష్ట్రాలకు కేటాయించే అధికారం దీనికి లేదు. ఇప్పుడు కేంద్ర ఆర్థిక మంత్రిత్వశాఖ రాష్ట్రాలకు అవసరమైన నిధులను సమకూరుస్తుంది.

‘నీతి’ స్వభావం (Nature of NITI) :

1. కేంద్ర ప్రభుత్వం నుంచి రాష్ట్రాలకు సలహాలను, సూచనలను ప్రణాళికా సంఘం అందచేసేది. కానీ, నీతి ద్వారా కేంద్ర రాష్ట్ర ప్రభుత్వాల మధ్య సిసలైన (genuine), నిరంతర భాగస్వామ్యం (continuing partnership) ఏర్పాటు చేయబడుతుంది.
2. వ్యూహాత్మక, సాంకేతిక సలహాలను కేంద్ర, రాష్ట్ర ప్రభుత్వాలకు అందజేసే ‘మేధో కేంద్రం’గా (think-tank) నీతిని రూపొందించే ప్రయత్నం జరుగుతోంది.
3. రాష్ట్రాల ఆర్థిక శక్తి పటిష్ఠమైన దేశ నిర్మాణానికి సహాయ పడుతుందన్న భావనను నీతి తెలియజేస్తుంది. ఈ దృష్టిలో సహకార సమాఖ్య వ్యవస్థను (co-operative fedaralism) భారతదేశంలో ప్రోత్సహించడానికి, బలపరచడానికి, రూపొందించడానికి నీతి సంస్థ తోడ్పడుతుంది.
4. గ్రామస్థాయి ప్రణాళికలను ఉన్నత స్థాయి ప్రణాళికలతో అనుసంధానం చేయడానికి అవసరమైన యంత్రాంగాన్ని నీతి అభివృద్ధి చేస్తుంది.
5. సమాజంలోని అన్ని వర్గాలు ఆర్థిక ప్రక్రియల ద్వారా ప్రయోజనాలు పొందడానికి ఈ సంస్థ కృషి చేస్తుంది.
6. ఒప్పందాల ద్వారా పరిజ్ఞానాన్ని, నవ కల్పనలను, వ్యవస్థాపక మద్దతును (entrepreneurial support) ఈ సంస్థ కల్పిస్తుంది.
7. ఆర్థికాభివృద్ధిని వేగవంతం చేయడానికి వివిధ రంగాల మధ్య ప్రభుత్వ శాఖల మధ్య పరిష్కార వేదికగా నీతి పనిచేస్తుంది.
8. ఉత్పాదక సామర్థ్య నిర్మాణాన్ని (capacity building) సృష్టించడానికి, పెంపొందించడానికి (upgradation) వివిధ కార్యక్రమాలను పర్యవేక్షించి (monitor) నిర్వహిస్తుంది.

నీతి లక్ష్యాలు :
మొదటి నుంచి ఆఖరి దశ వరకు సహాయకారిగా ఉన్న ప్రభుత్వ పాత్రను మార్చి రాష్ట్రాలు పటిష్టంగా ఉండేందుకు దోహదపడే రీతిలో ప్రభుత్వ పనితీరును మార్చడం.

1. వ్యవసాయదారులకు ప్రయోజనం కలుగచేసే విధంగా వ్యవసాయ ఉత్పత్తులను, ఆహార భద్రతను సమ్మిళితం చేయడం.
2. ప్రపంచ సమస్యలకు సంబంధించిన చర్చలలో భారతదేశాన్ని ప్రధాన సూత్రధారిగా (active player) రూపొందించడం.
3. ఆర్థికంగా ఉత్తేజితమైన మధ్య తరగతి (vibrant middle class) ప్రజలను ఉత్పత్తి ప్రక్రియలో సమర్థవంతంగా ఉపయోగించుకోవడం.
4. శాస్త్రీయ, మేధోపరమైన వ్యవస్థాపక శక్తులతో కూడిన మానవ మూలధనాన్ని (intellectual human capital) పెంపొందించడం.
5. అభివృద్ధి ప్రక్రియలో విదేశాల్లో స్థిరపడిన భారతీయులను (non-resident Indians) భాగస్వామ్యులను చేయడం.
6. పెరుగుతున్న పట్టణ ప్రాంతాలను ఆవాసయోగ్యంగా రూపొందించడానికి అవసరమైన ఆధునిక సాంకేతిక, పరిజ్ఞాన ఉపయోగితను మెరుగుపరచడం.
7. సాంకేతిక విజ్ఞానాన్ని ఉపయోగించడం ద్వారా సుపరిపాలనను ప్రోత్సహించడం.

నీతి వ్యవస్థ నిర్మాణం (Organisational Structure of NITI) :
కార్యాచరణ, సరళీకరణలతో కూడిన విజ్ఞాన కేంద్రంగా నిపుణులతో ఈ వ్యవస్థ నిర్మాణం జరుగుతుంది.

I. నీతి నిర్వహణ : ఇది కింది వారితో కూడి ఉంటుంది.

1. అధ్యక్షులు : దేశ ప్రధానమంత్రి
2. ఉపాధ్యక్షులు : ప్రధానమంత్రిచే నియమించబడే వ్యక్తి
3. సభ్యులు : 1. పూర్తి కాలపు సభ్యులు, 2. పూర్తి కాలం కాని సభ్యులు : దేశంలోని ప్రధాన విశ్వవిద్యాలయాలు, పరిశోధన సంస్థల నుంచి రొటేషన్ ప్రాతిపదికపై ఇద్దరు సభ్యులు.
4. ఎక్స్ అఫిషియో సభ్యులు: కేంద్ర మంత్రిమండలి నుంచి నలుగురికి మించకుండా ప్రధానమంత్రిచే నియమించబడే వ్యక్తులు.
5. ముఖ్య కార్య నిర్వహణ అధికారులు : భారత ప్రభుత్వ కార్యదర్శి స్థాయిలో నిర్దిష్ట కాల వ్యవధి కోసం ప్రధాన మంత్రిచే నియమించబడే వ్యక్తులు.

రాష్ట్ర ప్రభుత్వాల, కేంద్ర మంత్రుల సన్నిహిత సహకారంతో సంప్రదింపుల ద్వారా సమన్వయంతో నీతి (NITI) పని చేస్తుంది.

II. గవర్నింగ్ కౌన్సిల్(Governing Council):
గవర్నింగ్ కౌన్సిల్లో అన్ని రాష్ట్రాల ముఖ్యమంత్రులు, కేంద్ర ప్రాంతాల గవర్నర్లు ఉంటారు.

III. ప్రాంతీయ మండళ్ళు (Regional Councils) :
ప్రాంతీయ మండళ్ళు, ఒకటి కంటే ఎక్కువ రాష్ట్రాలు లేదా ప్రాంతాల నిర్దిష్ట సమస్యలను, అంశాలను పరిష్కరించడానికి ప్రయత్నిస్తాయి. ప్రాంతీయ మండలికి నిర్దిష్ట కాల వ్యవధి ఉంటుంది. ఈ మండళ్ళు వ్యూహాలను రూపొందించి అమలు చేస్తాయి. సంబంధిత మండలిలో ఏదో ఒక రాష్ట్ర ముఖ్యమంత్రి మండలికి సారధ్యం వహిస్తాడు. కేంద్రమంత్రులు, నిపుణులు, విద్యావేత్తలు మండలిలో సభ్యులుగా ఉంటారు.

ప్రశ్న 6.
భారతదేశంలో గ్రామీణ – పట్టణ వైవిధ్యాలకు కారణాలు (Rural Urban Divide in India) ఏవి ? వాటి నివారణా చర్యలు వివరించుము.
జవాబు. గామీణ, పట్టణ వైవిధ్యాలకు కారకాలు (Causes for the Rural, Urban Divide) : భారతదేశంలో గ్రామీణ, పట్టణ వైవిధ్యాలు చరిత్ర ప్రారంభం నుంచి ఉన్నాయి. అయితే, ఈ వైవిధ్యాలు అభివృద్ధి ప్రక్రియలో తీవ్ర స్థాయికి చేరి సవాళ్ళుగా మారుతున్నాయి. ఈ వైవిధ్యాలను ఈ కింద తెలిపిన ప్రజలు కారణాల ద్వారా తెలియచేయవచ్చు.

(ఎ) సహజమైన వ్యత్యాసాలు :
సహజ వనరులు, నీరు, మంచి వాతావరణం ఉన్న ప్రదేశాలలో పట్టణాలు, నగరాలు విస్తరించినట్లు చరిత్ర తెలియజేస్తుంది. ఈ చారిత్రక వెసులుబాటు అవస్థాపనా సౌకర్యాల పెరుగుదలకు సహాయపడింది. క్రమంగా పరిశ్రమలు, వాణిజ్యం, విద్య, ఆరోగ్య సౌకర్యాలు విస్తరించి పట్టణాల పెరుగుదలకు అనువైన పరిస్థితులను కల్పించింది. ఈ అంశాలే గ్రామీణ, పట్టణ ప్రాంతాల మధ్య వ్యత్యాసాలను పెంపొందించాయి.

(బి) ఆర్థికేతర కారకాలు :
సంప్రదాయాలు, విలువలు, ఉమ్మడి కుటుంబాలు, ప్రజల దృక్పథాలు సామాజిక ఆర్థిక గమనశీలతకు దోహదపడతాయి. గ్రామాలలో సామాజిక ఆంక్షలు, కుల విధానం, వేదాంత ధోరణి, న్యూనతా భావనలు గమనశీలతను, నవకల్పనలను అంతగా ప్రోత్సహించవు.

అదే పట్టణాలలో జన సాంద్రత ఎక్కువగా ఉండి భిన్న రూపాలలో వ్యక్తులు పోటీ స్ఫూర్తితో అనుబంధాలకు అతీతంగా జీవిస్తారు. ఉత్పత్తిలో ప్రత్యేకీకరణ ద్వారా విస్తృతమైన మార్కెట్లలో తమ ఉత్పత్తులకు డిమాండ్ను పొందగలుగుతారు. ఈ అంశాలన్నీ ఆర్థికాభివృద్ధికి దోహదపడతాయి.

(సి) ప్రభుత్వ విధానాలు :
అభివృద్ధి విధానాలలో ప్రభుత్వం పట్టణ ప్రయోజనాలకు మొగ్గు చూపడం కూడా వ్యత్యాసాలకు కారణం. నగరాలు, పట్టణాలలో అవస్థాపనా సౌకర్యాలు మెరుగు పడటానికి ప్రభుత్వం అధిక పెట్టుబడులను కేటాయిస్తుంది. పట్టణ ప్రజలకు అనుకూలంగా ఉన్న కొన్ని ప్రభుత్వ విధానాలు గ్రామాలలో రైతుల ఆదాయాలపై ప్రభావాన్ని చూపుతాయి.

ప్రభుత్వాలు అధిక సంఖ్యలో ఉన్న గ్రామీణ ప్రజల కంటే అధిక సంఖ్యలో ఉన్న పట్టణ ప్రజల సమస్యల పట్ల ఎక్కువ శ్రద్ధ చూపిస్తాయి. పట్టణాలలో విద్య, వైద్యం, ఆరోగ్యం వంటి సేవలపై కూడా ప్రభుత్వాలు ఎక్కువ మొత్తాలను ఖర్చు చేసి గ్రామాలను నిర్లక్ష్యం చేస్తాయి.

(డి) ఇతర అంశాలు :
నిరక్షరాస్యత, అధిక సంఖ్యలో శిశు మరణాలు, రక్త హీనతగల మహిళలు, శిశువులు ఎక్కువగా ఉండటం, రవాణా, వార్తా సౌకర్యాల కొరత, అల్ప ఆదాయాలు, అనిశ్చిత ఉపాధి దినాలు (uncertain wage employment days), తాగు నీరు, వైద్య సౌకర్యాల కొరత లాంటి సమస్యలతో భారతదేశంలోని గ్రామీణ ప్రజలు సతమతమవుతున్నారు. పట్టణాలలోని పేద ప్రజలు తమకంటే మెరుగైన జీవనాన్ని కొనసాగిస్తున్నట్లు అధిక శాతం గ్రామీణ ప్రజలు భావిస్తారు.

నివారణా చర్యలు :
ఈ కింద పేర్కొన్న నివారణ చర్యలు కూడా గ్రామీణాభివృద్ధికి సహాయపడుతూ గ్రామాల నుంచి పట్టణాలకు ప్రజల వలసలను తగ్గిస్తాయి.

1. జాతీయ గ్రామీణ ఉపాధి హామీ పథకం ద్వారా గ్రామీణ యువతకు వృత్తి, సేవా రంగాలకు ఉపయోగపడే శిక్షణను కల్పించాలి. రాజస్థాన్, అస్సాం వంటి రాష్ట్రాలలో ప్రవేశపెట్టిన ఈ విధమైన శిక్షణా కార్యక్రమాలు ఆశాజనకమైన ఫలితాలను ఇవ్వగలిగాయి.
2. చిన్న, సన్నకారు వ్యవసాయదారులకు పరపతి సౌకర్యాలను పెంచి వడ్డీ వ్యాపారులు, కమీషన్ ఏజెంట్ల ప్రాబల్యాన్ని తగ్గించడం, పంటల బీమా పథకాన్ని సమర్థవంతంగా అమలు చేస్తూ వ్యవసాయ ఉత్పత్తులకు లాభసాటి ధరలను కల్పించడం.
3. అవకాశం ఉన్నంత వరకు గ్రామీణ అవస్థాపనా రంగంలో ప్రైవేటు పెట్టుబడులను ప్రోత్సహించడం, ప్రభుత్వ-ప్రైవేటు భాగస్వామ్యంతో గ్రామీణ ప్రాంతాలలో అవస్థాపనా సౌకర్యాల అభివృద్ధిని పెంచే కృషిని ప్రోత్సహించడం.
4. గ్రామ ప్రాంతాలలో యువతకు నాణ్యమైన విద్య, శిక్షణ, నిపుణతలను కల్పించడం ద్వారా స్వయం ఉపాధిని పెంపొందించడం. స్థూల జాతీయోత్పత్తిలో కేవలం రెండు శాతం మాత్రమే భారతదేశంలో ఆరోగ్య, వైద్య రంగాలకు కేటాయించడం ఆ రంగాలను నిర్వీర్యం చేయడమే (దురదృష్టకరం.
5. గ్రామీణ ప్రాంతాలలో ప్రజారోగ్య వ్యవస్థ సమర్థవంతంగా లేకపోవడం వల్ల అది ప్రజల నమ్మకాన్ని పొందలేకపోయింది. మెరుగైన వైద్య, ఆరోగ్య సేవలు, గ్రామీణ ప్రాంతాలలో ఉత్పాదకత, సామాజిక భద్రతను తప్పనిసరిగా పెంచుతాయి.

స్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
నీతి ఆయోగ్పై లఘు వ్యాఖ్య రాయండి.
జవాబు.
ప్రణాళికా సంఘం స్థానంలో నీతి ఆయోగ్ సంస్థ (భారతదేశం పరివర్తన కోసం జాతీయ సంస్థ (National Institu- tion for Transforming India NITI Aayog)ను భారత ప్రభుత్వం జనవరి 1, 2015వ తేదీన స్థాపించింది. రాష్ట్ర ప్రభుత్వాలలో, ప్రధాన సంస్థలతో, నిపుణులతో, మేధావులతో విస్తృతంగా చర్చించి ఈ సంస్థను ఏర్పాటు చేశారు.

నీతి ఆయోగ్ విధులు (Functions of NITI Aayog) :

1. సహకార, పోటీ సమాఖ్యగా (co-operative and competitive federalism) భారతదేశం పరివర్తన చెందడానికి నీతి కృషి చేస్తుంది. ఆర్థికాభివృద్ధితో పాటు ప్రాధాన్యతలకు, వ్యూహాలకు సంబంధించిన జాతీయ ఎజెండాను దేశ ప్రధానికి, ముఖ్యమంత్రులకు అందజేస్తుంది.
2. కింది నుంచి పై స్థాయి వరకు ఒక వికేంద్రీకృత ప్రణాళికా నమూనాను (bottom-up model) ప్రవేశపెడుతుంది. జాతీయ, రాష్ట్రాల కోసం దూరదృష్టి (vision), ఊహాత్మక ప్రణాళికలను తయారు చేస్తుంది.
3. కేంద్ర, రాష్ట్ర మంత్రిత్వ శాఖలకు సహాయ పడేందుకు నిపుణులతో వాటి పరిధి, సంబంధిత ప్రణాళికలను వ్యూహాత్మక విధానాలను (domain strategies) రూపొందిస్తుంది. పరిశోధనాపరమైన మంచి ఫలితాలను ఇవ్వగలిగిన విధానాలకు సంబంధించిన విజ్ఞానాన్ని సేకరించి విస్తృతంగా కేంద్ర, రాష్ట్ర కూడలిగా ప్రభుత్వాలకు అందజేస్తుంది. సూక్ష్మంగా చెప్పాలంటే, విజ్ఞానం, నవకల్పనల కేంద్ర బిందువుగా (knowledge and innovation hub) నీతి వ్యవహరిస్తుంది.
4. సత్వర ఆర్థికాభివృద్ధి కోసం సమగ్ర, సంపూర్ణ పద్ధతులను (integraXed and holistic approach) ఈ సంస్థ ప్రవేశ పెడుతుంది. అంతర్రాష్ట్ర వివాదాలను లేదా వివిధ రంగాల మధ్య వివాదాలను నీతి పరిష్కరిస్తుంది.
5. ప్రపంచ స్థాయిలో అందుబాటులో ఉన్న నైపుణ్యాలను, వనరులను ప్రయోజనకరంగా వినియోగించడానికి సమన్వయ సంస్థ నోడల్ ఏజెన్సీగా వ్యవహరిస్తుంది. విధాన నిర్ణయాలు, కార్యక్రమాలు, నిపుణతలు, పాలనా వ్యవహారాలలో కేంద్ర, రాష్ట్ర ప్రభుత్వాలకు ఈ సంస్థ సలహాదారుగా పనిచేస్తుంది.
6. సాంకేతిక విజ్ఞానాల ప్రమాణాలను (technology upgradation), ఉత్పాదక శక్తుల నిర్మాణాలను (capacity building) అదనంగా పెంపొందించడానికి సహాయపడుతుంది.
7. ప్రభుత్వ విధానాలను, కార్యక్రమాలను ఎప్పటికప్పుడు పర్యవేక్షిస్తూ వాటి ప్రభావాలను (impact) సమీక్షిస్తుంది.

ప్రశ్న 2.
ప్రణాళిక అంటే ఏమిటి ? వివరించండి.
జవాబు.
ప్రణాళిక భావన :
మానవ ప్రవర్తనలో ప్రణాళిక అంతర్భాగం. ప్రతి దేశం తనదైన సరళిలో ప్రణాళికలను అమలుపరుస్తుంది. నిర్ణీత లక్ష్యంతో నిర్దిష్టంగా వ్యవహరించడమే ప్రణాళిక. ఆర్థిక ప్రణాళికను వివిధ ఆర్థిక వేత్తలు భిన్న రకాలుగా నిర్వచించారు. కాని, అన్ని నిర్వచనాలలో ఒక ఏకీకృత భావన ఇమిడి ఉంది. ‘నిర్ణీత కాలవ్యవధిలో నిర్ధిష్ట ప్రమాణాలను, లక్ష్యాలను సాధించడానికి ఆర్థిక వ్యవస్థను దేశంలోని ఒక కేంద్రీయ వ్యవస్థ నియంత్రించడమే ఆర్థిక ప్రణాళిక’.

తొడారో మహాశయుని ఉద్దేశంలో ఆర్థిక ప్రణాళిక అంటే ముందుగా నిర్ణయించబడిన లక్ష్యాలను సాధించడానికి బుద్ధిపూర్వకంగా ఒక దేశం లేదా ప్రాంతంలోని ప్రధాన ఆర్థికాంశాలను కొంతకాలంపాటు వినియోగం, పెట్టుబడి, పొదుపు, ఎగుమతులు, దిగుమతులు మొదలైన వాటిని ప్రభుత్వం ప్రభావితం చేయడం, నిర్వహించడం, నియంత్రించడం ప్రభుత్వపరమైన ఈ ప్రభావాలు, సూచనలు, నియంత్రణలకు చెందిన భావనలే సంక్షిప్తంగా ఆర్థిక ప్రణాళికల సారాంశం.

ప్రణాళిక (Plan) :
ప్రణాళికీకరణకు (Planning) ప్రధానమైన తేడా ఉంది. ప్రణాళిక ఒక పత్రం; ఆర్థిక కార్యకలాపాలను నిర్దేశించే నమూనా. ప్రణాళికీకరణలో ప్రణాళికలతోపాటు లక్ష్యసాధన దిశలో జరిగే కృషి ఉంటుంది. నిర్ణీత కాలపరిమితిలో ఎంపిక చేయబడిన లక్ష్యాలను సాధించడానికి ప్రణాళికలు మొత్తం ఆర్థిక వ్యవస్థకు వర్తిస్తాయి.

వివిధ రంగాలలో పెట్టుబడికోసం సేకరించిన ఆర్థిక వనరులు ప్రణాళికలో సూచించిన విధంగా కేటాయింపు జరుగుతుంది. జాతీయ ప్రయోజనాల ఆధారంగా నిర్దేశించబడిన లక్ష్యాలను సాధించడానికి ప్రణాళికలు ఉత్పత్తి పంపిణీలను నిర్దేశిస్తాయి.

ప్రశ్న 3.
సంతులిత ప్రాంతీయాభివృద్ధికి ప్రభుత్వం తీసుకున్న చర్యలను వివరించండి.
జవాబు.
సంతులిత ప్రాంతీయాభివృద్ధి అనగా అన్ని ప్రాంతాలు సమానంగా అభివృద్ధి చెందుతూ అన్ని ప్రాంతాలలో వనరుల లభ్యత ఒకే విధంగా ఉండవు. కాబట్టి అన్ని ప్రాంతాలు సమానంగా అభివృద్ధి చెందడం సాధ్యం కాదు. లభ్యమయ్యే వనరులను అభిలషణీయంగా ఉపయోగించకొనుటయే సంతులిత ప్రాంతీయాభివృద్ధి. దీనికోసం ప్రభుత్వం తీసుకొనే చర్యలు.

1. వెనుకబడిన రాష్ట్రాలకు కేంద్రం ఆర్థిక వనరులు బదిలీచేయడం.
2. వెనుకబడిన ప్రాంతాలకు ప్రాధాన్యత ఇచ్చి, ప్రభుత్వం పరిశ్రమలను స్థాపించుట.
3. వెనుకబడిన ప్రాంతాలకు, జిల్లాలకు అదనపు విత్త సదుపాయాల కల్పన.
4. వెనుకబడిన ప్రాంతాల్లో కావలసిన అవస్థాపనా సౌకర్యాలను కల్పించడం.
5. పారిశ్రామిక వికేంద్రీకరణను ప్రోత్సహించడం.
6. వెనుకబడిన ప్రాంతంలో పారిశ్రామిక క్షేత్రాలు ఏర్పాటు.
7. కొండ, గిరిజన ప్రాంతాలకోసం ప్రత్యేక పథకాలు.
8. చిన్నతరహా పరిశ్రమలకు తగిన ప్రోత్సహకాలు.
9. వెనుకబడిన ప్రాంతాలలో పరిశ్రమల స్థాపన, అభివృద్ధి కోశపరమైన ప్రోత్సహకాలు ఇవ్వడం అనగా సబ్సిడీలు, పన్ను రాయితీలు మొదలగునవి.

ప్రశ్న 4.
ఆర్థిక ప్రణాళికలకు సంబంధించిన వివిధ భావనలను తెలియజేయండి.
జవాబు.
నిర్ణీత కాల వ్యవధిలో నిర్దిష్ట ప్రమాణాలను, లక్ష్యాలను సాధించడానికి ఆర్థిక వ్యవస్థను దేశంలోని ఒక కేంద్రీయ వ్యవస్థ నియంత్రించడమే ఆర్థిక ప్రణాళిక.

1. పెట్టుబడిదారీ విధానంలో ప్రణాళిక :
సప్లయ్, డిమాండ్ రూపంలో ఉన్న మార్కెట్ శక్తులు, ఉత్పత్తి సంస్థలు స్వేచ్ఛ వినియోగదారుల ఎంపికలు పెట్టుబడిదారీ విధానానికి చోదక శక్తిగా పనిచేస్తాయి. లాభార్జన, స్వలాభాపేక్ష ఈ విధానాన్ని నడిపిస్తాయి. అందుకే భావనపరంగా పెట్టుబడిదారీ విధానానికి, ప్రణాళికలకు పొత్తు కుదరదు. ఈ విధానంలో ప్రభుత్వం ప్రధాన సౌకర్యాలను కల్పించే శాంతి భద్రతలను పరిరక్షించి ఆర్థిక వ్యవస్థను నడిపిస్తుంది.

2. ఎశ్రమ ఆర్థిక వ్యవస్థలో ప్రణాళిక :
ఈ ఆర్థిక వ్యవస్థలో ప్రభుత్వ, ప్రైవేటు రంగాలు కలిసి ఉంటాయి. భారతదేశం మిశ్రమ ఆర్థిక వ్యవస్థకు ఒక మంచి ఉదాహరణ. ఈ విధానంలో కేంద్ర ప్రణాళికా వ్యవస్థ ఆర్థిక ప్రణాళికలను రూపొందిస్తుంది. ఈ విధానంలో ప్రైవేటు రంగానికి అవసరమైన అవస్థాపనా సౌకర్యాలను ప్రభుత్వం చేకూరుస్తుంది. అయితే ప్రణాళికా లక్ష్యాలను దృష్టిలో ఉంచుకొని ప్రైవేటు రంగాన్ని ఎప్పటికప్పుడు ప్రభుత్వం నియంత్రణచేసి క్రమబద్ధీకరిస్తుంది.

3. సామ్యవాద వ్యవస్థలో ప్రణాళిక :
ఈ విధానంలో ఆర్థిక ప్రణాళికలు తప్పనిసరి. కేంద్రీయ ప్రణాళికా వ్యవస్థ ఆర్థిక వనరులను సమీకరించి దేశ ప్రయోజనాల దృష్టితో వివిధ రంగాలకు వనరులను కేటాయిస్తుంది. సామ్యవాద వ్యవస్థ ఆర్థిక ప్రణాళికలను యథాతథంగా అమలుచేస్తుంది.

4. ప్రజాస్వామిక ప్రణాళిక (Democratic Planning), అధీకృత ప్రణాళిక (Authoritarian) :
ప్రజాస్వామ్య ప్రణాళికలో ప్రభుత్వం ఉత్పత్తి సాధనాలన్నింటినీ నియంత్రణ చేయదు. ప్రజాభిప్రాయ పరిగణనలోకి తీసుకొని అధిక శాతం ప్రజలకు మేలు జరిగే విధంగా ప్రణాళికా లక్ష్యాలు నిర్దేశించబడతాయి. ఈ విధానంలో ఆర్థిక వ్యవస్థలో కొంతమేరకు స్వేచ్ఛ ఉంటుంది. 1990 సంవత్సరం తరువాత కొంత కాలంపాటు ఆనాటి రష్యాలో (USSR) అధీకృత ప్రణాళికా విధానం అమలు చేయబడింది.

5. కేంద్రీకృత, వికేంద్రీకృత ప్రణాళికలు (Centralised and Decentralised Planning) :
కేంద్రీకృత ప్రణాళిక ఇంతకు ముందు తెలియజేసినట్లు రష్యాలో ఉండేది. ఇది సామ్యవాద వ్యవస్థలో అమలుచేసే ప్రణాళిక. మిశ్రమ ఆర్థిక వ్యవస్థలో వికేంద్రీకృత ప్రణాళిక అమలులో ఉంటుంది. పరిపాలనా సంబంధమైన వివిధ యూనిట్లకు, కేంద్రీయ ప్రణాళికా వ్యవస్థకు మధ్య సమన్వయంతో వికేంద్రీకృత ప్రణాళిక పనిచేస్తుంది. మన దేశంలో ప్రణాళికా విధానం వికేంద్రీకృత రూపంలో ఉంది.

6. పై నుంచి, కింది నుంచి రూపొందించే ప్రణాళిక (Planning of Above and Below) :
ఈ విధానం పైనుంచి లేదా కింది నుంచి రూపొందించబడిన ప్రణాళికలను కలిగి ఉంటుంది. స్థానిక పరిస్థితుల, అవసరాల ఆధారంగా ప్రోత్సాహకరమైన ప్రణాళికలు కింద నుంచి ప్రణాళికల రూపంలో ఉంటాయి. ప్రజలు ప్రాంతీయ స్థాయిలో ప్రణాళికలను రూపొందిస్తారు. ప్రాంతీయ ప్రణాళికలను సమన్వయంచేసి జాతీయ ప్రణాళికలను తయారుచేసే విధానం కింది నుంచి సిద్ధం చేసిన ప్రణాళికల విధానంలో ఉంటుంది. ఇది ప్రజాస్వామ్య లక్ష్యాలకు అనుగుణంగా వాస్తవ పరిస్థితులను దృష్టిలో ఉంచుకొని తయారుచేసిన ప్రణాళికా విధానం.

7. దీర్ఘదర్శి ప్రణాళిక, వార్షిక ప్రణాళిక (Perspective Planning and Annual Planning) :
దీర్ఘదర్శి ప్రణాళిక 15 నుంచి 20 సంవత్సరాల కాలపరిమితితో ముందుచూపును కలిగి ఉంటుంది. దీర్ఘకాలంలో సాధించవలసిన లక్ష్యాలను ఈ ప్రణాళిక సూచిస్తుంది. దీర్ఘదర్శి ప్రణాళిక 3 నుంచి 5 సంవత్సరాల కాలపరిమితి కలిగిన స్వల్పకాల ప్రణాళికలుగా విభజించబడుతుంది. స్వల్పకాలిక ప్రణాళిక తిరిగి వార్షిక ప్రణాళికలుగా విడదీయ బడుతుంది. ఆచరణలో నిజానికి వార్షిక ప్రణాళికను దృష్టిలో ఉంచుకొంటారు. వార్షిక ప్రణాళిక ఆర్థిక కార్యకలాపాల సూచికగా గుర్తించబడుతుంది.

అదనపు ప్రశ్న:

ప్రశ్న 5.
భారతదేశంలో ప్రణాళికలలో సాధించిన విజయాలు మరియు వైఫల్యాలను వివరించుము.
జవాబు.
ఆర్థిక ప్రణాళిక అంటే ముందుగా నిర్ణయించిన లక్ష్యాలను సాధించడానికి బుద్ధిపూర్వకంగా ఒక దేశం లేదా ఒక ప్రాంతంలోని ప్రధాన ఆర్థికాంశాలను కొంతకాలం పాటు ప్రభుత్వం ప్రభావితం చేయడం, నిర్వహించడం, నియంత్రించడంను ఆర్థిక ప్రణాళిక అని అంటారు.

ప్రణాళికలు సాధించిన విజయాలు, వైఫల్యాలు :

1. విజయాలు :

1. నికర దేశీయ ఉత్పత్తి (Net Domestic Product), పొదుపు, పెట్టుబడులు, తలసరి ఆదాయంలో గణనీయమైన పెరుగుదల ఉంది.
2. భారతదేశం అన్ని మౌళిక, మూలధన వస్తు పరిశ్రమలలో, వినియోగ వస్తు పరిశ్రమలలో స్వయం సమృద్ధిని సాధించింది.
3. ఆహార ధాన్యాల ఉత్పత్తిలో స్వయం సమృద్ధి సాధించడంతో పాటు ఆహార భద్రతను కల్పిస్తుంది.
4. పారిశ్రామిక రంగంలో చెప్పుకోదగిన వస్తు వైవిధ్యత సాధ్యమైంది.
5. ప్రణాళికా కాలంలో అవస్థాపనా సౌకర్యాలు, రవాణా, నీటి పారుదల టెలికమ్యూనికేషన్ రంగాల విస్తరణ జరిగింది.
6. విద్యా రంగంలో అద్భుతమైన అభివృద్ధి జరిగింది. ముఖ్యంగా, శాస్త్ర, సాంకేతిక రంగంలో శిక్షణ పొందిన మానవ వనరులలో చెప్పుకోదగ్గ వృద్ధి చోటు చేసుకొంది. ప్రపంచ దేశాలలో సమాచార, సాంకేతిక రంగాలలో (information technology) అంతరిక్ష పరిశోధనలో ఒక ప్రధాన దేశంగా భారతదేశానికి ఒక గుర్తింపు వచ్చింది.

2. వైఫల్యాలు :

1. గ్రామీణ ప్రాంతాలలో పేదరిక భారం (incidence of poverty) సాపేక్షికంగా అధికంగా ఉంది.
2. నిరుద్యోగిత పెరుగుతున్నది. గ్రామీణ, పట్టణ ప్రాంతాలలో పేదరికానికి ప్రధాన కారణం నిరుద్యోగిత అనవచ్చు.
3. ఆదాయ అసమానతలు తగ్గలేదు. ఆర్థిక సంస్కరణల అమలు కాలంలో అసమానతలు మరింత పెరుగుతున్నాయి.
4. భూసంస్కరణలు ఆశించిన స్థాయిలో అమలు కాకపోవడం వల్ల భూయాజమాన్యంలో అసమానతలు (unequal land ownership) తొలగిపోలేదు.
5. ప్రాంతీయ అసమానతలు ఇంకా కొనసాగుతూనే ఉన్నాయి.

అతిస్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
సంతులిత ప్రాంతీయాభివృద్ధి.
జవాబు.
అన్ని ప్రాంతాలను ఒకే స్థాయిలో అభివృద్ధిచేయడం. ఒక్కో ప్రాంతం ఒక్కో కారణంగా అభివృద్ధిచెందగా, అదే విధంగా వెనుకబడి ఉంటుంది. కాబట్టి ఆయా ప్రాంతాలు ఎదుర్కొనే సమస్యలు అధ్యయనం చేసే ప్రత్యేకమైన పథకాలను అమలుపరచవలసి ఉంటుంది. అభివృద్ధి ఫలితాలు దేశ ప్రజలందరికి అందజేయడానికి, శ్రామిక శక్తి, సహజ వనరులను సంపూర్ణంగా వినియోగించు కోవడానికి ప్రాంతీయ అసమానతలు తొలగించి అన్ని ప్రాంతాలు సమంగా అభివృద్ధిచెందేలా చేయడం.

ప్రశ్న 2.
సమ్మిళిత వృద్ధి (Iriclusive growth).
జవాబు.
ఈ భావనలో వృద్ధి ఫలాలు జనాభాలో దిగువ వర్గాలకు అందడంతో పాటుగా మానసికేతర అంశాలు ఉంటాయి. ఆర్థికాభివృద్ధి ప్రక్రియలో ప్రతిఫలాలు పంపిణీ చేయకుండా గతంలో విస్మరించబడిన వర్గాల వారిని వృద్ధి ప్రక్రియలో భాగస్వాములను చేయడం సమ్మిళిత వృద్ధి లక్ష్యం. దీనివలన అనేక ఇతర ప్రయోజనాలు ఆర్థిక వ్యవస్థకు చేకూరుతాయి.

ప్రశ్న 3.
గ్రామీణ – పట్టణ ప్రాంతాల మధ్య వ్యత్యాసాలకు గల కారణాలు.
జవాబు.
పట్టణ జనాభా పెరుగుదలకు కారణాలు :
గ్రామల నుంచి ప్రజలు పట్టణాలకు వలస పోయి స్థిరపడటానికి గల ప్రధాన కారణాలను కింద విధంగా పేర్కొనవచ్చు.

1. గ్రామాలలో వ్యవసాయేతర రంగాలలో ఉపాధి అవకాశాలు తక్కువ. పట్టణాలలో ఉపాధి అవకాశాలు సాపేక్షంగా ఎక్కువ.
2. పారిశ్రామిక, సేవా రంగాల వృద్ధి విస్తరించడంతో విద్య, నైపుణ్యాలు కలిగిన గ్రామీణ యువత పట్టణాలకు ఆకర్షితులు అవుతున్నారు.
3. రవాణా, కమ్యూనికేషన్ల సౌకర్యాలతో పాటు విద్య, ఆరోగ్య సౌకర్యాలు పట్టణాలలో సుఖ జీవనానికి అవకాశం కల్పించడంతో కొందరు గ్రామీణ ప్రాంతాల నుంచి పట్టణాలకు తరలిపోతున్నారు.
4. పట్టణ ప్రాంతాలలో వ్యక్తిగత జీవనంలో ఇతరుల ప్రమేయం అతి స్వల్పంగా ఉంటుంది.
5. పట్టణ జీవన విధానం కొందరిని ఆకర్షించడంతో వలసలు పెరుగుతున్నాయి.

ప్రశ్న 4.
ప్రజాస్వామిక ప్రణాళిక, అధీకృత ప్రణాళిక.
జవాబు.
ప్రజాస్వామిక ప్రణాళిక (Democratic Planning), అధీకృత ప్రణాళిక (Authoritarian) :
“ప్రజాస్వామ్య ప్రణాళికలో ప్రభుత్వం ఉత్పత్తి సాధనాలన్నింటినీ నియంత్రణ చేయదు. ప్రజాభిప్రాయ పరిగణనలోకి తీసుకొని అధిక శాతం ప్రజలకు మేలు జరిగే విధంగా ప్రణాళికా లక్ష్యాలు నిర్దేశించబడతాయి.

ఈ విధానంలో ఆర్థిక వ్యవస్థలో కొంతమేరకు స్వేచ్ఛ ఉంటుంది. 1990 సంవత్సరం తరువాత కొంత కాలంపాటు ఆనాటి రష్యాలో (USSR) అధీకృత ప్రణాళికా విధానం అమలు చేయబడింది.

ప్రశ్న 5.
దీర్ఘకాలిక ప్రణాళిక, వార్షిక ప్రణాళిక.
జవాబు.
దీర్ఘదర్శి ప్రణాళిక, వార్షిక ప్రణాళిక (Perspective Planning and Annual Planning) :
దీర్ఘదర్శి ప్రణాళిక 15 నుంచి 20 సంవత్సరాల కాలపరిమితితో ముందుచూపును కలిగి ఉంటుంది. దీర్ఘకాలంలో సాధించవలసిన లక్ష్యాలను ఈ ప్రణాళిక సూచిస్తుంది.

దీర్ఘదర్శి ప్రణాళిక 3 నుంచి 5 సంవత్సరాల కాలపరిమితి కలిగిన స్వల్పకాల ప్రణాళికలుగా విభజించబడుతుంది. స్వల్పకాలిక ప్రణాళిక తిరిగి వార్షిక ప్రణాళికలుగా విడదీయబడుతుంది. ఆచరణలో నిజానికి వార్షిక ప్రణాళికను దృష్టిలో ఉంచుకొంటారు. వార్షిక ప్రణాళిక ఆర్థిక కార్యకలాపాల సూచికగా గుర్తించబడుతుంది.

ప్రశ్న 6.
భారతదేశ పరివర్తన కోసం జాతీయ సంస్థ (NITI Aayog).
జవాబు.
ప్రణాళికా సంఘం స్థానంలో నీతి ఆయోగ్ సంస్థ (భారతదేశం పరివర్తన కోసం జాతీయ సంస్థ (National Institu- tion for Transforming India NITI Aayog)ను భారత ప్రభుత్వం జనవరి 1, 2015వ తేదీన స్థాపించింది. రాష్ట్ర ప్రభుత్వాలలో, ప్రధాన సంస్థలతో, నిపుణులతో, మేధావులతో విస్తృతంగా చర్చించి ఈ సంస్థను ఏర్పాటు చేశారు.

Telangana TSBIE TS Inter 2nd Year Economics Study Material 3rd Lesson జాతీయాదాయం, పేదరికం, నిరుద్యోగిత Textbook Questions and Answers.

TS Inter 2nd Year Economics Study Material 3rd Lesson జాతీయాదాయం, పేదరికం, నిరుద్యోగిత

వ్యాసరూప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
భారతదేశపు జాతీయాదాయ ధోరణులను వివరించండి.
జవాబు.
నికర జాతీయోత్పత్తి, తలసరి ఆదాయాల ధోరణులు : భారతదేశంలో వాస్తవిక ఆదాయపు వృద్ధిని ప్రణాళికా బద్ధంగా అధ్యయనం చేసినట్లయితే ఆర్థిక ప్రణాళికీకరణ నేపథ్యంలో మొదటి మూడు దశాబ్దాల కాలంలో జాతీయాదాయంలోని సాలీనా పెరుగుదల రేటు అతి తక్కువగా అంటే సాలీనా 3.5 శాతంగా ఉన్నప్పటికీ, 1980-81 నుంచి జాతీయాదాయంలోని పెరుగుదల 5.9 శాతంగా ఉండటమనేది ఆశాజనకంగా ఉందని భావించవచ్చు.

గడచిన ఆరు దశాబ్దాల కాలంలో గల జాతీయాదాయ ధోరణుల విశ్లేషణ ఈ దేశపు వృద్ధి యొక్క ప్రధాన లక్షణాలను స్పష్టంగా తెలియజేస్తుంది. అవి : క్రమరహిత వృద్ధి, హెచ్చుకాని వృద్ధి రేటులు, 1991 సంస్కరణల తదనంతరం వృద్ధి తక్కువ బలహీనత (fragile)ను కలిగి ఉంది.

భారతదేశంలో ఆర్థిక ప్రణాళికీకరణకు బీజాలు పడినప్పటి నుంచి వ్యావసాయిక ఉత్పత్తిలో క్రమరహిత వృద్ధి పారిశ్రామిక ఉత్పత్తిలో లోటుపాట్లు ఉన్నప్పటికీ, నికర జాతీయోత్పత్తిలోని పెరుగుదల మందకొడిగానైనా కొనసాగింది. కొన్ని సంవత్సరాల పాటు బ్రిటిష్ పాలనలో ఉంటూ స్తబ్దతను చవిచూసిన ఆర్థిక వ్యవస్థలో ఈ రకమైన పెరుగుదలనేది ఆహ్వానించదగిన అభివృద్ధిగా చెప్పవచ్చు.

ఏది ఏమైనప్పటికీ, ఉత్పత్తి కారకాల దృష్ట్యా తలసరి నికర జాతీయోత్పత్తి వలెనే తలసరి జాతీయాదాయంలోని ధోరణులను పరిశీలించడం వల్ల ఆర్థిక వ్యవస్థ పని తీరును కచ్చితంగా తెలియజేయవచ్చు.

పట్టిక ప్రకారం 68 సంవత్సరాలకు సంబంధించిన (1950-51 నుంచి 2017-18 వరకు) దత్తాంశం ఆధారంగా, నికర జాతీయాదాయం స్థిర ధరల దృష్యా రూ.2,69, 724 కోట్ల నుంచి రూ. 1,14,04,413 కోట్ల మేరకు పెరిగింది. అదే కాలంలో వర్తమాన ధరల దృష్యా జాతీయాదాయం రూ. 9,829 కోట్ల నుంచి రూ.1,47,10,563 కోట్ల మేరకు పెరిగింది.

1950-51 లో స్థిర ధరల దృష్యా తలసరి ఆదాయం 1950-51 లో రూ.7,513 ఉన్నదల్లా 2017-18 వ సంవత్సరం నాటికి రూ. 86,668 మేరకు పెరిగింది. వర్తమాన ధరల దృష్యా కూడా గమనించినట్లయితే అది కాలంలో రూ. 274 నుంచి రూ.1,12,835 ల మేరకు పెరిగింది.

30 సంవత్సరాల కాల వ్యవధిని (1950-51 నుంచి 1980-81 వరకు) గమనించినట్లయితే జాతీయాదాయపు (1999-2000 -100) సాలుసరి వృద్ధి రేటు 3.5 శాతంగా ఉంది. తలసరి ఆదాయంలోని వృద్ధి రేటు కేవలం 1.4 శాతంగానే ఉంది. అదే కాలంలో వర్తమాన ధరల దృష్యా నికర జాతీయోత్పత్తి సాలుసరి వృద్ధి రేటు 9 శాతం ఉంటే తలసరి ఆదాయ వృద్ధి రేటు 6.7 శాతంగా ఉంది.

ఉత్పత్తి కారకాల దృష్ట్యా నికర జాతీయోత్పత్తి, తలసరి నికర జాతీయోత్పత్తి:

జాతీయాదాయ, తలసరి ఆదాయ వృద్ధిరేట్లు (శాతాలలో):

జాతీయాదాయం, తలసరి ఆదాయం వృద్ధి రేట్లను మూడు భాగాలుగా విభజించి చూసినట్లయితే మొదట పది సంవత్సరాల కాలంలో (1950-51 నుంచి 1960-61 వరకు) జాతీయాదాయం సగటున 4.2 శాతం మేరకు పెరిగింది. తరువాత కాలంలో తగ్గింది. సాలీనా 1960-61, 1970-71 మధ్య కాలంలో NNP వృద్ధి రేటు 3.5 శాతం మేరకు, తలసరి NNP 1.2 శాతం మేరకు తగ్గింది.

తదుపరి 10 సంవత్సరాల కాల వ్యవధిలో (1970-71 నుంచి 1980-81 వరకు) నికర జాతీయోత్పత్తిలోని పెరుగుదల రేటు 2.9 శాతం ఉంటే తలసరి NNP 0.6 శాతం మేరకు తగ్గింది. ఎనభైలలో వృద్ధి రేటుల విషయంలో చాలా ప్రస్ఫుటమైన పెరుగుదలను గమనించవచ్చు.

1999-2000 ధరల దృష్ట్యా 1980-81, 1990-91 కాలంలో నికర జాతీయోత్పత్తిలో పెరుగుదల రేటు సాలీనా 5.2 శాతం ఉంటే, తలసరి NNP సాలుసరి వృద్ధి రేటు 3 శాతం మేరకు పెరిగింది. భారతదేశ ఆర్థిక వ్యవస్థ ఆచార్య రాజ్ కృష్ణ సూచించిన 3 శాతం హిందూ వృద్ధి రేటు నుంచి బయటపడింది. కాబట్టి ఈ రకమైన వృద్ధి ఆరోగ్యకరమైన వృద్ధి రేటుగా చెప్పవచ్చు.

1990-91, 2000-01 మధ్య కాలంలో (1999-2000 ధరల దృష్ట్యా) నికర జాతీయోత్పత్తి సాలుసరి వృద్ధి రేటు 5.5 శాతం ఉంటే, తలసరి NNP 3.4 శాతంగా ఉంది. చివరి రెండు దశాబ్దాల కాలంలో (1980-81, 2000-01) NNP సాలుసరి వృద్ధి రేటు 5.6 శాతం అయితే, తలసరి NNP వృద్ధి రేటు 3.2 శాతంగా ఉంది. గత మూడు దశాబ్దాల జాతీయాదాయ ధోరణులను పోల్చిచూస్తే చివరి రెండు దశాబ్దాల్లో భారతదేశ ఆర్థిక వ్యవస్థ కొంత మేరకు మెరుగైందని చెప్పవచ్చు.

2000 – 01, 2004 – 05 మధ్య కాలంలో (1999 – 2000 ధరల దృష్ట్యా) వృద్ధి రేటు 6.4 శాతం మేరకు పెరిగింది, తలసరి NNP లోని సాలీనా వృద్ధి రేటు 4.7 శాతం మేరకు పెరిగింది. 2004 – 05, 2013-14 మధ్య కాలంలో (2004 – 05 ధరల దృష్యా) NNP లోని వృద్ధి రేటు మరింతగా అంటే 7.3 శాతం మేరకు పెరిగింది. తలసరి ఆదాయంలోని వృద్ధి రేటు 5.8 శాతం మేరకు పెరిగింది. అంటే జాతీయాదాయంలో, తలసరి ఆదాయంలో సాపేక్షికంగా చాలా పెరుగుదల ఏర్పడిందని పై గణాంకాలు తెలియచేస్తున్నాయి. దీనిని ఆరోగ్యకరమైన అభివృద్ధిగా పరిగణించవచ్చు.

ప్రశ్న 2.
జాతీయాదాయంలో రంగాల వారీగా వాటాలను సంక్షిప్తగా పరిశీలించండి.
జవాబు.
ఒక దేశంలో ఒక సంవత్సర కాలంలో ఉత్పత్తి అయిన అంతిమ వస్తు సేవల విలువను ఆ దేశపు జాతీయాదాయం అని అంటారు.

జాతీయాదాయంలో వివిధ రంగాల వాటా :
రంగాల వాటాల వారీగా జాతీయోత్పత్తి అధ్యయనం అనేది ఆర్థిక నిర్మితి స్వరూపాన్ని తెలియజేస్తుంది. జాతీయాదాయ ధోరణులు ఎలాంటి ప్రాధాన్యతను కలిగి ఉన్నాయో జాతీయాదాయపు వివిధ రంగాల వాటాల విశ్లేషణ కూడా అంతే ప్రాముఖ్యతను కలిగి ఉంది. ప్రణాళికల కాలంలో ప్రారంభమైన ఆర్థిక వృద్ధి ప్రక్రియ పర్యవసానమే పారిశ్రామిక పరమైన మూలం (industrial origin) ఆధారంగా జాతీయాదాయపు కూర్పు (composition) లోని నిర్మితిపరమైన మార్పును అర్థం చేసుకోవచ్చు.

1. ప్రాథమిక రంగపు వాటా : వ్యవసాయం, అడవులు, ఉద్యాన వనాలు, మత్స్య పరిశ్రమలను ప్రాథమిక రంగం కలిగి ఉంటుంది.

స్వాతంత్య్రానంతర కాలంలో జాతీయాదాయంలో ప్రాథమిక రంగపు వాటా గరిష్ఠంగా 1950-51 సంవత్సరంలో 57.2 శాతం ఉంటే, 2013-14 నాటికి కనిష్ఠంగా అంటే 13.9 శాతంగా ఉన్నదల్లా 2018-19 నాటికి 16.1 శాతం మేరకు పెరిగింది. జాతీయాదాయంలో ప్రాథమిక రంగం వాటా క్రమంగా తగ్గుతూ ఉన్నట్లు గమనించవచ్చు. వ్యవసాయ రంగపు ప్రతికూల వాతావరణ స్థితిగతుల, నిర్మితిపరమైన మార్పుల ఫలితమే వ్యావసాయిక రంగపు వాటాలో త్వరితగతిన సంభవించే తగ్గుదలకు ప్రధాన కారణంగా చెప్పవచ్చు.

ఇటీవల కాలంలో దేశ ఆర్థిక వ్యవస్థలో నిర్మాణాత్మక మార్పులు చోటు చేసుకొన్నాయి. రవాణా మరియు కం, బాంకింగ్ మరియు బీమా, ఇతర సేవల రంగాలు మొదలైనవి వ్యావసాయిక రంగం కంటే చాలా వేగంగా అభివృద్ధి చెందడం వల్ల దేశ జాతీయాదాయంలో వివిధ రంగాల వాటాల అంచనాలు ప్రభావితం అయ్యాయి.

2. ద్వితీయ రంగం వాటా :
ద్వితీయ రంగంలో గనులు మరియు క్వారీయింగ్, వస్తు తయారీ, నిర్మాణం, విద్యుత్, గ్యాస్, నీటి సరఫరా మొదలైనవి ఉంటాయి. జాతీయాదాయంలో ఈ రంగం యొక్క వాటా వృద్ధి క్రమంలో మొదట పెరుగుతుంది. 1950-51వ సంవత్సరంలో 15 శాతం ఉంటే, 1980-81 నాటికి 24 శాతం మేరకు, 2018-19 నాటికి 29.6 శాతం మేరకు పెరిగింది.

3. తృతీయ రంగం వాటా :
ఈ రంగపు వాటాలో భాగంగా వ్యాపారం, రవాణా, కమ్యూనికేషన్స్, స్టోరేజి, బాంకింగ్, బీమా, రియల్ ఎస్టేట్, సామాజిక, వైయక్తిక సేవలు ఉంటాయి. వీటి వాటా 1950-51 సంవత్సరంలో 25 శాతం ఉండగా, 2018-19 సంవత్సరం నాటికి 54, 3 శాతం మేరకు పెరిగింది. అంటే వాటి వాటా గణనీయంగా పెరిగిందని చెప్పవచ్చు. ఇలాంటి పెరుగుదలలో రవాణా విస్తరణ ప్రత్యేకించి రోడ్డు రవాణా, కమ్యూనికేషన్లు ప్రధాన కారకాలుగా ఉన్నాయి.

పారిశ్రామికీకరణ దశ పూర్తి కాకుండానే భారతదేశ ఆర్థిక వ్యవస్థ బాగా అభివృద్ధి చెందిన దేశాలైన యు.ఎస్.ఏ., కెనడా, యు.కె. లాంటి దేశాలలాగా పారిశ్రామిక పథకం ఉన్నతీకరణ వల్ల మారుతున్న జాతీయాదాయపు నిర్మితిని మరింతగా బలోపేతం చేయాల్సిన అవసరం ఉంది. అంటే వ్యవసాయాన్ని విస్మరించడమని అర్థం కాదు. కాని వ్యవసాయ ఆధారిత పరిశ్రమల పట్ల దృష్టిని సారిస్తూ .ఆర్థిక వ్యవస్థ పారిశ్రామికీకరణ దిశగా పయనించే విధంగా చేయాల్సి ఉంది. అంతేగాక, ఆర్థిక వ్యవస్థ సత్వర వృద్ధికిగాను పరిశ్రమలు వ్యవసాయానికి ఉత్పాదితాలను (inputs) సరఫరా చేయాల్సిన అవసరం ఉంది.

ప్రశ్న 3.
పంచవర్ష ప్రణాళికల కాలంలో జాతీయాదాయం మరియు తలసరి ఆదాయం వృద్ధి రేట్లను చర్చించండి.
జవాబు.
జాతీయాదాయం అనగా ఒక దేశంలో ఒక సంవత్సర కాలంలో ఉత్పత్తి అయిన అంతిమ వస్తు సేవల విలువగా చెబుతారు. అలాగే ఒక దేశపు జాతీయాదాయాన్ని ఆదేశపు జనాభాతో భాగిస్తే వచ్చే దానిని తలసరి ఆదాయంగా చెబుతారు. ఈ రెండు భావనలను ఒక దేశపు ఆర్థికాభివృద్ధి రేటును కొలవటానికి ఉపయోగిస్తారు.

పంచవర్ష ప్రణాళికల కాలంలో జాతీయాదాయం, తలసరి ఆదాయాల సాలుసరి వృద్ధి రేట్లు :
పంచవర్ష ప్రణాళికల కాలంలో జాతీయాదాయం, తలసరి ఆదాయాల సాలుసరి వృద్ధి రేట్లు క్రింది విధంగా వివరించవచ్చు.

వివిధ ప్రణాళికా కాలాలలోని సాలుసరి వృద్ధి రేట్లు:

మొదటి పంచవర్ష ప్రణాళికలో (1999-2000 ధరల దృష్యా) జాతీయాదాయం సంవత్సరానికి సగటు వృద్ధి రేటు 4.4 శాతంగా ఉన్నదల్లా, రెండవ ప్రణాళికా కాలం నాటికి 3.8 శాతం మేరకు తగ్గింది. ఏది ఏమైనప్పటికీ, మూడవ ప్రణాళికా కాలంలో జాతీయాదాయంలో సాలుసరి పెరుగుదల 2.6 శాతం మేరకు తగ్గింది. ఈ పెరుగుదల రేటు జనాభా వృద్ధిని తటస్థీకరించడానికి సరిపడేదిగా ఉంటుంది. ఈ ప్రణాళికా కాలంలో తలసరి ఆదాయ వృద్ధి రేటు 0.4 శాతంగా మాత్రమే ఉంది.

1965-66 సంవత్సరంలో ఏర్పడిన తీవ్రమైన క్షామం వల్ల వృద్ధి రేటు మందగించింది. దీని తరవాత మరొక క్షామం ఏర్పడటం వల్ల వ్యాపారంలో కూడా తిరోగమనం చోటు చేసుకోవడం వల్ల వృద్ధి రేటు మందగించింది. 1967-68 సంవత్సరం తరవాత ఆర్థిక వృద్ధి రేటు పెరుగుదల ప్రారంభమయ్యింది.

నాల్గవ ప్రణాళిక కాలంలో (1969-74) జాతీయాదాయపు సాలుసరి వృద్ధి రేటు 3.1 శాతానికి పడిపోగా, తలసరి ఆదాయపు సాలుసరి వృద్ధి రేటు 0.8 శాతంగా ఉంది. 1972-73, 1973-74 సంవత్సరాలలో ధరలలోని పెరుగుదల, ఉత్పాదక సామర్థ్యాన్ని పూర్తి స్థాయిలో వినియోగించుకోలేకపోవడం అనే ప్రధాన కారణాల వల్ల నాల్గవ ప్రణాళికా కాలంలో తక్కువ వృద్ధి రేటు నమోదైంది.

ఐదవ ప్రణాళికా కాలంలో (1974-79) జాతీయాదాయంలోని సాలుసరి సగటు పెరుగుదల 4.9 శాతం ఉంటే, తలసరి ఆదాయం మాత్రం కేవలం 2.6 శాతంగా ఉంది. సంక్షిప్తంగా చెప్పాలంటే, 5వ ప్రణాళికా కాలంలో ఆర్థిక వ్యవస్థ పని తీరు చాలా సంతృప్తికరంగా ఉంది. 6వ ప్రణాళికా కాలంలో (1980-85) భారతదేశ జాతీయాదాయపు వృద్ధి రేటు 5.4 శాతంగా నమోదు అయితే, తలసరి ఆదాయ వృద్ధి రేటు మాత్రం 3.1 శాతంగా ఉంది. 7వ ప్రణాళికా కాలంలో (1985 – 90) భారతదేశపు NNP సాలుసరి వృద్ధి రేటు 5.5 శాతం మేరకు పెరిగింది.

తలసరి NNP సాలుసరి వృద్ధి రేటు 3.3 శాతంగా ఉంది. కాని ఈ ప్రణాళికా కాలంలో NNP యొక్క ఆశించిన వృద్ధి రేటు 5 శాతం, తలసరి NNP యొక్క ఆశించిన వృద్ధి రేటు 3 శాతం. కాబట్టి, ఈ ప్రణాళికా కాలంలో ఆశించిన వృద్ధి రేటు కంటే వాస్తవిక వృద్ధి రేటు ఎక్కువగా ఉంది అని చెప్పవచ్చు. 8వ ప్రణాళికా కాలంలో (1992-97) జాతీయాదాయంలో 6. 7 శాతం, తలసరి ఆదాయంలో 4.5 శాతం వృద్ధిని సాధించింది. ఈ రకమైన ఆరోగ్యకరమైన ధోరణిని స్థిరంగా కొనసాగే విధంగా చూడటం అవసరం. 9వ ప్రణాళికా కాలంలో (1997-2002) జాతీయాదాయంలోని వృద్ధి రేటు 5.

3 శాతం ఉంటే, తలసరి ఆదాయంలోని వృద్ధి రేటు 3.3 శాతంగా ఉంది. ఈ ప్రణాళికా కాలంలోని వృద్ధి రేట్లను 8వ ప్రణాళికా కాలంలోని వృద్ధి రేట్లతో పోల్చినప్పుడు తగ్గినట్లు గమనించవచ్చు. 10వ ప్రణాళికా కాలంలో (2002-07) జాతీయాదాయంలోని ఫెరుగుదల ఇంతకు ముందెన్నడూ లేని విధంగా 7.8 శాతంగా ఉంటే, తలసరి ఆదాయం 6.1 శాతంగా ఉంది. 11వ ప్రణాళికా కాలంలో (2007-12) NNP లోని వృద్ధి రేటు 7.6 శాతం అయితే, తలసరి NNP లోని పెరుగుదల 6.2 శాతంగా ఉంది. ఈ ప్రణాళికా కాలంలో గత ప్రణాళికల వృద్ధి రేట్లను అధిగమించడం జరిగింది. 12వ ప్రణాళికా కాలంలో NNP లోని వృద్ధి రేటు 8 శాతంగా ఉంది.

ప్రశ్న 4.
ఆదాయ, సంపద పంపిణీలోని అసమానతలను ఏ విధంగా తగ్గించగలరో తెలియజేయండి.
జవాబు.
నివారణ చర్యలు :
భారతదేశపు పంచవర్ష ప్రణాళికల కాలాలలోని ప్రధాన లక్ష్యాల్లో ఆదాయ పంపిణీలోని అసమానతల నిర్మూలన ఒక ప్రధాన లక్ష్యంగా నిర్దేశింపబడింది. ప్రభుత్వం విడుదల చేసిన ప్రణాళికా డాక్యుమెంట్లను, విధానపరమైన తీర్మానాలను తరచి చూచినట్లయితే ఆదాయ అసమానతలను తగ్గించడానికి తీసుకొన్న పలుచర్యలను తెలుసుకొనుచున్నది.

1. భూసంస్కరణలు, వ్యావసాయిక భూపునఃపంపిణీ :
గ్రామీణ రంగంలో ముఖ్యంగా వ్యావసాయిక భూమి కేంద్రీకరణ వల్ల ఆదాయ అసమానతలు చోటు చేసుకొంటున్నాయి. జమీందారీ పద్ధతిని రద్దుచేయక ముందు పెద్ద మొత్తంలో భూమి అనుపస్థితి భూస్వాముల (absentee landlords) ఆధీనంలో ఉండటం వల్ల వ్యావసాయిక ఉత్పత్తిని అధిక మొత్తంలో భూస్వాములు తీసుకొని భూమిని సాగు చేసే సాగుదారులకు జీవనాధార స్థాయి మేరకే ఉత్పత్తిని ఇచ్చేవారు.

అందువల్ల భూస్వాముల, ఇతర మధ్యవర్తుల రద్దు, భూ కమతాలపై గరిష్ఠ పరిమితి చట్టాలను ప్రవేశపెడుతూ శాసనపరమైన చర్యలను ప్రభుత్వం తీసుకొంది.

2. ఏకస్వామ్య వ్యాపార కార్యకలాపాల నియంత్రణ :
ఆదాయ అసమానతలను తగ్గించడానికి ఏకస్వామ్య సంస్థల ప్రవృత్తులను నియంత్రించాల్సిన అవసరం ఉంది. 1969వ సంవత్సరంలో ఏకస్వామ్య వ్యాపార కార్యకలాపాల నియంత్రణ చట్టాన్ని (Mo- nopolies and Restrictive Trade Practices MRTP Act) ప్రవేశపెట్టారు.

3. ఉపాధి, వేతన విధానాలు :
నాలుగవ పంచవర్ష ప్రణాళికా కాలం నాటికి కూడా ఉద్యోగ కల్పన లక్ష్యానికి అంతగా ప్రాధాన్యతను ఇవ్వలేదు. ఏది ఏమైనప్పటికీ, నాలుగవ పంచవర్ష ప్రణాళికా ఆరంభం నుంచి గ్రామీణ తాత్కాలిక ఉపాధి పథకం (Crash Scheme for Rural Employment – CSRE), దుర్భిక్ష పీడిత ప్రాంతాల అభివృద్ధి పథకం (Drought Prone Areas Programme-DPAP).

ఇంజనీర్ల కోసం స్వయం ఉపాధి పథకాలు, నిరుద్యోగ విద్యావంతులకు ఉపాధి పథకాలు, పనికి ఆహార పథకం Food for Work Programme – FFWP మొదలైన కొన్ని ప్రత్యేకమైన పథకాలను ప్రవేశపెట్టారు. 1978-79 సమీకృత గ్రామీణాభివృద్ధి పథకాన్ని IRDP ప్రారంభించి ఆరవ ప్రణాళికా కాలం నాటికి దేశం మొత్తంలో ఈ పథకాన్ని విస్తరింపజేశారు.

సమీకృత గ్రామీణాభివృద్ధి పథకం, జాతీయ గ్రామీణ ఉపాధి హామీ పథకం National Rural Employment Programme – NREP గ్రామీణ భూమిలేని వారికి ఉపాధి హామీ పథకం Rural Landless Employment Guarantee Programme – RLEGP లాంటి పతకాలను ప్రవేశపెట్టి దేశంలో పేదరికం, నిరుద్యోగం, ఆదాయ అసమానతలను తగ్గించడానికి ప్రయత్నిస్తున్నారు. జవహర్ రోజ్ గార్ యోజనలో NREP, RLEGP లు ఏప్రిల్ 1, 1989న సమ్మిళితమయ్యాయి.

4. సాంఘిక భద్రతా చర్యలు :
సంఘటిత రంగంలోని శ్రామికుల భవిష్యత్తును దృష్టిలో పెట్టుకొని ప్రావిడెంట్ ఫండ్ చట్టం ద్వారా ప్రావిడెంట్ ఫండ్ లాభాలను కల్పిస్తున్నారు. ప్రభుత్వం ఉద్యోగ బీమా చట్టం సాంఘిక భద్రతా చర్యల్లో చాలా ముఖ్యమైంది. దీని ద్వారా శ్రామికులకు వైద్యం, అంగ వైకల్యం, గర్భిణీ స్త్రీలకు, అనారోగ్య కాలానికి, ఉద్యోగులపై ఆధారపడి ఉన్న వారికి ప్రయోజనం చేకూరే విధంగా సాంఘిక భద్రతా చర్యలను తీసుకొని పేదరికాన్ని, ఆదాయ అసమానతల తీవ్రతను పై చట్టాల అమలు ద్వారా తగ్గు ముఖం పట్టేలా ప్రయత్నాలు చేస్తున్నారు.

5. కనీస అవసరాల పథకం :
ప్రణాళిక రూపకర్తలు కనీస అవసరాల పథకాన్ని అయిదవ ప్రణాళికలో ప్రవేశపెట్టి, పేదరిక నిర్మూలనతో పాటు ఆర్థిక వృద్ధిని కూడా ఆశయంగా పెట్టుకున్నారు. ప్రభుత్వం 6వ పంచవర్ష ప్రణాళిక నుంచి ప్రభుత్వ ఏజన్సీల ద్వారా రాయితీ’ సేవలను కల్పించి పేద ప్రజల వినియోగ స్థాయిని పెంచి, గ్రామాల్లో, నగరాల్లో శ్రామికుల ఉత్పాదక సామర్థ్యం పెరిగేలా చర్యలు తీసుకొంటున్నారు.

6. గ్రామీణ పేదరిక నిర్మూలన పథకాలు :
భారతదేశంలో గ్రామీణ ప్రాంతాల్లో కఠోర పేదరికం ఉంది. గ్రామీణ ప్రాంతాల్లో భూమిలేని వ్యవసాయిక శ్రామికుల, సన్నకారు, ఉపాంత రైతులు, గ్రామీణ వృత్తుల వారు, షెడ్యూల్డ్ కులాలు, తెగల వారు చాలా పేదరికంలో ఉన్నారు. వీరి ఆదాయ స్థాయిని పెంపొందింపజేయడానికి ప్రభుత్వం ఈ క్రింది మూడు రకాలైన పథకాలను చేపడుతుంది. అవి :

1. గ్రామీణ పేద ప్రజల వనరుల – ఆదాయ అభివృద్ధి పథకాలు
2. ప్రత్యేక ప్రాంతాల అభివృద్ధి పథకాలు
3. అనుబంధ ఉద్యోగ అవకాశాలను సృష్టించే పనుల పథకాలు

7. పన్నుల వ్యవస్థ (Taxation) :
భారతదేశంలో ఉన్న పన్నుల వ్యవస్థలో ప్రత్యక్ష పన్నులకు పురోగామి స్వభావం ఉంటుంది. ప్రత్యక్ష పన్నుల వల్ల దేశంలో కొద్ది మంది చేతుల్లో కేంద్రీకృతమై ఉన్న సంపదను నిరోధించడానికి ఆస్కారం ఉంటుంది. అంటే ఆదాయ సంపద అసమానతలను తగ్గించవచ్చు. పన్నుల వ్యవస్థను పటిష్టం చేయడం ద్వారా నల్లధనాన్ని అరికట్టి, ఆదాయ-సంపద పంపిణీలో గల తీవ్ర వైషమ్యాలను రూపుమాపవచ్చు.

ప్రశ్న 5.
భారతదేశంలో నిరుద్యోగిత భారాన్ని వివరించండి.
జవాబు.
భారతదేశంలో నిరుద్యోగిత అంచనాలు :
1951 – 2011 మధ్య కాలంలో మన దేశంలో జనాభా గణనీయమైన రేటులో అంటే సాలీనా 2.1 శాతం మేరకు పెరిగింది: పర్యవసానంగా శ్రామిక మార్కెట్లో ఉద్యోగాన్వేషణ కోసం గల ప్రజల సంఖ్య అనూహ్యంగా త్వరితగతిన పెరిగింది. కాని ఆర్థిక వృద్ధి మందకొడిగా ఉండటం వల్ల దానికి అనుగుణంగా ఉద్యోగావకాశాలు పెరగలేదు. అందువల్ల ఒక ప్రణాళికా కాలం నుంచి మరొక ప్రణాళికా కాలం నాటికి నిరుద్యోగిత పరిమాణంలో పెరుగుదల చోటు చేసుకుంది.

1993 – 94 నుంచి 2004-2005 వరకు అంటే 11 సంవత్సరాల కాల వ్యవధిని సరళీకరణ కాలంగా పరిగణిస్తారు. అయితే 1977 – 78 నుంచి 1993 – 94 వరకు అన్ని రకాలైన నిరుద్యోగితలు తగ్గుదల ధోరణి కనపరిస్తే 1993-94, 2004-05 మధ్య కాలాలలో మాత్రం దానికి వ్యతిరేకమైన ధోరణి ప్రస్ఫుటంగా కనిపిస్తుంది. సాధారణ స్థితి నిరుద్యోగితను అనుసరించి 1977 – 78లో నిరుద్యోగిత 4.23 శాతం ఉంటే, 1993-94 నాటికి 2.56 శాతంకు తగ్గింది.

కాని 2004 – 05 నాటికి 3.06 శాతంకు పెరిగింది. 2011 – 12 లో ఈ పద్దతిని అనుసరించి నిరుద్యోగిత 2.7 శాతంగా అంచనా వేయబడింది. అత్యంత సమగ్ర నిరుద్యోగిత కొలమానం కూడా అంటే వర్తమాన రోజువారీ స్థితి (CDS) నిరుద్యోగిత రేటు 1977 – 78లో 8. 18 శాతం ఉంటే, 1993-94 నాటికి 6.03 శాతంకు తగ్గింది. కాని 2004-05 నాటికి మళ్ళీ నిరుద్యోగిత 8.28 శాతంకు పెరిగింది.

2004 – 05 తో పోల్చినప్పుడు 2011 – 12 సంవత్సరంలో CDS ప్రాతిపదికన గల నిరుద్యోగిత రేటు 6.6 శాతం అని అంచనా వేయబడింది. అంటే మళ్ళీ తగ్గుదల ధోరణి కనపరిచింది. పట్టణ, గ్రామీణ ప్రాంతాలలో ఈ రకమైన ధోరణిని గమనించవచ్చు. ఏది ఏమైనప్పటికీ, పట్టణ ప్రాంతాలలో CDS నిరుద్యోగిత రేటు 1993 – 94లో 7.43 శాతం ఉంటే, 2004 – 05 నాటికి 8.28 శాతం మేరకు అంటే చాలా కొద్దిగా మాత్రమే పెరిగింది.

ఈ పెరుగుదల రేట్లు గ్రామీణ ప్రాంతాలలో చాలా వేగవంతంగా ఉంది. 1993 – 94లో గ్రామీణ ప్రాంతాలలో 5.63 శాతం ఉంటే, 2004 – 05 నాటికి 8.28 శాతం మేరకు పెరిగింది. NSSO యొక్క 66వ రౌండులో నిరుద్యోగిత రేట్లు తగ్గినట్లు గమనించినప్పటికీ, గత కాలపు ధోరణి కంటే ఎలాంటి వ్యత్యాసం కనిపించలేదు.

ఎందుకంటే 2004-05, 2009-10 మధ్య కాలంలో అదనపు శ్రామిక శక్తి 9.2 మిలియన్లుగా ఉంది. ఇంతకు ముందున్న కాలంలో ఈ శ్రామిక శక్తి చాలా తక్కువగా ఉంది. గ్రామీణ మరియు పట్టణ ప్రాంతాలలో అన్ని నిరుద్యోగిత కొలమానాలలో ఈ రకమైన దృగ్విషయాన్ని గమనించవచ్చు.

ఆర్థిక సంస్కరణల మొదటి దశలో గ్రామీణ ఆర్థిక వ్యవస్థ సాపేక్షికంగా విస్మరించబడిందని చెప్పవచ్చు. సాధారణ ప్రధాన స్థితి (UPS) అనేది సంవత్సర కాలం పాటు బహిరంగ నిరుద్యోగిత కొలమానంగా ఉంటుంది. కాని వర్తమాన రోజు వారీ స్థితి (CDS) బహిరంగ నిరుద్యోగితనే కాకుండా అల్ప ఉద్యోగితను కూడా మదింపు చేస్తుంది.

1977-78లో పట్టణ ప్రాంతాలలో నిరుద్యోగిత రేటు 10.34 శాతం ఉంటే, అదే కాలంలో గ్రామీణ నిరుద్యోగిత రేటు 7.70 శాతంగా ఉంది (CDS ప్రాతిపదికన). 1987-88 నాటికి గ్రామీణ నిరుద్యోగిత రేటు చెప్పుకోదగిన విధంగా అంటే 5.25 శాతంగా ఉంది. కాని పట్టణ నిరుద్యోగిత 9.36 శాతంగా ఉంది. 1993-94 తరువాత సరళీకరణ కాలంలో గ్రామీణ నిరుద్యోగిత ముఖ్యమైన ప్రశ్న
5 భారతదేశంలో నిరుద్యోగిత భారాన్ని వివరించండి.

రేటు 8. 28 శాతమయ్యింది. 1993-94 నుంచి 2004-05 వరకు గల కాల వ్యవధిలో పట్టణ నిరుద్యోగిత 8.28 శాతమయ్యింది. వ్యవస్థీకృత రంగ నిరుద్యోగిత అధిక అనుపాతం వల్ల పట్టణ ప్రాంతాలలోని అధిక నిరుద్యోగిత స్థాయిలనేవి చోటు చేసుకొంటున్నాయి. తక్కువ ఉత్పాదకత కార్యకలాపాలలో నిమగ్నమయ్యే వారు సాపేక్షికంగా కొంత మందికే అవకాశం ఉన్నందువల్ల ప్రజలు ఉద్యోగులుగా లేదా నిరుద్యోగులుగా ఉండవలసి వస్తుంది.

గ్రామీణ ప్రాంతాలలో పురుషులలో, మహిళలలో సాధారణ స్థితి (PS + SS)ల దృష్ట్యా నిరుద్యోగిత రేట్లు వరుసగా 5.8 శాతంగా మరియు 3.8 శాతంగా ఉన్నాయి. అయితే పట్టణ ప్రాంతాలలో పురుషులలో, మహిళలలో వరుసగా 7.1 శాతంగా, 10.8 శాతంగా ఉన్నాయి అనే విషయం ద్వారా అవగతమవుతుంది.

ఒకవేళ వారపరమైన స్థితి దృష్ట్యా నిరుద్యోగిత రేట్ల పరిగణనలోకి తీసుకొన్నట్లైతే, గ్రామీణ ప్రాంతాలలో పురుషులలో, మహిళలలో ఈ నిరుద్యోగిత రేట్లు వరుసగా 8.8 శాతంగా, 7.7 శాతంగా ఉన్నాయి. అయితే పట్టణ ప్రాంతాలలో పురుషులలో ఈ నిరుద్యోగిత రేట్లు 8.8 శాతం కాగా మహిళలలో 12.8 శాతంగా ఉన్నాయి.

ప్రశ్న 6.
భారతదేశంలో పేదరికం, నిరుద్యోగితల నివారణ చర్యలను వివరించండి.
జవాబు.
పేదరిక నిర్మూలన కోసం ప్రణాళికా రూపకర్తలు 4 రకాలైన పథకాలను ప్రతిపాదించారు. అవి :

1. గ్రామీణ పేద ప్రజల కోసం ఆదాయ, వనరుల అభివృద్ధి పథకాలు.
2. ప్రత్యేక ప్రాంతాల అభివృద్ధి పథకాలు.
3. అనుబంధ ఉపాధి అవకాశాల కల్పనకు సంబంధించిన పని పథకాలు.
4. పేద ప్రజల ఉత్పాదక సామర్థ్యాన్ని పెంపొందించడానికి వినియోగస్థాయిని పెంచే కనీస సదుపాయాల పథకాలు.

1. ఆదాయ, వనరుల అభివృద్ధి పథకాలు :
భారతదేశంలో పలు ఆదాయ, వనరుల అభివృద్ధి పథకాలు అమలులో ఉన్నాయి. కొన్ని పథకాలు 1970 నుంచి, మరికొన్ని పథకాలను ఇటీవల ప్రవేశపెట్టారు. అందులో ముఖ్యమైనవి : సన్నకారు రైతుల అభివృద్ధి పథకం (SFDA), ఉపాంత రైతులు, వ్యవసాయ శ్రామికుల సంస్థ (MFAL), సమీకృత గ్రామీణాభివృద్ధి పథకం (IRDP), లాంటి వాటిని అమలు చేయడం ద్వారా గ్రామీణ పేద ప్రజల ఆదాయ, వనరులను అభివృద్ధి చేయడానికి కృషి జరిగింది.

2. ప్రత్యేక ప్రాంతాల అభివృద్ధి పథకాలు :
ఇందులో దుర్భిక్ష ప్రాంతాల అభివృద్ధి పథకం (DPAP), ఎడారి ప్రాంతాల అభివృద్ధి పథకం (DDP), అటవీ ప్రాంతాల అభివృద్ధి పథకం (HADP) మొదలైన పథకాలు ఉన్నాయి. వీటి ద్వారా అడవులు, పాడి మొదలైన వాటిని అభిలషణీయంగా వినియోగించుకొని పేద ప్రజల ఆదాయ స్థాయిని పెంపొందింపజేయడం ఈ ప్రత్యేక ప్రాంతాల అభివృద్ధి పథకాల ముఖ్య ఉద్దేశం.

3. ఉపాధి కల్పన లేదా జాతీయ గ్రామీణ ఉపాధి కల్పనా పథకం :
జాతీయ గ్రామీణ ఉపాధి పథకం (National Rural Employment Programme-NREP), గ్రామీణ భూమిలేని వారి ఉద్యోగితా హామీ పథకం (Rural Landless Employ- ment Guarantee Programme – RLEGP), పనికి ఆహార పథకం (Food for Work Programme – FWP), ప్రధానమంత్రి సమగ్ర పట్టణ పేదరిక నిర్మూలన పథకం (Prime Minister Integrated Urban Poverty Education Programme-PMIUPEP) మొదలైన పథకాల ద్వారా పేద ప్రజలకు అనుబంధ ఉపాధి అవకాశాలను కల్పించడమే లక్ష్యం.

జాతీయ గ్రామీణ ఉపాధి పథకం (NREP) తరువాతి కాలంలో మహాత్మాగాంధీ జాతీయ గ్రామీణ ఉపాధి కల్పనా పథకం (Mahatma Gandhi National Rural Employment Generation Programme – MGNREGP) o రూపాంతరం చెందింది.

4. కనీస అవసరాల పథకాలు, ఇరవై సూత్రాల పథకం :
వీటి ద్వారా ప్రజలకు కనీస అవసరాలను కల్పించి, పేద ప్రజల వినియోగస్థాయిని పెంచి, ఉత్పాదక సామర్థ్యాన్ని మెరుగుపరచడం ముఖ్య ఉద్దేశం. ప్రాథమిక విద్య, ఆరోగ్యం, నీటి సరఫరా, రోడ్లు, విద్యుద్దీకరణ, గృహాలు, పౌష్టిక ఆహారం మొదలైన కనీస అవసరాలను గ్రామీణ, పట్టణ ప్రాంతాల్లో నివసించే పేద ప్రజలకు కల్పించి, వారి సామర్థ్యాన్ని పెంపొందింపజేయడం ఈ పథకాల లక్ష్యం.

భారతదేశంలో ఇటీవల కాలంలో రెండు రకాలైన వ్యూహాలతో ప్రభుత్వం పేదరిక నిర్మూలన సమస్యకు ప్రయత్నిస్తుంది. అవి :
i) అధిక శ్రామిక శక్తికి ఉపాధిని కలుగజేసే విధంగా ఉత్పత్తి రంగాలను విస్తృత పరచడం.
ii) విద్య, నైపుణ్య కల్పన, ఆరోగ్య భద్రత ద్వారా పేదవారి సాధికారతను పెంచడం వల్ల, ఉత్పత్తి రంగాల్లో ప్రవేశించి, పోటీతత్త్వం ద్వారా అధిక ఆదాయాలను పొంది పేదరికం నుంచి బయటపడతారు. ఈ విధానం పేదరిక సమస్యను పరిష్కరిస్తుంది.

ప్రశ్న 7.
పేదరికంపై అభిజిత్ బెనర్జీ అభిప్రాయాలకు ఒక వ్యాఖ్యను రాయండి.
జవాబు.
అభిజిత్ వినాయక్ బెనర్జీ 1961 సంవత్సరంలో ఫిబ్రవరి 21న భారతదేశంలోని ముంబాయిలో జన్మించాడు. భారతదేశంలో పుట్టి అమెరికన్ ఆర్థికవేత్తగా ఎదిగి ఎస్తర్ డఫ్లూ మరియు మైకేల్ క్రెమేర్లతో పాటుగా ప్రపంచపు పేదరిక నిర్మూలనకుగాను క్రియాశీలకమైన, ప్రయోగాత్మకపరమైన దృక్పథాన్ని అభివృద్ధి చేసినందుకు గాను వారికి 2019వ సం||లో నోబుల్ బహుమతి గ్రహీతలుగా ప్రసిద్ధిగాంచినారు. మాసాచూస్చెట్స్ ఇనిస్టూట్యూట్ ఆఫ్ టెక్నాలజీ (MIT) లో బెనర్జీ ఆచార్యునిగా పనిచేస్తున్నాడు.

అనేక అంశాలలో విద్య, వైద్య మరియు ఆరోగ్య, ఋణ అందుబాటు మరియు నూతన సాంకేతికతల అన్వయింపులు మొదలగునవి పేదరికానికి నిజమైన కారణాలుగా ఉంటాయనే ప్రయోగాత్మక పరమైన దృక్పథాన్ని బెనర్జీ, డఫ్లూ మరియు మైకేల్ క్రెమేర్లు అన్వయించి విపులీకరించారు.

బెనర్జీ, డపూల ప్రకారం, “వాస్తవానికి కొంతమంది ప్రజలు తప్పనిసరిగా వారు చాలా కష్టించి పనిచేయగలుగుతారు. ఎందుకంటే వారు బలహీనులే గాకుండా సరిపడే ఆహారం లేకుండా (underfed) ఉంటారనేది వాస్తవం. అతి తక్కువ వ్యయంతో వారి యొక్క ప్రాథమిక అవసరాలను తీర్చుకోవడానికి మాత్రమే కష్టించి కనీస అవసరాలను పొందడానికి పనిచేయడం జరుగుతుంది.

కొన్ని ఇతర అత్యంత అవసరమయ్యే కొనుగోళ్ళు (గృహాల లాంటివి) మరియు ఆవశ్యకమయ్యే నిర్దిష్ట క్యాలరీల పరిమాణంను కొనుగోలు చేపట్టడానికి గాను బడ్జెట్లో పొందుపరచడంనే పేదరికానికి నిర్వచనంగా అర్థం చేసుకోవడం కొరకు గాను పేదరికానికి సంబంధించిన పేదరికపు రేఖలుగా చారిత్రాత్మకంగా పలు దేశాలలో గమనించవచ్చు”. అయితే ఈ నిర్వచనం ప్రకారం కొంతమందికి తగినంతగా తిండి లేకపోవడం వల్లనే వారిని ‘పేద’ వ్యక్తులుగా పేర్కొంటారు.

1. ఉత్పాదక ఆస్తులలో భూమి ఒక ఉత్పాదక ఆస్తిగా ఉంటుంది. ఒక దేశానికి మరొక దేశానికి గణనీయమైన వ్యత్యాసం ఉన్నప్పటికీ గ్రామీణ ప్రాంతాలలో ఎక్కువ శాతం మేరకు ప్రజలు ఏదో కొంత భూమిని కల్గి ఉంటారు. భూమి గాకుండా గ్రామీణ ప్రాంతాలలోని కడు పేద కుటుంబాలు కొద్దిలో కొద్దిగా అనశ్వర వస్తువుల లాంటి ఉత్పాదక ఆస్తులను కల్గి ఉంటారని బెనర్జీ, డపులు అభిప్రాయపడ్డారు.

2. కటిక పేదవారు విద్యపై అతి తక్కువగా ఖర్చు చేస్తారు. వీరు విద్యపై వెచ్చించే వ్యయం సాధారణంగా మొత్తం కుటుంబ బడ్జెట్లలో దాదాపుగా 2 శాతం మేరకు మాత్రమే ఉంటుంది. పేద కుటుంబాలలో పిల్లల విద్యపై తక్కువ ఖర్చు పెట్టడానికి ప్రధాన కారణం వారు ప్రభుత్వ బడులకు లేదా ఫీజు విధించని ఇతర బడులకు పోవడం. విద్యపై ఎక్కువ వెచ్చించే పేద కుటుంబాలు గల దేశాలలో ప్రభుత్వ బడులలో ఫీజులు ఉండడం ప్రధాన కారణంగా చెప్పవచ్చు (ముఖ్యంగా ఇండోనేషియా మరియు కొటేడి ఐవరీ ‘లాంటి దేశాలలో) అని బెనర్జీ అభిప్రాయపడ్డాడు.

3. పలు పేద కుటుంబాల వారు బహుళ వృత్తులను కలిగి ఉంటారనేది వాస్తవం అని బెనర్జీ, డఫ్లూ అభిప్రాయపడినారు. అయితే ఒక వ్యక్తి వ్యాపారంతో పాటు శ్రామికునిగా కూడా తన రెండు కార్యకలాపాలను నిర్వహించడంను ఒక ఉదాహరణగా చెప్పవచ్చు. దేశాలలో ప్రతిచోటా గానప్పటికీ, పలు ఇతర దేశాలలోని పట్టణ ప్రాంతాలలో ఏక కాలంలో బహుళ వృత్తులను కలిగి ఉండడమనేది సాధారణంగా ద్యోతకమవుతుందని బెనర్జీ, డపూలు అభిప్రాయపడినారు.

4. గ్రామీణ ప్రాంతాలలో మాత్రమే ఈ బహుళ వృత్తుల తీరు చాలా ప్రబలంగా ఉంటుందని కూడా అభిప్రాయపడినారు. బెనర్జీ ప్రకారం పేద కుటుంబాల వారు ఆర్థికపరమైన అవకాశాలను కల్గి ఉన్నప్పటికీ ప్రత్యేకీకరణను కలిగి ఉండరు. ప్రత్యేకీకరణను కలిగి లేకపోవడం వల్ల వారు దానికి మూల్యం చెల్లించాల్సి ఉంటుంది. సంవత్సరంలో సగటున 18 వారాల పాటు బయట ఉన్నప్పటికీ ఈ పలు పేద కుటుంబాల వారు బయట ఉద్యోగాలు నిర్వహించడం వల్ల సంపాదనలో వారు అధిక భాగాన్ని పొందగలుగుతున్నారు.

స్వల్పకాలిక వలసల వల్ల వారు వారి ఉద్యోగానికి సంబంధించిన అంశాలను మంచిగా నేర్చుకోవడానికి చాలా తక్కువ అవకాశం ఉంటుంది లేదా వారి యొక్క నిర్దిష్ట ప్రతిభలతో వారి ఉద్యోగాలను ముగించాల్సి ఉంటుంది లేదా ప్రోత్సహించబడుతుంది. అయితే వ్యవసాయేతర కార్యకలాపాలను నిర్వహించడానికి సాపేక్షికంగా పేద ప్రజలకు చాలా మట్టుకు తక్కువ నిర్దిష్టతను కలిగిన నైపుణ్యాలు అవసరమవుతాయి.

5. పేదవారికి అందుబాటులో ఉండే భౌతిక అవస్థాపనల లాంటి విద్యుచ్ఛక్తి, కుళాయి నీళ్లు, ప్రాథమిక పారిశుధ్యం (మరుగు దొడ్లకు అందుబాటులో ఉండడం లాంటివి)ల విషయంలో వివిధ దేశాల మధ్య గణనీయమైన వ్యత్యాసాలున్నాయి అని బెనర్జీ అభిప్రాయపడ్డాడు. కొన్ని కొన్ని ప్రభుత్వాలు విద్యుచ్ఛక్తి మరియు కుళాయి నీటి సౌకర్యాలనే ఈ రెండు కటిక పేదవారికి అందుబాటులో ఉండే విధంగా కృషిచేస్తున్నాయి.

సాధారణంగా గ్రామీణ పేదవారి (పారిశుధ్య సౌకర్యాలు లేకపోవడం వల్ల అదృష్టవశాత్తూ దాదాపుగా చాలా దట్టమైన చుట్టుప్రక్కల ప్రాంతాలలో ఉండడమనేది రోగ సంబంధిత పర్యావరణం ఘోరమైనదిగా ఉంటుంది) కంటే పట్టణ ప్రాంతపు పేదవారికి విద్యుచ్ఛక్తి మరియు కుళాయి నీటి సౌకర్యాలు ఎక్కువ మేరకు అందుబాటులో ఉంటాయి.

6. పలు అల్ప ఆదాయ దేశాలలో పేద కుటుంబాల వారికి ప్రాథమిక పాఠశాలలు, ప్రాథమిక ఆరోగ్య కేంద్రాలు అందుబాటులో ఉండే విధంగా ప్రభుత్వాలు కొన్ని ప్రయత్నాలు చేస్తూనే ఉన్నాయి. ఉదాహరణకు, భారతదేశంలో గల పెక్కు గ్రామాలలో ఒక కిలోమీటర్ లోపు ఒక బడి ఉంది మరియు ప్రతి 10,000ల మంది ప్రజలకు ఒక ఆరోగ్య ఉప కేంద్రం ఉంది. ఏది ఏమైనప్పటికీ, పేదవారికి చేయూతనిచ్చే సౌకర్యాలు అందుబాటులో ఉన్నప్పటికీ, వాటి నాణ్యత తక్కువ స్థాయిలో ఉండడమే గాకుండా, ఈ సౌకర్యాలు వారికి వాస్తవానికి ఏ మేరకు చేరబడుతున్నాయనేది స్పష్టంగా లేదు.

ప్రభుత్వ పాఠశాలలోని బోధనాపరమైన నాణ్యత తక్కువగా ఉండడం వల్ల, దాని యొక్క ప్రభావం నేర్చుకొనే స్థాయిలపై స్పష్టంగా ఉంటుంది. భారతదేశంలో 6-14 సంవత్సరాల మధ్యగల పిల్లలు పాఠశాలలలో 93.4 శాతం మేరకు నమోదు (అందులో 75 శాతం మంది పిల్లలు ప్రభుత్వ పాఠశాలలలో) చేసుకున్నప్పటికీ, ఇటీవల కాలంలో జాతీయ స్థాయిలో చేపట్టబడిన సర్వే ప్రకారం.

సెకండరీ గ్రేడ్ స్థాయిలో గల 7 నుండి 14 సం॥రాల మధ్యగల పిల్లలలో 34.9 శాతం మేరకు వారు కనీసం ఒక సులభమైన ఒక పేరాగ్రాఫ్ను చదవలేని వారుగా ఉన్నారు. అంతేగాక 41.1 శాతం మేరకు వ్యవకలనం చేయలేరు మరియు 65.5 శాతం మేరకు భాగాహారం చేయలేకపోతున్నారు. అంతేగాక, ప్రభుత్వ పాఠశాలలోని 6 నుండి 8 గ్రేడ్స్లో గల పిల్లలలో 22 శాతం మేరకు పిల్లలు రెండవ గ్రేడ్కు సంబంధించిన పాఠ్య పుస్తకం కూడా చదవలేకపోతున్నారని బెనర్జీ తన అనుభావిక అధ్యయన ఫలితాల ద్వారా రూఢీకరించాడు.

స్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
భారతదేశపు GDP లో ప్రభుత్వ, ప్రైవేట్ రంగాల వాటాలను తెలియజేయండి.
జవాబు.
స్వాతంత్ర్య సమయంలో ప్రభుత్వ రంగం నీటి పారుదల, విద్యుచ్ఛక్తి, రైల్వేలు, కమ్యూనికేషన్లు లాంటి కొన్ని విభాగాల కార్యకలాపాలకు మాత్రమే పరిమితమై ఉండేది. స్వాతంత్ర్యానంతరం ప్రభుత్వ రంగ కార్యకలాపాలు త్వరితగతిన విస్తరించాయి.

మన దేశంలో 1948, 1956లలోని మొదటి, రెండు పారిశ్రామిక తీర్మానాలు ప్రభుత్వ పరిధిని విస్తృత పరస్తూ ప్రైవేట్ రంగ కార్యకలాపాలను అతిగా నియంత్రించకుండా ఉండే విధంగా ఉంటాయి అని ధ్రువీకరిస్తూ భారతదేశంలో మిశ్రమ ఆర్థిక వ్యవస్థ ఏర్పడటానికి ప్రాధాన్యతను ఇచ్చాయి. ఈ రెండు పారిశ్రామిక తీర్మానాలు పరిశ్రమలను వివిధ రకాలుగా విభజించి, కొన్నింటిని పూర్తిగా ప్రభుత్వ రంగానికి, మరి కొన్నింటిని ఉమ్మడి రంగానికి అంటే ప్రభుత్వ, ప్రైవేట్ రంగాలకు ఇక మిగిలిన అన్నింటినీ కేవలం ప్రైవేట్ రంగానికి మాత్రమే అప్పగించాయి.

ప్రభుత్వ, ప్రైవేట్ రంగాలు రెండూ కలిసి జాతీయాదాయాన్ని ఉత్పత్తి చేస్తాయి. పంచవర్ష ప్రణాళికలు ప్రవేశపెట్టినప్పటి నుంచి ప్రభుత్వ ఆర్థిక కార్యకలాపాలు క్రమంగా పెరగడం వల్ల జాతీయాదాయంలో ప్రభుత్వ రంగం వాటా క్రమంగా పెరిగింది.

గత ఐదు దశాబ్దాల్లో జాతీయాదాయంలో ప్రభుత్వ రంగం వాటా నిలకడగా పెరిగినట్లు పట్టిక 3.5 ద్వారా స్పష్టంగా అర్థమవుతుంది. 1999-2000. ధరల దృష్ట్యా 1950-51లో స్థూల దేశీయోత్పత్తిలో ప్రభుత్వ రంగ వాటా 8 శాతం అయితే 2000-01 నాటికి 23.2 శాతం మేరకు పెరిగింది. అందువల్ల, జాతీయాదాయంలో ప్రభుత్వ రంగం ఐదింట ఒకటవ వంతు వాటాను కలిగి ఉంది.

స్థూల దేశీయోత్పత్తిలో ప్రభుత్వ ప్రైవేటు రంగాల వాటా:

ఆధారాలు :
i) CSO National Accounts statistics, 2011.
ii) Various Issues of Economic Survey.

వాస్తవానికి గడిచిన అయిదు దశాబ్దాల కాలంలో భారతదేశం జాతీయాదాయంలో ప్రైవేట్ రంగం వాటా అధికంగా ఉన్నట్లు పట్టిక 3.5 ద్వారా గమనించవచ్చు. 1950-51లో జాతీయాదాయంలో ప్రైవేట్ రంగం వాటా 92 శాతం అయితే, 1990-91 నాటికి 76.4 శాతం మేరకు తగ్గింది. ఆర్థిక సంస్కరణలను ప్రవేశపెట్టిన తరువాత జాతీయాదాయంలో ప్రైవేట్ రంగం వాటా పెరిగింది. 2000-01 నాటికి జాతీయాదాయంలో ప్రైవేట్ రంగం వాటా 76.8 శాతం ఉంటే 2008-09 నాటికి 79.8 శాతం, 2009-10 నాటికి 78.8 శాతం మేరకు పెరిగింది.

ప్రశ్న 2.
ఆదాయ, సంపద పంపిణీలోని అసమానతలకు గల ప్రధాన కారణాలను పరిశీలించండి.
జవాబు.
భారతదేశంలోని ఎగువ 10 శాతం వేతన జీవులు దిగువనున్న 10 శాతం మంది కంటే 12 రెట్లు అధికంగా ఉన్నారు. భారతదేశంలోని 100 మంది ధనికులు అందరి నికర ఆస్తుల విలువ 2011వ సంవత్సరంలో అధికంగా ఉంటే రూ. 12,06,375 కోట్లుగా ఉంది. వారి ఆదాయం దేశ దేశీయోత్పత్తిలో 17 శాతంగా ఉంది.

1. భూ యాజమాన్యంలోని అసమానతలు :
భారతదేశంలో బ్రిటీష్ వారి కాలంలో జమీందారి పద్ధతి వల్ల వ్యావసాయిక భూములు కొంత మంది చేతుల్లో కేంద్రీకృతమై ఉండేవి. స్వాతంత్య్రానంతరం జమీందారీ పద్ధతిని రద్దు చేసినప్పటికీ, భూ యజమాన్య కేంద్రీకరణ మాత్రం అదే విధంగా ఉంది. 2010-11లోని ఇటీవల దత్తాంశం ప్రకారం మొత్తం వ్యవసాయ యోగ్యమైన కమతాలలో 67 శాతం ఉపాంత కమతాలే. కాని 22.2 శాతం విస్తీర్ణత మాత్రమే సాగులో ఉంది.

2. ప్రైవేట్ కార్పోరేట్ రంగంలో ఆస్తుల కేంద్రీకరణ :
బడా పారిశ్రామిక వేత్తల చేతుల్లో ఆర్థిక సంపద, శక్తి అధికంగా కేంద్రీకరించబడింది. కాలగమనంలో వారు పెద్ద మొత్తంలో ఆస్తులను సంపాదించుకోవడంలో సఫలీకృతులయ్యారు. బ్యాంకుల, ఇతర విత్తపరమైన సంస్థల నుంచి సులభ విత్తం అందుబాటులో ఉండటమనేది వారు ఆస్తులను సంక్రమించుకొనేందుకు చేసే ప్రయత్నాలకు దోహదపడ్డాయి. అంతేకాకుండా మార్కెట్ నుంచి ఈక్విటీ మూలధనాన్ని వారు పెంచుకోగలిగారు.

NCAER ప్రకారం పట్టణ ప్రాంతాలలోని ఆస్తుల పంపిణీ చాలా మేరకు వైషమ్యాన్ని కలిగి ఉంది. ఈ సంవత్సరంలో ఎగువన ఉన్న 10 శాతం వారు పట్టణ ప్రాంతాలలోని మొత్తం సంవదలో 46.28 శాతం మేరకు వాటాను కలిగి ఉన్నారు. కాని దిగువన ఉన్న 60 శాతం వారు మొత్తం సంపదలో కేవలం 11.67 శాతం మేరకే వాటాను కలిగి ఉన్నారు.

3. వృత్తి పరమైన శిక్షణలోని అసమానతలు :
వ్యాపారస్థులు, ఇంజనీర్లు, న్యాయమూర్తులు, డాక్టర్లు, సమాచార సాంకేతిక రంగంలోని ఉద్యోగులు, ఇతర వృత్తి నైపుణ్యతగల నిపుణుల ఆదాయాలు తరచుగా పెరుగుతున్నాయి. దీనివల్ల ఆదాయ అసమానతలు పెరుగుతున్నాయి. కాబట్టి విద్య, శిక్షణలు కూడా మనదేశంలో ఆదాయ అసమానతలు తీవ్రతరమవ్వడానికి దోహదపడుతున్నాయి.

4. ద్రవ్యోల్బణం, ధరల పెరుగుదల :
1950 మధ్య కాలం నుంచి ధరలు నిరంతరంగా పెరగడం వల్ల శ్రామిక వర్గ వాస్తవిక ఆదాయం తగ్గుతుంది. కాని పారిశ్రామికవేత్తలు వ్యాపార వేత్తలు, అధిక మొత్తంలో మార్కెట్ మిగులు కలిగి ఉన్న పెద్ద వ్యవసాయదారులు ఈ ద్రవ్యోల్బణ పరమైన ప్రక్రియ వల్ల అధికంగా లబ్ధి పొందారు. భారతదేశంలో పునఃపంపిణీ ప్రభావాన్ని నియంత్రించడానికి ప్రయత్నం జరపకపోవడం వల్ల ఆదాయ అసమానతలు తీవ్రతరమవుతున్నాయి.

5. పరపతి సౌకర్యాల్లో అసమానత :
భారతదేశంలో ఆదాయ సంపద అసమానతలు, పరపతి సౌకర్యాలు అసంతులితంగా ఉండటం వల్ల అసమానతలు పెరుగుతున్నాయి అని చెప్పవచ్చు. పారిశ్రామిక సంస్థలు, వ్యాపార వేత్తలు మూలధనాన్ని చాలా సులభంగా పొందగలుగుతున్నారు. కాని వ్యవసాయదారులు, సన్నకారు, ఉపాంత రైతులు, వ్యవసాయ కూలీలు, చేతి వృత్తుల వారు వడ్డీ వ్యాపారస్థులపై ఆధారపడి ఉండటం వల్ల అనేక రకాలైన దోపిడీలకు గురి అవుతున్నారు.

6. పట్టణాల వైపు ప్రైవేట్ పెట్టుబడి :
ఇప్పటికీ, భారతదేశంలో 70 శాతం మంది ప్రజలు గ్రామాల్లో జీవిస్తున్నారు. కాని సుమారుగా 70 శాతం ప్రైవేటు పెట్టుబడి పట్టణ ప్రాంతాల్లోని పరిశ్రమలకు వెళుతుంది. కాబట్టి మన దేశంలోని పెట్టుబడి “పట్టణ పక్షపాత” వైఖరి కలిగినదిగా చెప్పవచ్చు.

7. ప్రభుత్వం పాత్ర :
భారతదేశంలో ఆర్థిక పరమైన మార్పుకు అగ్రగామిగా ప్రభుత్వం తరచుగా ఉంటుందని ప్రకటించుకొన్నప్పటికీ, ప్రభుత్వ పెట్టుబడి, ప్రైవేటు పెట్టుబడిని ప్రోత్సహించే విధంగా ఉంది. ఇటీవల కాలంలో ప్రవేశపెట్టిన సరళీకరణ, ప్రైవేటీకరణ ప్రపంచీకరణ, పెట్టుబడుల ఉపసంహరణ విధానాలు దేశంలో ఆదాయ-సంపద అసమానతలను పెంచడానికి దోహదపడుతున్నాయి.

ప్రశ్న 3.
వివిధ నిరుద్యోగిత రకాలను పరిశీలించండి.
జవాబు.
అమలులో ఉన్న వేతన రేటు వద్ద ఒక వ్యక్తికి పని చేయాలనే కోరిక ఉన్నప్పటికి, అతనికి ఉద్యోగావకాశం లభించకపోవడాన్ని నిరుద్యోగితగా చెప్పవచ్చు.

1. నిర్మితి సంబంధిత నిరుద్యోగిత (Structural Unemployment) :
ఈ రకమైన నిరుద్యోగిత దేశపు ఆర్థిక నిర్మితితో సంబంధం కలిగినదిగా ఉంటుంది. త్వరితగతిన పెరుగుతున్న జనాభా, వారిలో గమనశీలత లేకపోవడం వల్ల శ్రామిక డిమాండ్ కంటే శ్రామిక సప్లయ్ అధికంగా ఉండటం వల్ల ఆర్థిక వ్యవస్థలో నిరుద్యోగిత సమస్య ఏర్పడుతుంది. ఈ రకమైన నిరుద్యోగిత దీర్ఘకాలిక స్వభావాన్ని కలిగి ఉంటుంది. భారతదేశంలోని నిరుద్యోగిత ప్రధానంగా ఈ కోవలోకి వస్తుంది.

2. అల్ప ఉద్యోగిత (Under-Employment) :
శ్రామికుల అల్ప ఉద్యోగిత అంటే వారికి పని దొరుకుతుంది, కాని వారి శక్తి సామర్థ్యాలు అభిలషణీయమైన రీతిలో ఉపయోగించబడవు.

3. ప్రచ్ఛన్న నిరుద్యోగిత (Disguised Unemployment) :
ఉత్పత్తి ప్రక్రియలలో అవసరమయ్యే శ్రామికుల కంటే ఎక్కువ మంది ఉంటే వారిని ప్రచ్ఛన్న నిరుద్యోగులు అని అంటారు. పని చేస్తున్న మొత్తం శ్రామికుల్లో కొంత మందిని తొలగించినప్పటికీ ఉత్పత్తి ఏ మాత్రం తగ్గదు. అలాంటి వారిని ప్రచ్ఛన్న నిరుద్యోగులు అని అంటారు.

4. బహిరంగ (Open) నిరుద్యోగిత :
శ్రామికులు ఏ పనీ లేకుండా జీవించినట్లయితే వారికి చేయడానికి ఏ పనీ దొరకనట్లయితే, వారందరు కూడా బహిరంగ నిరుద్యోగిత కోవలోకి వస్తారు. విద్యను ఆర్జించిన వారు నిరుద్యోగులుగా ఉండటం, నైపుణ్యత లేని కారణంగా శ్రామిక నిరుద్యోగిత ప్రబలడం ఈ రకమైన నిరుద్యోగిత కోవలోకి వస్తాయి.

5. విద్యాయుత నిరుద్యోగిత (Educated Unemployment) :
విద్యనార్జించి లేదా తర్ఫీదు పొంది, నైపుణ్యతను కలిగి ఉన్న వ్యక్తికి అతని అర్హతలకు అనుగుణంగా ఉద్యోగం దొరకనట్లయితే, ఆ వ్యక్తిని విద్యనార్జించిన నిరుద్యోగి అని అంటారు. ప్రత్యేకించి, భారతదేశంలాంటి అభివృద్ధి చెందుతున్న దేశాలలో ఈ రకమైన నిరుద్యోగిత సమస్యగా ఉంది.

6. సంఘృష్ట నిరుద్యోగిత (Frictional) :
దేశంలోని శ్రామికులు ఒక వృత్తి నుంచి మరొక వృత్తికి మార్పు చెందే కాలంలో ఏర్పడిన నీరద్యోగితను సంఘృష్ట నిరుద్యోగిత అని అంటారు. శ్రామిక మార్కెట్లోని అసంపూర్ణతల వల్ల శ్రామికులకు ఉద్యోగ అవకాశాల గురించి సరైన అవగాహన లేకపోవడం వల్ల ఈ రకమైన నిరుద్యోగిత ఏర్పడుతుంది.

7. ఋతుపరమైన నిరుద్యోగిత (Seasonal) :
ఋతుగత మార్పులను అనుసరించి డిమాండ్లో చోటు చేసుకొనే మార్పు వల్ల ఈ నిరుద్యోగిత ఏర్పడుతుంది. శ్రామికులకు సంవత్సరమంతటా పని దొరకదు. సంవత్సరంలో కొన్ని కొన్ని ఋతువులలో మాత్రమే ఉద్యోగం దొరకుతుంది. సాధారణంగా వ్యావసాయిక రంగ ప్రాముఖ్యత గల దేశాలలో ఋతగత నిరుద్యోగిత అధికంగా ఉంటుంది.

8. చక్రీయ నిరుద్యోగిత (Cyclical Unemployment) :
అభివృద్ధి చెందిన దేశాలలోని వ్యాపార కార్యకలాపాల్లో మందకొడితనం ఏర్పడటం వల్ల సాధారణంగా ఏర్పడే నిరుద్యోగితను చక్రీయ నిరుద్యోగిత అని అంటారు. అన్ని దేశాలు వ్యాపార చక్రాల చట్రంలో ఉంటాయి.

9. సాంకేతిక పరమైన నిరుద్యోగిత (Technical) :
ఆర్థిక వ్యవస్థలో నూతన సాంకేతిక ప్రవేశం వల్ల శ్రామికులు తొలగించబడతారు. ఫలితంగా ఏర్పడే నిరుద్యోగితను సాంకేతికపరమైన నిరుద్యోగిత అని అంటారు.

ప్రశ్న 4.
భారతదేశంలో నిరుద్యోగితకు గల కారణాలను విశ్లేషించండి.
జవాబు.
అమలులో ఉన్న వేతన రేటు వద్ద ఒక వ్యక్తికి పని చేయాలనే కోరిక ఉన్నప్పటికి, అతనికి ఉద్యోగావకాశం లభించకపోవడాన్ని నిరుద్యోగితగా చెప్పవచ్చు.
1. ఉపాధి రహిత వృద్ధి :
భారతదేశ ప్రణాళికా కాలంలో మొదటి మూడు దశాబ్దాల కాలంలో GDP వృద్ధి రేటు తక్కువగా అంటే సాలుసరి 3.5 శాతంగా ఉంది. ఈ కాలంలో ఉద్యోగితా రేటు సాలీనా 2 శాతం మేరకు సహేతుకమైన రీతిలో పెరిగింది. కాని ఉద్యోగితా వృద్ధి రేటులో మాత్రం త్వరితగతిన తగ్గుదల నమోదైంది. సాధారణంగా ఆర్థిక వృద్ధి ఉద్యోగ అవకాశాలను కల్పించాల్సి ఉంటుంది. కాని, భారతదేశంలోని వృద్ధి చాలా కాలం నుంచి ఉపాధి రహితంగా ఉందనేది వాస్తవం. ఎందుకంటే ఉద్యోగావకాశాలు అశించిన విధంగా పెరగడం లేదు.

2. శ్రామిక శక్తిలోని పెరగుదల :
స్వాతంత్య్రం సిద్ధించినప్పటి నుంచి మరణాల రేటు తగ్గడం వల్ల జనాభా పరిణామ క్రమ సిద్ధాంతంలోని రెండవ దశను చేరుకొన్నాం. 1960వ దశాబ్దంలో జనాభా వృద్ధి రేటు సగటున 2.2 శాతం, శ్రామిక శక్తి సగటున 1.9 శాతం పెరిగింది. శ్రామిక శక్తి 1983-1993 కాలంలో జనాభా పరమైన, సాంఘిక కారణాల వల్ల చాలా అధికంగా పెరిగింది. తదుపరి కాలంలో శ్రామిక శక్తి తగ్గింది.

3. ప్రతికూల సాంకేతికత:
భారతదేశంలో మూలధనం కొరతగాను, శ్రమ అధికంగాను ఉంది. ఇలాంటి పరిస్థితుల్లో మార్కెట్ శక్తులు, సమర్థవంతంగా నిర్వహించబడితే దేశంలో శ్రమ సాంద్రత సాంకేతిక ఉత్పత్తి పద్ధతిని ఎంపిక చేసుకోవలసి వస్తుంది. కాని పారిశ్రామిక, వ్యావసాయిక రంగాల్లో ఉత్పత్తిదారులు శ్రమకు బదులుగా స్వయంచాలక యంత్ర శక్తిని ఉపయోగించడం వల్ల నిరుద్యోగ సమస్య పెరుగుతుంది.

4. ప్రతికూలమైన విద్యా వ్యవస్థ :
భారతదేశంలో విద్యా వ్యవస్థ లోపభూయిష్టంగా ఉంది. వాస్తవానికి ఇప్పుడున్న విద్యా వ్యవస్థను వలస వాద కాలంలో మన దేశంలో మెకాలే ప్రవేశపెట్టాడు. గున్నార్ మిర్దాల్ ప్రకారం భారతదేశంలో విద్యా విధానం మానవ వనురులను అభివృద్ధిపరిచే విధంగా లేదని, ఇది కేవలం ప్రభుత్వ, ప్రైవేట్ రంగాలలో గుమస్తాలను, సాధారణ తక్కువ స్థాయి కార్యనిర్వాహకులను మాత్రమే తయారు చేస్తుంది.

నవ్య ఆర్థిక సరళీకరణ విధానాల వల్ల ఆదాయ అసమానతలు పెరిగాయి. సాధారణంగా ఆదాయ అసమానతలు పెరగడం వల్ల పేదవారి కొనుగోలు శక్తి తగ్గుతుంది. ఫలితంగా, వస్తుత్పత్తికి డిమాండ్ తగ్గి తిరోగమన మాంద్య పరిస్థితులు చోటు చేసుకొని నిరుద్యోగిత పెరుగుతుంది.

ప్రశ్న 5.
నిరుద్యోగిత సమస్య యొక్క పర్యవసానాలను వివరించండి.
జవాబు.
భారతదేశంలో పలు కారణాల వల్ల ఏర్పడే పట్టణ, గ్రామీణ ప్రాంతాలలోని విస్తృత నిరుద్యోగిత ఒక సంక్లిష్ట సమస్య. నిరుద్యోగిత కేవలం వ్యక్తుల పైననే గాక వారి కుటుంబాలపై, దీర్ఘ కాలంలో వారు నివసిస్తున్న సమాజంపై కూడా ప్రభావాన్ని కనపరుస్తుంది. నిరుద్యోగిత వల్ల జీవనాధారం లేక పేదరికాన్ని అనుభవించడమే కాక నిరాశ, నిస్పృహలను, దుఃఖాలను కలగజేస్తుంది.

1. మానవ వనరులను కోల్పోవడం :
మానవ వనరులను కోల్పోవడంలో నిరుద్యోగిత సమస్య ప్రధాన కారణమవుతుంది. శ్రామికులు ఉద్యోగాన్వేషణలోనే వారి గరిష్ట సమయాన్ని వృధా చేస్తారు. ఇందువల్ల కొన్ని ఆర్థిక వ్యవస్థలలో ద్రవ్యోల్బణానంతర స్తబ్ధత అనే సమస్యకు దారితీస్తుందని ఫెల్ప్ (Phelps) అనే ఆర్థికవేత్త అభిప్రాయపడ్డాడు.

2. పేదరికపు పెరగుదల :
వ్యక్తి యొక్క అన్ని ఆదాయ వనరులను నిరుద్యోగిత హరించి వేస్తుంది. తత్ఫలితంగా వ్యక్తి పేదవాడు అవుతాడు. కాబట్టి, నిరుద్యోగిత పేదరికాన్ని ఉత్పన్నం చేస్తుందని చెప్పవచ్చు.

3. సాంఘిక సమస్యలు :
సమాజంలో పలు సాంఘిక సమస్యలు తలెత్తడానికి నిరుద్యోగిత కారణమవుతుంది, సామాజిక భద్రత కూడా దెబ్బతింటుంది.

4. రాజకీయ అస్థిరత :
దేశంలో రాజకీయ అస్థిరత చోటు చేసుకోవడానికి నిరుద్యోగిత కారణమవుతుంది. నిరుద్యోగ వ్యక్తులు ప్రతికూల సాంఘిక అంశాలతో సులభంగా ప్రభావితమవుతారు. అలాంటి వారు ప్రజాస్వామిక విలువల పట్ల, శాంతియుతమైన సాధనాల పట్ల నమ్మకాన్ని కోల్పోతారు.

5. శ్రమ దోపిడి :
నిరుద్యోగిత స్థితిలో ఉన్నప్పుడు సాధ్యమైనంత మేరకు గరిష్టంగా శ్రామికులు దోపిడికి గురి అవుతారు. శ్రామికులకు ఎవరికైతే పని కల్పించబడుతుందో వారు తక్కువ వేతనంతో బాటు వైవిధ్యభరితమైన షరతులలో పని చేయాల్సి ఉంటుంది. ఉద్యోగ భద్రత లేనందువల్ల శ్రామికులు యాజమానులకు తక్కువ వేతనంతో ఎక్కువ గంటలు పని చేయాల్సి ఉంటుంది.

6. జీవన ప్రమాణం :
నిరుద్యోగిత నెలకొని ఉన్న సమయాలలో ఉద్యోగాల కోసం పోటీ పెరగడమే కాకుండా వ్యక్తి యొక్క బేరమాడే శక్తి తగ్గుతుంది. అందువల్ల జీతాల, ప్యాకేజీల, ఆదాయాలతో ముడిపడి ఉన్న ప్రజల జీవన ప్రమాణం కూడా తగ్గుతుంది.

7. ఉద్యోగ వ్యత్యాసాలు :
ఒక వ్యక్తి దీర్ఘకాలం పాటు ఉద్యోగానికి ఆవల (బయట) ఉన్నట్లయితే మళ్ళీ ఉద్యోగాన్ని దొరక బట్టుకోవడమనేది కష్టంతో కూడుకొన్నది కావడం వల్ల శ్రామిక మార్కెట్లో ఉద్యోగ లభ్యత పరిస్థితి మరింత జటిలమవుతుంది. కొంత కాలం పాటు పనికి ఆవల ఉన్న వ్యక్తిని అతని తప్పు ఏమీ లేనప్పటికీ అతని సేవలను వినియోగించకోవడానికి యజమానులు ఎవరు కూడా సుముఖంగా ఉండరు.

8. నైపుణ్యాలు ఉపయోగితను కోల్పోవడం :
నిరుద్యోగులుగా ఉన్న కాలంలో వారు తమ నైపుణ్యాలను ఉపయోగించలేరు. నిరుద్యోగితా స్థితి చాలా కాలం పాటు కొనసాగినట్లయితే వారికున్న నైపుణ్యాలను కోల్పోవడం జరుగుతుంది.

ప్రశ్న 6.
భారతదేశంలో పేదరికానికి గల కారణాలను పరిశీలించండి.
జవాబు.
సమాజంలోని ఏ ప్రజలు అయితే తమ కనీస జీవితావసరాలను తీర్చుకోలేని స్థితిలో ఉంటారో దానిని పేదరికంగా చెప్పవచ్చు. ఏ సమాజంలోనైనా ఒక నిర్ణీత కనీస స్థాయిలో తమ జీవనాన్ని నిర్వహించుకోలేక, జీవనాధార వేతనం కూడ పొందలేక జీవితం గడుపుతున్న వారిని పేదవారుగా నమోదు చేయవచ్చు.

1. ఆర్థిక శక్తి కేంద్రీకరణ :
భారతదేశంలో ఆదాయ అసమానతలు అధికంగా ఉండటమే గాక గ్రామాల-నగరాల మధ్య గల వ్యత్యాసం అధికంగా ఉంది. 1990వ దశకం తరవాత ఆదాయ అసమానతలు క్రమంగా పెరుగుతున్నాయి. ధనవంతులు అభివృద్ధి ఫలితాల వల్ల లాభాన్ని పొందుతున్నారు, కాని పేదవారు నిరాశాపూరితంగా ఉన్నారు. అందువల్ల ఆదాయ-సంపద అసమానతలు, ఆర్థిక శక్తి కేంద్రీకరణం వల్ల ధనికులు మరింత ధనికులుగా, పేదవారు మరింత పేదవారిగా తయారవుతున్నారు.

2. సహజ వనరుల అల్ప వినియోగం :
దేశంలోని ప్రజల జీవన ప్రమాణ స్థాయిని పెంచుకోవాలంటే జాతీయాదాయ వృద్ధి రేటును పెంపొందించుకోవాల్సిన ఆవశ్యకత ఉంది. భారతదేశంలో నదుల నీరు, అటవీ సంపద, ఖనిజ సంపదలను సంపూర్ణంగా ఉపయోగించుకోకపోవడం వల్లనే 63 సంవత్సరాల ప్రణాళికా కాలం పూర్తి అయినప్పటికీ ఇంకా 19.3 శాతం ప్రజలు దారిద్ర్య రేఖ దిగువన జీవిస్తున్నారు.

3. అధిక జనాభా ఒత్తిడి :
భారతదేశంలో ప్రధాన సమస్య ఏమిటంటే మరణాల రేటు తగ్గి జననాల రేటు చాలా అధికంగా ఉండటం వల్ల 1951 నుంచి 2001 సంవత్సరం వరకు జనాభా సాలుసరి వృద్ధి రేటు 2.1 శాతంగా ఉంది. పెరుగుతున్న ప్రజల జీవన ప్రమాణ స్థాయి తగ్గకుండా ఉండాలి అంటే ఆర్థిక వృద్ధి రేటు అంతే వేగంగా పెరగాల్సి ఉంటుంది. పెరుగుతున్న జనాభాకు కావాల్సిన ఆహారం, గృహాలు, వైద్యం, విద్య మొదలైన కనీస సౌకర్యాలను కల్పించవల్సిన అవసరం ఉంది. జనాభా పెరుగుదల వల్ల శ్రామిక శక్తి పెరుగుతుంది.

తత్ఫలితంగా శ్రామికుల డిమాండ్ కంటే సప్లయి అధికమై దేశంలోని నిరుద్యోగం, పేదరికం అనే సమస్యలు పెరగుతున్నాయి. జనాభా వృద్ధి తలసరి జాతీయాదాయం వృద్ధి రేటు కంటే అధికంగా ఉండటం వల్ల ప్రజల తలసరి ఆదాయం తగ్గి జీవన వ్యయం తగ్గి పేదరికం పెరుగుతుంది.

4. నిరుద్యోగిత :
భారతదేశంలో అధిక శ్రామిక శక్తి ఉండటం వల్ల అందరికీ లాభదాయకమైన ఉపాధిని కల్పించడమనేది చాలా కష్టంతో కూడుకొన్న పనిగా చెప్పవచ్చు. మూలధన కొరతవల్ల పారిశ్రామికీకరణ మందకొడిగా తయారైనందువల్ల నిరుద్యోగిత ఏర్పడుతుంది. దేశంలోని మొత్తం శ్రామిక శక్తికి ఉపాధి అవకాశాలు కల్పించడానికి సరిపడే మూలధనం లేకపోవడం వల్ల పరిశ్రమలను విస్తరించలేకపోవడం జరుగుతుంది. తత్ఫలితంగా దేశంలో నిరుద్యోగిత పెరగడం వల్ల పేదరికం కూడా పెరుగుతుందని చెప్పవచ్చు. నిరుద్యోగుల సంఖ్య పెరగడం వల్ల పేదరికం తీవ్రత కూడా పెరుగుతుంది.

5. నాసిరకం విద్య :
పేదప్రజలు తక్కువ విద్యను అభ్యసించడం వల్ల దేశాల్లో పేదరికం పెరుగుతుంది. పేదప్రజల్లో సాపేక్షిక ఆదాయం తక్కువగా ఉండటానికి విద్యాపరమైన వ్యత్యాసాలు ప్రధాన కారణంగా ఉంటాయి.

6. నిత్యావసరాల లభ్యత తక్కువగా ఉండటం :
నిత్యావసర వస్తువుల లభ్యత తక్కువగా ఉండటం కూడా భారతదేశంలో పేదరికానికి ఒక ముఖ్యమైన కారణంగా చెప్పవచ్చు. నిత్యావసర వినియోగ వస్తువుల కొరత సరైన పంపిణీ విధానం లేనందువల్ల పేద ప్రజల జీవన ప్రమాణం తక్కువగా ఉంటుంది. ఎగువన ఉండే ధనికుల, అట్టడుగున ఉండే పేదవారి వినియోగ స్థాయిలలో వ్యత్యాసం అధికంగా ఉంది.

7. ద్రవ్యోల్బణం :
నిరంతర ధరల పెరుగుదల కూడా పేదరికానికి మరొక కారణం. ధరలు పెరగడం వల్ల ద్రవ్య కొనుగోలు శక్తి తగ్గుతుంది. ఫలితంగా దిగువ సమాజంలో మధ్య తరగతి, పేద ప్రజలు మరింత పేదవారు కావడానికి దారితీస్తుంది. అందువల్ల ద్రవ్యోల్బణం వల్ల దేశంలో పేదరికం మరింతగా పెరుగుతుందని చెప్పవచ్చు.

8. తక్కువ సాంకేతికత :
భారతదేశంలోని పేదరికానికి తక్కువ స్థాయి సాంకేతికత కూడా కారణం అవుతుందని చెప్పవచ్చు. అభివృద్ధి చెందిన దేశాలలోని సాంకేతికతతో పోల్చినట్లయితే తయారీ, వ్యవసాయ రంగంలో చాలా తక్కువ స్థాయి సాంకేతికతను వాడుతున్నారు. అంతేగాక, మార్కెట్ల సామర్థ్యం, వ్యవస్థాపన, నిర్వహణ, విత్త మార్కెట్లు చాలా తక్కువ స్థాయిలో ఉన్నాయి. తక్కువ సాంకేతికత ఫలితంగా తలసరి ఉత్పాదకత తక్కువ స్థాయిలో ఉంటుంది. పర్యవసానంగా, మూలధన ఉత్పాదకత తక్కువ స్థాయిలో ఉండి తక్కువ ఫలితాలు రావడం వల్ల మనదేశంలో మూలధన సంచయనం తక్కువగా ఉంది.

9. మూలధన కొరత :
ఆర్థిక వ్యవస్థ అభివృద్ధి మూలధన సంచయనంపై ఆధారపడి ఉంటుంది. భారతదేశంలో చాలామంది ప్రజలు నిరక్షరాస్యులు, తక్కువ నైపుణ్యత గల వారు కావడం వల్ల పురాతన మూలధన పరికరాలను, సాంప్రదాయిక ఉత్పత్తి పద్ధతులను ఎక్కువగా ఉపయోగిస్తున్నారు. తక్కువ ఉత్పాదకత వల్ల తక్కువ పొదుపు, తక్కువ పెట్టుబడి, తక్కువ మూలధన సంచయనాలను గమనించవచ్చు.

10. పంచవర్ష ప్రణాళికలు విఫలం చెందడం :
దేశంలో ప్రజలందరికీ కనీస జీవన స్థాయిని కల్పించడం పంచవర్ష ప్రణాళికల ముఖ్య లక్ష్యం. శ్రీమతి ఇందిరా గాంధీ “గరీబీ హఠావో” నినాదం ద్వారా పేదరిక నిర్మూలనకు ఎన్నో చర్యలను తీసుకొంది. పంచవర్ష ప్రణాళికల కాలంలో సాధించిన వృద్ధి రేటు పేదరికాన్ని సమూలంగా నిర్మూలించలేకపోయింది.

11. సరళీకరణ, ప్రైవేటీకరణ, ప్రపంచీకరణల అభివృద్ధి నమూనా:
ప్రజలకు అధిక సంఖ్యలో ఉపాధి అవకాశాలు కల్పించడంలో ప్రధాన వనరుగా ఉన్న వ్యవసాయం, వ్యవసాయాధారిత పరిశ్రమలను ఈ నమూనా విస్మరించింది. ఈ నమూనా మూలధన సాంద్రత అభివృద్ధి తీరును పరిగణనలోకి తీసుకోవడం వల్ల ఉపాధి కల్పన విషయంలో తీవ్ర భయాందోళనలకు దారితీసింది. దీని ఫలితంగా దేశంలో నిరుద్యోగిత పెరిగింది. ఈ వ్యూహానికి విస్తరణ ప్రభావం trickle down effect తక్కువగా ఉంటుంది. కాబట్టి, ఆర్థిక వ్యవస్థలో పేదరికం, నిరుద్యోగాలు పెరిగాయి.

12. సాంఘిక కారణాలు :
నిరక్షరాస్యత, అమాయకత్వం, మత, కుల, సంబంధిత ఆచారాలు, ఉమ్మడి కుటుంబ వ్యవస్థ మొదలైన వాటన్నింటివల్ల ఆధునిక సాంకేతికతను చేపట్టకపోవడం వల్ల గమనశీలత తగ్గి, ప్రజల ఆదాయాలు పెరగవు. అందువల్ల ప్రజలు కొన్ని స్వీయ నిర్ణయాల వల్ల పేదరికంలో ఉంటారు అనే దృక్పథాన్ని పరిగణించవలసి ఉంటుంది.

ప్రశ్న 7.
పేదరిక సమస్య పర్యవసానాలను చర్చించండి.
జవాబు.
ఏ పేదరికం అయినా కూడా ఒక దేశంలోని సాంఘిక, ఆర్థిక, రాజకీయ జీవనాలపై, తీవ్రమైన ఒత్తిడులకు కారణమవుతుంది. వాస్తవానికి, ఆర్థికాభివృద్ధి ప్రారంభ దశలలో పేదరిక విషవలయాలు ఏర్పడటానికి దోహదపడింది. ఉన్నవారు, లేనివారు అనే రెండు వర్గాలుగా మొత్తం సమాజం విభజితమైనది. ఉన్నవారు మాత్రమే విలాసపు జీవితం సమకూర్చే అన్ని సౌకర్యాలను అనుభవించేవారు. అయితే లేనివారు మాత్రం పేదరిక సమస్య వల్ల కనీసం కూడు, గుడ్డ, గూడు అనే ప్రాథమిక అవసరాలను తీర్చుకోలేకపోతున్నారు. ఫలితంగా, ఈ క్రింది ప్రతికూల ప్రభావాలు ఏర్పడుతున్నాయి.

1. అసమ అవకాశాలు :
సాధారణంగా ద్రవ్య సహాయం, వనరులు ఆధిక్యత వల్ల ఉన్నవారు అవకాశాలను మెరుగైన రీతిలో ఉపయోగించుకొంటారు. కాని పేదవారు మాత్రం కనీసం ప్రాథమిక అవసరాలను కూడా పొందలేరు. పర్యవసానంగా పేదవారు చాలా తీవ్రంగా లేమి ప్రభావానికి లోనవుతారు.

2. ఆర్థిక స్తోమత కేంద్రీకరణ :
కొద్ది మంది చేతుల్లో ఆర్థిక స్తోమత కేంద్రీకృతం కావడానికి తీవ్రమైన పేదరికం దోహదపడుతుంది. ధనికులు రాజకీయ ప్రాబల్యతను పొందడం కోసం వారి ఆర్థిక స్తోమతను ఉపయోగించుకొంటారు.

3. అసమర్థత (Inefficiency) :
పేదరికం ఉండటం వల్ల పేదవారు విద్య, ఇతర ప్రత్యేకమైన తర్ఫీదులు పొందడానికి గల అవకాశాలు మృగ్యమవుతాయి. ఒక వ్యక్తి సామర్థ్యాన్ని కలిగి ఉండటానికి కావలసిన బౌద్ధిక జ్ఞానం, భౌతిక శక్తి ఆవశ్యకత అందరూ గుర్తించిన అంశమే. సరైన అవగాహన, నైపుణ్యతను పెంచే శిక్షణ లేకపోవడం వల్ల మొత్తం ఉత్పత్తి ప్రక్రియ అసమర్థతకు లోనవుతుంది.

4. నిరుద్యోగ సమస్య :
పేదవారికి ఉపాధి అవకాశాలు పరిమితంగా ఉండటం వల్ల పేదరిక సమస్య, నిరుద్యోగిత సమస్యలు ఏర్పడటానికి దోహదపడుతున్నాయి. ఆర్థిక వ్యవస్థ బలోపేతం అయ్యే క్రమంలో నిరుద్యోగిత అనేది ఆటంకంగా పరిణమిస్తుంది. ఒక దేశం అన్ని అంశాలలో పురోగతిని సాధించే నేపథ్యంలో అధిక నిరుద్యోగిత అడ్డంకిగా నిలుస్తుంది.

5. ఆదాయ అసమానతలు, అభద్రత :
ఆదాయ అసమానతలు పెరగడానికి పేదరిక సమస్య దోహదపడటమే కాకుండా అభద్రతా భావాన్ని కూడా కలగజేస్తుంది.

6. సమాజం :
పేదరిక సమస్య సమాజంలోని కొన్ని రుగ్మతలకు కారణభూతం కావచ్చు. సమాజంలో పేదరికంలో ఉన్న ప్రజలలో ఎక్కువ మంది గృహ వసతి లేనివారిగా ఉండటం వల్ల వారందరు వీధుల్లోకి నెట్టివేయబడుతున్నారు. ఈ పేదరిక సమస్య సామాజిక అశాంతికి దారితీయడమే కాకుండా నేరాలు కూడా పెరగడానికి ఆస్కారం కావచ్చు.

7. పౌష్టిక ఆహార లోపం :
పేదరికపు అతి సామాన్య ప్రభావం పౌష్టిక ఆహార లోపం, ఈ సమస్య ప్రత్యేకించి పేదకుటుంబాల వారి పిల్లలలో కనిపిస్తుంది. పేదరికంలో నివసిస్తున్న ప్రజలకు కొనుగోలు శక్తి తక్కువైనందువల్ల పౌష్టిక ఆహారం చాలా అరుదుగా అందుబాటులో ఉంటుంది. సాధారణంగా పౌష్టిక ఆహారం అధిక ఖర్చుతో కూడుకొని ఉండటం వల్ల తక్కువ ఆదాయం గల కుటుంబాలు వాటిపై వెచ్చించడం సాధ్యపడదు. కాబట్టి, పేదవారు తక్కువ బలవర్ధకమైన ఆహారం కొనుగోలు చేస్తారు. పేదరికంలో ఉన్నవారు కొన్ని కొన్నిసార్లు చాలినంత మేరకు ఏది కూడా తినలేని విధంగా ఉండటం వల్ల పౌష్టిక ఆహార లోపంతో ఉంటారు.

8. ఆరోగ్యం :
పేదరికపు తీవ్ర ప్రభావాలు ఆరోగ్యంపై కూడా ఉంటాయి. పేదరికం వల్ల తరచుగా అనారోగ్యానికి గురి అవుతుండటం వల్ల వారి ఆయుఃప్రమాణం తగ్గడమే కాకుండా మందులపై అధిక వ్యయాన్ని వెచ్చించాల్సి ఉంటుంది. పేదవారి ఆరోగ్యకరమైన జీవన పర్యావరణ నిర్వహణకు గాను వనరులు లేకపోవడం వల్ల వారు రోగాల బారిన పడటమనేది సర్వసాధారణం.

9. విద్య :
పేదరికపు ప్రతికూల ప్రభావం విద్య మీద అధికంగా ఉంటుంది. పేదరికంలో ఉండే ఎక్కువ మంది ప్రజలు లేదా ప్రాయంలో బడికి పోలేకపోతున్నారు. పేదరికంలో ఉండే కుటుంబాలు అవసరమయ్యే బట్టలను లేదా బడికి పోవడానికి కావలసిన వాటిని వారి పిల్లలకు అందించలేకపోతున్నారు. ఇంకా కొన్ని కుటుంబాల వారు వారి పిల్లలను బడికి కూడా పంపలేక పోతున్నారు.

ప్రశ్న 8.
ప్రభుత్వంచే పరిగణనలోకి చేసుకోబడిన కొన్ని పేదరిక నిర్మూలన పథకాలను వివరించండి.
జవాబు.
భారతదేశంలోని పేదరిక నిర్మూలన, ఉపాధి కల్పన పథకాలు:

ప్రశ్న 9.
పేదరికపు పలు భావనలను విశ్లేషించండి.
జవాబు.
పేదరికం అనేది ఒక సామాజిక దృగ్విషయం. సమాజంలోని ఏ ప్రజలైతే తమ కనీస జీవితావసరాలను తీర్చుకోలేని స్థితిలో ఉంటారో, దానిని పేదరికంగా నిర్వచించవచ్చు. ఏ సమాజంలోనైనా ఒక నిర్ణీత కనీస స్థాయిలో తమ జీవనాన్ని నిర్వహించుకోలేక, జీవనాధార వేతనం కూడా పొందలేక జీవితం గడుపుతున్న వారిని పేదవారుగా నమోదు చేయవచ్చు.

పేదరికం రకాలు :
1. నిరుపేక్ష పేదరికం :
దేశంలోని ప్రజల కనీస అవసరాల పరిమాణాలను ముందుగా నిర్ణయించి తరువాత మార్కెట్ ధరల ఆధారంతో వాటి విలువను అంచనా వేసి కనీస జీవనావసర వినియోగాన్ని నిర్ధారిస్తారు. కనీస భౌతిక జీవనావసరాన్ని ద్రవ్య రూపంలో లెక్కించి కనీస జీవన వినియోగ వ్యయాన్ని నిర్ధారిస్తారు. నిర్ధారించిన కనీస ఆదాయం లేదా వినియోగం కంటే తక్కువగా పొందుతున్న ప్రజలను నిరపేక్ష పేదవారు అని అంటారు.

2. సాపేక్షిక పేదరికం :
సాపేక్షిక పేదరికాన్ని లెక్కించడానికి ప్రజల ఆదాయ పంపిణీని తులనాత్మకంగా అంచనావేసి ఎగువ 5 నుంచి 10 శాతం ప్రజల జీవన స్థాయితో పోల్చి చూసి దిగువ 5 నుంచి 10 శాతం ప్రజలను సాపేక్షిక పేదవారిగా పరిగణిస్తారు. లేదా, తక్కువ ఆదాయ స్థాయి గల ప్రజలను అధిక ఆదాయం పొందే వారితో పోల్చి, తక్కువ ఆదాయం పొందుతున్న ప్రజలను సాపేక్షకంగా పేదవారిగా పరిగణిస్తారు. తక్కువ ఆదాయం గల ప్రజల జీవన ప్రమాణం అధికంగా ఉన్నప్పటికీ అధిక ఆదాయ ప్రజల జీవన ప్రమాణంతో పోల్చి వారిని సాపేక్షిక పేదవారు అని అంటారు.

3. పేదరిక వ్యత్యాసపు సూచీ (Poverty Gap Index) :
పేదరికపు గీత దిగువన గల సగటు దూరం, ఆ గీతకు అనుపాతంగా తెలియజేసే దానిని (శూన్య పేదరిక వ్యత్యాసం పొందేవరకు పేదేతర వారిని లెక్కించుకొంటూ పోతే మొత్తం జనాభా దృష్ట్యా సగటు రూపొందించబడుతుంది) పేదరిక వ్యత్యాసపు సూచీగా నిర్వచిస్తారు.

ప్రతి పేద వ్యక్తి ఆదాయం, దారిద్య్ర రేఖ సూచించే ఆదాయానికి గల వ్యత్యాసాన్ని బదిలీ చేయడం ద్వారా ప్రతి పేద వ్యక్తికి గల ఆదాయం దారిద్ర్య రేఖ సూచించే ఆదాయానికి సమానమవుతుంది. కాబట్టి నిరపేక్ష దారిద్ర్యాన్ని అధిగమించవచ్చు. ఆ విధంగా పేదరిక వ్యత్యాసం పేదరికపు వ్యాప్తిని, తీవ్రతను ప్రతిభింబింప జేస్తుంది. కింది సూత్రం ఆధారంగా పేదరికపు వ్యత్యాసపు సూచీని గణన చేయవచ్చు :

పేదరికపు వ్యత్యాసం = పేదరికపు గీత – పేదవాడి సగటు వినియోగ వ్యయం / పేదరికపు గీత
లేదా G = \(\frac{Z-Y}{Z}\)

4. మానవ పేదరిక సూచీ (HPI) :
1997లో UNDP విడుదల చేసిన మానవాభివృద్ధి నివేదిక ‘మానవ పేదరిక సూచీ’ (Human Poverty Index – HPI) ని ప్రవేశ పెట్టింది. సమాజంలో పేదరికపు తీవ్రత పై సమష్టి అభిప్రాయానికి రావడం కోసం గుణాత్మక జీవనంలో వివక్షతకు సంబంధించిన వివిధ లక్షణాలన్నింటిని ఒక దగ్గర చేర్చి సంయుక్త సూచీని ఏర్పరిచారు.

2010 మానవాభివృద్ధి నివేదిక మానవ పేదరికపు సూచీ (HPI) స్థానంలో బహు పార్శ్వపు పేదరికపు సూచీ (Muli-dimen- sional Poverty Index – MPI) ని ప్రవేశపెట్టింది. బహు పార్శ్వపు పేదరికపు తలసరి లెక్క (జనాభాలో బహుపార్శ్వపు పేదరికాన్ని అనుభవిస్తున్న), బహు పార్శ్వపు దారిద్ర్యాన్ని అనుభవిస్తున్న ప్రతి గృహపు వివక్షతల సగటు సంఖ్య (వారి పేదరికపు తీవ్రతల లబ్దమే MPI).

ప్రశ్న 10.
భారతదేశంలో పేదరికపు భారాన్ని సంక్షిప్తంగా పరిశీలించండి.
జవాబు.
భారతదేశంలో పేదరిక భారం (Incidence of Poverty in India) : 1970 వ దశకం ప్రారంభం నుంచి ప్రణాళికా సంఘం పేదరిక సాంద్రతకు సంబంధించిన అంచనాలను గణన చేస్తుంది. 1973-74 ధరల దృష్ట్యా దారిద్ర్య రేఖ నిర్ధారణ కోసం గ్రామీణ ప్రజలకుగాను రూ. 49.63 తలసరి నెలవారి వ్యయం, పట్టణ ప్రజలకుగాను రూ.56.64 తలసరి నెలవారి వ్యయం పొందలేని వారిని దారిద్ర్య రేఖ కింద జీవించే వారుగా నిర్వచించవచ్చు. ధరలలో వస్తున్న మార్పుల దృష్ట్యా దారిద్ర్య రేఖను కాలానుసారంగా మారుస్తున్నారు.

రంగరాజన్ ప్యానల్ సూచన మేరకు 2011-12వ సంవత్సరానికి గాను ఎవరైతే గ్రామీణ ప్రాంతాలలో నెలవారి వ్యయం రూ.972; పట్టణ ప్రాంతాలలో నెలవారి వ్యయం రూ.1,407 చేయగలుగుతారో వారు పేదరిక నిర్వచనం పరిధిలోకి రారు. అందువల్ల, రంగరాజన్ కమిటీ ప్రకారం ఐదుగురు సభ్యులు కలిగిన కుటుంబం గ్రామీణ ప్రాంతాలలో రూ.4,760; పట్టణ ప్రాంతాలలో రూ.7,035 ల మేరకు వినియోగ వ్యయం చేయువారు పేదరికం పరిధిలోకి రారు.

ఒకవేళ రోజువారి ప్రాతిపదికన గణన చేసినచో 2011-12వ సంవత్సరంనకు గాను గ్రామీణ ప్రాంతాలలో తలసరి వినియోగ వ్యయం రూ. 32 రోజు ఒక్కింటికి; పట్టణ ప్రాంతాలలో రూ. 47 రోజు ఒక్కంటికి ఉన్నచో వారు పేదరికం పరిధిలోకి రారు. 2011-12వ సంవత్సరంనకు గాను తెండూల్కర్ పద్ధతి (అంచనా) ప్రకారం గ్రామీణ ప్రాంతాలలో రూ.816 మరియు పట్టణ ప్రాంతాలలో రూ.1,000 నెలసరి వ్యయం లేదా ఒకవేళ రోజు వారి ప్రాతిపదికన పరిగణనలోకి తీసుకొన్నచో, గ్రామీణ ప్రాంతాలలో తలసరి వ్యయం రోజు ఒక్కంటికి రూ.27 మరియు పట్టణ ప్రాంతాలలో రూ. 33గా ఉన్నచో, వారు పేదరికం పరిధిలోకి రారు. అయితే తెండూల్కర్ కమిటి దీనిని గ్రామీణ ప్రాంతాలకు గాను రూ. 4,080గా పట్టణ ప్రాంతాలకు రూ.5,000గా నిర్ధారించింది.

1973-74లో జనాభా సగం కంటే ఎక్కువ జనాభా దారిద్య్ర రేఖ దిగువన ఉన్నారు. నాలుగు దశాబ్దాల కాలంలో అంటే 1973-74 నుంచి 2011-12 వరకు గల పేదరికాన్ని గమనించినచో 1973-74లో 54.9 శాతం మేరకు ఉన్న పేదరికం 2011-12 నాటికి 21.92 శాతం మేరకు తగ్గింది అనే విషయం అర్థమవుతుంది. కానీ ఈ కాలంలో జనాభా గణనీయంగా పెరగడం వల్ల నిరపేక్ష పేదవారి సంఖ్య మాత్రం తగ్గలేదని చెప్పవచ్చు.

అతిస్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
జాతీయాదాయం.
జవాబు.
ఒక దేశంలో ఒక సంవత్సరకాలంలో ఉత్పత్తి చేయబడిన అంతిమ వస్తుసేవ నికర విలువ. రెండు మార్లు లెక్కించకుండా నిర్ణీత కాల వ్యవధిలో ఉత్పత్తి చేయబడిన వస్తుసేవల మొత్తం పరిమాణం.

ప్రశ్న 2.
తలసరి ఆదాయం.
జవాబు.
జాతీయాదాయమును దేశ జనాభాతో భాగిస్తే వచ్చే ఆదాయం.
తలసరి ఆదాయం = జాతీయాదాయం / దేశజనాభా.

ప్రశ్న 3.
నిరుద్యోగిత.
జవాబు.
అమలులో ఉన్న వేతన రేటు వద్ద ఒక వ్యక్తికి పనిచేయాలనే కోరిక ఉన్నప్పటికీ, అతనికి ఉద్యోగ అవకాశం లభ్యం కాకపోవడాన్నే నిరుద్యోగితగా చెప్పవచ్చు.

ప్రశ్న 4.
నిరంతర నిరుద్యోగిత.
జవాబు.
ఒక వ్యక్తి పనిచేయడానికి ఇష్టపడి, పని కోసం ప్రయత్నం చేసి సంవత్సరంలో అధిక కాలం ఖాళీగా ఉండటం. దీనిని బహిరంగ నిరుద్యోగిత అని కూడా అంటారు.

ప్రశ్న 5.
వార పరమైన స్థితి గల నిరుద్యోగిత.
జవాబు.
గత 7 రోజులలో ఒక వ్యక్తి కనీసం ఒక గంట పనిచేస్తే వారి పరమైన స్థితి ప్రకారం అతనిని ఉద్యోగిగా పరిగణిస్తారు.

ప్రశ్న 6.
నిర్మిత సంబంధిత నిరుద్యోగిత.
జవాబు.
ఇది దేశ ఆర్థిక నిర్మితతో సంబంధం కల్గి ఉంటుంది. త్వరితగతిన పెరుగుతున్న జనాభా, వారిలో గమనశీలత లేకపోవడం వల్ల శ్రామిక డిమాండ్ కంటే శ్రామిక సప్లయి అధికంగా ఉండటం వల్ల ఈ రకమైన నిరుద్యోగం ఏర్పడును. ఇది దీర్ఘ కాలికమైనది.

ప్రశ్న 7.
ఋతు సంబంధిత నిరుద్యోగిత.
జవాబు.
ఋతుగత మార్పులను అనుసరించి డిమాండ్లో చోటు చేసుకొనే మార్పు వల్ల ఈ నిరుద్యోగిత ఏర్పడుతుంది. వ్యావసాయ శ్రామికులకు సంవత్సరంలో 7 నుండి 8 మాసాల మేరకు పని దొరుకుతుంది. మిగతా సమయాలలో పని దొరకని శ్రామికులను ఋతుగత నిరుద్యోగులు అంటారు.

ప్రశ్న 8.
బహిరంగ నిరుద్యోగిత.
జవాబు.
శ్రామికులు ఏ పని లేకుండా జీవించినట్లయితే వారికి చేయడానికి ఏ పని దొరకనట్లయితే, వారందరూ కూడా బహిరంగ నిరుద్యోగిత కోవలోకి వస్తారు.

ప్రశ్న 9.
విద్యావంతుల నిరుద్యోగిత.
జవాబు.
విద్యనార్జించి లేదా తర్ఫదు పొంది, నైపుణ్యతను కల్గిన వ్యక్తికి అతని అర్హతలకు అనుగుణంగా ఉద్యోగం దొరికినట్లయితే, ఆ వ్యక్తి విద్యనార్జించిన నిరుద్యోగి అని అంటారు. మన దేశంలో ఇటువంటి నిరుద్యోగిత ఎక్కువగా ఉంటుంది.

ప్రశ్న 10.
చక్రీయ నిరుద్యోగిత.
జవాబు.
అభివృద్ధి చెందిన దేశాలలోని వ్యాపార కార్యకలాపాల్లో మందకొడితనం ఏర్పడటం వల్ల సాధారణంగా ఏర్పడే నిరుద్యోగతను చక్రీయ నిరుద్యోగిత అంటారు.

ప్రశ్న 11.
ప్రచ్ఛన్న నిరుద్యోగిత.
జవాబు.
ఉత్పత్తి ప్రక్రియలలో అవసరమైన శ్రామికుల కంటే ఎక్కువ మంది ఉండే వారిని ప్రచ్ఛన్న నిరుద్యోగులు అని అంటారు. వీరి ఉపాంత ఉత్పాదకత శూన్యంగా ఉంటుంది. వ్యవసాయరంగంలో ఈ రకమైన నిరుద్యోగిత ఉంటుంది.

ప్రశ్న 12.
సంఘృష్ట నిరుద్యోగిత.
జవాబు.
దేశంలోని శ్రామికులు ఒక వృత్తి నుంచి మరొక వృత్తికి మార్పుచెందే కాలంలో ఏర్పడిన నిరుద్యోగితను సంఘృష్ట నిరుద్యోగిత అంటారు. శ్రామిక మార్కెట్లోని అసంపూర్ణతల వల్ల శ్రామికులకు ఉద్యోగ అవకాశాల గురించి సరైన అవగాహన లేకపోవడం వల్ల ఈ రకమైన నిరుద్యోగిత ఏర్పడుతుంది.

ప్రశ్న 13.
అనుద్యోగిత.
జవాబు.
అనుద్యోగిత స్థితిలో ప్రజలు నిరుద్యోగులు కావచ్చు లేదా సంప్రదాయ 16 సంఘటిత రంగంలో పని చేస్తూండవచ్చు. లేదా ఈ రకమైన నిరుద్యోగిత అభివృద్ధి చెందుతున్న దేశాలలోనే ఉంటుంది.

ప్రశ్న 14.
అల్ప ఉద్యోగిత.
జవాబు.
శ్రామికుల అల్ప ఉద్యోగిత అంటే వారికి పని దొరకుతుంది. కాని వారి శక్తి సామర్థ్యాలు అభిలషణీయమైన రీతిలో ఉపయోగించబడవు.

ప్రశ్న 15.
సాంకేతిక పరమైన నిరుద్యోగిత.
జవాబు.
ఆర్థిక వ్యవస్థలో నూతన సాంకేతికత ప్రవేశం వల్ల శ్రామికులు తొలగించబడతారు. ఫలితంగా ఏర్పడే నిరుద్యోగితను సాంకేతిక పరమైన నిరుద్యోగిత అంటారు.

ప్రశ్న 16.
దారిద్ర్యరేఖ.
జవాబు.
గ్రామీణ ప్రజలకు గాను 49.63 తలసరి నెలవారి వ్యయం పట్టణ ప్రజలకు గాను, 756.64 తలసరి నెలవారి వ్యయం పొందేలేని వారిని దారిద్య్ర రేఖ క్రింద జీవించే వారిగా నిర్వచించవచ్చు.

ప్రశ్న 17.
పేదరిక వ్యత్యాసం.
జవాబు.
పేదరికపు గీత దిగువన గల సగటు దూరం, ఆ గీతల అనుపాతంగా తెలియజేసే దానిని పేదరిక వ్యత్యాసపు సూచీగా నిర్వచిస్తారు.

ప్రశ్న 18.
నిరపేక్ష పేదరికం.
జవాబు.
దేశంలోని ప్రజల కనీస అవసరాల (ధాన్యం, పప్పులు, పాలు, వెన్న మొదలైనవి) పరిమాణాలను ముందుగా నిర్ణయించి తరువాత మార్కెట్ ధరల ఆధారంతో వాటి విలువను అంచనా వేసి కనీస జీవనావసర వినియోగాన్ని నిర్ధారిస్తారు. ఈ కనీస జీవనాధార వినియోగ వ్యయాన్ని కూడా చేయలేని స్థితిని నిరపేక్ష పేదరికం అని అంటారు.

ఇండియన్ కౌన్సిల్ ఆఫ్ మెడికల్ రీసెర్చ్ ప్రకారం, ఈ భౌతిక పరిమాణాలు గ్రామీణ ప్రాంతాలలో 2,400 తలసరి క్యాలరీలుగా, పట్టణ ప్రాంతాలలో 2,100 తలసరి క్యాలరీలుగా ఉండాల్సి ఉంది. అంతకంటే తక్కువ క్యాలరీలను వినియోగించే వారందరూ పేదరికం కిందికి వస్తారు.

ప్రశ్న 19.
సాపేక్షిక పేదరికం:
జవాబు.
సాపేక్ష పేదరికాన్ని లెక్కించడానికి ప్రజల ఆదాయ పంపిణీని తులనాత్మకంగా అంచనా వేసి ఎగువ 5 నుంచి 10 శాతం ప్రజల జీవన స్థాయితో పోల్చి చూసి దిగువ 5 నుంచి 10 శాతం ప్రజలను సాపేక్షిక పేదవారిగా పరిగణిస్తారు. లేదా తక్కువ ఆదాయ స్థాయి గల ప్రజలను అధిక ఆదాయం పొందే వారితో పోల్చి, తక్కువ ఆదాయం పొందుతున్న ప్రజలను సాపేక్షికంగా పేదవారిగా పరిగణిస్తారు.

ప్రశ్న 20.
బహుపార్శ్వపు పేదరిక సూచీ.
జవాబు.
2010లో మానవాభివృద్ధి నివేదిక మానవ పేదరికపు సూచి స్థానంలో బహు పార్శ్యపు పేదరిక సూచీని ప్రవేశపెట్టారు. బహు పార్శ్వపు పేదరిక తలసరి లెక్క, బహు పార్శ్వపు దారిద్ర్యాన్ని అనుభవిస్తున్న ప్రతి గృహపు వివక్షతల సగటు సంఖ్య తీవ్రతల లబ్ధమే. ఈ సూచి మూడు అంశాలను కల్గి ఉంటుంది.
అవి : 1. వైద్యం, విద్య, జీవన ప్రమాణాలు.

TS Inter 2nd Year Maths 2A Textbook Solutions Pdf Download | TS Inter Maths 2A Study Material Pdf

TS Inter Second Year Maths 2A Important Questions | Maths 2A Important Questions Pdf 2022 TS

1. Maths 2A Complex Numbers Important Questions
2. Maths 2A De Moivre’s Theorem Important Questions
3. Maths 2A Quadratic Expressions Important Questions
4. Maths 2A Theory of Equations Important Questions
5. Maths 2A Permutations and Combinations Important Questions
6. Maths 2A Binomial Theorem Important Questions
7. Maths 2A Partial Fractions Important Questions
8. Maths 2A Measures of Dispersion Important Questions
9. Maths 2A Probability Important Questions
10. Maths 2A Random Variables and Probability Distributions Important Questions

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(b)

I.
Question 1.
Find the set of vaines of x for which the binomial expansions of the following are valid.
i) (2 + 3x)^{\(\frac{-2}{3}\)}
ii) (5 + x)^{\(\frac{3}{2}\)}
iii) (7 + 3x)^-5
iv) (4 – \(\frac{x}{3}\))^{\(\frac{-1}{2}\)}
Solution:
We know that
(2 + 3x)^{\(\frac{-2}{3}\)} = 2^{\(\frac{-2}{3}\)} (1 + \(\frac{3}{2}\)x)^{\(\frac{-2}{3}\)}
The expansion is valid only when |\(\frac{3}{2}\) x| < 1
⇒ |x| < \(\frac{2}{3}\)
⇒ x ∈ \(\left(\frac{-2}{3}, \frac{2}{3}\right)\).

ii) We know that (5 + x)^3/2
= 5^3/2 (1 + \(\frac{x}{5}\))^3/2
The expansion is valid only when
|\(\frac{x}{5}\)| < 1
⇒ |x| < 5
⇒ x ∈ (- 5, 5).

iii) We know that
(7 + 3x)^-5 = 7^-5 (1 + \(\frac{3 x}{7}\))^-5
The expansion is valid only when |\(\frac{3 x}{7}\)| < 1
⇒ |x| < \(\frac{7}{3}\)
⇒ x ∈ \(\left(\frac{-7}{3}, \frac{7}{3}\right)\)

iii) We know that (4 – \(\frac{x}{3}\))^{\(\frac{-1}{2}\)}
= \(4^{\frac{-1}{2}}\left(1-\frac{x}{12}\right)^{\frac{-1}{2}}\)
The expansion is valid only when |\(\frac{x}{12}\)| < 1
⇒ |x| < 12
⇒ x ∈ (- 12, 12).

Question 2.
i) 6th term of (1 + \(\frac{x}{2}\))^-5
ii) 7th term of (1 – \(\frac{x^2}{3}\))^-4
iii) 10th term of (3 – 4x)^{\(\frac{-2}{3}\)}
iv) 5th term of (7 + \(\frac{8 y}{3}\))^{\(\frac{7}{4}\)}
Solution:
i) General term in the expansion of (1 + x)^-n is
T_r+1 = (- 1)^r . ^n+r-1C_r . x^r
∴ 6th term of (1 + x)^-5 is
T₆ = (- 1)⁵ . ⁹C₅ (\(\frac{x}{2}\))^-5 (∵ n = r = 5)
= \(\frac{-63}{16}\) x⁵.

ii) General term in the expansion of (1 + x)^-n is
T_r+1 = (- 1)^r . ^n+r-1C_r . x^r
7th term in the eapansion of (1 – \(\frac{x^2}{3}\))^-4 is
T₇ = \({ }^9 C_6\left(\frac{x^2}{3}\right)^6\) (∵ n – 4; r = 6)
= \(\frac{28}{243}\) x¹²

iii) We know that
(3 – 4x)^{\(\frac{-2}{3}\)} = \(3^{\frac{-2}{3}}\left(1-\frac{4 x}{3}\right)^{\frac{-2}{3}}\)

iv) We know that (7 + \(\frac{8 y}{3}\))^{\(\frac{7}{4}\)}

Question 3.
Write down the first 3 terms In the expansion of
i) (3 +5x)^{\(\frac{-7}{3}\)}
ii) (1 + 4x)^-4
iii) (8 – 5x)^{\(\frac{2}{3}\)}
iv) (2 – 7x)^{\(\frac{-3}{4}\)}
Solution:
i) \((3+5 x)^{\frac{-7}{3}}=3^{\frac{-7}{3}}\left(1+\frac{5 x}{3}\right)^{\frac{-7}{3}}\)
We know that

ii) We know that
(1 + x)^-n = 1 – nx + \(\frac{\mathrm{n}(\mathrm{n}+1)}{2 !}\) x² – ………….
∴ (1 + 4x)^-4 = 1 – 4 (4x) + \(\frac{4(5)}{2}\) (4x)² – …………..
= 1 – 16x + 160x² – ……………
∴ The first 3 terms are 1, – 16x, 160x².

iii) (8 – 5x)^{\(\frac{2}{3}\)}

iv) \((2-7 x)^{\frac{-3}{4}}=2^{\frac{-3}{4}}\left[1-\frac{7 x}{2}\right]^{\frac{-3}{4}}\)
We know that

Question 4.
Find the general term ((r + i)th term) in the expansion of
i) (4 + 5x)^{\(\frac{-3}{2}\)}
ii) (1 – \(\frac{5 x}{3}\))^-3
iii) (1 + \(\frac{4 x}{5}\))^{\(\frac{5}{2}\)}
iv) (3 – \(\frac{5 x}{4}\))^{\(\frac{-1}{2}\)}
Solution:
i) We know that

ii) General term in the expansion (1 – x)^-n is

iii) General term in the expansion of (1 + X)^p/q is

iv) We know that

II.
Question 1.
Find the coefficient of x¹⁰ in the expansion of \(\frac{1+2 x}{(1-2 x)^2}\).
Solution:
We know that
\(\frac{1+2 x}{(1-2 x)^2}\) = (1 + 2x) (1 – 2x)^-2
= (1 + 2x) [1 + 2(2x) + 3 (2x)² + 4 (2x)³ + …………. + 10 (2x)⁹ + 11 (2x)¹⁰ + …………]
∴ The coefficient of x¹⁰ in \(\frac{1+2 x}{(1-2 x)^2}\) is
= 11 (2¹⁰) + 10 (2) (2⁹)
= 2¹⁰ (11 + 10)
= 21 × 2¹⁰.

Question 2.
Find the coefficient of x⁴ in the expansion of (1 – 4x)^-3/5.
Solution:
General term in the expansion of (1 – X)^{\(\frac{-p}{q}\)} is

Question 3.
i) Find the coefficient of x⁵
ii) Find the coefficient of x⁸ in (1 nt)2
iii) Find the coefficient of x in (2+3×9
Solution:
i) We know that
\(\frac{(1-3 x)^2}{(3-x)^{\frac{3}{2}}}=(1-3 x)^2\left[3-\left.x\right|^{\frac{-3}{2}}\right.\)

ii) We know that \(\frac{(1+x)^2}{\left(1-\frac{2}{3} x\right)^3}=(1+x)^2\left[1-\frac{2}{3} x\right]^{-3}\)

iii) We know that
\(\frac{(2+3 x)^3}{(1-3 x)^4}\) = (2 + 3x)³ [1 – 3x]^-4
= (8 + 36x + 54x² + 27x³) [1 + ⁴C (3x) + ⁵C₂ (3x)² + ⁶C₃ (3x)³ + ……….. + ^(r+3)C_r (3x)^r + …………..]
Clearly the coefficient of x^r in above expansion is
8 ^(r+3)C_r 3^r + 36 ^(r+2)C_r-1 3^r-1 + 54 ^(r+1)C_r-2 3^r-2 + 27 ^rC_r-3 3^r-2
for coefficient of x⁷, put r = 7
∴The coefficient of x⁷ in \(\frac{(2 x+3)^3}{(1-3 x)^4}\) is
8 ¹⁰C₇ 3⁷ + 36 ⁹C₆ 3⁶ + 54 ⁸C₅ 3⁵ + 27 ⁷C₄ 3⁴ = 8 ¹⁰C₃ 3⁷ + 36 ⁹C₃ 3⁶ + 54 ⁸C₃ 3⁵ + 27 ⁷C₃ 3⁴.

Question 4.
Find the coefficient of x³ in the expansion of \(\frac{\left(1+3 x^2\right)^{\frac{3}{2}}}{(3+4 x)^{\frac{1}{3}}}\).
Solution:
\(\frac{\left(1+3 x^2\right)^{\frac{3}{2}}}{(3+4 x)^{\frac{1}{3}}}\) = (1 + 3x)^3/2 (3 + 4x)^-1/3

III.
Question 1.
Find the sum of the infinite series:
i) 1 + \(\frac{1}{3}+\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}\) + ………….
ii) 1 – \(\frac{4}{5}+\frac{4 \cdot 7}{5 \cdot 10}-\frac{4 \cdot 7 \cdot 10}{5 \cdot 10 \cdot 15}\) + ………….
iii) \(\frac{3}{4}+\frac{3 \cdot 5}{4 \cdot 8}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12}\) + …………
iv) \(\frac{3}{4 \cdot 8}-\frac{3 \cdot 5}{4 \cdot 8 \cdot 12}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12 \cdot 16}\) – …………..
Solution:
i) Let y = 1 + \(\frac{1}{3}+\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}\) + ………….

ii) Let y = – \(\frac{4}{5}+\frac{4 \cdot 7}{5 \cdot 10}-\frac{4 \cdot 7 \cdot 10}{5 \cdot 10 \cdot 15}\) + ………….

iii) \(\frac{3}{4}+\frac{3 \cdot 5}{4 \cdot 8}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12}\) + …………

iv) Let y = \(\frac{3}{4 \cdot 8}-\frac{3 \cdot 5}{4 \cdot 8 \cdot 12}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12 \cdot 16}\) – …………..

Question 2.
If t = \(\frac{4}{5}+\frac{4 \cdot 6}{5 \cdot 10}+\frac{4 \cdot 6 \cdot 8}{5 \cdot 10 \cdot 15}\) + ……….. ∞, then prove that 9t = 16.
Solution:
Given
t = \(\frac{4}{5}+\frac{4 \cdot 6}{5 \cdot 10}+\frac{4 \cdot 6 \cdot 8}{5 \cdot 10 \cdot 15}\) + ……….. ∞

Question 3.
If x = \(\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}+\ldots\) then prove that 9x² + 24x = 11.
Solution:
Given x = \(\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}+\ldots\)

⇒ \(\frac{4}{3}\) + x = √3
⇒ 4 + 3x = 3√3
⇒ 16 + 9x² + 24x = 27
⇒ 9x² + 24x = 11.

Question 4.
If x = \(\frac{5}{(2 !) \cdot 3}+\frac{5 \cdot 7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots \ldots\) then find the value of x² + 4x.
Solution:
x = \(\frac{5}{(2 !) \cdot 3}+\frac{5 \cdot 7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots \ldots\)

∴ (1) ⇒ 2 + x = \(\left(1-\frac{2}{3}\right)^{-\frac{3}{2}}\)
⇒ 2 + x = \(\left(\frac{1}{3}\right)^{\frac{-3}{2}}\)
⇒ 2 + x = √27
⇒ x² + 4x = 23.

Question 5.
Find the sum to infinite terms of the series \(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1 \cdot 3}{1 \cdot 2} \cdot \frac{1}{10^4}+\frac{1 \cdot 3 \cdot 5}{1 \cdot 2 \cdot 3} \cdot \frac{1}{10^6}+\ldots\right)\)
Solution:
Let y = \(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1 \cdot 3}{1 \cdot 2} \cdot \frac{1}{10^4}+\frac{1 \cdot 3 \cdot 5}{1 \cdot 2 \cdot 3} \cdot \frac{1}{10^6}+\ldots\right)\)

Question 6.
Show that for any non-zero rational number x.
\(1+\frac{x}{2}+\frac{x(x-1)}{2 \cdot 4}+\frac{x(x-1)(x-2)}{2 \cdot 4 \cdot 6}+\ldots .\) = \(1+\frac{x}{3}+\frac{x(x+1)}{3 \cdot 6}+\frac{x(x+1)(x+2)}{3 \cdot 6 \cdot 9}+\ldots .\)
Solution:
L.H.S = \(1+\frac{x}{2}+\frac{x(x-1)}{2 \cdot 4}+\frac{x(x-1)(x-2)}{2 \cdot 4 \cdot 6}+\ldots .\)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Exercise 7(c)

I. Find the values of the following integrals.

Question 1.
\(\int_0^{\frac{\pi}{2}} \sin ^{10} x d x\) (May ’06; Mar. ’03)
Solution:

Question 2.
\(\int_0^{\frac{\pi}{2}} \cos ^{11} x d x\)
Solution:

Question 3.
\(\int_0^{\frac{\pi}{2}} \cos ^7 x \sin ^2 x d x\)
Solution:
\(\int_0^{\frac{\pi}{2}} \sin ^m x \cos ^n x d x\)

Question 4.
\(\int_0^{\frac{\pi}{2}} \sin ^4 x \cos ^4 x d x\)
Solution:

Question 5.
\(\int_0^\pi \sin ^3 x \cos ^6 x d x\)
Solution:
We have \(\int_0^{2 a} f(x) d x=2 \int_0^a f(x) d x\)
if f(2a – x) = f(x)

Question 6.
\(\int_0^{2 \pi} \sin ^2 x \cos ^4 x d x\)
Solution:
Take f(x) = sin²x cos⁴x
Then f(π – x) = sin²(π – x) cos⁴(π – x)
= sin²x cos⁴x
= f(x)

Question 7.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 \theta \cos ^7 \theta d \theta\)
Solution:
f(θ) = sin²θ cos⁷θ
f(-θ) = sin²(-θ) cos⁷(-θ)
= sin²θ cos⁷θ
= f(θ); and f is even

Question 8.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^3 \theta \cos ^3 \theta d \theta\)
Solution:
Let f(θ) = sin³θ cos³θ
∴ f(-θ) = sin³(-θ) cos³(-θ)
= -sin³θ cos³θ
= -f(θ)
∴ f is an odd function.
Hence \(\int_{-a}^a f(x) d x=0\) when f is odd.
∴ \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^3 \theta \cos ^3 \theta d \theta=0\)

Question 9.
\(\int_0^a x\left(a^2-x^2\right)^{\frac{7}{2}} d x\)
Solution:
Take x = a sin θ then dx = a cos θ dθ
Upper limit when x = a is θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is θ = 0

Let cos θ = t then -sin θ dθ = dt
Upper limit when θ = \(\frac{\pi}{2}\) is t = 0
Lower limit when θ = 0 is t = 1

Question 10.
\(\int_0^2 x^{\frac{3}{2}} \sqrt{2-x} d x\)
Solution:
Take x = 2 sin²θ, then dx = 4 sin θ cos θ dθ
Upper limit when x = 2 is sin²θ = 1 ⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is sin²θ = 0 ⇒ θ = 0

II. Evaluate the following integrals.

Question 1.
\(\int_0^1 x^5(1-x)^{\frac{5}{2}} d x\)
Solution:
Let x = sin²θ then dx = 2 sin θ cos θ dθ
Upper limit when x = 1 is θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is θ = 0

Question 2.
\(\int_0^4\left(16-x^2\right)^{\frac{5}{2}} d x\)
Solution:
Let x = 4 sin θ then dx = 4 cos θ dθ
Upper limit when x = 4 is θ = \(\frac{\pi}{2}\)
and Lower limit when x = 0 is θ = 0

Question 3.
\(\int_{-3}^3\left(9-x^2\right)^{\frac{3}{2}} x d x\)
Solution:
Let x = 3 sin θ then dx = 3 cos θ dθ
Upper limit when x = 3 is θ = \(\frac{\pi}{2}\)
and Lower limit when x = -3 is θ = \(-\frac{\pi}{2}\)

Question 4.
\(\int_0^5 x^3\left(25-x^2\right)^{\frac{7}{2}} d x\)
Solution:
Let x = 5 sin θ then
Upper limit when x = 5 is θ = \(\frac{\pi}{2}\)
and Lower limit when x = 0 is θ = 0

Question 5.
\(\int_{-\pi}^\pi \sin ^8 x \cos ^7 x d x\)
Solution:
Take f(x) = sin⁸x cos⁷x
then f(-x) = sin⁸(-x) cos⁷(-x)
= sin⁸x cos⁷x
= f(x)
f is an even function of x.
∴ \(\int_{-\pi}^\pi \sin ^8 x \cos ^7 x d x=2 \int_0^\pi \sin ^8 x \cos ^7 x d x\)
Now f(x) = sin⁸x cos⁷x
and f(π – x) = sin⁸(π – x) cos⁷(π – x)
= -sin⁸x cos⁷x
= -f(x)
Hence \(\int_0^\pi \sin ^8 x \cos ^7 x d x=0\)
∴ \(\int_{-\pi}^\pi \sin ^8 x \cos ^7 x d x=0\)
[By the result that f = [0, 2a] → R is integrable on [0, a] and if f(2a – x) = -f(x) ∀ x ∈ [a, 2a] then \(\int_0^{2 a} f(x) d x=0\)]

Question 6.
\(\int_3^7 \sqrt{\frac{7-x}{x-3}} d x\)
Solution:
Let x = 3 cos²θ + 7 sin²θ then
dx = -6 cos θ sin θ + 14 sin θ cos θ = 8 cos θ sin θ
Upper limit when x = 7 is
7 = 3 cos²θ + 7 sin²θ
⇒ 7(1 – sin²θ) = 3 cos²θ
⇒ cos θ = 0
⇒ θ = \(\frac{\pi}{2}\)
The lower limit when x = 3 is
3 = 3 cos²θ + 7 sin²θ
⇒ 3 sin²θ = 7 sin²θ
⇒ 4 sin²θ = 0
⇒ sin θ = 0
⇒ θ = 0

Question 7.
\(\int_2^6 \sqrt{(6-x)(x-2)} d x\)
Solution:
Put x = 2 cos²θ + 6 sin²θ
then dx = (-4 cos θ sin θ + 12 sin θ cos θ) dθ = 8 sin θ cos θ dθ
Upper limit when x = 6 is 6 = 2 cos²θ + 6 sin²θ
⇒ 6 cos²θ = 2 cos²θ
⇒ 4 cos²θ = 0
⇒ cos θ = 0
⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 2 is 2 = 2 cos²θ + 6 sin²θ
⇒ 2 sin²θ = 6 sin²θ
⇒ 4 sin²θ = 0
⇒ sin θ = 0
⇒ θ = 0

Question 8.
\(\int_0^{\frac{\pi}{2}} \tan ^5 x \cos ^8 x d x\)
Solution:

III. Evaluate the following integrals.

Question 1.
\(\int_0^1 x^{7 / 2}(1-x)^{5 / 2} d x\)
Solution:
Let x = sin²θ then dx = 2 sin θ cos θ dθ
Upper limit when x = 1 is sin²θ = 1 ⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is sin²θ = 0 ⇒ θ = 0

Question 2.
\(\int_0^\pi(1+\cos x)^3 d x\)
Solution:

Question 3.
\(\int_4^9 \frac{d x}{\sqrt{(9-x)(x-4)}}\)
Solution:
Take x = 4 cos²θ + 9 sin²θ then
dx = (-8 cos θ sin θ + 18 sin θ cos θ) dθ = 10 cos θ sin θ
Upper limit when x = 9 is 9 = 4 cos²θ + 9 sin²θ
⇒ 9(1 – sin²θ) = 4 cos²θ
⇒ 5 cos²θ = 0
⇒ cos θ = 0
⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 4 is 4 = 4 cos²θ + 9 sin²θ
⇒ 4(1 – cos²θ) = 9 sin²θ
⇒ 5 sin²θ = 0
⇒ sin θ = 0
⇒ θ = 0

Question 4.
\(\int_0^5 x^2(\sqrt{5-x})^7 d x\)
Solution:
Let x = 5 sin²θ then dx = 10 sin θ cos θ dθ
Upper limit when x = 5 is sin²θ = 1 ⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is sin²θ = 0 ⇒ θ = 0

Question 5.
\(\int_0^{2 \pi}(1+\cos x)^5(1-\cos x)^3 d \dot{x}\)
Solution:

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a)

I.
Question 1.
Expand the following using binomial theorem.
i) (4x + 5y)⁵
ii) \(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\)
iii) \(\left(\frac{2 p}{5}-\frac{3 q}{7}\right)^6\)
iv) (3x + x – x²)⁴
Solution:
i) we know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)
∴ (4x + 5y)⁷ = \({ }^7 \mathrm{C}_0\) (4x)⁷ + \({ }^7 \mathrm{C}_1\) (4x)⁶ (5y) + \({ }^7 \mathrm{C}_2\) (4x)⁵ (5y)² + \({ }^7 \mathrm{C}_3\) (4x)⁴ (5y)³ + \({ }^7 \mathrm{C}_4\) (4x)³ (5y)⁴ + \({ }^7 \mathrm{C}_5\) (4x)² (5y)⁵ + \({ }^7 \mathrm{C}_6\) (4x) (5y)⁶ + \({ }^7 \mathrm{C}_7\) (5y)⁷
= \(\sum_{r=0}^7{ }^7 C_r\) . (4x)^7-r . (5y)^r.

ii) We know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)

\(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\) = \({ }^5 C_0\left(\frac{2}{3} x\right)^5+{ }^5 C_1\left(\frac{2}{3} x\right)^4\left(\frac{7}{4} y\right)+{ }^5 C_2\left(\frac{2}{3} x\right)^3\left(\frac{7}{4} y\right)^2 +{ }^5 C_3\left(\frac{2}{3} x\right)^3\left(\frac{7}{4} y\right)^3\) + \({ }^5 C_4\left(\frac{2}{3} x\right)\left(\frac{7}{4} y\right)^4+{ }^5 C_5\left(\frac{7}{4} y\right)^5\)

= \(\sum_{r=0}^5{ }^5 C_r \cdot\left(\frac{2}{3} x\right)^{5-r} \cdot\left(\frac{7}{4} y\right)^r\)

iii) We know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)

iv) We know that
(3 + x – x²)⁴ = [3 + x (1 – x)]⁴
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)
∴ [3 + x (1 – x)]⁴ = \({ }^4 C_0\) 3⁴ + \({ }^4 C_1\)3³x (1 – x + \({ }^4 C_2\) 3²x² (1 – x)² + \({ }^4 C_3\) 3x³ (1 – x)³ + \({ }^4 C_4\) x⁴ (1 – x)⁴
= 81 + 108x (1 – x) + 54x² (1 – 2x + x²) + 12x³ (1 – 3x + 3x² – x³) + x⁴ (1 – 4x + 6x² – 4x³ + x⁵
= 81 + 108x – 54x² – 96x³ + 19x⁴ + 32x⁵ – 6x⁶ – 4x⁷ + x⁸.

Question 2.
Write down and simplify
i) 6th term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^y\)
ii) 7th term in (3x – 4y)¹⁰
iii) 10th term \(\left(\frac{3 p}{4}-5 q\right)^{14}\)
iv) rth term in \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) (1 ≤ r ≤ 9).
Solution:
i) r + 1th term n the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
∴ 6th term in the expansion of \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) is given by
T₆ = \({ }^9 C_5 \cdot\left(\frac{2 x}{3}\right)^4 \cdot\left(\frac{3 y}{2}\right)^5\)
= 189 . x⁴ . y⁵

ii) (r + 1)th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
7th term In the expansion of (3x – 4y)¹⁰ is given by
T₇ = \({ }^{10} \mathrm{C}_6\) (3x)⁴ (- 4y)⁶
= 280 . 12⁵ x⁴ y⁶.

iii) (r + 1)th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
10th term in the expansion of \(\left(\frac{3 p}{4}-5 q\right)^{14}\) is given by
T₁₀ = \({ }^{14} \mathrm{C}_9\left(\frac{3 p}{4}\right)^5\) (- 5q)⁹
= \(\frac{-(2002) \cdot 3^5 \cdot 5^9}{4^5}\) . p⁵ . q⁹.

iv) (r + )th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
∴ rth term in the expansion of \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) is given by
T_r = \({ }^8 C_{r-1}\left(\frac{3 a}{5}\right)^{9-r}\left(\frac{5 b}{7}\right)^{r-1}\).

Question 3.
Find the number of terms in the expansion of
i) \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\)
ii) (3p + 4q)¹⁴
iii) (2x + 3y + z)⁷
Solution:
1) The expansion of (x + a)ⁿ contains (n + 1) terms.
∴ Expansion of \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\) contains 10 terms.

ii) The expansion of (x + a)ⁿ contains (n + 1) terms.
∴ Expansion of (3p + 4q)¹⁴ contains 15 terms.

iii) Number of terms in the expansion of
(a + b + c)ⁿ = \(\frac{(n+1)(n+2)}{2}\)
∴ Expansion oF (2x + + z)⁷ contains \(\frac{(7+1)(7+2)}{2}\) = 36 terms.

Question 4.
Find the numerically greatest term(s) in the expansion of coefficients in (4x – 7y)⁴⁹ + (4x + 7y)⁴⁹.
Solution:
We know that
(4x – 7y)⁴⁹ = \({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ – \({ }^{49} \mathrm{C}_1\)(4x)⁴⁸ (7y) + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² – \({ }^{49} \mathrm{C}_3\) (4x)⁴⁶ (7y)³ + ……………. + \({ }^{49} \mathrm{C}_49\) (7y)⁴⁹ ………….(1)

(4x + 7y)⁴⁹ = \({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ + \({ }^{49} \mathrm{C}_1\)(4x)⁴⁸ (7y) + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² + \({ }^{49} \mathrm{C}_3\) (4x)⁴⁶ (7y)³ + ……………. + \({ }^{49} \mathrm{C}_49\) (7y)⁴⁹ ………….(2)

(1) + (2)
(4x – 7y)⁴⁹ + (4x + 7y)⁴⁹ = 2[\({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² + \({ }^{49} \mathrm{C}_4\) (4x)⁴⁵ (7y)⁴ + ………….. + \({ }^{49} \mathrm{C}_48\) (4x) (7y)⁴⁸]
which contains 25 non-zero coefficients.

Question 5.
Find the sum of last 20 coefficients in the expansion of (1 + x)³⁹.
Solution:
The last 20 coeffIcients in the expansion of (1 + x)³⁹ are \({ }^{39} \mathrm{C}_{20},{ }^{39} \mathrm{C}_{21}, \ldots \ldots \ldots,{ }^{39} \mathrm{C}_{39}\)
We know that

∴ The sum of last 20 coefficients in expansion of (1 + x)³⁹ is 2³⁸.

Question 6.
If A and B are coefficients of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^{2n – 1} respectively, then find the value of \(\frac{A}{B}\).
Solution:
Coefficient of xⁿ in the expansion of (1 + x)²ⁿ is \({ }^{2 n} C_n\).
Coefficient of xⁿ in the expansion of (1 + x)^{2n – 1} is \({ }^{2 n – 1} C_n\)
∴ A = \({ }^{2 n} C_n\) and B = \({ }^{2 n – 1} C_n\).
∴ \(\frac{A}{B}=\frac{{ }^{2 n} C_n}{2 n-1}=\frac{\frac{2 n !}{n ! n !}}{\frac{(2 n-1) !}{(n-1) ! \cdot n !}}\)
\(\frac{2 n !}{(2 n-1) ! n !} \cdot(n-1) !=\frac{2 n}{n}\)
\(\frac{A}{B}\) = 2.

II.
Question 1.
Find the coefficient of
i) x^-6 in \(\left(3 x-\frac{4}{x}\right)^{10}\)
ii) x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\)
iii) x² in \(\left(7 x^3-\frac{2}{x^2}\right)^9\)
iv) x^-7 in \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\)
Solution:
i) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
(r + 1)th term in the expansion of \(\left(3 x-\frac{4}{x}\right)^{10}\) is
T_r+1 = \({ }^{10} \mathrm{C}_{\mathrm{r}}\) . (3x)^10-r . (\(\frac{-4}{x}\))^r
T_r+1 = \({ }^{10} \mathrm{C}_{\mathrm{r}}\) . (3)^10-r . (- 4)^r . x^10-2r.
for coefficient of x^-6, 10 – 2r = – 6
⇒ 2r = 16
⇒ r = 8.
∴ Coefficient of x^-6 is \({ }^{10} \mathrm{C}_8\) . 3^10-8 . (- 4)⁸ = 405 × 4⁸.

ii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
(r + 1)th term in the expansion of \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) is
T_r+1 = \({ }^{13} C_r \cdot\left(2 x^2\right)^{13-r} \cdot\left(\frac{3}{x^3}\right)^r\)
T_r+1 = \({ }^{13} C_r \) . 2^13-r . 3^r . x^26-5r
For coefficients of x¹¹, 26 – 5r = 11
⇒ 5r = 15
⇒ r = 3.
Coefficient of x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) is \({ }^{13} C_3 \) . 2^13-3 . 3³
= 286 . 2¹⁰ . 3³.

iii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
∴ General term in the expansion of \(\left(7 x^3-\frac{2}{x^2}\right)^9\) is
T_r+1 = \({ }^9 C_r \cdot\left(7 x^3\right)^{9-r}\left(\frac{-2}{x^2}\right)^r\)
= \({ }^9 C_r\) 7^9-r (- 2)^r . x^27-5r
for coefficient of x², 27 – 5r = 2
⇒ 5r = 25
⇒ r = 5.
∴ Coefficient of x² is \({ }^9 \mathrm{C}_5\) . 7⁴ . (- 2)⁵
= – 126 . 7⁴ . 2⁵.

iv) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)\) is
T_r+1 = \(={ }^7 C_r \cdot\left(\frac{2}{3} x^2\right)^{7-r} \cdot\left(\frac{-5}{4 x^5}\right)^r\)
= \({ }^7 \mathrm{C}_{\mathrm{r}} \cdot\left(\frac{2}{3}\right)^{7-\mathrm{r}}\left(\frac{-5}{4}\right)^{\mathrm{r}} \mathrm{x}^{14-7 \mathrm{r}}\)
For coefficient of x^-7, 14 – 7r = – 7
⇒ 7r = 21
⇒ r = 3
∴ Coefficient of x^-7 is \({ }^7 C_3 \cdot\left(\frac{2}{3}\right)^4 \cdot \frac{(-5)^3}{4^3}\)
= \(-\frac{35 \times 16 \times 125}{81 \times 64}=\frac{-4375}{324}\).

Question 2.
Find the term independent of x in the expansion of
i) \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\)
ii) \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
iii) \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\)
iv) \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\)
Solution:
i) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\) is
T_r+1 = \({ }^{10} C_r \cdot\left(\frac{\sqrt{x}}{3}\right)^{10-r} \cdot\left(\frac{-4}{x^2}\right)^r\)
= \({ }^{10} C_r \cdot \frac{x^{\frac{10-r}{2}}}{3^{10-r}} \cdot \frac{(-4)^r}{x^{2 r}}\)
= \({ }^{10} C_r \cdot \frac{(-4)^r}{3^{10-r}} \cdot x^{\frac{10-5 r}{2}}\)
For the independent term (i.e., the coefficient of x⁰)
put \(\frac{10-5 r}{2}\) = 0
⇒ r = 2.
∴ Term independent of ‘x’ in the expansion is
T3 = \({ }^{10} C_2 \frac{(-4)^2}{3^8} \times x^0=\frac{80}{729}\).

ii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\) is
T_r+1 = \({ }^{25} C_r\left(\frac{3}{\sqrt[3]{x}}\right)^{25-r} \cdot(5 \sqrt{x})^r\)
= \({ }^{25} C_r\) . 3^25-r . 5^r . x^{(5r – 50)/6}
For the independent term,
(i.e., coefficient of x⁰)
Put \(\frac{5 r-50}{6}\) = 0
⇒ r = 10.
∴ Term independent of ‘x’ in the expansion is T₁₁ = \({ }^{25} \mathrm{C}_{10}\) . 3¹⁵ . 5¹⁰.

iii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\) is
T_r+1 = \({ }^{14} C_r \cdot\left(4 x^3\right)^{14-r} \cdot\left(\frac{7}{x^2}\right)^r\)
= \({ }^{14} C_r\) . 4^14-r . 7^r . x^42-5r.
For the independent term, (i.e., coefficient of x⁰)
Put 42 – 5r = 0
which is impossible as ‘r’ is integer.
∴ Term independent of ‘x in the expansion is ‘0’.

iv) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\) is
T_r+1 = \({ }^9 C_r\left(\frac{2 x^2}{5}\right)^{9-r} \cdot\left(\frac{15}{4 x}\right)^r\)
= \({ }^9 \mathrm{C}_{\mathrm{r}}\left(\frac{2}{5}\right)^{9-\mathrm{r}} \cdot\left(\frac{15}{4}\right)^{\mathrm{r}} \cdot \mathrm{x}^{18-3 \mathrm{r}}\)
For the independent term, (i.e. coefficient of x⁰)
Put 18 – 3r = 0
⇒ r = 6
Term independent of ‘x’ in the expansion is
T₇ = \({ }^9 \mathrm{C}_6 \cdot\left(\frac{2}{5}\right)^3 \cdot\left(\frac{15}{4}\right)^6\)
= \(\frac{3^7 \cdot 5^3 \cdot 7}{2^7}\).

Question 3.
Find the middle term(s) in the expansion of
i) \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
ii) \(\left(4 a+\frac{3}{2} b\right)^{11}\)
iii) (4x² + 5x³)¹⁷
iv) \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\)
Solution:
i) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3 x}{7}-2 y\right)^{10}\) is
T_r+1 = \({ }^{10} C_{\mathrm{r}} \cdot\left(\frac{3 \mathrm{x}}{7}\right)^{10-\mathrm{r}}(-2 \mathrm{y})^{\mathrm{r}}\)
The expansion has 11 (odd number) terms.
Hence T₆ is the only middle term.
Thus r = 5
∴ Middle term in the expansion is
T₆ = \(-10 C_5\left(\frac{6}{7}\right)^5\) . x⁵ . y⁵.

ii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion \(\left(4 a+\frac{3}{2} b\right)^{11}\) is
T_r+1 = \(\)
The expansion has 12 (even numbers) terms.
Hence T₆ and T₇ are the middle terms.
Thus r = 5 and r = 6
when r = 5,
T₆ = \({ }^{11} C_5 \cdot(4 a)^6 \cdot\left(\frac{3}{2} b\right)^5\)
= 77 × 2⁸ . 3⁶ . a⁶ . b⁵.
when r = 6,
T₇ = \({ }^{11} C_6(4 a)^5 \cdot\left(\frac{3}{2} b\right)^6\)
= 77 × 2⁵ . 3⁷ . a⁵ . b⁶.

iii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of (4x² + 5x³)¹⁷ is
T_r+1 = \({ }^{17} \mathrm{C}_r\) . (4x²)^17-r . (5x³)^r.
The expansion has 18 (even number) terms.
Hence T₉ and T₁₀ are the middle terms.
Thus r = 8 and r = 9
When r = 8.
T₉ = \({ }^{17} \mathrm{C}_8\) . (4x²)⁹ . (5x³)⁸
= \({ }^{17} \mathrm{C}_8\) . 4⁹ . 5⁸ . x⁴²
When r = 9,
T10 = \({ }^{17} \mathrm{C}_9\) (4x²)⁸ (3)⁹
= \({ }^{17} \mathrm{C}_9\) . 4⁸ . 5⁹ . x⁴³

iv) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\) is
T_r+1 = \({ }^{20} C_r \cdot\left(\frac{3}{a^3}\right)^{20-r} \cdot\left(5 a^4\right)^r\)
The expansion has 21 (odd number) terms. Hence, T₁₁ is the only middle term
Thus r = 10
∴ Middle term in the expansion is
T₁₁ = \({ }^{20} C_{10} \cdot\left(\frac{3}{a^3}\right)^{10} \cdot\left(5 a^4\right)^{10}\)
= \({ }^{20} C_{10}\) . 15¹⁰ . a¹⁰.

Question 4.
Find the numerically greatest term(s) in the expansion of
i) (4 + 3x)¹⁵ when x = \(\frac{7}{2}\).
ii) (3x + 5y)¹² when x = \(\frac{1}{2}\), y = \(\frac{4}{3}\)
iii) (4a – 6b)¹³ when a = 3, b = 5.
iv) (3 + 7x)ⁿ when x = \(\frac{4}{5}\), n = 5.
Solution:
i) We know that (4 + 3x)¹⁵ = 4¹⁵ \(\left(1+\frac{3 x}{4}\right)^{15}\)
First we find the numerically greatest term in the expansion of \(\left(1+\frac{3 x}{4}\right)^{15}\)
Let X = \(\frac{3 x}{4}\)
x = \(\frac{7}{2}\), |X| = \(\left|\frac{3}{4} \times \frac{7}{2}\right|=\frac{21}{8}\)
Now \(\frac{(n+1)|X|}{1+|X|}=\frac{16 \times \frac{21}{8}}{1+\frac{21}{8}}=\frac{336}{29}\)
not an integer.
Its integral part m = \(\left[\frac{336}{29}\right]\) = 11.
∴ T_m+1, i.e., T₁₂ is the numerically greatest term in the binomial expansion of \(\left(1+\frac{3 x}{4}\right)^{15}\)
∴ T₁₂ = \({ }^{15} C_{11}\left(\frac{3 x}{4}\right)^{11}\)
= \({ }^{15} \mathrm{C}_{11}\left(\frac{21}{8}\right)^{11}\)
∴ Numerically greatest term in the expansion 01(4 + 3x)¹⁵ = \({ }^{15} C_{11}\left(4^{15}\right) \frac{21^{11}}{8^{11}}\)
= \({ }^{15} C_{11} \cdot \frac{21^{11}}{2^3}\).

ii) We know that
(3x + 5y)¹² = (3x)¹² . (1 + \(\frac{5 y}{3 x}\))¹²
First we find the numerically greatest term in the expansion of (1 + \(\frac{5 y}{3 x}\))¹²

iii) We know that
(4a – 6b)¹³ = (4a)¹³ (1 – \(\frac{6 b}{4 a}\))¹³
First we find the numerically greatest term in the expansion of (1 – \(\frac{6 b}{4 a}\))¹³
Let X = – \(\frac{6 b}{4 a}\)
As a = 3 and b = 5, |X| = \(\frac{5}{2}\)

∴ The numerically greatest terms in the expansion of (4a – 6b)¹³ are T₁₀ and T₁₁.
T₁₀ = – 12¹³ . ¹³C₉ . \(\left(\frac{5}{2}\right)^9\)
= – ¹³C₉ . (12)⁴ . (30)⁹
and T₁₁ = 12¹⁰ . ¹³C₁₀ . \(\left(\frac{5}{2}\right)^10\)
= 143 . 2¹⁷ . 3¹³ . 5¹⁰.

iv) We know that (3 + 7x)ⁿ = 3ⁿ (1 + \(\frac{7}{3}\) x)ⁿ
First we find numerically greatest term in the expansion of (1 + \(\frac{7}{3}\) x)ⁿ
Let X = \(\frac{7}{3}\) x
As x = \(\frac{4}{5}\), |X| = \(\frac{28}{15}\) and
\(\frac{(n+1)|X|}{1+|X|}=\frac{56}{5}\) and n = 15.

Its integral part,
m = \(\left[\frac{(\mathrm{n}+1)|\mathrm{X}|}{1+|\mathrm{X}|}\right]\) = 11
∴ T_m+1 i.e., T₁₂ is numerically greatest term in the expansion of (1 + \(\frac{7}{3}\) x)ⁿ
T₁₂ = ¹⁵C₁₁ . \(\left(\frac{28}{15}\right)^{11}\)
∴ The numerically greatest terms in the expansion of (3 + 7x)ⁿ is
T₁₂ = 3¹⁵ . ¹⁵C₁₁ . \(\left(\frac{28}{15}\right)^{11}\)
= ¹⁵C₁₁ . \(\left(\frac{28}{5}\right)^{11}\) . 3⁴.

Question 5.
Prove the following:
i) 2 . C₀ + 5 . C₁ + 8. C₂ + ……………. + (3n + 2) C_n = (3n + 4) 2^n-1
ii) C₀ – 4 C₁ + 7 . C₂ – 10 . C₃ + ……………. = 0,
if n is an even positive Integer.
iii) \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\)
iv) \(C_0+\frac{3}{2} \cdot C_1+\frac{9}{3} \cdot C_2+\frac{27}{4} \cdot C_3+\ldots \ldots+\frac{3^n}{n+1} C_n=\frac{4^{n+1}-1}{3(n+1)}\)
v) C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ………….. + 2ⁿ . C_n = 3ⁿ
Solution:
i) We know that
C₀ = C_n, C₁ = C_n-1, ………… C_r = C_n-r
Let S = 2 . C₀ + 5 . C₁ + 8 . C₂ + ………….. + (3n – 1) . C_n-1 + (3n + 2) C_n ………….(1)
∴ S = (3n + 2) C₀ + (3n – 1)C₁ + (3n – 4)C₂ + …………. + 5 . C_n-1 + 2 . C_n ………….(2)
(1) + (2) ⇒ 2S = (3n + 4) . C₀ + (3n + 4) . C₁ + (3n + 4) . C₂ + …………… (3n + 4) . C_n
= (3n + 4) (C₀ + C₁ + C₂ + …………… + C_n)
⇒ 2S = (3n + 4) . 2ⁿ
⇒ S = (3n + 4) . 2^n-1
∴ 2 . C₀ + 5 . C₁ + 8 . C₂ + ………… + (3n + 2) . C_n = (3n + 4) . 2^n-1

ii) We know that 1, 4, 7, 10, ………… are in A.P.
(n + 1)th term,
T_n+1 = 1 + (n)3 = 3n + 1
∴ C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……….. (n + 1) terms.
= \(\sum_{r=0}^n(-1)^r(3 r+1) C_r\)
= \(3 \sum_{r=0}^n(-1)^r r \cdot C_r+\sum_{r=0}^n(-1)^r \cdot C_r\)
= 3 (0) + 0 = 0
∴ C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……….. = 0.

iii) Given L.H.S

iv) Given L.H.S

v) L.HS = C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ……….. + 2ⁿ . C_n
= C₀ + C₁ . 2 + C₂ . 2² + C₃ . 2³ + ………. + C_n 2ⁿ
= (1 + 2)ⁿ
= 3ⁿ = R.H.S
∴C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ……….. + 2ⁿ . C_n = 3ⁿ.

Question 6.
Find the sum of the following:
i) \(\frac{{ }^{15} C_1}{{ }^{15} C_0}+2 \frac{{ }^{15} C_2}{{ }^{15} C_1}+3 \frac{{ }^{15} C_3}{{ }^{15} C_2}+\ldots+15 \frac{{ }^{15} C_{15}}{{ }^{15} C_{14}}\)
ii) C_n . C₃ + C₁ .C₄ + C₂ . C₅ + + …………… + C_n-3 . C_n
iii) 2² C₀ + 3² C₁ + 4² C₂ + …………. + (n + 2)² C_n
iv) 3C₀ + 6C₁ + 12C₂ + ……………. + 3 . 2ⁿ C_n
Solution:
i) We know that

ii) (1 + x)ⁿ = C₀ + C₁x + C₂x² + …………. + C_nxⁿ …………..(1)
(x + 1)ⁿ = C₀xⁿ + C₁x^{n – 1} + C₂₃x^n-2 + …………… + C_n …………….. (2)
(1) x (2) = (1 + x)²ⁿ
= (C₀ + C₁x + C₂x² + ……….. + C_nxⁿ) (C₀x + C₁x^n-1 + C₂x^n-2 + C₃x^n-3 + ………….. + C_n]
Comparing coefficients of x^n-3 on bothsides,
²ⁿC_n-3 = C₀ . C₃ + C₁ . C₄ + C₂ . C₅ + …………. + C_n-3 . C_n
i.e., C₀. C₃ + C₁ . C₄ + C₂. C₅ + …………… + C_n-3 . C_n = ²ⁿC_n-3 = ²ⁿC_n+3
[∵ ⁿC_r = ⁿC_n-r].

iii) 2² C₀ + 3² C₁ + 4² C₂ + …………. + (n + 2)² C_n

= n (n – 1) 2^n-2 + 5 n 2^n-1 + 4 (2ⁿ)
= 2^n-2 [n (n – 1) + 10n + 16]
= (n² + 9n . 16) 2^n-2.

iv) 3 . C₀ + 6 . C₁ + 12 . C₂ + ……………. + 3 . 2ⁿ C_n
= \(\sum_{r=0}^n 3 \cdot 2^r \cdot C_r\)
= \(3 \sum_{r=0}^n 2^r \cdot C_r\)
= 3 [1 + C₁ (2) + C₂ (2²) + C₃ (2³) + …………. + C_n 2ⁿ]
= 3 [1 + 2]ⁿ
= 3 . 3ⁿ
= 3ⁿ⁺¹.

Question 7.
Using binomial theorem prove that 50ⁿ – 49n – 1 is divisible by 49² for all positive integers n.
Solution:
We know that,
50ⁿ – 49n – 1
= (1 + 49)ⁿ – 49n – 1
= [1 + ⁿC₁ . 49 + ⁿC₂ . 49² + ⁿC₃ . 49³ + ………… + 49ⁿ] – 49n – 1
= ⁿC₂ . 49² + ⁿC₃ . 49³ + …………… + ⁿC_n . 49ⁿ
= 49² [ⁿC₂ + ⁿC₃ . 49 + ……….. + ⁿC_n . 49^n-2]
= 49² (a positive integer)
Hence 50ⁿ 49n – 1 is divisible by 49² ∀n ∈ N.

Question 8.
Using binomial theorem prove that 5⁴ⁿ + 52n – 1 is divisible by 676 for all positive integers n.
Solution:
We know that, 5⁴ⁿ + 52n – 1
= (5²)²ⁿ + 52n – 1
= (25)²ⁿ+ 52n – 1
= (26 – 1)²ⁿ+ 52n – 1
= ²ⁿC₀ (26)²ⁿ – ²ⁿC₁ (26)^2n-1 + ²ⁿC₂ (26)^2n-2 + …………. + ²ⁿC_2n-2(26)² – ²ⁿC_2n-1 (26) + ²ⁿC_2n + 52n – 1
= 26²ⁿ + ²ⁿC₁ (26)^2n-1 + ²ⁿC₂ (26)^2n-2 + …………….. + ²ⁿC_2n-2 (26)²
= 26² [26^2n-2 – ²ⁿC₁ 26^2n-3 + ²ⁿC₂ 26^2n-4 + ……… + ²ⁿC_2n-2]
= 676 (some integer)
∴ 5⁴ⁿ + 52n – 1 is divisible by 676, ∀n ∈ N.

Question 9.
If (1 + x + x²)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_2nx²ⁿ, then prove that
i) a₀ + a₁ + a₂ + ……….. + a_2n = 3ⁿ
ii) a₀ + a₂ + a₄ + ………… + a_2n = \(\frac{3^n+1}{2}\)
iii) a₁ + a₃ + a₅ + ……………. + a_2n-1 = \(\frac{3^n-1}{2}\)
iv) a₀ + a₃ + a₆ + a₉ + ………… = 3^n-1
Solution:
Given (1 + x + x²)^{n/sup> = a₀ + a₁x + a₂x2 + ………….. + a_2nx2n
i) Subtituting x = 1 in (I), we have
a₀ + a₁ + a₂ + ……….. + a_2n = 3n …………. (1)
Substituting x = – 1 in (I), we have
a₀ – a₁ + a₂ + ……….. + a_2n = 1 …………….(2)}

ii) (1) + (2)
⇒ 2a₀ + 2a₂ + 2a₄ + ……….. + 2a_2n = 3ⁿ + 1
⇒ a₀ + a₂ + a₄ + ……….. + a_2n = \(\frac{3^n+1}{2}\)

iii) (1) – (2)
⇒ 2a₁ + 2a₃ + 2a₅ + ……….. + 2a_2n-1 = 3ⁿ – 1
⇒ a₁ + a₃ + a₅ + ……….. + a_2n-1 = \(\frac{3^n-1}{2}\)

iv) Substituting x = ω, in (1), we have
a₀ + a₁ω + a₂ω² + ……….. + a_2nω²ⁿ = 0
(∵ 1 + ω + ω² = 0)

Substituting x = ω² in (1), we have
a₀ + a₁ω² + a₂ω⁴ + a₃ω⁶ + ……….. + a_2nω⁴ⁿ = 0 …………… (4)
(1) + (3) +(4):
3a₀ + a₁ (1 + ω + ω²) + a₂ (1 + ω + ω²) + a₃ (1 + ω³ + ω⁶) + ………… + a_2n (1 + ω²ⁿ + ω⁴ⁿ) = 3ⁿ
⇒ 3a₀ + 3a₃ + 3a₆ + 3a₉ + …………. = 3ⁿ
(∵ 1 + ω + ω² = 0 and ω³ = 1)
⇒ a₀ + a₃ + a₆ + a₉ + ……….. = 3^n-1

Question 10.
If (1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……………+ b₂₁ x²¹, then find the value of
i) b₀ + b₂ + b₄ + ……………. + b₂₀
ii) b₁ + b₃ + b₅ + ……………. + b₂₁
Solution:
Given
(1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……………+ b₂₁ x²¹ ……………(1)
Substituting x = 1 in (1),
we get b₀ + b₁ + b₂ + ……………. + b₂₁ = 4⁷ ……….(2)
Substituting x = – 1 in (1),
we get b₀ – b₁ + b₂ + ……………. – b₂₁ = 0 …………… (3)
i) (2) + (3)
⇒ 2b₀ + 2b₂ + 2b₄ + ……………. + b₂₀ = 4⁷
⇒ b₀ + b₂ + b₄ + ……………. + b₂₀ = 2¹³.

ii) (2) – (3)
⇒ 2b₁ + 2b₃ + 2b₅ + ……………. + 2b₂₁ = 4⁷
⇒ b₁ + b₃ + b₅ + ……………. + b₂₁ = 2¹³.

Question 11.
If the coefficients of x¹¹ and x¹² in the binomial expansion of \(\left(2+\frac{8 x}{3}\right)^n\) are equal, find n.
Solution:
We know that \(\left(2+\frac{8 x}{3}\right)^n=2^n\left(1+\frac{4 x}{3}\right)^n\)
Coefficient of x¹¹ in the expansion of \(\left(2+\frac{8 x}{3}\right)^n\) is ⁿC₁₁ . 2ⁿ . (\(\frac{4}{3}\))¹¹
Coefficient of x¹² in the expansion of \(\left(2+\frac{8 x}{3}\right)^n\) is ⁿC₁₂ . 2ⁿ . (\(\frac{4}{3}\))¹²
Given coefficients of x¹¹ and x¹² are same
⇒ ⁿC₁₁ . 2ⁿ . (\(\frac{4}{3}\))¹¹ = ⁿC₁₂ . 2ⁿ . (\(\frac{4}{3}\))¹²
⇒ \(\frac{n !}{(n-11) ! 11 !}=\frac{n !}{(n-12) ! 12 !}\left(\frac{4}{3}\right)\)
⇒ 12 = (n – 11) \(\frac{4}{3}\)
⇒ 9 = n – 11
⇒ n = 11 + 9 = 20.

Question 12.
Find the remainder when 2²⁰¹³ is divided by 17.
Solution:
We have 2²⁰¹³
= 2 (2²⁰¹²)
= 2 (2⁴)²⁰³
= 2 (16)⁵⁰³
= 2 (17 – 1)²⁰³
= 2 [⁵⁰³C₀ 17⁵⁰³ – ⁵⁰³C₁ 17⁵⁰² + ⁵⁰³C₂ 17⁵⁰¹ – ……….. + ⁵⁰³C₅₀₂ 17 – ⁵⁰³C₅₀₃]
= 2 [⁵⁰³C₀ 17⁵⁰³ – ⁵⁰³C₁ 17⁵⁰² + ⁵⁰³C₂ 17⁵⁰¹ – ……….. + ⁵⁰³C₅₀₂ 17 – ⁵⁰³C₅₀₃] – 2
= 17m – 2 where ‘m is some integer
∴ 2²⁰¹³ = 17m – 2 (or) 17k + 15
∴ The remainder is – 2 or 15.

Question 13.
If the coefficient of (2r + 4)th term and (3r + 4)th term in the expansion of (1 + x)²¹ are equal, find r.
Solution:
We know that coefficient of (r + 1)th term of (1 + x)ⁿ is ⁿC_r.
∴ Coefficient of (2r + 4)th term 0f (1 + x)²¹ is ²¹C_2r+3
Also coefficient of (3r + 4)th term of (1 +x)²¹ is ²¹C_3r+3.
Given coefficient of (2r + 4)th term and (3r + 4)th terms in the expansion of (1 + x)²¹ are equal.
∴ ²¹C_2r+3 = ²¹C_3r+4
∴ Either 2r + 3 = 3r + 3 0r 2r + 3 + 3 = 21
If 2r + 3 = 3r + 3 then r = 0,
If 2r + 3 + 3r = 21 then r = 3.
∴ r = 0 or r = 3.

III.
Question 1.
If the coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in AP. then prove that n² – 4m + 398 = 0.
Solution:
Coefficient of x^r in the expansion of (1 + x)ⁿ is ⁿC_r.
Given coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in A.P., then
2(ⁿC₁₀) = ⁿC₉ + ⁿC₁₁
⇒ \(2 \frac{n !}{(n-10) ! 10 !}=\frac{n !}{(n-9) ! 9 !}+\frac{n !}{(n-11) !+11 !}\)
⇒ \(\frac{2}{10(n-10)}=\frac{1}{(n-9)(n-10)}+\frac{1}{11 \times 10}\)
⇒ \(\frac{2}{(n-10) 10}=\frac{110+(n-9)(n-10)}{110(n-9)(n-10)}\)
⇒ 22 (n – 9) = 110 + n² – 19n + 90
⇒ n² – 41n + 398 = 0.

Question 2.
If 36, 84, 126 are three successive binomial coefficients in the expansion of (1 + then find n.
Solution:
Let us consider ⁿC_r-1, ⁿC_r and ⁿC_r+1 as three successive binomial coefficients of (1 + xy)ⁿ.
i.e., ⁿC_r-1 = 36; ⁿC_r-1 = 84 and ⁿC_r-1 = 126
Consider \(\frac{{ }^{n_C} C_r}{{ }^n C_{r-1}}=\frac{84}{36}\)
⇒ \(\frac{n-r+1}{r}=\frac{7}{3}\)
⇒ 3n + 3 = 10r …………..(1)
Similarly,
\(\frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{126}{84}\)
⇒ \(\frac{\mathrm{n}-\mathrm{r}}{\mathrm{r}+1}=\frac{3}{2}\)
⇒ 2n = 5r + 3 ………….(2)
⇒ 2n = 5 \(\left(\frac{3 \mathrm{n}+3}{10}\right)\) + 3 (∵ from (1))
⇒ n = 9.

Question 3.
If the 2nd, 3rd and 4th terms in the expansion of (a + x)ⁿ are respectively 240, 720, 1080. find a, x, n.
Solution:
General term in the expansion of (a + x)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
∴ 2nd term,T₂ = ⁿC₁ . a^n-1 . x …………..(1)
3rd term, T₃ = ⁿC₂ . a^n-2 . x² ………..(2)
4th term, T₄ = ⁿC₃ . a^n-3 . x³ …………(3)
Given T₂ = 240, T₃ = 720, T₃ = 1080
From (1) and (2),

Sub. n = 5 in (1), we get
5 . a⁴ . x = 240 ………..(6)
Substituting n = 5 in (4), we get x = \(\frac{3 a}{2}\) ………….(7)
Substituting x = \(\frac{3 a}{2}\) in (6),
we get 5 . a⁴ = 240
⇒ a⁵ = 32
⇒ a = 2
Substituting in (7), we get x = 3
∴ a = 2; x = 3 and n = 5.

Question 4.
If the coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are in A.P., then show that n² – (4r + 1)n + 4r² – 2 = 0.
Solution:
We know that, the general term, (r + 1)th term in the expansion of (1 + x)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r
∴ The coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are ⁿC_r-1, ⁿC_r and ⁿC_r+1
Given ⁿC_r-1, ⁿC_r & ⁿC_r+1 are in A.P.

⇒ 2(n – r + 1) (r + 1) = r (r + 1) + (n – r) (n – r + 1)
⇒ 2nr + 2n – 2r² – 2r + 2r + 2 = r² + r + n² – nr + n – nr + r² + r
⇒ n² – n (4r + 1) + 4r² – 2 = 0.

Question 5.
Find the sum of the coefficients of x³² and x^-18 in the expansion of (2x³ – \(\frac{3}{x^2}\))¹⁴.
Solution:
The general term in (2x³ – \(\frac{3}{x^2}\))¹⁴ is
T_r+1 = ¹⁴C_r (2x³)^14-r (\(\frac{-3}{x^2}\))^r
T_r+1 = (- 1)^r . ¹⁴C_r . 2^14-r . 3^r . x^42-5r ………….(1)
For coefficient of x³², put
42 – 5r = 32
⇒ r = 2
Substituting r = 2 in (1), we get
T₃ = ¹⁴C₂ . 2¹² . 3² . x³²
∴ Coefficient of x³² is ¹⁴C₂ . 2¹² . 3² ………(2)
For coefficient of x^-18, put
42 – 5r = 18
⇒ r=12
Substituting r = 12 in (1), we get
T₁₃ = ¹⁴C₂ . 2² . 3¹² . x^-18
∴ Coefficient of x^-18 is ¹⁴C₁₂ . 2² . 3¹² ………….(3)
Hence sum of the coefficients of x³² and x^-18 is
¹⁴C₂ . 2¹² . 3² + ¹⁴C₁₂ . 2² . 3¹²
= ¹⁴C₂ . 2² . 3² (2¹⁰ + 3¹⁰)
= 91 × 36(2¹⁰ + 3¹⁰).

Question 6.
If P and Q are the sum of odd terms and the sum of even terms respectively in the expansion of (x + a)ⁿ then prove that
i) P² – Q² = (x² – a²)ⁿ
ii) 4PQ (x + a)²ⁿ – (x – a)²ⁿ
Solution:
We know that,
(x + a)ⁿ = ⁿC₀ xⁿ + ⁿC₁ x^n-1 . a + ⁿC₂ x^n-2 . a² + ………….. + ⁿC_n-1 x a^n-1 + ⁿC_n aⁿ
= (ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………) + (ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..)
∴ (x + a)ⁿ = P + Q
∴ Sum of odd terms,
P = ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………
Sum of even terms,
Q = ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..
∴ (x + a)ⁿ = P + Q
We know that
(x – a)ⁿ = ⁿC₀ xⁿ a – ⁿC₁ x^n-1 a + ⁿC₂ x^n-2 a¹² – ⁿC₃ x^n-3 a³ + ……………. + ⁿC_n (- 1)ⁿ aⁿ
= (ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………) – (ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..)
⇒ (x – a)ⁿ = P – Q

i) P² – Q² = (P + Q) (P – Q)
= (x + a)ⁿ (x – a)ⁿ
⇒ P² – Q² = (x² – a²)ⁿ

ii) 4PQ = (P + Q)² – (P – Q)²
= [(x + a)ⁿ]² – [(x – a)ⁿ]²
⇒ 4PQ = (x + a)²ⁿ – (x – a)²ⁿ

Question 7.
If the coefficients of 4 consecutive terms in the expansion of (1 + x)ⁿ are a₁, a₂, a₃, a₄ respectively, then show that \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\)
Solution:
Given a₁, a₂, a₃, a₄ are the coefficients of 4 consecutive terms in (1 + x)ⁿ respectively.
Let a₁ = ⁿC_r-1
a₂ = ⁿC_r
a₃ = ⁿC_r+1
a₄ = ⁿC_r+2

Question 8.
Prove that (²ⁿC₀)² – (²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ……….. + (²ⁿC_2n)² = (- 1)^{n 2n}C_n.
Solution:
We know that
(x + 1)²ⁿ = ²ⁿC₀ x²ⁿ + ²ⁿC₁ x^2n-1 + ²ⁿC₂ x^2n-2 + …………… + ²ⁿC_2n ……………(1)
(1 – x)²ⁿ = ²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² – …………… + ²ⁿC_2n x²ⁿ ……………(2)
From (1) and (2),
(1 – x)²ⁿ (1 + x)²ⁿ = (²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² + ……………… + ²ⁿC_2n x²ⁿ)
⇒ (1 – x²)²ⁿ = [²ⁿC₀ x²ⁿ + ²ⁿC₁ x^2n-1 + ²ⁿC₂ x^2n-2 + …………… + ²ⁿC_2n] . [²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² + …………… + ²ⁿC_2n x²ⁿ]
Equating coefficient of x²ⁿ on both sides, we get
(- 1)ⁿ . ²ⁿC_n = (²ⁿC₀)² + ((²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ………….. + (²ⁿC_2n)²

Question 9.
Prove that
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n) = \(\frac{(\mathbf{n}+1)^{\mathbf{n}}}{\mathbf{n} !}\) . C₀ . C₁ . C₂ ………….. C_n.
Solution:
Given L.H.S
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n)

= R.H.S
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n) = \(\frac{(\mathbf{n}+1)^{\mathbf{n}}}{\mathbf{n} !}\) . C₀ . C₁ . C₂ ………….. C_n.

Question 10.
Find the term independent of x in (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ.
Solution:
We know that (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ = (\(\frac{1}{3 x}\))ⁿ (1 + 3x)²ⁿ
= \(\frac{1}{3^n \cdot x^n} \sum_{r=0}^{2 n}\left({ }^{2 n} C_r\right)(3 x)^r\)
For the term, independent of x put r = n.
∴ The term independent of x in (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ is \(\frac{1}{3^n}\) ²ⁿC_n . 3ⁿ.

Question 11.
Show that the middle term In the expansion of (1 + x)²ⁿ is \(\frac{1 \cdot 3 \cdot 5 \ldots \ldots(2 n-1)}{n !}\) (2x)ⁿ.
Solution:
The expansion of (1 + x)²ⁿ contains 2n + 1 terms.
∴ Middle term is (n + 1)th term

Question 12.
If (1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² …………… + a₂₀x²⁰, then prove that
i) a₀ + a₁ + a₂ + …………… + a₂₀ = 2¹⁰
ii) a₀ – a₁ + a₂ – a₃ + …………. + a₂₀ = 4¹⁰
Solution:
Given
(1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² …………… + a₂₀x²⁰ …………….(1)
i) Put x = 1, in (1), we get
(1 + 3 – 2)¹⁰ = a₀ + a₁ + a₂ + …………… + a₂₀
⇒ a₀ + a₁ + a₂ + …………… + a₂₀ = 2¹⁰.

ii) Put x – 1 in (1), we get
(1 – 3 – 2)¹⁰ = a₀ – a₁ + a₂ – a₃ + …………. + a₂₀
a₀ – a₁ + a₂ – a₃ + …………. + a₂₀ = 4¹⁰.

Question 13.
If (3√3 + 5)^{2n + 1} = x and f = x – [x] (where [x] the integral part of x), find the value of x.f.
Solution:
Given (3√3 + 5)^{2n + 1} = x
and f = x – [x]
∴ 0 < f < 1
Let us consider F = (3√3 + 5)^{2n + 1}
We know that
5 < 3√3 < 6 = 0 < 3√3 – 5 < 1
⇒ 0 < (3√3 – 5)^{2n + 1} < 1
⇒ 0 < F < 1
⇒ – 1 < – F < 0
Let x = I + f (where E is an integer)
Now
i + f – F = (3√3 + 5)^{2n + 1} + (3√3 – 5)^{2n + 1}
= [^{2n + 1}C₀ (3√3)²ⁿ⁺¹ + ^{2n + 1}C₁ (3√3)²ⁿ . 5 + ^{2n + 1}C₂ (3√3) . 5² + …………..] – [^{2n + 1}C (3√3)²ⁿ⁺¹ – ^{2n + 1}C₁ (3√3)²ⁿ . 5 + ^{2n + 1}C₂ (3√3)^2n-1 . 5² – …………]
= 2 [^{2n + 1}C₁ (3√3) 5 + ^{2n + 1}C₃ (3√3)^2n-2 5³ + …………. + ^{(2n + 1)}C_(2n+1) (5)²ⁿ⁺¹]
= 2k, where k is an integer
∴ I + f – F is an even integer
⇒ f – F is also integer.
∴ (1) + (2)
⇒ – 1 < f – F < 1
⇒ f – F = 0
⇒ f = F
∴ x . f = x . F
= (3√3 + 5)^{2n + 1} . (3√3 – 5)^{2n + 1}
= (27 – 25)^{2n + 1}
= 2^{2n + 1}.

Question 14.
If R, n are posilve integers, n is odd, 0< F < 1 and if (5√5 + 11) = R + F, then prove that
i) R is an even integer and
ii) (R + F). F = 4ⁿ
Solution:
Given R, n are positive integers, 0 < F < 1 and
(5√5 + 11)ⁿ = R + F …………….(1)
i) Consider (5√5 – 11)ⁿ = f …………….(2)
We know that 11 < 5√5 < 12
⇒ 0 < 5√5 – 11 < 1
⇒0 < (5√5 – 11)ⁿ < 1
⇒ 0 < f < 1
⇒ – 1 < – f < 0 ………….(3)
From (1) and (3)
– 1 < F -f < 1 ……………(4)
Also R + F – f
= (5√5 + 11)ⁿ – (5√5 – 11)ⁿ
= [ⁿC₀ (5√5)ⁿ + ⁿC₁ (5√5)^n-1 (11) + ⁿC₂ (5√5)^n-2 . 11² + ⁿC₃ (5√5)^n-3 . 11³ + ………… + ⁿC_n (11)ⁿ] – [ⁿC₀ (5√5)ⁿ – ⁿC₁ (5√5)^n-1 (11) + ⁿC₂ (5√5)^n-2 . 11² – ⁿC₃ (5√5)^n-3 . 11³ + ………….. + (- 1)ⁿC_n (11)ⁿ]
= 2 [ⁿC₁ (5√5)^n-1 (11) + ⁿC₃ (5√5)^n-3 (11)³ + ……………]
= 2k, where k is an integer (∵ f is odd)
∴ R + F – f is an even Integer.
⇒ F – f is also an interger. (∵ R is integer)
From (4), we have F – f = 0
⇒ F = f
∴ R is an even Integer.

ii) Now (R + F) . F
= (5√5 + 11)ⁿ (5√5 + 11)ⁿ
= ((5√5)² – 11²)ⁿ = 4ⁿ
∴ (R + F) . F = 4ⁿ.

Question 15.
If I, n are positive Integers, 0 < f < 1 and if (7 + 4√3) = I + f, then show that
i) I is an odd integer and
ii) (I + f) (I – f) =
Solution:
Given I and n are positve integers.
0 < f < I and (7 + 4√3)ⁿ = I + f ………….(1)

i) Let us consider (7 – 4√3)ⁿ = F
We know that 6 < 4√3 < 7
⇒ – 7 < – 4√3 < – 6
⇒ 0 < 7 – 4√3 < 1
⇒ 0 < (7 – 4√3)ⁿ < 1
⇒ 0 < F < 1
we have 0 < F + f < 2 …………(2)
Now I + f + F = (7 + 4√3)ⁿ + (7 – 4√3)ⁿ
= [ⁿC₀ 7ⁿ + ⁿC₁ 7^n-1 (4√3) + ⁿC₂ 7^n-2 (4√3)² + ………….. + ⁿC_n (4√3)ⁿ] + [ⁿC₀ 7ⁿ – ⁿC₁ 7^n-1 (4√3) + ⁿC₂ 7^n-2 (4√3)² – ………….. + ⁿC_n (- 1)ⁿ (4√3)ⁿ]]
= 2[ⁿC₀ 7ⁿ + ⁿC₂ 7^n-2 (4√3)² + ⁿC₄ 7^n-4 (4√3)⁴ + ……………]
= 2k, where k is an integer.
∴ I + f + F is an even integer.
∴ f + F is also an integer. (∵ I is an integer)
from (2) we have f + F = I ………..(3)
∴ I + I is an even integer
⇒ I is an odd integer.

ii) Also (I + f) (I – f) = (I + f) F
= (7 + 4√3)ⁿ (7 – 4√3)ⁿ
= (7² – (4√3)²)ⁿ = 1.

Question 16.
If n is a Positive integer, prove that \(\sum_{r=1}^n \mathbf{r}^3 \cdot\left(\frac{{ }^n C_r}{{ }^n C_{r-1}}\right)^2=\frac{n(n+1)^2(n+2)}{12}\).
Solution:
We know that \(\frac{{ }^{{ }^r} C_r}{{ }^n C_{r-1}}=\frac{n-r+1}{r}\)

Question 17.
Find the number of irrational terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰.
Solution:
Number of terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰ are 101.
General term in the expansion of (x + y)ⁿ is
T_r+1 = ⁿC_r x^n-r . y^r
∴ General term in the expansion of (5^1/6 + 2^1/8)¹⁰⁰
T_r+1 = ¹⁰⁰C_r . \(\left(5^{\frac{1}{6}}\right)^{100-r} \cdot\left(2^{\frac{1}{8}}\right)^r\)
= ¹⁰⁰C_r . \(\cdot 5^{\frac{100-r}{6}} \cdot 2^{\frac{r}{8}}\)
For T_r+1 to be a rational.
Clearly ‘r’ is a multiple of 8 and 100 – r is a multiple of 6
∴ r = 16, 40, 64. 88.
Number of rational terms are 4.
∴ Number of irrational terms are 101 – 4 = 97.

Students must practice this TS Intermediate Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Exercise 7(a)

I. Evaluate the following integrals as the limit of a sum.

Question 1.
\(\int_0^5(x+1) d x\)
Solution:
We use the following formula for p = 5
and f(x) = x² + 1, x ∈ [0, 5] and f is continuous over [0, 5].

Question 2.
\(\int_0^4 x^2 d x\)
Solution:

II. Evaluate the following integrals as the limit of a sum.

Question 1.
\(\int_0^4\left(x+e^{2 x}\right) d x\)
Solution:
Here p = 4, and f(x) = x + e^2x

Question 2.
\(\int_0^1\left(x-x^2\right) d x\)
Solution:
Here p = 1 and f(x) = x – x²

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(d)

I. Evaluate the following integrals.

Question 1.
\(\int \frac{1}{\sqrt{2 x-3 x^2+1}} d x\)
Solution:

Question 2.
\(\int \frac{\sin \theta}{\sqrt{2-\cos ^2 \theta}} d \theta\)
Solution:
Let cos θ = t, then sin θ dθ = -dt

Question 3.
\(\int \frac{\cos x}{\sin ^2 x+4 \sin x+5} d x\)
Solution:
Let sin x = t, then cos x dx = dt

Question 4.
\(\int \frac{d x}{1+\cos ^2 x}\)
Solution:
Dividing by cos²x we get

Question 5.
\(\int \frac{d x}{2 \sin ^2 x+3 \cos ^2 x}\)
Solution:
Dividing by cos²x we get

Question 6.
\(\int \frac{1}{1+\tan x} d x\)
Solution:

write cos x = A(sin x + cos x) + B \(\frac{\mathrm{d}}{\mathrm{dx}}\)(sin x + cos x)
= A(sin x + cos x) + B(cos x – sin x)
Comparing coefficients of cos x and sin x on both sides
A – B = 0 and A + B = 1
Solving 2A = 1 ⇒ A = \(\frac{1}{2}\)
∴ B = \(\frac{1}{2}\)
∴ cos x = \(\frac{1}{2}\)(sin x + cos x) + \(\frac{1}{2}\)(cos x – sin x)

= \(\frac{1}{2}\)x + \(\frac{1}{2}\) log|sin x + cos x| + c
[∵ sin x + cos x = t ⇒ (cos x – sin x) dx = dt in second integral]

Question 7.
\(\int \frac{1}{1-\cot x} d x\)
Solution:

Let sin x = A(sin x – cos x) + B \(\frac{\mathrm{d}}{\mathrm{dx}}\)(sin x – cos x)
= A(sin x – cos x) + B(cos x + sin x)
Comparing coefficients of sin x and cos x on both sides we get
A + B = 1 and -A + B = 0
solving B = \(\frac{1}{2}\) and A = \(\frac{1}{2}\)

= \(\frac{1}{2}\)x + \(\frac{1}{2}\) log|sin x – cos x| + c
[∵ sin x – cos x = t ⇒ (cos x + sin x) dx = dt in second integral]

II. Evaluate the following integrals.

Question 1.
\(\int \sqrt{1+3 x-x^2} d x\) (May ’11)
Solution:

Question 2.
\(\int\left(\frac{9 \cos x-\sin x}{4 \sin x+5 \cos x}\right) d x\) (New Model Paper)
Solution:
Let 9 cos x – sin x = A(4 sin x + 5 cos x) + B \(\frac{\mathrm{d}}{\mathrm{dx}}\)(4 sin x + 5 cos x)
∴ 9 cos x – sin x = A(4 sin x + 5 cos x) + B(4 cos x – 5 sin x) …….(1)
Comparing coefficients of cos x and sin x on both sides
5A + 4B = 9 …….(2)
and 4A – 5B = -1 ……….(3)
Solving (2) and (3)

= x + log|4 sin x + 5 cos x| + c
(∵ 4 sin x + 5 cos x = t ⇒ (4 cos x – 5 sin x) dx = dt in second integral)

Question 3.
\(\int \frac{2 \cos x+3 \sin x}{4 \cos x+5 \sin x} d x\)
Solution:
Let 2 cos x + 3 sin x = A(4 cos x + 5 sin x) + B \(\frac{d}{d x}\)(4 cos x + 5 sin x)
= A(4 cos x + 5 sin x) + B(-4 sin x + 5 cos x) ……..(1)
Comparing coefficients of cos x and sin x on both sides we get
4A + 5B = 2 ………(2)
and 5A – 4B = 3 ………(3)
Solving (2) and (3) we get

Question 4.
\(\int \frac{1}{1+\sin x+\cos x} d x\)
Solution:

Question 5.
\(\int \frac{1}{3 x^2+x+1} d x\)
Solution:

Question 6.
\(\int \frac{d x}{\sqrt{5-2 x^2+4 x}}\)
Solution:
Consider 5 – 2x² + 4x = 5 – (2x² – 4x)

III. Evaluate the following integrals.

Question 1.
\(\int \frac{x+1}{\sqrt{x^2-x+1}} d x\)
Solution:

Question 2.
∫(6x + 5) \(\sqrt{6-2 x^2+x}\) dx (Mar. ’09)
Solution:
Let 6x + 5 = A \(\frac{\mathrm{d}}{\mathrm{dx}}\)(6 – 2x² + x) + B
= A(-4x + 1) + B
Equating the coefficients of x and constant terms
-4A = 6 ⇒ A = \(-\frac{3}{2}\)
and A + B = 5
⇒ B = 5 + \(\frac{3}{2}\) = \(\frac{13}{2}\)

Question 3.
\(\int \frac{d x}{4+5 \sin x}\)
Solution:

Question 4.
\(\int \frac{1}{2-3 \cos 2 x} d x\) (June ’10)
Solution:
Let tan x = t then sec²x dx = dt

Question 5.
∫x\(\sqrt{1+x-x^2}\) dx (May ’12)
Solution:
Let x = A \(\frac{\mathrm{d}}{\mathrm{dx}}\)(1 + x – x²) + B = A(1 – 2x) + B
Comparing the coefficient of x, constant terms on both sides

Question 6.
\(\int \frac{d x}{(1+x) \sqrt{3+2 x-x^2}}\) (New Model Paper)
Solution:

Question 7.
\(\int \frac{d x}{4 \cos x+3 \sin x}\)
Solution:

Question 8.
\(\int \frac{1}{\sin x+\sqrt{3} \cos x} d x\) (May ’12)
Solution:

Question 9.
\(\int \frac{d x}{5+4 \cos 2 x}\) (Mar. ’11)
Solution:

Question 10.
\(\int \frac{2 \sin x+3 \cos x+4}{3 \sin x+4 \cos x+5} d x\) (Mar. ’11)
Solution:
Since there exist constants in both the numerator and denominator, we determine constants A, B, and C such that
2 sin x + 3 cos x + 4 = A \(\frac{\mathrm{d}}{\mathrm{dx}}\)(3 sin x + 4 cos x + 5) + B (3 sin x + 4 cos x + 5) + C
= A(3 cos x – 4 sin x) + B(3 sin x + 4 cos x + 5) + C …….(1)
Comparing both sides the coefficients of sin x, cos x, and constants
-4A + 3B = 2
⇒ 4A – 3B + 2 = 0 ……..(2)
3A + 4B – 3 = 0 ……….(3)
5B + C – 4 = 0 ………(4)
Solving (2) and (3)

Question 11.
\(\int \sqrt{\frac{5-x}{x-2}} d x\) on (2, 5).
Solution:

Question 12.
\(\int \sqrt{\frac{1+x}{1-x}} d x\) on (-1, 1).
Solution:

Question 13.
\(\int \frac{d x}{(1-x) \sqrt{3-2 x-x^2}}\) on (-1, 3).
Solution:

Question 14.
\(\int \frac{d x}{(x+2) \sqrt{x+1}}\) on (-1, ∞).
Solution:
Let x + 1 = t² then dx = 2t dt

Question 15.
\(\int \frac{d x}{(2 x+3) \sqrt{x+2}}\) on I ⊂ (-2, ∞) \ {\(-\frac{3}{2}\)}
Solution:
Let x + 2 = t² then dx = 2t dt
and 2x + 3 = 2(t² – 2) + 3 = 2t² – 1

Question 16.
\(\int \frac{1}{(1+\sqrt{x}) \sqrt{x-x^2}} d x\) on (0, 1).
Solution:
Put x = t² then dx = 2t dt

Question 17.
\(\int \frac{d x}{(x+1) \sqrt{2 x^2+3 x+1}}\) on I ⊂ R \ [-1, \(-\frac{1}{2}\)]
Solution:
Let x + 1 = \(\frac{1}{t}\)

Question 18.
\(\int \sqrt{e^x-4} d x\) on \(\left[\log _e 4, \infty\right)\).
Solution:
Let e^x – 4 = t² then ex dx = 2t dt

Question 19.
\(\int \sqrt{1+\sec x} d x\) on \(\left[\left(2 n-\frac{1}{2}\right) \pi,\left(2 n+\frac{1}{2}\right) \pi\right]\), n ∈ Z.
Solution:

Question 20.
\(\int \frac{d x}{1+x^4}\) on R.
Solution:

Students must practice this TS Intermediate Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Exercise 7(b)

I. Evaluate the following definite integrals.

Question 1.
\(\int_0^a\left(a^2 x-x^3\right) d x\)
Solution:

Question 2.
\(\int_2^3 \frac{2 x}{1+x^2} d x\) (Mar. ’12)
Solution:
Let 1 + x² = t, then 2x dx = dt
Upper limit t = 1 + 9 = 10 when x = 3
Lower limit t = 1 + 4 = 5 when x = 2

= log 10 – log 5
= log 2

Question 3.
\(\int_0^\pi \sqrt{2+2 \cos \theta} d \theta\)
Solution:

Question 4.
\(\int_0^\pi \sin ^3 x \cos ^3 x d x\)
Solution:
I = \(\int_0^\pi \sin ^3 x \cos ^3 x d x\)

Question 5.
\(\int_0^2|1-x| d x\)
Solution:

Question 6.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos x}{1+e^x} d x\)
Solution:

Question 7.
\(\int_0^1 \frac{d x}{\sqrt{3-2 x}}\)
Solution:
Let 3 – 2x = t² then -2 dx = 2t dt
∴ Upper limit t² = 1 ⇒ t = 1
and Lower limit t² = 3 ⇒ t = √3

Question 8.
\(\int_0^a(\sqrt{a}-\sqrt{x})^2 d x\)
Solution:

Question 9.
\(\int_0^{\frac{\pi}{4}} \sec ^4 \theta d \theta\)
Solution:

Question 10.
\(\int_0^3 \frac{x}{\sqrt{x^2+16}} d x\)
Solution:
Let x² + 16 = t2
Upper limit: x = 3
t² = 25
⇒ t = 5
⇒ 2x dx = 2t dt
Lower limit; x = 0 ⇒ t = 4
∴ \(\int_4^5 \frac{t d t}{t}=[t]_4^5\) = 1

Question 11.
\(\int_0^1 x e^{-x^2} d x\)
Solution:
Let x² = t then x dx = \(\frac{1}{2}\) dt
Upper limit x = 1 ⇒ t = 1
Lower limit x = 0 ⇒ t = 0

Question 12.
\(\int_1^5 \frac{d x}{\sqrt{2 x-1}}\)
Solution:
Let 2x – 1 = t² then 2 dx = 2t dt
⇒ dx = t dt
Upper limit when x = 5
⇒ t² = 9
⇒ t = 3
Lower limit when x = 1
⇒ t² = 1
⇒ t = 1 (taking positive values in [1, 5])

II. Evaluate the following integrals.

Question 1.
\(\int_0^4 \frac{x^2}{1+x} d x\)
Solution:

Question 2.
\(\int_{-1}^2 \frac{x^2}{x^2+2} d x\)
Solution:

Question 3.
\(\int_0^1 \frac{x^2}{x^2+1} d x\) (New Model Paper, TET, Mar. ’11)
Solution:

Question 4.
\(\int_0^{\frac{\pi}{2}} x^2 \sin x d x\)
Solution:
Applying integration by parts
taking u = x² and v = sin x we get

Question 5.
\(\int_0^4|2-x| d x\) (May ’11)
Solution:
If x > 2 then |2 – x| = -(2 – x) = x – 2
If x < 2 then |2 – x| = 2 – x

Question 6.
\(\int_0^{\frac{\pi}{2}} \frac{\sin ^5 x}{\sin ^5 x+\cos ^5 x} d x\)
Solution:

Question 7.
\(\int_0^{\frac{\pi}{2}} \frac{\sin ^2 x-\cos ^2 x}{\sin ^3 x+\cos ^3 x} d x\) (New Model Test Paper & Mar. ’12)
Solution:

Evaluate the following limits.

Question 8.
\(\lim _{n \rightarrow \infty} \frac{\sqrt{n+1}+\sqrt{n+2}+\ldots+\sqrt{n+n}}{n \sqrt{n}}\)
Solution:
For determining the limit we use the result that if f is continuous on [0, 1] and

Question 9.
\(\lim _{n \rightarrow \infty}\left[\frac{1}{n+1}+\frac{1}{n+2}+\ldots .+\frac{1}{6 n}\right]\)
Solution:

Question 10.
\(\lim _{n \rightarrow \infty} \frac{1}{n}\left[\tan \frac{\pi}{4 n}+\tan \frac{2 \pi}{4 n}+\ldots+\tan \frac{n \pi}{4 n}\right]\)
Solution:

Question 11.
\(\lim _{n \rightarrow \infty} \sum_{i=1}^n \frac{i^3}{i^4+n^4}\)
Solution:

Question 12.
\(\lim _{n \rightarrow \infty} \sum_{i=1}^n \frac{i}{n^2+i^2}\)
Solution:
\(\lim _{n \rightarrow \infty} \sum_{i=1}^n \frac{1}{n^2+i^2}\)
Dividing the numerator and denominator by n² we get

Let 1 + x² = t then x dx = \(\frac{1}{2}\) dt
Upper limit when x = 1 is t = 2
Lower limit when x = 0 is t = 1

Question 13.
\(\lim _{n \rightarrow \infty}\left(\frac{1+2^4+3^4+\ldots+n^4}{n^5}\right)\)
Solution:

Question 14.
\(\lim _{n \rightarrow \infty}\left[\left(1+\frac{1}{n^2}\right)\left(1+\frac{2^2}{n^2}\right) \cdots \cdot\left(1+\frac{n^2}{n^2}\right)\right]^{\frac{1}{n}}\)
Solution:

Question 15.
\(\lim _{n \rightarrow \infty}\left[\frac{(n)^{\frac{1}{n}}}{n}\right]\)
Solution:

III. Evaluate the following integrals.

Question 1.
\(\int_0^{\frac{\pi}{2}} \frac{d x}{4+5 \cos x}\) (Mar. ’93)
Solution:

Question 2.
\(\int_a^b \sqrt{(x-a)(b-x)} d x\)
Solution:

Question 3.
\(\int_0^{\frac{1}{2}} \frac{x \sin ^{-1} x}{\sqrt{1-x^2}} d x\)
Solution:
Let sin^-1x = θ then sin θ = x and dx = cos θ dθ
Upper limit, sin θ = \(\frac{1}{2}\) ⇒ θ = \(\frac{\pi}{6}\)
Lower limit, sin θ = 0 ⇒ θ = 0

Question 4.
\(\int_0^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16 \sin 2 x} d x\) (Apr. ’01)
Solution:

Question 5.
\(\int_0^{\frac{\pi}{2}} \frac{a \sin x+b \cos x}{\sin x+\cos x} d x\)
Solution:

Question 6.
\(\int_0^a x(a-x)^n d x\)
Solution:

Question 7.
\(\int_0^2 x \sqrt{2-x} d x\)
Solution:

Question 8.
\(\int_0^\pi x \sin ^3 x d x\)
Solution:

Question 9.
\(\int_0^\pi \frac{x}{1+\sin x} d x\) (May ’11)
Solution:

Question 10.
\(\int_0^\pi \frac{x \sin ^3 x}{1+\cos ^2 x} d x\) (Mar. ’11)
Solution:
Let I = \(\int_0^\pi \frac{x \sin ^3 x}{1+\cos ^2 x} d x\)

Question 11.
\(\int_0^1 \frac{\log (1+x)}{1+x^2} d x\) (New Model Paper & Mar. ’10)
Solution:
Put x = tan θ then dx = sec²θ dθ
Upper limit when x = 1 is θ = \(\frac{\pi}{4}\)
and Lower limit when x = 0 is θ = 0

Question 12.
\(\int_0^\pi \frac{x \sin x}{1+\cos ^2 x} d x\) (Apr. ’99)
Solution:

Question 13.
\(\int_0^{\frac{\pi}{2}} \frac{\sin ^2 x}{\cos x+\sin x} d x\)
Solution:

Question 14.
\(\int_0^\pi \frac{1}{3+2 \cos x} d x\)
Solution:

Question 15.
\(\int_0^{\frac{\pi}{4}} \log (1+\tan x) d x\)
Solution:

Question 16.
\(\int_{-1}^{\frac{3}{2}}|x \sin \pi x| d x\)
Solution:
We have |x sin πx| = x sin πx when -1 ≤ x ≤ 1
= -x sin πx when 1 < x ≤ \(\frac{3}{2}\)

Question 17.
\(\int_0^1 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right) d x\)
Solution:
Let x = tan θ then dx = sec²θ dθ
Upper limit when x = 1 is θ = \(\frac{\pi}{4}\)
and Lower limit when x = 0 is θ = 0

Question 18.
\(\int_0^1 x \tan ^{-1} x d x\)
Solution:
Let x = tan θ then dx = sec²θ dθ
Upper limit when x = 1 is θ = \(\frac{\pi}{4}\)
and Lower limit when x = 0 is θ = 0
∴ \(\int_0^1 x \tan ^{-1} x d x=\int_0^{\frac{\pi}{4}} \theta \tan \theta \sec ^2 \theta d \theta\)
using integration by parts by taking u = θ and v = tan θ sec²θ we get

Question 19.
\(\int_0^\pi \frac{x \sin x}{1+\cos ^2 x} d x\)
Solution:

Question 20.
Suppose that f : R → R is a continuous periodic function and T is its period of it. Let a ∈ R. Then prove that for any positive integer n, \(\int_a^{a+n T} f(x) d x=n \int_a^{a+T} f(x) d x\).
Solution:

(∵ f is a continuous function with period T)
Consider \(\int_{a+r T}^{a+(r+1) T} f(x) d x\) and (1 < r < r+1 < n)
take x = y + rT and dx = dy
Upper limit when x = a + rt + T is y = a + T
The lower limit when x = a + rT is y = a

(∵ f is periodic ⇒ f(y + rT) = f(y)
Similarly, we can prove that each integral of (1) is equal to \(\int_a^{a+T} f(x) d x\)
Hence \(\int_a^{a+n T} f(x) d x=n \int_a^{a+n T} f(x) d x\)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(c)

I. Evaluate the following integrals.

Question 1.
∫x sec²x dx on I ⊂ R – {\(\frac{(2 n+1) \pi}{2}\) : n is an integer}.
Solution:
We use the formula for integration by parts which state that

Question 2.
\(\int e^x\left(\tan ^{-1} x+\frac{1}{1+x^2}\right) d x\), x ∈ R.
Solution:

Question 3.
\(\int \frac{\log x}{x^2} d x\) on(0, ∞).
Solution:

Question 4.
∫(log x)² dx on (0, ∞).
Solution:
Take (log x)² = u and 1 = v.
Then by integration by parts,
∫(log x)² . 1 . dx = (log x)² . x – ∫2 (log x) \(\frac{1}{x}\) . x dx
= x(log x)² – 2 ∫log x . 1 . dx
= x(log x)² – 2[logx . x – ∫\(\frac{1}{x}\) . x dx]
= x(log x)² – 2x[log x] + 2x + c

Question 5.
∫e^x (sec x + sec x tan x) dx on I ⊂ R – {(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
Let f(x) = sec x then f'(x) = sec x tan x
∴ Using ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫e^x (sec x + sec x tan x) dx = e^x sec x + c

Question 6.
∫e^x cos x dx on R.
Solution:
Let I = ∫e^x cos x dx
and take u = e^x and v = cos x.
Then using integration by parts,
I = e^x (sin x) – ∫e^x sin x dx
= e^x (sin x) – [e^x(-cos x) – ∫e^x (-cos x) dx]
= e^x sin x + e^x cos x – ∫e^x cos x dx
= e^x (sin x + cos x) – 1
2I = e^x (sin x + cos x)
I = \(\frac{1}{2}\) e^x (sin x + cos x) + c
∴ ∫e^x cos x dx = \(\frac{1}{2}\) e^x (sin x + cos x)

Question 7.
∫e^x (sin x + cos x) dx on R.
Solution:
Take f(x) = sin x then f'(x) = cos x
So by using formula ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫e^x (sin x + cos x) dx = e^x sin x + c.

Question 8.
∫(tan x + log sec x) e^x dx on ((2n – \(\frac{1}{2}\))π, (2n + \(\frac{1}{2}\))π), n ∈ Z.
Solution:
Take f(x) = log|sec x| then f'(x) = \(\frac{1}{\sec x}\) (sec x tan x) = tan x
So by the formula ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫(tan x + log sec x) e^x dx = e^x log|sec x| + c

II. Evaluate the following integrals.

Question 1.
∫xⁿ log x dx on (0, ∞), n is a real number and n ≠ -1.
Solution:
Take u = log x and v = xⁿ
applying integration by parts,

Question 2.
∫log(1 + x²) dx on R.
Solution:
Take log(1 + x²) = u and 1 = v then
using integration by parts, we get

Question 3.
∫√x log x dx on (0, ∞).
Solution:
Take u = log x and v = x^1/2 and
using integration by parts, we get

Question 4.
\(\int e^{\sqrt{x}} d x\) on (0, ∞).
Solution:

Question 5.
∫x² cos x dx on R.
Solution:
Take x² = u and cos x = v,
and using integration by parts, we get
∫x² cos x dx = x² (sin x) – ∫2x sin x dx
= x² sin x – [2x(-cos x) – ∫2 . (-cos x) dx]
= x² sin x + 2x cos x – 2∫cos x dx
= x² sin x + 2x cos x – 2 sin x + c

Question 6.
∫x sin²x dx on R.
Solution:

Question 7.
∫x cos²x dx on R.
Solution:

Question 8.
∫cos√x dx on R.
Solution:
∫cos√x dx = ∫\(\frac{1}{\sqrt{x}}\) √x cos√x dx
Taking √x = t, we get \(\frac{1}{2 \sqrt{x}}\) dx = dt
⇒ \(\frac{\mathrm{dx}}{\sqrt{\mathrm{x}}}\) = 2 dt
∴ ∫cos √x dx = 2∫t cos t dt
using Integration by parts,
= 2[t(sin t) – ∫1 . sin t dt]
= 2[t sin t + cos t + c]
= 2[√x sin √x + cos √x ] + c

Question 9.
∫x sec²2x dx on I ⊂ R \ {(2nπ + 1) \(\frac{\pi}{4}\) : n ∈ Z}
Solution:
Taking x = u and sec²2x = v,
and applying integration by parts we get
∫x sec²2x dx = x(\(\frac{1}{2}\) tan 2x – ∫1 . \(\frac{1}{2}\) tan 2x dx
= \(\frac{x}{2}\) tan 2x – \(\frac{1}{2}\) ∫tan 2x dx
= \(\frac{x}{2}\) tan 2x – \(\frac{1}{4}\) log|sec 2x| + c

Question 10.
∫x cot²x dx on I ⊂ R \ {nπ : n ∈ Z).
Solution:
∫x cot²x dx = ∫x(cosec²x – 1) dx = ∫x cosec²x dx – ∫x dx
Taking u = x and v = cosec²x on the first integral
and using integration by parts we get
∫x cot²x dx = x(-cot x) – ∫1 . (-cot x) dx – \(\frac{x^2}{2}\)
= -x cot x + ∫cot x dx – \(\frac{x^2}{2}\)
= -x cot x + log|sin x| – \(\frac{x^2}{2}\) + c

Question 11.
∫e^x (tan x + sec²x) dx on I ⊂ R \ {(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
Let f(x) = tan x, then f'(x) = sec²x
So by the formula ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫e^x (tan x + sec²x) dx = e^x tan x + c

Question 12.
∫\(e^x\left(\frac{1+x \log x}{x}\right) d x\) on (0, ∞). (Mar. ’13)
Solution:

Question 13.
∫e^ax sin bx dx on R, a, b ∈ R.
Solution:
Let I = ∫e^ax sin bx dx
Taking u = e^ax and v = sin bx
and applying integration by parts

Question 14.
\(\int \frac{x e^x}{(x+1)^2} d x\) on I ⊂ R \ {-1}.
Solution:

Question 15.
\(\int \frac{d x}{\left(x^2+a^2\right)^2}\), (a > 0) on R.
Solution:
Take substitution x = a tan θ
so that dx = a sec²θ dθ

Question 16.
∫e^x log(e^2x + 5e^x + 6) dx on R.
Solution:

Question 17.
\(\int e^x \frac{(x+2)}{(x+3)^2} d x\) on I ⊂ R \ {-3}.
Solution:

Question 18.
∫cos(log x) dx on (0, ∞).
Solution:
Let I = ∫cos (log x) dx = ∫cos (log x) . 1 dx
Take u = cos (log x) and v = 1
and using integration by parts successively.
I = cos (log x) . x – ∫-sin (log x) \(\frac{1}{x}\) . x . dx
= x cos (log x) + ∫sin(log x) dx
= x cos (log x) + sin (log x) . x – ∫cos (log x) \(\frac{1}{x}\) . x . dx
= x cos (log x) + x . sin(log x) – ∫cos (log x) dx
= x [cos (log x) + sin (log x)] – ∫cos (log x) dx
= x [cos (log x) + sin (log x)] – I
∴ 2I = x [cos (log x) + sin (log x)]
⇒ I = \(\frac{x}{2}\) [cos (log x) + sin (log x)] + c
∴ ∫cos (log x) dx = \(\frac{x}{2}\) [cos (log x) + sin (log x)] + c

III. Evaluate the following integrals.

Question 1.
∫x tan^-1x dx, x ∈ R.
Solution:
Let u = tan^-1x and v = x then using integration by parts

Question 2.
∫x² tan^-1x dx, x ∈ R.
Solution:
Take u = tan^-1x and v = x²
and apply integration by parts we get

Question 3.
\(\int \frac{\tan ^{-1} x}{x^2} d x\), x ∈ I ⊂ R \ {0}.
Solution:

Question 4.
∫x cos^-1x dx, x ∈ (-1, 1).
Solution:
Let cos^-1x = θ then cos θ = x
⇒ dx = -sin θ dθ
∴ ∫x cos^-1x dx = ∫θ cos θ (-sin θ dθ) – \(\frac{1}{2}\) ∫θ sin 2θ dθ
Using integration by parts by taking u = θ, v = sin 2θ we get

Question 5.
∫x² sin^-1x dx, x ∈ (-1, 1).
Solution:
Let sin^-1x = θ then sin θ = x
⇒ dx = cos θ dθ
∴ ∫x² sin^-1x dx = ∫θ sin²θ cos θ dθ
Using integration by parts
by choosing functions u = θ and v = sin²θ cos θ, we get

Question 6.
∫x log(1 + x) dx, x ∈ (-1, ∞).
Solution:
Take u = log(1 + x) and v = x
and apply integration by parts

Question 7.
∫sin√x dx on (0, ∞).
Solution:
\(\int \frac{\sqrt{x}}{\sqrt{x}} \sin \sqrt{x} d x\)
Let √x = t then \(\frac{1}{2 \sqrt{x}}\) dx = dt
⇒ \(\frac{d x}{\sqrt{x}}\) = 2 dt
∴ ∫sin √x dx = 2∫t sin t dt,
using Integration by parts by taking u = t and v = sin t, we get
= 2[t(-cos t) – ∫1 . (-cos t) dt]
= 2[-t cos t + ∫cos t dt]
= 2[-t cos t + sin t] + c
= 2[sin √x – √x cos √x ] + c

Question 8.
∫e^ax sin(bx + c) dx, (a, b, c ∈ R, b ≠ 0) on R.
Solution:
Let I = ∫e^ax sin (bx + c) dx, taking u = e^ax and v = sin (bx + c)
and applying integration by parts,

Question 9.
∫a^x cos 2x dx on R (a > 0 and a ≠ 1).
Solution:
Let I = ∫a^x cos 2x dx
using integration by parts by taking cos 2x = u and a^x = v, we have

Question 10.
\(\int \tan ^{-1}\left(\frac{3 x-x^3}{1-3 x^2}\right) d x\) on I ⊂ R – \(\left\{-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right\}\).
Solution:

Question 11.
∫sinh^-1x dx on R.
Solution:
Take sinh^-1x = u and v = 1,
Applying integration by parts we get

Question 12.
∫cosh^-1x dx on [1, ∞).
Solution:
∫cosh^-1x dx = ∫cosh^-1x . 1 . dx
Take u = cosh^-1x and v = 1 then

Question 13.
∫tanh^-1x dx on (-1, 1).
Solution:
∫tanh^-1x dx = ∫tanh^-1x . 1 . dx
Take u = tanh^-1x and v = 1
and apply integration by parts we get