TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(b)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(b)

I.
Question 1.
Find the set of vaines of x for which the binomial expansions of the following are valid.
i) (2 + 3x)^{\(\frac{-2}{3}\)}
ii) (5 + x)^{\(\frac{3}{2}\)}
iii) (7 + 3x)^-5
iv) (4 – \(\frac{x}{3}\))^{\(\frac{-1}{2}\)}
Solution:
We know that
(2 + 3x)^{\(\frac{-2}{3}\)} = 2^{\(\frac{-2}{3}\)} (1 + \(\frac{3}{2}\)x)^{\(\frac{-2}{3}\)}
The expansion is valid only when |\(\frac{3}{2}\) x| < 1
⇒ |x| < \(\frac{2}{3}\)
⇒ x ∈ \(\left(\frac{-2}{3}, \frac{2}{3}\right)\).

ii) We know that (5 + x)^3/2
= 5^3/2 (1 + \(\frac{x}{5}\))^3/2
The expansion is valid only when
|\(\frac{x}{5}\)| < 1
⇒ |x| < 5
⇒ x ∈ (- 5, 5).

iii) We know that
(7 + 3x)^-5 = 7^-5 (1 + \(\frac{3 x}{7}\))^-5
The expansion is valid only when |\(\frac{3 x}{7}\)| < 1
⇒ |x| < \(\frac{7}{3}\)
⇒ x ∈ \(\left(\frac{-7}{3}, \frac{7}{3}\right)\)

iii) We know that (4 – \(\frac{x}{3}\))^{\(\frac{-1}{2}\)}
= \(4^{\frac{-1}{2}}\left(1-\frac{x}{12}\right)^{\frac{-1}{2}}\)
The expansion is valid only when |\(\frac{x}{12}\)| < 1
⇒ |x| < 12
⇒ x ∈ (- 12, 12).

Question 2.
i) 6th term of (1 + \(\frac{x}{2}\))^-5
ii) 7th term of (1 – \(\frac{x^2}{3}\))^-4
iii) 10th term of (3 – 4x)^{\(\frac{-2}{3}\)}
iv) 5th term of (7 + \(\frac{8 y}{3}\))^{\(\frac{7}{4}\)}
Solution:
i) General term in the expansion of (1 + x)^-n is
T_r+1 = (- 1)^r . ^n+r-1C_r . x^r
∴ 6th term of (1 + x)^-5 is
T₆ = (- 1)⁵ . ⁹C₅ (\(\frac{x}{2}\))^-5 (∵ n = r = 5)
= \(\frac{-63}{16}\) x⁵.

ii) General term in the expansion of (1 + x)^-n is
T_r+1 = (- 1)^r . ^n+r-1C_r . x^r
7th term in the eapansion of (1 – \(\frac{x^2}{3}\))^-4 is
T₇ = \({ }^9 C_6\left(\frac{x^2}{3}\right)^6\) (∵ n – 4; r = 6)
= \(\frac{28}{243}\) x¹²

iii) We know that
(3 – 4x)^{\(\frac{-2}{3}\)} = \(3^{\frac{-2}{3}}\left(1-\frac{4 x}{3}\right)^{\frac{-2}{3}}\)

iv) We know that (7 + \(\frac{8 y}{3}\))^{\(\frac{7}{4}\)}

Question 3.
Write down the first 3 terms In the expansion of
i) (3 +5x)^{\(\frac{-7}{3}\)}
ii) (1 + 4x)^-4
iii) (8 – 5x)^{\(\frac{2}{3}\)}
iv) (2 – 7x)^{\(\frac{-3}{4}\)}
Solution:
i) \((3+5 x)^{\frac{-7}{3}}=3^{\frac{-7}{3}}\left(1+\frac{5 x}{3}\right)^{\frac{-7}{3}}\)
We know that

ii) We know that
(1 + x)^-n = 1 – nx + \(\frac{\mathrm{n}(\mathrm{n}+1)}{2 !}\) x² – ………….
∴ (1 + 4x)^-4 = 1 – 4 (4x) + \(\frac{4(5)}{2}\) (4x)² – …………..
= 1 – 16x + 160x² – ……………
∴ The first 3 terms are 1, – 16x, 160x².

iii) (8 – 5x)^{\(\frac{2}{3}\)}

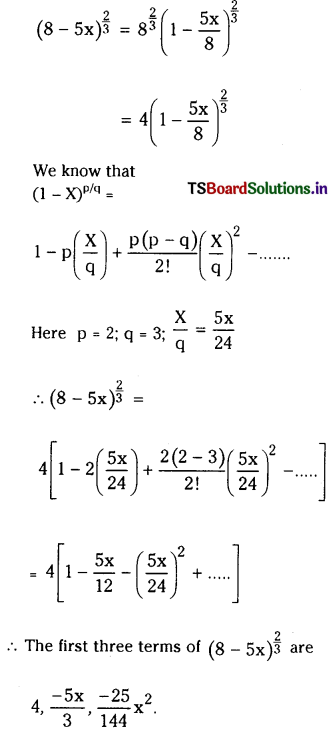
iv) \((2-7 x)^{\frac{-3}{4}}=2^{\frac{-3}{4}}\left[1-\frac{7 x}{2}\right]^{\frac{-3}{4}}\)
We know that

Question 4.
Find the general term ((r + i)th term) in the expansion of
i) (4 + 5x)^{\(\frac{-3}{2}\)}
ii) (1 – \(\frac{5 x}{3}\))^-3
iii) (1 + \(\frac{4 x}{5}\))^{\(\frac{5}{2}\)}
iv) (3 – \(\frac{5 x}{4}\))^{\(\frac{-1}{2}\)}
Solution:
i) We know that

ii) General term in the expansion (1 – x)^-n is

iii) General term in the expansion of (1 + X)^p/q is

iv) We know that

II.
Question 1.
Find the coefficient of x¹⁰ in the expansion of \(\frac{1+2 x}{(1-2 x)^2}\).
Solution:
We know that
\(\frac{1+2 x}{(1-2 x)^2}\) = (1 + 2x) (1 – 2x)^-2
= (1 + 2x) [1 + 2(2x) + 3 (2x)² + 4 (2x)³ + …………. + 10 (2x)⁹ + 11 (2x)¹⁰ + …………]
∴ The coefficient of x¹⁰ in \(\frac{1+2 x}{(1-2 x)^2}\) is
= 11 (2¹⁰) + 10 (2) (2⁹)
= 2¹⁰ (11 + 10)
= 21 × 2¹⁰.

Question 2.
Find the coefficient of x⁴ in the expansion of (1 – 4x)^-3/5.
Solution:
General term in the expansion of (1 – X)^{\(\frac{-p}{q}\)} is

Question 3.
i) Find the coefficient of x⁵
ii) Find the coefficient of x⁸ in (1 nt)2
iii) Find the coefficient of x in (2+3×9
Solution:
i) We know that
\(\frac{(1-3 x)^2}{(3-x)^{\frac{3}{2}}}=(1-3 x)^2\left[3-\left.x\right|^{\frac{-3}{2}}\right.\)

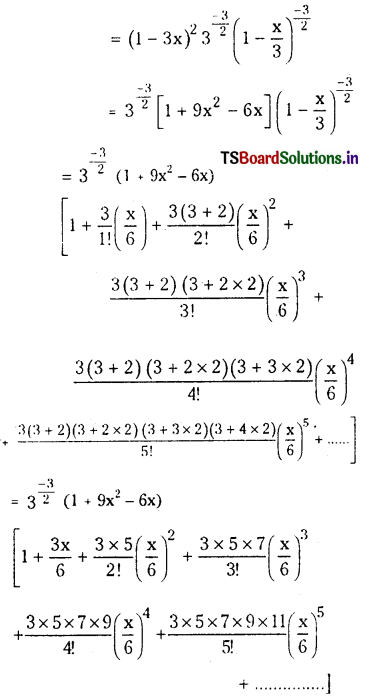
ii) We know that \(\frac{(1+x)^2}{\left(1-\frac{2}{3} x\right)^3}=(1+x)^2\left[1-\frac{2}{3} x\right]^{-3}\)

iii) We know that
\(\frac{(2+3 x)^3}{(1-3 x)^4}\) = (2 + 3x)³ [1 – 3x]^-4
= (8 + 36x + 54x² + 27x³) [1 + ⁴C (3x) + ⁵C₂ (3x)² + ⁶C₃ (3x)³ + ……….. + ^(r+3)C_r (3x)^r + …………..]
Clearly the coefficient of x^r in above expansion is
8 ^(r+3)C_r 3^r + 36 ^(r+2)C_r-1 3^r-1 + 54 ^(r+1)C_r-2 3^r-2 + 27 ^rC_r-3 3^r-2
for coefficient of x⁷, put r = 7
∴The coefficient of x⁷ in \(\frac{(2 x+3)^3}{(1-3 x)^4}\) is
8 ¹⁰C₇ 3⁷ + 36 ⁹C₆ 3⁶ + 54 ⁸C₅ 3⁵ + 27 ⁷C₄ 3⁴ = 8 ¹⁰C₃ 3⁷ + 36 ⁹C₃ 3⁶ + 54 ⁸C₃ 3⁵ + 27 ⁷C₃ 3⁴.

Question 4.
Find the coefficient of x³ in the expansion of \(\frac{\left(1+3 x^2\right)^{\frac{3}{2}}}{(3+4 x)^{\frac{1}{3}}}\).
Solution:
\(\frac{\left(1+3 x^2\right)^{\frac{3}{2}}}{(3+4 x)^{\frac{1}{3}}}\) = (1 + 3x)^3/2 (3 + 4x)^-1/3

III.
Question 1.
Find the sum of the infinite series:
i) 1 + \(\frac{1}{3}+\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}\) + ………….
ii) 1 – \(\frac{4}{5}+\frac{4 \cdot 7}{5 \cdot 10}-\frac{4 \cdot 7 \cdot 10}{5 \cdot 10 \cdot 15}\) + ………….
iii) \(\frac{3}{4}+\frac{3 \cdot 5}{4 \cdot 8}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12}\) + …………
iv) \(\frac{3}{4 \cdot 8}-\frac{3 \cdot 5}{4 \cdot 8 \cdot 12}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12 \cdot 16}\) – …………..
Solution:
i) Let y = 1 + \(\frac{1}{3}+\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}\) + ………….

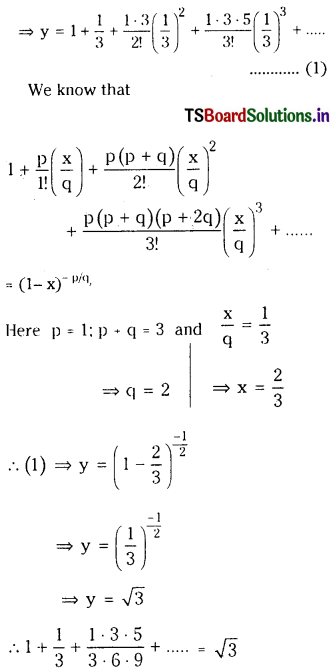
ii) Let y = – \(\frac{4}{5}+\frac{4 \cdot 7}{5 \cdot 10}-\frac{4 \cdot 7 \cdot 10}{5 \cdot 10 \cdot 15}\) + ………….

iii) \(\frac{3}{4}+\frac{3 \cdot 5}{4 \cdot 8}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12}\) + …………

iv) Let y = \(\frac{3}{4 \cdot 8}-\frac{3 \cdot 5}{4 \cdot 8 \cdot 12}+\frac{3 \cdot 5 \cdot 7}{4 \cdot 8 \cdot 12 \cdot 16}\) – …………..

Question 2.
If t = \(\frac{4}{5}+\frac{4 \cdot 6}{5 \cdot 10}+\frac{4 \cdot 6 \cdot 8}{5 \cdot 10 \cdot 15}\) + ……….. ∞, then prove that 9t = 16.
Solution:
Given
t = \(\frac{4}{5}+\frac{4 \cdot 6}{5 \cdot 10}+\frac{4 \cdot 6 \cdot 8}{5 \cdot 10 \cdot 15}\) + ……….. ∞

Question 3.
If x = \(\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}+\ldots\) then prove that 9x² + 24x = 11.
Solution:
Given x = \(\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}+\ldots\)

⇒ \(\frac{4}{3}\) + x = √3
⇒ 4 + 3x = 3√3
⇒ 16 + 9x² + 24x = 27
⇒ 9x² + 24x = 11.

Question 4.
If x = \(\frac{5}{(2 !) \cdot 3}+\frac{5 \cdot 7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots \ldots\) then find the value of x² + 4x.
Solution:
x = \(\frac{5}{(2 !) \cdot 3}+\frac{5 \cdot 7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots \ldots\)

∴ (1) ⇒ 2 + x = \(\left(1-\frac{2}{3}\right)^{-\frac{3}{2}}\)
⇒ 2 + x = \(\left(\frac{1}{3}\right)^{\frac{-3}{2}}\)
⇒ 2 + x = √27
⇒ x² + 4x = 23.

Question 5.
Find the sum to infinite terms of the series \(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1 \cdot 3}{1 \cdot 2} \cdot \frac{1}{10^4}+\frac{1 \cdot 3 \cdot 5}{1 \cdot 2 \cdot 3} \cdot \frac{1}{10^6}+\ldots\right)\)
Solution:
Let y = \(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1 \cdot 3}{1 \cdot 2} \cdot \frac{1}{10^4}+\frac{1 \cdot 3 \cdot 5}{1 \cdot 2 \cdot 3} \cdot \frac{1}{10^6}+\ldots\right)\)

Question 6.
Show that for any non-zero rational number x.
\(1+\frac{x}{2}+\frac{x(x-1)}{2 \cdot 4}+\frac{x(x-1)(x-2)}{2 \cdot 4 \cdot 6}+\ldots .\) = \(1+\frac{x}{3}+\frac{x(x+1)}{3 \cdot 6}+\frac{x(x+1)(x+2)}{3 \cdot 6 \cdot 9}+\ldots .\)
Solution:
L.H.S = \(1+\frac{x}{2}+\frac{x(x-1)}{2 \cdot 4}+\frac{x(x-1)(x-2)}{2 \cdot 4 \cdot 6}+\ldots .\)