TS Inter 2nd Year Maths 2A Measures of Dispersion Important Questions

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 8 Measures of Dispersion to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Measures of Dispersion Important Questions

Question 1.
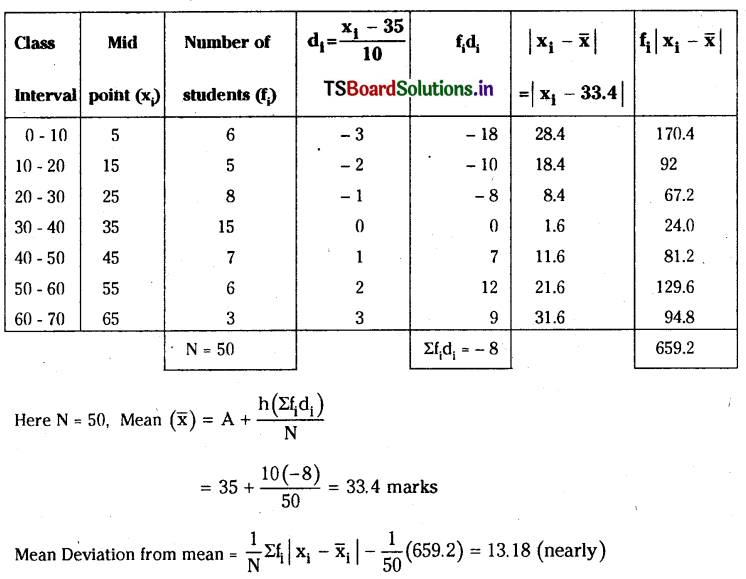
Find the mean deviation from the mean of the following data, using the step deviation method.

Solution:

Question 2.
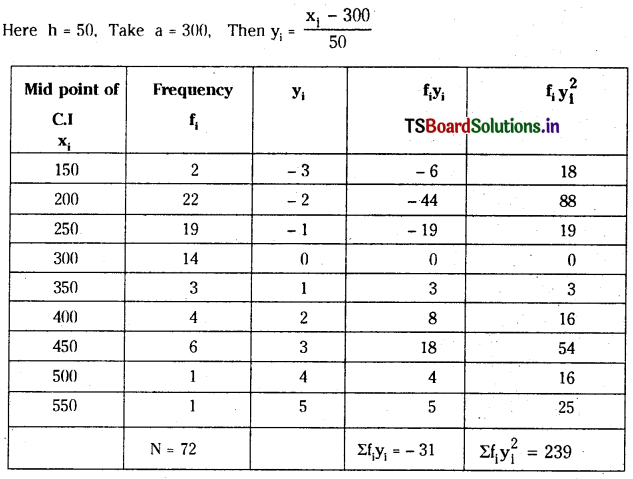
The following table gives the daily wages of workers in a factory. Compute the standard deviation and the coefficient of variation of the wages of the workers.

Solution:
We shall solve this problem using the step deviation method, since the mid points of the class intervals are numerically large.

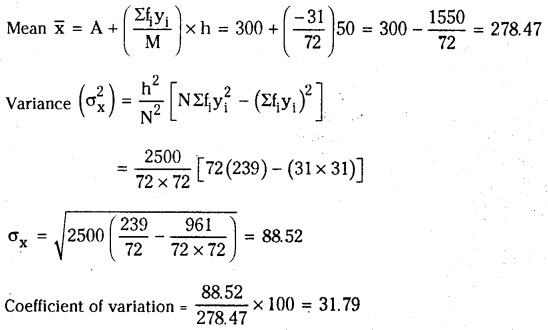
Question 3.
An analysis of monthly wages paid to the workers of two firms A and B belonging to the same industry gives the following data.

	Firm A	Firm B
Number of workers The average daily wage (Rs.) Variance of distribution of wages	500 186 81	600 175 100

i) Which firm A or B, has greater variability in individual wages?
ii) Which firm lias a larger wage bill?
Solution:

Since C.V. of firm B is greater than CV. of firm A, we can say that firm B has greater variability in individual wages.

(ii) Firm A has number of workers i.e., wage earners (n₁) = 500
Its average daily wage, say \(\overline{\mathbf{x}}_1\) Rs. 186
Since Average daily wage = \(\frac{Total Wages Paid}{no.of Workers}\), it follows that total wages paid to the workers
n₁\(\overline{\mathbf{x}}_1\) = 500 x 186 – Rs.93,000
Firm B has number of wage earners (n₂) – 600
Average daily wage, say \(\overline{\mathbf{x}}_2\) = Rs 175
∴ Total daily wages paid to the workers n₂\(\overline{\mathbf{x}}_2\) 600 x 175 = Rs. 1,05,000
Hence we see that firm B has larger wage bill.

Question 4.
The variance of 20 observations is 5. If each of the observations is multiplied by 2, find the variance of the resulting observations.
Solution:
Let the given observations be x₁, x₂ ……………….. x₂₀ and \(\overline{\mathbf{x}}\) be their mean.
Given that n = 20 and variance = 5

Note: From this example we note that, if each observation in a data is multiplied by a constant k, then the variance of the resulting observations is k² time that of the variance of original observations.

Question 5.
If each of the observations x₁, x₂, ………………….., x_n is increased by k, where k is a positive or negative number, their show that the variance remains unchanged.
Solution:
Let \(\overline{\mathbf{x}}\) be the mean of x₁, x₂, ………………….., x_n. Then their variance is given by
\(\sigma_1^2=\frac{1}{n} \sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^2\)
If to each observation we add a constant k, then the new (changed) observations will be y_i = x_i+k …………….. (1)

Thus the variance of the new observations is the same as that of the original observations.
Note: We note that adding (or subtracting) a positive number to (or form) each of the given set of observations does not affect the variance.

Question 6.
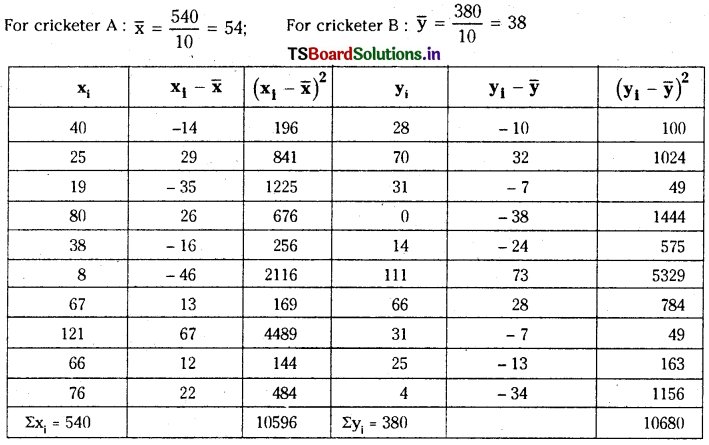
The scores of two cricketers A and B in 10 innings are given below. Find who is a better run getter and who is a more consistent player.

Solution: