TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(c)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Exercise 7(c)

I. Find the values of the following integrals.

Question 1.
\(\int_0^{\frac{\pi}{2}} \sin ^{10} x d x\) (May ’06; Mar. ’03)
Solution:

Question 2.
\(\int_0^{\frac{\pi}{2}} \cos ^{11} x d x\)
Solution:

Question 3.
\(\int_0^{\frac{\pi}{2}} \cos ^7 x \sin ^2 x d x\)
Solution:
\(\int_0^{\frac{\pi}{2}} \sin ^m x \cos ^n x d x\)

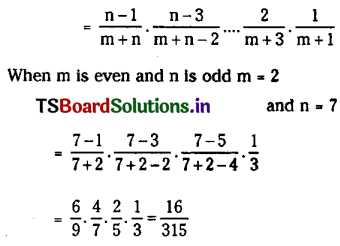
Question 4.
\(\int_0^{\frac{\pi}{2}} \sin ^4 x \cos ^4 x d x\)
Solution:

Question 5.
\(\int_0^\pi \sin ^3 x \cos ^6 x d x\)
Solution:
We have \(\int_0^{2 a} f(x) d x=2 \int_0^a f(x) d x\)
if f(2a – x) = f(x)

Question 6.
\(\int_0^{2 \pi} \sin ^2 x \cos ^4 x d x\)
Solution:
Take f(x) = sin²x cos⁴x
Then f(π – x) = sin²(π – x) cos⁴(π – x)
= sin²x cos⁴x
= f(x)

Question 7.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 \theta \cos ^7 \theta d \theta\)
Solution:
f(θ) = sin²θ cos⁷θ
f(-θ) = sin²(-θ) cos⁷(-θ)
= sin²θ cos⁷θ
= f(θ); and f is even

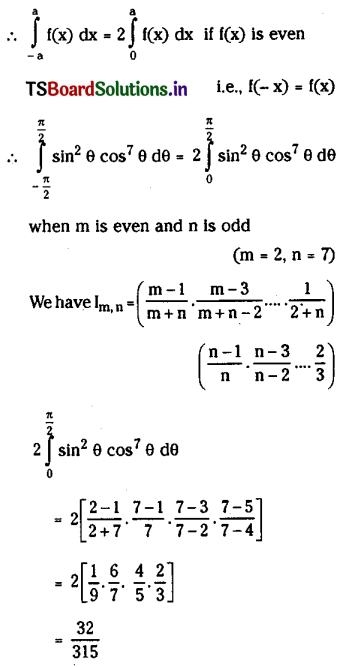
Question 8.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^3 \theta \cos ^3 \theta d \theta\)
Solution:
Let f(θ) = sin³θ cos³θ
∴ f(-θ) = sin³(-θ) cos³(-θ)
= -sin³θ cos³θ
= -f(θ)
∴ f is an odd function.
Hence \(\int_{-a}^a f(x) d x=0\) when f is odd.
∴ \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^3 \theta \cos ^3 \theta d \theta=0\)

Question 9.
\(\int_0^a x\left(a^2-x^2\right)^{\frac{7}{2}} d x\)
Solution:
Take x = a sin θ then dx = a cos θ dθ
Upper limit when x = a is θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is θ = 0

Let cos θ = t then -sin θ dθ = dt
Upper limit when θ = \(\frac{\pi}{2}\) is t = 0
Lower limit when θ = 0 is t = 1

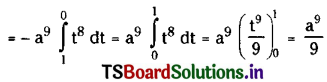
Question 10.
\(\int_0^2 x^{\frac{3}{2}} \sqrt{2-x} d x\)
Solution:
Take x = 2 sin²θ, then dx = 4 sin θ cos θ dθ
Upper limit when x = 2 is sin²θ = 1 ⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is sin²θ = 0 ⇒ θ = 0

II. Evaluate the following integrals.

Question 1.
\(\int_0^1 x^5(1-x)^{\frac{5}{2}} d x\)
Solution:
Let x = sin²θ then dx = 2 sin θ cos θ dθ
Upper limit when x = 1 is θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is θ = 0

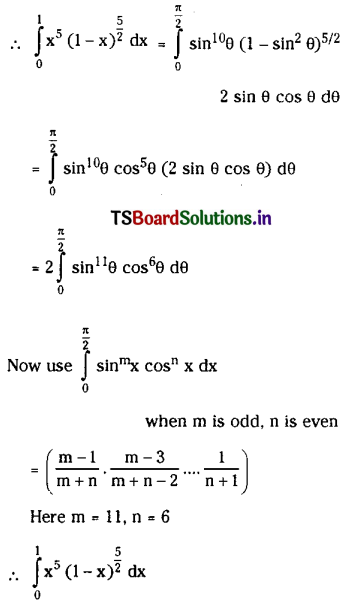
Question 2.
\(\int_0^4\left(16-x^2\right)^{\frac{5}{2}} d x\)
Solution:
Let x = 4 sin θ then dx = 4 cos θ dθ
Upper limit when x = 4 is θ = \(\frac{\pi}{2}\)
and Lower limit when x = 0 is θ = 0

Question 3.
\(\int_{-3}^3\left(9-x^2\right)^{\frac{3}{2}} x d x\)
Solution:
Let x = 3 sin θ then dx = 3 cos θ dθ
Upper limit when x = 3 is θ = \(\frac{\pi}{2}\)
and Lower limit when x = -3 is θ = \(-\frac{\pi}{2}\)

Question 4.
\(\int_0^5 x^3\left(25-x^2\right)^{\frac{7}{2}} d x\)
Solution:
Let x = 5 sin θ then
Upper limit when x = 5 is θ = \(\frac{\pi}{2}\)
and Lower limit when x = 0 is θ = 0

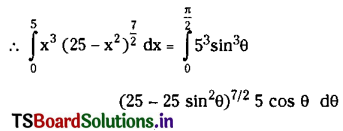
Question 5.
\(\int_{-\pi}^\pi \sin ^8 x \cos ^7 x d x\)
Solution:
Take f(x) = sin⁸x cos⁷x
then f(-x) = sin⁸(-x) cos⁷(-x)
= sin⁸x cos⁷x
= f(x)
f is an even function of x.
∴ \(\int_{-\pi}^\pi \sin ^8 x \cos ^7 x d x=2 \int_0^\pi \sin ^8 x \cos ^7 x d x\)
Now f(x) = sin⁸x cos⁷x
and f(π – x) = sin⁸(π – x) cos⁷(π – x)
= -sin⁸x cos⁷x
= -f(x)
Hence \(\int_0^\pi \sin ^8 x \cos ^7 x d x=0\)
∴ \(\int_{-\pi}^\pi \sin ^8 x \cos ^7 x d x=0\)
[By the result that f = [0, 2a] → R is integrable on [0, a] and if f(2a – x) = -f(x) ∀ x ∈ [a, 2a] then \(\int_0^{2 a} f(x) d x=0\)]

Question 6.
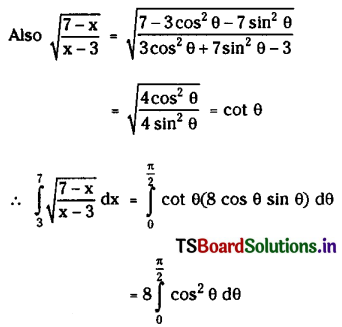
\(\int_3^7 \sqrt{\frac{7-x}{x-3}} d x\)
Solution:
Let x = 3 cos²θ + 7 sin²θ then
dx = -6 cos θ sin θ + 14 sin θ cos θ = 8 cos θ sin θ
Upper limit when x = 7 is
7 = 3 cos²θ + 7 sin²θ
⇒ 7(1 – sin²θ) = 3 cos²θ
⇒ cos θ = 0
⇒ θ = \(\frac{\pi}{2}\)
The lower limit when x = 3 is
3 = 3 cos²θ + 7 sin²θ
⇒ 3 sin²θ = 7 sin²θ
⇒ 4 sin²θ = 0
⇒ sin θ = 0
⇒ θ = 0

Question 7.
\(\int_2^6 \sqrt{(6-x)(x-2)} d x\)
Solution:
Put x = 2 cos²θ + 6 sin²θ
then dx = (-4 cos θ sin θ + 12 sin θ cos θ) dθ = 8 sin θ cos θ dθ
Upper limit when x = 6 is 6 = 2 cos²θ + 6 sin²θ
⇒ 6 cos²θ = 2 cos²θ
⇒ 4 cos²θ = 0
⇒ cos θ = 0
⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 2 is 2 = 2 cos²θ + 6 sin²θ
⇒ 2 sin²θ = 6 sin²θ
⇒ 4 sin²θ = 0
⇒ sin θ = 0
⇒ θ = 0

Question 8.
\(\int_0^{\frac{\pi}{2}} \tan ^5 x \cos ^8 x d x\)
Solution:

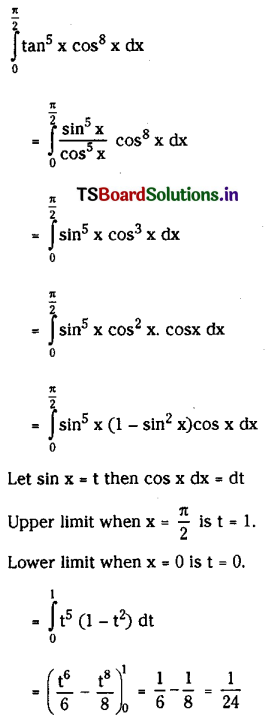
III. Evaluate the following integrals.

Question 1.
\(\int_0^1 x^{7 / 2}(1-x)^{5 / 2} d x\)
Solution:
Let x = sin²θ then dx = 2 sin θ cos θ dθ
Upper limit when x = 1 is sin²θ = 1 ⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is sin²θ = 0 ⇒ θ = 0

Question 2.
\(\int_0^\pi(1+\cos x)^3 d x\)
Solution:

Question 3.
\(\int_4^9 \frac{d x}{\sqrt{(9-x)(x-4)}}\)
Solution:
Take x = 4 cos²θ + 9 sin²θ then
dx = (-8 cos θ sin θ + 18 sin θ cos θ) dθ = 10 cos θ sin θ
Upper limit when x = 9 is 9 = 4 cos²θ + 9 sin²θ
⇒ 9(1 – sin²θ) = 4 cos²θ
⇒ 5 cos²θ = 0
⇒ cos θ = 0
⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 4 is 4 = 4 cos²θ + 9 sin²θ
⇒ 4(1 – cos²θ) = 9 sin²θ
⇒ 5 sin²θ = 0
⇒ sin θ = 0
⇒ θ = 0

Question 4.
\(\int_0^5 x^2(\sqrt{5-x})^7 d x\)
Solution:
Let x = 5 sin²θ then dx = 10 sin θ cos θ dθ
Upper limit when x = 5 is sin²θ = 1 ⇒ θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is sin²θ = 0 ⇒ θ = 0

Question 5.
\(\int_0^{2 \pi}(1+\cos x)^5(1-\cos x)^3 d \dot{x}\)
Solution: