TS Inter 2nd Year Maths 2A Random Variables and Probability Distributions Important Questions

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 10 Random Variables and Probability Distributions to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Random Variables and Probability Distributions Important Questions

Question 1.
A cubical die is thrown. Find the mean and variance of X, giving the number on the face that shows up.
Solution:
Let S be the sample space and X be the random variable associated with S, where P(X) is given by the following table.

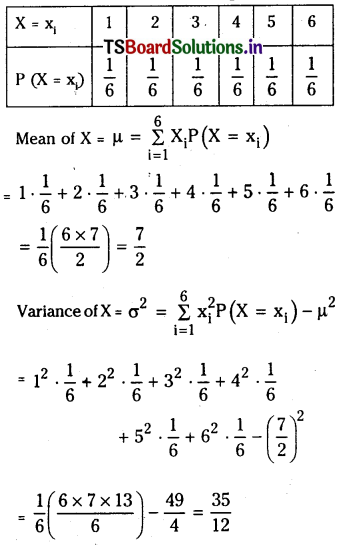
Question 2.
The probability distribution of a random variable X is given below:

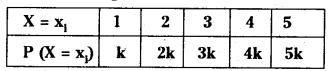
Find the value of k and the mean and variance of X.
Solution:

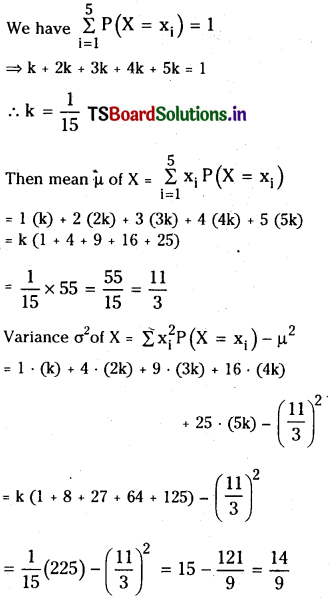
Question 3.
If x is a random variable with probability distribution p(X=k)=\(\frac{(k+1) c}{2^k}\) k = 0,1,2 ………… then find c.
Solution:
Since p(X=k)=\(\frac{(k+1) c}{2^k}\) k = 0,1,2 ……….. is the probability distribution of x

Question 4.
Let X be a random variable such that
P(x=-2) = P(X = -1) = P(X=2)
P(X = 1) = \(\frac{1}{6}\) and P(X = 0) \(\frac{1}{3}\)
Find the mean and variance of X.
Solution:

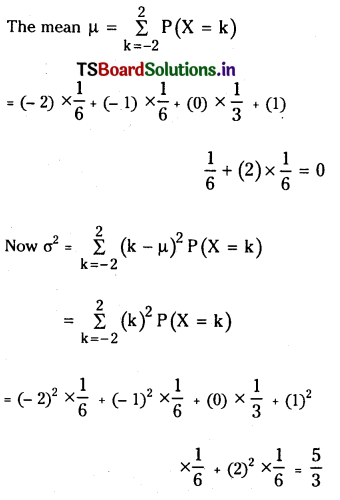
Question 5.
Two dice are roiled at random. Find the probability distribution of the sum of the numbers on them. Find the mean of the random variable.
Solution:
When two dice are rolled, the sample space S consists of 6 x 6 = 36 sample points
S = ((1, 1), (1, 2), (1, 6), (2, 1), (2, 6),(6, 6)).
Let X denote the sum of the numbers on the two dice. Then the range of X = {(2, 3, 4 , 12)}
The probability distribution for X is given here under:

Question 6.
8 coins are tossed simultaneously. Find the probability of getting atleast 6 heads.
Solution:
In the experiment of tossing a coin, the probability of getting a head \(\frac{1}{2}\) and the probability of getting a tail \(\frac{1}{2}\). The probability of getting r heads in a random throw of 8 coins is

Question 7.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X≥1).
Solution:
Here x = B(n,p) is specified by np = 4 = μ and npq = σ² = 3

Question 8.
The probability that a person chosen at random is left handed (in hand wilting) is 0.1. What is the probability that in a group of 10 people, there is one who is left handed.
Solution:
Heye n = 10, find p =\(\frac{1}{10}\) = 0.1.
Hence q = 0.9
We have to find P(X = 1); the probability that
exactly one out of 10 is left handed
P(X = 1) = ¹⁰C₁ p¹ q^10-1
= 10 x 0.1 x (0.9)⁹ = (0.9)⁹

Question 9.
In a book of 450 pages, there are 400 typo graphical errors. Assuming that the number of errors per page follow the Poisson law, find the probability that a random sample of 5 pages will contain no typo graphical error.
Solution:
The average number of errors per page in the book is \(\lambda=\frac{400}{450}=\frac{8}{9}\)
The probability that there are r errors per page:

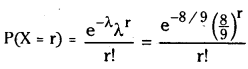
Hence P(X=0) = e^-8/9
The required probability that a random sample of 5 pages will contain no error is [P(X) = 0)]⁵ = (e^-8/9)⁵

Question 10.
The deficiency of red cells In the blood cells is determined by examining a specimen of blood under a microscope. Suppose a small fixed volume contains on an average 20 red cells for normal persons. Using the Poisson distribution, find the probability that a specimen of blood taken from a normal person will contain less than 15 red cells.
Solution:
Here λ = 20.
Let P(X = r) denote the probability that a specimen taken from a normal person will contain r red cells.
Then we have P(X < 15)

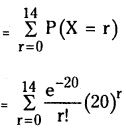
Question 11.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5).
Solution: