TS Inter 2nd Year Maths 2A Partial Fractions Important Questions

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 7 Partial Fractions to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Partial Fractions Important Questions

Question 1.
Resolve \(\frac{5 x+1}{(x+2)(x-1)} \) into partial fraction.
Solution:
Let \(\frac{5 x+1}{(x+2)(x-1)}=\frac{A}{x+2}+\frac{B}{x-1}\)
where A and B are non-zero numbers to be determined.
Then \(\frac{5 x+1}{(x+2)(x-1)}=\frac{A(x-1)+B(x+2)}{(x+2)(x-1)}\)
∴ A(x – 1)+B(x+2)5x+1
Putting x = 1 in (1), we get
3B = 5 +1 i.e.., B = 2
Putting x = – 2 in (1) we get
– 3A=-.9 i.e., A=3
∴ \(\frac{5 x+1}{(x+2)(x-1)}=\frac{3}{x+2}+\frac{2}{x-1}\)

Question 2.
Resolve \(\frac{2 x+3}{5(x+2)(2 x+1)}\) into partial fraction.
Solution:
Let \(\frac{2 x+3}{(x+2)(2 x+1)}=\frac{A}{x+2}+\frac{B}{2 x+1}\)
where A and B are non-zero real numbers, to be determined.

Question 3.
Resolve \(\frac{13 x+43}{2 x^2+17 x+30}\) into partial fraction.
Solution:
We have 2x² + 17x + 34) = (2x + 5) (X + 6)

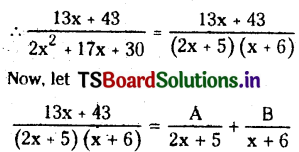
∴ 13x+43 = A(x+6) + B(2x+ 5)
= (A + 2B)x + (6A + 5B)
Comparing the coefficients of like powers of x, we have
A+2B=13 and 6A+5B = 43
Solving these two equations.
we get A = 3 and R = 5
∴ \(\frac{13 x+43}{2 x^2+17 x+30}=\frac{3}{2 x+5}+\frac{5}{x+6}\)

Question 4.
Resolve \(\frac{x^2+5 x+7}{(x-3)^3}\) into partial fraction
Solution:

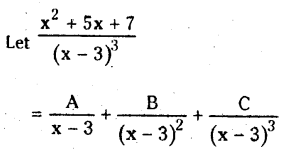
where A, B and C are constants determined.
∴ \(\frac{\mathrm{x}^2+5 \mathrm{x}+7}{(\mathrm{x}-3)^3}=\frac{\mathrm{A}(\mathrm{x}-3)^2+\mathrm{B}(\mathrm{x}-3)+\mathrm{C}}{(\mathrm{x}-3)^3}\)
∴ x²+ 5x + 7 = A x² +(B – 6A)x  + (9A – 3B + C)
Now comparing the cçefficients of like powers of x in (1), we get
A=1,B – 6A = 5, 9A – 3B +C = 7
Solving these equations, we get
A = 1, B = 11, C = 31

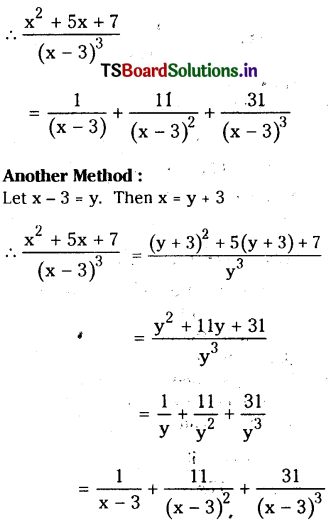
Question 5.
Resolve \(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}\) into partial fraction
Solution:
Here (2x + 3) is a linear factor and (x + 3) is, a repeated linear factor. We apply Rules I and-II, and write
\(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}\)

Question 6.
Resolve \(\frac{1}{(x-1)^2(x-2)}\) into partial fraction
Solution:

Equating the corresponding coefficients, we have
A+C=0, – 3A+ B – 2C = 0 2A-2B+C= 1
Solving these equations, we get
A= -1, B = – 1, C = 1

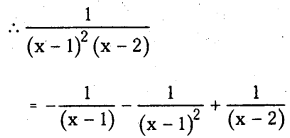
Question 7.
Resolve \(\frac{3 x-18}{x^3(x+3)}\) into partial fraction
Solution:

Equating the corresponding coefficients, we have
A+D = 0, 3AB=0, 3B+C=3, 3C=-18
Solving these equations, we get
A=-1,B=3,C=-6, D=1
∴ \(\frac{3 x-18}{x^3(x+3)}=\frac{-1}{x}+\frac{3}{x^2}-\frac{6}{x^3}+\frac{1}{(x+3)}\)

Question 8.
Resolve \(\frac{x-1}{(x+1)(x-2)^2}\) into partial fraction
Solution:

Question 9.
Resolve \(\frac{2 x^2+1}{x^3-1}\) into partial fraction
Solution:

∴ 2x²+1=(A+B)x²+(A-B+C)x+(A-C)
∴ Comparing the corresponding coefficients, we have
A B = 2, A – B + C = 0, A-C = 1
Solving these equations, we get
A = 1, B = 1, C = 0
∴ \(\frac{2 x^2+1}{\left(x^3-1\right)}=\frac{1}{x-1}+\frac{x}{x^2+x+1}\)

Question 10.
Resolve \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) into partial fraction.
Solution:

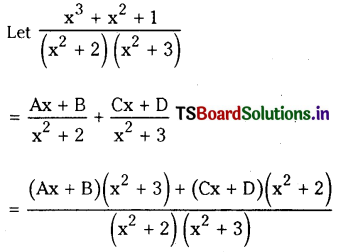
∴ x³+x²+1(A+C)x³+(B+D)x²+(3A+2C)x+(3B+2D) = 1
Comparing the corresponding coefficients, we have
A+C = 1, B+D = 1, 3A+2C = 0,3B+2D = 1
Solving these equations, we get
A=-2, B=-1,C=3,D= 2

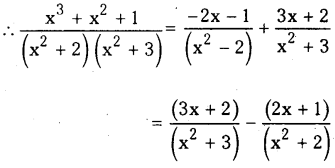
Question 11.
Resolve \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}\) into partial fraction.
Solution:
x⁴ +x² +1=(x +1) – x
(x²+x+ t)(x²-x+ 1)

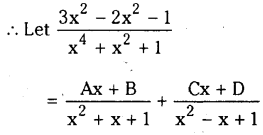
= (Ax+B)(x²-x+1)+(Cx+D)(x²+x+1)
=3x – 2x – 1 ……………….. (1)
Comparing the coefficients of
x³, x² , x and constants in (1), we get
A+C = 3 …………………….. (2)
– A+B+C+D – 2 …………………. (3)
A – B+C+D = 0 …………………… (4)
B+D = – 1 …………………… (5)
From (2), C = 3 – A …………………… (6)
and from (5), D = – 1 – B …………………… (7)
Putting these values in (3) we get
– A+ B + 3 – A – 1 – B  – 2
∴  – 2A = – 4 or A = 2
Similarly from (4) we get
A-B + 3 – A – 1 -B= 0
∴ – 2B=- 2 or B = 1
∴ From (6); C = 3 – A= 3 – 2= 1
and from(7); D= – 1 – B= – 1  – 1 = – 2
∴ \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{2 x+1}{x^2+x+1}+\frac{x-2}{x^2-x+1}\)
To find the partial fractions of \(\frac{f(x)}{g(x)}\), when g(x) contains repeated irreducible factor, we use the following rule.

Question 12.
Resolve \(\frac{x^4+24 x^2+28}{\left(x^2+1\right)^3}\) into partial fraction.
Solution:

Comparing the corresponding coefficients.
we have
A = 0, B = 1. 2A C =0, 2B + D = 24,
A+C+E = 0 , B + D+F=28 .
Solving these equations, we get
A = 0,B = 1, C = 0, D= 22, E = 0, F=,5

Question 13.
Resolve \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) into partial fraction.
Solution:

Question 14.
Resolve  \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\) into partial fraction.
Solution:
The given fraction is improper with degree of the numerator equal to degree of denominator.

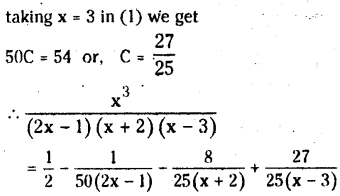
Question 15.
Resolve \(\frac{x^4}{(x-1)(x-2)}\) into partial fraction.
Solution:
By dividing x⁴ with (x – 1) (x -2) we get

Question 16.
Find the coefficient of x⁴ in the expansion of  \(\frac{3 x}{(x-2)(x+1)}\) in powers of specifying the interval in which the expansion is valid.
Solution:
Resolving the given fraction into partial fractions we get

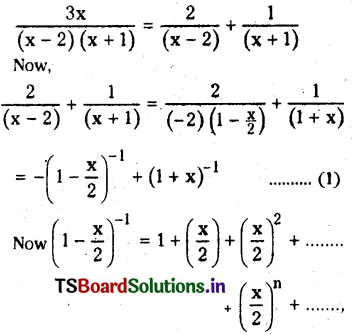
Question 17.
Find the coefficient of xⁿ in the power series of expansion of \(\frac{x}{(x-1)^2(x-2)}\) specifying the region in which the expansion is valid.
Solution:
Resolving the given fraction into partial fractions, we get