TS Inter 2nd Year Maths 2A Complex Numbers Important Questions

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 1 Complex Numbers to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Complex Numbers Important Questions

Question 1.
Express \(\frac{4+2 i}{1-2 i}+\frac{3 r 4 i}{2+3 i}\) in the form a + bi, a ∈ R, b ∈ R.
Solution:

Question 2.
Find the real and Imaginary parts of the complex number \(\frac{a+i b}{a-i b}\)
Solution:

Question 3.
Express (1 – i)³(1+i) in the of on a+ib.
Solution:
(1 – i)³ (1 + i) = (1 -i)² (1 – 1) (1 + 1)
– (1 +i² – 2i)(1²– i²)
(1 – 1 – 2i) (1 +1) 2(0 – 2i)
= 0  – 4i = 0 + (i – 4)

Question 4.
Find the multiplicative Inverse of 7 + 24i.
Solution:
Since \((x+i y)\left(\frac{x-i y}{x^2+y^2}\right)=1\) it follows that the multiplicative inverse of
(x+iy) is \(\frac{x-i y}{x^2+y^2}\)
Hence the multiplicative inverse of 7 + 24i is
\(\frac{7-24 i}{(7)^2+(24)^2}=\frac{7-24 i}{49+576}=\frac{7-241}{625}\)

Question 5.
Determine the locus of z, z ≠ 2i, such that Re \(\left(\frac{z-4}{z-2 i}\right)=0\)
Solution:
Let z = x + iy, then


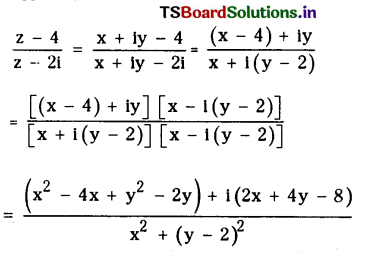
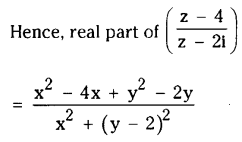
The ratio on the R.H.S is zero
i.e., x² – 4x + y² – = 0 if and only if (x – 2)² (y – 1)² =5.
⇔ x,y≠(0, 2) and (x – 2)²+(y – 1)²=5
Hence the locus of the given point representing the complex number is the circle with (2, 1) as centre and \(\sqrt{5}\) units as radius except for the point (0, 2).

Question 6.
If 4x+i(3x – y) = 3 – 6i where x and y are real numbers, then find the values of x and y.
Solution:
We have 4x+i(3x-y)=3+i(-6).
Equating the real and imaginary parts in the above equation, we get
4x = 3, 3x  – y = – 6. Upon solving the simultaneous equations, we get
x = 3/4 and y = 33/4.

Question 7.
If z=2 – 3i, then show that z² – 4z+ 13=0.
Solution:
z = 2 – 3i ⇒ z – 2= – 3i = (z -2)²=(-3i)²
⇒ z² + 4 – 4z = – 9
⇒ z²– 4z+ 13=0

Question 8.
Find the complex conjugate of (3+4i) (2-3i).
Solution:
The given complex number
(3+4i) (2-3i) = 6 – 9i + 8i + 12 = 18 – i
Its complex conjugate = 18 + i.

Question 9.
Show that \(z_1=\frac{2+11 i}{25}, \quad z_2=\frac{-2+i}{(1-2 i)^2}\)
Solution:

Since this complex number is the conjugate of \(\frac{2+11 i}{25}\) the given complex numbers z₁, z₂ are conjugate to each other.

Question 10.
Find the square roots of (-5+ 12f).
Solution:
From 1.2.8, we have

Question 11.
Write \(z=-\sqrt{7}+i \sqrt{21}\) in the polar form.
Solution:

Question 12.
Express – 1 – i in polar form with principal value of the amplitude.
Solution:
Let  – 1  – 1 = r (cos θ + i sin θ).
Then – i = rcosθ,- 1 = r sinθ and tanθ = 1 …………….. (1)
∴ r² = 2, i.e., r = ± \(\sqrt{2}\)
Since r is positive, r = \(\sqrt{2}\)
Since ‘θ’ satisfies – π ≤ 0 < π, the value of θ satisfying the equation (1) is θ \(=\frac{-3 \pi}{4}\)
∴ \(-1-i=\sqrt{2}\left[\cos \left(-\frac{3 \pi}{4}\right)+i \sin \left(\frac{-3 \pi}{4}\right)\right]\)

Question 13.
If the amplitude of \(\left(\frac{z-2}{z-6 i}\right)=\frac{\pi}{2}\),find its locus.
Solution:

The points satisfying (1) and (2) constitute the arc of the circle x² + y² – 2x – Gy = 0 intercepted by the diameter
3x + y – 6 = 0 not containing the origin and excluding the points (0, 6) and (2, 0). Hence this arc is the required locus.

Question 14.
Show that the equation of any circle in the complex plane is of the form
\(\mathbf{z} \overline{\mathbf{z}}+\mathbf{b} \overline{\mathbf{z}}+\overline{\mathbf{b}} \mathbf{z}+\mathrm{c}=\mathbf{0},(\mathbf{b} \in \mathrm{C} ; c \in R)\)
Solution:
Assume the general form of the equation of a circle in Cartesian coordinates as
x²+y²+2gx+2fy+c=0, (g,f ∈ R) …………………. (1)
To write this equation in the complex variable form.
Let (x, y) = z. Then

Question 15.
Show that the complex numbers z satisfying \(z^2+\bar{z}^2=2\) constitute a hyperbola.
Solution:
Substituting z = x + ¡y in the given equation \(z^2+\bar{z}^2=2\) we obtain the Cartesian form of the given equation.
∴ (x+iy)²+(x-iy)²=2
i.e., x² – y² + 2 ixy + x² – y² – 2ixy = 2
or 2x² + 2(iy)² = 2
i.e., x² – y² = 1
Since this equation denotes a hyperbola, all the complex numbers satisfying \(z^2+\bar{z}^2=2\) constitute the hyperbola x² – y² = 1.

Question 16.
Show that the points In the Argand diagram represented by the complex numbers 1 + 3i, 4 – 3i, 5 – 5i are collinear.
Solution:
Let the three complex numbers be represented in the Argand plane by the points
P, Q, R respectively. Then P = (1, 3),Q = (4, – 3) and R = (5, – 5).
The slope of the line segment joining P, Q is \(\frac{3+3}{1-4}=\frac{6}{-3}=-2\)
Similarly, the slope of the line segment joining Q, R is \(\frac{-3+5}{4-5}=\frac{2}{-1}=-2\). Since the slope of PQ is the slope of QR, the points P, Q, R are collinear.

Question 17.
Find the equation of the straight line joining the points represented by (-4 + 3i), (2-3i) in the Argand plane.
Solution:
Take the given points as A= – 4 + 3i = (-4,3)  B=2-3i = (2,-3).
Then the equation of the straight line \(\overline{\mathrm{AB}}\) is
y – 3 = \(\frac{3+3}{-4-2}\) (x +4)
i.e, x + y +1 = 0

Question 18.
z=x+iy represents a point in the Argand plane. Find the locus of z such that lzl = 2.
Solution:
Let z = x + ¡y, Then |z|=2 if and only if
|x + iy| = 2 if and only if 4x² + y² = 2 if and only if x² + y² = 4.
x² + y² = 4 represents a circle with centre at (0,0) and radius 2.
∴ The locus of |z|=2 is the circle x²+ y² = 4.

Question 19.
The point P represents a complex number z in the Argand plane. If the amplitude of \(\mathrm{z} is \frac{\pi}{4}\), determine the locus of P.
Solution:
Let z=x+i y

Question 20.
If the point P denotes the complex number z=x+iy in the Argand plane and if \(\frac{z-i}{z-1}\) is a purely imaginary number, find the locus of P.
Solution:
We note that \(\frac{z-1}{z-1}\) is not defined If z = 1.

i.e., x² + y²– x- y = 0 and (x, y) ≠ (1, 0).
∴ The locus of P is the circle
x² + y²– x – y = 0 excluding the point (1, 0).

Question 21.
Describe geometrically the following subsets of C:
(i) { z ∈ C| | z – 1+i | = 1
(ii) { z ∈ C| | z + 1+i| ≤ 3
Solution:
(i) Let S = {z ∈ C| | z – 1+i | = 1)
If we write z (x, y), then

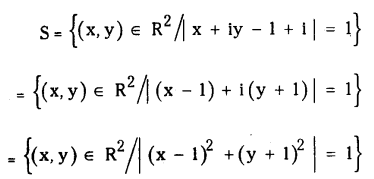
Hence S is a circle with centre (1, – 1) and radius 1 unit.

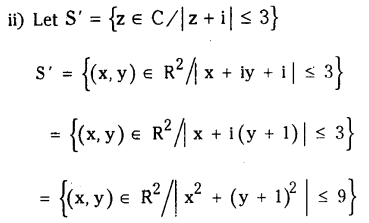
Hence s’ is the closed circular disc with centre at (0, – 1) and radius 3 units.