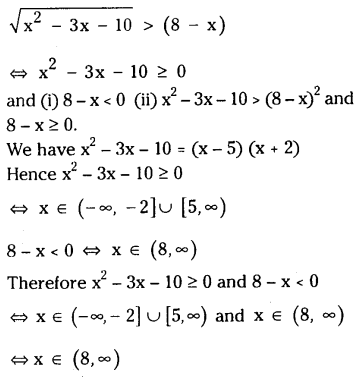TS Inter 2nd Year Maths 2A Quadratic Expressions Important Questions

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 3 Quadratic Expressions to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Quadratic Expressions Important Questions

Question 1.
Find the roots of the equation
3x² + 2x – 5 = 0.
Solution:
The roots of the quadratic equation
ax + bx + c = 0 are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
Here a = 3, b = 2 and c = – 5.
Therefore the roots of the given equation are

Hence 1 and – \(\frac{5}{3}\) are the roots of the given equation.

Another method:
We can also obtain these roots in the following way.
3x² + 2x – 5 = 3x² + 5x -3x – 5
= x(3x+5) – 1 (3x+5)
= (x-1) (3x + 5)
= 3 (x – 1) \(\left(x+\frac{5}{3}\right)\)
Since 1 and \(\frac{5}{3}\) are the zeros of 3x² + 2x – 5, they are the roots of 3x² + 2x – 5 = 0.

Question 2.
Find the roots of the equation
4x²– 4x + 17 = 3x² – 10x – 17.
Solution:
Given equation can be rewritten as x² + 6x + 34 = 0.
The roots of the quadratic equation, ax² + bx + c = 0 are
\(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
Therefore the roots of the given equation are

Hence the roots of the given equation are
– 3 + 5i and -3-5i

Question 3.
Find the roots of the equation
\(\sqrt{3} x^2+10 x-8 \sqrt{3}=0\)
Solution:
The roots of the quadratic equation a+ b

Question 4.
Find the nature of the roots of 4x² – 20x + 25 = 0.
Solution:
Here a = 4, b = -20 and c = 25
Hence Δ = b² – 4ac = (-20)²– 4 (4) (25) = 0
Since Δ is zero and a, b, c are real, the roots of the given equation are real and equal.

Question 5.
Find the nature of the roots of 3x² + 7x + 2 = 0.
Solution:
Here a=3, b=7 and c=2
Hence = b² – 4ac
= (7)² 4(3) (2) = 25 = 5²  > 0.
Since Δ = 5 is a square number, the roots of the given equation are rational and unequal.

Question 6.
For what values of m, the equation x² – 2 (1 + 3m) x + 7 (3 + 2m) = 0 will have equal roots?
Solution:
The given equation will have equal roots if its discriminant is 0.
Here Δ = {- 2(1+3m))}² + 4(1) 7(3 + 2m)
= 4(1+3m)² – 28 (3+2m) = 4(9m² – 8m – 20)
= 4 (m – 2) (9m + 10) = 36 (m – 2) m + \(\left(m+\frac{10}{9}\right)\)
Hence Δ = 0 ⇔ m = 2 or m= \(-\frac{10}{9}\)
Therefore the roots of the given equation are equal \(\left\{-\frac{10}{9}, 2\right\}\)

Question 7.
If α and β are the roots of ax² +bx + c = 0, find the values of α² + β² and α³ + β³ in terms of a, b, c.
Solution:
From the hypothesis

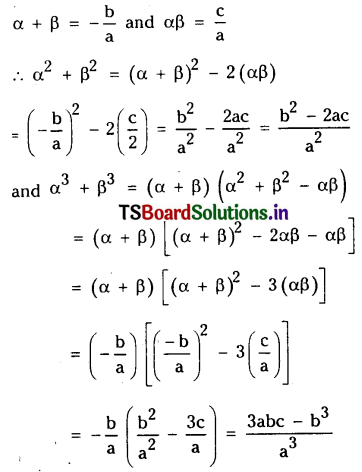
Question 8.
Form a quadratic equation whose roots are 2\(\sqrt{3}\) -5 and -2\(\sqrt{3}\) – 5.
Solution:

Question 9.
Let α and β be the roots of the quadratic equation ax² + bx + c = 0. If c ≠ 0, then form the quadratic equation whose roots are \(\frac{1-\alpha}{\alpha}\) and \(\frac{1-\beta}{\beta}\)
Solution:
From the hypothesis we have

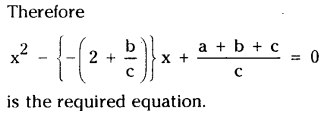
Question 10.
Find a quadratic equation, the sum of whose roots is I and the sum of the squares of the roots is 13.
Solution:
Let a and 3 be the roots of a required equation

Therefore x² – a + x a = 0 becomes  – x  – 6 = 0. This is a required equation.
Equations reducible to quadratic equations: We now explain by some illustrations how to solve some equations which are reducible to quadratic equations by suitable substitutions.

Question 11.
Solve \(x^{\frac{2}{3}}+x^{\frac{1}{3}}\) – 2 = 0.
Solution:
On taking \(\mathrm{x}^{\frac{1}{3}}\) = t, the given equation becomes
t² + t – 2= 0, which is a quadratic equation in t.
Hence a complex number a is a solution of the equation.
\(x^{\frac{2}{3}}+x^{\frac{1}{3}}\) – 2 = 0, if there exists λ such that λ² + λ -2 = 0 and λ³ = α.
Therefore the set of all solutions of the given equation is

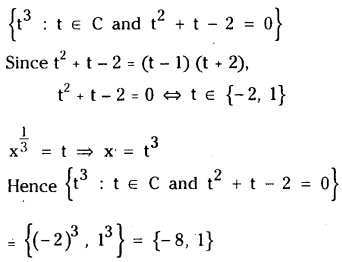
Therefore the solution set of the given equation is { – 8, 1}.

Question 12.
Solve 7^1+x +7^1-x = 50 for real x.
Solution:
The given equation can be written as

X = – 1 or x = 1
Therefore the solution set of the given equation is (-1, 1).

Question 13.
Solve \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\)
Solution:
On taking \(\sqrt{\frac{x}{1-x}}=t\) the given equation becomes

Question 14.
Find all numbers which exceed their square root by 12.
Solution:
Let x be any such number.
Then \(x = \sqrt{\mathrm{x}}\) + 12 ie., x – 12 = \(x = \sqrt{\mathrm{x}}\)
On squaring both sides and simplifying we obtain (x – 12)²
i.e., x²  – 24x 144 = x
i.e., x² – 25x + 144 = 0
i.e.,x (x – 16) – 9(x – 16) = 0
i.e., (x – 16) (x – 9) = 0
The roots of the equation (x – 16) (x – 9) = 0 are 9 and 16.
But x = 9 does not satisfy equation (1), while x = 16 satisfies (1). Therefore the required number is 16.

Question 15.
Prove that there is a unique pair of consecutive positive odd integers such that the sum of their squares is 290 and find it.
Solution:
Since two consecutive odd integers differ by
2, we have to prove that there is a unique
positive odd integer x such that
⇔ x²+(x+2)²=290 ……………. (1)
⇔ x²+ (x + 2)² = 290
⇔x² + x² + 4x + 4 = 290
⇔ 2x² + 4x – 286 = 0
⇔ x² + 2x – 143 = 0
⇔ x²+ 13x – 11x – 143 = 0
⇔ x(x + 13) – 11 (x + 13) = 0
⇔ (x+ 13)(x – 11)=0
⇔ x∈( – 13,11)
Hence 11 is the only positive odd integer satisfying equation (1).
Therefore (11, 13) is the unique pair of integers which satisfies the given condition.

Question 16.
The cost of a piece of cable wire is Rs. 35/-. If the length of the piece of wire is 4 meters more and each meter costs Rs. 1/- less, the cost would remain unchanged. What is the length of the wire?
Solution:
Let the length of the piece of wire be ‘l’ meters and the cost of each meter be Rs. x I –
By the given conditions lx = 35 ……………………. (1)
Also, (1+ 4) (x – 1) = 35
i.e., lx – 1 + 4x – 4 = 35 ……………………… (2)
From (1) and (2), 35 – l + 4x – 4 = 35
i.e., 4x = l + 4
Therefore \(x=\frac{l+4}{4}\)
On substituting this value of ‘x’ in (1) and simplifying, we get
\(l\left(\frac{l+4}{4}\right)=35\)
i.e., l² + 4l- 140 = 0
i.e., l² + 14l – 10l- 140 = 0
i.e., l(l+ 14)-10 (1+ 14)=0
i.e., (l+ 14) (1- 10) = 0
The roots of the equation (l + 14) (l- 10) = 0 are-14 and 10.
Since the length can not be negative, i = 10
Therefore the length of the piece of wire is 10 metres.

Question 17.
One fourth of a herd of goats was seen in the forest. Twice the square root of the number in the herd had gone up the bill and the remaining l5goatswere on the bank of the flyer. Find the total number of goats
Solution:
Let the number of goats in the herd be ‘x’.
By the given conditions, the number of goats seen in the forest is \(\frac{x}{4}\) the number of goats gone up the hill is \(2 \sqrt{x}\) and the number of the remaining goats which were on the bank of the river is 15.
Therefore \(\frac{x}{4}\) + \(2 \sqrt{x}\) + 15 = X
i.e., x + \(8 \sqrt{x}\) + 60 = 4x
i.e., 3x – \(8 \sqrt{x}\) –  60 = 0.
On taking \(\sqrt{x}\) = t, this equation becomes
3t² – 8t – 60 = 0
i.e., 3t²– 18t+ 10t – 60 = 0
i.e.,3t(t – 6)+ 10(t – 6)=0
i.e.,(t – 6)(3t+ 10)=0
The roots of the equation (t – 6) (3t + 10) = 0 are 6 and \(-\frac{10}{3}\)
Hence 3x – \(8 \sqrt{x}\) – 60 = 0 = \(\sqrt{x}\) = 36
(since \(\sqrt{x}\) is non-negative)⇔ x = 36
Therefore the total number of goats in the herd is 36

Question 18.
In a cricket match Anli took one wicket less than twice the number of wickets taken by Ravi. If the product of the number of wickets taken by them is 15, find the number of wickets taken by each of them.
Solution:
Let the number of wickets taken by Anil and
Ravi be x and y respectively.
Then x = 2y – 1 …………… (1)
xy = 15 ……………(2)
From (1) and (2), (2y – 1) y = 15
i.e., 2y²-y-15=0
i.e., 2y²-6y + 5y- 15 = 0
i.e., 2y(y-3) + 5 (y-3) = 0
i.e., (y-3)(2y + 5)= 0
The roots of the equation (y – 3) (2y + 5) = 0 are 3 and \(-\frac{5}{2}\)
Since the number of wickets must be positive integer y = 3.
From (2) we get 3x = 15, i.e., x = 5
Therefore the wickets taken by Anil and Ravi are 5 and 3 respectively.

Question 19.
Some points on a plane are marked and they are connected pairwise by line segments. if the total number of line segments formed is 10, find the number of marked points on the plane.
Solution:
Let the number of points marked on the plane be ‘x’. Since each point is joined to the remaining (x – 1) points, the number of line segments having a given point as an end point is (x – 1). Hence the total number of line segments formed appears to be x (x – 1).
But in this counting, each line segment is counted exactly twice at each of its end points. Hence the total number of line
segments actually formed is \(\frac{x(x-1)}{2}\)
Therefore by hypothesis \(\frac{x(x-1)}{2}\) = 10
i.e., x – x – 20 = 0
i.e., (x – 5) (x +4) = 0
The roots of the equation (x – 5) (x + 4) = 0 are – 4 and 5.
x can not be negative, so x = 5.
Therefore the number of points marked on the plane is 5.

Question 20.
Suppose that the quadratic equations ax² + bx +c = 0 and bx² + cx + a = 0 have a common root. Then show that
a³ + b³ + C³ = 3abc.
Solution:
The condition for two quadratic equations

Question 21.
For what values of x the expression – 5x – 14 is positive?
Sol.
Since x² – 5x  – 14 = (x + 2) (x – 7), the roots of the equation x² – 5x – 14 = 0 are – 2 and 7.
Flere the coefficient of x² is 1, which is positive.
Hence x² – 5x – 14 is positive when x < – 2 or x> 7.

Question 22.
For what values of x the expression  – 6x²+2x – 3 is negative?
Solution:
– 6x + 2x – 3 = 0 can be written as
6x² – 2x + 3= 0.
The roots of this equation are
\(\frac{2 \pm \sqrt{(-2)^2-4(6)(3)}}{2(6)}\)
Therefore the roots of – 6x²+2x – 3 = 0 are non-real complex numbers.
Here the coefficient of x² is – 6 which is negative.
Hence – 6x² + 2x – 3 < 0 for all x R

Question 23.
Find the value of x at which the following expressions have maximum or minimum.

(i) x²+5x+6
(ii) 2x – x²+7
Solution:
(i) In the expression x²+5x+6, the coefficient of x² is positive.
So x² + 5x + 6 has absolute minimum at
x – (since b=5, a= 1).

(ii) In the expression 2x – x² + 7, the coefficient of x2 is negative.
So 2x – x² + 7 has an absolute maximum at
\(x=-\frac{2}{2(-1)}=1\) (since b=2, a-1).

Question 24.
Find the maximum or minimum value of the quadratic expression.
(i) 2x – 7 – 5 x 2
(ii) 3x² + 2x + 11
Solution:
(i) Comparing the given expression with ax² + bx + C,
we have a = -5, b = 2 and c = – 7.

Question 25.
Find the changes in the sign of 4x – 5x² + 2 for x ∈ R and find the extreme value.
Solution:
Comparing the given expression with
ax² + bx+c, we have a = – 5 < 0.
The roots of the equation 5x² – 4x – 2 = 0 are \(\frac{2 \pm \sqrt{14}}{5}\)
Therefore, when \(\frac{2-\sqrt{14}}{5}<x<\frac{2+\sqrt{14}}{5}\) the sign of 4x – 5x² + 2 is positive and when
\(x<\frac{2-\sqrt{14}}{5} \text { or } x>\frac{2+\sqrt{14}}{5}\) the sign of 4x – 5x² + 2 is negitive
Since a < 0, the maximum value of the expression 4x – 5x² + 2 is

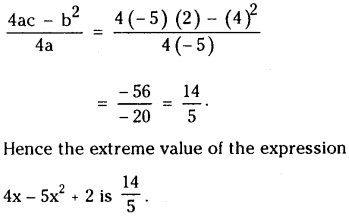
Question 26.
Show that none of the values of the function \(\frac{x^2+34 x-71}{x^2+2 x-7}\) over R lies between 5 and 9.
Solution:
Let y₀ be a value of the given function.
Then ∋ x₀ ∈ R such that
\(y_0=\frac{x_0^2+34 x_0-71}{x_0^2+2 x_0-7}\)
If y₀ = 1, then clearly y₀ ∉(5,9).
Suppose that y₀ ≠ 1.
Then the equation y₀ (x² + 2x – 7) = x² + 34x – 71 is a quadratic equation and x₀ is a real root of it.
Therefore(y₀ -1)x²+(2y₀ – 34)x – (7y₀ – 71)
= 0 is a quadratic equation having a real root x₀.
Since all the coefficients of this quadratic equation are real, the other root of the equation is also real.
Therefore
Δ = (2y₀ – 34)² +4 (y₀ -1) (7y₀ – 71) ≥ 0.
On simplifyìng this we get
y²₀ – 14y₀ + 45 ≥ 0
i.e., (y₀-5) (y₀– 9) ≥ 0
Therefore y₀ ≤ 5 or y₀ ≥ 9.
Hence y₀ does not lie in (5, 9).
Hence none of the values of the given function over R lies between 5 and 9.

Question 27.
Find the maximum value of the function
\(\frac{x^2+14 x+9}{x^2+2 x+3}\) over R.
Solution:
Since the discriminant of x² + 2x + 3 is negative, x² + 2x + 3 is never zero on R.

The above inequality is true even when y₀ = 1.
Hence the range of the given function on R is a subset of [- 5, 4].
For m = 4, the equation (1 – m) x² + (14 – 2m) x+ 9 – 3m = 0 is a quadratic equation with real coefficients and discriminant zero and hence has only one root which is real. Let it be α.
Then for m = 4, we have (1 – m) α² + (14 – 2m) α + 9 – 3m = 0.
Hence \(\frac{\alpha^2+14 \alpha+9}{\alpha^2+2 \alpha+3}=m=4\)
Hence 4 is in the range of the given function.
Since the range is a subset of [-5, 4] and 4 is in the range, 4 is the absolute maximum value given function over R.

Question 28.
Find the solution set of x² + x – 12 ≤ 0 by both algebraic and graphical methods.
Solution:
Algebraic Method:
We have x² + x – 12 (x + 4) (x – 3)
Hence – 4 and 3 are the roots of the equation x² + x – 12 = 0
Since the coefficient of x² in the quadratic expression x² + x – 12 = 0 is positive, x² + x – 12 is negative if – 4 < x < 3 and positive if either x < – 4 or x > 3.
Hence x² + x – 12 ⇔ -4 ≤ x ≤ 3
Therefore the solution set is
{ x ∈ R : – 4 ≤ x ≤ 3}
Graphical Method:
Let y = f(x) x² – x – 12
The values of y at some selected values of x are given in the following table:

The graph of the function y = f(x) is drawn using the above tabulated values.

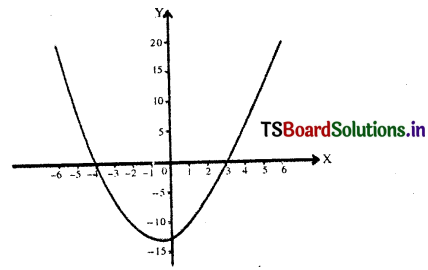
Therefore from the graph of y = f(x we observe that
y = x² – x – 12 ≤ 0 if i – 4 ≤ x≤3
Hence the solution set is {x ∈ R : – 4 ≤ x ≤ 3}.

Question 29.
Find the set of values of x for which the inequalities x²-3x-10<0, 10x – x²-16>0 hold simultaneously.
Solution:
We have x² -3x – 10 (x + 2) (x – 5)
Flence – 2 and 5 are the roots of the equation x²-3x-10= 0.
Since the coefficient of x² in the quadratic 30. expression x² – 3x -10 is positive.
x²-3x-10<0 =-2<x<5
We have 10x – x²-16 = – (x – 2)(x – 8)
Hence 2 and 8 are the roots of the equation
10x – x² – 16 = 0.
Since the coefficient of x² in the quadratic expression 10x – x² -16 is negative.
10x- x²-16>0=2 < x< 8
Hence x² -3x -10 < 0 and
⇔ X∈ (-2,5)∩(2,8)
Therefore the solution set is {x∈R : 2 < x < 5}.
10x – x² – 16 >0

Question 30.
Solve the inequation \(\sqrt{x+2}>\sqrt{8-x^2}\)
Solution:

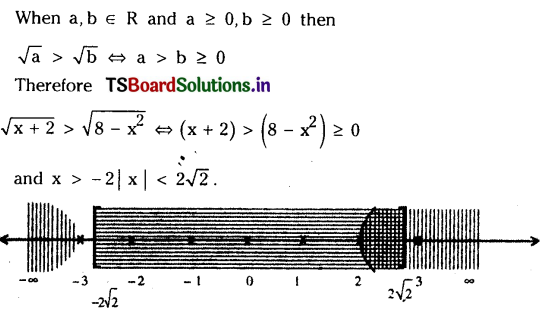
We have (x + 2) >(8-x²)
⇔ x²+ x – 6>0
Now x² + x-6 = (x + 3)(x-2)
Since -3 and 2 are the roots of the equation
x² + x – 6 = 0 and the coefficient of x² in x² + x – 6 is positive

Question 31.
Solve the inequation
\(\sqrt{(x-3)(2-x)}<\sqrt{4 x^2+12 x+11}\)
Solution:
The given inequation is equivalent to the following two inequalities.
(x-3) (2-x) ≥ 0 and (x – 3)(2-x)4x²+ 12x+11
(x – 3)(2- x)≥ 0 (x-2)(x-3)≤0
– x²+ 5x- 6<4x² + 12x+ 11
⇔ 5x² + 7x + 17 > 0
The discriminant of the quadratic expression 5x² + 7x + 17 is negative.
Hence 5x² + 7x + 17 > 0 ∀x ∈ R.
Hence the solution set of the given inequation is {x ∈R :2 ≤ x ≤ 3}.

Question 32.
Solve the inequation
\(\frac{\sqrt{6+x-x^2}}{2 x+5} \geq \frac{\sqrt{6+x-x^2}}{x+4}\)
Solution:

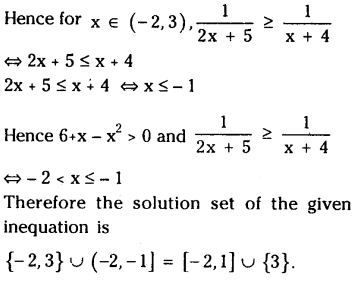
Question 33.
Solve the inequation
\(\sqrt{x^2-3 x-10}>(8-x)\)
Solution: