Srinivas

The multiple-choice format of TS 6th Class Science Bits with Answers 11th Lesson Water in Our Life allows students to practice decision-making and selecting the most appropriate answer.

TS 6th Class Science Bits 11th Lesson Water in Our Life

Question 1.
A unit for measuring volumes of liquids
A) gallon
B) litre
C) cusecs
D) all
Answer:
D) all

Question 2.
Water level in the reservoirs is measured in ………………….
A) miles
B) feet
C) centimetres
D) milli metres
Answer:
B) feet

Question 3.
Water released from dams and projects during floods is measured in
A) cusec
B) litres
C) gallons
D) A and C
Answer:
A) cusecs

Question 4.
Liquids are measured in ……………..
A) centimetres
B) milli metres
C) gallons
D) metres
Answer:
C) gallons

Question 5.
Long periods of less rainfall causes
A) floods
B) droughts
C) cyclones
D) mansoons
Answer:
B) droughts

Question 6.
One of the following is not a reason for scarcity of water
A) deforestation
B) lack of rains
C) drying of water bodies
D) heavy floods
Answer:
D) heavy floods

Question 7.
Excessive rainfall in an area leads to
A) drought
B) floods
C) migration
D) none
Answer:
B) floods

Question 8.
Factors responsible for floods are
A) Intensity and duration of rainfall
B) Soil condition
C) Presence of plants or trees on the ground
D) All of them
Answer:
D) All of them

Question 9.
Find the mis-matched pair
1. Water in reservoir is measured in – feet
2. Water released from dams – liters
3. Liquids are measured in – liters or milliliters
A) 1
B) Both 1 & 2
C) 2
D) 3
Answer:
C) 2

Question 10.
Read the following.
1. Sea water is readily available for drinking
2. River water should be purified before drinking
3. Water in ponds and puddles is usually fresh water
Find the correct sentences from above
A) 1 & 2
B) 2 & 3
C) 1
D) 1 & 3
Answer:
B) 2 & 3

Question 11.
One of the following is not a fresh water body?
1. Puddle
2. Pond
3. River
4. Ocean
A) 4
B) 3
C) 1
D) 2
Answer:
A) 4

Question 12.
The consequences of drought
1. Very difficult to get food and fodder
2. Drinking water is sufficient
3. People travel long distances for water
4. Soil becomes wet and fertile
A) 1 & 2 are correct
B) 2 & 4 are correct
C) 1 & 3 are correct
D) 3 & 4 are correct
Answer:
C) 1 & 3 are correct

Question 13.
Area of the earth’s surface covered by water.
A) 34
B) 23
C) 14
D) 13
Answer:
A) 34

Question 14.
The percentage of water by weight in the human body is…………
A) 50%
B) 60%
C) 70%
D) 80%
Answer:
C) 70%

Question 15.
Fruit that contains large amount of water.
A) Mango
B) Apple
C) Watermelon
D) Guava
Answer:
C) Watermelon

Question 16.
Of the water available on the earth, the percentage of fresh water ……………
A) 1%
B) 2%
C) 3%
D) 4%
Answer:
A) 1%

Question 17.
The taste of sea water is ……
A) sweet
B) salty
C) sour
D) bitter
Answer:
B) salty

Question 18.
Why don’t we drink sea water?
A) because of sweet taste
B) because of salinity
C) because of sour taste
D) sea water with more minerals
Answer:
B) because of salinity

Question 19.
If several borewells are dug and underground water is tapped constantly what will happen to the source of ground water?
A) depletion of ground water occurs
B) depletion of rain
C) sudden decrease in water level of rivers
D) sudden increase in underground waters
Answer:
A) depletion of ground water occurs

Question 20.
Why are people ready to pay money for water along with other commodities?
A) Water is available in excessive amounts.
B) Water scarcity occurs
C) Water bodies became dry
D) Water bodies became contaminated
Answer:
D) Water bodies became contaminated

Question 21.
Water level in well increases during rainy season. Why?
A) due to direct rainfall into the well
B) over flow of river water to wells
C) rise of ground water revel leads to rise in water level of wells
D) A or B options
Answer:
C) rise of ground water revel leads to rise in water level of wells

Question 22.
What will happen if the source of ground water is tapped constantly?
A) Ground water level decreases
B) Ground water level increases
C) More rainfall occurs
D) Earth will be free of pollution
Answer:
A) Ground water level decreases

Question 23.
What happens if there is less rainfall or too much rainfall?
A) Water bodies are filled with rain water
B) Scarcity of food and drinking water problem will arise
C) All the crops are grown easily
D) Water will be useful for several years
Answer:
B) Scarcity of food and drinking water problem will arise

Question 24.
i) Water level in the water bodies depends on rainfall.
ii) Water level in the water bodies go up in summer.
A) Both the sentences are true
B) Both the sentences are false
C) Sentence – (i) is false, sentence – (ii) is true
D) Sentence – (i) is true, sentence – (ii) is false
Answer:
D) Sentence – (i) is true, sentence – (ii) is false

Question 25.
i) Sea water is salty and is not fit for drinking.
ii) Water used by us in our daily life is not salty.
A) Both sentences are false
B) Both sentences are true
C) Sentence – (i) is true, sentence – (ii) is false
D) Sentence – (i) is false, sentence – (ii) is true
Answer:
B) Both sentences are true

Question 26.
What have you done to measure the amount of water wasted by you?
A) Measured the time the tap was left open
B) A bucket was kept under the tap while using water
C) Measured the water used and wasted by other students
D) All the above
Answer:
D) All the above

Question 27.
The sequence of steps properly involved in observing the quantity of water mentioned on the label?
i) Water bottles are collected
ii) Labels are observed
iii) Observing their quantity
A) i, ii, iii
B) iii, ii, i
C) ii, iii, i
D) i, iii, ii
Answer:
A) i, ii, iii

Question 28.
What activities are considered to measure the amount of water used by us daily?
1. Drinking
2. Toilets
3. Bathing
4. Washing
The related activities for measuring?
A) 1,2,3
B) 2,3,4
C) 1,2,3,4
D) 2&3
Answer:
C) 1,2,3,4

Question 29.
Tapping of ground water by………………. is a tough job.
A) digging pit
B) digging well or borewell
C) fish tank
D) reservoir
Answer:
B) digging well or borewell

Question 30.
Rainfall is less and farmers are largely dependent on irrigation using to raise crops.
A) underground water
B) river water
C) salty water
D) lake water
Answer:
A) underground water

Question 31.
You found that paid water is purchased in shops through
A) Packets
B) Disposable bottles
C) Cans
D) All the above
Answer:
D) All the above

Read the given lines.
Sea water is salty but water used by us for our daily purposes is not salty. Water in ponds, pudd’es, rivers is fresh water.

Question 32.
Which water is not useful for drinking?
A) sea water
B) ocean water
C) well water from saline sou
D) all the above
Answer:
D) all the above

Read the given lines
Water level in the water sources depends on rainfall. Water levels in wells go up in the rainy season and go down in the summer season. :

Question 33.
Generally the water level in water sources depends upon
A) Rainfall during rainy season
B) Rainfall during winter season
C) Rainfall during summer season
D) Rainfall during dry condition
Answer:
A) Rainfall during rainy season

Question 34.
What are the places in which water is widely used other than our domestic purposes?
A) Vehicle washing shed
B) Industries
C) Houses
D) A & B
Answer:
D) A & B

Question 35.
These districts are treated as drought prone areas
A) Anantapur
B) Prakasham
C) A and B
D) Vest Godavari
Answer:
C) A and B

Question 36.
The place is determined as drought hit area by no rain fall for a period of
A) 1 to 2 years
B) 2 or 3 years
C) 4 to 5 ears
D) 6 months to 1 year
Answer:
C) 4 to 5 ears

Question 37.
Read the passage and answer the question.
During droughts it is very difficult to get food and fodder. Drinking water is scarce. What will people do in drought hit areas? ( )
A) People migrate longer distances for work
B) People stay back to get water
C) Nothing will happen to people in drought hit areas
D) People pray to god to get rains
Answer:
A) People migrate longer distances for work

Question 38.

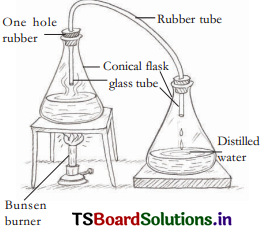
What is the method to be implemented in the place of ‘?‘ empty box?
A) cleaning
B) aeration
C) sublimation
D) distillation
Answer:
B) aeration

Question 39.
The above picture tells us

A) floods
B) walk in sea
C) tap water burst
D) water in the summer
Answer:
B) walk in sea

Question 40.
Everyone should have the aim for conserving this resource for future generations .
A) water
B) plastic
C) synthetic material
D) polymers
Answer:
A) water

Question 41.
These are the suitable slogans for conserving water resources …..
1. Save water for future
2. Use water unnecessarily as much as possible
3. Every drop of water counts – let us save
4. Let us save water – save our lives
Suitable slogans are
A) 1,2 & 3
B) 2,3 & 4
C) 1,3 & 4
D) 1,2 & 4
Answer:
C) 1,3 & 4

The multiple-choice format of TS 6th Class Science Bits with Answers 9st Lesson Plants: Parts and Functions allows students to practice decision-making and selecting the most appropriate answer.

TS 6th Class Science Bits 9th Lesson Plants: Parts and Functions

Question 1.
The main root part of the plant
A) Tap root
B) Fibrous root
C) Ciliated root
D) Fat root system
Answer:
A) Tap root

Question 2.
The roots present in grass
A) Tap root
B) Fibrous roots
C) Fat root system
D) Trunk root
Answer:
B) Fibrous roots

Question 3.
Roots which store food
A) storage roots
B) tuberous roots
C) hard roots
D) soft roots
Answer:
B) tuberous roots

Question 4.
One plant doesn’t possess tap root system
A) Neem
B) Rice plant
C) Guava
D) Mango
Answer:
B) Rice plant

Question 5.
This helps in anchoring the plant body to the soil
A) root
B) stem
C) branch
D) twig
Answer:
A) root

Question 6.
The number of root systems
A) 2
B) 1
C) 4
D) 3
Answer:
A) 2

Question 7.
The minerals present in the soil are absorbed by
A) Stem
B) Leaf
C) Root
D) Fruit
Answer:
C) Root

Question 8.
In some plants, food is stored in roots. These roots are called …………
A) Tap roots
B) Tuberous roots
C) Fibrous roots
D) None
Answer:
B) Tuberous roots

Question 9.
Example for Tuberous root
A) Carrot
B) Raddish
C) Beetroot
D) All
Answer:
D) All

Question 10.
The stalk like structure of leaf :
A) vein
B) midrib
C) palm
D) petiole
Answer:
D) petiole

Question 11.
…… acts as a skeleton of the leaf and gives it a shape and support
A) Petiole
B) Stalk
C) Venation
D) Midrib
Answer:
C) Venation

Question 12.
The flat portion of the leaf
A) Petiole
B) Edge
C) Midrib
D) Lamina
Answer:
D) Lamina

Question 13.
Which part connects leaf lamina with stem?
A) Petiole
B) Midrib
C) Vein
D) Edge
Answer:
B) Midrib

Question 14.
The long vein present in the middle of the leaf is
A) Midrib
B) Lamina
C) Vein
D) Petiole
Answer:
A) Midrib

Question 15.
Leaf prepares food by the process of
A) Digestion
B) Photosynthesis
C) Respiration
D) Excretion
Answer:
B) Photosynthesis

Question 16.
Reticulate venation is present in the plants having the following root system.
A) Tap Root system
B) Fibrous Root system
C) System of Rootlets
D) Adventitious root system
Answer:
A) Tap Root system

Question 17.
Carrot, sweet potato are good examples of ………….
A) leaves
B) storage stem
C) tuberous roots
D) All
Answer:
C) tuberous roots

Question 18.
One of the following parts is not an aerial part of the plant.
A) Leaves
B) Flower
C) Tuberous stem
D) Branch
Answer:
C) Tuberous stem

Question 19.
In a plant leaves and flowers grow from the
A) branch
B) stem
C) roots
D) apex
Answer:
B) stem

Question 20.
Branches are absent in this plant
A) Sugarcane
B) Tulasi
C) Hibiscus
D) Rose
Answer:
A) Sugarcane

Question 21.
We will see a on the stem of potato.
A) root
B) blade
C) patch
D) scar
Answer:
D) scar

Question 22.
These attract insects for pollination
A) flowers
B) fruits
C) seeds
D) leaves
Answer:
A) flowers

Question 23.
Potato is a modified.
A) root
B) leaf
C) stem
D) seed
Answer:
C) stem

Question 24.
One of the following is not a modified stem
A) Garlic
B) Carrot
C) Ginger
D) Potato
Answer:
B) Carrot

Question 25.
Colourful structures of the flower
A) Sepals
B) Pollens
C) Buds
D) Petals
Answer:
D) Petals

Question 26.
Example for parallel leaf venation having plant is
A) Mango
B) Neem
C) Jowar
D) Hibiscus
Answer:
C) Jowar

Question 27.
Banana oil is made from …………….
A) Bananas
B) Banyan tree
C) Petroleum
D) Banana plant
Answer:
C) Petroleum

Question 28.
Find the mis-matched pair …………….
(i) Grass – parallel venation
(ii) Mango – parallel venation
(iii) Sugarcane – parallel venation
(iv) Neem – reticulate venation
A) i
B) ii
C) iii
D) iv
Answer:
B) ii

Question 29.
Match the following.

List-I	List-II
1. Carrot	a) Stem
2. Potato	b) Fibrous roots
3. Grass	c) Tuberous roots

A) 1 – a, 2 – b, 3 – c
B) 1 – b, 2 – c, 3 – a
C) 1 – b, 2 – a, 3 – c
D) 1 – c, 2 – a, 3 – b
Answer:
D) 1 – c, 2 – a, 3 – b

Question 30.
Find the odd one out regarding types of plants and their nature ( )

Answer:

Question 31.
Find the modified stems among the following

(i) Turmeric	(A) i, iv, v, iii
(ii) Beet root	(B) ii, iii & iv
(iii) Radish	(C) i, iii, iv, v, vi
(iv) Potato	(D) i, iv, v, vi
(v) Garlic
(vi) Ginger

Answer:
C) i, iii, iv, v, vi

Question 32.
a) Stomata are bean shaped structures
b) They help in exchanging of food. Which is correct?
A) Both a & b are correct
B) a is correct h is wrong
C) Both a & b are wrong
D) a is wrong h is correct
Answer:
B) a is correct h is wrong

Question 33.
a) The arrangement of veins in the lamina is called venation
b) Venation acts like a skeleton of leaf.
A) Both a & b are wrong
B) a is wrong b is correct
C) a is correct b is wrong
D) Both a & b are correct
Answer:
D) Both a & b are correct

Question 34.
Scaly leaves are not present in
A) Grass
B) Mango
C) Paddy
D) A or C
Answer:
B) Mango

Question 35.
1) Water is released from plant in the form of vapours.
2) Excess water is released from the plant through the stomata.
3) Transpiration helps in removal of excess water from plants.
A) all sentences are correct
B) sentence I is correct
C) 2 & 3 are correct
D) All are wrong
Answer:
A) all sentences are correct

Question 36.
If leaves are absent in the mango tree,
A) the plant won’t prepare water
B) the plant will die
C) photosynthesis decreases
D) respiration increases
Answer:
B) the plant will die

Question 37.
Why do leaves have stomata?
A) To receive carbondioxide
B) To release oxygen
C) To prepare food
D) All the above
Answer:
D) All the above

Question 38.
………. carries the water absorbed by the roots to different parts of the plant
A) root
B) leaf
C) branch
D) stem
Answer:
D) stem

Question 39.
If transpiration is not done in the plants
A) the plants do not prepare food properly
B) the plants cannot maintain water percentage
C) water imbalance occurs in the plant
D) all the above
Answer:
D) all the above

Question 40.
The incorrect function of the leaf among the following statements.
A) Preparation of starch by photosynthesis
B) Exchange of gases through stomata
C) Elimination of water vapour through transpiration
D) Restrict water transportation
Answer:
D) Restrict water transportation

Question 41.
What would happen if stomata are absent in leaves?
A) Transpiration does not occur
B) No gas exchange occurs
C) Water transportation does not occur
D) All of the above
Answer:
D) All of the above

Question 42.
Leaf : Photosynthesis : Root ………..
A) Food preparation
B) Water preparation
C) Taking water and minerals
D) Food releasing
Answer:
C) Taking water and minerals

Question 43.
Pistils have three parts. They are
A) stigma, ovule, style
B) ovary, seed, petal:
C) petiole, stigma, style
D) stigma, style, ovary
Answer:
D) stigma, style, ovary

Question 44.
Why don’t all the plants have the same kind of leaves?
A) Based on the place and conditions the leaves are modified
B) Based on the stem they grow roots
C) Roots develop leaves
D) Stem produces leaves
Answer:
A) Based on the place and conditions the leaves are modified

Question 45.
Choose the correct answer
A) All roots are similar in paddy
B) Potato is a stern tuber
C) Grass has reticulate venation
D) Tamarind has fibrous root system
Answer:
A) All roots are similar in paddy

Question 46.
If you don’t know the name of a collected plant what would you do?
A) We will ask our teacher
B) We will ask the gardener
C) We will ask the farmer
D) Above all
Answer:
D) Above all

Question 47.
What is the nature of the root system that you observed in Tridax plant.
A) Tap root system – main root with lateral roots
B) Fibrous root system – main root with lateral roots
C) Tap root system — Root hairs
D) Lateral root system with tap roots
Answer:
A) Tap root system – main root with lateral roots

Question 48.
What is the purpose of adding ink in the tumbler?

A) In order to observe minerals and food that is absorbed by plant
B) In order to observe water and minerals absorbed by roots of plant
C) In order to cut the stem of a plant
D) In order to cut the leaves of a plant
Answer:
B) In order to observe water and minerals absorbed by roots of plant

Question 49.
What aspects are considered in observing the similarities among leaves of different plants? ( )
1. Leaf base, Petiole, Lamina
2. Leaf shape, Leaf edge
3. Leaf life, Place of leaf on stem
A) 1 and 3
B) 1 and 2
C) 2 and 3
D) 1,2 and 3
Answer:
B) 1 and 2

Question 50.
If you want to observe types of venation in leaves what leaves are to be collected?
A) Mango and Grass
B) Grass and Paddy
C) Grass and Hvdrilla
D) Mango and Guava
Answer:
A) Mango and Grass

Question 51.
Write the steps involved in observing stomata in leaves
1. Fleshy leaf is taken
2. Put a drop of water on it
3. Peel the outer layer of the leaf
4. Observe it under microscope
5. Place it on a slide.
A) 1, 2, 3, 4, 5
B) 5, 4, 3, 2, 1
C) 4, 5, 2, 3,1
D) 1, 3, 2, 5, 4
Answer:
D) 1, 3, 2, 5, 4

Question 52.
Where do we see traditional cottage industry where pictures of various mythological figures are drawn with bright colours on dried leaves
A) Warangal
B) Mahaboob nagar
C) Khammam
D) None
Answer:
A) Warangal

Question 53.
Read the given lines.
Some plants store food in roots and stems. Some plants like radish, carrot,beetroot store food materials in their roots. What is the special feature in the plants like radish, carrot, beetroot etc?
A) Roots of these plants store water
B) Roots of these plants store food
C) Stem of these plants store food
D) Leaf of these plants store food
Answer:
B) Roots of these plants store food

Question 54.

Neem	Reticulate venation
Grass	Parallel venation
Tulasi	Reticulate venation

Based on the information studied by you what type of venation is seen in the plant Sapota? ( )
A) Parallel venation
B) Parallel venation or Reticulate venation
C) Reticulate venation
D) Horizontal venation
Answer:
C) Reticulate venation

Question 55.
Read the table

Parthenium (Congress weed)	Tap root system
Paddy	Fibrous root system
Tridax	Tap root system

What types of root system is seen in plants like grass or rice? ( )
A) Tap root system
B) Fibrous root system
C) Tap root it Fibrous root system
D) Upper tap root system
Answer:
B) Fibrous root system

Question 56.
Read the given lines.
There are variations in the size and shape of plants but generally all plants havel roots, stems and leaves.
What do plants generally have?
A) Roots
B) Fruits & buds
C) Leaves & stem
D) All the above
Answer:
D) All the above

Question 57.
Read the given lines.
The long vein present in the middle of the leaf lamina is called midrib. The branches arising from the midrib are called veins. Veins in the leaf are very helpful in ?
A) Giving shape and support
B) Supply material
C) A & B
D) Taking gases
Answer:
C) A & B

Question 58.
Venation of the leaf in the picture is?

A) Reticulate
B) Parallel
C) Circular
D) Linear
Answer:
A) Reticulate

Question 59.
Find the type of venation.

A) Reticulate venatiori
B) Parallel venation
C) Palmate venation
D) Pinnate venation
Answer:
B) Parallel venation

Question 60.
The following diagram represents

A) Osmosis
B) Photosynthesis
C) Transpiration
D) Respiration
Answer:
C) Transpiration

Question 61.
The given picture of root system is present in

A) Mango – Tap root system
B) Grass – Tap root system
C) Neem – Fibrous root system
D) Palm tree – Tap root system
Answer:
A) Mango – Tap root system

Question 62.
What is the use of given diagram present in plants?

A) it is a stomata – for exchanging gases
B) It is a root – for exchanging food
C) It is a stomata – for transpiration
D) It is a leaf – for photosynthesis
Answer:
D) It is a leaf – for photosynthesis

Question 63.
……. helps in exchange of gases in trees
A) Stem
B) Root
C) Stomata
D) Branch
Answer:
C) Stomata

Question 64.
We enjoy the beauty of nature through these components of plant?
A) Leaf
B) Flowers
C) Roots
D) Stem
Answer:
B) Flowers

Question 65.
How do plants help us?
A) By giving food and air
B) By giving air and water
C) By cleaning environment
D) A and C
Answer:
D) A and C

Question 66.
Find the correct sentence on plants and their role in the nature.
A) They give air to breathe
B) They make us to survive on the earth
C) Both
D) They confront our lives
Answer:
C) Both

Question 67.
Leaves expel excess water through the stomata. What do we call this process?
A) Condensation
B) Melting
C) Evaporation
D) Transpiration
Answer:
D) Transpiration

Question 68.
Which of the following plant preserves food in the stem?
A) Ginger
B) Carrot
C) Beetroot
D) Radish
Answer:
A) Ginger

Regular practice with TS 6th Class Science Bits with Answers 8th Lesson Fibre to Fabric improves students’ confidence and readiness for assessments and examinations.

TS 6th Class Science Bits 8th Lesson Fibre to Fabric

Question 1.
Separation of seeds from the cotton is called
A) Ginning
B) twisting
C) weaving
D) spinning
Answer:
A) Ginning

Question 2.
Golden fibre
A) Cotton yarn
B) Chemical yarn
C) Wool
D) Jute yarn
Answer:
D) Jute yarn

Question 3.
This is not a plant fibre
A) Nylon
B) Hemp
C) Flax
Answer:
A) Nylon

Question 4.
Synthetic fibre
A) Silk
B) Jute
C) Acrylic
D) Hemp
Answer:
C) Acrylic

Question 5.
Which of the following was used to spin yarn?
A) Charka
B) Takli
C) Gear
D) A & B
Answer:
D) A & B

Question 6.
Cotton is obtained from
A) flowers
B) fruits
C) leaves
D) stems
Answer:
B) fruits

Question 7.
Cotton plants are usually cultivated in
A) Red soil
B) Sand
C) Black soil
D) Hill areas
Answer:
C) Black soil

Question 8.
Ginning is the process associated with
A) Cotton
B) Jute
C) Mango
D) Coconut
Answer:
A) Cotton

Question 9.
The fruits of the cotton plant are called
A) cotton bolls
B) coconut bolls
C) stems
D) roots
Answer:
A) cotton bolls

Question 10.
Arranging of yarn horizontally and vertically to make fabric
A) weaving
B) spinning
C) retting
D) none
Answer:
A) weaving

Question 11.
Looms operated by the electrical motors
A) Electric loom
B) Power loom
C) Handloom
D) Charka
Answer:
B) Power loom

Question 12.
Examples of the products made from Jute
A) Tables, door curtains
B) Buckets, Pens
C) Chairs, CPUs
D) Gunny bags, floor mats, chappals
Answer:
D) Gunny bags, floor mats, chappals

Question 13.
Read the table and choose the correct options for blanks.

Fabric	Things
Cotton	a) ………………..
Silk	b) Kurta, Sarees
Linen	c) Trousers

A) Towels
B) Sarees
C) Parachutes
D) A & B
Answer:
D) A & B

Question 14.

Seasons	Clothes we wear
a) Winter	Cotton
b) Rainy	Silk
c) Summer	Cotton

Find the mismatched one from the above table.
A) a
B) b
C) c
D) a & c
Answer:
A) a

Question 15.
Match the following:
1) Cotton ( ) a) Moths
2) Polyester ( ) b) Heavier fabrics
3) Silk ( ) c) Light fabrics
A) 1 – c, 2 – a, 3 – b
B) 1 – c, 2 – b, 3 – a
C) 1 – b 2 – a, 3 – c
D) 1 – b, 2 – c, 3 – a
Answer:
D) 1 – b, 2 – c, 3 – a

Question 16.
Read the following sentences that explains natural fibres.
i) Absorb more water
ii) Less time taken to dry
iii) Very smooth to touch
iv) Chemicals are used to make
A) All are true
B) Only (i) is true
C) Only (iii) & (iv) are true
D) Only (i) & (iv) are true
Answer:
B) Only (i) is true

Question 17.
The following one is not a natural fibre
A) Cotton
B) Silk
C) Terylene
D) Decron
Answer:
C) Terylene

Question 18.
Silk : insect : : Wool
A) sheep
B) plant
C) cotton
D) snake
Answer:
A) sheep

Question 19.
Why do we dye the yarns?
A) to get soft enough to make fabric
B) to get strong enough to make hag
C) to make weak and soft
D) to get strong enough to make fabric
Answer:
D) to get strong enough to make fabric

Question 20.
Jute fibre is derived from which part of the jute plant?
A) Leaves
B) Peel of the stem
C) Root
D) Seed
Answer:
B) Peel of the stem

Question 21.
Find the odd one out regarding types of fibres.
A) Cotton
B) Wool
C) Silk
D) Terylene
Answer:
D) Terylene

Question 22.
Read the sentences:
a) Fabrics are not only used for making clothes.
b) The material used for making school bags Is a kind of fabric
A) Both (a) and (b) are correct
B) (a) is correct (b) is wrong
C) (a) is wrong (b) is correct
D) Both (a) and (b) are wrong
Answer:
A) Both (a) and (b) are correct

Question 23.
Pick the correct question for clarifying doubt on woollen fabrics
A) How do we collect woollen from plants?
B) Which animals fibre is used as wool?
C) How silk worm gives woollen?
D) Is cotton gives perfect wool?
Answer:
B) Which animals fibre is used as wool?

Question 24.

Property	Natural fabric	Artificial fabric
Water absorbing nature	More	Less
Stretching capacity of yarn	less	high
Result after burning	ash forms	melts

If the fibre is less water absorbed, high in stretching and melts on burning. What is it ?
A) Natural fibre
B) Artificial fibre
C) Synthetic fibre
D) B & C
Answer:
D) B & C

Question 25.
If you want to see handloom industry where should you visit ?
A) Gadwal
B) Siricilla
C) Venkatagiri
D) All these places
Answer:
D) All these places

Question 26.
……….. is a type of rough cotton fabric used in book binding.
A) Coconut fibre
B) Jute
C) Calico
D) Date palm
Answer:
C) Calico

Question 27.
After washing, cotton clothes get
A) expanded
B) wrinkled
C) stretched
D) burnt
Answer:
B) wrinkled

Question 28.
Suppose a student burnt a cloth of silk what type of smell he might have observed ?
A) burning of feather
B) burning of skin
C) burning of leaves
D) burning of cloth
Answer:
A) burning of feather

Question 29.
Suppose you washed cotton shirt and polyester shirt. You kept them in the sun. Which one becomes dry earlier?
A) polyester
B) cotton
C) both A & B
D) they won’t dry
Answer:
A) polyester

Question 30.
The thread like structures you observed in the fabric
A) retting
B) clown
C) roughage
D) yarn
Answer:
D) yarn

Question 31.
If you touch these clothes you feel soft sense.
A) cotton
B) silk
C) wool
D) jute
Answer:
B) silk

Question 32.
Jute Is grown in soil.
A) clay
B) loam
C) loose
D) alluvial
Answer:
D) alluvial

Question 33.
In Andhra Pradesh cotton is widely grown in district.
A) Ananthapur
B) Prakasam
C) East Godavari
D) Srikakulam
Answer:
B) Prakasam

Question 34.
Paddy, chilli and other commercial crops are usually packed in bags.
A) polythene
B) synthetic
C) gunny
D) fibre
Answer:
C) gunny

Question 35.
Generally weaving of clothe is done on
A) cart
B) takli
C) looms
D) charka
Answer:
C) looms

Question 36.
What will you do before Inserting the thread into the needle?
A) Twist the end
B) Wet the end
C) A or B
D) Stretch the end of the thread
Answer:
C) A or B

Question 37.
When you touch silky clothes how do you feel?
A) Slippery
B) Shiny
C) Coarse to touch
D) A and B
Answer:
D) A and B

Question 38.
Find the correct order for making cotton yam.
A) Cotton boils → Remove seeds → Separate cotton
B) Remove seeds → Cotton boils → Separate cotton
C) Separate cotton → Remove seeds → Cotton boils
D) Cotton seeds → Cotton plants → Yarn
Answer:
A) Cotton boils → Remove seeds → Separate cotton

Question 39.
What did you observe while burning the polyester cloth?
A) Gives ash
B) Gives water
C) Gives pungent smell
D) Gives different colours
Answer:
C) Gives pungent smell

Question 40.
What did you observe while burning the silk and cotton fabric?
A) Gives ash
B) Gives colours
C) Release water
D) No change
Answer:
D) No change

Question 41.
The fibre used for making Khaddar
A) Woollen
B) Cotton
C) Silk
D) Nylon
Answer:
B) Cotton

Question 42.
What can we do to make the cotton yarn strong enough?
A) dryed and coated with oils
B) dryed and coated with chemicals
C) dryed and coated with water
D) soaked in the petrol

S.No.	Character	Natural fabric	Artificial fabric
1.	Water absorbing nature	yes	no
2.	Time taken to dry	long	short
3.	Smell while burning	no	yes (pungent)
4.	Result after burning	ash	melts
5.	Stretching capacity of yarn	less	high
6.	Smoothness	rough	smooth

Answer:
B) dryed and coated with chemicals

Question 43.
An example for natural fibre of plant origin.
A) Cotton
B) Silk
C) Rayon
D) Nylon
Answer:
A) Cotton

Question 44.
Do you find any relation between smoothness and time to dry?
A) They are inversly related
B) As smoothness increases, time to dry increases
C) No relation
D) Sometimes increases, sometimes decreases
Answer:
A) They are inversly related

Question 45.
Which fabrics give ash when they are burn?
A) cotton
B) rayon
C) nylon
D) polyster
Answer:
A) cotton

Question 46.
Read the lines and answer the question given below.
There are thread like structures in the fabric. These threads are called yarn.

Q. Fabric is made up of ………….
A) Cloth
B) Yarn
C) Seed
D) Plant
Answer:
B) Yarn

Question 47.
When we burn fabric made up of artificial fibre it gives a pungent smell.
Q. The fibre gives pungent smell in burning.
A) Synthetic fibre
B) Natural fibre
C) Coarse fibre
D) Silk fibre
Answer:
A) Synthetic fibre

Question 48.
Read the table :

Cotton	Blankets
Coconut	Coir
Jute	Bags
Calico	Book binding

The fabric used in book binding
A) Coir
B) Cotton
C) Calico
D) Jute
Answer:
C) Calico

Question 49.
Why do our farmers dry the stems of Red Sorrel (Gongura)?
A) To collect wool
B) To collect jute
C) To collect cotton
D) To collect silk
Answer:
B) To collect jute

Question 50.
Why should we wear woollen clothes in winter?
A) To retain our body heat
B) To keep our body cool
C) To stop air from our body
D) B and C
Answer:
A) To retain our body heat

Question 51.
If we wear woollen clothes in summer season. What will happen?
A) Our body becomes cool
B) Our body becomes ice
C) Our body feels much suffocate
D) Cool air enters into our organs
Answer:
C) Our body feels much suffocate

Question 52.
Find the wrong sentence.
A) Hemp and flax are animal fibres
B) Jute is a plant fibre
C) Cotton is taken from plant
D) Silk is obtained from silk moth
Answer:
A) Hemp and flax are animal fibres

Question 53.
Some sentences about artificial fibres.
i) Smooth to touch
ii) Less time to dry
iii) Absorbs less water
iv) More stretching capacity
A) i, ii, iii only
B) ii, iii, iv
C) iii, iv
D) i, iv only
Answer:
A) i, ii, iii only

Question 54.

1	Yarn making	?
2	Power looms	Weaving fabrics
3	Chemicals	Synthetic fibres
4	Wool	Sheep

A) Colouring
B) Dying
C) Spinning
D) Ginning
Answer:
C) Spinning

Question 55.
Find the mismatched pair.
1) Nylon – Parachute ropes
2) Cotton – Towels
3) Wool – Summer clothes
A) 1
B) 2
C) 3
D) 1&3
Answer:
C) 3

Question 56.
Find the given diagram related to spinning of thread.

A) Takli
B) Charka
C) Ratnam
D) Dredging
Answer:
A) Takli

Question 57.
The given picture shows

A) net of ball making
B) metallic wire making
C) mat making
D) all the above
Answer:
C) mat making

Question 58.
Now a days weaving is done on
A) power looms
B) wooden loom
C) stick looms
D) charkha
Answer:
A) power looms

Question 59.
Jute is collected from
A) plants
B) animals
C) A & B
D) chemicals
Answer:
A) plants

Question 60.
What is the change that we see in wearing garments from ancient period to modern age?
1) Ancient people used to wear animal skin as clothes.
2) Clothes were also made from metal.
3) Ancient people started wearing fibres.
4) Different types of clothes were worn by ancient people.
A) 1 & 3 sentences correct
B) 1 & 2 sentences correct
C) 2 & 3 sentences correct
D) 1 & 4 sentences correct
Answer:
B) 1 & 2 sentences correct

Question 61.
In order to decrease child labour In textile and handloom industry one of these activities is helpful.
A) Voluntary organisations uy to eradicate it.
B) Government should take remedial measures.
C) Government should encourage child labour.
D) A and B sentences are reliable.
Answer:
D) A and B sentences are reliable.

Question 62.
Why people use cotton clothes in summer season?
1) to keep body cool.
2) To keep body warmth and humid
3) To absorb sweat.
4) To leave more sweat out.
5) To absorb more heat.
Correct sentences are
A) 1, 3 sentences
B) 1, 2 only
C) 2, 3 only
D) 1, 2, 4 only
Answer:
A) 1, 3 sentences

Question 63.
To protect our environment we should do one of the following.
A) Using cloth bags instead of polythene bags.
B) Using plastic bags instead of cloth bags.
C) Leaving garbage everywhere in the surroundings.
D) Using synthetic clothes widely.
Answer:
A) Using cloth bags instead of polythene bags.

Question 64.
What is the advantage of natural fibre compared to artificial fibres?
A) They easily decomposed in the soil.
B) They are environmentally and eco-friendly factors.
C) Both A & B sentences.
D) They are hard and durable.
Answer:
C) Both A & B sentences.

Regular practice with TS 6th Class Science Bits with Answers 7th Lesson Separation of Substances improves students’ confidence and readiness for assessments and examinations.

TS 6th Class Science Bits 7th Lesson Separation of Substances

Question 1.
The components of Indian Ink can be identified using this technique
A) Filtration
B) Chromatography
C) Evaporation
D) Decantation
Answer:
B) Chromatography

Question 2.
Which of the following is not dissolved in water?
A) Sugar
B) Cooking oil
C) Salt
D) Lemon Juice
Answer:
B) Cooking oil

Question 3.
Concrete is a ……………..
A) mixture
B) man-made substance
C) natural product
D) A and B
Answer:
D) A and B

Question 4.
When the sugar falls in the red gram in your house, you separate the sugar by following
A) with magnet
B) sieving
C) sublimation
D) chromatography
Answer:
B) sieving

Question 5.
Which method helps to separate the husk from grain?
A) Grain and husk are equal in weight
B) Winnowing method
C) The weight of husk is less than the grain
D) None of the above
Answer:
C) The weight of husk is less than the grain

Question 6.
The impurities and bran present in flour can be removed by
A) Filtration
B) Evaporation
C) Churning
D) Sieving
Answer:
D) Sieving

Question 7.
Muddy water is taken in a beaker and allowed to stand. Then the mud settles down. The phenomenon is called (or) Mud and sand are separated from water by using this method.
A) Decantation
B) Sedimentation
C) Evaporation
D) Winnowing
Answer:
B) Sedimentation

Question 8.
Sand and salt are separated from its mixture using the principle
A) decantation and then evaporation
B) evaporation and then decantation
C) evaporation and condensation
D) sieving and winnowing
Answer:
A) decantation and then evaporation

Question 9.
Sieving is used when components of mixture have
A) same particle size
B) different particle sizes
C) same or different particle sizes
D) none
Answer:
B) different particle sizes

Question 10.
Your mother adds the following ingredients for smell while cooking biryani
A) Dal-Chilli powder
B) Onions – Dal
C) Cloves – Cardamom
D) Salt-Chilli powder
Answer:
C) Cloves – Cardamom

Question 11.
If crystallization process is not done in the nature, we can’t obtain…
A) Sea water
B) Sugar from sugarcane
C) Salt from sea water
D) Urea from crop
Answer:
C) Salt from sea water

Question 12.
The method of ……….. is used in the process of preparing cheese (paneer) in our houses.
A) decantation
B) filtration
C) sublimation
D) crystallisation
Answer:
B) filtration

Question 13.
Salt is separated from salt water by
A) crystallisation
B) filtration
C) sedimentation
D) sieving
Answer:
A) crystallisation

Question 14.
The reverse process of ‘evaporation’ is
A) filtration
B) decantation
C) boiling
D) condensation
Answer:
D) condensation

Question 15.
When the heavier component of a mixture settles down after water is added to it is called ……….
A) Sublimation
B) Filteration
C) Sedimentation
D) Crystallisation
Answer:
C) Sedimentation

Question 16.
Impurities settle at the bottom when muddy water was kept over night in a bucket. The clear water was then poured off from the top. The
process of separation used in this example is called
A) Filteration
B) Decantation
C) Winnowing
D) Sublimation
Answer:
B) Decantation

Question 17.
Separation of colours from a mixture of colours is called …….
A) Sublimation
B) Chromatography
C) Decantation
D) Crystallization
Answer:
B) Chromatography

Question 18.
Chromatography: colour: sedimentation ………
A) sand and mud
B) husk and paddy
C) flour and sugar
D) sugar and salt
Answer:
A) sand and mud

Question 19.
Find out the odd one regarding separation of mixture
A) Sublimation
B) Rectification
C) Crystallization
D) Distillation
Answer:
B) Rectification

Question 20.
If oil is mixed with water, how can you separate it?
A) by sublimation
B) by decantation
C) by sedimentation
D) by filtration
Answer:
D) by filtration

Question 21.
The result of conducting Chromatography is ……….
A) All colours are mixed
B) Colours are separated
C) New colours are formed without separation
D) No change observed
Answer:
B) Colours are separated

Question 22.
The following method is used to separate colour from the mixture
A) Sedimentation
B) Filtration
C) Chromatography
D) Winnowing
Answer:
C) Chromatography

Question 23.
Mud is separated by this process
A) Sedimentation
B) Winnowing
C) Crystallisation
D) Distillation
Answer:
A) Sedimentation

Question 24.
Identify the correct sentence.
A) Colours are separated by chlorography
B) Colours are separated by chromatography
C) Colours are separated by achlorography
D) Colours are separated by chromography
Answer:
B) Colours are separated by chromatography

Question 25.
Match the following.
a) Hand picking ( ) i) Soil and water separation
b) Sedimentation ( ) ii) Husk from grain
c) Winnowing ( ) iii) Stones from rice
A) a-i, b-ii, c-iii
B) a-iii, b-ii, c-i
C) a-ii, b-iii, c-i
D) a-iii, b-i, c-ii
Answer:
B) Colours are separated by chromatography

Question 26.
Mixture of substances present in the coffee.
A) Coffee powder, water, sugar, milk
B) Salt, water, coffee powder
C) Salt, water, coffee powder
D) Salt, sugar water, coffee powder
Answer:
A) Coffee powder, water, sugar, milk

Question 27.
Match the following.
a) Crystallisation ( ) i) Prepare pure water
b) Distillation ( ) ii) Camphor vapourisation
c) Sublimation ( ) iii) Salt from water
A) a – i,b – ii,c – iii
B) a – iii,b – i,c – ii
C) a – ii,b – i,c – iii
D) a – i,b – iii,c – ii
Answer:
B) a – iii,b – i,c – ii

Question 28.
Read the following sentences. Find the correct sentences.
i) Chromatography is done with chalk piece
ii) Sublimation is the technique for salt and water
iii) We can separate stones and paddy from rice
iv) Winnowing helps us to separate husk from grain
A) i, ii, iii
B) i, iii, iv
C) i, iii only
D) ii, iii, iv
Answer:
B) i, iii, iv

Question 29.
Substances that are mixed in lemon water.
A) lemon juice
B) salt or sugar
C) water
D) all the above
Answer:
D) all the above

Question 30.
One of the following is not a man-made substance
A) laddu
B) animal body
C) jam
D) curd
Answer:
B) animal body

Question 31.
Find out the wrong statement.
A) Husk is separated from grain by winnowing
B) Flour is separated from red gram by crystallisation
C) Stones are separated from rice by hand picking
D) Salt is obtained by evaporation of sea water.
Answer:
B) Flour is separated from red gram by crystallisation

Question 32.
Identify the correct statement of the following.
I) Salt is separated from salt solution by crystallization.
Il) Sugar is separated from tea by filtration.
A) I, Il are correct
B) I, II are not correct
C) I is correct, is not correct
D) I is not correct,is correct
Answer:
C) I is correct, is not correct

Question 33.
The correct question to clarify doubt on distillation.
A) How can we use drinking water?
B) What material is used for chromatography to get distilled water?
C) How can we get distilled water?
D) A or B
Answer:
C) How can we get distilled water?

Question 34.
What will be the consequence if there is no crystallisatlon in the nature?
A) We can’t find the colours
B) We can’t get distilled water
C) We can’t separate pure rice
D) We can’t get salt from sea water
Answer:
D) We can’t get salt from sea water

Question 35.
Find the odd one out regarding mixtures of substances.
A) Coffee
B) Tea
C) Lemon Juice
D) Water
Answer:
D) Water

Question 36.
Read the given sentences.
Lakshmi says that sedimentation and decantation are used at home while cleaning
rice and pulses for cooking.
A) Sentence is wrong based on the process
B) Sentence is correct based on the process
C) Sentence is incomplete based on the method
D) Sentence gave wrong information
Answer:
A) Sentence is wrong based on the process

Question 37.
Read the given sentences.
a) Chromatography is used to separate the colours
b) Camphor is vapourised by sublimation
A) Both the sentences are wrong
B) (a) is correct (b) is wrong
C) (b) is correct (a) is correct
D) Both the sentences are correct
Answer:
D) Both the sentences are correct

Question 38.
Filter paper for mud water. Then what is for chromatography?
A) Chalk powder
B) Funnel
C) Chalk piece
D) Sieve plate
Answer:
C) Chalk piece

Question 39.
When a few plants are Infested …………… is an excellent method of controlling pests.
A) hand picking
B) crystallization
C) chromatography
D) sedimentation
Answer:
A) hand picking

Question 40.
How can you separate stones, the mixture combining pebbles and other organic matter?
A) distillation
B) crystallization
C) decantation
D) hand picking
Answer:
D) hand picking

Read the given paragraph and answer the question:
On a windy day, a farmer stands on a high platform and allows the mixture of grain and husk to drop slowly from the flat pan. The wind carries the husk forward and the grain fall vertically downward. A separate heap of grain is formed.

Question 41.
Which method of separation is explained in the given paragraph?
A) sieving
B) flat falling
C) winnowing
D) hand moving
Answer:
C) winnowing

Question 42.
A filter paper can be used to separate
A) salt from salt solution
B) seeds and solid particles of pulp in the vegetable juice
C) muddy particles from muddy water
D) decoction from boiled tea leaves.
Answer:
B) seeds and solid particles of pulp in the vegetable juice

Question 43.
The method commonly employed by farmers to separate husk from grains is
A) sieving
B) threshing
C) winnowing
D) hand picking
Answer:
D) hand picking

Question 44.
Camphor and powdered salt mixture is separated by
A) sublimation
B) filtration
C) winnowing
D) chromatography
Answer:
A) sublimation

Question 45.
On large scale, milk or curd is to separate the butter.
A) hand picked
B) centrifuged
C) decanted
D) filtered
Answer:
B) centrifuged

Question 46.
The principle in the process of sedimentation is
A) Gravity
B) Attraction
C) Repulsion
D) Condensation
Answer:
A) Gravity

Question 47.
Find out the correct order of an experiment
a) Pour some water in a plate
b) Take a whole stick of white chalk
c) Observe the colour pattern formed on chalk
d) Put an ink mark on the curved surface of chalk
Chalk is placed in the water
A) b, d, a, e, c
B) a, e, c, d, b
C) d, c, e, b, a
D) c, e, b, a, d
Answer:
A) b, d, a, e, c

Question 48.
When you kept the camphor in open air, it disappears after some hours. Name the phenomenon.
A) Sublimation
B) Distillation
C) Crystallization
D) Evaporation
Answer:
A) Sublimation

Question 49.
Find the part in the given diagram of chromatography?

A) Chalk mark
B) Ink mark
C) Water mark
D) Oil mark
Answer:
B) Ink mark

Question 50.
What is the purpose of keeping cotton ply at the end of the funnel?

A) To prevent loss of vapourised camphor
B) To release loss of vapourised camphor
C) To stop solid camphor from escaping
D) To prevent loss of heat
Answer:
A) To prevent loss of vapourised camphor

Question 51.
The conical flask receiving water from heated conical flask in the distillation process is .
A) With full of impurities
B) With full of salt
C) With full of crystals
D) Without impurities
Answer:
D) Without impurities

Question 52.
The leaves are separated from the tea by the method of
A) Chromatography
B) Sieving
C) Hand picking
D) Filtration
Answer:
D) Filtration

Question 53.
What process is involved in the sublimation?
A) Changing from solid state to gaseous state
B) Changing from liquid state to solid state
C) Changing from gaseous state to liquid state
D) Changing from liquids to gaseous state
Answer:
A) Changing from solid state to gaseous state

Question 54.
Find out the correct order of an experiment
a) Stir the solution with a glass rod.
b) You will find salt crystals and powder in the dish
c) Heat some salt water in a beaker
d) Continue heating till all the water in the beacker has evaporated
A) c, a, d, b
B) d, a, b, c
C) a, c, d, b
D) d, c, b, a
Answer:
A) c, a, d, b

Question 55.
Which substance is used instead of water to do evaporation experiment?
A) Sand
B) Soda water
C) Rice
D) Piece of chalk
Answer:
B) Soda water

Question 56.
The process of separation of sugar and flour is
A) Filtration
B) Sieving
C) Winnowing
D) Chromatography
Answer:
B) Sieving

Question 57.
Which substance given below undergoes sublimation
A) camphor
B) water
C) kerosene
D) crystal violet
Answer:
A) camphor

Question 58.
Generally we see sublimation process here in our surroúndings
A) lighting camphor in the temples
B) incense sticks formers
C) salt crystallization
D) drinking water
Answer:
A) lighting camphor in the temples

Question 59.
People prefer ………… and methods at home to clean rice and pulses for cooking
A) sedimentation, sublimation
B) sublimation, distillation
C) distillation, crystallisation
D) sedimentation, decantation
Answer:
D) sedimentation, decantation

Read the given lines.
Before administering injections to patients, doctors mix injection powder with some liquid.

Question 60.
What is the liquid along with injections used by doctors?
A) Filtration
B) Distilled water
C) Boiled water
D) Mud water
Answer:
B) Distilled water

Question 61.
Sublimation — Camphor
Crystallisation — Sea water
Winnowing — Husk from gram
What do we get from salt water by the process of Crystallisation?
A) Salt
B) Soil
C) Water
D) Rocks
Answer:
A) Salt

Read the given lines.
Filter paper is a sieve made of paper which has very fine holes. We can filter very small particles using this type of sieve.

Question 62.
What method is done to separate flour from mustard seeds?
A) Sedimentation
B) Distillation
C) Sieving
D) Decantation
Answer:
C) Sieving

Question 63.
Given picture shows heating of camphor on ……….

A) sublimation
B) sedimentation
C) crystallization
D) distillation
Answer:
A) sublimation

Question 64.
The given picture explains the process of …………….

A) sublimation
B) filtration
C) chromatography
D) sublimation
Answer:
C) chromatography

Question 65.
What is done through the apparatus shown In the given picture?

A) decantation
B) decantation
C) sedimentation
D) crystallisation
Answer:
B) decantation

Question 66.
I Identify the figure.
A) Sedimentation
B) Decantation
C) Crystallization
D) Distillation
Answer:
B) Decantation

Question 67.
The process which is shown in the diagram is …………..

A) Chromatography
B) Hand picking
C) Sieving
D) Winnowing
Answer:
C) Sieving

Question 68.
The experiment indicated in the following diagram.

A) Preparation of distilled water
B) Sublimation
C) Condensation of sugar
D) Preparation of salt water
Answer:
A) Preparation of distilled water

Question 69.
What is the man doing in the picture?

A) Decantation
B) Distillation
C) Winnowing
D) Chromatography
Answer:
C) Winnowing

Question 70.
For administering injections doctors use
A) Salt water
B) Distilled water
C) Sea water
D) Sugar water
Answer:
B) Distilled water

Question 71.
One of the following is not a hand picking technique.
A) Stones from rice
B) Rotten fruits from fresh fruits
C) Separating oranges and apples
D) Separate husk from grains
Answer:
D) Separate husk from grains

Question 72.
Different types of separation techniques help us
A) to get desirable quantities of material
B) to remove good varieties
C) to get undesirable material
D) to follow various techniques
Answer:
A) to get desirable quantities of material

Regular practice with TS 6th Class Science Bits with Answers 6th Lesson Habitat improves students’ confidence and readiness for assessments and examinations.

TS 6th Class Science Bits 6th Lesson Habitat

Question 1.
Components of a habitat
A) temperature
B) moisture
C) shelter
D) above all
Answer:
D) above all

Question 2.
AIl habitats are grouped into
A) terrestrial
B) aquatic
C) A and B
D) air habitat
Answer:
C) A and B

Question 3
Habitats show the of nature.
A) environment
B) plants
C) animals
D) diversity
Answer:
D) diversity

Question 4.
Our intestine is a habit at for
A) several animals
B) several microbes
C) several plants
D) none of the above
Answer:
B) several microbes

Question 5.
One of the following is a reptile
A) Wolf
B) Parrot
C) Garden Lizard
D) House fly
Answer:
C) Garden Lizard

Question 6.
An example that belongs to aquatic habitat is
A) hydrill
B) vallisneria
C) lotus
D) all
Answer:
D) all

Question 7.
Organism that lives in the bottom of the pond is
A) fis
B) lotus
C) hydrilla
D) whirling beetle
Answer:
C) hydrilla

Question 8.
Desert animal
A) Rat
B) Camel
C) Horse
D) Cow
Answer:
B) Camel

Question 9.
Organism lives in underground
A) Cat
B) Earthworm
C) Hen
D) Dog
Answer:
B) Earthworm

Question 10
Identify the plant which float on the surface of the pond.
1) Hydrilla
2) Pistia
3) Lotus
4) Vallisneria
A) 1,2,3
B) 2,3
C) 3
D) 2
Answer:
D) 2

Question 11.
Identify the plant which is not a hydrophyte (water plant)
A) Hydrilla
B) Tulasi (Holy basil)
C) Lotus
D) Vallisneria
Answer:
B) Tulasi (Holy basil)

Question 12.
In the following which belongs to desert habitat?
A) elephant
B) horse
C) camel
D) lion
Answer:
C) camel

Question 13.
An example of terrestrial habitat
A) forest
B) pond
C) sea
D) river
Answer:
A) forest

Question 14.
……………. is the suitable place for cockroaches.
A) Wet and dark
B) Dry and dark
C) Wet and light
D) A and B
Answer:
B) Dry and dark

Question 15.
Which of the following is a desert plant?
A) Cactus
B) Acaria
C) Aloevera
D) All of these
Answer:
D) All of these

Question 16.
The birds and animals take temporary habitat in our school during midday meal
A) Crow
B) Dog
C) House-flies
D) All
Answer:
D) All

Question 17.
Identify desert plant
A) Cactus and Aloevera
B) Neem and Teakwood
C) Mango
D) Apple and Guava
Answer:
A) Cactus and Aloevera

Question 18.
Ozone day is celebrated on
A) September -16
B) October -16
C) November -16
D) December -16
Answer:
A) September -16

Question 19.
Birds from Siberia come to Kolleru lake. This is
A) Change of habitat for laying eggs
B) Distance from hunters
C) For maintaining ecological balance
D) To entertain visitors
Answer:
A) Change of habitat for laying eggs

Question 20.
All habitats on land collectively known as
A) Desert habitat
B) Terrestrial habitat
C) Aquatic habitat
D) Forest habitat
Answer:
B) Terrestrial habitat

Question 21.
Hydrilla plant grows
A) on water
B) on the land
C) in water
D) at any place
Answer:
C) in water

Question 22.
The plants that are grown in our house.
A) Peepal
B) Tamarind
C) Neem
D) Crotan
Answer:
A) Peepal

Question 23.
The following plants need less water.
A) Desert plants
B) Water plants
C) Terrestrial plants
D) Garden plants.
Answer:
A) Desert plants

Question 24.
Example of aquatic plant.
A) Hydrilla
B) Hydra
C) Rose
D) Hibiscus
Answer:
A) Hydrilla

Question 25.
Read the following sentences.
a) In orchards, farmers grow a single type of fruit plants.
b) In a mango orchards different types of trees can be grown.
A) both a and b are true
B) a is true, b is false
C) a is false, b is true
D) both a and b are false
Answer:
B) a is true, b is false

Question 26.
The animal that lives on both terrestrial and aquatic habitats
A) Bird
B) Frog
C) Leech
D) Fish
Answer:
B) Frog

Question 27.
This is not an aquatic habitat
A) lake
B) canal
C) river
D) desert
Answer:
D) desert

Question 28.
If pond habitat is destroyed
A) fish will die
B) birds will die
C) insects disappear
D) trees will die
Answer:
A) fish will die

Question 29.
This is not a pet animal
A) Cow
B) Dog
C) Tiger
D) Cat
Answer:
C) Tiger

Question 30.
Identify the odd one.
A) Hydrilla
B) Lotus
C) Vallisnaria
D) Tamarind
Answer:
D) Tamarind

Question 31.
Identify the plant which is different from other plants.
A) Aloevera
B) Opuntia
C) Vallisnaria
D) Cactus
Answer:
C) Vallisnaria

Question 32.
If we disturb the habitat of any organism what would happen?
A) Organism will die
B) It will impact other organisms in the habitat
C) No change will occur
D) All the organisms will be happy
Answer:
B) It will impact other organisms in the habitat

Question 33.
The components of a habitat are
A) air
B) water and food
C) shelter
D) all the above
Answer:
D) all the above

Question 34.
Hydrilla plants are formed in habitat.
A) sand
B) tree
C) aquatic
D) desert
Answer:
C) aquatic

Question 35.
If you want to create habitat for birds what would you do?
A) growing trees
B) cutting trees
C) sowing trees
D) killing trees
Answer:
A) growing trees

Read the paragraph and answer the questions (36- 38).
The plants that grow ¡n coastal regions differ from those of Telangana or Rayalaseema.

Question 36.
What will you understand from the above sentence?
A) Difference in states
B) Difference in plants
C) Diversity of habitat
D) Diversity of land
Answer:
C) Diversity of habitat

Question 37.
Battameka pitta is seen in district.
A) Krishna
B) Kurnool
C) Vizag
D) Hyderabad
Answer:
B) Kurnool

Question 38.
We can see mangroves only in districts
A) coastal
B) deccan
C) mountain
D) desert
Answer:
A) coastal

Question 39.
During the months of October to March birds like appear near Kolleru lake.
A) Pelican
B) Peacocks
C) Sparrows
D) Vultures
Answer:
A) Pelican

Question 40.
Identify the animal belongs to pond habitat.

A) Lion
B) Crow
C) Fish
D) Elephant
Answer:
C) Fish

Question 41.
Identify the given diagrams.
A) Cockroach; Dragonfly
B) Dragon fly; House fly
C) House fly; Cockroach
D) Pond skater; Dragonfly
Answer:
D) Pond skater; Dragonfly

Question 42.
Identify the given plant.
A) Pistia
B) Lotus
C) Ichornia
D) Hydrilla
Answer:
A) Pistia

Question 43.
Interdependency of organisms is disappearing due to
A) Industrialisation
B) Pollution
C) Man made activities
D) Any one of the above
Answer:
C) Man made activities

Question 44.
All the desert animals can adjust in any dry habitat. Can a human being adjust?

A) Yes
B) No
C) Can’t say
D) Yes / No
Answer:
B) No

Question 45.
A beautiful habit at

A) An orchand
B) Dry land
C) Dumping yard
D) B and C
Answer:
A) An orchand

Question 46.
The barks bear green velvety growth that are seen in
A) Summer season
B) Autumn season
C) Rainy season
D) Dry condition
Answer:
C) Rainy season

Question 47.
……………. is voluntary organisation to work for animal rights and protection
A) Red Cross
B) Green Cross
C) Blue Cross
D) All
Answer:
C) Blue Cross

Question 48.
Good example for diversity of habItat
A) Grapes grown in Telangana and Andhra
B) Apples grown in Kashmiî but not in A.P.
C) Lions are seen all over India.
D) Buttameka pitta is in all the states.
Answer:
B) Apples grown in Kashmiî but not in A.P.

Question 49.
Unharmed habit at leads to
A) better war
B) better food searching
C) unfavourable life
D) better life
Answer:
D) better life

Question 50.

Parts	Terrestrial plant (Tulasi)	Aquatic plant (Hydrilla)
Stem Leaf	hard flattened	Slender ?

A) Scaly
B) Large
C) Hard
D) Long
Answer:
A) Scaly

Telangana SCERT TS 6th Class Telugu Guide Pdf Download ఉపవాచకం 5th Lesson వాగ్గేయకారుడు రామదాసు Textbook Questions and Answers.

TS 6th Class Telugu Guide ఉపవాచకం 5th Lesson వాగ్గేయకారుడు రామదాసు

కింది ప్రశ్నలకు పది లేక పన్నెండు వాక్యాలలో సమాధానాలు రాయండి.

ప్రశ్న 1.
వాగ్గేయకారుడు రామదాసు పాఠ్యభాగ సారాంశాన్ని రాయండి.
జవాబు.
పరిచయం : భారతదేశంలోని పవిత్రమైన నదుల్లో ఒకటైన గోదావరీ తీరంలోని భద్రాచలంలో వెలసిన శ్రీరాముని సేవించి తరించిన భక్తుడు, వాగ్గేయకారుడు అయిన రామదాసు జీవిత విశేషాలే ఈ పాఠ్యభాగం. ఇందులో రామదాసు బాల్యం, విద్యాభ్యాసం, తాగక మంత్రోపదేశం, తహసీలుదారు ఉద్యోగం, రామదాసు కావడం, చెరసాల జీవితం, రామలక్ష్మణులు విడిపించడం అనే అంశాలు ఉన్నాయి.

బాల్యం, విద్యాభ్యాసం : ఖమ్మం జిల్లాలోని నేలకొండపల్లి గ్రామంలో క్రీ.శ. 17వ శతాబ్దంలో కంచెర్ల లింగన్న, కామమ్మ దంపతులు తమ కుమారుడికి గోపన్న అని పేరు పెట్టారు. రఘునాథ భట్టాచార్యుల వద్ద బాలరామాయణం చదువుకున్న గోపన్న అన్ని శాస్త్రాలలో పండితుడేకాక రాముడికి భక్తుడు కూడా అయ్యాడు.

తారక మంత్రోపదేశం : కబీరుదాసు చేసి తారకమంత్ర ఉపదేశాన్ని ఆనందతన్మయంతో పారాయణ చేశాడు. నిత్యం భజన కాలక్షేపాలు, అన్న సంతర్పణల వల్ల ఆస్తి తరిగిపోవటంతో ఉద్యోగం కోసం గోలకొండ కోటలో ముఖ్య ఉద్యోగులైన అక్కన్న మాదన్నలను ఆశ్రయించాడు.

తహసీలుదారు ఉద్యోగం : గొప్పవాడైన తానాషా ప్రభువు అక్కన్న మాదన్నల సూచనల మేరకు గోపన్నను భద్రాచలానికి తహసీలుదారుగా నియమించాడు.

రామదాసు కావడం : గోపన్న తహసీలుదారుగా తన బాధ్యతలను చక్కగా నిర్వహించటంతో పాటు భద్రాచల రామచంద్రుడి సేవలు, రామకోటి రాయడం కూడా కొనసాగించాడు. ఒకసారి రామకోటి పూర్తిచేసిన సందర్భంగా అన్న సమారాధన ఏర్పాటు చేసినప్పుడు అక్కడ అన్నం వార్చిన గంజిగుంటలో పడి అతని కుమారుడు మరణించాడు. గోపన్న చేసిన ప్రార్థనతో ఆ బాలుడు తిరిగి బతకడం వల్ల నాటినుండి గొప్ప భక్తుడైన గోపన్న రామదాసుగా పిలవబడ్డాడు.

చెరసాల జీవితం : ప్రభువు అనుమతి లేకుండా ప్రజల డబ్బును ఆలయ నిర్మాణానికి ఖర్చుపెట్టడం వల్ల రామదాసు జైలు జీవితం గడిపాడు.

రామలక్ష్మణులు విడిపించడం : రామదాసు భక్తి ప్రపత్తులకు మెచ్చి రామలక్ష్మణులే స్వయంగా వచ్చి సేవకుల వేషంలో వెళ్ళి తానాషాకు డబ్బు కట్టడం వల్ల రాజు రామదాసును విడిపించి పశ్చాత్తాపపడ్డాడు.

ముగింపు : దాశరథి శతకం, ఎన్నో కీర్తనలు రచించిన రామదాసు కవిగా, రామభక్తుడిగా, గొప్ప వాగ్గేయకారుడిగా పేరుపొందాడు.

ప్రశ్న 2.
తానాషా ప్రభువు గొప్పదనం తెలపండి.
జవాబు.
పరిచయం: గోల్కొండ రాజ్యాన్ని పాలించిన చిట్టచివరి రాజు అబుల్ హసన్ కుతుబ్షా. ఎంతో ఉత్తముడై తన ప్రజలందరినీ నిష్పక్షపాత బుద్ధితో పాలించి ప్రజలచేత తానాషా (మంచిరాజు) అనే బిరుదును పొందాడు.

అక్కన్న మాదన్నలు : ముస్లిం అయిన తానాషా ప్రభువుకి హిందువులైన అక్కన్న మాదన్నలు మంత్రులుగా ఎంతో విశ్వాసంతో సేవ చేశారు. ఇది గిట్టని ఢిల్లీ పాదుషా ఔరంగజేబు హెచ్చరించినా అక్కన్న మాదన్నలను వదులుకోని స్నేహశీలి, గొప్పవ్యక్తి తానాషా. అక్కన్న మాదన్నల సూచన మేరకు భద్రాచలానికి తహసీలుదారుగా నియమించి కంచెర్ల గోపన్నకు మేలు చేశాడు.

రామదాసు చెర : రామదాసు ప్రజల సొమ్ముతో ఆలయాన్ని నిర్మించి తనకు ఎంతో కీర్తి తెచ్చినందుకు లోపల్లోపల సంతోషించాడు తానాషా. కానీ తక్కిన తహసీలుదార్లు కూడా ఇలాగే చేస్తే ప్రభుత్వ ఖజానా ఖాళీ అయిపోతుందేమోననే భయంతో రామదాసును చెరసాలలో బంధించాడు.

శ్రీరామ లక్ష్మణ దర్శనం : రామదాసును విడిపించమని చెప్పి డబ్బు చెల్లించడానికి వచ్చి రామలక్ష్మణులు సేవకుల రూపంలో తానాషాకు దర్శనం ఇచ్చారు. తానాషా వెంటనే రామదాసును చెరనుంచి విడిపించి రాజమర్యాదలు చేశాడు. పశ్చాత్తాపం : మహాభక్తుడైన రామదాసును చెరలో చిత్రహింసలు పెట్టినందుకు తానాషా ఎంతో పశ్చాత్తాపపడ్డాడు. అందుకే రామలక్ష్మణులు తనకు చెల్లించిన డబ్బుతో పాటు పట్టువస్త్రాలు గూడా ఇచ్చి భద్రాచలాన్ని శ్రీరామచంద్రునికి మాన్యంగా ప్రకటించాడు.

ముగింపు : స్నేహానికి, మంచితనానికి మారుపేరైన తానాషా హిందూ ముస్లింల ఐకమత్యానికి, తెలుగు భాష అభివృద్ధికి పాటుపడిన మహానుభావుడు.

పరిచిత గద్యభాగాలు

1. కింది పేరా చదవండి. ప్రశ్నలకు జవాబులు రాయండి.

తల్లిదండ్రులు ఆ బిడ్డకు ‘గోపన్న’ అనే పేరు పెట్టారు. గోపన్నకు తగిన వయస్సు రాగానే ఉపనయనం చేశారు. అయిదో ఏటనే అక్షరాభ్యాసం చేశారు. శాస్త్ర పండితులయిన రఘునాథ భట్టాచార్యుల వంటి వైష్ణవదీక్షా గురువులు గోపన్నకు బాల రామాయణాన్ని తాత్పర్య సహితంగా చెప్పటం జరిగింది. అందువల్ల చిన్నతనం నుంచే గోపన్న మనసులో శ్రీరాముడి మహిమలు నాటుకొనిపోయాయి. ఎప్పుడూ సీతారాముల విగ్రహాలకు భక్తితో పూజలు చేసేవాడు. తన స్నేహితులతో రామభజనలు చేసేవాడు.

రామకోటి రాసేవాడు. ఐదేళ్ళ వయసులోనే గోపన్నకు ఎంత రామభక్తి ఉండేదంటే, తాను గూడా ఆ రాముడున్న కాలంలోనే పుట్టి ఉంటే సుగ్రీవుడు, ఆంజనేయుడు వలె భక్తితో శ్రీరాముడిని సేవించే భాగ్యం లభించేది గదా అని అనుకునేవాడు. ఈ విధంగా ఎంత రామభక్తి పరాయణుడైనా, గోపన్న సర్వశాస్త్రాలను నేర్చుకొని తల్లిదండ్రులను తృప్తి పరిచాడు. కాని విద్యావంతుడు, దైవభక్తియుక్తుడైన పుత్రుడి అభివృద్ధిని చూసి ఆనందించే భాగ్యం ఆ తల్లిదండ్రులకు లేదు. కొద్ది రోజులకే వారు కన్నుమూశారు.

ప్రశ్నలు :

1. అక్షరాభ్యాసం అంటే ఏమిటి ?
జవాబు.
‘ఓ నమః’ అంటూ పలకమీద రాయించి చదువు నేర్పడం మొదలు పెట్టడాన్ని అక్షరాభ్యాసం అంటారు.

2. గోపన్నకు బాలరామాయణాన్ని తాత్పర్యసహితంగా బోధించిన గురువు ఎవరు?
జవాబు.
గోపన్నకు బాలరామాయణాన్ని తాత్పర్య సహితంగా బోధించిన గురువు పేరు రఘునాథ భట్టాచార్యులు

3. సీతారాముల విగ్రహాలకు పూజలతో పాటు గోపన్న ఇంకేమి చేసేవాడు ?
జవాబు.
స్నేహితులతో భజనలు చేసేవాడు. ‘రామకోటి’ రాసేవాడు.

4. రామకోటి అంటే ఏమిటి ?
జవాబు.
శ్రీరామ అనే మూడు అక్షరాల నామాన్ని కోటిసార్లు రాయడాన్ని ‘రామకోటి’ అంటారు.

5. గోపన్న చక్కగా చదువుకోవడం చూసి ఎవరు తృప్తిపడ్డారు ?
జవాబు.
గోపన్న చక్కగా చదువుకోవడం చూసి అతని తల్లిదండ్రులు తృప్తిపడ్డారు.

2. కింది పేరాను చదవండి. ఖాళీలను పూరించండి.

అక్కన్న – మాదన్నలనే వాళ్ళు తానాషా కొలువులో ఉండేవాళ్ళు. వాళ్ళలో అక్కన్న మంత్రిగా, దండనాయకుడిగా కూడా బాధ్యతలు నిర్వహించాడు. మాదన్న ప్రధానమంత్రి. మాదన్న అసలు పేరు సూర్యప్రకాశరావు. ఈ అన్నదమ్ములిద్దరూ ఔరంగజేబు దాడుల నుంచి గోల్కొండ రాజ్యాన్ని కాపాడటంలో ప్రధాన పాత్ర వహించారు. మహారాష్ట్ర నాయకుడు శివాజీకీ తానాషాకూ సంధి జరిపారు. అక్కన్న మాదన్నలు బతికి ఉన్నంతకాలం ఢిల్లీ సుల్తాను, గోల్కొండను ఆక్రమించుకోలేకపోయాడు. వాళ్ళ అన్నదమ్ములు కాకపోయినా ఒకరినుంచి మరొకరిని వేరుచేయలేనంత సన్నిహితంగా కలిసిపోయారు. వీరి హత్య జరిగిన అనంతరమే ఔరంగజేబు తానాషాను బందీ చేయగలిగాడు. ఒక ముస్లిం రాజ్యానికి మంత్రులుగా హిందువులుండటం ఔరంగజేబు సహించలేకపోయాడు. అక్కన్న మాదన్నలను వదిలించుకొమ్మని ఔరంగజేబు ఎంత చెప్పినా తానాషా వారిని వదులుకోలేదు. అక్కన్న మాదన్నలకు తానాషాతో గల అనుబంధం హిందూ, ముస్లింల ఐకమత్యాన్ని, స్నేహసౌహార్ద్రతలను చాటుతున్నది.

ఖాళీలు:

1. అక్కన్న మాదన్నలు గోల్కొండ రాజ్యాన్ని………………….. దాడుల నుంచి కాపాడారు.
2. ఔరంగజేబు ముస్లిం రాజ్యానికి హిందువులు …………….. ఉండటం సహించలేకపోయాడు.
3. తానాషా కొలువులో అక్కన్న …………….. పదవులు నిర్వహించాడు.
4. తానాషా ప్రధానమంత్రి అయిన సూర్యప్రకాశరావు ………………….. పేరుతో ప్రసిద్ధుడు.
5. అక్కన్న మాదన్నలు తానాషాకి ………………. తో సంధి జరిపారు.
జవాబు.
1. అక్కన్న మాదన్నలు గోల్కొండ రాజ్యాన్ని ఔరంగజేబు దాడుల నుంచి కాపాడారు.
2. ఔరంగజేబు ముస్లిం రాజ్యానికి హిందువులు మంత్రులుగా ఉండటం సహించలేకపోయాడు.
3. తానాషా కొలువులో అక్కన్న మంత్రి, దండనాయకుడు పదవులు నిర్వహించాడు.
4. తానాషా ప్రధానమంత్రి అయిన సూర్యప్రకాశరావు మాదన్న పేరుతో ప్రసిద్ధుడు.
5. అక్కన్న మాదన్నలు తానాషాకి శివాజీ తో సంధి జరిపారు.

3. ఈ క్రింది పేరాను చదివి తప్పు / ఒప్పులను గుర్తించుము

దక్షిణ భారత రాజ్యాల్లో గోల్కొండ రాజ్యం కూడా ఒకటి. గోల్కొండను పాలించిన రాజులు ప్రజల హితం కోరిన వారు. ధర్మబద్ధంగా పాలించారు. ఆ రాజుల మాతృభాష తెలుగుకాదు. అయినా వాళ్ళలో కొందరు తెలుగు నేర్చుకొని తెలుగు భాషను ప్రోత్సహించి తెలుగు కావ్యాల్ని అంకితంగా తీసుకున్నారు గూడా. తెలుగు చాటువుల్లో కనిపించే ‘మల్కిభరాముడు’ గోల్కొండ ప్రభువైన ‘ఇబ్రహీం కులీకుతుబ్షా’ అన్నది అందరికీ తెలిసిన విషయమే. మహ్మద్ కులీకుతుబ్షా కాలంలోనే నేటి హైదరాబాద్ నగరం నిర్మాణమయింది. గోల్కొండ రాజ్యాన్ని పాలించిన చిట్ట చివరి రాజు అబుల్ హసన్ కుతుబ్షా.

ప్రశ్నలు :

1. గోల్కొండను పాలించిన రాజులు ప్రజలహితం కోరినవారు
2. గోల్కొండ రాజ్యాన్ని పాలించిన చిట్ట చివరి రాజు కులీకుతుబ్షా
3. ఇబ్రహీం కుతుబ్షా కాలంలో హైదరాబాద్ నగరం నిర్మాణమయింది
4. గోలకొండ రాజుల మాతృభాష తెలుగు కాదు
5. ఇబ్రహీం కుతుబ్షాకు మల్కిభరాముడని పేరు.
జవాబు.
1. గోల్కొండను పాలించిన రాజులు ప్రజలహితం కోరినవారు (ఒప్పు)
2. గోల్కొండ రాజ్యాన్ని పాలించిన చిట్ట చివరి రాజు కులీకుతుబ్షా (తప్పు)
3. ఇబ్రహీం కుతుబ్షా కాలంలో హైదరాబాద్ నగరం నిర్మాణమయింది (తప్పు)
4. గోలకొండ రాజుల మాతృభాష తెలుగు కాదు (ఒప్పు)
5. ఇబ్రహీం కుతుబ్షాకు మల్కిభరాముడని పేరు. (ఒప్పు)

4. కింది పేరాను చదవండి. ఖాళీలను పూరించండి.

ఇంటి భారమంతా గోపన్న మీద పడింది. బంధుమిత్రుల సలహామీద గోపన్న పెండ్లి చేసుకున్నాడు. భార్య కమల సౌందర్యవతి. సకల సద్గుణాలు గల ఇల్లాలు. ఆ దంపతులిద్దరూ ఇంటికి వచ్చే అతిథులను సేవించుకుంటూ అన్నప్రదానం చేసేవారు. ఒకనాడు కబీరుదాసు గోపన్న ఇంటి సమీపంలోకి హరినామ సంకీర్తన చేసుకుంటూ వచ్చాడు. ఇంట్లో నుండి బయటికి వచ్చి గోపన్న కబీరును చూశాడు. అతడు కూడా గోపన్నను చూచి చేతులు చాచి పిలిచాడు. గోపన్నలో భగవద్భక్తి లక్షణాలు కనిపించాయి కబీరుకు. గోపన్నా! నీలో శాంతి, సౌమనస్యం వంటి సద్గుణాలున్నాయి. నీకు అఖండయోగం, శ్రీరామచంద్రుడి అనుగ్రహం కలుగుతాయి.

ఖాళీలు:

1. గోపన్న భార్య పేరు …………….
2. గోపన్నలో కబీరుకు ……………. లక్షణాలు కనిపించాయి.
3. హరినామ సంకీర్తన చేసుకుంటూ …………….. గోపన్న ఇంటి సమీపంలోకి వచ్చారు.
4. ఇంటికి వచ్చే అతిథులను సేవించుకుంటూ ……………. చేసేవారు.
5. నీకు అఖండ యోగం, ……………. అనుగ్రహం కలుగుతాయి అని కబీరు చెప్పాడు.
జవాబు.
1. గోపన్న భార్య పేరు కమల.
2. గోపన్నలో కబీరుకు భగవద్భక్తి లక్షణాలు కనిపించాయి.
3. హరినామ సంకీర్తన చేసుకుంటూ కబీరు గోపన్న ఇంటి సమీపంలోకి వచ్చారు.
4. ఇంటికి వచ్చే అతిథులను సేవించుకుంటూ అన్నదానం చేసేవారు.
5. నీకు అఖండ యోగం, శ్రీరామచంద్రుడి అనుగ్రహం కలుగుతాయి అని కబీరు చెప్పాడు.

Telangana SCERT TS 6th Class Telugu Guide Pdf Download ఉపవాచకం 4th Lesson తెలంగాణ పల్లెలు-సంస్కృతి Textbook Questions and Answers.

TS 6th Class Telugu Guide ఉపవాచకం 4th Lesson తెలంగాణ పల్లెలు-సంస్కృతి

1. కింది ప్రశ్నలకు పది లేక పన్నెండు వాక్యాలలో సమాధానాలు రాయండి.

ప్రశ్న 1.
‘తెలంగాణ పల్లెలు – సంస్కృతి’ పాఠ్యభాగ సారాంశాన్ని రాయండి.
జవాబు.
పరిచయం : తెలంగాణ సంస్కృతికి ఆట, పాట, భాష, యాస ఇప్పటికీ సజీవంగా ఉన్న పల్లెలే పట్టుగొమ్మలు. పల్లెలు వివిధ పండుగలతో, రకరకాల కులవృత్తుల ప్రజలతో, పాడి పంటలతో, ఆటపాటలతో, పెళ్ళిళ్ళు పేరంటాళ్ళతో, ఉ మ్మడి కుటుంబాలతో, వినోద ప్రదర్శనలతో ఎప్పుడూ కళకళలాడుతూ ఉంటాయి.

పండగలు : సంవత్సరంలో రెండు పంటలు పండించే రైతులు పంట చేతికి వచ్చిన ఆనందంతో పదిమందిని పిలిచి కడుపునిండా భోజనం పెట్టగానే కొత్త పండుగ అంటారు. భక్తి శ్రద్ధలతో, నియమనిష్ఠలతో రైతులు వ్యవసాయపు పనులు మొదలుపెట్టే పవిత్ర దినాన్ని సాగువాటు లేక ఏరువాక అంటారు.

కులవృత్తులు : పల్లెల్లో ఎవరికి వారే తమ తమ కులాలకు సంబంధించిన వస్తువులను తయారు చేసి వాటిని అవసరమైన వారికి ఇచ్చి వారి దగ్గర తమకు అవసరమైన వస్తువులను, సేవలనుగాని తిరిగి పొందే వస్తుమార్పిడి పద్ధతి ఉండేది. గ్రామ ప్రజలకు అవసరాలు తీర్చడం కోసం వడ్రంగులు కర్ర పనిముట్లను, కమ్మరి వాళ్ళు ఇనుప వస్తువులనూ, కుమ్మరులు మట్టివస్తువులనూ, అవుసుల వాళ్ళు బంగారు నగలను తయారు చేయగా, కోమట్లు ఇతర సరుకులను, రైతులు ఆహార ధాన్యాలను, కూరగాయలను సమకూర్చేవారు.

పాడి పంటలు : ఊర్లో నాలుగు పాడి బర్రెలు ఉంటే ఊరందరికీ పాలు, పెరుగు, చల్ల పంచబడుతుంది.

ఆటపాటలు : పల్లెలో ఆడుకునే గోటీలు, చిర్ర గోనె, కబడ్డి, ఓమన గుంటలు, గచ్చకాయలు, తొక్కుడు బిళ్ళ మొదలైన ఆటల వల్ల శరీరం గట్టిబడటమే కాకుండా మానసిక ఎదుగుదల కూడా కలిగేది. ఇంకా బతుకమ్మ, కోలాటం, జాజిరి, అలావా వంటి ఆటల్లో పాటలుకూడా పాడడం వల్ల సంగీత సాహిత్యాలలో చరిత్ర ప్రవేశం లభించేవి. వాటివల్ల ఆచార వ్యవహారాలు తెలియడమే కాక గ్రహణ శక్తి, ఆలోచనా పరిధి, భాషా పరిజ్ఞానం పెరిగేవి.

పెళ్ళిళ్ళు : ఎవరింట్లో పెళ్ళి జరిగినా పందిళ్ళు వేయడం, విస్తళ్ళు కుట్టడం, వడ్లు దంచడం, బియ్యం ఏరడం, సన్నాయి వాయించడం, పూలు అల్లివ్వడం, పత్రికలు పంచడం మొదలైన పనులలో ఊరి వాళ్ళందరూ పాలుపంచుకొనే వాళ్ళు.

ఉమ్మడి కుటుంబాలు : ప్రతి ఇంట్లో తాతయ్య, నాయనమ్మలు, పెద్దమ్మ, పెద్దనాయనలు, అత్తయ్య, మామయ్యలు, పిల్లలు మొదలైన వారంతా ఉమ్మడిగా కలిసే ఉండేవారు. తాతలు, అవ్వలు చెప్పే నీతికథల ద్వారా పిల్లలు కష్టం, సుఖం, శ్రమ, నీతి, వినయం, మర్యాద వంటి మంచి విషయాలు నేర్చుకొనేవారు.

ముగింపు :పల్లెల్లో నాటకాలు, యక్షగానాలు, బుర్రకథలు, చెంచు బాగోతాల ద్వారా ప్రజలు వినోదంతో పాటు సందేశాన్ని కూడా పొందేవారు.

ప్రశ్న 2.
తెలంగాణ పల్లెల్లో జరుపుకునే పండగల గురించి రాయండి.
జవాబు.
పరిచయం : పాడి పంటలతో తులతూగే తెలంగాణ పల్లెలు పండుగరోజుల్లో ఆటపాటలతో కళకళలాడుతూఉంటాయి. వీటిలో కొత్త పండుగ, సాగువాటు ముఖ్యమైన పండుగలు.

కొత్త పండుగ : కొత్త వడ్లను దంచి, కొత్త బియ్యం తీసి, వండి పదిమందిని పిలిచి, కడుపు నిండా భోజనం పెట్టి పంచడమే కొత్త పండుగ. ఏడాదిలో రెండుసార్లు పంట చేతికి వస్తుంది. కాబట్టి కొత్త పండుగను రెండుసార్లు చేసుకుంటారు. కడుపునిండా అన్నం దొరకని కాలంలో ప్రజలకు ‘కొత్త’ ఒక పెద్ద పండుగ. కుండను దేవుడిగా పూజించే తెలంగాణ సంస్కృతిలో పండుగలకు, శుభకార్యాలకు ‘కూరాడు’ పేరుతో కుండను పూజిస్తారు.

సాగువాటు : ఏరువాక, ఏరొక అని కూడా పిలిచే సాగువాటు అంటే రైతు వ్యవసాయం పనులు మొదలుపెట్టే పవిత్రమైన రోజు. ఈ రోజున రైతు దంపతులు తెల్లారకుండానే నిద్రలేచి తలస్నానం చేసి దేవునికి మొక్కుకుంటారు. ముందురోజే కడిగి కొమ్ములకు రంగులు వేసిన ఎద్దులనూ, శుభ్రం చేసి ఉంచిన నాగలి, పార, తట్ట, కొడవలి వంటి పనిముట్లను తీసుకొని తెల్లవారకుండానే రైతు పొలం వెడతాడు. పొలంలో నాగలికట్టి దున్నడం గానీ, నాలుగు తట్టల మట్టిని తవ్విపోయడం గానీ చేసే ఆ రోజున రైతు ఎవ్వరితోనూ మాట్లాడాడు. రైతు ఇంటికి వచ్చేవరకూ ఇంట్లో ఎవ్వరూ నిద్రపోరు.

ముగింపు : ఈ విధంగా తెలంగాణ సంస్కృతిలో వ్యవసాయానికి సంబంధించిన పండుగల ప్రాధాన్యం తెలుస్తుంది.

ప్రశ్న3.
కులవృత్తుల ద్వారా పల్లె ప్రజల మధ్య ఏర్పడే అనుబంధాలను వివరించండి.
జవాబు.
పరిచయం : పల్లెల్లో పూర్వం ఎవరికి వారు తమ తమ కులాలకు సంబంధించిన వస్తువులు తయారు చేసి, ఆ వస్తువులను ఇచ్చి తమకు అవసరమైన వాటిని తీసుకునేవారు. కొందరు తమ సేవలను అందించేవారు.

వస్తువుల తయారీ : వడ్రంగి వాళ్ళు రైతుకు కావలసిన నాగండ్లను, గొర్రులను, ఇతర కర్ర పనిముట్లను తయారు చేసి ఇచ్చేవారు. కమ్మరివాళ్ళు కర్రు, కొడవలి, పార, గడ్డపార, బండికమ్ములు మొదలైన ఇనుప వస్తువులను తయారు చేసి ఇచ్చేవారు. కుమ్మరివాళ్ళు కుండ, గురిగి, పటువ, ఎసుల, కాగు, గూన వంటి మట్టి వస్తువులనూ, అవుసుల వాళ్ళు బంగారు నగలనూ తయారుచేసేవారు.

సేవలు అందించడం : సవరం పనిచేసి మంగలివాళ్ళు, బట్టలు నేసి పద్మశాలి వాళ్ళు, తట్టబుట్టలను అల్లి మేదరి వాళ్ళూ, ఎరుకలవాళ్ళు, బట్టలను కుట్టి మేర వాళ్ళు పల్లె ప్రజలకు అవసరమైన ఆహారధాన్యాలు, కూరగాయలు పండించేవారు. రైతులు పండించిన పల్లికాయలు, నువ్వులు, కుసుమలను, గానుగ పడితే వాటివల్ల అటు మనుషులకు నూనె, ఇటు పశువులకు మేత దొరికింది.

వస్తు మార్పిడి : పల్లెల్లో డబ్బుతో పని లేకుండా ఆయా వృత్తుల ప్రజలు తమ దగ్గర ఉన్నది. ఇతరులకు ఇచ్చి వారి దగ్గర తమకు అవసరమైనది తీసుకొనేవారు. వ్యవసాయంతో, కుల వృత్తులతో సంబంధం లేని కళాకారులు తమ కళానైపుణ్యంతో ప్రజలను మెప్పించి వారి నుంచి తమ అవసరాలకు సరిపడా వస్తువులనూ, ధాన్యాన్ని సేకరించేవారు. ముగింపు : ఈ విధంగా ప్రజల్లో ఈ ఇచ్చిపుచ్చుకునే విధానం వల్ల బలమైన అనుబంధాలు ఏర్పడేవి.

పరిచిత గద్యభాగాలు

1. కింది గద్యభాగాన్ని చదవండి. ప్రశ్నలకు సమాధానం రాయండి.

తెలంగాణ సంస్కృతికి పల్లెలు పట్టుగొమ్మలు. ఆట, పాట, భాష, యాస, ఇప్పటికీ పల్లెల్లో సజీవంగా ఉన్నాయి. రైతులు, వివిధ వృత్తుల వారు ఒకరికొకరు సహకరించుకుంటూ బతికేవాళ్ళు. పల్లెల్లో ప్రజలంతా ప్రధానంగా వ్యవసాయం మీద ఆధారపడి జీవించేవారు. ఊరిమీది చెరువుతో, ఊరి కింది వాగుతో వారు సహజీవనం చేసేవారు. వివిధ కులాల వారు తమ వృత్తికి సంబంధించిన వస్తువులు తయారు చేసేవారు. వస్తుమార్పిడి జరిగేది. రైతు పండించిన పంటలో అందరికీ భాగం దక్కేది. పండుగలు, జాతరలు, పెండ్లిండ్లకు అన్ని వృత్తుల వారి భాగస్వామ్యం ఉండేది. ప్రతి పండుగలో పాట ఒక భాగమైపోయేది. పాటలేని పండుగలు, వేడుకలు తెలంగాణలో లేనేలేవు.

ప్రశ్న 1.
పల్లెల్లో ప్రజలందరూ ప్రధానంగా దేనిమీద ఆధారపడి జీవించేవారు ?
జవాబు.
పల్లెల్లో ప్రజలందరూ ప్రధానంగా వ్యవసాయం మీద ఆధారపడి జీవించేవారు.

ప్రశ్న 2.
వృత్తి పనివారు తమ వస్తువులను ఇతరులకు ఇచ్చి ఇతరులు మంచి వస్తువులను తాము తీసుకోవడానికి ఏమని పేరు?
జవాబు.
వృత్తి పనివారు తమ వస్తువులను ఇతరులకు ఇచ్చి ఇతరుల నుంచి వస్తువులను తాము తీసుకోవడానికి వస్తుమార్పిడి అని పేరు.

ప్రశ్న 3.
తెలంగాణ సంస్కృతికి పట్టుగొమ్మలు ఏవి ?
జవాబు.
తెలంగాణ సంస్కృతికి పల్లెలు పట్టుగొమ్మలు.

ప్రశ్న 4.
ప్రతి పండుగలో ఏది ఒక భాగమై పోయింది ?
జవాబు.
ప్రతి పండుగలో పాట ఒక భాగమైపోయింది.

ప్రశ్న 5.
ఇప్పటికీ పల్లెల్లో సజీవంగా ఉన్నవి ఏవి ?
జవాబు.
ఆట, పాట, భాష, యాస ఇప్పటికీ పల్లెల్లో సజీవంగా ఉన్నాయి.

2. కింది పేరాను చదవండి. ప్రశ్నలకు జవాబులు గుర్తించండి.

రైతుకు కావలసిన నాగండ్లను, గొర్రులను, ఇతర కర్ర పనిముట్లను వడ్రంగి వాళ్లు తయారు చేసి ఇచ్చేవారు. కర్రు, కొడవలి, పార, గడ్డపార, బండికమ్ములు మొదలైన ఇనుప వస్తువులను కమ్మరి వాళ్ళు తయారు చేసి ఇచ్చేవారు. కుండ, గురిగి, పటువ, ఎసుల, కాగు, గూన వంటి మట్టివస్తువులను కమ్మరివాళ్ళు తయారు చేసి ఇచ్చేవారు. బంగారు నగలను అవుసుల వాళ్ళు తయారు చేసేవారు. మంగలివాళ్లు సవరం పని చేస్తే, పద్మశాలివాళ్ళు బట్టలు నేసేవారు. మేదరివాళ్ళ, ఎరుకలవాళ్ళు తట్టబుట్టలను అల్లేవారు. బట్టలను మేరవాళ్ళు కుట్టేవాళ్ళు, కోమటివాళ్ళు అందరికి కావలసిన ఇతర సరుకులను అమ్మేవారు. రైతులు వీళ్లనుంచి తనకు కావలసిన వస్తువులను తీసుకుని పొలం దున్ని పంటను పండించేవారు. పండించిన పంటను అన్ని కులాల వారికి ‘ఎరం’ పేరుతో పంచేవారు. ఈ ధాన్యాన్ని ఆయా కులాలవారు తమ తిండికి సరిపోను నిలువ చేసుకుని మిగతాది షావుకారికి అమ్మి ఇతర వస్తువులు తీసుకునేవారు.

ప్రశ్నలు:

1. బట్టలు నేసేవారిని ఏమంటారు ?
(అ) మంగలి వాళుళ
(ఆ) మేదరి వాళ్ళు
(ఇ) పద్మశాలి వాళ్ళు
(ఈ) కుమ్మరి వాళ్ళు
జవాబు.
(ఇ) పద్మశాలి వాళ్ళు

2. కింది వాటిలో కుమ్మరివాళ్ళు తయారు చేయని వస్తువు ఏది ?
(అ) బంగారు నగలు
(ఆ) కాగు
(ఇ) కుండ
(ఈ) పటువ
జవాబు.
(అ) బంగారు నగలు

3. మేదరివాళ్ళు ఎరుకలవాళ్ళు ఏమి చేసేవారు ?
(అ) బట్టలు కుట్టడం
(ఆ) తట్ట బుట్టలను అమ్మడం
(ఇ) పంటలు పండించడం
(ఈ) తట్టబుట్టలను అల్లడం
జవాబు.
(ఈ) తట్టబుట్టలను అల్లడం

4. పండించిన పంటను అన్ని కులాల వారికి పంచడానికి ఏమని పేరు ?
(అ) శిరం
(ఆ) ఎరం
(ఇ) వరం
(ఈ) గరం
జవాబు.
(ఆ) ఎరం

5. కర్ర పనిముట్లను ఎవరు తయారు చేస్తారు ?
(అ) వడ్రంగులు
(ఆ) కుమ్మరులు
(ఇ) కమ్మరులు
(ఈ) రైతులు
జవాబు.
(అ) వడ్రంగులు

3. కింది పేరా చదవండి. ఖాళీలను పూరించండి.

చెరువు నీళ్లను పొలాలకు సమంగా పంచడానికి ‘పెద్ద నీరటికాడు’ ఉండేవాడు. ఇతడు తూములను జాగ్రత్తగా చూసుకొంటూ నీళ్లను కాలువలకు సమంగా పంచేవాడు. ఒక్కొక్క కాలువకు ఒక నీరటికాడు ఉండేవాడు. అతడు కాలువల్లోని నీటిని పొలాలకు సమానంగా పంచేవాడు. వీరిద్దరు కలిసి నీటిచుక్కను కూడా వృధా పోనీయకుండా పంటచేలకు, కాలువలకు ఉపయోగించేవారు. ‘పెద్ద నీరటికాడు’ పదవి వంశపారంపర్యంగా వచ్చేది. కాని చిన్న నీరటి గాళ్లను ఆయా పొలాల రైతులే నియమించుకునేవారు.

ఖాళీలు:

1. కాలువల్లోని నీటిని పొలాలకు సమానంగా పంచేవాడు …………………
2. పెద్ద నీరటికాడు ……………….. నీళ్ళను పొలాలకు సమంగా పంచేవాడు.
3. చిన్న నీరటిగాళ్లను …………………. నియమించుకుంటారు.
4. నీరటిగాళ్ళు ………………… వృథా చేయరు.
5. తూములను జాగ్రత్తగా చూసుకుంటూ నీళ్లను కాలువలకు సమంగా పంచేవాడు ………………
జవాబు.
1. కాలువల్లోని నీటిని పొలాలకు సమానంగా పంచేవాడు నీరటికాడు
2. పెద్ద నీరటికాడు చెరువు నీళ్ళను పొలాలకు సమంగా పంచేవాడు.
3. చిన్న నీరటిగాళ్లను పొలాల రైతులే నియమించుకుంటారు.
4. నీరటిగాళ్ళు చుక్క నీటిని వృథా చేయరు.
5. తూములను జాగ్రత్తగా చూసుకుంటూ నీళ్లను కాలువలకు సమంగా పంచేవాడు పెద్ద నీరటికాడు

4. క్రింది పేరాను చదివి ‘5’ ప్రశ్నలు తయారు చేయండి.

సాగువాటు అంటే రైతు వ్యవసాయం పనులు మొదలు పెట్టేరోజన్న మాట. దీన్ని ఎరువాక పండుగ అని కూడా అంటారు. రైతు వ్యవసాయం పని చేయని రోజంటూ ఉండదు. కాని సంవత్సరంలో ఒక మంచి రోజు చూసుకొని నాగలి కట్టి నాలుగు సాళ్లు దున్ని పారతో నాలుగుసార్తు తవ్వి భూదేవతను మొక్కుకుంటాడు. సాగువాటు అనేది రైతు జీవితంలో ఒక భాగంగా పల్లె సంస్కృతికి అద్దం పడుతుంది. ఆరోజు రైతు దంపతులు కూరుకు రాత్రే నిద్ర లేస్తారు. తలంటుస్నానం చేస్తారు. దేవుడికి మొక్కుకుంటారు.
జవాబు.
1. రైతు వ్యవసాయ పనులు మొదలుపెట్టే రోజును ఏమంటారు ?
2. సాగువాటుకు మరో పేరేమిటి ?
3. రైతు సాగువాటు రోజు ఏ దేవతకు మొక్కుకుంటాడు ?
4. ఎవరు పని చేయని రోజంటు ఉండదు ?
5. ఎరువాక రైతు జీవితంలో దేనికి అద్దం పడుతుంది ?

5. కింది పేరా చదవండి. ఖాళీలను పూరించండి.

పల్లెల్లో ప్రజలు నాటకాలు, యక్షగానాలు, బుర్రకథలు, ఒగ్గుకథలు, చిందుబాగోతాలతో కాలక్షేపం చేసేవారు. వీటితో ప్రజలకు మంచి సందేశం అందేది. రాత్రంత మెలకువతో ఉండి నాటకాలు, బాగోతాలు చూసేవారు. ఎండకాలం వచ్చిందంటే చాలు ఏ చెట్టుకిందనో, కూలిన గోడలమధ్యనో బాగోతాలు ఆడేవారు. ఆ పాటలు విన్న పిల్లలు మరునాడు ఏచూరు కిందనో అరుగులమీదనో అదే పాటలతో ఆటలను ఆడేవారు. ఇప్పుడు ఇంటింటా టీవీలు, సినిమాలు వచ్చాయి. టీవీల్లో అసభ్య సన్నివేశాలతో సీరియళ్లు వస్తున్నాయి. అవి మనుషుల్లో జుగుప్సను, దురాలోచనలను పెంచుతున్నాయి. కారణాలు ఏవైనా పల్లెల సంస్కృతి కనుమరుగైపోతున్నది.

ఖాళీలు

1. రాత్రంత మెలకువతో ఉండి నాటకాలు, ……………………. చూసేవారు.
2. ఇప్పుడు ఇంటింటా ……………… సినిమాలు వచ్చాయి.
3. కారణాలు ఏవైన ……………. కనుమరుగై పోతున్నది.
4. పిల్లల్లో దురాలోచనలను కలుగజేసేవి …………….
5. చెట్టు కిందనో, కూలిన గోడల మధ్యనో ……………. ఆడేవారు
జవాబు.
1. రాత్రంత మెలకువతో ఉండి నాటకాలు, బాగోతాలు చూసేవారు.
2. ఇప్పుడు ఇంటింటా టీవీలు సినిమాలు వచ్చాయి.
3. కారణాలు ఏవైన పల్లెల సంస్కృతి కనుమరుగై పోతున్నది.
4. పిల్లల్లో దురాలోచనలను కలుగజేసేవి సినిమాలు టీవీలలో వచ్చే అసభ్య సన్నివేశాలు
5. చెట్టు కిందనో, కూలిన గోడల మధ్యనో బాగోతాలు ఆడేవారు

6. క్రింది పేరాను చదివి ఐదు ప్రశ్నలు తయారు చేయండి.

పల్లెల్లో ఆటపాటలు విభిన్నంగా ఉండేవి. గోటీలు, చిర్రగోనె, కబడ్డి, గుడ్డిరాజు, ఓమనగుంటలు, గచ్చకాయలు, తొక్కుడు బిళ్ళ, పరమపదసోపానపటం, పచ్చీసు, అష్టా చెమ్మ, మట్టికుప్పలు, రేసు, కాశెపుల్ల, దాల్దడి దస్సన్న పొడి వంటి ఆటలతో శారీరక దృఢత్వమే కాదు మానసిక ఎదుగుదల ఉండేది. కలిసి ఆడటం వలన స్నేహం బలపడేది. జీవితంలో పోటీ తత్వం పెరిగేది. బతుకమ్మ, కోలాటం, జాజిరి, అలావా, చప్పట్లు వంటి ఆటల్లో పాటలు కూడా ఉండేవి. పాటను, ఆటను కలిపి లయబద్ధంగా ఆడి పాడటంలో సంగీతం, సాహిత్యాల్లో ప్రవేశం లభించేది. గ్రహణశక్తి పెరిగేది. పాటల ద్వారా మంచి విషయాలు, చరిత్ర తెలిసేది. ఆలోచనా పరిధి విస్తరించేది. తరం నుంచి తరానికి ఆచార వ్యవహారాలు తెలిసేవి. భాషా పరిజ్ఞానం అలవడేది.
జవాబు.
1. లయబద్ధంగా ఆడి పాడటంలో దేనిలో ప్రవేశం లభించేది ?
2. తరం నుంచి తరానికి ఏమి తెలిసేవి ?
3. పల్లెల్లో ఆటలు ఎలా ఉండేవి ?
4. కలిసి ఆడటం వలన ఏం బలపడేది ?
5. పాటల ద్వారా ఏఏ విషయాలు తెలిసేవి ?

Telangana SCERT TS 6th Class Telugu Guide Pdf Download ఉపవాచకం 3rd Lesson ఎలుకమ్మ పెళ్ళిTextbook Questions and Answers.

TS 6th Class Telugu Guide ఉపవాచకం 3rd Lesson ఎలుకమ్మ పెళ్ళి

కింది ప్రశ్నలకు పది లేక పన్నెండు వాక్యాలలో సమాధానాలు రాయండి.

ప్రశ్న 1.
ఎలుకమ్మ పెళ్ళి పాఠ్యభాగ సారాంశం రాయండి.
జవాబు.
పరిచయం : సంతానం లేని బ్రహ్మయ్య తమకు దొరికిన ఎలుక పిల్లను భార్య కోరిక మేరకు తన మంత్రశక్తితో చిన్న పాపగా మార్చి పెంచి పెద్ద చేసి పెళ్ళి జేయడమే ఈ పాఠ్యభాగంలోని ప్రధానాంశం.

మూషిక బాల సహజ లక్షణం : ఆ పాపకు మూషిక బాల అని పేరు పెట్టి బ్రహ్మయ్య దంపతులు అల్లారుముద్దుగా పెంచుకుంటున్నారు. పెరిగి పెద్ద అయిన ఆ పాప ఎప్పుడూ అటూ ఇటూ తిరుగుతూండడం, ప్రతి వస్తువునూ కొరకడం, చిరుతిండ్ల కోసం వెతకడం, రంధ్రాలున్న చోట ఆడుకోవడం, పిల్లలు కనిపిస్తే భయపడడం వంటి ఎలుక లక్షణాలతో ప్రవర్తించేది.

మూషికబాల వినాయక భక్తి : మూషిక బాల ఒకసారి హఠాత్తుగా అమ్మానాన్నలకు చెప్పకుండా శివాలయానికి వెళ్ళి అక్కడ జరిగే నవరాత్రి ఉత్సవాలలో వినాయకుని విగ్రహానికి పూజలు చేసింది. నవరాత్రులు పూర్తయ్యాక కూడా ఆమె పొద్దస్తమానం శివాలయంలోని వినాయక విగ్రహం దగ్గరే ఆనందంగా గడిపేది.

మూషిక బాల చదువు సంధ్యలు : మూషిక బాలను బడిలో చేర్పించినా కూడా గుడికి వెళ్ళటం మాత్రం మానేది కాదు. బాగా అల్లరి చేస్తూ పుస్తకాలు అన్నీ కొరికేది. ఒకసారి వాళ్ళ టీచరు తోటి బాలలతో విహార యాత్రకు తీసుకెళ్ళినప్పుడు ఒక బాలిక వలలో చిక్కుకుపోతే తన పదునైన పళ్ళతో వలను కొరికి ఆమెను రక్షించింది.

మూషిక బాల పెళ్ళి : బ్రహ్మయ్య తన మంత్రశక్తితో సూర్యుణ్ణి వీరుడిగా తెచ్చి పెళ్ళి చేసుకోమని కూతురుని అడిగితే మిరుమిట్లు గొలిపే ఆ వెలుగులను భరించలేనన్నది. నల్లగా ఉన్నాడని మేఘుణ్ణి, నిలకడ లేని వాడని వాయుదేవుణ్ణి, మృదుత్వం లేకుండా బండబారినట్లున్నాడని మేరు పర్వతుణ్ణి ఆమె పెళ్ళాడటానికి ఒప్పుకోలేదు. చివరికి మూషిక రాజును చూసి వలచి వరించింది.

ప్రశ్న 2.
మూషిక బాల స్వభావాన్ని వివరించండి.
జవాబు.
పరిచయం : తుంగభద్రా నది ఒడ్డున ఉన్న గ్రామంలో నివసిస్తున్న సంతానం లేని బ్రహ్మయ్య దంపతులకు తమ కుటీరం ముందు ఒక ఎలుక పిల్ల కనిపించింది. దానికి సపర్యలు చేసిన బ్రహ్మయ్య భార్య కోరిక మేరకు తన మంత్రశక్తితో ఆ ఎలుకపిల్లను చిన్న పాపగా మార్చి మూషిక బాల అని పేరు పెట్టాడు.

ప్రవర్తన : అల్లారుముద్దుగా పెరిగి పెద్దదైన మూషిక బాల ఎప్పుడూ ఒకచోట స్థిరంగా ఉండేది కాదు. కనిపించిన వస్తువులన్నింటినీ కొరకడం, చిరుతిండ్ల కోసం వెతకడం, పచ్చి కూరగాయలు తినడం, పప్పు డబ్బాలు వెతకడం, వడ్ల బస్తాల దగ్గర, బియ్యం బస్తాల దగ్గర తిరగడం, రంధ్రాలున్న చోటనే ఆడుకోవడం, పిల్లలు కనిపిస్తే భయంతో ఉరకడం, మూషిక బాలకు సహజ లక్షణాలుగా మారిపోయాయి.

వినాయక భక్తి : మూషిక బాల ఒకసారి తల్లిదండ్రులకు చెప్పాపెట్టకుండా శివాలయానికి వెళ్ళి అక్కడ నవరాత్రి మండపంలోని వినాయకుని విగ్రహం ముందు పూజారితో పాటు పూజలు చేసింది.

చదువు సంధ్యలు : మార్పు వస్తుందని భావించి బళ్ళో వేసినా ఆమె గుడికి వెళ్ళడం మాత్రం మానలేదు.

వివాహం : మూషిక బాలకు గొప్ప వరుణ్ణి తేవాలని తండ్రి ప్రయత్నించినా ఆమె సూర్యుణ్ణి, మేఘుణ్ణి, వాయుదేవుణ్ణి, మేరు పర్వతుణ్ణి తిరస్కరించి మూషికరాజును పెళ్ళి చేసుకుంది.

ప్రశ్న 3.
ఎలుకమ్మ ఎవరిని ఎందుకు వరించింది ?
జవాబు.
పరిచయం : మూషిక బాలకు పెళ్ళీడు రాగానే పెళ్ళి చేయాలనుకున్నారు బ్రహ్మయ్య దంపతులు. సూర్యుణ్ణి పెళ్ళి కొడుకుగా తీసుకు వచ్చాడు తండ్రి. కానీ మూషిక బాల తండ్రి తీసుకు వచ్చిన సూర్యుడు, మేఘుడు, వాయుదేవుడు, మేరు పర్వతుడు వంటి గొప్ప వరులను తిరస్కరించి మూషిక రాజును వరించింది.

సూర్యుడు : తండ్రి వరుడుగా తెచ్చిన సూర్యుణ్ణి చూసి బాగానే ఉన్నాడు కానీ అతని మిరుమిట్లు గొలిపే కాంతిని తాను భరించలేనన్నది మూషిక బాల.

మేఘుడు : మేఘుణ్ణి చూసిన మూషిక బాల వరుడు అందగాడే గాని నల్లగా ఉన్నాడు అని తిరస్కరించింది.

వాయుదేవుడు : ఇతడు అందగాడే గానీ ఇతనికి అస్సలు నిలకడలేదు. ఈయనకంటే మంచివాడూ, గొప్పవాడూ లేడా అని తండ్రిని ప్రశ్నించింది మూషిక బాల.

మేరు పర్వతుడు : మేరు పర్వతుడు మృదుత్వం లేకుండా బండబారినట్లుండడం వల్ల మూషిక బాలకు నచ్చలేదు. మూషికరాజు : మూషిక రాజును చూసీ చూడగానే మూషికబాల సిగ్గుతో తలవంచుకొని వినయంగా నమస్కరించింది. ఈ అందగాణ్ణి పెండ్లి చేసుకోవడానికి అనుమతించండి అన్నది మూషిక బాల.

ముగింపు : అందరికంటే ధనవంతుడూ, యోగ్యుడూ, చక్కని అందగాడూ, చదువుకున్న వాడయిన వరుణ్ణి తేవాలనుకున్నా మూషికబాల మూషిక రాజుని పెళ్ళాడింది కదా! అని బ్రహ్మయ్య దంపతులు ఆశ్చర్యపోయారు.

పరిచిత గద్యభాగాలు

1. కింది పేరాను చదవండి. ప్రశ్నలకు జవాబులు గుర్తించండి.

ధనం లేకపోయినా బ్రహ్మయ్యకు కొన్ని అపూర్వశక్తులున్నాయి. ఒకరోజున బ్రహ్మయ్య కుటీరం ముందర కూర్చొని ఉన్నాడు. కాకి ఒకటి ఎలుక పిల్లను ముక్కున కరుచుకొని వెళ్ళుతుండగా జారి బ్రహ్మయ్య ఇంటిముందర పడింది. వెంటనే బ్రహ్మయ్య, అతని భార్య దాన్ని పైకి తీసి ఒళ్ళంతా తుడిచి చక్కగా నిమిరారు. భార్య భర్తను చూసి, ‘మనకు పిల్లలు లేరు కదా! మీ మంత్రశక్తిని ఉపయోగించి ఈ ఎలుకను పాపగా మార్చండి” అన్నది.

భార్య మాట కాదనలేక, ‘సరే, నీ ఇష్టం!’ అన్నాడు బ్రహ్మయ్య. ఏదో మంత్రం జపించి కమండలంలోని నీళ్ళను చిట్టెలుకమీద చల్లాడు. వెంటనే ఆ ఎలుక చిన్న పాపగా మారిపోయింది. బ్రహ్మయ్య భార్య ఆనందించింది. ఆ పాపను అల్లారుముద్దుగా పెంచసాగింది. వాళ్ళిద్దరూ ఆ పాపకు ‘మూషిక బాల’ అని పేరు పెట్టారు.

1. బ్రహ్మయ్య ఇంటి ముందర ఏమి పడింది ?
(అ) కాకిపిల్ల
(ఆ) కోకిల పిల్ల
(ఇ) ఎలుక పిల్ల
(ఈ) పక్షి పిల్ల
జవాబు.
(ఇ) ఎలుక పిల్ల

2. కింది వాటిలో బ్రహ్మయ్యకు లేనిది ఏమిటి ?
(అ) ధనం
(ఆ) విద్య
(ఇ) మంత్రశక్తి
(ఈ) తెలివి
జవాబు.
(అ) ధనం

3. బ్రహ్మయ్య చిట్టెలుకను ఎట్లా మార్చాడు ?
(అ) పెద్ద ఎలుక
(ఆ) పక్షిలా
(ఇ) చిలుకలా
(ఈ) చిన్న పాపలా
జవాబు.
(ఈ) చిన్న పాపలా

4. ఎలుకను ముక్కున కరుచుకొని వెడుతున్నది ఏది ?
(అ) చిలుక
(ఆ) కాకి
(ఇ) పిల్లి
(ఈ) గద్ద
జవాబు.
(ఆ) కాకి

5. చిన్న పాపకు పెట్టిన పేరు ఏమిటి ?
(అ) హంసరాజు
(ఆ) మూషిక బాల
(ఇ) వెన్నెల బాల
(ఈ) హిమబాల
జవాబు.
(ఆ) మూషిక బాల

2. కింది పేరా చదవండి. ఖాళీలను పూరించండి.

“మీరు చెప్పిన గుర్తులన్నీ ఉన్న బాలికను నేను శివాలయంలోనే చూశాను. ఆలయ ప్రాంగణంలో వినాయక నవరాత్రుల సందర్భంగా పెద్ద వినాయక విగ్రహం ఒకటి ఏర్పాటు చేశారు. నిన్న ఉదయం నుంచి ఆ బాలిక అక్కడే ఉన్నది” అని అసలు సంగతి చెప్పింది ఆ మనిషి. వెంటనే బ్రహ్మయ్య, అతని భార్య శివాలయానికి పోయారు. అక్కడ మూషిక బాల పూజారి దగ్గరే కూర్చుని, పూజలో అతనికి సాయంచేస్తున్నది. భక్తులకు ప్రసాదాలు ఇస్తున్నది. తదేకంగా వినాయకుణ్ణి చూస్తూ తన్మయమై పోతున్నది.
తల్లిదండ్రులను చూసి, తననక్కడి నుంచి తోలుకొని పోతారేమోనని భయంతో దేవుడి విగ్రహం వెనుకకు పోయి దాక్కున్నది.

ఖాళీలు :

1. వినాయక నవరాత్రుల సందర్భంగా వినాయక విగ్రహాన్ని ఏర్పాటు చేసిన చోటు ………………
2. మూషిక బాల …………… దగ్గరే కూర్చొని ఉన్నది.
3. మూషిక బాల ……………. ను చూస్తూ తన్మయమై పోతున్నది.
4. బాలిక శివాలయంలో ………………. నుంచి ఉన్నది.
5. తల్లిదండ్రులు తనను తీసుకుపోతారేమోనని ……………. వెనుక దాక్కున్నది.
జవాబు.
1. వినాయక నవరాత్రుల సందర్భంగా వినాయక విగ్రహాన్ని ఏర్పాటు చేసిన చోటు శివాలయం
2. మూషిక బాల పూజారి దగ్గరే కూర్చొని ఉన్నది.
3. మూషిక బాల వినాయకుణ్ణి ను చూస్తూ తన్మయమై పోతున్నది.
4. బాలిక శివాలయంలో నిన్న ఉదయం నుంచి ఉన్నది.
5. తల్లిదండ్రులు తనను తీసుకుపోతారేమోనని దేవుడి విగ్రహం వెనుక దాక్కున్నది.

3. క్రింది పేరాను చదివి ‘ఐదు’ ప్రశ్నలు తయారు చేయండి.

మూషికబాల నాలుగో తరగతిలో ఉండగా ఒక సంఘటన జరిగింది. బడిపిల్లలను తీసుకొని వాళ్ళ టీచర్ అడవిలోని చెరువు దగ్గరికి పిక్నిక్కు పోయారు. దారిలో గీత అనే ఒక బాలిక ప్రమాదవశాత్తూ, ఆ అడవిలో వేటగాడు పన్నిన వలలో ఇరుక్కున్నది. ఎంత మంది ప్రయత్నించినా ఆ వలనుంచి గీతను తప్పించలేకపోయారు. అప్పుడు మూషిక బాల తన పదునైన పండ్లతో ఆ వల తాళ్ళను క్షణాల్లో కొరికి, గీతను కాపాడింది. దాంతో పిల్లలందరికి మూషిక బాల పట్ల ప్రత్యేక అభిమానం ఏర్పడింది. పరుగు పందెంలో కూడా ప్రతిసారీ మూషిక బాలదే మొదటి బహుమతి. మెల్లమెల్లగా మూషిక బాలకు చదువు పట్ల ఇష్టం పెరిగి కళాశాల విద్య కూడా నిరాఘాటంగా పూర్తిచేసింది.

ప్రశ్నలు :
1. సంఘటన జరిగినపుడు మూషికబాల ఏ తరగతిలో ఉంది ?
2. బడి పిల్లలు టీచర్తో కలిసి ఎక్కడికి పోయారు ?
3. ప్రమాదంలో చిక్కుకున్న బాలిక పేరు ఏమిటి ?
4. గీతను ప్రమాదం నుండి తప్పించింది ఎవరు ?
5. మూషిక బాలకు దేని పట్ల ఇష్టం పెరిగింది ?

4. క్రింది పేరాను చదివి, ఇచ్చిన ఖాళీలను పూర్తి చేయండి.

కొంతకాలం గడిచింది. పాప పెరిగి పెద్దదయింది. ఎప్పుడూ ఒక చోట స్థిరంగా ఉండకుండా తిరగడం అలవాటయింది. కనిపించిన వస్తువులన్నీ కొరుకడం, చిరుతిండ్లకోసం వెతుకడం, పచ్చికూరగాయలు తినడం, పప్పుడబ్బాలు వెతకడం, వడ్ల బస్తాల దగ్గర, బియ్యం బస్తాల దగ్గర తిరుగడం, రంధ్రాలున్న చోటనే ఆటలాడుకోవడం, పిల్లులు కనిపిస్తే భయంతో ఉరకడం, మూషిక బాలకు సహజలక్షణాలుగా మారిపోయాయి.

ఖాళీలు :

1. మూషిక బాల ………………. కనిపిస్తే భయంతో ఉరకడం చేసేది
2. ఒక చోట ………………. ఉండకుండా తిరగడం అలవాటయింది.
3. ……………….. ఉన్న చోట ఆటలాడుకునేది.
4. కనిపించిన వస్తువులన్నీ …………………. చేసేది.
5. ……………. కోసం వెదికేది
జవాబు.
1. మూషిక బాల పిల్లులు కనిపిస్తే భయంతో ఉరకడం చేసేది
2. ఒక చోట స్థిరంగా ఉండకుండా తిరగడం అలవాటయింది.
3. రంధ్రాలు ఉన్న చోట ఆటలాడుకునేది.
4. కనిపించిన వస్తువులన్నీ కొరుకడం చేసేది.
5. చిరుతిండ్లు కోసం వెదికేది

Regular practice with TS 6th Class Science Bits with Answers 5th Lesson Materials and Things improves students’ confidence and readiness for assessments and examinations.

TS 6th Class Science Bits 5th Lesson Materials and Things

Question 1.
Eco-friendly products are
A) wood
B) jute
C) A & B
D) plastic
Answer:
C) A & B

Question 2.
Find the transparent substances correctly:
A) Oil paper, stone
B) Glass, polythene cover
C) Stone, tracing paper
D) Water
Answer:
B) Glass, polythene cover

Question 3.
One of the following is not made of wood
A) Chair
B) Table
C) Glass
D) Bench
Answer:
D) Bench

Question 4.
Example for opaque substance
A) Rubber
B) Oil paper
C) Plastic cover
D) Glass
Answer:
B) Oil paper

Question 5.
Identify the object which is made up of more than one material.
A) Wooden bowl
B) Ceramic bowl
C) Chair
D) Plastic mug
Answer:
C) Chair

Question 6.
Which one is opaque substance?
A) Glass
B) Water
C) Oil paper
D) Wood
Answer:
D) Wood

Question 7.
Oil paper is substance.
A) Translucent
B) Opaque
C) Transparent
D) Above all
Answer:
C) Transparent

Question 8.
One of the following is not translucent substance
A) Oil paper
B) Window glass
C) A & B
D) Wood
Answer:
B) Window glass

Question 9.
One of the followings not transparent substance
A) Oil paper
B) Bus front glass
C) Polythene paper
D) Air
Answer:
B) Bus front glass

Question 10.
If you threw the paper bowl into water
A) It will sink
B) It will float
C) It will bounce back
D) Nothing happen
Answer:
D) Nothing happen

Question 11.
Identify the transparent object from below given options.
A) Oil paper
B) Glass before the bus driver
C) Face mirror
D) Rough glass
Answer:
B) Glass before the bus driver

Question 12.
The materials which don’t change their shape
A) liquids
B) gases
C) solids
D) none of them
Answer:
C) solids

Question 13.
The fumes of candle is a good example of
A) liquid
B) solid
C) mixed
D) gas
Answer:
D) gas

Question 14.
Which of the following floats on water?
A) leaf
B) iron nail
C) stone
D) cell phone
Answer:
A) leaf

Question 15.
Example of soluble substance
A) sugar
B) sand
C) saw dust
D) oil
Answer:
A) sugar

Question 16.
The material that does not dissolve in water
A) insoluble
B) soluble
C) opaque
D) transparent
Answer:
A) insoluble

Question 17.
Salt is soluble in
A) kerosene
B) water
C) petrol
D) oil
Answer:
B) water

Question 18
Floats on water
A) Iron nail
B) stone
C) rice
D) oil
Answer:
D) oil

Question 19.
The water floating object Is
A) Wood
B) Stone
C) Iron nail
D) Potato
Answer:
A) Wood

Question 20.
Density of water is
A) 1 gm/ml
B) 2 gm/ml
C) 3 gm/ml
D) 4 gm/ml
Answer:
A) 1 gm/ml

Question 21.
You will see the type of glass in shopping malls
A) Transparent
B) Opeque
C) Translucent
D) Hand glass
Answer:
A) Transparent

Question 22.
……………. is insoluble in water
A) Sugar
B) Saw dust
C) Salt
D) All the above
Answer:
B) Saw dust

Question 23.
Which of the following is not a liquid?
A) Water
B) Milk
C) Mercury
D) Salt
Answer:
D) Salt

Question 24.
Read the following sentences.
i) Lemon juice is soluble in water
ii) Salt is insoluble in water.
iii) Sugar is soluble in water
Correct sentences from above.
A) i & ii
B) i & iii
C) ii & iii
D) i, ii & iii
Answer:
B) i & iii

Question 25.
Find out the odd one regarding solubility of substance.
A) sugar
B) salt
C) sand
D) camphor
Answer:
C) sand

Question 26.
Pick up the correct sentence.
A) Kerosone is insoluble in water
B) Oil is soluble in water
C) Sand is completely soluble in water
D) Dissolved substances are stones
Answer:
A) Kerosone is insoluble in water

Question 27.
“All the materials that float cannot be made to sink” The above sentence is ………..
A) wrong
B) right
C) can’t say
D) either right or wrong
Answer:
A) wrong

Question 28.
Why doesn’t sand mix with water?
A) It has soluble capacity
B) It has melting capacity
C) It is insoluble in water
D) A & B
Answer:
C) It is insoluble in water

Question 29.
Find out the wrong match.

1	Mirror	Glass, Wood
2	Door	Wood, Paint
3	Towel	Metal, Rubber
4	Pot	Clay

A) 1
B) 2
C) 3
D) 4
Answer:
C) 3

Question 33.
Water is a liquid. Then it dissolves
A) all the substances
B) only some substances
C) no substances
D) A & C
Answer:
B) only some substances

Question 34.
The substance which is available in three states
A) Oil
B) Dalda
C) Petrol
D) Water
Answer:
D) Water

Question 35.
Solid material among the following
A) Water
B) Water vapour
C) Ice
D) Oil
Answer:
C) Ice

Question 36.
What question will you ask your teacher about state of the material?
A) How many states of materials are available in nature?
B) What is the use of gases?
C) How can you hold material?
D) Into how many states, liquids are classified
Answer:
A) How many states of materials are available in nature?

Question 37.
What will happen if some substances are not soluble in water?
A) They will float
B) We can’t eat substances
C) They will sink
D) A & C
Answer:
D) A & C

Question 38.
Can you make a chair with glass or mud ? If not why?
A) We can’t make. Because mud is a loose soil
B) We can make. Because mud is a hard soil
C) We can’t make. Because mud is a hard soil
D) We can make. Because mud is loose soil.
Answer:
A) We can’t make. Because mud is a loose soil

Question 39.
If you put a wood piece in salt water
A) sinks in water
B) floats on water
C) dissolves in water
D) remains in the middle
Answer:
B) floats on water

Question 40.
Identify mis – matched Rair.
A) Tansparent – mirror of us
B) Opaque-wood
C) Translucent-stone
D) Reflecting matter – wood
Answer:
C) Translucent-stone

Question 41.
Water bottle is made up of
A) three different materials
B) two different materials
C) one material
D) A & C
Answer:
C) one material

Question 42.
The item which are made of wood
A) Chair
B) Doors & Chairs
C) iron nails
D) Glass
Answer:
B) Doors & Chairs

Question 43.
If you want to see the objects unclearly we should use
A) Translucent substances
B) Transparent substances
C) Opaque substances
D) All
Answer:
A) Translucent substances

Question 44.
The colour of smoke comes from extinguished candle wick
A) grey
B) black
C) blue
D) white
Answer:
D) white

Question 45.
Material is converted from liquid to solid on
A) boiling
B) heating
C) cooling
D) pressing
Answer:
C) cooling

Question 46.
What did you use to make a paper translucent?
A) water
B) oil
C) salt
D) sugar
Answer:
B) oil

Question 47.
Arrange the order of sentences for doing the candle and burn matching stick experiment
i) See a column of white smoke
ii) Hold a burning matchstick
iii) Extinguish the flame
iv) Keep burning matchstick close to smoke.
A) i, iii, ii, iv
B) iv, iii, ii, i
C) ii, iii, i, iv
D) iv, iii, i, ii
Answer:
C) ii, iii, i, iv

Question 48.
What will you observe from the experiment candle burning match stick?
A) Solid can he converted into liquid
B) A solid can be converted into liquid and then gases
C) A solid can be converted into semi-solid
D) A solid cannot be converted
Answer:
B) A solid can be converted into liquid and then gases

Question 49.
Iron nail is put in water. Empty iron tin is put in water.
A) Iron nail floats
Empty iron tin sinks

B) Iron nail floats
Empty iron tin floats

C) Iron nail sinks
Empty iron tin sinks

D) Iron nail sinks
Empty iron tin floats
Answer:
D) Iron nail sinks
Empty iron tin floats

Question 50.
Transparent substances are mostly used here
A) Saloon shops
B) Packing of sweets by shop keeper
C) Bus windows
D) All the above
Answer:
D) All the above

Question 51.
Read the sentence and answer the question.
We sort material as solids, liquids and gases based on their state at normal temperature.
What factor mainly influences the state of material?
A) Light
B) Temperature
C) Humidity
D) Rain
Answer:
B) Temperature

Question 52.

Solids	Liquids	Gases
stone	milk	smoke
chalk piece	water	air
wood	kerosene	gas in cylinder

Air is a good example for …………… state of material. ( )
A) gaseous
B) liquid
C) solid
D) opaque
Answer:
A) gaseous

Question 53.

Leather	Shoes, bags, belt
Ceramic	Cups, plates, saucers
Rock	Idols, rollers, bricks

What do we use to make plates?
A) Ceramic
B) Leather
C) Rock
D) Stone
Answer:
A) Ceramic

Question 54.

Bicycle	Wood, metal, rubber, paint
Pot	Clay, paint
Door	Wood, paint

Wood is used in making ……………..
A) Bicycle, pot
B) Pot, door
C) Bicycle, door
D) Pot, door, cycle
Answer:
C) Bicycle, door

Question 55.

Glassjar	Transparent
Steel glass	Opaque
Bus window glass	Transparent
Oil paper	Transparent

Which are transparent?
A) Glass jar, bus, window glass
B) Oil paper
C) Steel glass
D) Oil papers, steel glass
Answer:
A) Glass jar, bus, window glass

Question 56.
This is an opaque material
A) Glass
B) Plastic used for lamination
C) Water
D) Wood
Answer:
D) Wood

Question 57.
A person is easily observing outside environment from his closed window. So it is made up of
A) Glass
B) Iron sheet
C) Wood
D) Aluminium
Answer:
A) Glass

Question 58.
You construct the windows with the following object to see the inner objects outside and outer objects inside ……….
A) Glass
B) Metal sheet
C) Thermacol
D) Plywood
Answer:
A) Glass

Question 59.
Which of the following jars is used by a shopkeeper to exhibit sweets?
A) Glass jar
B) Wooden jar
C) Iron jar
D) Steel jar
Answer:
A) Glass jar

Question 60.
Which of the following material is used to make a boat?
A) Wood
B) Cement
C) Paper
D) Glass
Answer:
A) Wood

Question 61.
The opaque substance that protects house
A) water
B) walls
C) curtains
D) glass
Answer:
B) walls

Question 62.
Gin wants to use mirror in his house for light, at the same time the things should not be seen from outside. Which type of mirrors are to be used?
A) Transparent
B) Opaque
C) Translucent
D) None of the above
Answer:
C) Translucent

Question 63.
Floating a ship on surface of sea water is an amazing work and hardship behind it. This creditgoesto
A) The scientists who designed it
B) The people who sail in it
C) The people who built it
D) The businessman who built it
Answer:
A) The scientists who designed it

Question 64.
Wooden piece sinks but not wooden bowl. The reason is
A) material in one shape will sink in water but float when they are in other shape
B) material sinks in other shape.
C) material floats in any shape
D) material sinks or floats in any shape
Answer:
A) material in one shape will sink in water but float when they are in other shape

Telangana SCERT TS 6th Class Telugu Guide Pdf Download ఉపవాచకం 2nd Lesson మన జాతర-జన జాతర Textbook Questions and Answers.

TS 6th Class Telugu Guide ఉపవాచకం 2nd Lesson మన జాతర-జన జాతర

ప్రశ్న 1.
మన జాతర-జన జాతర పాఠ్యభాగ సారాంశం రాయండి.
(లేదా)
సమ్మక్క-సారక్కల గురించి రాయండి.
జవాబు.
పరిచయం : వరంగల్ జిల్లాలోని మేడారంలో రెండేళ్ళకోసారి మూడు రోజులపాటు జరిగే సమ్మక్క-సారక్క జాతర గురించిన విశేషాలను ఈ పాఠ్య భాగంలో వివరించారు.
సమ్మక్క-సారక్క అనే తల్లీకూతుళ్ళు వీరవనితలు. 12వ శతాబ్దంలో కరీంనగర్ జిల్లా పాలవాస ప్రాంతాన్ని పాలించిన మేడరాజు అనే గిరిజన దొర అడవిలో పులుల మధ్య ఆడుకుంటున్న చిన్నపిల్లను సమ్మక్క అని పేరు పెట్టి పెంచాడు. మేడారం రాజు అయిన పగిడిద్దరాజును పెళ్ళిచేసుకుని నాగులమ్మ, సారలమ్మ, జంపన్న అనే ముగ్గురు పిల్లల్ని కన్నది. మేడారం మహారాణిగా ప్రజల మేలుకోసం ఎన్నో మంచి పనులు చేసింది.

కాకతీయుల దండయాత్ర : మేడరాజుకు ఆశ్రయం ఇచ్చాడనీ, కప్పం కట్టలేదనీ, స్వతంత్రం ప్రకటించుకున్నాడని మేడారం రాజుపై కాకతీయ ప్రతాపరుద్రుడు యుద్ధానికి సైన్యాన్ని పంపాడు. అంత పెద్ద సైన్యాన్ని ఓడించలేక పగిడిద్దరాజు, జంపన్న వీరమరణం పొందినా సమ్మక్క మాత్రం వీరోచితంగా పోరాడింది. చివరికి కాకతీయ సైనికుల దొంగ దెబ్బవల్ల గాయపడి చిలకలగుట్ట మీదికి వెళ్ళి మాయమయ్యింది. కులదైవం కలలో కనిపించి సమ్మక్క దేవత అని చెప్పడంతో రాజు జాతరకు ఏర్పాట్లు చేయమని ఆదేశించాడు.

జాతర జరిగే విధానం : నియమనిష్ఠలతో గిరిజన పురోహితులు పవిత్రమైన చిలకలగుట్ట మీది నుంచి పసుపు కుంకుమ భరిణను, వెదురుగడను తెచ్చి గద్దెపై నిలపడంతో జాతర మొదలవుతుంది. దేవతల వన ప్రవేశంతో ముగిసే ఈ జాతరలో ప్రజలు బంగారం అని పిలిచే బెల్లాన్ని తమ బరువు సరిపడా తూచి పంచి తమ మొక్కులు తీర్చుకుంటారు.

పరిచిత గద్యభాగాలు

1. కింది పేరా చదవండి. ప్రశ్నలకు సరియైన జవాబులు గుర్తించండి.

ఆమెకు పెండ్లి వయస్సు వచ్చింది. మేడరాజు మేనల్లుడు పగిడిద్దరాజు. ఇతడు కాకతీయులకు సామంతరాజుగా ఉండి మేడారంను పాలిస్తుండేవాడు. పగిడిద్దరాజుకు సమ్మక్కనిచ్చి పెళ్లి చేశారు. సమ్మక్క మేడారం రాజ్యంలోకి అడుగు పెట్టింది. వీరికి నాగులమ్మ, సారలమ్మ అనే ఇద్దరు బిడ్డలు, జంపన్న అనే కొడుకు పుట్టారు. సమ్మక్క ప్రజల పక్షం | వహించి పరిపాలనలో మార్పులు చేసింది. గిరిజనుల కోసం ఎన్నో సంస్కరణలు ప్రవేశపెట్టింది. ప్రజల బాగోగులు స్వయంగా తెలుసుకున్నది. మహారాణులంటే మేడల్లోనే ఉంటారు. ప్రజలకు కనిపించరు. కాని మేడారం మహారాణి సమ్మక్క మాత్రం ఎప్పుడు ప్రజల మధ్యనే ఉండేది.

1. మేడరాజు ఎవరికి మేనమామ ?
(అ) జంపన్న
(ఆ) సమ్మక్క
(ఇ) పగిడిద్దరాజు
(ఈ) సారలమ్మ
జవాబు.
(ఇ) పగిడిద్దరాజు

2. మేడారం మహారాణి ఎవరు ?
(అ) సమ్మక్క
(ఆ) సారక్క
(ఇ) అమ్మక్క
(ఈ) చిన్నక్క
జవాబు.
(అ) సమ్మక్క

3. పగిడిద్దరాజు ఎవరికి సామంతుడు ?
(అ) నిజాం నవాబుకు
(ఆ) ఢిల్లీ సుల్తానులకు
(ఇ) చాళుక్యులకు
(ఈ) కాకతీయులకు
జవాబు.
(ఈ) కాకతీయులకు

4. పరిపాలనలో సమ్మక్క ఎవరి పక్షం వహించింది ?
(అ) భర్త పక్షం
(ఆ) ప్రజల పక్షం
(ఇ) బిడ్డల పక్షం
(ఈ) తండ్రి పక్షం
జవాబు.
(ఆ) ప్రజల పక్షం

5. మహారాణులు సాధారణంగా ఎక్కడ ఉంటారు ?
(అ) ప్రజల మధ్యన
(ఆ) యుద్ధరంగంలో
(ఇ) మేడల్లో
(ఈ) గుడిసెల్లో
జవాబు.
(ఇ) మేడల్లో

2. కింది పేరా చదవండి. ఖాళీలను పూరించండి.

యుద్ధంలో ముందుండి పోరాడుతారు తప్ప వెనకనుంచి వచ్చి దెబ్బకొట్టరు. ఇది యుద్ధనీతి. సమ్మక్క పోరాటాన్ని చూసి కాకతీయ సైన్యం ఆందోళన చెందింది. ఒక సైనికుడు దొంగచాటుగా వెనుకనుంచి వెళ్లి బల్లెంతో వీపులో పొడిచాడు. గాయపడిన సమ్మక్క గుర్రంమీద ఈశాన్య దిక్కున ఉన్న చిలకలగుట్టమీదికి పోయింది. ఎంత వెతికినా మళ్ళీ ఎవరికీ కనిపించలేదు. ఆమెకోసం వెదుకుతున్న గిరిజనులకు ఓ నెమలినార చెట్టు, దానికింద ఓ పుట్ట. పుట్టమీద ఓ కుంకుమ భరిణ కనిపించింది. ఆ భరిణలో పసుపు, కుంకుమ, చెట్ల మూలికలు కనిపించాయి. సమ్మక్క తల్లి దేవతారూపం పొందిందని గిరిజనులు నమ్మారు.

ఖాళీలు :
1. చిలకలగుట్ట ఉన్న దిక్కు …………………….
2. సమ్మక్క కోసం వెతుకుతున్న గిరిజనులకు పుట్టమీద కనిపించినది ………………..
3. యుద్ధంలో …………….. పోరాడడం యుద్ధనీతి.
4…………………. పోరాటాన్ని చూసి కాకతీయ సైన్యం ఆందోళన చెందింది.
5. సమ్మక్క తల్లి ………………. రూపం పొందిందని గిరిజనులు నమ్మారు.
జవాబు.
1. చిలకలగుట్ట ఉన్న దిక్కు ఈశాన్యం.
2. సమ్మక్క కోసం వెతుకుతున్న గిరిజనులకు పుట్టమీద కనిపించినది కుంకుమ భరిణ
3. యుద్ధంలో ముందుండి పోరాడడం యుద్ధనీతి.
4. సమ్మక్క పోరాటాన్ని చూసి కాకతీయ సైన్యం ఆందోళన చెందింది.
5. సమ్మక్క తల్లి దేవతా రూపం పొందిందని గిరిజనులు నమ్మారు.

పై పేరాననుసరించి తప్పు ( X ), ఒప్పు ( √ ) లను గుర్తించండి.

6. యుద్ధంలో వెనుక నుంచి దెబ్బకొడతారు. (X)
7. సమ్మక్క పోరాటాన్ని చూసి, కాకతీయ సైన్యం ఆనందించింది. (X)
8. సైనికుడు దొంగ దెబ్బతీశాడు. ( √ )
9. సమ్మక్క యుద్ధంలో మరణించింది. (X)
10. గిరిజనులు సమ్మక్క తల్లి దేవతగా మారిందని నమ్మారు. ( √ )

3. క్రింది గద్యాన్ని చదవండి. దాని కింద ఇవ్వబడిన పదాల నుండి సరైన పదాన్ని ఎన్నుకొని సంబంధిత ఖాళీలను పూరించండి.

12వ శతాబ్దంలో పూర్వపు కరీంనగర్ జిల్లా పొలవాస ప్రాంతాన్ని గిరిజన దొర మేడరాజు పాలిస్తుండేవాడు. అతడికి ……………… లేదు. ఒకనాడు (2) ……………….. మధ్య ఆడుకుంటున్న చిన్న పిల్లను చూశాడు. దేవుడిచ్చిన వరంగా భావించి ఆ (3) ……………
ఇంటికి తెచ్చి సాదుకున్నాడు. (4) …………….. అని పేరు పెట్టుకున్నాడు. చిన్నప్పటి నుండి సమ్మక్క చెట్ల వైద్యం చేస్తూ, తోటి (5) ………………… ను రక్షించేది. (పాప, వేట, శతాబ్దం, జాతర, గిరిజనుల, బాగోగులు, సమ్మక్క, సంతానం)
జవాబు.
12వ శతాబ్దంలో పూర్వపు కరీంనగర్ జిల్లా పొలవాస ప్రాంతాన్ని గిరిజన దొర మేడరాజు పాలిస్తుండేవాడు. అతడికి సంతానం లేదు. ఒకనాడు వేట మధ్య ఆడుకుంటున్న చిన్న పిల్లను చూశాడు. దేవుడిచ్చిన వరంగా భావించి ఆ పాప ఇంటికి తెచ్చి సాదుకున్నాడు. సమ్మక్క అని పేరు  పెట్టుకున్నాడు. చిన్నప్పటి నుండి సమ్మక్క చెట్ల వైద్యం చేస్తూ, తోటి గిరిజనులను ను రక్షించేది.

 

4. క్రింది గద్యాన్ని చదివి, తప్పు – ఒప్పులను గుర్తించండి.

జాతరకు ప్రత్యేకంగా గిరిజన పురోహితులు ఉంటారు. వారు నియమ నిష్ఠలతో జాతర కార్యక్రమం చేస్తారు. చిలకల గుట్టను గిరిజనులు పవిత్రమైనదిగా భావిస్తారు. ఆ గుట్ట పైకి ఎవరూ పోరు. జాతర ముందర ఒక కోయ యువకుడు చిలకల గుట్ట మీదికి పోయి పసుపు కుంకుమ ఉన్న భరిణను, వెదురుగడను తెచ్చి గద్దెలపై నిలపడంతో జాతర మొదలవుతుంది. అతడు పూనకంతో ఉంటాడు. సమ్మక్క గాయపడ్డ చోటును తల్లి గద్దె అని, సారలమ్మ వీరమరణం పొందిన చోటును పిల్ల గద్దె అని అంటారు. ఈ తతంగాన్ని ‘దేవతలను ఆహ్వానించడం’ అంటారు. తర్వాత భక్తులు గద్దెలను దర్శించుకోవడం మొదలవుతుంది. మూడవనాడు దేవతల వనప్రవేశంతో జాతర ముగుస్తుంది.

తప్పు ( X ), ఒప్పు( √ ) లను గుర్తించండి.

1. చిలకల గుట్టపైకి ఎవరైన పోతారు (X)
2. జాతరలో కోయ యువకుడు పూనకంతో ఉంటాడు. (√)
3. పసుపు, కుంకుమ భరిణ, వెదురుగోడ చిలకల గుట్టపై ఉంటాయి. (√)
4. దేవతల ఆహ్వానం తర్వాతనే భక్తులు గద్దెలను దర్శించుకుంటారు. (√)
5. మేడారం జాతర ఏడవ రోజుకు ముగుస్తుంది. (X)

5. ఈ క్రింది పేరాను చదివి ప్రశ్నలకు సమాధానాలు రాయండి.

జయశంకర్ జిల్లా తాడ్వాయి మండలం మేడారం గ్రామం దగ్గర అడవి మధ్యలో ‘చిలకల గట్టు’ ఉన్నది. చుట్టు దట్టమైన అడవి. ఇక్కడ రెండేండ్లకొకసారి మూడు రోజులపాటు జాతర జరుగుతుంది. మాఘశుద్ధ పౌర్ణమి (ఫిబ్రవరి నెలలో) మొదలకొని మూడు రోజుల పాటు జరిగే ఈ జాతరనే సమ్మక్క – సారక్క జాతర అంటారు. ఇది పూర్తిగా గిరిజన సంప్రదాయరీతిలో జరిగే జాతర. కేవలం మన రాష్ట్రం నుంచేకాక పొరుగు రాష్ట్రాలైన ఆంధ్రప్రదేశ్, మహారాష్ట్ర, చత్తీస్గఢ్, జార్ఖండ్, మధ్యప్రదేశ్ రాష్ట్రాలనుండి కూడా లక్షల మంది వచ్చి మొక్కు తీర్చుకుంటారు.

ప్రశ్న 1.
సమ్మక్క – సారక్క జాతర ఎన్ని రోజులు జరుగుతుంది ?
జవాబు.
మూడు రోజులు జరుగుతుంది.

ప్రశ్న 2.
జాతరకు ఏయే రాష్ట్రాల నుండి భక్తులు వస్తారు ?
జవాబు.
ఆంధ్ర ప్రదేశ్, మహారాష్ట్ర, చత్తీస్ గఢ్, జార్ఖండ్, మధ్యప్రదేశ్.

ప్రశ్న 3.
గిరిజన సంప్రదాయంలో జరిగే జాతర ఏది ?
జవాబు.
సమ్మక్క – సారక్క జాతర

ప్రశ్న 4.
సమ్మక్క – సారక్క జాతర ఎప్పుడు జరుగుతుంది ?
జవాబు.
మాఘశుద్ధ పౌర్ణమి (ఫిబ్రవరి నెలలో)

ప్రశ్న 5.
మేడారం ఏ జిల్లాలో ఉంది ?
జవాబు.
జయశంకర్ జిల్లాలో ఉంది.

6. క్రింది పేరాను చదివి, ఇచ్చిన ఖాళీలను పూర్తి చేయండి.

గిరిజనులు దేవతామూర్తులుగా కొలిచి ఆరాధించే సమ్మక్క, సారక్కలు ఇద్దరూ తల్లీకూతుళ్ళు. గిరిజన హక్కుల కోసం ఎదురుతిరిగి పోరాడిన వీర వనితలు. 12వ శతాబ్దంలో పూర్వపు కరీంనగర్ జిల్లా “పొలవాస” ప్రాంతాన్ని మేడరాజు పాలిస్తుండేవాడు. అతనికి సంతానం లేదు. ఒకనాడు వేటకు వెళ్లి అడవిలో పులుల మధ్య ఆడుకుంటున్న చిన్న పిల్లను చూశాడు. దేవుడిచ్చిన వరంగా భావించి, ఆ పాపను ఇంటికి తెచ్చి సాదుకున్నాడు. సమ్మక్క అని పేరు పెట్టుకున్నాడు. చిన్నప్పటి నుంచి సమ్మక్క చెట్ల వైద్యం చేస్తూ తోటి గిరిజనులను రక్షించేది. ఆమెకు మహిమలు ఉన్నాయని, దేవతామూర్తి అని గిరిజనులు భావించేవారు. సమ్మక్క గిరిజన గూడేనికి తలలో నాలుకయింది. ఆమెకు పెండ్లి వయసు వచ్చింది. మేడరాజు మేనల్లుడు పగిడిద్దరాజు.

ఖాళీలు :
1. సమ్మక్క, సారక్కలను గిరిజనులు …………… గా కొలుస్తారు.
2. “పొలవాస” ప్రాంతాన్ని ……………..రాజు పాలించేవాడు.
3. అడవిలో పాప ………………… మధ్య ఆడుకుంటుంది.
4. సమ్మక్క …………… వైద్యం చేసేది.
5. మేడరాజు మేనల్లుడు ………………
జవాబు.
1. సమ్మక్క, సారక్కలను గిరిజనులు దేవతామూర్తులుగా గా కొలుస్తారు.
2. “పొలవాస” ప్రాంతాన్ని మేడరాజు రాజు పాలించేవాడు.
3. అడవిలో పాప పులుల మధ్య మధ్య ఆడుకుంటుంది.
4. సమ్మక్క చెట్ల వైద్యం వైద్యం చేసేది.
5. మేడరాజు మేనల్లుడు పగిడిద్దరాజు

Telangana SCERT TS 8th Class Hindi Guide Pdf 9th Lesson मैं सिनेमा हूँ Textbook Questions and Answers.

TS 8th Class Hindi 9th Lesson Questions and Answers Telangana मैं सिनेमा हूँ

प्रश्न :

प्रश्न 1.
चित्र में क्या – क्या दिखायी दे रहे हैं?
उत्तर :
चित्र में एक नाटक प्रदर्शन, उसको देखने वाले बचे और बडे – बडे लोग आदि दिखायी दे रहे हैं।

प्रश्न 2.
वे क्या – क्या कर रहे हैं ?
उत्तर :
कुछ छात्र नाटक प्रदर्शन कर रहे हैं। और बाकी सभी लोग नाटक को देख रहे हैं।

प्रश्न 3.
नाटक में क्या बताया जा रहा होगा ?
उत्तर :
यह नाटक विश्व साक्षरता दिवस के उपलक्ष्य में प्रसारित कर रहे हैं। इसीलिए इसमें साक्षरता का संदेश ही बताया जा रहा होगा।

सुनो – बोलो :

प्रश्न 1.
चित्र के बारे में बातचीत कीजिए।
उत्तर :
गौतम और सुरेश के बीच में इस चित्र के बारे में बातचीत चल रहा है। वह इस प्रकार है

• गौतम : सुरेश, क्या तुमने इस चित्र को देखा ?
• सुरेश : हाँ, खूब देख लिया।
• गौतम : तो बताओ कि चित्र में क्या है ?
• सुरेश : एक सिनेमाघर है।
• गौतम : बहुत अच्छा। तुमने सचमुच ठीक कहा।
• सुरेश : सिनेमा घर में पर्दा बहुत अच्छा दिखाई देता है न ?
• गौतम : हाँ ! वह तो चाँदी से बनाया गया है।
• सुरेश : अरे गौतम सिनेमाघर में कुर्सियाँ बहुत अच्छी नज़र आ रही है न ?
• गौतम : हाँ ! वे तो कीमती कुर्सियाँ है।

प्रश्न 2.
सिनेमा देखना आपको कैसा लगता है? क्यों ?
उत्तर :
सिनेमा देखना मुझे बहुत अच्छा लगता है। क्योंकि सिनेमा आजकल के मनोरंजन साधनों में एक है। इसके द्वारा समय का सदुपयोग होता है। मानसिक थकावट दूर हो जाती है।

पढ़ो :

अ. पाठ में आये अंग्रेजी शब्दों के अर्थ शब्दकोश में ढूँढ़िए। वाक्य में प्रयोग किजिए।
उत्तर :
जैसे : प्रोजेक्टर = प्रक्षेपक ; प्रक्षेपक की सहायता से परदे पर सिनेमा दिखायी देता है।
पाइरेटेड – चोरी की हुई फ़िल्म – पाइरेटेड सिनेमा मत देखो।
पैरेसी – चोरी – पुलीस पैरेसी सिनेमा को पकड लेते हैं।
फ़्लिम – सिनेमा – यह नयी फ़िल्म है।
सी.डी – कैसेट ड्राइव – रामू हमेशा सी.डी देखता रहता है।

आ. राजा हरिश्चंद्र भारत की पहली मूक फ़िल्म थी । उसी तरह पहली बोलती फ़िल्म थी – ‘आलम आरा।’ अब नीचे दिखाये गये पोस्टर के आधार पर प्रश्नों के उत्तर दीजिए।

उत्तर :
1. सिनेमाघर का नाम मैजेस्टिक सिनेमाघर है।
2. जुबेदा, विट्ठल, पृथ्वीराज कपूर तथा अन्य पात्र हैं।
3. सिनेमा देखने का समय प्रतिदिन शाम को 5.30,6.00 और रात 10.30 . बजे है।
4. मूक चित्र केवल मूकी होते हैं। बोलती फ़िल्में बातचीत या टाकी के होते हैं।

लिखो :

अ. नीचे दिये गये प्रश्नों के उत्तर लिखिए।

प्रश्न 1.
निर्देशक और सिनेमा एक – दूसरे से कैसे जुडे रहते हैं?
उत्तर :
निर्देशक और सिनेमा एक – दूसरे से जुडे रहते हैं। निर्देशक के बिना सिनेमा और सिनेमा के बिना निर्देशक नही हैं। वार्तव में सिनेमा का केंद्रबिंदु निर्देशक ही है। वह सिनेमा के निर्माण से जुडे सभी लोगों, जैसे नायक-नायिका, पात्र, संगीत निर्देशक, कथाकार, संवाद लेखक, कैमरामेन आदि को एक सूत्र में बाँधकर सिनेमा को साकार रूप देता है। सिनेमा बनाने में हजारों लोगो की मेहनत जुडी होती है। सिनेमा से उनके जीविका चलती है। उनकी मेहनत पर ही सिनेमा का भविष्य निर्भर रहता है।

प्रश्न 2.
पाइरेटेड सिनेमा से आप क्या समझते हैं?
उत्तर :
चोरी की हुई फ़िल्म को पाइरेटेड सिनेमा कहते हैं।

आ. इस पाठ का सारांश अपने शद्दों में लिखिए।
उत्तर :
सभी को सिनेमा देखना अच्छा लगता है। छुट्टियों के समय में तो सब सिनेमा देखते हैं। इसे देखने में उत्सुक रहते हैं। सिनेमा हमें आनंदित करता है। यह हमारे मनोरंजन का साधन है।
सिनेमा का जन्म विदेश में हुआ है। भारत में इसे लाने का श्रेय श्री दादा साहेब फ़ाल्के को जाता है। सन् 1913 में उन्होंने राजा हरिश्चंद्र नाम से एक सिनेमा का निर्माण किया। यही भारत का पहला सिनेमा है।
सिनेमा बनाने वाले को निर्माता कहते हैं। सिनेमा पहले-पहले मूक थे। बाद में टाकी आ गये। उसके बाद में रंगों के सिनेमा आये। सिनेमा हास्य तथा दुख दोनों भावों के होते हैं।
सिनेमाओं में कल्पना तथा प्रेरणा दोनों हैं। सिनेमा को बनाने में कई लोगों का योगदान है। कहानीकार कहानी लिखता है। निर्माता, उस कहानी को खरीदकर सिनेमा बनाता है।
निर्माता की निर्देशक सहायता करता है। यूँ तो केंद्रबिंदु निर्देशक ही है। नायक – नायिका, पात्र, संगीत निर्देशक, कथाकार, संवाद लेखक कैमरामेन आदि भी सिनेमा के प्राण हैं।
सिनेमां के बुरे और अच्छे दोनों रूप होते हैं। अच्छाई को ग्रहण करें। बुराई को छोड़ दे। पाइरेटेड चित्र न देखें। इन्हें देखना – दिखाना दोनों शासन अपराध है।

शब्द अंडार :

अ. निम्न लिखित शब्दों को वाक्य में प्रयोग कीजिए।

1. मनोरंजन : सिनेमा से मनोरंजन मिलता है।
2. उत्सुक : वह गीत गाने में उत्सुक है।
3. विदेश : आम फल को विदेश लोग भी बहुत पसंद करते हैं।
4. श्रेय : तंदुरुस्ती के लिए टहलना श्रेय है।
5. प्रशंसा : अच्छे काम करने वालों की प्रशंसा करनी चाहिए।
6. भविष्य : आज के बच्चे ही भविष्य के नागरिक हैं।
7. उज्ञल : उज्चल भविष्य के लिए खूब परिश्रम करना चाहिए।

सृजनात्मक अभिव्यक्ति :

अ. नीचे दी गयी जानकारी से एक पोस्टर बनाइए।
फ़िल्म का नाम – (अपने मनपसंद पात्रों के नाम लिखो।)
प्रारंभ करने की तिथि – (अपना मनपसंद दिनांक डालो।)
पात्रों के नाम – (अपने मनपसंद पात्रों के नाम लिखो।)
निर्देशक का नाम – (अपने मनपसंद निर्देशक का नाम लिखो।)
सिनेमाघर का नाम – (अपने मनपसंद सिनेमाघर का नाम लिखो।)
सिनेमा की विशेषता – (अपनी ओर से सिनेमा की विशेषता लिखो।)
उत्तर :

प्रशंसा :

अ. अपने मनपसंद सिनेमा के बारे में लिखिए।
उत्तर :
मैं ने तेलुगु का एक सिनेमा देखा। नाम था ‘भक्त प्रहल्लाद।’ यह भक्त प्रहल्लाद की कहानी है। भक्त प्रहल्लाद राक्षस राजा हिरण्य कश्यप का पुत्र का नाम था।
हिरण्य कश्यप तीन लोकों में वही राजा और देव मानता था। और सबको मानने को कहता था। लेकिन उसका बेटा प्रहल्काद भगवान विष्णु के सिवा और किसी को भगवान या देव नहीं समझता है।
इसलिए राजा हिरण्य कश्यप अपने बेटे को कई दंड देता है। एक बार साँप से काटवाने का आदेश देता है। साँप काटने से भी भगवान विष्णु की कृपा से वह जीवित होता है। दूसरी बार सागर में फेंक दिये जाते हैं तो इस बार लक्ष्मी देवी उसकी रक्षा करती है।
एक बार हाथी के पैरों के नीचे दबा दिया जाता है। लेकिन उसे विष्णु की कृपा से कुछ नहीं होता और एक बार विष पिलाया जाता है फिर भी भगवान श्री महाविष्णु की कृपा से प्रहल्लाद को कुछ नही होता।
अंत में प्रहल्लाद के पिता हिरण्य कश्यप भगवान विष्णु को कंभे में दिखाने को कहता है तो प्रहल्ताद कहता है कि भगवान विष्णु अवश्य ही कंभे में है।
तो हिरण्य कश्यप ने गदे से कंभे को मारता है तो श्रीविष्णु नरसिंह के अवतार में प्रकट होकर उसे मार देते हैं।

भषा की बात :

अ. नीचे दिया गया अनुच्छेद पढ़िए।
“प्रोजेक्टर से मैं चलता हैँ
परदे पर में दिखता हूँ।
मनोरंजन सबका करता हूँ
जल्दी बताओ कौन हैँ में?

ऊपर दिये गये अनुच्छेद में चलता हूँ, दिखता हूँ, करता हूँ, बताओ, हूँ ये सारे शब्द किसी काम का होना प्रकट करते हैं। ऐसे शब्द ही क्रिया शब्द कहलाते हैं। क्रिया के दो प्रकार हैं। वे है –
1. अकर्मक क्रिया 2. सकर्मक क्रिया
1. अकर्मक क्रिया : जहाँ कर्ता के व्यापार का फल कर्ता पर पड़े उसे अकर्मक क्रिया कहते हैं। जैसे : मैं प्रोजेक्टर से चलता हुँ। ‘चलता हूँ’, क्रिया का व्यापार ‘में’ पर पड़ रहा है। जैसे:
लड़का हँसता है।
लड़का दौड़ता है।

2. सकर्मक क्रिया : जहाँ कर्ता के व्यापार का फल कर्म पर पडे उसे सकर्मक क्रिया कहते हैं। जैसे : निर्माता उस कहानी को खरीदता है। ‘खरीदता है’ क्रिया का व्यापार कर्म ‘कहानी’ पर पड़ रहा है।
जैसे:
राकेश चित्र बनाता है।
लड़की रोटी खाती है।

आ. पाठ में आये हूए अन्य तीन क्रिया शब्द ढूँढ़िए। वाक्य प्रयोग कीजिए।
जैसे : देखना – में सिनेमा देखना चाहता हूँ।
उत्तर :

1. पहचानना – अब मुझे कोई भी पहचान नहीं सकते हैं।
2. करना – सिनेमा सबका मनोरंजन करता है।
3. बताना – वह कुछ बताना चाहता है।
4. लाना – तुम मेरे लिए क्या लाते हो?
5. लिखना – राम पाठ लिखता है।
6. खरीदना – में कलम खरीदना चाहता हूँ।
7. देना – आज रवि सभा में सेमिनार देनेवाला है।
8. बेचना – मैं इसे बेचना चाहता हूँ।

परियोजना कार्य :

अ. हिदी समाचार चैनल के पाँच मुख्य समाचार लिखिए।
उत्तर :
विद्यार्थी कृत्य।

Essential Material for Examination Purpose :

1. पढ़ो
पठित – गद्यांश

नीचे दिये गये गद्यांश को पढ़कर प्रश्नों के उत्तर एक वाक्य में लिखिए।

1. मेरा जन्म विदेश में हुआ। किंतु भारत में मुझे लाने का श्रेय मेरे पितामह दादा साहेब फाल्के को जाता है। सन् 1913 में उन्होंने राजा हरिश्चंद्र के नाम से मुझे आपके सामने लाया। देश – विदेश के समाचार पत्रों में मेरे लाड़ले दादा साहेब फाल्के की खूब प्रशंसा की गयी। मेरी खुशी का ठिकाना न रहा । उन्होंने मेरा भविष्य उज्जवल कर दिया ।

प्रश्न :
1. किसका जन्म विदेश में हुआ?
2. भारत में सिनेमा कौन लाया ?
3. पहली भारतीय फ़िल्म का नाम क्या था ?
4. भारतीय सिनेमा के पितामह कौन हैं?
5. यह गद्यांश किस पाठ से है?
उत्तर :
1. सिनेमा का जन्म विदेश में हुआ।
2. भारत में सिनेमा दादा साहेब फाल्के लाये।
3. पहली भारतीय फ़िल्म का नाम राजा हरिश्चंद्र था।
4. भारतीय सिनेमा के पितामह दादा साहेब फाल्के हैं।
5. यह गद्यांश ‘मैं सिनेमा हूँ’ पाठ से है।

II. कहानीकार एक अच्छी कहानी लिखता है। निर्माता उस कहानी को खरीदता है। निर्माता मुझे बनाने से लेकर सिनेमाघरों तक पहुँचाने वाला महत्वपूर्ण व्यक्ति है।

प्रश्न :
1. एक अच्छी कहानी कौन लिखता है ?
2. सिनेमा बनानेवाले को क्या कहते हैं ?
3. कहानी को कौन खरीदता है?
4. दुनिया में अच्छाई और बुराई दोनों भी है। (भाववाचक संज्ञा पहचानिए।)
5. यह गद्यांश किस पाठ से है?
उत्तर :
1. एक अच्छी कहानी कहानीकार लिखता है।
2. सिनेमा बनानेवाले को निर्माता कहते है।
3. कहानी को निर्माता खरीदता है।
4. अच्छाई, बुराई।
5. यह गद्यांश ‘मैं सिनेमा हूँ’ पाठ से है।

अपठित – गद्यांश :
नीचे दिये गये गद्यांश को पढ़कर प्रश्नों के उत्तर एक वाक्य में लिखिए।

I. उसके घर में पिता थे, माँ थी और एक गुडिया – सी बहन थी । वह सारे घर का दुलारा था। एक दिन की बात है। बह बीमार पडा। माँ ने उसका खाना बिलकुल बंदकर दिया। पर उसका बार-बार कुछ खाने को माँगना छोटी बहन से न सहा गया। बह चुपके से गुड और चने चुरा लाई और खिला दी अपने भैया को । उसके बाद भिया का बुखार बढ़ गया पर वह तो खिला ही चुकी थी । अपने भाई के संतोष के लिए वह माँ – बाप का गुस्सा भी सहने को तैयार थी ।

प्रश्न :
1. उसके घर में कितने लोग और कौन – कौन थे ?
2. एक दिन उसे क्या हुआ ?
3. बीमार पडने से मॉ ने क्या किया ?
4. उसकी बहन ने क्या किया ?
5. गुड और चने खाने से क्या परिणाम हुआ?
उत्तर :
1. उसके घर में तीन लोग पिता, मौं और बहन थीं।
2. एक दिन वह बीमार हो गया।
3. बीमार पडने से माँ ने उसका खाना बिलकुल बंद कर दिया।
4. उसकी बहन ने उसे चुपके से गुड और चने खिलाये।
5. गुड और चने खाने से भैया का बुखार और बढ़ गया।

II. खेलकूद और व्यायाम से हमारा शरीर और मन स्वस्थ रहता है। खुली हवा के बिना तो मनुष्य शरीर स्वस्थ नहीं बन सकता। इसके लिए घर हवादार होना चाहिए। प्रातः काल खुली हवा में टहलना भी स्वास्थ्य के लिए लाभदायक है।
यह हमेशा याद रखना चाहिए कि अच्छा स्वास्थ्य ही सुखमय जीवन का आधार है। एक प्रचलित कहावत है – “मन चंगा तो कटौती में गंगा।”

प्रश्न :
1. हमारा शरीर और मन किनसे स्वरथ रहता है ?
2. किसके बिना तो मनुष्य का शरीर स्वस्थ नहीं बन संकता ?
3. घर कैसा होना चाहिए ?
4. सुखमय जीवन का आधार क्या है?
5. प्रचलित कहावत क्या है?
उत्तर :
1. खेलकूद और व्यायाम से हमारा शरीर और मन स्वस्थ रहता है।
2. खुली हवा के बिना तो मनुष्य का शरीर स्वस्थ नहीं बन सकता।
3. घर हवादार होना चाहिए।
4. स्वारथ्य सुखमय जीवन का आधार है।
5. प्रचलित कहावत है – “मन चंगा तो कटौती में गंगा।”

III. प्रथम पृष्ठ पर मुख्य – मुख्य समाचार होते हैं। व्यापार और खेलकूद के समाचार दूसरे – तीसरे पृष्ठों पर दिये जाते हैं। साथ ही व्यंग्य चित्र और विज्ञापनों के चित्र भी होते हैं, जिससे समाचार पत्र और भी आकर्षक लगता है। प्रायः सभी समाचार – पत्रों में बच्चों का भी पृष्ठ होता है, जिसमें मनोरंजक कहानियाँ, कविताएँ तथा चुटकुले आदि होते हैं। बच्चों के लिए समाचार भी दिये जाते हैं। कभी – कभी बच्चों के चित्रों के साथ उनके द्वार लिखी गयी रचनाएँ भी छापी जाती हैं।

प्रश्न :
1. मुख्य – मुख्य समाचार किस पृष्ठ पर होते हैं ?
2. दूसरे – तीसरे पृष्ठों पर किसके समाचार दिये जाते हैं ?
3. किनसे समाचार पत्र और भी आकर्षक लगता है?
4. सभी समाचार पत्रों में किनके लिए भी पृष्ठ होते हैं ?
5. इस अनुच्छेद में किसके बारे में बताया गया है ?
उत्तर :
1. मुख्य – मुख्य समाचार प्रथम पृष्ठ पर होते हैं।
2. दूसरे – तीसरे पृष्ठों पर व्यापार और खेलकूद के समाचार दिये जाते हैं।
3. व्यंग्य और विज्ञापनों के चित्रों से समाचार पत्र और भी आकर्षक लगता है।
4. सभी समाचार पत्रों में बच्चों के लिए भी पृष्ठ होते हैं।
5. इस अनुच्छेद में समाचार पत्रों के बारे में बताया गया है।

II. लिखो :

लघु प्रश्न :

प्रश्न 1.
सिनेमा का हमसे क्या निवेदन है?
उत्तर :
सिनेमा हम से इस प्रकार निवेदन करता है कि “मेरी अच्छाई को स्वीकार करो । मुझे सिनेमा घरों में ही देखो। पाइरेटेड (चोरी की हुई फ़िल्म) बिलकुल मत देखो। पैरेसी सी.डी को न तो खरीदे और न ही बेचे’।

प्रश्न 2.
हमें सिनेमा कहाँ देखना चाहिए? क्यों ?
उत्तर :
हमें सिनेमा केवल सिनेमाघरों में ही देखना चाहिए। क्योंकि निर्माता कई करोडों रुपये खर्च करके सिनेमाओं का निर्माण करते हैं। इसलिए पैरेसी फ़िल्म न देखना चाहिए। यह शासन विरुद्ध भी है।

प्रश्न 3.
सिनेमाघर कैसा होता है? बताओ।
उत्तर :
सिनेमाघर बहुत अच्छा होता है। सिनेमाघर बहुत बडा तथा विशाल होता है। सिनेमाघरों में जमीन टिकट, बेंच टिकट, कुर्सी टिकट, बाल्कनी टिकट और रिजर्वड टिकट आदि होते हैं। अंदर के चारों ओर के दीवारों को स्पीकर भी होते हैं।

प्रश्न 4.
दादा साहेब फ़ाल्के कौन थे ?
उत्तर :
भारत में सिनेमा को लाने का श्रेयकर्ता श्री दादा साहेब फ़ाल्के थे। इन्होंने सन् 1913 में भारत में राजा हरिश्चंद्र नामक एक सिनेमा बनाया।

प्रश्न 5.
सिनेमा में कैसे भाव देखने को मिलते हैं ?
उत्तर :
सिनेमा में सभी भाव देखने को मिलते हैं। सिनेमा में हास्य है तो दुख भी है। इसमें कल्पना है तो प्रेरणा भी है।

लघु निबंध प्रश्न :

प्रश्न 1.
किसी देखे हुये सिनेमा की कहानी सुनाओ।
उत्तर :
में ने तेलुगु का एक सिनेमा देखा। नाम था ‘भक्त प्रहल्लाद।’ यह भक्त प्रहल्लाद की कहानी है। भक्त प्रहल्लाद राक्षस राजा हिरण्य कश्यप का पुत्र का नाम था।
हिरण्य कश्यप तीन लोकों में वही राजा और देव मानता था। और सबको मानने को कहता था। लेकिन उसका बेटा प्रहल्लाद भगवान विष्णु के सिवा और किसी को भगवान या देव नहीं समझता है।
इसलिए राजा हिरण्य कश्यप अपने बेटे को कई दंड देता है। एक बार साँप से काटवाने का आदेश देता है। साँप काटने से भी भगवान विष्णु की कृपा से वह जीवित होता है। दूसरी बार सागर में फेंक दिये जाता है तो इस बार लक्ष्मी देवी उसकी रक्षा करती है।
एक बार हाथी के पैरों के नीचे दबा दिया जाता है। लेकिन उसे विष्णु की कृपा से कुछ नहीं होता और एक बार विष पिलाया जाता है फिर भी भगवान श्री महाविष्णु की कृपा से प्रहल्गाद को कुछ नहीं होता।
अंत में प्रहल्भाद के पिता हिरण्य कश्यप भगवान विष्णु को कंभे में दिखाने को कहता है तो प्रहक्काद कहता हैं कि भगवान विष्णु अवश्य ही कंभे में हैं।
तो हिरण्यकश्यप गदे से कंभे को मारा तो श्रीविष्णु नरसिंह के अवतार में प्रकट होकर उसे मार देते हैं।

III. सृजनात्मक अभिव्यति :

प्रश्न 1.
किसी एक विज्ञान यात्रा का वर्णन करते हुये अपने पिताजी का नाम एक पत्र लिखिए।
उत्तर :

हैदराबाद,
दि. ××××

पूज्य पिताजी,
सादर प्रणाम । मैं यहाँ कुशल हूँ। आशा करता हूँ कि आप सब वहाँ कुशल हैं। मैं यहाँ खूब पढ रहा हूँ।
पाठशाला की ओर से पिछले सप्ताह हम विज्ञान यात्रा के लिए विशाखपट्टणम गये। इसे वैजाग भी कहते हैं। यह एक सुन्दर और बडा शहर है। सागर के किनारे पर है। यहाँ अनेक दर्शनीय स्थान हैं। हम नौकाश्रय में गये और अनेक विज्ञानदायक बातें जानलीं। कैलासगिरि उद्यानवन, विमानाश्रय आदि हमने देखे। सिंहाचलम, अरकु आदि प्रदेशों में हम गये। हमें बहुत आनंद मिला है।
माताजी को मेरे प्रणाम और बहन रम्या को आशीश कहना।

आपका प्रिय पुत्र,
××××

पता :
जी. माधवराव,
घ.नं 31-8-4/9,
वरंगल।

సారాంశము :

ప్రియమైన పిల్లల్లారా ! నమస్తే ఎలా ఉన్నారు ?
నన్ను గుర్తుపట్టలేదా ? ఏమీ విషయం లేదులే. “ప్రొజెక్టర్తో నేను నడుస్తాను.
తెరపై నేను కనిపిస్తాను.
అందరి మనస్సులను రంజింపచేస్తాను.
(అందరికీ మనోరంజనం కల్గిస్తాను)
త్వరగా చెప్పండి, నేనెవరిని?
శభాష్. మీరు సరిగా చెప్పారు. నేను సినిమాను. మీ అందరికీ నన్ను చూడడం బాగుంటుంది కదా! నాకు కూడా మిమ్మల్ని కలవడం బాగుంటుంది. సెలవు దినాలలో నన్ను మీరు చూడడానికి ఉత్సాహం చూపిస్తారు కదా ! నాకు కూడా మిమ్మల్ని ఆనందింపజేయడం చాలా బాగుంటుంది.
నేను విదేశంలో జన్మించాను. కానీ భారతదేశంలోకి తీసుకువచ్చిన ఘనత నా తండ్రిగారైన దాదాసాహెబ్ ఫాల్కే గారికి చెందుతుంది. 1913 సం॥లో ఆయన “రాజా హరిశ్చంద్ర’ పేరుతో నన్ను మీ దగ్గరికి తెచ్చెను. దేశవిదేశాలకు చెందిన వార్తాపత్రికల్లో నా ప్రియమైన గారాల దాదాసాహెబ్ ఫాల్కే గారిని బాగా ప్రశంసించిరి. సంతోషానికి అవధులు లేవు. ఆయన నా భవిష్యత్తును ఉజ్వలింపచేసిరి.
నన్ను ఎంతగా పొగిడినా నన్ను నిర్మించినది మానవుడే కదా. ఆయనే నిర్జీవంగా ఉన్న నాకు ప్రాణం పోసెను. ఒకప్పుడు నేను మూగదాన్ని. కానీ ఆయన నాకు మాట్లాడే శక్తినిచ్చెను. రంగులు నింపెను. నా జీవితంలో వసంతాన్ని
నింపెను.
నాలో అన్ని భావాలు చూడడానికి లభిస్తాయి – నాలో హాస్యం ఉన్నది – దుఃఖం (ఏడుపు) ఉన్నది. నాలో కల్పన ఉన్నది. ప్రేరణ కూడా ఉన్నది. కాని నన్ను నిర్మించడంలో ఎంతోమంది ప్రజల ప్రమేయం (భాగస్వామ్యం) ఉంటుంది.
కథా రచయిత ఒక చక్కని కథ వ్రాస్తాడు. నిర్మాత ఆ కథను కొంటాడు. నిర్మాత అనునతడు నన్ను కొనుగోలు చేసిన దగ్గరి నుండి సినిమా హాళ్ళకు పంపించే వరకు ఉన్నటువంటి మహత్వపూర్ణమైన వ్యక్తి.

నిర్మాత తన ఈ పనిని పూర్తి చేయుటకు దర్శకుని సహాయం తీసుకుంటాడు. వాస్తవంగా నా కేంద్రబిందువు దర్శకుడే. అతడు నా నిర్మాణంలో ముడిపడియున్న ప్రజలందరినీ – నాయకుడు, నాయకురాలు, ఇతర పాత్రధారులు, సంగీత దర్శకుడు, కథా రచయిత, డైలాగ్ రైటర్, కెమేరామెన్ మొ॥గు వారిని ఒకే సూత్రంలో బంధించి నాకు సాకార రూపాన్ని కల్గిస్తారు. నన్ను నిర్మించడంలో వేలకొలది ప్రజల కృషి జోడించబడి యుంటుంది. నాతో వారికి జీవనోపాధి కలుగుతుంది. వారి కృషి మీదనే నా భవిష్యత్తు ఆధారపడి ఉంటుంది.
–
పిల్లల్లారా ! నాది ఒకటే కోరిక. అది ఏమనగా అందరినీ సంతోషపెట్టడమే. ప్రపంచంలో మంచి-చెడు రెండూ ఉంటాయి. అదే విధంగా నాకు మంచి చెడు రెండు రూపాలు ఉన్నాయి. నేను మీతో విన్నవించుకునేది ఏమనగా నాలోని మంచిని గ్రహించండి. నన్ను సినిమా థియేటర్లలోనే చూడండి. ఈ రోజున కొంతమంది ప్రజలు నన్ను దొంగిలించి (పైరసీ) చూస్తున్నారు. నన్ను ఇలాగ చూడవద్దు. ఈ విధంగా చూడడం మరియు చూపడం రెండూ చట్టరీత్యా నేరమే. అందువలన పైరసీ సీడీలు కొనవద్దు, అమ్మవద్దు.
పిల్లల్లారా ! మీరు నన్ను ఎంత చూస్తే ఆనందం లభిస్తుందో అంతవరకే చూడండి. మీరు నా మాట తప్పనిసరిగా అంగీకరిస్తారని ఆశిస్తున్నాను.

वचन :

• बच्चा – बच्चे
• वह् – वे
• छुट्टी – छुट्टियाँ
• मनुष्य – मनुष्य
• सूत्र – सूत्र
• मैं – हम
• इस – ये
• पत्र – पत्र
• क्षमता – क्षमताएँ
• यह – ये
• परदा – परदे
• खुशी – खुशियाँ
• घर – घर

उल्टे शब्द :

• बच्चे × बूढे
• अच्छा × बुरा
• देश × विदेश
• खुशी × दुखी
• मूक × बोल
• खरीदना × बेचना
• वास्तव × अवार्तव
• स्वीकार × अस्वीकार/इनकार
• पहचचान × भूल
• आनंद × दुख
• सामने × पीछे
• जीव × निर्जीव
• क्षमता × अक्षमता
• महत्वपर्ण × महत्वहीन
• साकार × निराकार
• आशा × निराशा
• जलि × धीरे
• जन्म × मृत्य/मरण
• प्रशंसा × निदा
• दनाना × बिगाइना
• हास्य × दुख
• सहायता × हानि
• अच्छाई × पुराई
• अवश्य × अनावश्य

उपसर्ग :

• मनोरंजन – मन:
• निर्माता – निर
• योगदान – योग
• कथाकार – कथा
• निवेदन – नि
• विदेश – वि
• निर्जीव – निर
• सिनेमाघर – सिनेमा
• साकार – सा
• स्वीकार – स्वी
• उज्ञवल – उ
• सजीव – स
• महत्वपूर्ण – महत्व
• निर्भर – नि

प्रत्यय :

• अच्छाई – ई
• पैरेसी – ई
• जीविका – इका
• निर्जीव – जीव
• प्रेरणा – आ
• महत्त्वपूर्ण – पूर्ण
• ठिकाना – आ
• पितामह् – मह
• बुराई – ई
• कथाकार – कार
• निर्भर – भर
• सजीव – जीव
• योगदान – दान
• पहुँचानेवाला – वाला
• मनोरंजन – रंजन
• सिनेमाधर – घर्
• कैमेरामेन – मेन
• खुशी – ई
• क्षमता – ता
• कहानीकार – कार
• सहायता – ता
• आनंदित – इत्त

लिंग :

• बच्ता – बची
• मामा – मामी
• भाई – बहिन
• अभिनेता – अभिनेत्री
• लेखक – लेखिका
• संवाद लेखक – संवाद लेखिका
• प्यारा – प्यारी
• चाचा – चाची
• नायक – नायिका
• राजा – रानी
• सेवक – सेविका
• कैमेरा मेन – कैमेरा र्त्री
• दादा – दादी
• काका – काकी
• नेता – नेत्री
• पिता – माता
• निर्देशक – निर्देशिका

पर्यायवाची शब्द :

• बच्चे – लडके
• छटी – विराम
• मनुष्य – आदमी
• संवाद – वार्तालाप
• व्यक्ति – आदमी
• आनंद – संत्रोष
• समाचार – खबर
• नायक – अभिनेता
• कानून – शासन
• मदट – सदायता
• प्रशंसा – स्तुति
• खुशी – संतोष
• नायिका – अभिनेत्री
• कहानी – कथा

संधि विच्छेद :

• सिनेमाघर = सिनेमा + घर
• आनंदित = आनंद + इत
• कहानीकार = कहानी + कार
• कैमेरामेन = कैमेरा + मेन
• कहानीकार = कहानी + कार
• पितामह = पिता + मह
• महत्वपूर्ण = महत्व + पूर्ण

वाक्य प्रयोग :

1. खरीदना – में आम खरीदना चाहता हूँ।
2. निर्देशक – निर्देशक के आदेशों के अनुसार नायक को चलना है।
3. साकार – वह सत्य का साकार रूप है।
4. आनंद – सिनेमा से हमें आनंद मिलता है।
5. प्रशंसा – अध्यापिका जी ने लडकी की प्रशंसा की।

मुहावरे वाले शब्द :

1. प्रशंसा करना = स्तुति करना ; बच्चों के भाषण सुनकर अध्यापिका ने उनकी बड़ी प्रशंसा की।
2. जी लगना = मन लगना ; मुझे सिनेमा पर जी नहीं लगता।
3. जीविका चलाना = जीवन चलाना, रोटी कमाना ; जीविका चलाने के लिए कई मार्ग हैं।
4. खुशी का ठिकाना न रहना = अति प्रसत्न होना ; यह बात सुनकर उसके खुशी का ठिकाना नहीं रहा।

शब्दार्थ (అర్ధములు) (Meanings) :