TS Inter 2nd Year Maths 2A De Moivre’s Theorem Important Questions

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 2 De Moivre’s Theorem to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A De Moivre’s Theorem Important Questions

Question 1.
Simplify \(\frac{(\cos \alpha+i \sin \alpha)^4}{(\sin \beta+i \cos \beta)^8}\)
Solution:

Question 2.
If m,n are integers and x = cos α + i sin α, y = cos β + i sin β then prove that
x^m yⁿ + \(\frac{1}{x^m y^n}\) = cos (mα +nβ) and
x^m yⁿ – \(\frac{1}{x^m y^n}\) = 2i sin (mα +nβ)
Solution:

Question 3.
If n is a positive Integer, show that \((1+i)^n+(1-i)^n=2^{\frac{n+2}{2}} \cos \left(\frac{n \pi}{4}\right)\)
Solution:

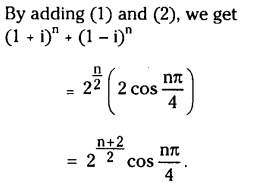
Question 4.
If n is an Integer then show that
(1 + cos θ + i sin θ)ⁿ + (1 + cos θ – i sin θ)ⁿ \(=2^{n+1} \cos ^n\left(\frac{\theta}{2}\right) \cos \left(\frac{n \theta}{2}\right)\)
Solution:
L.H.S
(1 + cos θ + i sin θ)ⁿ + (1 + cos θ – i sin θ)ⁿ

Question 5.
If cos α+cos β + cos γ = 0 = sin α + sin β + sin γ, Prove that cos² α +cos² β +cos γ = \(\frac{3}{2}\) sin² α + sin² β + sin² γ.
Solution:

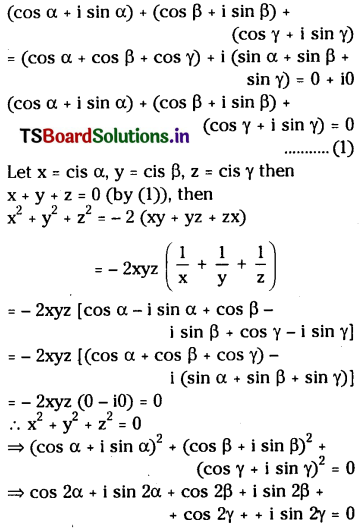
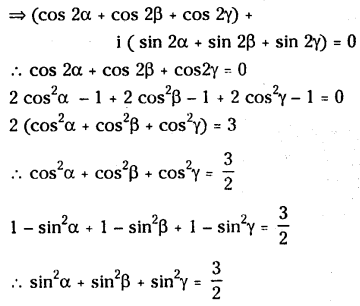
Question 6.
Find all the values of \((\sqrt{3}+i)^{1 / 4}\)
Solution:
The modulus amplitude form of

Question 7.
Find all the roots of the equation
x¹¹ – x⁷ + x⁴ -1 = 0
Solution:
x¹¹ – x⁷ + x⁴ -1  = x⁷(x⁴-1) +1 (x⁴– 1) = (x⁴-1)(x⁷. 1)
Therefore the roots of the given equations are precisely the roots of unity and 7th roots of – 1.
They are cis = \(\frac{2 \mathrm{k} \pi}{4} \) = cis \(\frac{\mathrm{k} \pi}{4}\) k∈{0,1,2,3} and

Question 8.
If 1, ω, ω² are the cube roots of unity, prove that

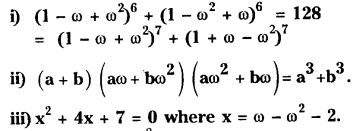
Solution:

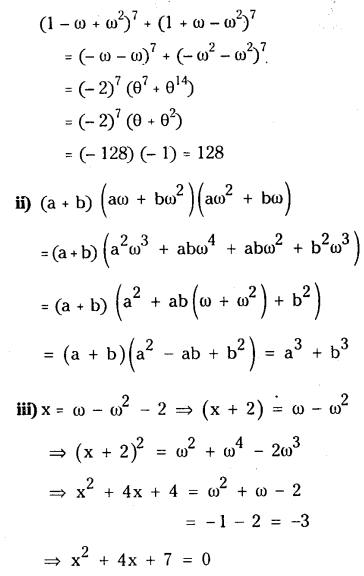
Question 9.
If α, β are the roots of the equation x² + x + 1 = 0 then prove that α⁴ + β⁴ + α^-1 = β^-1
Solution:
Since α, β are the complex cube roots of unity,
we may take α = ω, β = ω²