TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(a)

I.
Question 1.
Expand the following using binomial theorem.
i) (4x + 5y)⁵
ii) \(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\)
iii) \(\left(\frac{2 p}{5}-\frac{3 q}{7}\right)^6\)
iv) (3x + x – x²)⁴
Solution:
i) we know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)
∴ (4x + 5y)⁷ = \({ }^7 \mathrm{C}_0\) (4x)⁷ + \({ }^7 \mathrm{C}_1\) (4x)⁶ (5y) + \({ }^7 \mathrm{C}_2\) (4x)⁵ (5y)² + \({ }^7 \mathrm{C}_3\) (4x)⁴ (5y)³ + \({ }^7 \mathrm{C}_4\) (4x)³ (5y)⁴ + \({ }^7 \mathrm{C}_5\) (4x)² (5y)⁵ + \({ }^7 \mathrm{C}_6\) (4x) (5y)⁶ + \({ }^7 \mathrm{C}_7\) (5y)⁷
= \(\sum_{r=0}^7{ }^7 C_r\) . (4x)^7-r . (5y)^r.

ii) We know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)

\(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\) = \({ }^5 C_0\left(\frac{2}{3} x\right)^5+{ }^5 C_1\left(\frac{2}{3} x\right)^4\left(\frac{7}{4} y\right)+{ }^5 C_2\left(\frac{2}{3} x\right)^3\left(\frac{7}{4} y\right)^2 +{ }^5 C_3\left(\frac{2}{3} x\right)^3\left(\frac{7}{4} y\right)^3\) + \({ }^5 C_4\left(\frac{2}{3} x\right)\left(\frac{7}{4} y\right)^4+{ }^5 C_5\left(\frac{7}{4} y\right)^5\)

= \(\sum_{r=0}^5{ }^5 C_r \cdot\left(\frac{2}{3} x\right)^{5-r} \cdot\left(\frac{7}{4} y\right)^r\)

iii) We know that
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)

iv) We know that
(3 + x – x²)⁴ = [3 + x (1 – x)]⁴
(x + a)ⁿ = \({ }^{\mathrm{n}} \mathrm{C}_0\) xⁿ + \({ }^n C_1\) x^n-1 a + \({ }^n C_2\) x^n-2 a² + ……………. + \({ }^n C_r\) + \({ }^n C_n\)
∴ [3 + x (1 – x)]⁴ = \({ }^4 C_0\) 3⁴ + \({ }^4 C_1\)3³x (1 – x + \({ }^4 C_2\) 3²x² (1 – x)² + \({ }^4 C_3\) 3x³ (1 – x)³ + \({ }^4 C_4\) x⁴ (1 – x)⁴
= 81 + 108x (1 – x) + 54x² (1 – 2x + x²) + 12x³ (1 – 3x + 3x² – x³) + x⁴ (1 – 4x + 6x² – 4x³ + x⁵
= 81 + 108x – 54x² – 96x³ + 19x⁴ + 32x⁵ – 6x⁶ – 4x⁷ + x⁸.

Question 2.
Write down and simplify
i) 6th term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^y\)
ii) 7th term in (3x – 4y)¹⁰
iii) 10th term \(\left(\frac{3 p}{4}-5 q\right)^{14}\)
iv) rth term in \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) (1 ≤ r ≤ 9).
Solution:
i) r + 1th term n the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
∴ 6th term in the expansion of \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) is given by
T₆ = \({ }^9 C_5 \cdot\left(\frac{2 x}{3}\right)^4 \cdot\left(\frac{3 y}{2}\right)^5\)
= 189 . x⁴ . y⁵

ii) (r + 1)th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
7th term In the expansion of (3x – 4y)¹⁰ is given by
T₇ = \({ }^{10} \mathrm{C}_6\) (3x)⁴ (- 4y)⁶
= 280 . 12⁵ x⁴ y⁶.

iii) (r + 1)th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
10th term in the expansion of \(\left(\frac{3 p}{4}-5 q\right)^{14}\) is given by
T₁₀ = \({ }^{14} \mathrm{C}_9\left(\frac{3 p}{4}\right)^5\) (- 5q)⁹
= \(\frac{-(2002) \cdot 3^5 \cdot 5^9}{4^5}\) . p⁵ . q⁹.

iv) (r + )th term in the expansion of (x + a)ⁿ is given by
T_r+1 = \({ }^n C_r\) . x^n-r . a^r
∴ rth term in the expansion of \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) is given by
T_r = \({ }^8 C_{r-1}\left(\frac{3 a}{5}\right)^{9-r}\left(\frac{5 b}{7}\right)^{r-1}\).

Question 3.
Find the number of terms in the expansion of
i) \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\)
ii) (3p + 4q)¹⁴
iii) (2x + 3y + z)⁷
Solution:
1) The expansion of (x + a)ⁿ contains (n + 1) terms.
∴ Expansion of \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\) contains 10 terms.

ii) The expansion of (x + a)ⁿ contains (n + 1) terms.
∴ Expansion of (3p + 4q)¹⁴ contains 15 terms.

iii) Number of terms in the expansion of
(a + b + c)ⁿ = \(\frac{(n+1)(n+2)}{2}\)
∴ Expansion oF (2x + + z)⁷ contains \(\frac{(7+1)(7+2)}{2}\) = 36 terms.

Question 4.
Find the numerically greatest term(s) in the expansion of coefficients in (4x – 7y)⁴⁹ + (4x + 7y)⁴⁹.
Solution:
We know that
(4x – 7y)⁴⁹ = \({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ – \({ }^{49} \mathrm{C}_1\)(4x)⁴⁸ (7y) + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² – \({ }^{49} \mathrm{C}_3\) (4x)⁴⁶ (7y)³ + ……………. + \({ }^{49} \mathrm{C}_49\) (7y)⁴⁹ ………….(1)

(4x + 7y)⁴⁹ = \({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ + \({ }^{49} \mathrm{C}_1\)(4x)⁴⁸ (7y) + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² + \({ }^{49} \mathrm{C}_3\) (4x)⁴⁶ (7y)³ + ……………. + \({ }^{49} \mathrm{C}_49\) (7y)⁴⁹ ………….(2)

(1) + (2)
(4x – 7y)⁴⁹ + (4x + 7y)⁴⁹ = 2[\({ }^{49} \mathrm{C}_0\) (4x)⁴⁹ + \({ }^{49} \mathrm{C}_2\) (4x)⁴⁷ (7y)² + \({ }^{49} \mathrm{C}_4\) (4x)⁴⁵ (7y)⁴ + ………….. + \({ }^{49} \mathrm{C}_48\) (4x) (7y)⁴⁸]
which contains 25 non-zero coefficients.

Question 5.
Find the sum of last 20 coefficients in the expansion of (1 + x)³⁹.
Solution:
The last 20 coeffIcients in the expansion of (1 + x)³⁹ are \({ }^{39} \mathrm{C}_{20},{ }^{39} \mathrm{C}_{21}, \ldots \ldots \ldots,{ }^{39} \mathrm{C}_{39}\)
We know that

∴ The sum of last 20 coefficients in expansion of (1 + x)³⁹ is 2³⁸.

Question 6.
If A and B are coefficients of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^{2n – 1} respectively, then find the value of \(\frac{A}{B}\).
Solution:
Coefficient of xⁿ in the expansion of (1 + x)²ⁿ is \({ }^{2 n} C_n\).
Coefficient of xⁿ in the expansion of (1 + x)^{2n – 1} is \({ }^{2 n – 1} C_n\)
∴ A = \({ }^{2 n} C_n\) and B = \({ }^{2 n – 1} C_n\).
∴ \(\frac{A}{B}=\frac{{ }^{2 n} C_n}{2 n-1}=\frac{\frac{2 n !}{n ! n !}}{\frac{(2 n-1) !}{(n-1) ! \cdot n !}}\)
\(\frac{2 n !}{(2 n-1) ! n !} \cdot(n-1) !=\frac{2 n}{n}\)
\(\frac{A}{B}\) = 2.

II.
Question 1.
Find the coefficient of
i) x^-6 in \(\left(3 x-\frac{4}{x}\right)^{10}\)
ii) x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\)
iii) x² in \(\left(7 x^3-\frac{2}{x^2}\right)^9\)
iv) x^-7 in \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\)
Solution:
i) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
(r + 1)th term in the expansion of \(\left(3 x-\frac{4}{x}\right)^{10}\) is
T_r+1 = \({ }^{10} \mathrm{C}_{\mathrm{r}}\) . (3x)^10-r . (\(\frac{-4}{x}\))^r
T_r+1 = \({ }^{10} \mathrm{C}_{\mathrm{r}}\) . (3)^10-r . (- 4)^r . x^10-2r.
for coefficient of x^-6, 10 – 2r = – 6
⇒ 2r = 16
⇒ r = 8.
∴ Coefficient of x^-6 is \({ }^{10} \mathrm{C}_8\) . 3^10-8 . (- 4)⁸ = 405 × 4⁸.

ii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
(r + 1)th term in the expansion of \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) is
T_r+1 = \({ }^{13} C_r \cdot\left(2 x^2\right)^{13-r} \cdot\left(\frac{3}{x^3}\right)^r\)
T_r+1 = \({ }^{13} C_r \) . 2^13-r . 3^r . x^26-5r
For coefficients of x¹¹, 26 – 5r = 11
⇒ 5r = 15
⇒ r = 3.
Coefficient of x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) is \({ }^{13} C_3 \) . 2^13-3 . 3³
= 286 . 2¹⁰ . 3³.

iii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
∴ General term in the expansion of \(\left(7 x^3-\frac{2}{x^2}\right)^9\) is
T_r+1 = \({ }^9 C_r \cdot\left(7 x^3\right)^{9-r}\left(\frac{-2}{x^2}\right)^r\)
= \({ }^9 C_r\) 7^9-r (- 2)^r . x^27-5r
for coefficient of x², 27 – 5r = 2
⇒ 5r = 25
⇒ r = 5.
∴ Coefficient of x² is \({ }^9 \mathrm{C}_5\) . 7⁴ . (- 2)⁵
= – 126 . 7⁴ . 2⁵.

iv) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)\) is
T_r+1 = \(={ }^7 C_r \cdot\left(\frac{2}{3} x^2\right)^{7-r} \cdot\left(\frac{-5}{4 x^5}\right)^r\)
= \({ }^7 \mathrm{C}_{\mathrm{r}} \cdot\left(\frac{2}{3}\right)^{7-\mathrm{r}}\left(\frac{-5}{4}\right)^{\mathrm{r}} \mathrm{x}^{14-7 \mathrm{r}}\)
For coefficient of x^-7, 14 – 7r = – 7
⇒ 7r = 21
⇒ r = 3
∴ Coefficient of x^-7 is \({ }^7 C_3 \cdot\left(\frac{2}{3}\right)^4 \cdot \frac{(-5)^3}{4^3}\)
= \(-\frac{35 \times 16 \times 125}{81 \times 64}=\frac{-4375}{324}\).

Question 2.
Find the term independent of x in the expansion of
i) \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\)
ii) \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
iii) \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\)
iv) \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\)
Solution:
i) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\) is
T_r+1 = \({ }^{10} C_r \cdot\left(\frac{\sqrt{x}}{3}\right)^{10-r} \cdot\left(\frac{-4}{x^2}\right)^r\)
= \({ }^{10} C_r \cdot \frac{x^{\frac{10-r}{2}}}{3^{10-r}} \cdot \frac{(-4)^r}{x^{2 r}}\)
= \({ }^{10} C_r \cdot \frac{(-4)^r}{3^{10-r}} \cdot x^{\frac{10-5 r}{2}}\)
For the independent term (i.e., the coefficient of x⁰)
put \(\frac{10-5 r}{2}\) = 0
⇒ r = 2.
∴ Term independent of ‘x’ in the expansion is
T3 = \({ }^{10} C_2 \frac{(-4)^2}{3^8} \times x^0=\frac{80}{729}\).

ii) General term in the expansion of (x + a)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\) is
T_r+1 = \({ }^{25} C_r\left(\frac{3}{\sqrt[3]{x}}\right)^{25-r} \cdot(5 \sqrt{x})^r\)
= \({ }^{25} C_r\) . 3^25-r . 5^r . x^{(5r – 50)/6}
For the independent term,
(i.e., coefficient of x⁰)
Put \(\frac{5 r-50}{6}\) = 0
⇒ r = 10.
∴ Term independent of ‘x’ in the expansion is T₁₁ = \({ }^{25} \mathrm{C}_{10}\) . 3¹⁵ . 5¹⁰.

iii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\) is
T_r+1 = \({ }^{14} C_r \cdot\left(4 x^3\right)^{14-r} \cdot\left(\frac{7}{x^2}\right)^r\)
= \({ }^{14} C_r\) . 4^14-r . 7^r . x^42-5r.
For the independent term, (i.e., coefficient of x⁰)
Put 42 – 5r = 0
which is impossible as ‘r’ is integer.
∴ Term independent of ‘x in the expansion is ‘0’.

iv) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\) is
T_r+1 = \({ }^9 C_r\left(\frac{2 x^2}{5}\right)^{9-r} \cdot\left(\frac{15}{4 x}\right)^r\)
= \({ }^9 \mathrm{C}_{\mathrm{r}}\left(\frac{2}{5}\right)^{9-\mathrm{r}} \cdot\left(\frac{15}{4}\right)^{\mathrm{r}} \cdot \mathrm{x}^{18-3 \mathrm{r}}\)
For the independent term, (i.e. coefficient of x⁰)
Put 18 – 3r = 0
⇒ r = 6
Term independent of ‘x’ in the expansion is
T₇ = \({ }^9 \mathrm{C}_6 \cdot\left(\frac{2}{5}\right)^3 \cdot\left(\frac{15}{4}\right)^6\)
= \(\frac{3^7 \cdot 5^3 \cdot 7}{2^7}\).

Question 3.
Find the middle term(s) in the expansion of
i) \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
ii) \(\left(4 a+\frac{3}{2} b\right)^{11}\)
iii) (4x² + 5x³)¹⁷
iv) \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\)
Solution:
i) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3 x}{7}-2 y\right)^{10}\) is
T_r+1 = \({ }^{10} C_{\mathrm{r}} \cdot\left(\frac{3 \mathrm{x}}{7}\right)^{10-\mathrm{r}}(-2 \mathrm{y})^{\mathrm{r}}\)
The expansion has 11 (odd number) terms.
Hence T₆ is the only middle term.
Thus r = 5
∴ Middle term in the expansion is
T₆ = \(-10 C_5\left(\frac{6}{7}\right)^5\) . x⁵ . y⁵.

ii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion \(\left(4 a+\frac{3}{2} b\right)^{11}\) is
T_r+1 = \(\)
The expansion has 12 (even numbers) terms.
Hence T₆ and T₇ are the middle terms.
Thus r = 5 and r = 6
when r = 5,
T₆ = \({ }^{11} C_5 \cdot(4 a)^6 \cdot\left(\frac{3}{2} b\right)^5\)
= 77 × 2⁸ . 3⁶ . a⁶ . b⁵.
when r = 6,
T₇ = \({ }^{11} C_6(4 a)^5 \cdot\left(\frac{3}{2} b\right)^6\)
= 77 × 2⁵ . 3⁷ . a⁵ . b⁶.

iii) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of (4x² + 5x³)¹⁷ is
T_r+1 = \({ }^{17} \mathrm{C}_r\) . (4x²)^17-r . (5x³)^r.
The expansion has 18 (even number) terms.
Hence T₉ and T₁₀ are the middle terms.
Thus r = 8 and r = 9
When r = 8.
T₉ = \({ }^{17} \mathrm{C}_8\) . (4x²)⁹ . (5x³)⁸
= \({ }^{17} \mathrm{C}_8\) . 4⁹ . 5⁸ . x⁴²
When r = 9,
T10 = \({ }^{17} \mathrm{C}_9\) (4x²)⁸ (3)⁹
= \({ }^{17} \mathrm{C}_9\) . 4⁸ . 5⁹ . x⁴³

iv) General term in the expansion of (x + a)ⁿis
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
General term in the expansion of \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\) is
T_r+1 = \({ }^{20} C_r \cdot\left(\frac{3}{a^3}\right)^{20-r} \cdot\left(5 a^4\right)^r\)
The expansion has 21 (odd number) terms. Hence, T₁₁ is the only middle term
Thus r = 10
∴ Middle term in the expansion is
T₁₁ = \({ }^{20} C_{10} \cdot\left(\frac{3}{a^3}\right)^{10} \cdot\left(5 a^4\right)^{10}\)
= \({ }^{20} C_{10}\) . 15¹⁰ . a¹⁰.

Question 4.
Find the numerically greatest term(s) in the expansion of
i) (4 + 3x)¹⁵ when x = \(\frac{7}{2}\).
ii) (3x + 5y)¹² when x = \(\frac{1}{2}\), y = \(\frac{4}{3}\)
iii) (4a – 6b)¹³ when a = 3, b = 5.
iv) (3 + 7x)ⁿ when x = \(\frac{4}{5}\), n = 5.
Solution:
i) We know that (4 + 3x)¹⁵ = 4¹⁵ \(\left(1+\frac{3 x}{4}\right)^{15}\)
First we find the numerically greatest term in the expansion of \(\left(1+\frac{3 x}{4}\right)^{15}\)
Let X = \(\frac{3 x}{4}\)
x = \(\frac{7}{2}\), |X| = \(\left|\frac{3}{4} \times \frac{7}{2}\right|=\frac{21}{8}\)
Now \(\frac{(n+1)|X|}{1+|X|}=\frac{16 \times \frac{21}{8}}{1+\frac{21}{8}}=\frac{336}{29}\)
not an integer.
Its integral part m = \(\left[\frac{336}{29}\right]\) = 11.
∴ T_m+1, i.e., T₁₂ is the numerically greatest term in the binomial expansion of \(\left(1+\frac{3 x}{4}\right)^{15}\)
∴ T₁₂ = \({ }^{15} C_{11}\left(\frac{3 x}{4}\right)^{11}\)
= \({ }^{15} \mathrm{C}_{11}\left(\frac{21}{8}\right)^{11}\)
∴ Numerically greatest term in the expansion 01(4 + 3x)¹⁵ = \({ }^{15} C_{11}\left(4^{15}\right) \frac{21^{11}}{8^{11}}\)
= \({ }^{15} C_{11} \cdot \frac{21^{11}}{2^3}\).

ii) We know that
(3x + 5y)¹² = (3x)¹² . (1 + \(\frac{5 y}{3 x}\))¹²
First we find the numerically greatest term in the expansion of (1 + \(\frac{5 y}{3 x}\))¹²

iii) We know that
(4a – 6b)¹³ = (4a)¹³ (1 – \(\frac{6 b}{4 a}\))¹³
First we find the numerically greatest term in the expansion of (1 – \(\frac{6 b}{4 a}\))¹³
Let X = – \(\frac{6 b}{4 a}\)
As a = 3 and b = 5, |X| = \(\frac{5}{2}\)

∴ The numerically greatest terms in the expansion of (4a – 6b)¹³ are T₁₀ and T₁₁.
T₁₀ = – 12¹³ . ¹³C₉ . \(\left(\frac{5}{2}\right)^9\)
= – ¹³C₉ . (12)⁴ . (30)⁹
and T₁₁ = 12¹⁰ . ¹³C₁₀ . \(\left(\frac{5}{2}\right)^10\)
= 143 . 2¹⁷ . 3¹³ . 5¹⁰.

iv) We know that (3 + 7x)ⁿ = 3ⁿ (1 + \(\frac{7}{3}\) x)ⁿ
First we find numerically greatest term in the expansion of (1 + \(\frac{7}{3}\) x)ⁿ
Let X = \(\frac{7}{3}\) x
As x = \(\frac{4}{5}\), |X| = \(\frac{28}{15}\) and
\(\frac{(n+1)|X|}{1+|X|}=\frac{56}{5}\) and n = 15.

Its integral part,
m = \(\left[\frac{(\mathrm{n}+1)|\mathrm{X}|}{1+|\mathrm{X}|}\right]\) = 11
∴ T_m+1 i.e., T₁₂ is numerically greatest term in the expansion of (1 + \(\frac{7}{3}\) x)ⁿ
T₁₂ = ¹⁵C₁₁ . \(\left(\frac{28}{15}\right)^{11}\)
∴ The numerically greatest terms in the expansion of (3 + 7x)ⁿ is
T₁₂ = 3¹⁵ . ¹⁵C₁₁ . \(\left(\frac{28}{15}\right)^{11}\)
= ¹⁵C₁₁ . \(\left(\frac{28}{5}\right)^{11}\) . 3⁴.

Question 5.
Prove the following:
i) 2 . C₀ + 5 . C₁ + 8. C₂ + ……………. + (3n + 2) C_n = (3n + 4) 2^n-1
ii) C₀ – 4 C₁ + 7 . C₂ – 10 . C₃ + ……………. = 0,
if n is an even positive Integer.
iii) \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\)
iv) \(C_0+\frac{3}{2} \cdot C_1+\frac{9}{3} \cdot C_2+\frac{27}{4} \cdot C_3+\ldots \ldots+\frac{3^n}{n+1} C_n=\frac{4^{n+1}-1}{3(n+1)}\)
v) C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ………….. + 2ⁿ . C_n = 3ⁿ
Solution:
i) We know that
C₀ = C_n, C₁ = C_n-1, ………… C_r = C_n-r
Let S = 2 . C₀ + 5 . C₁ + 8 . C₂ + ………….. + (3n – 1) . C_n-1 + (3n + 2) C_n ………….(1)
∴ S = (3n + 2) C₀ + (3n – 1)C₁ + (3n – 4)C₂ + …………. + 5 . C_n-1 + 2 . C_n ………….(2)
(1) + (2) ⇒ 2S = (3n + 4) . C₀ + (3n + 4) . C₁ + (3n + 4) . C₂ + …………… (3n + 4) . C_n
= (3n + 4) (C₀ + C₁ + C₂ + …………… + C_n)
⇒ 2S = (3n + 4) . 2ⁿ
⇒ S = (3n + 4) . 2^n-1
∴ 2 . C₀ + 5 . C₁ + 8 . C₂ + ………… + (3n + 2) . C_n = (3n + 4) . 2^n-1

ii) We know that 1, 4, 7, 10, ………… are in A.P.
(n + 1)th term,
T_n+1 = 1 + (n)3 = 3n + 1
∴ C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……….. (n + 1) terms.
= \(\sum_{r=0}^n(-1)^r(3 r+1) C_r\)
= \(3 \sum_{r=0}^n(-1)^r r \cdot C_r+\sum_{r=0}^n(-1)^r \cdot C_r\)
= 3 (0) + 0 = 0
∴ C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……….. = 0.

iii) Given L.H.S

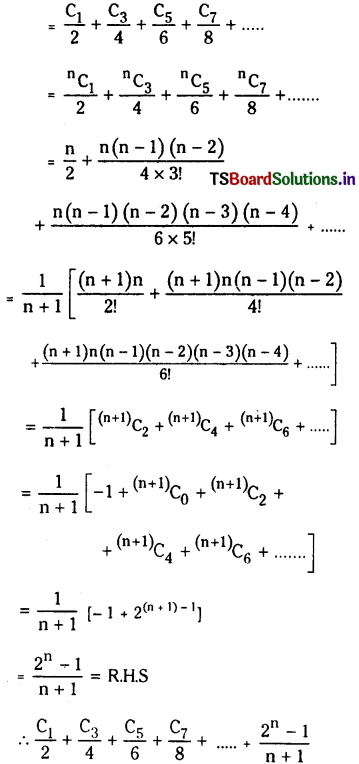
iv) Given L.H.S

v) L.HS = C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ……….. + 2ⁿ . C_n
= C₀ + C₁ . 2 + C₂ . 2² + C₃ . 2³ + ………. + C_n 2ⁿ
= (1 + 2)ⁿ
= 3ⁿ = R.H.S
∴C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ……….. + 2ⁿ . C_n = 3ⁿ.

Question 6.
Find the sum of the following:
i) \(\frac{{ }^{15} C_1}{{ }^{15} C_0}+2 \frac{{ }^{15} C_2}{{ }^{15} C_1}+3 \frac{{ }^{15} C_3}{{ }^{15} C_2}+\ldots+15 \frac{{ }^{15} C_{15}}{{ }^{15} C_{14}}\)
ii) C_n . C₃ + C₁ .C₄ + C₂ . C₅ + + …………… + C_n-3 . C_n
iii) 2² C₀ + 3² C₁ + 4² C₂ + …………. + (n + 2)² C_n
iv) 3C₀ + 6C₁ + 12C₂ + ……………. + 3 . 2ⁿ C_n
Solution:
i) We know that

ii) (1 + x)ⁿ = C₀ + C₁x + C₂x² + …………. + C_nxⁿ …………..(1)
(x + 1)ⁿ = C₀xⁿ + C₁x^{n – 1} + C₂₃x^n-2 + …………… + C_n …………….. (2)
(1) x (2) = (1 + x)²ⁿ
= (C₀ + C₁x + C₂x² + ……….. + C_nxⁿ) (C₀x + C₁x^n-1 + C₂x^n-2 + C₃x^n-3 + ………….. + C_n]
Comparing coefficients of x^n-3 on bothsides,
²ⁿC_n-3 = C₀ . C₃ + C₁ . C₄ + C₂ . C₅ + …………. + C_n-3 . C_n
i.e., C₀. C₃ + C₁ . C₄ + C₂. C₅ + …………… + C_n-3 . C_n = ²ⁿC_n-3 = ²ⁿC_n+3
[∵ ⁿC_r = ⁿC_n-r].

iii) 2² C₀ + 3² C₁ + 4² C₂ + …………. + (n + 2)² C_n

= n (n – 1) 2^n-2 + 5 n 2^n-1 + 4 (2ⁿ)
= 2^n-2 [n (n – 1) + 10n + 16]
= (n² + 9n . 16) 2^n-2.

iv) 3 . C₀ + 6 . C₁ + 12 . C₂ + ……………. + 3 . 2ⁿ C_n
= \(\sum_{r=0}^n 3 \cdot 2^r \cdot C_r\)
= \(3 \sum_{r=0}^n 2^r \cdot C_r\)
= 3 [1 + C₁ (2) + C₂ (2²) + C₃ (2³) + …………. + C_n 2ⁿ]
= 3 [1 + 2]ⁿ
= 3 . 3ⁿ
= 3ⁿ⁺¹.

Question 7.
Using binomial theorem prove that 50ⁿ – 49n – 1 is divisible by 49² for all positive integers n.
Solution:
We know that,
50ⁿ – 49n – 1
= (1 + 49)ⁿ – 49n – 1
= [1 + ⁿC₁ . 49 + ⁿC₂ . 49² + ⁿC₃ . 49³ + ………… + 49ⁿ] – 49n – 1
= ⁿC₂ . 49² + ⁿC₃ . 49³ + …………… + ⁿC_n . 49ⁿ
= 49² [ⁿC₂ + ⁿC₃ . 49 + ……….. + ⁿC_n . 49^n-2]
= 49² (a positive integer)
Hence 50ⁿ 49n – 1 is divisible by 49² ∀n ∈ N.

Question 8.
Using binomial theorem prove that 5⁴ⁿ + 52n – 1 is divisible by 676 for all positive integers n.
Solution:
We know that, 5⁴ⁿ + 52n – 1
= (5²)²ⁿ + 52n – 1
= (25)²ⁿ+ 52n – 1
= (26 – 1)²ⁿ+ 52n – 1
= ²ⁿC₀ (26)²ⁿ – ²ⁿC₁ (26)^2n-1 + ²ⁿC₂ (26)^2n-2 + …………. + ²ⁿC_2n-2(26)² – ²ⁿC_2n-1 (26) + ²ⁿC_2n + 52n – 1
= 26²ⁿ + ²ⁿC₁ (26)^2n-1 + ²ⁿC₂ (26)^2n-2 + …………….. + ²ⁿC_2n-2 (26)²
= 26² [26^2n-2 – ²ⁿC₁ 26^2n-3 + ²ⁿC₂ 26^2n-4 + ……… + ²ⁿC_2n-2]
= 676 (some integer)
∴ 5⁴ⁿ + 52n – 1 is divisible by 676, ∀n ∈ N.

Question 9.
If (1 + x + x²)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_2nx²ⁿ, then prove that
i) a₀ + a₁ + a₂ + ……….. + a_2n = 3ⁿ
ii) a₀ + a₂ + a₄ + ………… + a_2n = \(\frac{3^n+1}{2}\)
iii) a₁ + a₃ + a₅ + ……………. + a_2n-1 = \(\frac{3^n-1}{2}\)
iv) a₀ + a₃ + a₆ + a₉ + ………… = 3^n-1
Solution:
Given (1 + x + x²)^{n/sup> = a₀ + a₁x + a₂x2 + ………….. + a_2nx2n
i) Subtituting x = 1 in (I), we have
a₀ + a₁ + a₂ + ……….. + a_2n = 3n …………. (1)
Substituting x = – 1 in (I), we have
a₀ – a₁ + a₂ + ……….. + a_2n = 1 …………….(2)}

ii) (1) + (2)
⇒ 2a₀ + 2a₂ + 2a₄ + ……….. + 2a_2n = 3ⁿ + 1
⇒ a₀ + a₂ + a₄ + ……….. + a_2n = \(\frac{3^n+1}{2}\)

iii) (1) – (2)
⇒ 2a₁ + 2a₃ + 2a₅ + ……….. + 2a_2n-1 = 3ⁿ – 1
⇒ a₁ + a₃ + a₅ + ……….. + a_2n-1 = \(\frac{3^n-1}{2}\)

iv) Substituting x = ω, in (1), we have
a₀ + a₁ω + a₂ω² + ……….. + a_2nω²ⁿ = 0
(∵ 1 + ω + ω² = 0)

Substituting x = ω² in (1), we have
a₀ + a₁ω² + a₂ω⁴ + a₃ω⁶ + ……….. + a_2nω⁴ⁿ = 0 …………… (4)
(1) + (3) +(4):
3a₀ + a₁ (1 + ω + ω²) + a₂ (1 + ω + ω²) + a₃ (1 + ω³ + ω⁶) + ………… + a_2n (1 + ω²ⁿ + ω⁴ⁿ) = 3ⁿ
⇒ 3a₀ + 3a₃ + 3a₆ + 3a₉ + …………. = 3ⁿ
(∵ 1 + ω + ω² = 0 and ω³ = 1)
⇒ a₀ + a₃ + a₆ + a₉ + ……….. = 3^n-1

Question 10.
If (1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……………+ b₂₁ x²¹, then find the value of
i) b₀ + b₂ + b₄ + ……………. + b₂₀
ii) b₁ + b₃ + b₅ + ……………. + b₂₁
Solution:
Given
(1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……………+ b₂₁ x²¹ ……………(1)
Substituting x = 1 in (1),
we get b₀ + b₁ + b₂ + ……………. + b₂₁ = 4⁷ ……….(2)
Substituting x = – 1 in (1),
we get b₀ – b₁ + b₂ + ……………. – b₂₁ = 0 …………… (3)
i) (2) + (3)
⇒ 2b₀ + 2b₂ + 2b₄ + ……………. + b₂₀ = 4⁷
⇒ b₀ + b₂ + b₄ + ……………. + b₂₀ = 2¹³.

ii) (2) – (3)
⇒ 2b₁ + 2b₃ + 2b₅ + ……………. + 2b₂₁ = 4⁷
⇒ b₁ + b₃ + b₅ + ……………. + b₂₁ = 2¹³.

Question 11.
If the coefficients of x¹¹ and x¹² in the binomial expansion of \(\left(2+\frac{8 x}{3}\right)^n\) are equal, find n.
Solution:
We know that \(\left(2+\frac{8 x}{3}\right)^n=2^n\left(1+\frac{4 x}{3}\right)^n\)
Coefficient of x¹¹ in the expansion of \(\left(2+\frac{8 x}{3}\right)^n\) is ⁿC₁₁ . 2ⁿ . (\(\frac{4}{3}\))¹¹
Coefficient of x¹² in the expansion of \(\left(2+\frac{8 x}{3}\right)^n\) is ⁿC₁₂ . 2ⁿ . (\(\frac{4}{3}\))¹²
Given coefficients of x¹¹ and x¹² are same
⇒ ⁿC₁₁ . 2ⁿ . (\(\frac{4}{3}\))¹¹ = ⁿC₁₂ . 2ⁿ . (\(\frac{4}{3}\))¹²
⇒ \(\frac{n !}{(n-11) ! 11 !}=\frac{n !}{(n-12) ! 12 !}\left(\frac{4}{3}\right)\)
⇒ 12 = (n – 11) \(\frac{4}{3}\)
⇒ 9 = n – 11
⇒ n = 11 + 9 = 20.

Question 12.
Find the remainder when 2²⁰¹³ is divided by 17.
Solution:
We have 2²⁰¹³
= 2 (2²⁰¹²)
= 2 (2⁴)²⁰³
= 2 (16)⁵⁰³
= 2 (17 – 1)²⁰³
= 2 [⁵⁰³C₀ 17⁵⁰³ – ⁵⁰³C₁ 17⁵⁰² + ⁵⁰³C₂ 17⁵⁰¹ – ……….. + ⁵⁰³C₅₀₂ 17 – ⁵⁰³C₅₀₃]
= 2 [⁵⁰³C₀ 17⁵⁰³ – ⁵⁰³C₁ 17⁵⁰² + ⁵⁰³C₂ 17⁵⁰¹ – ……….. + ⁵⁰³C₅₀₂ 17 – ⁵⁰³C₅₀₃] – 2
= 17m – 2 where ‘m is some integer
∴ 2²⁰¹³ = 17m – 2 (or) 17k + 15
∴ The remainder is – 2 or 15.

Question 13.
If the coefficient of (2r + 4)th term and (3r + 4)th term in the expansion of (1 + x)²¹ are equal, find r.
Solution:
We know that coefficient of (r + 1)th term of (1 + x)ⁿ is ⁿC_r.
∴ Coefficient of (2r + 4)th term 0f (1 + x)²¹ is ²¹C_2r+3
Also coefficient of (3r + 4)th term of (1 +x)²¹ is ²¹C_3r+3.
Given coefficient of (2r + 4)th term and (3r + 4)th terms in the expansion of (1 + x)²¹ are equal.
∴ ²¹C_2r+3 = ²¹C_3r+4
∴ Either 2r + 3 = 3r + 3 0r 2r + 3 + 3 = 21
If 2r + 3 = 3r + 3 then r = 0,
If 2r + 3 + 3r = 21 then r = 3.
∴ r = 0 or r = 3.

III.
Question 1.
If the coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in AP. then prove that n² – 4m + 398 = 0.
Solution:
Coefficient of x^r in the expansion of (1 + x)ⁿ is ⁿC_r.
Given coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in A.P., then
2(ⁿC₁₀) = ⁿC₉ + ⁿC₁₁
⇒ \(2 \frac{n !}{(n-10) ! 10 !}=\frac{n !}{(n-9) ! 9 !}+\frac{n !}{(n-11) !+11 !}\)
⇒ \(\frac{2}{10(n-10)}=\frac{1}{(n-9)(n-10)}+\frac{1}{11 \times 10}\)
⇒ \(\frac{2}{(n-10) 10}=\frac{110+(n-9)(n-10)}{110(n-9)(n-10)}\)
⇒ 22 (n – 9) = 110 + n² – 19n + 90
⇒ n² – 41n + 398 = 0.

Question 2.
If 36, 84, 126 are three successive binomial coefficients in the expansion of (1 + then find n.
Solution:
Let us consider ⁿC_r-1, ⁿC_r and ⁿC_r+1 as three successive binomial coefficients of (1 + xy)ⁿ.
i.e., ⁿC_r-1 = 36; ⁿC_r-1 = 84 and ⁿC_r-1 = 126
Consider \(\frac{{ }^{n_C} C_r}{{ }^n C_{r-1}}=\frac{84}{36}\)
⇒ \(\frac{n-r+1}{r}=\frac{7}{3}\)
⇒ 3n + 3 = 10r …………..(1)
Similarly,
\(\frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{126}{84}\)
⇒ \(\frac{\mathrm{n}-\mathrm{r}}{\mathrm{r}+1}=\frac{3}{2}\)
⇒ 2n = 5r + 3 ………….(2)
⇒ 2n = 5 \(\left(\frac{3 \mathrm{n}+3}{10}\right)\) + 3 (∵ from (1))
⇒ n = 9.

Question 3.
If the 2nd, 3rd and 4th terms in the expansion of (a + x)ⁿ are respectively 240, 720, 1080. find a, x, n.
Solution:
General term in the expansion of (a + x)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r . a^r
∴ 2nd term,T₂ = ⁿC₁ . a^n-1 . x …………..(1)
3rd term, T₃ = ⁿC₂ . a^n-2 . x² ………..(2)
4th term, T₄ = ⁿC₃ . a^n-3 . x³ …………(3)
Given T₂ = 240, T₃ = 720, T₃ = 1080
From (1) and (2),

Sub. n = 5 in (1), we get
5 . a⁴ . x = 240 ………..(6)
Substituting n = 5 in (4), we get x = \(\frac{3 a}{2}\) ………….(7)
Substituting x = \(\frac{3 a}{2}\) in (6),
we get 5 . a⁴ = 240
⇒ a⁵ = 32
⇒ a = 2
Substituting in (7), we get x = 3
∴ a = 2; x = 3 and n = 5.

Question 4.
If the coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are in A.P., then show that n² – (4r + 1)n + 4r² – 2 = 0.
Solution:
We know that, the general term, (r + 1)th term in the expansion of (1 + x)ⁿ is
T_r+1 = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\) . x^n-r
∴ The coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are ⁿC_r-1, ⁿC_r and ⁿC_r+1
Given ⁿC_r-1, ⁿC_r & ⁿC_r+1 are in A.P.

⇒ 2(n – r + 1) (r + 1) = r (r + 1) + (n – r) (n – r + 1)
⇒ 2nr + 2n – 2r² – 2r + 2r + 2 = r² + r + n² – nr + n – nr + r² + r
⇒ n² – n (4r + 1) + 4r² – 2 = 0.

Question 5.
Find the sum of the coefficients of x³² and x^-18 in the expansion of (2x³ – \(\frac{3}{x^2}\))¹⁴.
Solution:
The general term in (2x³ – \(\frac{3}{x^2}\))¹⁴ is
T_r+1 = ¹⁴C_r (2x³)^14-r (\(\frac{-3}{x^2}\))^r
T_r+1 = (- 1)^r . ¹⁴C_r . 2^14-r . 3^r . x^42-5r ………….(1)
For coefficient of x³², put
42 – 5r = 32
⇒ r = 2
Substituting r = 2 in (1), we get
T₃ = ¹⁴C₂ . 2¹² . 3² . x³²
∴ Coefficient of x³² is ¹⁴C₂ . 2¹² . 3² ………(2)
For coefficient of x^-18, put
42 – 5r = 18
⇒ r=12
Substituting r = 12 in (1), we get
T₁₃ = ¹⁴C₂ . 2² . 3¹² . x^-18
∴ Coefficient of x^-18 is ¹⁴C₁₂ . 2² . 3¹² ………….(3)
Hence sum of the coefficients of x³² and x^-18 is
¹⁴C₂ . 2¹² . 3² + ¹⁴C₁₂ . 2² . 3¹²
= ¹⁴C₂ . 2² . 3² (2¹⁰ + 3¹⁰)
= 91 × 36(2¹⁰ + 3¹⁰).

Question 6.
If P and Q are the sum of odd terms and the sum of even terms respectively in the expansion of (x + a)ⁿ then prove that
i) P² – Q² = (x² – a²)ⁿ
ii) 4PQ (x + a)²ⁿ – (x – a)²ⁿ
Solution:
We know that,
(x + a)ⁿ = ⁿC₀ xⁿ + ⁿC₁ x^n-1 . a + ⁿC₂ x^n-2 . a² + ………….. + ⁿC_n-1 x a^n-1 + ⁿC_n aⁿ
= (ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………) + (ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..)
∴ (x + a)ⁿ = P + Q
∴ Sum of odd terms,
P = ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………
Sum of even terms,
Q = ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..
∴ (x + a)ⁿ = P + Q
We know that
(x – a)ⁿ = ⁿC₀ xⁿ a – ⁿC₁ x^n-1 a + ⁿC₂ x^n-2 a¹² – ⁿC₃ x^n-3 a³ + ……………. + ⁿC_n (- 1)ⁿ aⁿ
= (ⁿC₀ xⁿ + ⁿC₂ x^n-2 a² + ⁿC₄ x^n-4 a⁴ + …………) – (ⁿC₁ x^n-1 a + ⁿC₃ x^n-3 a³ + ⁿC₅ x^n-5 a⁵ + …………..)
⇒ (x – a)ⁿ = P – Q

i) P² – Q² = (P + Q) (P – Q)
= (x + a)ⁿ (x – a)ⁿ
⇒ P² – Q² = (x² – a²)ⁿ

ii) 4PQ = (P + Q)² – (P – Q)²
= [(x + a)ⁿ]² – [(x – a)ⁿ]²
⇒ 4PQ = (x + a)²ⁿ – (x – a)²ⁿ

Question 7.
If the coefficients of 4 consecutive terms in the expansion of (1 + x)ⁿ are a₁, a₂, a₃, a₄ respectively, then show that \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\)
Solution:
Given a₁, a₂, a₃, a₄ are the coefficients of 4 consecutive terms in (1 + x)ⁿ respectively.
Let a₁ = ⁿC_r-1
a₂ = ⁿC_r
a₃ = ⁿC_r+1
a₄ = ⁿC_r+2

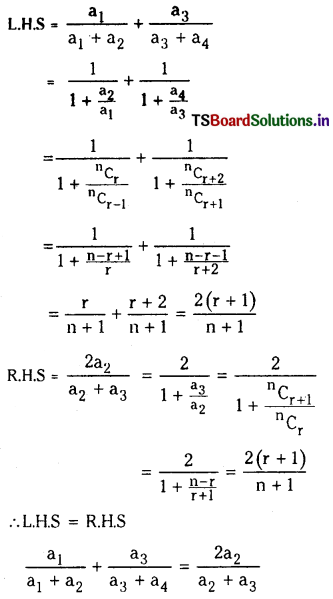
Question 8.
Prove that (²ⁿC₀)² – (²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ……….. + (²ⁿC_2n)² = (- 1)^{n 2n}C_n.
Solution:
We know that
(x + 1)²ⁿ = ²ⁿC₀ x²ⁿ + ²ⁿC₁ x^2n-1 + ²ⁿC₂ x^2n-2 + …………… + ²ⁿC_2n ……………(1)
(1 – x)²ⁿ = ²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² – …………… + ²ⁿC_2n x²ⁿ ……………(2)
From (1) and (2),
(1 – x)²ⁿ (1 + x)²ⁿ = (²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² + ……………… + ²ⁿC_2n x²ⁿ)
⇒ (1 – x²)²ⁿ = [²ⁿC₀ x²ⁿ + ²ⁿC₁ x^2n-1 + ²ⁿC₂ x^2n-2 + …………… + ²ⁿC_2n] . [²ⁿC₀ – ²ⁿC₁ x + ²ⁿC₂ x² + …………… + ²ⁿC_2n x²ⁿ]
Equating coefficient of x²ⁿ on both sides, we get
(- 1)ⁿ . ²ⁿC_n = (²ⁿC₀)² + ((²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ………….. + (²ⁿC_2n)²

Question 9.
Prove that
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n) = \(\frac{(\mathbf{n}+1)^{\mathbf{n}}}{\mathbf{n} !}\) . C₀ . C₁ . C₂ ………….. C_n.
Solution:
Given L.H.S
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n)

= R.H.S
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) ………….. (C_n-1 + C_n) = \(\frac{(\mathbf{n}+1)^{\mathbf{n}}}{\mathbf{n} !}\) . C₀ . C₁ . C₂ ………….. C_n.

Question 10.
Find the term independent of x in (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ.
Solution:
We know that (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ = (\(\frac{1}{3 x}\))ⁿ (1 + 3x)²ⁿ
= \(\frac{1}{3^n \cdot x^n} \sum_{r=0}^{2 n}\left({ }^{2 n} C_r\right)(3 x)^r\)
For the term, independent of x put r = n.
∴ The term independent of x in (1 + 3)ⁿ (1 + \(\frac{1}{3 x}\))ⁿ is \(\frac{1}{3^n}\) ²ⁿC_n . 3ⁿ.

Question 11.
Show that the middle term In the expansion of (1 + x)²ⁿ is \(\frac{1 \cdot 3 \cdot 5 \ldots \ldots(2 n-1)}{n !}\) (2x)ⁿ.
Solution:
The expansion of (1 + x)²ⁿ contains 2n + 1 terms.
∴ Middle term is (n + 1)th term

Question 12.
If (1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² …………… + a₂₀x²⁰, then prove that
i) a₀ + a₁ + a₂ + …………… + a₂₀ = 2¹⁰
ii) a₀ – a₁ + a₂ – a₃ + …………. + a₂₀ = 4¹⁰
Solution:
Given
(1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² …………… + a₂₀x²⁰ …………….(1)
i) Put x = 1, in (1), we get
(1 + 3 – 2)¹⁰ = a₀ + a₁ + a₂ + …………… + a₂₀
⇒ a₀ + a₁ + a₂ + …………… + a₂₀ = 2¹⁰.

ii) Put x – 1 in (1), we get
(1 – 3 – 2)¹⁰ = a₀ – a₁ + a₂ – a₃ + …………. + a₂₀
a₀ – a₁ + a₂ – a₃ + …………. + a₂₀ = 4¹⁰.

Question 13.
If (3√3 + 5)^{2n + 1} = x and f = x – [x] (where [x] the integral part of x), find the value of x.f.
Solution:
Given (3√3 + 5)^{2n + 1} = x
and f = x – [x]
∴ 0 < f < 1
Let us consider F = (3√3 + 5)^{2n + 1}
We know that
5 < 3√3 < 6 = 0 < 3√3 – 5 < 1
⇒ 0 < (3√3 – 5)^{2n + 1} < 1
⇒ 0 < F < 1
⇒ – 1 < – F < 0
Let x = I + f (where E is an integer)
Now
i + f – F = (3√3 + 5)^{2n + 1} + (3√3 – 5)^{2n + 1}
= [^{2n + 1}C₀ (3√3)²ⁿ⁺¹ + ^{2n + 1}C₁ (3√3)²ⁿ . 5 + ^{2n + 1}C₂ (3√3) . 5² + …………..] – [^{2n + 1}C (3√3)²ⁿ⁺¹ – ^{2n + 1}C₁ (3√3)²ⁿ . 5 + ^{2n + 1}C₂ (3√3)^2n-1 . 5² – …………]
= 2 [^{2n + 1}C₁ (3√3) 5 + ^{2n + 1}C₃ (3√3)^2n-2 5³ + …………. + ^{(2n + 1)}C_(2n+1) (5)²ⁿ⁺¹]
= 2k, where k is an integer
∴ I + f – F is an even integer
⇒ f – F is also integer.
∴ (1) + (2)
⇒ – 1 < f – F < 1
⇒ f – F = 0
⇒ f = F
∴ x . f = x . F
= (3√3 + 5)^{2n + 1} . (3√3 – 5)^{2n + 1}
= (27 – 25)^{2n + 1}
= 2^{2n + 1}.

Question 14.
If R, n are posilve integers, n is odd, 0< F < 1 and if (5√5 + 11) = R + F, then prove that
i) R is an even integer and
ii) (R + F). F = 4ⁿ
Solution:
Given R, n are positive integers, 0 < F < 1 and
(5√5 + 11)ⁿ = R + F …………….(1)
i) Consider (5√5 – 11)ⁿ = f …………….(2)
We know that 11 < 5√5 < 12
⇒ 0 < 5√5 – 11 < 1
⇒0 < (5√5 – 11)ⁿ < 1
⇒ 0 < f < 1
⇒ – 1 < – f < 0 ………….(3)
From (1) and (3)
– 1 < F -f < 1 ……………(4)
Also R + F – f
= (5√5 + 11)ⁿ – (5√5 – 11)ⁿ
= [ⁿC₀ (5√5)ⁿ + ⁿC₁ (5√5)^n-1 (11) + ⁿC₂ (5√5)^n-2 . 11² + ⁿC₃ (5√5)^n-3 . 11³ + ………… + ⁿC_n (11)ⁿ] – [ⁿC₀ (5√5)ⁿ – ⁿC₁ (5√5)^n-1 (11) + ⁿC₂ (5√5)^n-2 . 11² – ⁿC₃ (5√5)^n-3 . 11³ + ………….. + (- 1)ⁿC_n (11)ⁿ]
= 2 [ⁿC₁ (5√5)^n-1 (11) + ⁿC₃ (5√5)^n-3 (11)³ + ……………]
= 2k, where k is an integer (∵ f is odd)
∴ R + F – f is an even Integer.
⇒ F – f is also an interger. (∵ R is integer)
From (4), we have F – f = 0
⇒ F = f
∴ R is an even Integer.

ii) Now (R + F) . F
= (5√5 + 11)ⁿ (5√5 + 11)ⁿ
= ((5√5)² – 11²)ⁿ = 4ⁿ
∴ (R + F) . F = 4ⁿ.

Question 15.
If I, n are positive Integers, 0 < f < 1 and if (7 + 4√3) = I + f, then show that
i) I is an odd integer and
ii) (I + f) (I – f) =
Solution:
Given I and n are positve integers.
0 < f < I and (7 + 4√3)ⁿ = I + f ………….(1)

i) Let us consider (7 – 4√3)ⁿ = F
We know that 6 < 4√3 < 7
⇒ – 7 < – 4√3 < – 6
⇒ 0 < 7 – 4√3 < 1
⇒ 0 < (7 – 4√3)ⁿ < 1
⇒ 0 < F < 1
we have 0 < F + f < 2 …………(2)
Now I + f + F = (7 + 4√3)ⁿ + (7 – 4√3)ⁿ
= [ⁿC₀ 7ⁿ + ⁿC₁ 7^n-1 (4√3) + ⁿC₂ 7^n-2 (4√3)² + ………….. + ⁿC_n (4√3)ⁿ] + [ⁿC₀ 7ⁿ – ⁿC₁ 7^n-1 (4√3) + ⁿC₂ 7^n-2 (4√3)² – ………….. + ⁿC_n (- 1)ⁿ (4√3)ⁿ]]
= 2[ⁿC₀ 7ⁿ + ⁿC₂ 7^n-2 (4√3)² + ⁿC₄ 7^n-4 (4√3)⁴ + ……………]
= 2k, where k is an integer.
∴ I + f + F is an even integer.
∴ f + F is also an integer. (∵ I is an integer)
from (2) we have f + F = I ………..(3)
∴ I + I is an even integer
⇒ I is an odd integer.

ii) Also (I + f) (I – f) = (I + f) F
= (7 + 4√3)ⁿ (7 – 4√3)ⁿ
= (7² – (4√3)²)ⁿ = 1.

Question 16.
If n is a Positive integer, prove that \(\sum_{r=1}^n \mathbf{r}^3 \cdot\left(\frac{{ }^n C_r}{{ }^n C_{r-1}}\right)^2=\frac{n(n+1)^2(n+2)}{12}\).
Solution:
We know that \(\frac{{ }^{{ }^r} C_r}{{ }^n C_{r-1}}=\frac{n-r+1}{r}\)

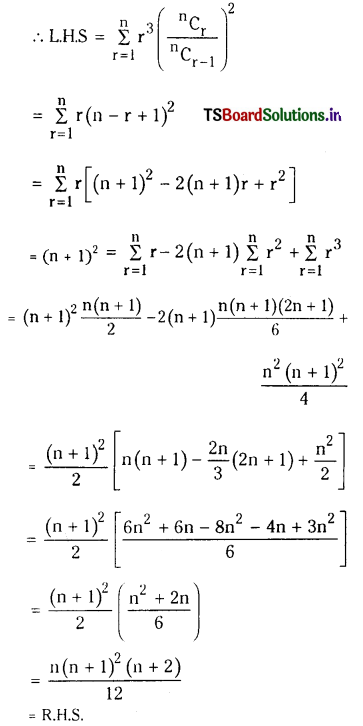
Question 17.
Find the number of irrational terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰.
Solution:
Number of terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰ are 101.
General term in the expansion of (x + y)ⁿ is
T_r+1 = ⁿC_r x^n-r . y^r
∴ General term in the expansion of (5^1/6 + 2^1/8)¹⁰⁰
T_r+1 = ¹⁰⁰C_r . \(\left(5^{\frac{1}{6}}\right)^{100-r} \cdot\left(2^{\frac{1}{8}}\right)^r\)
= ¹⁰⁰C_r . \(\cdot 5^{\frac{100-r}{6}} \cdot 2^{\frac{r}{8}}\)
For T_r+1 to be a rational.
Clearly ‘r’ is a multiple of 8 and 100 – r is a multiple of 6
∴ r = 16, 40, 64. 88.
Number of rational terms are 4.
∴ Number of irrational terms are 101 – 4 = 97.