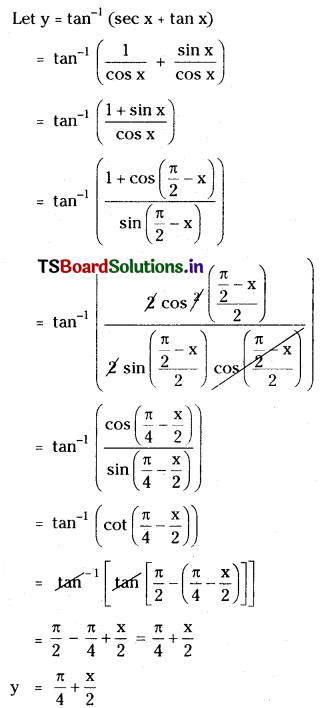
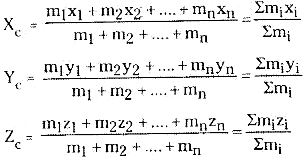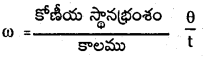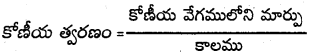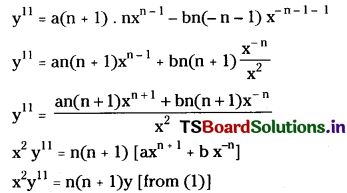Here students can locate TS Inter 1st Year Physics Notes 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం to prepare for their exam.
TS Inter 1st Year Physics Notes 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం
→ ద్రుఢ వస్తువు : పరిపూర్ణమైన, నిర్దిష్టమైన మార్పుచెందని ఆకారం కలిగి ఉండే వస్తువును ఒక ద్రుఢ వస్తువుకు ఆదర్శ నమూనాగా తీసుకుంటారు. ఇటువంటి వస్తువులో కణముల మధ్య దూరము మారదు అని భావిస్తారు.
→ స్థానాంతరణ గమనము : ఈ విధమైన చలనంలో వస్తువు మొత్తం ఒకచోటు నుండి మరొకచోటుకు స్థానభ్రంశం చెందుతుంది.
→ శుద్ధ స్థానాంతరణ గమనంలో ఏ క్షణంలోనైనా వస్తువులోని అన్ని కణాలు ఒకే వేగాన్ని కలిగి ఉంటాయి.
→ భ్రమణాక్షము : వస్తువు స్థానాంతరణ చలనం నిరోధించడానికి దానిని ఒక సరళరేఖపరంగా స్థిరంగా ఉంచాలి. కాని వస్తువు ఇటువంటి సరళరేఖపరంగా తనచుట్టూ తాను తిరిగే అవకాశం ఉంది.
“వస్తువు తన చుట్టూ తాను ఏ సరళరేఖపరంగా చలించుతుందో దానిని భ్రమణాక్షము అంటారు”.
→ భ్రమణ గమనము : ఒక స్థిరమైన అక్షం పరంగా భ్రమణం చెందే ద్రుఢ వస్తువులోని కణాలు భ్రమణ అక్షానికి లంబతలంలో భ్రమణాక్షంపై గల బిందువులను కేంద్రంగా చేసుకొని నియమిత వృత్తాకారమార్గంలో చలిస్తాయి. ఈ విధమైన చలనాన్ని భ్రమణ గమనము అంటారు.
Note :
- కొన్ని సందర్భాలలో భ్రమణ గమనము స్థిరమైన అక్షం వెంబడి కాకుండా ఒక స్థిర బిందువు ఆధారంగా కూడా ఉండవచ్చు.
- కీలకంలేని లేదా భ్రమణాక్షం స్థిరంగా బిగించకుండా ఉన్న ద్రుఢ వస్తువు గమనం కేవలం స్థానాంతరణ గమనం లేదా స్థానాంతరణ గమనము మరియు భ్రమణ గమనముల సంయోగాన్ని కలిగి ఉంటుంది. వస్తువును ఏదో విధంగా బిగించితే దానికి భ్రమణ గమనం మాత్రమే ఉంటుంది.
→ ద్రవ్యరాశి కేంద్రము : ఏదైనా వస్తువు లేదా కణ వ్యవస్థ మొత్తం ద్రవ్యరాశి ఒక బిందువు వద్ద కేంద్రీకృతమైనట్లుగా భావిస్తే అటువంటి బిందువును ద్రవ్యరాశి కేంద్రం అంటారు. అన్ని బాహ్యబలాలు ఇటువంటి బిందువు వద్దనే ప్రయోగించినట్లుగా ఆ వస్తువు లేదా వ్యవస్థ గమనంలో ఉంటుంది.
→ గరిమనాభి : వస్తువులోని ఏ బిందువు పరంగా మొత్తం గురుత్వ బలభ్రామకం శూన్యమవుతుందో ఆ బిందువును వస్తువు గరిమనాభిగా నిర్వచించవచ్చు.
గరిమనాభివద్ద నికర బలభ్రామకం τ = Σ(ri × mi) g = 0
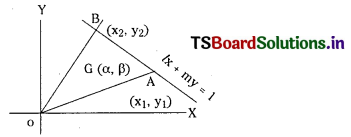
→ ద్రవ్యరాశి కేంద్ర నిరూపకాలు : m1, m2 క అను రెండు వస్తువులు ఒక మూల బిందువు నుండి x1, x2 దూరాలలో ఉంటే ఆ వ్యవస్థ ద్రవ్యరాశి కేంద్రము xc = \(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
అనగా ద్రవ్యరాశి కేంద్రము మూలబిందువు నుండి వస్తువులోని అన్నికణముల ద్రవ్యరాశి భ్రామకాల మొత్తము మరియు వస్తువు ద్రవ్యరాశికి గల నిష్పత్తిగా భావించవచ్చు.
Note:
- సమాన ద్రవ్యరాశులు గల రెండు వస్తువులు m, m లు ‘x’ దూరంలో ఉంటే వాటి ద్రవ్యరాశి కేంద్రం కచ్చితంగా వాటి మధ్య బిందువు వద్ద ఉంటుంది.
- మూడు సమాన ద్రవ్యరాశులు గల వస్తువులను ఒక త్రిభుజం శీర్షాల వద్ద ఉంచితే ఆ వ్యవస్థ ద్రవ్యరాశి కేంద్రం ఆ త్రిభుజ కేంద్రాభం (centroid) వద్ద ఉంటుంది.
ద్రవ్యరాశి కేంద్ర నిరూపకాలకు సమీకరణాలు. అనేక వస్తువులు లేదా కణాలు m1, m2, త్రిదిశాత్మకంగా తీసుకుంటే ఆ వ్యవస్థ ద్రవ్యరాశి కేంద్ర x, y మరియు z నిర్దేశకాలు
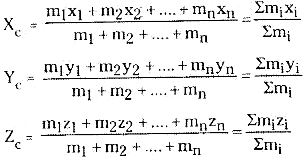

→ ద్రవ్యరాశి కేంద్ర లక్షణాలు :
- వ్యవస్థ మొత్తం ద్రవ్యరాశి దాని ద్రవ్యరాశి కేంద్రం వద్దనే కేంద్రీకృతమైనట్లుగా ప్రవర్తిస్తుంది.
- వ్యవస్థపైగల మొత్తం బాహ్యబలం ద్రవ్యరాశి కేంద్రం వద్దనే ప్రయోగించినట్లుగా వస్తువు ప్రవర్తన ఉంటుంది. బాహ్య = M. ‘a’; ‘a’ ద్రవ్యరాశి కేంద్రత్వరణము.
- అంతర్గత బలాలు ద్రవ్యరాశి కేంద్ర గమనాన్ని ప్రభావితం చేయలేవు.
- స్థానాంతరణ మరియు భ్రమణ గమనం కలిగి ఉన్న సంక్లిష్ట చలనాలలో, ద్రవ్యరాశి కేంద్రం స్థానాంతరణ గమనమే. వస్తువు మొత్తం స్థానాంతరణ గమనం అవుతుంది.
- ఒక కణ వ్యవస్థ మొత్తం ద్రవ్యవేగము ఆ వ్యవస్థ మొత్తం ద్రవ్యరాశి మరియు ద్రవ్యరాశి కేంద్రాల వేగాల లబ్ధానికి సమానము p̅ = MV.
- ద్రవ్యరాశి కేంద్ర నిరూపకాలు మనం ఎంచుకున్న నిర్దేశచట్రంపై ఆధారపడవు.
→ సదిశల సదిశా లబ్ధము : రెండు సదిశలు ā మరియు b̅ లను మరల సదిశ ఏర్పడేవిధంగా గుణించడాన్ని సదిశల సదిశాలబ్ధము అంటారు. దీనిని ā cross b̅ అని అంటారు.
ā × b̅ = |ā||b̅| sinθ. n̅ ఇందులో n̅ ఇచ్చిన సదిశల తలానికి లంబదిశలో గల ప్రమాణ సదిశ.
Note : సదిశల సదిశా లబ్ధము ā × b̅ ను వజ్రంబ్ధము అని కూడా అంటారు.
సదిశా లబ్ధ నియమాలు :
- సదిశా లబ్ధము స్థిత్యంతర న్యాయాన్ని పాటించదు. అనగా ā × b̅ + b̅ × ā కాని ā × b̅ = – (b̅ × ā)
- సదిశా లబ్దము విభాజక న్యాయాన్ని పాటిస్తుంది అనగా ā × (b̅ + c̅) = (a̅ × b̅) + (a̅ × c̅)
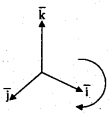
- ఏవైనా సదిశలను i̅, j̅ మరియు K̅ల సంయోగంగా చూపినపుడు సదిశాలబ్ధము కుడిచేతి మర నిబంధనను పాటిస్తుంది.
- ఒక తలంలో గల రెండు ప్రమాణ సదిశలను సవ్యదిశలో గుణిస్తే అది ఆ తలానికి లంబదిశలో గల వేరొక ప్రమాణ సదిశను ఇస్తుంది.
అనగా i × j = k, j × k = i మరియు k × i = j
రెండు ప్రమాణ సదిశలను అపసవ్యదిశలో గుణిస్తే – గుర్తుతో మూడవ ప్రమాణ సదిశను ఇస్తుంది. j × i = -k, k × j = -i, k × t = -j. - సమాంతర ప్రమాణ సదిశల సదిశా లబ్ధము సున్న
అనగా i × i = j × J = k × k = 0
→ కోణీయ స్థానభ్రంశము (θ) : భ్రమణ గమనంలో ఉన్న వస్తువు వృత్త కేంద్రం వద్ద చేసిన కోణాన్ని కోణీయ స్థానభ్రంశము ‘θ’ అంటారు. ప్రమాణము రేడియన్.
కోణీయ వేగము (ω) : కోణీయ స్థానభ్రంశంలోని మార్పు రేటును కోణీయవేగం అంటారు.
కోణీయ వేగములు α = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) ప్రమాణము రేడియన్ / సెకను
Note : భ్రమణ గమనంలో ఉన్న వస్తువులోని అన్ని కణాలు ఒకే పరిమాణం గల కోణీయ స్థానభ్రంశము (θ) మరియు కోణీయ వేగము (ω) వంటి రాశులను కలిగి ఉంటాయి.
→ కోణీయ త్వరణము : కోణీయ వేగంలో మార్పు రేటును కోణీయ త్వరణం అంటారు.
కోణీయ త్వరణము α = \(\frac{d \omega}{d t}=\frac{d^2 \theta}{d t^2}\) ప్రమాణము రేడియన్ / సె2
→ బలభ్రామకము లేదా టార్క్ (τ) : మూలబిందువు (0) పరంగా స్థాన సదిశను r̅ కలిగిన ఒక వస్తువు లేదా కణంపై బలము F̅ ను ప్రయోగిస్తే, r̅ మరియు F̅ ల వజ్రలబ్ధాన్ని టార్క్
టార్క్ τ = r̅ × F̅ = |r̅||F|sin θ n̅
టార్క్ సదిశరాశి. దీని దిశ I, F ల తలానికి లంబంగా ఉంటుంది.
టార్క్క ప్రమాణము న్యూటన్ – మీటరు. D.F = ML2 T-2
Note : టార్క్ పని, శక్తిలకు మితిఫార్ములాలు ఒక్కటే.
→ కోణీయ ద్రవ్యవేగము (1) : m ద్రవ్యరాశి గల ఒక కణం ద్రవ్యవేగము మరియు అది మూలబిందువు నుండి 7 దూరంలో ఉంటే P మరియు T ల వజ్ర లబ్దాన్ని కోణీయ ద్రవ్యవేగంగా నిర్వచించినారు.
కోణీయ ద్రవ్యవేగము ‘L’ = r̅ × p̅ = |r̅||p̅|sin θ. n̅ ఇది సదిశరాశి. D.F = ML2T-1
→ L, α ల మధ్య సంబంధము : కోణీయ ద్రవ్యవేగంలోని మార్పురేటు వస్తువుపై ప్రయోగించిన బాహ్య టార్కుక సమానము.
టార్కు τ = \(\frac{d \overline{\mathrm{L}}}{d \mathrm{t}}=\frac{\mathrm{d}}{\mathrm{dt}}\)(r̅ × p̅)
→ కోణీయ ద్రవ్యవేగనిత్యత్వ నియమము : ఏదైనా వస్తువు లేదా కణంపై ప్రయోగించిన బాహ్య టార్క్ సున్న అయితే ఆ వస్తువు కోణీయ ద్రవ్యవేగము స్థిరము.
అనగా బాహ్య టార్క్ సున్న అయితే వ్యవస్థలో గల కణముల కోణీయ ద్రవ్యవేగములలో మొత్తం మార్పు సున్న i.e. τ = 0 అయితే
\(d \bar{L}_1+d \bar{L}_2+\ldots d \bar{L}_n=\sum_{1=1}^n d \bar{L}_1\) = 0
Note : కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమము స్థానాంతరణ గమనంలోని రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని పోలి ఉంటుంది.
→ ద్రుఢ వస్తువుల సమాతాస్థితి : కాలంతోపాటు వస్తువు రేఖీయ మరియు కోణీయ ద్రవ్యవేగాలు మార్పులేకుండా స్థిరంగా ఉంటే ఆ వస్తువుకు రేఖీయ త్వరణము మరియు టార్క్లు సున్న. అటువంటి వస్తువు సమతాస్థితిలో ఉన్నది అంటారు.

→ వస్తువు సమతాస్థితికి కావలసిన నియమాలు :
- ఒక వస్తువుపై ప్రయోగించిన బలాల సదిశా మొత్తము సున్న కావలెను.
\(\bar{F}_1+\bar{F}_2+\bar{F}_3+\bar{F}_n=\sum_{i=1}^n \bar{F}_i\) = 0 అయితే ఆ వస్తువు స్థానాంతరణ సమతాస్థితిని కలిగి ఉంటుంది. - ఏదైనా వస్తువుపై ప్రయోగించిన టార్క్ సదిశా మొత్తం సున్న అయితే ఆ వస్తువు భ్రమణ సమతాస్థితిని పొందుతుంది.
τ1 + τ2 + …………. + τn = \(\sum_{i=1}^n {τ}_i\) = 0 అయితే ఆ వస్తువు భ్రమణ సమతాస్థితిలో ఉంటుంది.
→ బలభ్రామకముల సూత్రాలు : యాంత్రిక సమతాస్థితిలో ఉన్న ఒక వ్యవస్థ ఆధారం వద్ద కీలకం ప్రతిచర్యా బలం R మరియు బలాలు F1, F2, అయితే
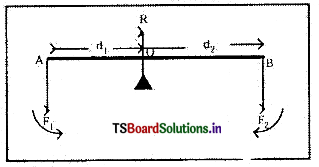
- స్థానాంతరణ సమతాస్థితి కోసం R – F1 – F2 = 0 అనగా ఊర్ధ్వదిశలో బలాలు మొత్తం, అధోదిశలో బలాల మొత్తానికి సమానము.
- భ్రమణ సమతాస్థితి కోసం d1F1 – d2F2 = 0 అనగా ఊర్ధ్వ దిశలో బలభ్రామకాల మొత్తం అధో దిశలో బలభ్రామకాల మొత్తానికి సమానము.
→ యాంత్రిక లాభం : భ్రమణ సమతాస్థితి వద్ద d1F1 = d2F2, లేదా \(\frac{F_1}{F_2}=\frac{d_2}{d_1}\) దీనిని యాంత్రిక లాభం అంటారు. అనగా పెద్ద భారాన్ని చిన్న యత్నబలంతో ఎత్తవచ్చని అర్థము.
→ జడత్వ భ్రామకము (I) : భ్రమణ గమనంలో గల వస్తువు జడత్వాన్ని కొలవడానికి జడత్వ భ్రామకాన్ని వాడతారు. వస్తువు మొత్తం ద్రవ్యరాశి భ్రమణ అక్షం నుండి R దూరంలో ఉన్నదని భావిస్తే భ్రమణ అక్షపరంగా దాని జడత్వ భ్రామకము
I = MR2. ప్రమాణము కి.గ్రా. మీ2, D.F: ML2
Note : వస్తువు ద్రవ్యరాశిలాగా జడత్వ భ్రామకము స్థిరరాశి కాదు.
I విలువ భ్రమణాక్షము, వస్తువు ద్రవ్యరాశి మరియు వస్తువులో ద్రవ్యరాశి వితరణ (distribution) లపై ఆధారపడును.
→ భ్రమణ వ్యాసార్ధము (k) : ఏ బిందువు ద్రవ్యరాశి మొత్తం వస్తువు ద్రవ్యరాశికి సమానమో, ఏ బిందువువరంగా జడత్వభ్రామకం వస్తువు మొత్తం జడత్వ భ్రామకానికి సమానమో, ఆ బిందువు ద్వారా పోయే అక్షానికి, భ్రమణాక్షానికి మధ్య ఉన్న లంబదూరాన్ని ఆ అక్షపరంగా వస్తువు భ్రమణ వ్యాసార్ధంగా నిర్వచించినారు.
→ గతిపాలక చక్రం : వాహనాల వేగంలో హఠాత్తుగా వచ్చే మార్పులు నిరోధించడానికి అత్యధిక జడత్వ భ్రామకం కలిగిన వృత్తాకార బిళ్ళ చక్రాలను వాడతారు. వీటిని గతిపాలక చక్రాలు అంటారు. గతిపాలక చక్రం వేగంలో మార్పులు క్రమేణా కలిగేటట్లు చేసి వాహనాల కుదుపులను తగ్గిస్తుంది.
→ లంబాక్ష సిద్ధాంతము : ఒక పలక తలానికి లంబంగా ఉన్న ఒక అక్షపరంగా జడత్వ భ్రామకం ఆ అక్షంతో అనుషక్తంగా ఉన్న పలక తలంలోని రెండు పరస్పర లంబ అక్షముల పరంగా గల జడత్వ భ్రామకాల మొత్తానికి సమానము.
Iz = Ix + Iy
→ సమాంతరాక్ష సిద్ధాంతము : ఏదైనా ఒక అక్షం పరంగా ఒక వస్తువు జడత్వ భ్రామకం (I’z) ఆ అక్షానికి సమాంతరంగా ఉండి వస్తువు ద్రవ్యరాశి కేంద్రం ద్వారా పోయే అక్షపరంగా వస్తువు జడత్వ భ్రామకం (Iz) మరియు వస్తువు ద్రవ్యరాశి (m) ను అక్షముల మధ్యదూర వర్గం (R2) చేత గుణించి కలుపగా వచ్చు మొత్తానికి సమానము. అనగా I’z = Iz + MR2
→ దొర్లుడు గమనము : దొర్లుడు గమనము అనేది స్థానాంతరణ గమనము మరియు భ్రమణ గమనముల సంయోగము.
→ దొర్లుడు గమనం గతిజశక్తి (R.K.E) : దొర్లుడు గమనంలో ఉన్న వస్తువుకు స్థానాంతరణ గమనం వల్ల గతిజశక్తి (1/2mv2) మరియు భ్రమణ గమనం వల్ల భ్రమణ గతిజశక్తి (\(\frac{1}{2}\)Iω2) ఉంటాయి.
దొర్లుడు గమనంలో వస్తువు మొత్తం గతిజశక్తి K.ER = \(\frac{1}{2}\) mv2 + \(\frac{1}{2}\) Iω2

→ రెండు కణాల వ్యవస్థలో ద్రవ్యరాశులు m1, m2, వాటి స్థానాలు x1, మరియు x2 అయితే,
a) ద్రవ్యరాశి కేంద్రం నిరూపకాలు xc = \(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
b) నిరూపక వ్యవస్థ మూలబిందువు m1 తోటి ఏకీభవించితే
Xc = \(\frac{\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\) లేక xc = \(\frac{\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\) ఇక్కడ.d = m, m, ల మధ్యదూరం
c) ద్రవ్యరాశి కేంద్రం నుండి వస్తువుల దూరాల మధ్య నిష్పత్తి \(\frac{d_1}{d_2}=\frac{m_2}{m_1}\)
→ అనేక కణాల వ్యవస్థకు

f) ద్రవ్యరాశి కేంద్రం ద్రవ్యవేగం Pc = mvc = \(\sum_{\mathbf{l}=1}^{\mathbf{n}}\)mivi లేదా mvc = m1v1 + m2v2 + …….. + mnvn లేదా \(\overline{\mathrm{P}}_{\mathrm{C}}=\overline{\mathrm{P}}_1+\overline{\mathrm{P}}_2+\ldots . . \overline{\mathrm{P}}_{\mathrm{n}}\)
g) ద్రవ్యరాశి కేంద్రం త్వరణం a = \(\frac{F_C}{M}=\sum_{i=1}^n a_i m_i\)
∴ a = \(\frac{m_1 a_1+m_2 a_2+m_3 a_3+\ldots .+m_n a_n}{m_1+m_2+m_3+\ldots . .+m_n}\)
→ వజ్ర లబ్ధము (లేదా) సదిశా లబ్ధము : Ā × B̅ = |Ā| |B̅| sin θ. n̂ గా నిర్వచించినారు; n̂ ఏకాంక లంబ సదిశ.
→ సజాతి ఏకాంక సదిశల వజ్ర లబ్ధం సున్న. అనగా ī ī = j̅· j̅ = k̅·k̅ = 0
సమాంతర సదిశల మధ్య వజ్ర లబ్ధం శూన్యం.
→ i̅ × j̅ = k̅, j̅ × k̅ =j̅ మరియు k̅ × j̅ = j̅;
→ Ā = x1 ī + y1 j̅ + z1 k̅ మరియు B = x2 ī + y2 j̅ + z2 k̅ అయితే
Ā × B̅ = \(\left|\begin{array}{ccc}
\mathrm{i} & \mathrm{j} & \mathrm{k} \\
\mathrm{x}_1 & \mathrm{y}_1 & \mathrm{z}_1 \\
\mathrm{x}_2 & \mathrm{y}_2 & \mathrm{z}_2
\end{array}\right|\) = (y1z2 – y2z1) ī – (x1z2 – x2z1) j̅ + (x1y2 − x2y1)k̅
→ కోణీయ వేగం
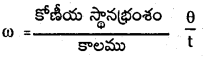
ω = \(\frac{\theta}{t}\)
చిన్న కోణములకు ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\); యూనిట్ : రేడియన్ / సె
ω = \(\frac{\theta}{t}\) లేదా ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\); లేదా ω = \(\frac{2 \pi n}{t}\) (n = భ్రమణాల సంఖ్య)
→ కోణీయ త్వరణం
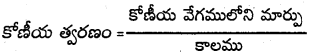
α = \(\frac{\omega_2-\omega_1}{t}\) లేదా α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\), యూనిట్ : రేడియన్ / సె2
→ v మరియు ω మధ్య సంబంధము V = rω;
→ త్వరణము a = rα
→ అభికేంద్ర త్వరణము ac = rω2 = vω = \(\frac{\mathrm{v}^2}{\mathrm{r}}\); అపకేంద్ర బలం = \(\frac{\mathrm{mv}^2}{\mathrm{r}}\) = mrω2
→ తిరుగుతున్న గ్రామ్ ఫోన్ రికార్డుపై నాణెము నుంచిన అది జారిపోకుండా ఉండుటకు fs = μsN = mrω2
μsmg = mrω2 ⇒ μs = \(\frac{\mathrm{r} \omega^2}{\mathrm{~g}}\)

→ mద్రవ్యరాశి గల వస్తువు క్షితిజతలంలో వృత్తాకారంలో తిరుగుతూ M ద్రవ్యరాశి గల వస్తువు భారాన్ని నిలుపు చేసిన Mg = mrω2 లేదా కోణీయ వేగము ω = \(\sqrt{\frac{M g}{m r}}\)
→ టార్క్ τ = r̅ × F̅ = |r̅||F̅| sin θ. ఇది ఎంత శక్తితో వస్తువు తిప్పబడినదో తెలియజేస్తుంది.
→ బలయుగ్మ భ్రామకము బలము × బలదిశల మధ్య లంబదూరం.
→ జడత్వ భ్రామకము I = \(\sum_{i=1}^n\)miri2 లేదా I = MR2
→ జడత్వ భ్రామకము I = MR2 = MK2 అయిన, K ని భ్రమణ వ్యాసార్ధము అంటారు.
→ సమాంతర అక్ష సిద్ధాంతము నుండి I = IG + MR2
→ లంబ అక్ష సిద్ధాంతము నుండి Iz = Ix + Iy
→ సన్నని కడ్డీ జడత్వ భ్రామకము :
a) సన్నని కడ్డీ మధ్య బిందువు ద్వారా పోతూ పొడవుకు లంబముగా ఉన్న అక్షముపై జడత్వ భ్రామకము
I = \(\frac{\mathrm{M} l^2}{12}\); K = \(\frac{l}{\sqrt{12}}\)
b) కడ్డీ చివర ఉన్న బిందువు ద్వారా పోతూ పొడవుకు లంబంగా ఉన్న అక్షముపై జడత్వ భ్రామకం
I = \(\frac{\mathrm{m} l^2}{3}\); K = \(\frac{l}{\sqrt{3}}\)
→ రింగు జఢత్వ భ్రామకము :
a) రింగు కేంద్రము గుండాపోతూ దాని తలమునకు లంబంగా ఉన్న అక్షం పరంగా జడత్వ భ్రామకం I = MR2, K = R
b) ఏదైనా వ్యాసం పరంగా రింగు జడత్వ భ్రామకం I = \(\frac{\mathrm{MR}^2}{2}\); K = \(\frac{\mathrm{R}}{\sqrt{2}}\)
c) రింగు తలంలోని ఏదైనా స్పర్శరేఖ పరంగా జడత్వ భ్రామకం I = \(\frac{3}{2}\)MR2; K = \(\sqrt{\frac{3}{2}}\)R
→ గుండ్రని పళ్ళెము జడత్వ భ్రామకం :
a) గుండ్రని పళ్ళెం కేంద్రం గుండా పోతూ తలానికి I = \(\frac{\mathrm{MR}^2}{2}\); K = \(\frac{\mathrm{MR}^2}{2}\)
లంబంగా ఉన్న అక్షం పరంగా జడత్వ భ్రామకం
b) పళ్ళెంలోని ఏదైనా వ్యాసం పరంగా జడత్వ భ్రామకం I = \(\frac{\mathrm{MR}^2}{4}\); K = \(\frac{\mathrm{R}}{2}\)
c) పళ్ళెం తలంలోని స్పర్శరేఖ పరంగా జడత్వ భ్రామకం I = \(\frac{5}{4}\)MR2; K = \(\frac{5}{4}\)R
→ సమతల పటలము యొక్క జడత్వ భ్రామకము :
a) సమాంతరంగా మధ్యబిందువు ద్వారా పోయే అక్షం పరంగా I = M\(\sqrt{\frac{l^2+b^2}{12}}\); K = \(\sqrt{\frac{l^2+b^2}{12}}\)
b) పొడవుకు సమాంతరంగా మధ్యబిందువు ద్వారా పోయే అక్షం పరంగా I = \(\frac{\mathrm{Mb}^2}{12}\); K = \(\frac{b}{\sqrt{12}}\)
c) వెడల్పుకు సమాంతరంగా మధ్యబిందువు ద్వారా పోయే అక్షం పరంగా I = \(\frac{b}{\sqrt{12}}\); K = \(\frac{l}{\sqrt{12}}\)
→ ఘనగోళం యొక్క జడత్వ భ్రామకం :
a) వ్యాసం పరంగా జడత్వ భ్రామకం I = \(\frac{2}{5}\)MR2; K = \(\sqrt{\frac{2}{5}}\)R
b) ఏదైనా స్పర్శరేఖ పరంగా I = \(\frac{7}{5}\)MR2; K = \(\sqrt{\frac{7}{5}}\)R
→ గుల్లగోళం యొక్క జడత్వ భ్రామకం :
a) వ్యాసం పరంగా జడత్వ భ్రామకం I = \(\frac{2}{3}\)MR2; K = \(\sqrt{\frac{2}{3}}\)R
b) ఏదైనా స్పర్శరేఖ పరంగా జడత్వ భ్రామకం I = \(\frac{7}{3}\)MR2; K = \(\sqrt{\frac{5}{3}}\)R
→ ఘన స్థూపం జడత్వ భ్రామకం:
a) స్థూపం అక్షం పరంగా జడత్వ భ్రామకం I = \(\frac{\mathrm{MR}^2}{2}\); K = \(\frac{\mathrm{R}}{\sqrt{2}}\)
b) పొడవుకు లంబంగా, కేంద్రం ద్వారా పోయే అక్షం పరంగా జడత్వ భ్రామకం I = M\(\left(\frac{l^2}{12}+\frac{\mathrm{R}^2}{4}\right)\)
K = \(\sqrt{\frac{l^2}{12}+\frac{\mathrm{R}^2}{4}}\)
→ గుల్ల స్థూపము జడత్వ భ్రామకం :
a) స్థూపం అక్షం పరంగా జడత్వ భ్రామకం I = MR2; K = R
b) పొడవుకు లంబంగా, కేంద్రం పోయే అక్షం పరంగా I = M\(\left(\frac{l^2}{12}+\frac{\mathrm{R}^2}{2}\right)\); K = \(\sqrt{\frac{l^2}{12}+\frac{\mathrm{R}^2}{2}}\)

→ కోణీయ ద్రవ్యవేగం L̅ = Iω
→ కోణీయ ద్రవ్యవేగం మరియు టార్క్ మధ్య సంబంధం, τ = \(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}=\frac{\mathrm{L}_2-\mathrm{L}_1}{\mathrm{t}}\)
→ కోణీయ త్వరణం మరియు టార్క్ మధ్య సంబంధం, τ = Iα.
→ కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం
I1ω1 + I2ω2 = స్థిరం (వస్తువుపై బాహ్య టార్క్ పనిచేయనపుడు).
![]()