TS Inter 1st Year Physics Notes Chapter 5 గమన నియమాలు

Here students can locate TS Inter 1st Year Physics Notes 5th Lesson గమన నియమాలు to prepare for their exam.

TS Inter 1st Year Physics Notes 5th Lesson గమన నియమాలు

→ బలము : ఒక వస్తువును గమనంలోకి తేవాలన్నా లేదా గమనంలో గల వస్తువును విరామ స్థితికి తేవాలన్నా బలం అనేది అవసరం.
కావున ఒక వస్తువు యొక్క స్థితిని మార్చునది లేక మార్చుటకు ప్రయత్నించే భౌతికరాశిని బలంగా నిర్వచించారు. ఇది సదిశరాశి.

→ న్యూటన్ నియమాలు :
న్యూటన్ మొదటి నియమం : బాహ్యబలం పనిచేయనంతవరకు నిశ్చలస్థితిలో ఉన్న వస్తువు నిశ్చలస్థితిలోను, జ గమనంలో ఉన్న వస్తువు సమవేగంతో ఋజుమార్గంలోను చలిస్తుంది.

→ మొదటి నియమం యొక్క ప్రాముఖ్యత : ఇది జడత్వము మరియు బలాలను నిర్వచిస్తుంది.

→ న్యూటన్ రెండవ నియమము : వస్తువు ద్రవ్యవేగంలోని మార్పురేటు వస్తువుపై ప్రయోగించిన బాహ్యబలానికి అనులోమానుపాతంలో ఉండి, బాహ్యబలం పనిచేసే దిశలోనే పనిచేస్తుంది.
అనగా \(\frac{\mathrm{d} \overline{\mathrm{P}}}{\mathrm{dt}}\) ∝ F లేదా F = k\(\frac{\mathrm{d} \overline{\mathrm{P}}}{\mathrm{dt}}\) లేదా F = k.ma లేదా F = ma (∵ k = 1)

→ ప్రాముఖ్యత : న్యూటన్ రెండవ నియమం ద్రవ్యవేగాన్ని నిర్వచిస్తుంది మరియు బలానికి ఒక సమీకరణమును ఉత్పాదిస్తుంది.
న్యూటన్ మూడవ నియమము : ప్రతి చర్యకూ ఎల్లపుడూ దానికి సమానము, వ్యతిరేకము అయిన ప్రతిచర్య
ఉంటుంది.
చర్య = – ప్రతిచర్య. న్యూటన్ మూడవ నియమం నుండి బలం ఎల్లపుడూ జతలు, జతలుగా పనిచేయును అని తెలుస్తుంది.

→ జడత్వం : జడత్వం అంటే మార్పుకు నిరోధం. వస్తువు తనంతట తానుగా తన స్థితిని మార్చుకోజాలని వస్తు ధర్మాన్ని జడత్వం అంటారు. వస్తువు జడత్వాన్ని ద్రవ్యరాశి ‘m’ తో కొలుస్తారు.

→ ద్రవ్యవేగము (P̅): ఒక వస్తువు ద్రవ్యరాశి m మరియు వేగము ల ల లబ్దాన్ని ద్రవ్యవేగము అంటారు. ఇది రాశి.
ద్రవ్యవేగము P̅ = mu, ప్రమాణము కి.గ్రా. -మీటరు/సెకను.

→ ద్రవ్యవేగము కొన్ని పరిశీలనలు :
1) సమాన పరిమాణంగల బలాన్ని వేరు వేరు ద్రవ్యరాశులు గల వస్తువులపై ప్రయోగిస్తే ఎక్కువ ద్రవ్యరాశి గల వస్తువు తక్కువ వేగాన్ని, తక్కువ ద్రవ్యరాశి గల వస్తువు ఎక్కువ వేగాన్ని పొందుతాయి. కాని ఆ రెండింటికి ద్రవ్యవేగంలో మార్పు సమానము. ఎందుకనగా ద్రవ్యవేగంలో మార్పు బాహ్యబలానికి అనులోమానుపాతంలో ఉంటుంది (న్యూటన్ రెండవ నియమము).

2) వేగంగా చలించే క్రికెట్ బంతిని తక్షణం ఆపడంకన్నా చేతులను బంతి దిశలో వెనుకకు లాగడం వల్ల తక్కువ బలం వాడి క్యాచ్ పట్టుకోవచ్చు.
తక్షణం బంతిని ఆపితే కాల అవధి Δt తక్కువ.
F = \(\frac{\mathrm{mv}-\mathrm{mu}}{\Delta \mathrm{t}}\) ఎక్కువ
చేతులు వెనుకకు కొంతదూరం జరపడంవల్ల కాలవ్యవధి Δt పెరుగును.
∴ ఆపడానికి కావలసిన బలం F = \(\frac{\mathrm{mv}-\mathrm{mu}}{\Delta \mathrm{t}}\) తక్కువ.
పై రెండు సందర్భాలలోను mυ – mu సమానము కాని Δt మారింది..

→ న్యూటన్ రెండవ నియమం ప్రకారము అంతర్గత బలాలు వ్యవస్థ ద్రవ్యవేగాన్ని మార్చలేవు.
ఉదా : తుపాకినుండి బులెట్లు పేల్చితే బులెట్ ఎక్కువ వేగంతో ముందుకు వెళుతుంది. తుపాకి తక్కువ వేగంతో వెనక్కి వెళుతుంది. కాని ఈ రెంటికి ద్రవ్యవేగము సమానవ

→ ప్రచోదనము : ఒక వస్తువుపై అత్యధిక బలం అతిస్వల్పకాలం పాటు పనిచేస్తే బలము మరియు కాలముల లబ్ధాన్ని ప్రచోదనము అంటారు. ఇది ద్రవ్యవేగంలో మార్పుకు సమానము.
ప్రచోదనము = బలం × కాలవ్యవధి ద్రవ్యవేగంలో మార్పు
ప్రచోదనం సదిశరాశి. ప్రమాణము న్యూటన్ – సెకను.

→ న్యూటన్ మూడవ నియమం ప్రకారము బలాలు ఎప్పుడూ జంటగానే ఏర్పడతాయి. చర్య ప్రతిచర్య.

→ సాధారణంగా చర్య, ప్రతిచర్యలు వేరు వేరు వ్యవస్థలపై పనిచేయడం వల్ల చలనం సాధ్యపడుతుంది.

→ చర్య, ప్రతిచర్య ఒకే వస్తువు లేదా వ్యవస్థపై పనిచేసే సందర్భాలలో ఆ వస్తువు సమతాస్థితిలో ఉంటుంది.

→ ద్రవ్యవేగ నిత్యత్వ నియమము: అన్యోన్య చర్య జరిపే కణాలు ఉన్న విముక్త వ్యవస్థ మొత్తం ద్రవ్యవేగము నిత్యత్వంగా (స్థిరంగా) ఉంటుంది.
ద్రవ్యవేగ నిత్యత్వ నియమము స్థితిస్థాపక, అస్థితి స్థాపక అభిఘాతాలకు వర్తిస్తుంది.

→ స్పర్శబలాలు : ఒక వస్తువు మరొక వస్తువుతో స్పర్శలో ఉంటే (అనగా తాకుతూ ఉంటే) వాటి మధ్య ఏర్పడే బలాలను స్పర్శబలాలు అంటారు. ఇవి న్యూటన్ మూడవ నియమాన్ని సంతృప్తిపరిచే విధంగా ఉంటాయి.

• స్పర్శ తలాలకు లంబంగా ఉండే స్పర్శాబలాలను అభిలంబ చర్య (Normal reaction) అంటారు.
• స్పర్శ తలాలకు సమాంతరంగా ఉండే స్పర్శాబలాలను ఘర్షణ (Friction) అంటారు.
• స్పర్శబలాలు ఘన పదార్థముల మధ్య మరియు ప్రవాహి (Fluid) లో మునిగి ఉన్న వస్తువుల మధ్య కూడా ఏర్పడతాయి.

→ ఘర్షణ : స్పర్శలో ఉన్న రెండు తలాల మధ్య సాపేక్ష గమనాన్ని వ్యతిరేకించే బలాన్ని ఘర్షణ లేదా ఘర్షణ బలం అంటారు. ఇది స్పర్శ తలాలకు సమాంతరంగా పనిచేస్తుంది.

→ స్థితిక ఘర్షణ : విరామ స్థితిలో గల, వస్తువుల మధ్య ఘర్షణను స్థితిక ఘర్షణ అంటారు. ఇది వస్తువుల మధ్య జరగబోయే చలనాన్ని వ్యతిరేకిస్తుంది.
వస్తువుపై అనువర్తిత బలం ప్రయోగించినపుడు మాత్రమే స్థితిక ఘర్షణ బలం పనిచేయడం ప్రారంభిస్తుంది. ఈ బలాలు అనువర్తిత బలంతో పాటు ఒక సీమాంత విలువ వరకు పెరుగుతాయి. గరిష్ఠ స్థితిక ఘర్షణ (f_s)_max విలువ అభిలంబ ప్రతిచర్య (N) కు అనులోమానుపాతంలో ఉంటుంది.
(f_s)_max = μ_kN

→ గతిక ఘర్షణ : గమనంలోకి వచ్చిన తరువాత స్పర్శ తలాల మధ్య సాపేక్ష చలనాన్ని నిరోధించే బలాన్ని గతిక ఘర్షణ బలం అంటారు.
f_k = μ_kN
గతిక ఘర్షణ గుణకం μ_k విలువ స్టైతిక ఘర్షణ గుణకం μ_s, కన్నా తక్కువ.

→ దొర్లుడు ఘర్షణ : వస్తువుల మధ్య దొర్లుడు చలనం ఉన్నపుడు దొర్లుడు చలనాన్ని వ్యతిరేకిస్తూ స్పర్శ తలాలకు సమాంతరంగా పనిచేసే బలాన్ని దొర్లుడు ఘర్షణ అంటారు.
వస్తువు దొర్లుతున్నపుడు స్పర్శ తలాలు స్వల్పంగా విరూపణం చెందుతాయి. ఫలితంగా వస్తువులు పరిమిత తలంలోనే స్పర్శలో ఉంటాయి. దొర్లుడు ఘర్షణ బలం వస్తువుల మధ్య గల స్పర్శతలం వైశాల్యం మీద ఆధారపడుతుంది.

→ బాల్ బేరింగులు : యంత్రాలలో కదిలే భాగాల మధ్య బాల్ బేరింగులు అమర్చడం వలన స్పర్శలోని తలాల మధ్య దొర్లుడు ఘర్షణ ఏర్పడుతుంది. దొర్లుడు ఘర్షణ గుణకం తక్కువ కావున వస్తువుల మధ్య ఘర్షణ తగ్గుతుంది.

→ క్షితిజ సమాంతర రోడ్డుపై కారు గమనం : క్షితిజ సమాంతరంగా ఉన్న రోడ్డుపై వృత్తాకార మార్గంలో చలించే వస్తువు (కారు) పై మూడు బలాలు పనిచేస్తాయి.

• కారు భారము (mg)
• అభిలంబ ప్రతిచర్య (N)
• ఘర్షణ బలం (f)

ఈ రకమైన చలనంలో కారు టైర్లకు, రోడ్డుకు మధ్య గల ఘర్షణబలం అభికేంద్రబలాన్ని సమకూరుస్తుంది.
ఇటువంటి మార్గంలో కారు సురక్షితంగా ప్రయాణించాలి. అంటే \(\frac{\mathrm{mv}^2}{\mathrm{R}}\) = μmg కావాలి.
లేదా కారు సురక్షిత వేగము V = \(\sqrt{\mu g R}\)

→ గట్టు కట్టిన రోడ్డు మీద కారు గమనం : వంపు మార్గాలలో ప్రమాదాలు నివారించడానికి రహదారిని క్షితిజ సమాంతర దిశకు కొంత కోణంలో రహదారి వెలుపలి అంచు కొంచెం ఎత్తులో ఉండేటట్లు కొంత కోణం 6తో నిర్మిస్తారు. దీనిని రహదారిని గట్టు కట్టడం అంటారు.
రహదారిని గట్టు కట్టడం వల్ల సురక్షిత వేగం పెరుగుతుంది. వంపు మార్గంలో ఈ గట్టు కట్టిన రహదారి సురక్షిత వేగము V₀ = \(\sqrt{g R \tan \theta}\). ఈ వేగంతో రహదారిపై వాహనాలు ప్రయాణిస్తే టైర్లలో అరుగుదల తక్కువ. వంపుమార్గంలో కావలసిన అభికేంద్రబలాన్ని టైర్లు, రోడ్డుకు మధ్య గల ఘర్షణ బలం వల్ల కాక గురుత్వ ఆకర్షణ వల్ల కలుగుతుంది.

→ ద్రవ్యవేగం P̅ = ద్రవ్యరాశి x వేగము, P̅ = mv
ప్రమాణము : kg m/sec. మితి ఫార్ములా : MLT^-1

→ న్యూటన్ రెండవ నియమం ప్రకారము F ∝ \(\frac{\mathrm{d} \overrightarrow{\mathrm{P}}}{\mathrm{dt}}=\mathrm{m} \frac{\mathrm{d} \overrightarrow{\mathrm{v}}}{\mathrm{dt}}\) లేదా F = ma = m\(\frac{(v-u)}{t}\)
ప్రమాణము : కి.గ్రా. మీ/సె² న్యూటన్, మితి ఫార్ములా = MLT^-2

→ తీగ లేదా దారము గుండా కలుగజేయు బలమును తన్యత అంటారు T = F.

→ వస్తువును స్వేచ్ఛగా వ్రేలాడదీసిన T – mg = 0
∴ తన్యత T = mg.

→ తీగ ద్వారా వ్రేలాడదీయబడిన వస్తువును త్వరణం చెందించితే, T = mg + ma_లేదా T = m(g + a) ‘+’ ⇒ ఊర్ధ్వ దిశ, ‘-‘ ⇒ అధోఃదిశ; ‘a’ ఫలిత త్వరణము.

→ ఒక వస్తువు క్షితిజ సమాంతర తలం మీద రెండవ వస్తువు క్షితిజ లంబంగా వేలాడుతుంటే

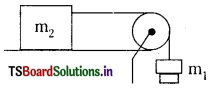
• త్వరణము a = \(\frac{m_1 g}{m_1+m_2}\)
• తీగయందు తన్యత T = \(\frac{2 m_1 m_2 g}{m_1+m_2}\)

→ రెండు వస్తువులు M₁ మరియు M₂ లు స్పర్శించబడితే

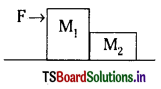
• F బలము ప్రయోగించుట వలన వ్యవస్థ త్వరణము a = \(\frac{F}{M_1+M_2}\)
• రెండు వస్తువుల మధ్య స్పర్శాబలము f = \(\frac{\mathrm{M}_2 \mathrm{~F}}{\mathrm{M}_1+\mathrm{M}_2}\) (F పై M₁ వలన)

→ m ద్రవ్యరాశి గల వస్తువును లిప్ట్ యందు ‘a’ త్వరణముతో తీసికొనిపోయిన

• ఊర్ధ్వ దిశలో గమనములో ఉన్నపుడు దృశ్యభారము W₁ = m(g + a) లేదా W₁ = W (1 + \(\frac{a}{g}\))
• అధోః దిశలో ‘a’ త్వరణముతో గమనములో ఉన్నప్పుడు W₁ = m(g – a) లేదా W₁ = W(1 – \(\frac{a}{g}\))
  గమనిక : దృశ్య భారమును నేల కలుగజేసిన ప్రతిచర్య బలము (N) అని కూడా అంటారు.

→ ప్రచోదనము (J) = బలము X కాలము = ద్రవ్యవేగంలోని మార్పు. J = m\(\frac{(v-u)}{t}\) × t = mv – mu

→ ద్రవ్యవేగ రేఖీయ నిత్యత్వ నియమము ప్రకారము
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂, i.e., అభిఘాతము యందు ద్రవ్యవేగ మొత్తము స్థిరము.

→ ఘర్షణ బలం F ∝ లంబ ప్రతిచర్య N i.e., F ∝ N

→ ఘర్షణ గుణకం

ఎ) క్షితిజ సమాంతర తలం మీద లంబ చర్య N = mg = వస్తువు భారం
బి) వాలు తలం మీద లంబ ప్రతిచర్య N = mg cos θ
ఇక్కడ θ = వాలు తలం కోణం

→ ప్రశాంతత కోణము యొక్క టాంజెంట్ ప్రమేయము (tan θ), ఘర్షణ గుణకమునకు సమానము ∴ μ_s = tan θ.

→ నున్నని క్షితిజ సమాంతర తలంపై త్వరణం a = \(\frac{F}{m}\)

→ గరుకు క్షితిజ సమాంతర తలంపై త్వరణం a = \(\frac{F}{m}\) – μ_kg
(μ_k = గతిక ఘర్షణ గుణకం, F = ప్రయోగించి బలం)
గమనిక :
\(\frac{F}{m}\) < μ_kg అయినచో వస్తువు కదలదు.

1) నున్నని వాలుతలం వెంబడి క్రిందకు జరిగే చలనం విషయంలో :
ఎ) త్వరణం a = g sin θ.
బి) వాలుతలం క్రిందకు చేరు సమయానికి పొందు వేగం v = \(\sqrt{2 g l \sin \theta}=\sqrt{2 g h}\)

2) వాలుతలం వెంబడి పైకి చలించునపుడు :
ఎ) త్వరణం a = -g sin θ.
బి) u తొలివేగం అయితే వాలుతలం పైకి చేరటానికి పట్టేకాలం t = \(\frac{u}{g \sin \theta}\)
(కాని పైకి చేరటానికి కావలసిన కనీస తొలివేగం u = \(\sqrt{2 g l \sin \theta}\).

→ లాన్ లర్ చలనము :
1) m ద్రవ్యరాశి గల లాన్లర్ను F బలముతో లాగునపుడు
ఎ) క్షితిజ సమాంతర అంశ బలము F_x = F cos θ.
బి) లంబ ప్రతిచర్య N = mg – F sin θ.

2) F బలంతో తోసినప్పుడు
సి) క్షితిజ సమాంతర అంశ బలము F_x = F cos θ
డి) లంబ ప్రతిచర్య N = mg + F sin θ.