TS Inter 1st Year Maths 1B Differentiation Important Questions Short Answer Type

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Differentiation Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Differentiation Important Questions Short Answer Type

Question 1.
Find the derivative of x³ from the first principle. [Mar. ’15 (TS), ’98]
Solution:
Let f(x) = x³ then f(x + h) = (x + h)³

Question 2.
Find the derivative of \(\sqrt{x+1}\) from the first principle. [Mar. ’12, ’05]
Solution:

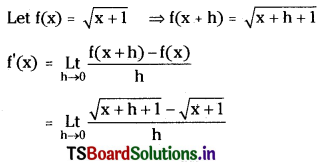
Question 3.
Find the derivative of sin 2x from the first principle. [B.P. May ’15 (TS), ’10, ’91; Mar. ’02; Mar. ’18 (AP)]
Solution:
Let f(x) = sin 2x
f(x + h) = sin 2(x + h) = sin 2x + 2h

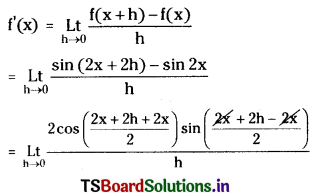
Question 4.
Find the derivative of cos ax from the first principle. [May ’14; Mar. ’13 (old), ’13, ’11, ’09]
Solution:
Let f(x) = cos ax
f(x + h) = cos a(x + h) = cos(ax + ah)

Question 5.
Find the derivative of tan 2x from the first principle. [Mar. ’14, ’13 (old). ’05; May ’13. ’11; May ’15 (AP)]
Solution:
Let f(x) = tan 2x
f(x + h) = tan 2(x + h) = tan (2x + 2h)

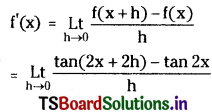
Question 6.
Find the derivative of sec 3x from the first principle. [Mar. ’16 (AP), ’12, ’08]
Solution:
Let f(x) = sec 3x
f(x + h) = sec 3(x + h) = sec (3x + 3h)

Question 7.
Find the derivative of x sin x from the first principle. [Mar. ’18, ’15 (AP), ’10; May ’09]
Solution:
Let f(x) = x sin x
f(x + h) = (x + h) sin (x + h)

Question 8.
Find the derivative of cos²x from the first principle. [Mar. ’19 (TS); May ’08, ’04]
Solution:

Question 9.
Find the derivative of log x from the first principle. [Mar. ’03]
Solution:
Given, f(x) = log x
Now, f(x + h) = log (x + h)

∴ f is differentiable at x and f'(x) = \(\frac{1}{x}\)

Question 10.
Prove that \(\frac{d}{d x} \mathbf{u v}=\mathbf{u} \frac{d v}{d x}+v \frac{d u}{d x}\). [May ’97]
(Or)
If f, g are two differentiable functions at x then fg is differentiable at x. then show that (fg)’ (x) = f(x) g'(x) + g(x) f'(x).
Solution:
Since f and g are two differentiable functions at x, f'(x) and g'(x) exist.


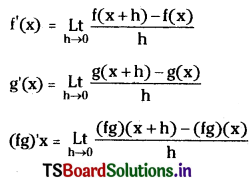
= f(x + 0) . g'(x) + g(x) . f'(x)
= f(x) . g'(x) + g(x) . f'(x)
∴ fg is differentiable at x and (fg)’ (x) = f(x) g'(x) + g(x) f'(x).

Question 11.
Prove that \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\). [May ’04, ’98]
(Or)
If f, g are two differentiable functions at x and g(x) ≠ 0 then \(\frac{f}{g}\) is differentiable at x, then show that \(\left(\frac{f}{g}\right)^{\prime}(x)=\frac{g(x) f^{\prime}(x)-f(x) g^{\prime}(x)}{[g(x)]^2}\)
Solution:
Since f, g are differentiable at x and f'(x), g'(x) exists.

Question 12.
Find the derivative of \(\cos ^{-1}\left(\frac{b+a \cos x}{a+b \cos x}\right)\), (a > 0, b > 0). [May ’09]
Solution:
Let y = \(\cos ^{-1}\left(\frac{b+a \cos x}{a+b \cos x}\right)\)
Differentiating on both sides with respect to ‘r’ to ‘x’

Question 13.
If xy = ex-y, then show that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)^2}\). [Mar. ’08, ’07, ’96, ’88; May ’00, ’95]
Solution:
Given, x^y = e^x-y
Taking logarithms on both sides,
log(x^y) = log(e^x-y)
y log x = (x – y) log e
y log x = x – y
y + y log x = x
y(1 + log x) = x
y = \(\frac{x}{1+\log x}\)
Differentiating on both sides with respect to ‘x’

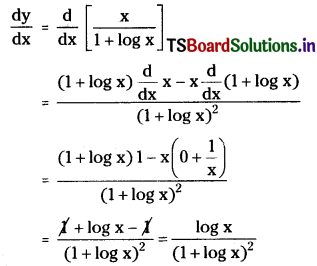
Question 14.
If sin y = x sin (a + y), then show that \(\frac{d y}{d x}=\frac{\sin ^2(a+y)}{\sin a}\). [Mar. ’95, May ’87]
Solution:
Given, sin y = x sin (a + y)
x = \(\frac{\sin y}{\sin (a+y)}\)
Differentiating on both sides with respect to ‘x’.

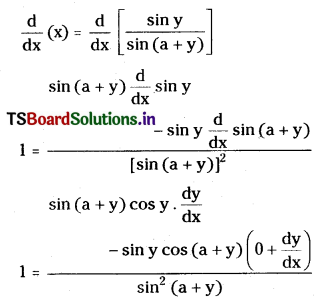
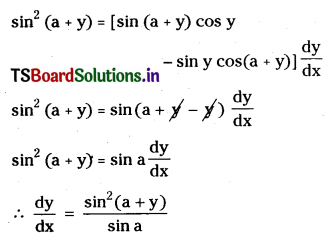
Question 15.
Differentiate \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\) with respect to \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\). [Mar. ’13 (Old); May ’04, ’95]
Solution:

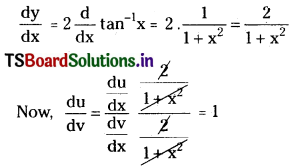
Question 16.
Find the derivative of tan^-1(sec x + tan x). [May ’97]
Solution:

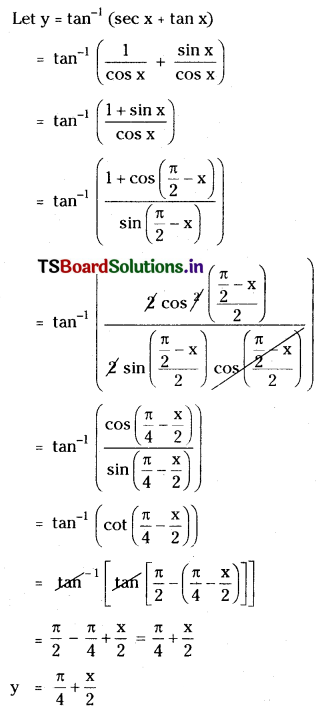
Question 17.
If x = a (cos t + t sin t), y = a (sin t – t cos t) then find \(\frac{d \mathbf{y}}{d \mathbf{x}}\). [Mar. ’16 (TS), May ’08, ’00, ’93]
Solution:
Given that x = a(cos t + t sin t)
Differentiating on both sides with respect to ‘t’.

Question 18.
If x = a(t – sin t), y = a(1 + cos t) then find \(\frac{d^2 \mathbf{y}}{\mathbf{d x}^2}\). [May ’02]
Solution:
Given, x = a(t – sin t)
Differentiating on both sides with respect to ‘x’.
\(\frac{\mathrm{dx}}{\mathrm{dt}}\) = a(1 – cos t)
y = a(1 + cos t)
Differentiating on both sides with respect to ‘x’.
\(\frac{\mathrm{dy}}{\mathrm{dt}}\) = a(0 – sin t) = -a sin t

Question 19.
Find the second order derivative of \(\tan ^{-1}\left(\frac{1+x}{1-x}\right)\). [May ’12]
Solution:
Given, f(x) = \(\tan ^{-1}\left(\frac{1+x}{1-x}\right)\)
Differentiating on both sides with respect to ‘x’.

Again differentiating on both sides with respect to ‘x’.
f”(x) = \(-\frac{1}{\left(1+x^2\right)^2}(0+2 x)=\frac{-2 x}{\left(1+x^2\right)^2}\)

Question 20.
If y = ae^nx + be^-nx, then prove that y” = n2y. [Mar. ’15 (AP); May ’14]
Solution:
Given y = ae^nx + be^-nx ………(1)
Differentiating on both sides with respect to ‘x’.
y’ = ae^nx (n) + be^-nx (-n)
y’ = n ae^nx – n be^-nx
again differentiating on both sides with respect to ‘x’
y” = na . e^nx (n) – n be^-nx (-n)
= n² ae^xnx + n2be^-nx
= n² (ae^nx + be^-nx)
= n²y (∵ from 1)
∴ y” = n²y

Question 21.
If y = axⁿ⁺¹ + bx^-n then prove that x²y¹¹ = n(n + 1)y. [May ’10; Mar. ’06]
Solution:
Given, y = axⁿ⁺¹ + bx^-n …….(1)
Differentiating on both sides with respect to ‘x’.
y¹ = a . (n + 1) x^n+1-1 + b(-n) x^-n-1
= a(n + 1)xⁿ – bn . x^-n-1
Again differentiating on both sides with respect to ‘x’.

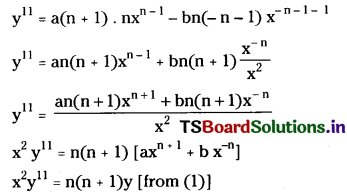
Question 22.
If y = a cos x + (b + 2x) sin x, then prove that y¹¹ + y = 4 cos x. [May ’07]
Solution:
Given, y = a cos x + (b + 2x) sin x ………(1)
Differentiating on both sides with respect to ‘x’.
y¹ = a(-sin x) + (b + 2x) cos x + sin x (0 + 2 . 1)
y¹ = -a sin x + (b + 2x) cos x + 2 sin x
Again differentiating of both sides with respect to ‘x’.
y¹¹ = -a cos x + (b + 2x) (-sin x) + cos x (0 + 2 . 1) + 2 cos x
= -a cos x – (b + 2x) sin x + 2 cos x + 2 cos x
= -a cos x – (b + 2x) sin x + 4 cos x
= -[a cos x + (b + 2x) sin x] + 4 cos x
y¹¹ = -y + 4 cos x [∵ from (1)]
y¹¹ + y = 4 cos x

Question 23.
If ax² + 2hxy + by² = 1 then prove that \(\frac{d^2 y}{d x^2}=\frac{h^2-a b}{(h x+b y)^3}\). [Mar. ’08; May ’97]
Solution:
Given, ax² + 2hxy + by² = 1 ……..(1)
Differentiating on both sides with respect to ‘x’.

Question 24.
Find the derivative of cot x from the first principle. [Mar. ’19, ’17 (AP)]
Solution: