TS Inter 1st Year Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(a)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(a)

Question 1.
Find the acute angle between the pair of lines represented by the following equations. (V.S.A.Q.)
(i) x² – 7xy + 12y² = 0
Answer:
x² – 7xy + 12y² = 0
Comparing with ax² + 2hxy + by²
We get a = 1, b = 12, h = \(\frac{-7}{2}\)

(ii) y² – xy – 6x² = 0
Answer:
y² – xy – 6x² = 0
a = – 6, h = – \(\frac{1}{2}\), b = 1

(iii) (x cos α – y sin α)² = (x² + y²) sin² α
Answer:
(x cos α – y sin α)² = (x² + y²) sin2 α
x² cos² α + y² sin² α – 2xy cos α sin α
= x² sin² α + y² sin² α
= x² (cos² α – sin² α) – 2xy cos α sin α = 0
⇒ x² cos 2α – xy sin 2α = 0
Here a = cos 2α, b = 0, h = –\(\frac{1}{2}\) sin 2α
∴ tan θ = \(\left|\frac{2 \sqrt{h^2-a b}}{a+b}\right|\) = \(\left|\frac{2 \sqrt{\frac{1}{4} \sin ^2 2 \alpha}}{\cos 2 \alpha}\right|\)
= tan 2α
∴ θ = 2α

(iv) x² + 2xy cot α – y² = 0
Answer:
x² + 2xy cot α – y² = 0
Here a = 1, b = – 1, h = cot α
tan θ = \(\left|\frac{2 \sqrt{h^2-a b}}{a+b}\right|\) = \(\left|\frac{2 \sqrt{\cot ^2 \alpha+1}}{0}\right|\) = ∞
∴ θ = \(\frac{\pi}{2}\)

II.
Question 1.
Show that the following pairs of straight lines have the same set of angular bisectors (that is they are equally inclined to each other) (S.A.Q.)
(i) 2x² + 6xy + y² = 0
4x² + 18xy + y² = 0
(ii) a²x² + 2h(a + b)xy + b²y² = 0
ax² + 2hxy + by² = 0, a + b ≠ 0
(iii) ax² + 2hxy + by² + λ(x² + y²) = 0 (λ ∈ R)
ax² + 2hxy + by² = 0
Answer:

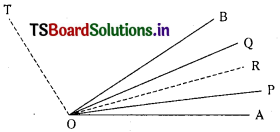
(i) Given equation 2x² + 6xy + y² = 0 represents combined equation of OA and OB.
Equation of pair of bisectors is
3(x² – y²) = (2 – 1)xy
⇒ 3(x² – y²) = xy ………………. (1)
Combined equation of OP and OQ is
4x² + 18xy + y² = 0
Equation to the pair of bisectors is
9(x² – y²) = (4 – 1)xy
⇒ 9(x² – y²) = 3xy
⇒ 3(x² – y²) = xy ………………… (2)
(1) and (2) denote the same lines.
∴ OA, OB and OP, OQ are inclined to each other. OR and OT are angular bisectors.

(ii) Given equation is a²x² + 2h(a + b)xy + b²y² = 0
represents combined equation of OA, OB.
∴ Equation to the pair of bisectors is
h(a + b) (x² – y²) = (a² – b²) xy
⇒ h(a + b) (x² – y²) = (a – b) (a + b) xy
⇒ h(x² – y²) = (a – b)xy …………………. (1)
Combined equation of OP, OQ is
ax² + 2hxy + by² = 0
Equation to the pair of bisectors is
\(\frac{x^2-y^2}{a-b}=\frac{x y}{h}\)
⇒ h(x² – y²) = (a – b)xy ………………….. (2)
(1), (2) represent the same equation.
Hence the pairs of lines have the same set of angular bisectors.

(iii) Equation to the pair of bisectors of the equation
ax² + 2hxy + by² + λ(x² + y²) = 0
⇒ x²(a + λ) + 2hxy + y²(b + λ) = 0 is

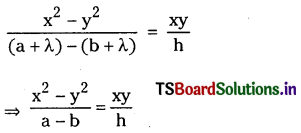
⇒ h(x² – y²) – xy(a – b) = 0 ………………. (1)
Equation to the pair of bisectors of
ax² + 2hxy + by² = 0 is \(\frac{x^2-y^2}{a-b}=\frac{x y}{h}\)
⇒ h(x² – y²) – xy(a – b) = 0
(1), (2) represent the same equation.
Hence the pairs of lines have the same set of angular bisectors.

Question 2.
Find the value of h, if the slopes of the lines represented by 6x² + 2hxy + y² = 0 are in the ratio 1 : 2. (S.A.Q.)
Answer:
Combined equation of the lines is
6x² + 2hxy + y² = 0
Suppose the slopes of two lines represented by the above equation be m₁ and m₂.
Then m₁ + m₁ = \(\frac{-2 h}{1}\), m₁m₂ = 6
Given that m₁ : m₂ = 1 : 2 ⇒ \(\frac{\mathrm{m}_1}{\mathrm{~m}_2}=\frac{1}{2}\)
⇒ m₂ = 2m₁
∴ 3m₁ = – 2h; 2m₁² = 6

Question 3.
If ax² + 2hxy + by² = 0 represents two straight lines such that the slope of one line is twice the slope of the other. Prove that 8h² = 9ab. (S.A.Q.)
Answer:
Combined equation of the lines is
ax² + 2hxy + by² = 0 ……………… (1)
Suppose y = m₁x and y = m₂x are the lines represented by (1).

Question 4.
Show that the equation of the pair of straight lines passing through the origin and making an angle of 30° with the line 3x – y – 1 = 0 is 13x² + 12xy – 3y² = 0. (S.A.Q.)
Answer:

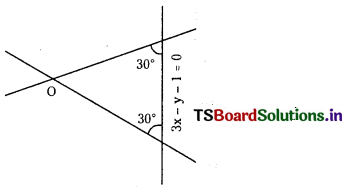
Given equation of the straight line is
3x – y – 1 = 0 ………………….. (1)
Let the slope of (1) be m₁. Then m₁ = 3 Suppose the slope of the line passing through the origin making an angle 30° be ‘m’.
∴ Equation of the line passing through the origin with slope ’m’ is y = mx and
m = \(\frac{\mathrm{y}}{\mathrm{x}}\) …………………… (2)
Suppose angle between lines (1) and (2) be θ then tan θ =

⇒ 9m² + 6m + 1 = 3m² – 18m + 27
⇒ 6m² + 24m – 26 = 0
⇒ 3m² + 12m – 13 = 0
⇒ \(3\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^2+12\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\) – 13 = 0 [∵ From (2)]
⇒ 3y² + 12xy – 13x² = 0
⇒ 13x² – 12xy – 3y² = 0

Question 5.
Find the equation to the pair of straight lines passing through the origin and making an acute angle a with the straight line x + y + 5 = 0. (SA.Q.)
Answer:
Given equation of the line is x + y + 5 = 0 ………………… (1)

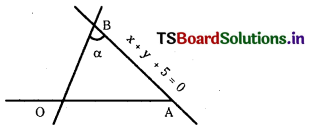
Let the slope of the given line be m₁ then m₁ = – 1. If m is the slope of the line making angle a with the line (1), then the equation of the line passing through the origin is
y = mx ⇒ m = \(\frac{y}{x}\) ………………….. (2)
If α is the angle between the lines (1) ans (2)

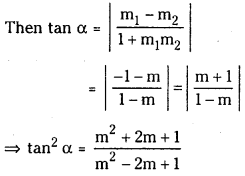
⇒ (m² – 2m + 1)tan² α = m² + 2m + 1
⇒ m²(1 – tan² α) + 2m(1 + tan² α) + (1 – tan²α)= 0 ……………… (3)
From (2) we have
\(\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^2\) (1 – tan² α) + 2\(\frac{y}{x}\)(1 + tan² α)
+ (1 – tan² α) = 0
⇒ (1 – tan² α)y² + 2xy(1 + tan² α) + x²(1 – tan² α) = 0 …………….. (4)

Case (i): If α = \(\frac{\pi}{4}\) then from (4)
2xy (1 + 1) = 0
⇒ 4xy = 0 ⇒ xy = 0

Case (ii): If α ≠ \(\frac{\pi}{4}\) then
x²+ 2xy\(\left(\frac{1+\tan ^2 \alpha}{1-\tan ^2 \alpha}\right)\) + y² = 0
⇒ x²+ 2xy\(\frac{1}{\cos 2 \alpha}\) + y² = 0
⇒ x²+ 2xy sec 2α + y² = 0
So if α ≠ \(\frac{\pi}{4}\) then the combined equation of lines is x² + 2xy sec 2α + y² = 0 and if α = \(\frac{\pi}{4}\) then the equation is xy = 0.

Question 6.
Show that the straight lines represented by (x + 2a)² – 3y² = 0 and x = a form an equilateral triangle. (S.A.Q.)
Answer:

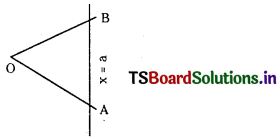
Given equation of pair of lines is
(x + 2a)² – 3y² = 0
⇒ (x + 2a + √3 y) (x + 2a – √3y) = 0
Equation of OA is x + √3 y + 2a = 0 ………………. (1)
Equation of OB is x – √3y + 2a = 0 ………………. (2)
Equation of AB is x – a = 0 ………………… (3)
Use the formula for
cos θ = \(\left|\frac{a_1 a_2+b_1 b_2}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\right|\)
Between (1) and (3) lines
cos ∠OAB = \(\frac{|1+0|}{\sqrt{1+3} \sqrt{1}}=\frac{1}{2}\) = cos 60°
∴ ∠OAB = 60°
Similarly angle between (2) and (3) is
cos ∠OBA = \(\frac{|1+0|}{\sqrt{1+3} \sqrt{1}}=\frac{1}{2}\) = cos 60°
∴ ∠OBA = 60°
∴ ∠AOB = 180° – (∠OBA + ∠OAB)
= 180° – (60° + 60°) = 60°
∴ ∆ AOB is an equilateral triangle.

Question 7.
Show that the pair of bisectors of the angles between the straight lines (ax + by)2 = c (bx – ay)2, c > 0 are parallel and perpen¬dicular to the line ax + by + k = 0.(S.A.Q.)
Answer:
Combined equation of the given lines is
(ax + by)² = c(bx – ay)²
⇒ a²x² + 2abxy + b²y²
= c(b²x² – 2abxy + a²y²)
⇒ (a² – cb²)x² + 2ab(1 + c) xy + (b² – ca²)y² = 0 ……………… (1)
Using the standard equation of bisectors,
(x² – y²)h = xy(a – b)
Equation of bisectors of angles between the lines (1) is
(x² – y²) ab (1 + c) = (a² – cb² – b² + ca²)xy
= [a² – b² + c(a² – b²)]xy
= (a² – b²) (1 + c) xy
⇒ ab(x² – y²) = (a² – b²)xy
⇒ ab(x² – y²) – (a² – b²)xy = 0
⇒ abx² – aby² – a²xy + b²xy = 0
⇒ ax(bx – ay) + by (bx – ay) = 0
⇒ (ax + by) (bx – ay) = 0
Hence the equation of bisectors represented by (1) are ax + by = 0 ………………. (2)
bx – ay = 0 ………………….. (3)
Given equation of the line is
ax + by + k = 0 …………………… (4)
ax + by = 0 is parallel to ax + by + k = 0 and bx – ay = 0 is perpendicular to ax + by + k = 0.

Question 8.
The adjacent sides of a parallelogram are 2x² – 5xy + 3y² = 0 and one diagonal is x + y + 2 = 0. Find the vertices and the other diagonal. (S.A.Q.)
Answer:

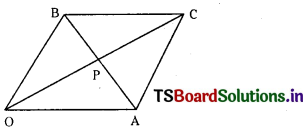
The given equation is
2x² – 5xy + 3y² = 0 ……………… (1)
Which represent lines OA and OB respectively in the figure.
Equation of AB is x + y + 2 = 0
⇒ y = – (x + 2) ………………. (2)
∴ From (1)
⇒ 2x² + 5x(x + 2) + 3(x + 2)² = 0
⇒ 2x² + 5x² + 10x + 3(x² + 4x + 4) = 0
⇒ 10x² + 22x +12 = 0
⇒ 5x² + 11x + 6 = 0
⇒ 5x² + 5x + 6x + 6 = 0
⇒ 5x(x + 1) + 6(x + 1) = 0
⇒ (x + 1) (5x + 6) = 0
⇒ x = – 1 or x = \(\frac{-6}{5}\)
Also from (2), y = -(x + 2)
x = -1 ⇒ y = – 1

Question 9.
Find the centroid and the area of the triangle formed by the following lines.
(i) 2y² – xy – 6x² = 0, x + y + 4 = 0
(ii) 3x² – 4xy + y² = 0, 2x – y = 6 (S.A.Q.)
Answer:
(i)

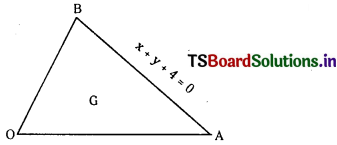
The equation 2y² – xy – 6x² = 0
represents combined equation of OA and OB and equation of AB is x + y + 4 = 0
⇒ y = – (x + 4) …………….. (2)
From (1) 2(x + 4)² + x(x + 4) – 6x² = 0
⇒ 2(x² + 8x + 16) + x² + 4x – 6x² = 0
⇒ 3x² – 20x – 32 = 0
⇒ 3x² – 20x – 32 = 0
⇒ (3x + 4) (x – 8) = 0
⇒ x = – \(\frac{4}{3}\)

Case (i): x = – \(\frac{4}{3}\)
∴ y = – (x + 4)
= – \(\left(-\frac{4}{3}+4\right)\) = – \(\frac{8}{3}\)
∴ Co-ordinates of A = \(\left(-\frac{4}{3},-\frac{8}{3}\right)\)

Case (ii): x = 8 ⇒ y = – (8 + 4) = – 12
∴ Co-ordinates of B = (8, -12)
Let G be the centroid of ∆OAB

(ii) The equation 3x² – 4xy + y² = 0 ……………… (1)
represents pair of lines OA and OB.
Equation of AB is 2x – y = 6
⇒ y = 2x – 6 ……………. (2)
From (1) 3x² – 4x(2x – 6) + (2x – 6)² = 0
⇒ 3×2² – 8x² + 24x + 4x² – 24x + 36 = 0
⇒ – x² + 36 = 0 ⇒ x² – 36 = 0
⇒ (x + 6) (x – 6) = 0 ⇒ x = 6 or – 6
If x = 6 ⇒ y = 12 – 6 = 6
∴ Co-ordinates of A = (6, 6)
x = – 6 ⇒ y = -12 – 6 = -18
∴ Co-ordinates of B = (-6, -18)
∴ Co-ordinates of G = \(\left(\frac{0+6-6}{3}, \frac{0+6-18}{3}\right)\)
= (0, -4)
∴ Area of ∆OAB = \(\frac{1}{2}\) |₁y₂ – x₂yi I
= \(\frac{1}{2}\) |6 (- 18) – (- 6)6|
= \(\frac{1}{2}\) |- 108 + 36| = \(\frac{1}{2}\) (72) = 36 sq. units.

Question 10.
Find the equation of the pair of lines intersecting at (2, -1) and (S.A.Q.)
(i) Perpendicular to the pair 6x² – 13xy – 5y² = 0 and
(ii) Parallel to the pair 6x² – 13xy – 5y² = 0
Answer:
Given equation 6x² – 13xy – 5y² = 0 represents lines OA and OB.
(i) Equation of the pair of lines through
(x₁, y₁) and perpendicular to ax² + 2hxy + by² = 0 is b(x – x₁)²] a(y – y₁)² = 0
⇒ -5(x – 2)² + 13 (x – 2) (y + 1) + 6(y + 1)² = 0
⇒ -5(x² – 4x + 4) + 13 (xy + x – 2y – 2) + 6(y² + 2y + 1) = 0
⇒ -5x² + 20x – 20 + 13xy + 13x – 26y – 26 + 6y² + 12y + 6 = 0
⇒ 5x² – 13xy – 6y² – 33x + 14y + 40 = 0

(ii) Equation of the pair of lines through (x₁, y₁) and parallel to ax² + 2hxy + by² = 0 is
a(x – x₁)² + 2h (x – x₁) (y – y₁) + b(y – y₁)² = 0
⇒ 6(x – 2)² – 13 (x – 2) (y + 1) – 5(y + 1)² = 0
⇒ 6(x² – 4x + 4) – 13 (xy – 2y + x – 2) – 5(y² + 2y + 1) = 0
⇒ 6x² – 13xy – 5y² – 37x + 16y + 45 = 0

Question 11.
Find the equation of the bisector of the acute angle between the lines (S.A.Q.)
3x – 4y + 7 = 0 and 12x + 5y – 2 = 0.
Answer:
Given equations of lines are
3x – 4y + 7 = 0 ……………….. (1)
12x + 5y – 2 = 0 ………………… (2)
The equation of bisectors of angles between

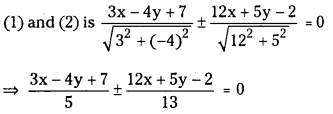
⇒ 13(3x – 4y + 7) ± 5(12x + 5y – 2) = 0
⇒ (39x – 52y + 91) ± (60x + 25y – 10) = 0
∴ (39x – 52y + 91) + (60x + 25y – 10) = 0
⇒ 99x – 27y + 81 = 0
⇒ 11x – 3y + 9 = 0 ………………….. (3)
Also (39x – 52y + 91) – (60x + 25y – 10) = 0
⇒ – 21x – 77y + 101 = 0
⇒ 21x + 77y – 101 = 0 ………………….. (4)
Let θ be the angle between (1) and (4) then

∴ (4) is an obtuse angled bisector then (3) will be the acute angled bisector.
∴ 11x – 3y + 9 = 0 is the acute angled bisector.

Question 12.
Find the equation of the bisector of the obtuse angle between the lines x + y – 5 = 0 and x – 7y + 7 = 0 (S.A.Q.)
Answer:
Given equations of lines are
x + y – 5 = 0 ………………. (1)
and x – 7y + 7 = 0 ………………….. (2)
The equation of bisectors of angles between (1) and (2) is

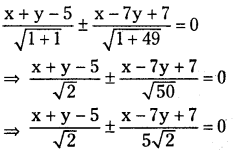
⇒ 5x + 5y – 25 ± (x – 7y + 7) = 0
(i) (5x + 5y – 25) + (x – 7y + 7) = 0
⇒ 6x – 2y – 18 = 0
⇒ 3x – y – 9 = 0 …………………. (3)
(ii) (5x + 5y – 25) – (x – 7y + 7) = 0
⇒ 4x + 12y – 32 = 0
⇒ x + 3y – 8 = 0 ……………… (4)
Let θ be the angle between (1) and (4)
Then

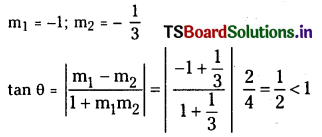
∴ (4) is an acute angle bisector and hence (3) is an obtuse angle bisector.
∴ 3x – y – 9 = 0 is the obtuse angle bisector.

III.
Question 1.
Show that the lines represented by (lx + my)² – 3 (mx – ly)² = 0 and lx + my + n = 0 form an equilateral triangle with area \(\frac{n^2}{\sqrt{3}\left(l^2+m^2\right)}\). (S.A.Q.)
Answer:
The equation (lx + my)² – 3(mx – ly)² = 0 represents combined equation of lines OA and OB.
∴ (l²x² + m²y² + 2lmxy) – 3(m²x² – 2lmxy + l²y²) = 0
⇒ x²(l² – 3m²) + 8lmxy + (m² – 3l²)y² = 0 ……………….. (1)
Angle between lines represented by (1) by the formula cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^2+4 h^2}}\)

∴ θ = 60° which is the angle between OA and OB,
∴ ∠AOB = 60°
Combined equation of the bisectors of OA
and OB is h(x² – y²) = (a – b)xy
⇒ 4lm(x² – y²) = (l² – 3m² – m² + 3l²) xy
⇒ 4lm(x² – y²) = 4 (l² – m²) xy
⇒ lmx² – (l² – m²) xy – lmy² = 0
⇒ (lx + my) (mx – ly) = 0
⇒ lx + my = 0 and mx – ly = 0
∴ The bisector mx – ly = 0 is perpendicular to AB whose equation is lx + my + n = 0
∴ ∠OBA = 60°
∴ OAB is an equilateral triangle,
p = length of the perpendicular from O to AB.
= \(\frac{|\mathrm{n}|}{\sqrt{l^2+\mathrm{m}^2}}\)
∴ Area of ∆OAB = \(\frac{\mathrm{p}^2}{\sqrt{3}}=\frac{\mathrm{n}^2}{\sqrt{3}\left(l^2+\mathrm{m}^2\right)}\) sq.units

Question 2.
Show that the straight lines represented by 3x² + 48xy + 23y² = 0 and 3x – 2y + 13 = 0 form an equilateral triangle of area \(\frac{13}{\sqrt{3}}\) = sq.units. (E.Q.)
Answer:
The equation 3x² + 48xy + 23y² = 0 ……………… (1)
represents lines OA, OB.
Equation of AB is 3x – 2y + 13 = 0 — (2)
From (1) we.can express the equation as
(9x² – 12xy + 4y²) – 3 (4x² + 9y² + 12xy) = 0
⇒ (3x – 2y)² – 3 (2x + 3y)² = 0
⇒ [(3x – 2y) + √3 (2x + 3y)] [(3x – 2y) – √3 (2x + 3y)] = 0
⇒ [(3 + 2√3)x + (3√3 – 2) y] [(3 – 2√3 ) x – (3√3 + 2) y] = 0
∴ Equation of OA is
(3 – 2√3 ) x + (3√3 – 2) y = 0 ………………… (3)
Equation of OB is
(3 – 2√3) x – (3√3 + 2) y = 0 ……………… (4)
Angle between (2) and (3) is cos θ

Question 3.
Show that the equation of the pair of lines bisecting the angles between the pair of bisectors of the angles between the pair of lines ax² + 2hxy + by² = 0 is (a – b) (x² – y²) + 4hxy = 0. (S.A.Q.)
Answer:
Equation of the given lines is
ax² + 2hxy + by² = 0
Equation of the pair of bisectors is
(x² – y²) h = (a – b) xy — (1)
hx² – hy² – (a – b) xy = 0
Equation to the pair of bisectors of (1) is
– \(\frac{(a-b)}{2}\) (x² – y²) = (h + h)xy
⇒ (a – b) (x² – y²) + 4hxy = 0
∴ Equation of the pair of bisectors of the pair of bisectors of lines ax² + 2hxy + by² = 0 is (a – b) (x² – y²) + 4hxy = 0

Question 4.
If one line of the pair of lines ax² + 2hxy + by² = 0 bisects the angle be-tween the coordinate axes, prove that (a + b)² = 4h². (S.A.Q.) (June ’04)
Answer:
The angular bisectors of the coordinate axes are y = x and y = – x
Case (i) : When y = x is one of the lines of
ax² + 2hxy + by² = 0 then
ax² + 2hx (x) + bx² = 0
⇒ a + 2h + b = 0 …………………. (1)
Case (ii) : When y = – x is the other line of
ax² + 2hxy + by² = 0 then
ax² + 2hx(-x) + bx² = 0
⇒ a – 2h + b = 0 ………………… (2)
From (1) and (2)
[(a + b) + 2h] [(a + b) – 2h] = 0
⇒ (a + b)² – 4h² = 0
⇒ (a + b)² = 4h²

Question 5.
If (α, β) is the centroid of the triangle formed by the lines ax² + 2hxy + by² = 0 and lx + my = 1, prove that (E.Q.)
\(\frac{\alpha}{b l-h m}=\frac{\beta}{a m-h l}=\frac{2}{3\left(b l^2-2 h l m+a m^2\right)}\)
Answer:

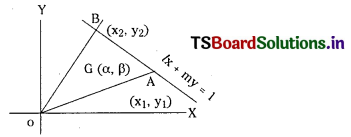
Combined equation of OA and OB is
ax² + 2hxy + by² = 0 …………………. (1)
Equation of AB is lx + my = 1 ……………………. (2)
⇒ my = 1 – lx
⇒ y = \(\frac{1-l \mathrm{x}}{\mathrm{m}}\) ……………………… (3)
From (1) ax² + 2hx \(\left(\frac{1-l x}{m}\right)\) + b\(\left(\frac{1-l x}{m}\right)^2\) = 0
⇒ am²x² + 2hmx (1 – lx) + b (1 – lx)² = 0
⇒ (am² – 2hml + bl²) x² + 2hmx – 2blx + b = 0
⇒ (am² – 2hml + bl²) x² + 2x (hm – bl) + b = 0
Let the coordinates of point of intersection of lines (1) with (2) be A (x₁, y₁) and B (x₂, y₂).
Then x₁ + x₂ = \(\frac{-2(\mathrm{hm}-\mathrm{b} l)}{\mathrm{am}^2-2 \mathrm{hm} l+\mathrm{b} l^2}\)
= \(\frac{2(\mathrm{~b} l-\mathrm{hm})}{\mathrm{am}^2-2 \mathrm{~h} / \mathrm{m}+\mathrm{b} l^2}\) …………………… (4)
A(x₁, y₁) and B(x₂, y₂) lies on (2)
∴ lx₁ + my₁ = 1
lx₂ + my₂ = 1
⇒ l(x₁ + x₂) + m (y₁ + y₂) = 2
⇒ m (y₁ + y₂) = 2 – l(x₁ + x₂)

Question 6.
Prove that the distance from the origin to the orthocentre of the triangle formed by the lines \(\frac{x}{\alpha}+\frac{y}{\beta}\) = 1 and ax² + 2hxy + by² = 0 is (α² + β²)^1/2 \(\left|\frac{(a+b) \alpha \beta}{a \alpha^2-2 h \alpha \beta+b \beta^2}\right|\).
Answer:

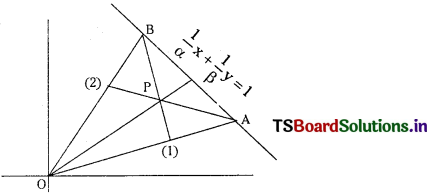
Let OA and OB be the lines through the origin denoted by ax² + 2hxy + by² = 0 given by
l₁x + m₁y = 0 ………………. (1)
l₂x + m₂y = 0 ……………… (2)
∴ (l₁x + m₁y) (l₂x + m₂y) = ax² + 2hxy + by²
∴ l₁l₂ = a, m₁m₂ = b, l₁m₂ + l₂m₁ = 2h
Given line is \(\frac{1}{\alpha}\) x + \(\frac{1}{\beta}\) y = 1
Solving (1) and (3) we get the coordinates of A

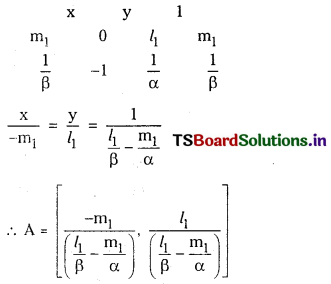
Let B be the point of intersection of (2) and (3) Let P be the orthocentre of ∆AOB.

⇒ l₂y (l₁α – m₁β) + αβl₁l₂
= m₂x (l₁α – m₁β) + αβm₁m₂
= m₂x (l₁α – m₁β) – l₂y (l₁α – m₁β)
= – αβl₁l₂ – αβm₁m₂

Question 7.
The straight line lx + my + n = 0 bisects an angle between the pair of lines of which one is px + qy + r = 0. Show that the other line is (px + qy + r) (l² + m²) – 2 (lp + mq) (lx + my + n) = 0. (E.Q.)
Answer:
Let (α, β) be any point on the bisector
lx + my + n = 0 and lα + mβ + n = 0 ……………… (1)
The other line passes through the intersection of px + qy + r = 0 and lx + my + n = 0. This will be of the form p + λq = 0.
⇒ (px + qy + r) + λ(lx + my + n) = 0 ………………. (2)
Given px + qy + r = 0 ………………….. (3)
is one of the lines in pair of lines. If (α, β) is a point on the bisector then its perpendicular distance from lines (2) and (3) are same.

Simplifying and squaring on both sides,
(p + λl)² + (q + λm)² = p² + q²
⇒ (p² + 2pλl + λ²l²) + (q² + 2q λm + λ²m²) = p² + q²
⇒ 2 λ (pi + qm) + λ² (l² + m²) = 0
∴ 2λ (pl + qm) = – λ² (l² + m²)
⇒ λ = – 2 \(\left(\frac{\mathrm{p} l+\mathrm{qm}}{l^2+\mathrm{m}^2}\right)\)
∴ From equation (2), the equation of other line is (px + qy + r) – \(\frac{2(\mathrm{p} l+\mathrm{qm})}{l^2+\mathrm{m}^2}\) (lx + my + n) = 0
⇒ (px + qy + r) (l² + m²) – 2 (lp + qm) (lx + my + n) = 0