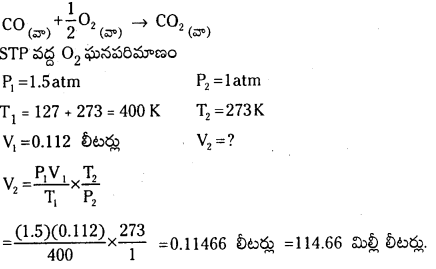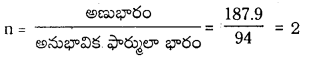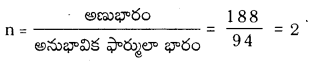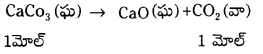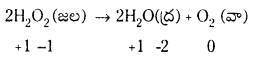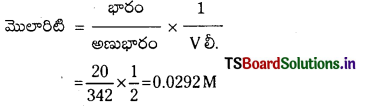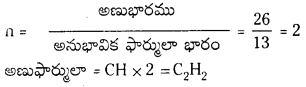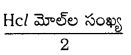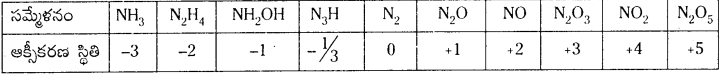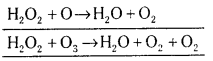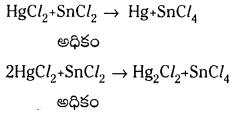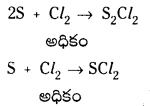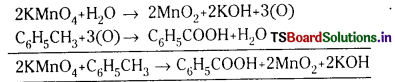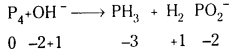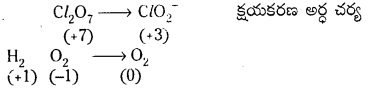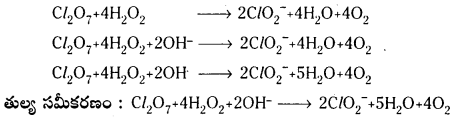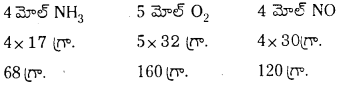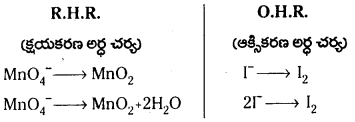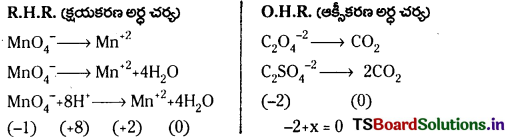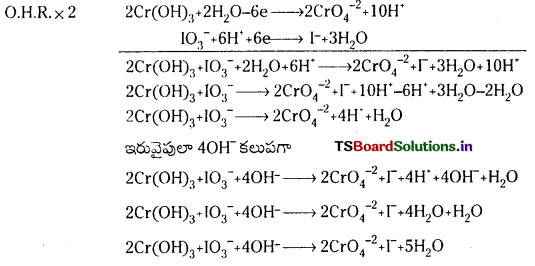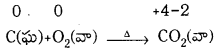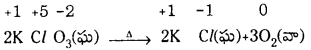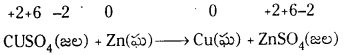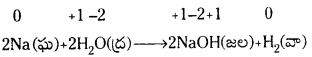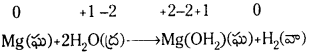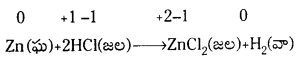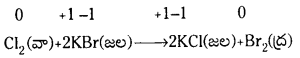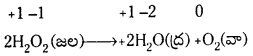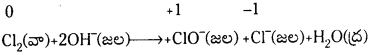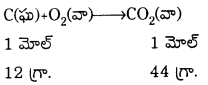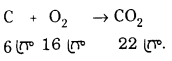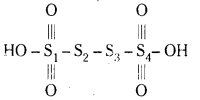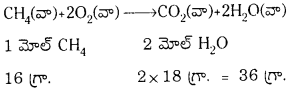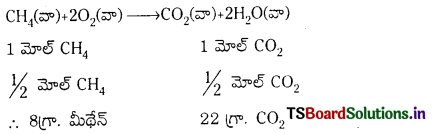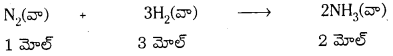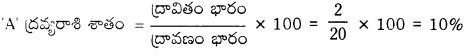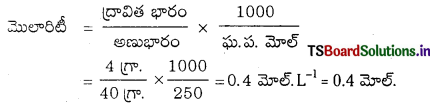Telangana TSBIE TS Inter 1st Year Chemistry Study Material 5th Lesson స్టాయికియోమెట్రీ Textbook Questions and Answers.
TS Inter 1st Year Chemistry Study Material 5th Lesson స్టాయికియోమెట్రీ
అత్యంత లఘు సమాధాన ప్రశ్నలు
ప్రశ్న 1.
540 గ్రాముల గ్లూకోజ్లో ఎన్ని మోల్ల గ్లూకోజ్ ఉంది?
జవాబు:

ప్రశ్న 2.
0.1 మోల్ సోడియం కార్బొనేటు భారాన్ని లెక్క కట్టండి.
జవాబు:
భారం = మోల్ల సంఖ్య × గ్రా. అణుభారం = 0.1 × 106 = 10.6 గ్రా.

ప్రశ్న 3.
5.23 గ్రా.ల గ్లూకోజ్లో ఎన్ని అణువులు ఉంటాయి?
జవాబు:
అణువుల సంఖ్య = మోల్ల సంఖ్య × 6.023 × 1023
= \(\frac{5.23}{180}\) × 6.023 × 1023
= 1.75 × 1022 అణువులు
ప్రశ్న 4.
S.T.P. వద్ద 1.12 × 10-7 CC ల వాయువులో ఉండే అణువుల సంఖ్యను లెక్కించండి.
జవాబు:
అణువుల సంఖ్య = \(\frac{1.12 \times 10^{-7}}{22.4 \times 10^3}\) × 6.023 × 1023
= \(\frac{11.2}{22.4}\) × 6.023 × 1022 × 10-3 × 10-7
= 3.01 × 1012 మోల్ ల
గమనిక : మోల్ల సంఖ్య =
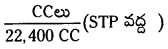
ప్రశ్న 5.
ఒక సమ్మేళనం అనుభావిక ఫార్ములా CH2O. దాని అణుభారం 90. ఆ సమ్మేళనం అణు ఫార్ములాను కనుక్కోండి.
జవాబు:
అనుభావిక ఫార్ములా భారం = 12 +2+16=30
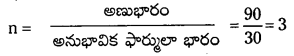
అణుఫార్ములా = 3 × అనుభావిక ఫార్ములా
= 3 × CH2O = C3H6O3
ప్రశ్న 6.
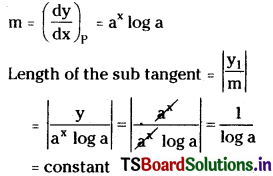
కింది సమీకరణాన్ని ఆక్సిడేషన్ సంఖ్య పద్ధతిలో తుల్యం చేయండి. (March 2013)
జవాబు:
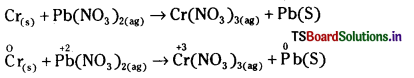
ఆక్సీకరణ ప్రక్రియ 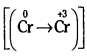 లో మార్పు 3 యూనిట్లు క్షయకరణ ప్రక్రియ [(pb+2 → Pb0)] లో మార్పు 2 యూనిట్లు. ఆక్సీకరణ ప్రక్రియలో ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పు, క్షయకరణ ప్రక్రియలో వచ్చిన ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పుకు సమానం చేయాలి. తగిన సంఖ్యలతో గుణించాలి.
లో మార్పు 3 యూనిట్లు క్షయకరణ ప్రక్రియ [(pb+2 → Pb0)] లో మార్పు 2 యూనిట్లు. ఆక్సీకరణ ప్రక్రియలో ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పు, క్షయకరణ ప్రక్రియలో వచ్చిన ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పుకు సమానం చేయాలి. తగిన సంఖ్యలతో గుణించాలి.
2Cr + 3Pb(NO3)2(ag) → 2Cr(NO3)3(ag) + 3Pb(s)
ప్రశ్న 7.
0.795 గ్రా.ల CuO ని Cu, H2O లుగా క్షయకరణం చేయడానికి STP వద్ద ఘ.ప. H2 అవసరం అవుతుంది.
జవాబు:
CuO, H2 ల మధ్య చర్య CuO + H2 → Cu + H2O
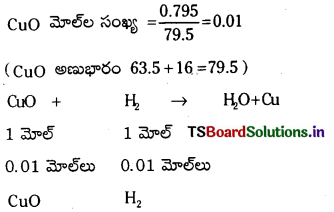
0.01 మోల్ల CuO ను క్షయకరణం చేయడానికి 0.01 మోల్ల H2 అవసరం.
STP వద్ద ఘనపరిమాణం = మోల్ల సంఖ్య × 22.4 లీ. = 0.01 × 22.4 లీ. = 0.224 లీ.
ప్రశ్న 8.
100 ml ల ఎసిటిలీన్ ని పూర్తిగా దహనం చేయడానికి కావలసిన O2 ఘనపరిమాణాన్ని STP వద్ద లెక్కకట్టండి.
జవాబు:

22,400 మి.లీ. ఎలిటిలీన్ ను దహనం చేయడానికి STP వద్ద అవసరమయ్యే ఆక్సిజన్ \(\frac{5}{2}\) × 22,400 మి.లీ.
100mlల ఎసిటిలీన్ (STP వద్ద) దహనం చేయడానికి అవసరమయ్యే ఆక్సిజన్ = \(\frac{100 \mathrm{ml}}{22,400 \mathrm{ml}}\) × \(\frac{5}{2}\) × 22,400 మి.లీ.
= \(\frac{500}{2}\) మి.లీ. = 250 మి.లీ.

ప్రశ్న 9.
ప్రస్తుత కాలంలో ఎలక్ట్రాన్ సాంద్రత తగ్గుదలను ఆక్సీకరణం అనీ, ఎలక్ట్రాన్ సాంద్రత పెరగడాన్ని క్షయకరణం అనీ అంటారు. దీనిని మీరు సమర్ధించండి.
జవాబు:
H2 + Cl2 → 2Hcl ఈ చర్యలో ఎలక్ట్రాన్ బదిలీ లేదు. కానీ క్లోరిన్ అధిక ఋణవిద్యుదాత్మకత వల్ల క్లోరిన్ వద్ద ఎలక్ట్రాన్ సాంద్రత పెరుగుతుంది. హైడ్రోజన్ వద్ద ఎలక్ట్రాన్ సాంద్రత తగ్గుతుంది. అందువల్ల క్లోరిన్ క్షయకరణం చెందినట్టు, హైడ్రోజన్ ఆక్సీకరణం చెందినట్టు పరిగణించవచ్చు.
ప్రశ్న 10.
ఆక్సీకరణ – క్షయకరణ భావం అంటే ఏమిటి? ఉదాహరణ ఇవ్వండి.
జవాబు:
CuSO4 (జ. ద్రా.) + Zn (ఘ) → Zn SO4 (ద్ర) Cu (ఘ) (లేదా) Cu++ + Zn → Zn++ + Cu
ఈ చర్యలో Cu++ ఆక్సీకరణ సంఖ్య “+2” నుండి “0” కు తగ్గింది. “Zn” అక్సీకరణ సంఖ్య “0” నుండి “+2” కి పెరిగింది. ఆక్సీకరణ సంఖ్యలో పెరుగుదలను ఆక్సీకరణమనీ, తగ్గుదలను క్షయకరణమనీ భావిస్తారు.
ఈ చర్యలో “Zn” Zn++. గా ఆక్సీకరణ చెందింది.
Cu++, Cu గా క్షయకరణం చెందింది.
ప్రశ్న 11.
సోడియమ్ సల్ఫేట్ (Na2SO4) లోని వివిధ మూలకాల ద్రవ్యరాశి శాతాలను గణించండి.
జవాబు:
Na2 SO4 అణుభారం = 2 (23) + 32 + 16(4) = 46 + 32 + 64 = 142 gms
సోడియం ద్రవ్యరాశి శాతం = \(\frac{100}{142}\) × 46 = 32.38%
సల్ఫర్ ద్రవ్యరాశి శాతం = \(\frac{100}{142}\) × 32 = 22.54%
ఆక్సిజన్ ద్రవ్యరాశి శాతం = \(\frac{100}{142}\) × 64 = 45.08%
ప్రశ్న 12.
సార్థక అంకెలు అంటే మీరు ఏమి చెబుతారు?
జవాబు:
ప్రాయోగిక లేదా సిద్ధాంత రీత్యా రాబట్టిన విలువల్లో అనిశ్చితత్వం ఉంటుంది. దానిని సార్థక అంకెలతో సూచిస్తారు. ఖచ్చితంగా తెలిసిన అర్థవంతమైన అంకెలను సార్థక అంకెలు అంటారు. ఒక సంఖ్యలోని అనిశ్చితత్వాన్ని దానికి కొన్ని అంకెలు రాసిన తర్వాత చివరి అంకె అనిశ్చితమై ఉంటుంది. ఈ విధంగా ఒక ప్రయోగ విలువను 11.2ml అని రాస్తే అందులో పదకొండు నిశ్చయంగా తెలిసింది. చివరి అంకె రెండు అనిశ్చితమైనది. ఇందులో అనిశ్చితత్వం ±1 ఉంటుంది. ప్రత్యేకించి చెబితే తప్ప ఆఖరి అంకెలో అనిశ్చితత్వం ±1 ఉంటుందని అర్థం చెప్పుకోవాలి.
ప్రశ్న 13.
కాంతివేగం 3.0 × 108m.s-1 అయితే 2 నానో సెకండ్లలో అది ప్రయాణించే దూరాన్ని లెక్కించండి.
జవాబు:
కాంతి ప్రయాణించిన దూరం = కాంతివేగం × ప్రయాణించిన కాలం
= 3 × 108 × 2 × 10-9 = 0.6 మీటర్లు
కావున కాంతి 2 నానో సెకండ్లలోనూ 0.6 మీటర్ల దూరం ప్రయాణిస్తుంది.
లఘు సమాధాన ప్రశ్నలు
ప్రశ్న 14.
సోడియంకార్బొనేట్ తయారీ నెలకు సుమారు 424 × 106 g. మిథైల్ ఆల్కహాల్ 320 × 106 g. అయితే ఏది ఎక్కువ మోల్లు తయారవుతుంది?
జవాబు:
నెలలో తయారైన సోడియం కార్బొనేట్ మోల్ సంఖ్య = \(\frac{424 \times 10^6}{106}\) = 4 × 106
నెలలో తయారైన మిథైల్ ఆల్కహాల్ మోత్ల సంఖ్య = \(\frac{320 \times 10^6}{32}\) = 107
కావున తయారయ్యే మిథైల్ ఆల్కహాల్ మోల్ల సంఖ్య ఎక్కువ.
ప్రశ్న 15.
1.5 atm పీడనం, 1270ల C వద్ద 0.112 లీటర్ల O2 పూర్తిగా చర్య జరిపి CO2 ఏర్పడడానికి STP వద్ద CO ఘనపరిమాణం కనీసం ఎంత కావాలి?
జవాబు:
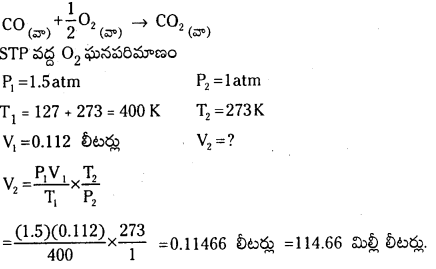
సమీకరణం ప్రకారం
కావల్సిన CO ఘనపరిమాణం 2 × O2 ఘనపరిమాణం = 114.66 × 2 = 229.32 మిల్లీ లీటర్లు.
ప్రశ్న 16.
కర్బన సమ్మేళనంలోని మూలకాల రసాయన విశ్లేషణ చేశారు. భారాత్మకంగా వాటి సంఘటన శాతాలు కింది విధంగా ఉన్నాయి. కార్బన్ 10.06%, హైడ్రోజన్ = 0.84%, క్లోరిన్ = 89.10% సమ్మేళనం అనుభావిక ఫార్ములాను కనుక్కోండి.
జవాబు:
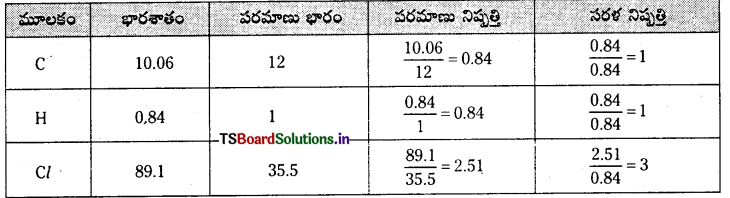
అనుభావిక ఫార్ములా = CHCl3
ప్రశ్న 17.
ఒక కర్బన సమ్మేళనాన్ని విశ్లేషించగా కింది సంఘటన శాతాలను ఇచ్చింది. కార్బన్ 14.5%, హైడ్రోజన్ 1.8%, క్లోరిన్ 64.46%, ఆక్సిజన్ 19.24% అయితే సమ్మేళనం అనుభావిక ఫార్ములా కనుక్కోండి.
జవాబు:
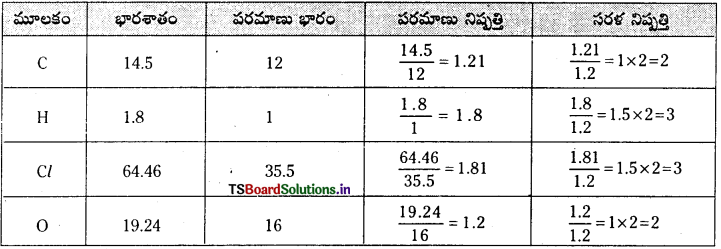
అనుభావిక ఫార్ములా = C2H3Cl3O2
ప్రశ్న 18.
కింది సంఘటన శాతం ఉన్న సమ్మేళనపు అనుభావిక ఫార్ములాను కనుక్కోండి. పొటాషియం K = 26.57%, క్రోమియం Cr = 35.36%, ఆక్సిజన్ (O) 38.07% [K, Cr, O ల పరమాణు భారాలు వరుసగా 39, 52, 16 ఉంటాయి ] అనుభావిక ఫార్ములా కనుక్కోండి.
జవాబు:
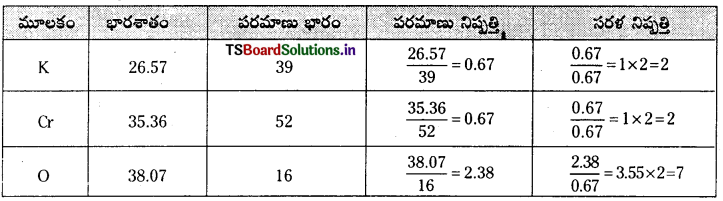
అనుభావిక ఫార్ములా = K2 Cr2 O7
ప్రశ్న 19.
ఒక కర్బన సమ్మేళనం 12.8% కార్బన్, 2.1% హైడ్రోజన్, 85.1% బ్రోమీన్ ఉంటాయి. దాని అణుభారం 187.9 అణుఫార్ములాను కనుక్కోండి.
జవాబు:
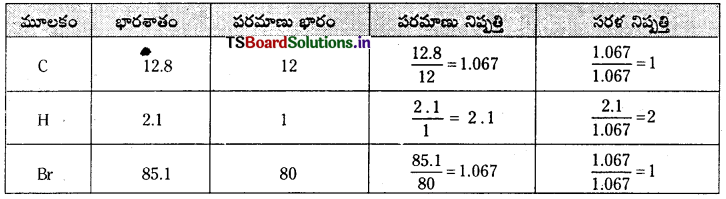
అనుభావిక ఫార్ములా = CH2Br
అనుభావిక ఫార్ములా భారం = 12 + 2 × 1 + 80 = 94
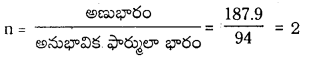
అణుఫార్ములా = అనుభావిక ఫార్ములా × n = CH2 Br × 2 = C2H4Br2

ప్రశ్న 20.
ఒక కార్బనిక సమ్మేళనం అనుభావిక ఫార్ములా CH2 Br. O. 188 g ల సమ్మేళనం 14 °C ఉష్ణోగ్రత వద్ద, 752 mm ల పీడనం వద్ద 24.2 c.cల గాలిని స్థానభ్రంశం చేసింది. అయితే సమ్మేళనం అణుఫార్ములాను కనుక్కోండి. (జలబాష్ప పీడనం 14°C వద్ద 12mm )
జవాబు:
పొడివాయువు పీడనం = వాయువు పీడనం – నీటి ఆవిరి సంతృప్తి పీడనం ‘
= 752 – 12 = 740 mm
PV = nRT ఆదర్శ వాయు సమీకరణము
PV = \(\frac{\mathrm{W}}{\mathrm{M}}\)RT
W = 0.188 V = \(\frac{24.2}{1000}\)Lt
P = \(\frac{740}{760}\) T = 273 + 14 = 287K
M = ?
M = \(\frac{0.188 \times 0.0821 \times 287 \times 760 \times 1000}{740 \times 24.2}\) = 188
అనుభావిక ఫార్ములా = CH2Br
అనుభావిక ఫార్ములా భారం = 12 + 2 + 80 = 94
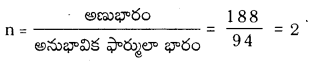
అణుఫార్ములా = అనుభావిక ఫార్ములా × 2
= CH2Br × 2 = C2H4Br2
ప్రశ్న 21.
420 Kg ల Hclని తయారు చేయడానికి 90% H2SO4 ఎంత అవసరమవుతుంది?
జవాబు:
2NaCl + H2SO4 → Na2SO4 + 2Hcl
Hcl మోల్ల సంఖ్య = \(\frac{420 \times 10^3}{36.5}\) = 11.5 × 103
రెండు మోల్ల Hcl తయారు చేయడానికి అవసరమైన H2SO4 మోల్ల సంఖ్య =1
11.5 × 103 మోల్లు తయారు చేయడానికి అవసరమయ్యే
H2SO4 మోల్ల సంఖ్య = \(\frac{11.5 \times 10^3}{2}\) = 5.75 × 103
H2SO4 భారం = మోల్ల సంఖ్య × 98 = 5.75 × 103 × 98 = 563.5 Kg
H2SO,4 90% కావున, H2SO4 భారం = \(\frac{563.5 \times 100}{90}\) = 627 Kg
ప్రశ్న 22.
ఒక అంతరిక్ష ప్రయాణీకుడికి 34g ల సుక్రోజ్ను దహనం చేయడం వల్ల వచ్చే శక్తి తన శరీరానికి ఒక గంటకు అవసరమవుతుంది. ఒక రోజుకు తనకు కావలసిన శక్తి కోసం అతడు ఎంత ఆక్సిజన్ను తనతో తీసుకుపోవాలి?
జవాబు:
ఒకరోజుకు అవసరమయ్యే సుక్రోజ్ భారం 34 × 24 = 816 గ్రా.
సుక్రోజ్ మోత్ల సంఖ్య = \(\frac{\mathrm{W}}{\mathrm{M} \cdot \mathrm{Wt}}\) = \(\frac{816}{342}\) = 2.385
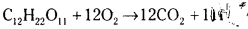
1 మోల్ సుక్రోజ్ను దహనం చేయడానికి కావలసిన ఆక్సిజన్ 12 మోల్లు.
2.385 మోల్లకు కావలసిన 02 = \(\frac{2.355 \times 12}{1}\) = 28.63
ఆక్సిజన్ భారం = మోల్ల సంఖ్య × అణుభారం
= 28.63 × 32 = 916.2 గ్రా.
ప్రశ్న 23.
4 గ్రా. CaCO3ని వేడిచేస్తే STP వద్ద వెలువడే CO2 ఘ.ప. ఎంత?
జవాబు:
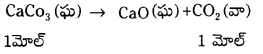
100 గ్రా. CaCO3 వేడిచేయడం వల్ల వెలువడే CO2 ఘ.ప. STP వద్ద 22.4 Lt
4 గ్రా. CaCO3 వేడిచేయడం వల్ల వెలువడే CO2 ఘ.ప. STP వద్ద 22.4 Lt
\(\frac{4 \times 22.4}{100}\) = 0.896 Lt
ప్రశ్న 24.
50 గ్రా. గంధక నమూనా(S) గాలిలో మండిస్తే 4% నమూనా మిగిలిపోయింది. STP వద్ద 21% ఆక్సిజన్ ఘ.ప. గల గాలి ఘ.ప. లెక్కించండి.
జవాబు:
సల్ఫర్ నమూనా భారం = 50 గ్రా. ; మిగిలిన సల్ఫర్ భారం = 2 గ్రా.; చర్యపొందిన సల్ఫర్ = 50 – 2 = 48 గ్రా.
S + O2 → SO2
సల్ఫర్ మోల్ల సంఖ్య = \(\frac{48}{32}\) = 1.5
ఆక్సిజన్ మోల్ల సంఖ్య = 1.5
STP వద్ద ఆక్సిజన్ ఘ.ప. = 22.4 × 1.5 = 33.6 Lit
గాలి ఘ.ప. = \(\frac{33.6 \times 100}{21}\) = 160 లీ.
ప్రశ్న 25.
20°C, 770mm Hg పీడనం వద్ద 10 cc మీథేనన్ను పూర్తిగా దహనం చేయడానికి STP పరిస్థితిలో కావలసిన ఆక్సిజన్ ఘన పరిమాణాన్ని లెక్కించండి.
జవాబు:
మీథేన్ దహనం CH4 + 2O2 → CO2 + 2H2O
CH4 మోల్ల సంఖ్య = \(\frac{\mathrm{PV}}{\mathrm{RT}}\) = \(\frac{770}{760} \times \frac{10}{82.1 \times 293}\) = 4 × 10-4
ఆక్సీజన్ మోల్లు = 2 × 4 × 10-4 = 8 × 10-4
STP వద్ద O2 ఘ.ప. = 8 × 10-4 × 22,400 = 18.88 cc
మరొక పద్ధతి :
STP వద్ద మీథేన్ ఘ.ప. లెక్కించాలి.
\(\frac{P_1 V_1}{T_1}\) = \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\)
V2 = \(\frac{770 \times 10}{293} \times \frac{273}{760}\) = 9.44 cc
STP వద్ద O2, ఘ. ప. = 2 × CH4 ఘ. ప.
= 2 × 9.44 = 18.88 cc
ప్రశ్న 26.
27°C, 760mm Hg పీడనం వద్ద 0.6 గ్రా. మెగ్నీషియంపై అధిక సజల Hcl సమక్షంలో వెలువడే H2 ఘ.ప. గణించండి.
జవాబు:
Mg + 2Hcl → MgCl2 + H2
Mg మోల్ల సంఖ్య = \(\frac{0.6}{24}\) = 0.025
సమీకరణం ప్రకారం
1 మోల్ Mg – 1 మోల్ H2 ను ఇస్తుంది.
0.025Mg – 0.0025 H2 ను ఇస్తుంది.
PV = nRT
P = 760 mm = 1 atm n = 0.025
T = 27 + 273 = 300K R = 0.0821
V = \(\frac{\mathrm{nRT}}{\mathrm{P}}\) = \(\frac{0.025 \times 0.0821 \times 300}{1}\) = 0.615L
ప్రశ్న 27.
అంశమాపక పద్ధతిలో గాల్వనో ఘటంలో రిడాక్స్ చర్యల పాత్రను వివరించండి.
జవాబు:
ఒక ద్రావణానికి మరియొక ద్రావణాన్ని వాటి మధ్య చర్య పూర్తి అయ్యే వరకు కలపడాన్ని అంశమాపనం అంటారు. చర్య పూర్తయ్యే స్థానాన్ని ‘అంతిమస్థానం’ అంటారు. కొన్ని అంశమాపన చర్యలలో ఎలక్ట్రాన్ బదిలీ జరిగి, ఆక్సీకరణ – క్షయకరణ మార్పులు జరుగుతాయి. ఇటువంటి చర్యలలో అంతిమ స్థానాన్ని రంగు మార్పు ద్వారా గుర్తించవచ్చు.
ఉదా : 1) KMnO4 పాల్గొనే చర్యలలో అంతిమస్థానం వద్ద గులాబి రంగు ఏర్పడుతుంది.
2) కొన్ని చర్యలలో రిడాక్స్ సూచికల రంగు మార్పు ద్వారా అంతిమస్థానాన్ని గుర్తిస్తారు.
డైక్రోమేటుతో జరిగే చర్యలలో డైఫినైల్ ఎమీన్ సూచిక ఆక్సీకరణం చెంది గాఢమైన నీలిరంగుని ఇస్తుంది.
3) అయోడోమెట్రీ అంశమాపనంలో Cut ను లెక్కించుట.
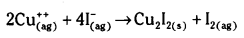
ఏర్పడిన అయొడిన్ స్టార్చ్ నీలిరంగునిస్తుంది.
రిడాక్స్ అంశమాపనాలలో \(\mathrm{MnO}_4^{-}\), \(\mathrm{Cr}_2 \mathrm{O}_7^{2-}\) ఆక్సీకరణకారకాలుగాను, \(\mathrm{S}_2 \mathrm{O}_3^{2-}\) క్షయకరణ కారకం గాను పనిచేస్తాయి.
గాల్వనిక్ ఘటాలలో రిడాక్స్ చర్యల పాత్ర
కాపర్సల్ఫేటు ద్రావణంలో జింక్ పలకను ఉంచితే రిడాక్స్ చర్య జరుగుతుంది.
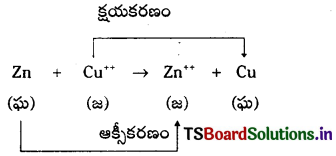
ఇదే చర్యను గాల్వానిక్ ఘటంలో జరుపుతారు. రసాయనశక్తిని విద్యుత్ శక్తిగా మార్చే విద్యుత్ రసాయన ఘటాన్ని గాల్వానిక్ ఘటం అంటారు.
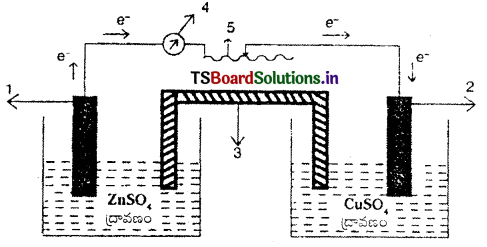
- జింక్ (ఆనోడ్)
- రాగి (కాథోడ్)
- లవణవారధి
- అమ్మీటరు
- రియోస్టాట్
ఎడమవైపు ZnSO4 ద్రావణంలో జింక్ పలక ఉంచబడినది. కుడివైపు CuSO, ద్రావణంలో Cu పలక ఉంచబడినది. ఎడమవైపు ఆక్సీకరణ చర్య జరుగుతుంది.
Zn → Zn++ + 2e–
ఈ చర్యలో విడుదలయిన ఎలక్ట్రాన్లు తీగగుండా ప్రవహించి Cu++ ను Cu గా క్షయకరణం చేస్తాయి.
Cu++ + 2e → Cu
ఈ విధంగా రెండు బీకర్లలోను రిడాక్స్ చర్యలు జరుగుతాయి. రెండు బీకర్లలోను ఉన్న Zn/Zn++ Cu++/Cu లను రిడాక్స్ జంటలు అంటారు. ఈ జంటల వల్ల ఎలక్ట్రిక్ పొటెన్షియల్ ఏర్పడుతుంది. తీగల ద్వారా ఎలక్ట్రాన్ ప్రవాహం వల్ల విద్యుత్ ప్రవాహం ఏర్పడుతుంది. రెండు అర్థఘటాలను లవణ వారధి కలుపుతుంది.
ప్రశ్న 28.
మోలార్ ద్రవ్యరాశిని నిర్వచించి వివరించండి.
జవాబు:
పరమాణువులు, అణువులు, కణాలు, ఎలక్ట్రానులు అయాన్ లు మొదలైన వాటికి మోల్ భావనను వాడతారు. SI పద్ధతిలో మోల్ (mol) ఒక పదార్థపు మౌలికమైన భౌతిక పరిమాణాన్ని చెప్పడానికి ప్రవేశపెట్టబడింది.
ఖచ్ఛితంగా 12g (లేదా 0.012 కి.గ్రా) ల 12C ఐసోటోపులో ఉండే పరమాణువులకు సమాన సంఖ్యలో కణాలు లేదా వస్తువులు ఉన్న పదార్థ పరిమాణాన్ని ఒక మోల్ అంటారు. ఒక మోల్ కార్బన్ భారం 12 గ్రా. దానిలో ఉండే పరమాణువుల సంఖ్య = 6.0221367 × 1023 mol-1
మోలార్ ద్రవ్యరాశి : ఒక మోల్ పదార్థం ద్రవ్యరాశిని గ్రాములలో చెబితే అది మోలార్ ద్రవ్యరాశి అవుతుంది.
నీటి మోలార్ ద్రవ్యరాశి = 18.02 గ్రా.
నీటి అణు ద్రవ్యరాశి = 18.02 amu.
మోలార్ ద్రవ్యరాశి సంఖ్యాత్మకంగా పరమాణు ద్రవ్యరాశి లేదా అణుద్రవ్యరాశి లేదా ఫార్ములా ద్రవ్యరాశికి సమానం.
వాటి యూనిట్ ‘u’.
సోడియం క్లోరైడ్ అణుద్రవ్యరాశి = 58.5amu.

ప్రశ్న 29.
అసౌష్ఠవ విఘటన చర్యలు (అననుపాత చర్యలు) (డిస్ ప్రపోర్షనేషన్ చర్యలు) ఏవి? ఉదాహరణలివ్వండి.
జవాబు:
కొన్ని చర్యలలో ఒకే మూలకం ఒకేసారి ఆక్సీకరణ – క్షయకరణ చర్యలకు లోనవుతుంది. ఈ చర్యలను అననుపాత చర్యలు అంటారు.
ఉదా :
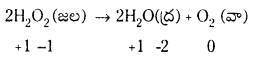
ఈ చర్యలో పెరాక్సైడ్లోని ఆక్సిజన్ -1 స్థితిలో ఉంటుంది. దాని స్థితి O2లో సున్నకు పెరుగుతుంది. H2O లో -2కు తగ్గుతుంది. ఈ చర్యలో ఆక్సిజన్ అననుపాత చర్యకు గురి అయినది.

హాలోజన్లు క్షారాలతో చర్యలో అననుపాత విఘటన చర్య జరుగుతుంది.
పై చర్యలో క్లోరిన్ \(\mathrm{ClO}_3^{-}\) గా ఆక్సీకరణం చెందినది. అదే సమయంలో Cl– గా క్షయకరణం కూడా చెందినది.
ప్రశ్న 30.
కంప్రపోర్షనేషన్ (సహానుపాత) చర్యలను ఉదాహరణలతో వివరించండి.
జవాబు:
ఒకే మూలకం వేరు వేరు ఆక్సీకరణ స్థితులలో ఆక్సీకరణ – క్షయకరణ చర్యకు లోనై ఒకే ఉత్పన్నాన్ని ఏర్పరుస్తుంది. ఈ చర్యలో మూలకస్థితి మధ్యంతర ఆక్సీకరణ స్థితిలో ఉంటుంది.
ప్రశ్న 31.
69.9% Fe, 30.1% O2 గల ఐరన్ ఆక్సైడ్ అనుభావిక ఫార్ములా కనుక్కోండి.
జవాబు:

అనుభావిక ఫార్ములా = Fe2O3
ప్రశ్న 32.
82.0245 గ్రా.మోల్’ మోలార్ ద్రవ్యరాశి గల సోడియం ఎసిటేట్ 500 ml 0.375 మోలార్ జల ద్రావణాన్ని తయారుచేయడానికి కావలసిన సోడియం ఎసిటేటు ద్రవ్యరాశిని గణించండి.
జవాబు:
ద్రావిత భారం = మోలారిటి × ఘ.ప. లీటర్లలో × గ్రా. అణుభారం
= 0.375 × \(\frac{500}{1000}\) × 82.0245 గ్రా
CH3COONa భారం = 15.375 గ్రాములు.
∴ 500 mL 0.375M సోడియం ఎసిటేటు ద్రావణాన్ని తయారుచేయడానికి కావలసిన సోడియం ఎసిటేటు ద్రవ్యరాశి 15.375 గ్రాములు.
ప్రశ్న 33.
20 గ్రా. షుగర్ (C12H22O11) ని 2L నీటిలో కరిగిస్తే వచ్చే గాఢత ఎంత?
జవాబు:
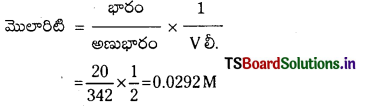
ప్రశ్న 34.
ఈ క్రింది వాటిలో ఎన్ని సార్థక అంకెలు ఉన్నాయో తెలపండి.
(i) 0.0025
జవాబు:
0.0025లో సార్థక సంఖ్యలు 2
(ii) 208
జవాబు:
208లో సార్థక సంఖ్యలు 3
(iii) 5005
జవాబు:
5005లో సార్థక సంఖ్యలు 4
(iv) 1,26,000
జవాబు:
1,26,000లో సార్థక సంఖ్యలు 6
(v) 500.0
జవాబు:
500.0లో సార్థక సంఖ్యలు 4
(vi) 2.0034
జవాబు:
2.0034 లో సార్థక సంఖ్యలు 5
ప్రశ్న 35.
ఈ క్రింది వాటిని మూడు సార్థక అంకెల వరకు సరిదిద్దండి.
(i) 34.216
(ii) 10.4107
(iii) 0.04597
(iv) 2808
జవాబు:
(i) 34.216 సరిచేయగా 34.2
(ii) 10.4107 సరిచేయగా 10.4
(iii) 0.04597 సరిచేయగా 0.046
(iv) 2808 సరిచేయగా 2.81 × 103
ప్రశ్న 36.
0.040 మోల్ భాగం ఉన్న ఇథనోల్ జల ద్రావణంలో ఇథనోల్ మొలారిటీని గణించండి (నీటి సాంద్రతను ఒకటిగా తీసుకోండి)
జవాబు:
ఇథనోల్ మోల్ల సంఖ్య = 0.04. నీటి మోల్ల సంఖ్య = 1 – 0.04 = 0.996.
మోల్ల సంఖ్య × గ్రాము అణుభారము = 0.996 × 18 గ్రాములు. (నీటి సాంద్రత ఒకటిగా తీసుకోవడమైనది)
నీటి ఘనపరిమాణం = 0.996 × 18 మిల్లీలీటర్లు. (నీటి
మొలారిటీ = మోల్ల సంఖ్య + ఘనపరిమాణం లీటర్లలో
= మోల్ల సంఖ్య × 1000/ఘ.ప. మి.లీ
= 0.04 × 1000/0.996 × 18 మి.లీ.
= 2.223 M
ప్రశ్న 37.
కింది పట్టికలోని దత్తాంశాలనుపయోగించి ప్రకృతి సిద్ధంగా లభించే ఆర్గాన్ ఐసోటోప్ల మోలార్ ద్రవ్యరాశిని గణించండి.
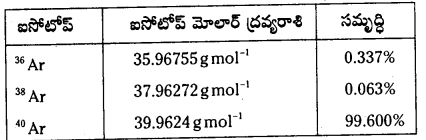
జవాబు:
ఆర్గాన్ మోలార్ ద్రవ్యరాశి :
= \(\frac{(35.96755 \times 0.337)+(37.96272 \times 0.063)+(39.9624 \times 99.6)}{100}\)
= 39.947
ప్రశ్న 38.
వెల్డింగ్ చేసే వాయు ఇంధనంలో కార్బన్, హైడ్రోజన్ మాత్రమే ఉంటాయి. కొద్ది నమూనాను ఆక్సిజన్ సమక్షంలో మండిస్తే 3.38g కార్బన్ డై ఆక్సైడ్, 0.690g నీరు ఏర్పడ్డాయి. మరి ఏ యితర ఉత్పన్న పదార్థం రాలేదు. 10.0L (STP వద్ద కొలిచిన) ఈ వెల్డింగ్ వాయువు 11.6g బరువు ఉన్నది. దాని
(i) అనుభావిక ఫార్ములా
(ii) వాయువు ద్రవ్యరాశి
(iii) అణుఫార్ములా గణించండి.
జవాబు:
CO2 మోల్ ల సంఖ్య = \(\frac{3.38}{44}\) = 0.07682; H2O మోల్ల సంఖ్య = \(\frac{0.69}{18}\) = 0.03833
CO2, H2Oల మోల్ల నిష్పత్తి 0.07682; 0.03833 = 2 : 1
కార్బన్, హైడ్రోజన్ పరమాణువుల నిష్పత్తి = 1 : 1
అణుభావిక ఫార్ములా = CH
పది లీటర్ల వాయువు భారం STP వద్ద 11.6 గ్రాములు.
STP వద్ద 22.4 లీటర్ల వాయువు భారాన్ని అణుభారంగా తీసుకోవచ్చు.
∴ అణుభారం = \(\frac{22.4 \times 11.6}{10}\) = 26
అణుభావిక ఫార్ములా భారం = 12 + 1 = 13
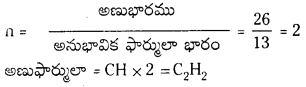
ప్రశ్న 39.
కాల్షియం కార్బొనేట్ సజల Hclతో చర్య జరిపి Cacl2ను, CO2ను ఇచ్చే రసాయన చర్య,
CaCO3(ఘ) + 2Hcl(జల) → CaCl2 (జల) + CO2(వా) + H2O(ద్ర).
25mlల 0.75M Hcl సజల ద్రావణంతో పూర్తిగా చర్య జరగడానికి కావలసిన CaCO3 ద్రవ్యరాశి ఎంత?
జవాబు:
CaCO3 ద్రవ్యరాశి = మోల్ల సంఖ్య ×100 గ్రా.
సమీకరణం ప్రకారం, CaCO3 మోత్ల సంఖ్య
= 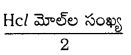
Hcl మోల్ల సంఖ్య = మోలారిటి × ఘ.ప. లీటర్లలో
= M × V లీ.
= 0.75 × \(\frac{25}{1000}\) = 0.01875
CaCO3 మోల్ల సంఖ్య = \(\frac{0.01875}{2}\) = 0.009375
CaCO3 భారం = 0.009375 × 100 = 0.9375 గ్రా.

ప్రశ్న 40.
50ml 0.1N సోడియం కార్బొనేట్ ద్రావణానికి 150ml నీటిని కలిపితే వచ్చిన ద్రావణం నార్మాలిటీని గణించండి.
జవాబు:
విలీనానికి ముందు నార్మాలిటి విలీనానికి తరువాత నార్మాలిటి
N1 V1 = N2V2
50 × 0.1 = N2 × 200
N2 = \(\frac{50 \times 0.1}{200}\) = 0.025 N
ప్రశ్న 41.
200 mL 0.2N NaOH ద్రావణాన్ని తటస్థీకరించడానికి కావలసిన 0.1N సల్ఫ్యూరిక్ ఆమ్లం ఘనపరిమాణాన్ని
జవాబు:
ఆమ్ల తుల్యాంకాలు = క్షార తుల్యాంకాలు
N1V1 = N2V2
0.1 × V1 = 0.2 × 200ml
V1 = \(\frac{0.2 \times 200}{0.1}\)
= 2 × 200 = 400m L
ప్రశ్న 42.
250 mL ల 0.2 N NaOHని తటస్థీకరించడానికి ఎంత నార్మాలిటీ గల 50 mL H2SO4 కావాలి?
జవాబు:
ఆమ్ల తుల్యాంకాలు = క్షార తుల్యాంకలు
ఆమ్ల మిల్లీ తుల్యాంకాలు – క్షార మిల్లీ తుల్యాంకాలు
N1V1 = N2V2
N1.50mL = 0.2 × 250ml
N1 = \(\frac{0.2 \times 250}{50}\) = 1N
గమనిక : మిల్లీ మోల్ల సంఖ్య = మిల్లీ లీటర్లు × మోలారిటి
మిల్లీ తుల్యాంకాలు = మిల్లీ లీటర్లు × నార్మాలిటి
మోల్ల సంఖ్య = మొలారిటీ × లీటర్లలో ఘ.ప.
ప్రశ్న 43.
100 mL ల 0.1 M H2C2O42H2O ద్రావణంతో సల్ఫ్యూరిక్ ఆమ్లం సమక్షంలో చర్య జరపడానికి కావలసిన 0.1 M KMnO4 ద్రావణం ఘనపరిమాణాన్ని గణించండి.
జవాబు:
2KMnO4 + 3H2SO4 + 5H2C2O4 → K2SO4 + 2MnSO4 + 8H2O + 10CO2
\(\frac{\mathrm{M}_1 \mathrm{~V}_1}{\mathrm{n}_1}\) = \(\frac{\mathrm{M}_2 \mathrm{~V}_2}{\mathrm{n}_2}\)
M1 = ఆగ్జాలికామ్లం మొలారిటి M2 = KMnO4 మొలారిటి
V1 = ఆగ్జాలికామ్లం ఘ. ప. V2 = ?
n1 = ఆగ్జాలికామ్లం మోల్ ల సంఖ్య n2 = ?
\(\frac{0.1 \times 100}{5}\) = \(\frac{0.1 \times V_2}{2}\)
V2 = \(\frac{0.1 \times 100 \times 2}{5 \times 0.1}\) = 40ml
ప్రశ్న 44.
కింది పదార్థాల్లో కింద గీతతో చూపించిన మూలకాల ఆక్సీకరణ స్థితులు వ్రాయండి.
(a) NaH2PO4
(b) NaHSO4
(c) H4P2O7
(d) K2MnO4
(e) CaO2
(f) NaBH4
(g) H2S2O7
(h) KAl(sO4)2.12H2O
జవాబు:
(a) NaH2PO4
+1+2+x+8 = 0
x-5= 0 x = +5
ఫాస్పరస్ ఆక్సీకరణ సంఖ్య = +5
(b) NaHSO4
1+1+x-8 = 0
x-6 = 0 x=+6
సల్ఫర్ ఆక్సీకరణ సంఖ్య = +6
(c) H4P2O7
+4+2x+-14 = 0
2x – 10 = 0 x = \(\frac{10}{2}\) = +5
H4P2O7 P ఆక్సీకరణ సంఖ్య = +5
(d) K2MnO4
Mn ఆక్సీకరణ సంఖ్య = x అనుకొనుము.
+2+x-8 = 0
x-6 = 0 x=+6
K2MnO4 Mn ఆక్సీకరణ సంఖ్య = +6
(e) CaO2
(Ca) క్షార మృత్తిక లోహాల ఆక్సీకరణ స్థితి = +2
‘O’ ఆక్సీకరణ స్థితి = x
+2 + 2x = 0 2x = -2 x = -1
CaO2 లో O ఆక్సీకరణ స్థితి = -1
(f) NaBH4
+ 1+x+-4 = 0
x-3= 0 x=+3
NaBH4 లో బోరాన్ ఆక్సీకరణ సంఖ్య = +3
(g) H2S2O7
+2+2x-14= 0
2x-12= 0 2x= +12 x=+6
H2S2O7 లో ‘S’ ఆక్సీకరణ సంఖ్య = +6
(h) KAl(sO4)2.12H2O
\(\mathrm{SO}_4^{–}\) లో ‘S’ ఆక్సీకరణ సంఖ్య ఇచ్చిన పదార్థంతో ‘S’ ఆక్సీకరణ సంఖ్య = +6
x-8=-2
x=+6
ప్రశ్న 45.
కింది పదార్థాల్లో కింద గీతతో చూపించిన మూలకాల ఆక్సీకరణ స్థితులను వివరించండి. మీరిచ్చిన ఆక్సీకరణ స్థితులను ఎలా వివరిస్తారు?
a) KI3
b) H2S4O6
c) Fe3O4
జవాబు:
a) Kl3 → K+ + \(\mathrm{l}_3^{-}\)
\(\mathrm{l}_3^{-}\) ion I– మరియు I2 ల కలయిక వల్ల ఏర్పడుతుంది.
I– ఆక్సీకరణస్థితి-1. I2 ఆక్సీకరణ స్థితి 0.
b) H2S4O6
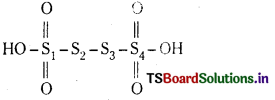
S2, S3 ల ఆక్సీకరణ సంఖ్యలు సున్న.
S1, S4ల ఆక్సీకరణ సంఖ్యలు +5.
సరాసరి ఆక్సీకరణ సంఖ్య = \(\frac{10}{4}\) = +2.5
c) Fe3O4 లో FeO, Fe2O3లు ఉంటాయి.
FeO లో Fe ఆక్సీకరణ స్థితి = +2
Fe2O3 లో Fe ఆక్సీకరణ స్థితి = +3
సరాసరి ఆక్సీకరణ సంఖ్య = \(\frac{+2-2 \times 3}{3}\) = \(\frac{8}{3}\) = 2.67 3
ప్రశ్న 46.
కింది ఆక్సీకరణ – క్షయకరణ చర్యలను వివరించండి.
a) Cuo(ఘ) + H2(వా) → Cu(ఘ) + H2O(వా)
b) Fe2O3(ఘ) + 3CO(వా) → 2 Fe(ఘ) + 3CO2(వా)
c) 4Bcl3 (వా) + 3Li AlH4 → 2B2H6(వా) + 3 Lic (ఘ) + 3AlCl3
d) 2K(ఘ) + F2(వా) → 2K+F–(ఘ)
e) 4NH3 (వా) + 5O2 (వా) → 4NO (వా) + 6H2O(వా)
జవాబు:
a) Cu+2 → Cu0 – క్షయకరణం
\(\mathrm{H}_2^0\) → 2H+ – ఆక్సీకరణం
∴ ఇది రిడాక్స్ చర్య.
b) Fe+3 → Fe– క్షయకరణం
C+2 → C+4 – ఆక్సీకరణం
∴ ఇది రిడాక్స్ చర్య
c) ఈ చర్యలో ఏ పరమాణువుకు ఆక్సీకరణ సంఖ్యలో మార్పులేదు.
∴ ఇది రిడాక్స్ చర్య కాదు.
d) K0 → K+ – ఆక్సీకరణం
F0 → F– – క్షయకరణం
∴ ఇది రిడాక్స్ చర్య.
e) N-3 → N+2 – ఆక్సీకరణం
O0 → O-2 – క్షయకరణం
∴ ఇది రిడాక్స్ చర్య.
ప్రశ్న 47.
ఫ్లోరిన్ మంచుతో చర్య జరిపి కింది మార్పును ఇస్తుంది. H2O(ఘ) + F2(వా) → 2HF(వా) + HOF(వా) దీనిని రిడాక్సు చర్యగా చూపండి.
జవాబు:
H2O లోని O–H బంధంలో ఆక్సిజన్ వద్ద ఎలక్ట్రాన్ సాంద్రత కన్నా OF బంధంలో -0- వద్ద ఎలక్ట్రాన్ సాంద్రత తక్కువ. అందువల్ల 0 – ఆక్సీకరణం చెందుతుంది. F2 లో F ఎలక్ట్రాన్ సాంద్రత కన్నా HOF లో F వద్ద ఎలక్ట్రాన్ సాంద్ర” పెరుగుతుంది. ఇది క్షయకరణం. కనుక ఈ చర్య క్షయకరణం.
O-2 → O0 – ఆక్సీకరణం
F → F– – క్షయకరణం
∴ ఇది రిడాక్స్ చర్య.

ప్రశ్న 48.
H2SO5, Cr2, \(\mathrm{O}_7^{2-}\) లలో \(\mathrm{NO}_3^{-}\) లలో S, Cr, N ల ఆక్సీకరణ సంఖ్యలను, నిర్మాణాలను వ్రాయండి.
జవాబు:
H2SO5 దీనిని H2SO3.(O2)
ఆక్సీకరణ సంఖ్య +2+x-6-2 = 0
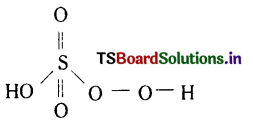
x = +6
కనుక H2SO5 లో పెరాక్సీ బంధం ఉంటుంది.
(ii)
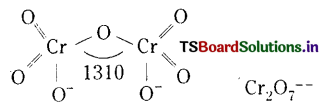
Cr2\(\mathrm{O}_7^{-}\)
Cr ఆక్సీకరణ సంఖ్య = x
O ఆక్సీకరణ సంఖ్య = -2
2x – 14 = -2 (అయాన్ పై ఆవేశం)
2x = 14 – 2 = 12
x = \(\frac{12}{2}\) = +6
క్రోమియం ఆక్సీకరణ సంఖ్య = +6
(iii) N\(\mathrm{O}_3^{-}\)
నైట్రోజన్ ఆక్సీకరణ స్థితి = x
ఆక్సిజన్ ఆక్సీకరణ స్థితి = -2
x-6 = -1
x = +5
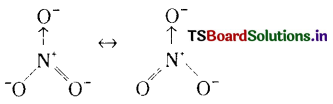
ప్రశ్న 49.
కింది సంయోగ పదార్థాల ఫార్ములాలు వ్రాయండి.
a) మెర్క్యూరీ (II) క్లోరైడు
b) నికెల్ (II) సల్ఫేటు
c) టిన్ (IV) ఆక్సైడ్
d) థాలియం (I) సల్ఫేటు
e) ఐరన్ (III) సల్ఫేటు
f) క్రోమియం (III) ఆక్సైడ్
జవాబు:
a) Hg+2.Cl–
ఫార్ములా HgCl2
b) Ni+2S \(\mathrm{O}_4^{2-}\)
ఫార్ములా NiSO4
c) Sn-4.O-2 Sn2O4
లేదా SnO2
d) Tl+1.S\(\mathrm{O}_4^{-2}\)
ఫార్ములా Tl2.SO4
e) Fe+3S\(\mathrm{O}_4^{-2}\)
ఫార్ములా Fe2(SO4)3
f) Cr+3.O-2
ఫార్ములా Cr2.O3
ప్రశ్న 50.
కార్బన్ –4 నుంచి + 4 వరకు నైట్రోజన్ -3 నుండి + 5 వరకు ఆక్సీకరణ స్థితులు చూపే పదార్థాల పట్టిక ఇవ్వండి.
జవాబు:
కింది పదార్థాలలో -4 నుండి + 4 వరకు ఆక్సీకరణ సంఖ్యలను కార్బన్ ప్రదర్శిస్తుంది.
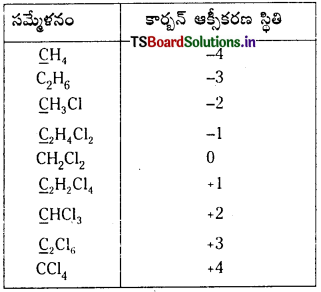
నైట్రోజన్ (-3 నుండి +5)
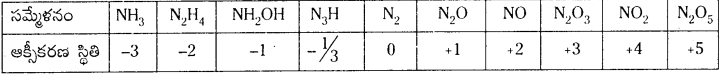
ప్రశ్న 51.
SO2, H2O2 లు ఆక్సీకరణులుగాను, క్షయకరణులుగాను పనిచేస్తాయి. కాని HNO3 కేవలం ఆక్సీకరణిగానే పనిచేస్తుంది. ఎందువల్ల ?
జవాబు:
SO2లో సల్ఫర్ ఆక్సీకరణ స్థితి +4. సల్ఫర్కు ఆక్సీకరణ స్థితిని +6 వరకు పెంచుకొనగలదు. అందువల్ల అది క్షయకరణిగా పనిచేయగలదు. అంతేగాక దాని ఆక్సీకరణ సంఖ్య 0 లేదా -2 వరకు తగ్గవచ్చు. కనుక ఆక్సీకరణి గా కూడా పనిచేయగలదు. అదేవిధంగా హైడ్రోజన్ పెరాక్సైడ్ ఆక్సిజన్ ఆక్సీకరణ స్థితి -1. ఈ ఆక్సీకరణ స్థితి ( కు పెరగవచ్చు లేదా -2కు తగ్గవచ్చు. ఈ విధంగా SO2 మరియు H2O,లు ఆక్సీకరణులుగాను మరియు క్షయకరణులుగాను కూడా పనిచేస్తాయి.
HNO3లో నైట్రోజన్ ఆక్సీకరణస్థితి +5. ఇది నైట్రోజన్ యొక్క గరిష్ఠ ఆక్సీకరణ స్థితి. కనుక దాని ఆక్సీకరణ స్థితి పెరిగే అవకాశం లేదు. కాబట్టి HNO3 క్షయకరణిగా పనిచేయలేదు.
ఆక్సీకరణ స్థితి తగ్గే అవకాశం ఉన్నందువల్ల ఆక్సీకరణిగా మాత్రమే పనిచేయగలదు.
ప్రశ్న 52.
a) 6CO2 (వా) +6H2O(ద్ర) → C6H12O6(జల) + 6O2(వా)
b) O3(వా) + H2O2(ద్ర) → H2O(ద్ర) + 2O2(వా)
పైన ఇచ్చిన చర్యలను కింది విధంగా రాస్తే ఇంకా ఎక్కువ అర్థవంతంగా ఉంటుంది. ఎందువల్ల?
a) 6CO2 (వా) + 12H2O(ద్ర) → C6H12O6(జల) + 6H2O(ద్ర) + 6O2 (వా)
b) O3(వా) + H2O2(ద్ర) → H2O(ద్ర) + O2(వా) + O2(వా)
(a), (b) చర్యాగతుల శోధనకు సాంకేతిక ప్రక్రియలను వివరించండి.
జవాబు:
మొక్కలు, గాలిలోని CO2ను, భూమి నుండి నీరును సూర్యరశ్మి, క్లోరోఫిల్లల సమక్షంలో గ్రహించి కార్బోహైడ్రేటులను సంశ్లేషిస్తాయి. ఈ చర్యలో ఆక్సిజన్ విడుదల అవుతుంది. ఆక్సిజన్ నీటి నుండి విడుదలవుతుంది. CO2 నుండి కాదు. చర్య (a) లో 6H2O అణువులు 3O2 అణువులను మాత్రమే విడుదల చేయగలవు. కావున పై సమీకరణం కన్నా కింది విధంగా వ్రాయుట అర్థవంతం.
6CO2 (వా) + 12H2O (ద్ర) → C6H12O6(జల) + 6H2O (ద్ర) → 618O2(వా)
O18 ఐసోటోప్ గల నీరు ఈ విషయాన్ని స్పష్టం చేస్తుంది
6CO2 (వా) + 12H2O18 (ద్ర) → C6H12O6(జల) + 6H2O (ద్ర) + 618O2(వా)
ఈ చర్య H2O18 వాడినపుడు \(\mathrm{O}_2^{18}\) విడుదల అవుతుంది
(b)
O3 → O2 + (O)
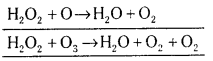
ఈ చర్యలో ఒక ఆక్సిజెన్ నుండి మరియొకటి నుండి విడుదల అవుతుంది ఈ విషయాన్ని ద్వారా నిరూపితమవుతుంది.
ప్రశ్న 53.
AgF2 చాలా అస్థిరమైనది. అది ఏర్పడితే ఒక బలమైన ఆక్సీకరణిగా పనిచేస్తుంది ఎందువల్ల?
జవాబు:
AgF2 అనేది అస్థిరమైనది. దీనిలో Ag, Ag+2 స్థితిలో ఉన్నది. ఇది స్థిరమైన Ag+ గా మారుతుంది. అందువల్ల అది అస్థిరమైనది. AgF గాను, మరియు F గాను విఘటనం చెందుతుంది. విడుదలయిన ఫ్లోరిన్ బలమైన ఆక్సీకరణి. కనుక AgF2 బలమైన ఆక్సీకరణిగా పనిచేస్తుంది.
2AgF2 → 2AgF + F2
ప్రశ్న 54.
ఒక ఆక్సీకరణి, ఒక క్షయకరణిల మధ్య చర్య జరిగితే క్షయకరణి అధికంగా ఉన్నపుడు తక్కువ ఆక్సీకరణ స్థితి సంయోగ పదార్థం, ఆక్సీకరణి అధికంగా ఉంటే ఎక్కువ ఆక్సీకరణ స్థితి సంయోగ పదార్థం ఏర్పడతాయి. దీనిని కనీసం మూడు ఉదాహరణలతో వివరించండి.
జవాబు:
HgCl2 మరియు SnCl2 చర్యలో, HgCl2 ఆక్సీకరణిగాను SnCl2 క్షయకరణిగాను పనిచేస్తాయి. SnCl2 అధికంగా ఉన్నపుడు ఏర్పడిన ఉత్పన్నం అల్ప ఆక్సీకరణ స్థితిలో ఉంటుంది. కాని HgCl2 అధికంగా ఉన్నపుడు ఏర్పడిన ఉత్పన్నంలో Hg అధిక ఆక్సీకరణ స్థితిలో ఉంటుంది.
1.
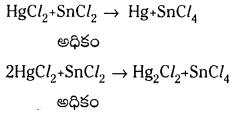
2. ఫాస్పరస్, క్లోరిన్ల చర్యలో ఫాస్పరస్ క్షయకరణి, క్లోరిన్ ఆక్సీకరణి. క్లోరిన్ స్వల్ప పరమాణంలో ఉన్నప్పుడు ఏర్పడే ఉత్పన్నం PCl5 కాని క్లోరిన్ అధికంగా ఉన్నప్పుడు PCl5 ఉత్పన్నంగా ఏర్పడుతుంది.
P4 + 6Cl2 → 4PCl3
P4 + 10Cl2 → 4PCl5
a) CuO(ఘ) + H2(వా) → Cu(ఘ) + H2O(వా)
ఈ చర్యలో Cu ఆక్సీకరణ సంఖ్య + 2 నుంచి 0కు తగ్గింది. H2 ఆక్సీకరణ స్థితి 0 నుండి +1 కు పెరిగింది. అందువల్ల ఇది రీడాక్సు చర్య.
b) Fe2O3(ఘ) + 3CO(వా) → 2Fe(ఘ) +3CO2(వా)
ఈ చర్యలో Fe ఆక్సీకరణ స్థితి +3 నుండి 0 కు తగ్గింది. కార్బన్ ఆక్సీకరణ స్థితి + 2 నుండి +4కు పెరిగింది. అందువల్ల రీడాక్సు చర్య.
c) 4BCl3 (వా) + 3LiAlH4(ఘ) → 2B2H6(వా) + 2LiCl(ఘ) + 3AlCl3 (ఘ)
LiAlH4లో Hydrogen H– ion గా ఉంటుంది. B2H6 లో కూడా హైడ్రోజన్ మీద కొంత ఋణావేశం ఉంటుంది. అందువల్ల ఎలక్ట్రాన్ సాంద్రత H వద్ద తగ్గుతుంది. కనుక ఆక్సీకరణం.
BCl3 నుండి B2H6కు B వద్ద ఎలక్ట్రాన్ సాంద్రత పెరుగుతుంది. అందువల్ల క్షయకరణం. అందువల్ల ఇది ఒక రిడాక్సు చర్య.
d) 2K(s) + F2(వా) → 2K+F–(s)
ఈ చర్యలో K ఎలక్ట్రాన్ కోల్పోతుంది. కనుక ఆక్సీకరణం.
F ఎలక్ట్రాను గ్రహిస్తుంది. కనుక క్షయకరణం. K → K+ ఆక్సీకరణం F2 → 2F–క్షయకరణం.
e) 4NH3 (వా) + 502 (వా) → 4NO (వా) + 6H2O(వా)
NH3 → NO లో N ఆక్సీకరణ స్థితి – 3 నుండి +2 గా మారుతుంది. కనుక ఆక్సీకరణం O2 → H2O చర్యలో O ఆక్సీకరణ స్థితి సున్న నుండి -2కు తగ్గింది.
3. అధికంగా ఉన్న ద్రవ సల్ఫర్ లోనికి క్లోరినన్ను పంపించినపుడు సల్ఫర్ మోనోక్లోరైడు ఏర్పడుతుంది. కాని అధికంగా క్లోరిన్ ఉన్నప్పుడు సల్ఫర్ డై క్లోరైడ్ ఏర్పడుతుంది.
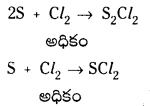
ప్రశ్న 55.
కింది వాటిని ఏ విధంగా వివరిస్తారు?
a) క్షారీకృత KMnO4 అమ్లీకృత KMnO4లు ఆక్సీకరణులైనా టోలీన్ నుంచి బెంజోయిక్ ఆమ్లం తయారీలో ఆల్కహాలిక్ KMnO4 ను ఆక్సీకరణిగా వాడతారు. ఎందువల్ల? చర్యకు తుల్య ఆక్సీకరణ – క్షయకరణ సమీకరణం రాయండి.
b) మూలక రసాయన మిశ్రమంలో క్లోరైడ్ ఉంటే దానికి గాఢ సల్ఫ్యూరిక్ ఆమ్లం కలిపినపుడు ఘాటైన వాసన గల HCl వాయువు వెలువడుతుంది. ఐతే మిశ్రమంలో బ్రోమైడ్ లవణం ఉంటే ఎర్రటి బ్రోమిన్ వస్తుంది. ఎందువల్ల?
జవాబు:
a) ఆమ్లీకృత KMnO4 కర్బన పదార్థాలను CO2 మరియు నీరుగా ఆక్సీకరణం చేస్తుంది. క్షారయుత పెర్మాంగనేటు, కర్బన పదార్థాలను ఆల్డిహైడ్లుగాను, ఆమ్లాలుగానూ ఆక్సీకరణం చేస్తుంది. ఈ కారణం వల్ల టోలీన్ నుండి బెంజాయిక్ ఆమ్లం తయారీలో క్షారయుత పెర్మాంగనేటును ఉపయోగిస్తారు.
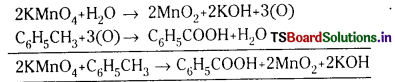
b) అల్పబాష్పశాలి ఆమ్లాలు లవణాలతో చర్యపొందినపుడు అధిక బాష్పశీలి ఆమ్లాలు ఏర్పడతాయి. క్లోరైడు, బ్రోమైడ్ లవణాలు గాఢ H2SO4 తో చర్య జరిపినపుడు అధిక భాష్పశీలి Hcl మరియు HBr లు ఏర్పడతాయి. అయితే HCl, Cl2 గా ఆక్సీకరణం చెందదు. కాని HBr ను H2SO4, Br2 గా ఆక్సీకరణం చెందిస్తుంది.
కనుక H2SO4, HBrను ఎరుపురంగు Br2 గా ఆక్సీకరణం చేస్తుంది.
2Nacl + H2SO4 → Na2SO4 + 2Hcl
2KBr + H2SO4 → K2SO4 + 2HBr
2HBr + H2SO4 → 2H2O + SO2 + Br2

ప్రశ్న 56.
కింది చర్యలలో ఆక్సీకరణి, క్షయకరణి, ఆక్సీకరణం చెందిన పదార్థం, క్షయకరణం చెందిన పదార్థం తెలపండి.
a) 2AgBr(ఘ) + C6H6O2 → 2Ag(ఘ) + 2HBr(జల) + C6H4O2(జల)
b) HCHO(ద్ర) + 2[Ag(NH3)2]+ (జల) + 30H– (జల) → 2Ag(ఘ) + HCOO– (జల) + 4NH3 (జల) + 2H2O(ద్ర)
c) HCHO(ద్ర) + 2Cu++ (జల) + 50H– (జల) → Cu2O(ఘ) +HCOO– (జల) + 3H2O(ద్ర)
d) N2H4(ద్ర) + 2H2O2(ద్ర) → N2(వా) + 4H2O(ద్ర)
e) Pb(ఘ) + PbO2(ఘ) + 2H2SO4(జల) → PbSO4 (ఘ) + 2H2O(ద్ర)
జవాబు:
ఆక్సీకరణం చెందే పదార్థం క్షయకరణి. క్షయకరణం చెందే పదార్థం ఆక్సీకరణి.
a) ఈ చర్యలో Ag+ → Ag గా మారింది. క్షయకరణం చెందింది. అందువల్ల Ag+ ఆక్సీకరణి. C6H6O2 లోని C ఆక్సీకరణం చెందింది. C6H6O2 క్షయకరణి.
b) HCHO → HCOO– గా ఆక్సీకరణం చెందింది. అందువల్ల HCHO క్షయకరణి. అమ్మోనికల్ సిల్వర్ నైట్రేటులో Ag+ గా Ag క్షయకరణం చెందింది. అందువల్ల (Ag(NH3)2]+ ఆక్సీకరణి.
Cu++ → Cu2O గా క్షయకరణం చెందినది.
c) HCHO → HCOO గా ఆక్సీకరణం చెందినది.
కావున Cu++ ఆక్సీకరణి. HCHO క్షయకరణి.
d) N2H4(ద్ర) + 2H2O2(ద్ర) → N2 (వా) + 4H2O(ద్ర)
N2H4 → N2 ; ఆక్సీకరణ చర్య
2H2O2 → 2H2O; క్షయకరణ చర్య
N2H4 క్షయకరణి. H2O2 ఆక్సీకరణి
e) Pb ఆక్సీకరణం చెందుతుంది. కనుక క్షయకరణి. PbO2 → PbSO4 గా క్షయకరణం చెందుతుంది. కావున PbO2 ఆక్సీకరణి.
ప్రశ్న 57.
2S2\(\mathrm{O}_3{ }^{2-}\)(జల) + I2(ఘ) → S4\(O_6^{2-}\)(జల) + 2I– (జల)
S2\(\mathrm{O}_3^{2-}\)(జల) + 2Br2(ద్ర) → 5H2O(ద్ర) → 2S\(\mathrm{O}_4^{2-}\) (జల) + 4Br– (జల) + 10H+ (జల)
లలో Br2, I2లు వేరు వేరు విధానాల్లో చర్య జరుపుతున్నాయి. ఎందువల్ల?
జవాబు:
అయోడిన్ బలహీన ఆక్సీకరణి కాగా బ్రోమీన్ బలమైన ఆక్సీకరణి. అందువల్ల అయోడిన్ చర్యలో సల్ఫర్ ఆక్సీకరణ స్థితి S2\(\mathrm{O}_3{ }^{2-}\) లో + 2 నుండి S4\(\mathrm{O}_6{ }^{2-}\) లో +2.5కు మారుతుంది. కాని Br2 బలమైన ఆక్సీకరణి కనుక సల్ఫర్ను అత్యధిక ఆక్సీకరణ స్థితికి +6 కు ఆక్సీకరణం చేస్తుంది. S2\(\mathrm{O}_3{ }^{2-}\), S\(\mathrm{O}_4{ }^{2-}\) మారేవరకు చర్య జరుగుతుంది.
ప్రశ్న 58.
హాలోజన్లలో ఫ్లోరిన్ బలమైన ఆక్సీకరణి. హైడ్రోహాలిక్ సంయోగ పదార్థాలలో హైడ్రో అయోడిక్ ఆమ్లం బలమైన క్షయకరణి వివరించండి.
జవాబు:
హాలోజన్ల ఆక్సీకరణ సామర్థ్యం ఫ్లోరిన్ నుండి అయోడిన్క తగ్గుతుంది.
Fl2 > Cl2 > Br2 > I2
దీనికి కారణం, F2, నుండి I2 కు ఋణ విద్యుదాత్మకతలు మరియు ఎలక్ట్రాన్ గ్రాహ్య ఎంథాల్పీలు క్రమంగా తగ్గడమే. హాలైడులను హాలోజన్లుగా F2 ఆక్సీకరణం చేస్తుంది.
2Kcl + F2 → 2KF + Cl2
2kBr + F2 → 2KF + Br2
2KI + F2 → 2KF + I2
క్లోరిన్ Brను, Iను మాత్రమే స్థానభ్రంశం చెందించగలదు.
2kBr + Cl2 → 2Kcl + Br2
2KI + Cl2 → 2Kcl + I2
అదేవిధంగా I– ను I2గా Br2 ఆక్సీకరణం చెందిస్తుంది.
2KI + Br2 → 2KBr + I2
అయొడిన్ హాలైడులను స్థానభ్రంశం చేయలేదు.
హైడ్రోజన్ హాలైడులలో క్షయకరణ సామర్థ్యం HF నుండి HI కు పెరుగుతుంది. దీనికి కారణం హైడ్రోజన్ హాలైడ్లలో బంధ దూరం పెరుగుదలతో ఉష్ణ స్థిరత్వం తగ్గడమే. అందువల్ల HF ను ఆక్సీకరణం చేయటం కష్టం. HI ను సులభంగా ఆక్సీకరణం చెందించవచ్చు. ఈ కారణంగా HI బలమైన క్షయకరణి.
ప్రశ్న 59.
కింది చర్య ఎందుకు జరుగుతుంది?
Xe\(\mathrm{O}_6^{4-}\) (జల) + 2F– (జల) + 6H+ (జల) → XeO3(వా) + F2(వా) + 3H2O(ద్ర)
ఈ చర్య నుంచి Na4 XeO6 అనే పదార్థం (దీనిలో Xe\(O_6^{4-}\) ఒక విభాగం) గురించి ఏమని నిర్ధారించవచ్చు.
జవాబు:
Xe\(\mathrm{O}_6^{4-}\) అయాన్ చాలా బలమైన ఆక్సీకరణి. F2 కన్నా బలమైనది. అందువల్ల అది F– ను ఆమ్లయానకంలో F2 గా ఆక్సీకరణం చేయగలదు. Na4 XeO6 అయానిక పదార్థం.
ప్రశ్న 60.
క్రింది చర్యలను పరిశీలించండి.
a) H3PO2(జల) + 4AgNO3(జల) + 2H2O(ద్ర) → H3PO4(జల) + 4Ag(ఘ) + 4HNO3
b) H3PO2(జల) + 2CuSO4 (జల) + 2H2O(ద్ర) → H3PO4 (జల) + 2Cu(ఘ) + 2H2SO4(జల)
c) C6H5CHO(ద్ర) + 2[Ag\(\left(\mathrm{NH}_3\right)_2{ }^{+}\) (జల) + 3OH– (జల) → C6H5COO– (జల) + 2Ag(ఘ) + 4NH3(జల) + 2H2O(ద్ర)
d) C6H5CHO(ద్ర) + 2Cu2+ (జల) 5OH– (జల) → మార్పులేదు.
ఈ చర్యల గురించి Ag+, Cu++ల ప్రవృత్తి గురించి మీరు ఏమని నిర్ధారించగలరు.
జవాబు:
ఆమ్లయానకంలో A+, Cu++ ఒకే రకమైన పై చర్యలలో ఆక్సీకరణ సామర్ధ్యాన్ని ప్రదర్శిస్తాయి. క్షారయానకంలో Ag+ బలమైన ఆక్సీకరణి. Cu++ బెంజాల్ డిహైడ్ ను క్షారయానకంలో ఆక్సీకరణం చెందించుట లేదు. అందువల్ల బలహీనమైన ఆక్సీకరణి.
ప్రశ్న 61.
కింది ఆక్సీకరణ – క్షయకరణ చర్యలను అయాన్-ఎలక్ట్రాన్ పద్ధతి ద్వారా తుల్యం చేయండి.
a) Mn\(\mathrm{O}_4^{-}\) (జల) + I–(జల) → MnO2(ఘ) + I2(ఘ) (క్షార యానకంలో)
b) Mn\(\mathrm{O}_4^{-}\) (జల) + SO2 (వా) → Mn2+(జల) + HS\(\mathrm{O}_4^{-}\) (జల) (ఆమ్ల ద్రావణంలో)
c) H2O2(జల) + Fe2+(జల) → Fe3+ (జల) + H2O(ద్ర) (ఆమ్ల ద్రావణంలో)
d) Cr2\(\mathrm{O}_7^{2-}\) + SO2(వా) → Cr3+ (జల) + S\(\mathrm{O}_4^{2-}\) (జల) (ఆమ్ల ద్రావణంలో)
జవాబు:
a) Mn\(\mathrm{O}_4^{-}\) (జల) + I– (జల) → MnO2(ఘ) + I2 (మ) (క్షార యానకంలో)
1వ దశ : మొదట సంక్షిప్త అయానిక సమీకరణాన్ని రాయండి.
Mn\(\mathrm{O}_4^{-}\) (జల) + I– (జల) → MnO2(ఘ) + I2(ఘ)
2వ దశ : రెండు అర్ధ చర్యలను వ్రాయండి.
ఆక్సీకరణ అర్ధ చర్య :
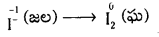
క్షయకరణ అర్ధ చర్య :

3వ దశ : I పరమాణువులను తుల్యం చేయాలి.
2I– (జల) → I2(ఘ)
4వ దశ : చర్య క్షార యానకంలో జరుగుతుంది కాబట్టి O పరమాణువులను తుల్యం చేయడానికి క్షయకరణ అర్ధ చర్యలో OH– అయాన్లను తగిన సంఖ్యలో కలపాలి.
Mn\(\mathrm{O}_4^{-}\)(జల) → MnO2(ఘ) + 2OH–(ద్ర)
H పరమాణువులను తుల్యం చేయడానికి ఎడమ ప్రక్కన రెండు H2O అణువులను కలపాలి.
Mn\(\mathrm{O}_4^{-}\) (జల) + 2H2O (జల) → MnO2(ఘ) + 2OH–
H, O పరమాణువులను దాగుడుమూతల పద్ధతిలో తుల్యం చేయాలి.
Mn\(\mathrm{O}_4^{-}\) (జల) + 2H2O(జల) → MnO2(ఘ) + 4OH–(జల)
5వ దశ : రెండు అర్ధచర్యలలోని ఆవేశాలను తుల్యం చేయాలి.
2I–(జల) → I2(ఘ) + 2e–
Mn\(\mathrm{O}_4^{-}\) (జల) + 2H2O(ద్ర ) +3e– → MnO2 (ఘ) + 4OH–(జల)
విడుదలయిన ఎలక్ట్రాన్ల సంఖ్య, గ్రహించిన ఎలక్ట్రాన్ల సంఖ్యను తుల్యం చేయాలి. ఆక్సీకరణ అర్ధచర్యను 3 పెట్టి క్షయకరణ అర్ధ చర్యను 2 పెట్టి హెచ్చవేయాలి.
6I–(జల) → 3I2(ఘ) + 6e–
2Mn\(\mathrm{O}_4^{-}\) (జల) + 4H,O(ద్ర) + 6e– → 2MnO2(ఘ) + 80H–(జల)
6వ దశ : రెండు అర్ధ చర్యలను కలిపితే మొత్తం మీది చర్య వస్తుంది. రెండు వైపుల ఎలక్ట్రాన్లను కొట్టివేయాలి.
6I–(జల) + 2Mn\(\mathrm{O}_4^{-}\) (జల) + 4H2O(ద్ర) → 3I2 (ఘ) + 2MnO2(ఘ) + 8OH–(జల)
7వ దశ : చివరగా సమీకరణాన్ని పరమాణువులు, ఆవేశాల పరంగా సరిచూసుకోవాలి.
b) Mn\(\mathrm{O}_4^{-}\) (జల) + SO2(వా) → Mn2+(జల) + HS\(\mathrm{O}_4^{-}\) (జల) (ఆమ్ల ద్రావణంలో)
1వ దశ : మొదటగా సంక్షిప్త అయానిక సమీకరణాన్ని రాయండి.
2వ దశ : రెండు అర్ధ చర్యలను రాయండి.
ఆక్సీకరణం చర్య : 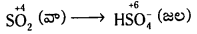
క్షయకరణం చర్య : 
3వ దశ : O2 పరమాణువులను ఆక్సీకరణ అర్ధ చర్యలో తుల్యం చేయడానికి ఎడమవైపు 2H2O రాయాలి.
SO2 + 2H2O → HSO–
H పరమాణువులను తుల్యం చేయడానికి H+లు కలపాలి.
SO2 + 2H2O → HS\(\mathrm{O}_4^{-}\) + 3H+
క్షయకరణ అర్ధ చర్యలో O, H లను తుల్యం చేయాలి.
Mn\(\mathrm{O}_4^{-}\) → Mn++ + 4H2O
చర్య ఆమ్ల యానకంలో జరుగుతున్నది. కాబట్టి H+ లను ఉపయోగించి Hలను తుల్యం చేయాలి.
Mn\(\mathrm{O}_4^{-}\) + 8H+ → Mn++ + 4H2O
4వ దశ : రెండు చర్యలలోని విద్యుదావేశాలను తుల్యం చేయాలి.
SO2 + 2H2O → HSO4 + 3H+ + 2e–
Mn\(\mathrm{O}_4^{-}\) + 8H+ + 5e– → Mn++ + 4H2O
5వ దశ : ఎలక్ట్రాన్లను తుల్యం చేయడానికి ఆక్సీకరణ అర్ధ చర్యను 5 చేత, క్షయకరణ అర్ధ చర్యను 2 చేత గుణించాలి.
5SO2 + 10H2O → 5HS\(\mathrm{O}_4^{-}\) + 15H+ + 10e–
2Mn\(\mathrm{O}_4^{-}\) + 16H+ + 10e– → 2Mn++ + 8H2O
6వ దశ : పై రెండు అర్ధ చర్యలను కలపాలి.
5SO2 + 2Mn\(\mathrm{O}_4^{-}\) + 2H2O + H+ → 5HS\(\mathrm{O}_4^{-}\) + 2Mn++
c) H2O2(జల) + Fe++(జల) → Fe3+ (జల) + H2O(ద్ర) (ఆమ్ల ద్రావణంలో)
1వ దశ : ఆక్సీకరణ అర్ధ చర్య : Fe2+ (జల) → Fe3+ (జల)
క్షయకరణ అర్ధ చర్య : H2\(\mathrm{O}_2^{-1}\) (జల) → H2O-2
2వ దశ : ‘O’ పరమాణువులను తుల్యం చేయాలి.
H2O2 → H2O + H2O
H2O2 → 2H2O
‘H’ పరమాణువులను తుల్యం చేయాలి.
H2O2 + 2H+ → 2H2O
3వ దశ : విద్యుదావేశాలను తుల్యం చేయాలి.
Fe2+(జల) → Fe3+(జల) + e–
H2O2 + 2H+ + 2e– → 2H2O
4వ దశ : ఎలక్ట్రాన్లను తుల్యం చేయాలి.
2Fe2+ → 2Fe3+ + 2e–
H2O2 + 2H+ + 2e– → 2H2O
5వ దశ : పై తుల్య చర్యలను కలపాలి.
2Fe2+ + H2O2 + 2H+ → 2 Fe3+ + 2H2O
d) Cr2\(\mathrm{O}_7^{2-}\) + SO2(వా) → Cr3+ + \(\mathrm{SO}_4{ }^{2-}\) (ఆమ్ల ద్రావణంలో)
1వ దశ :
ఆక్సీకరణ అర్ధ చర్య : SO2 → S\(\mathrm{O}_4^{2-}\)
క్షయకరణ అర్ధ చర్య: Cr2\(\mathrm{O}_7^{2-}\) → Cr3-
2వ దశ : O, H మినహా ఇతర పరమాణువులను తుల్యం చేయాలి.

ప్రశ్న 62.
కింది సమీకరణాలను క్షార యానకంలో అయాన్-ఎలక్ట్రాన్ పద్ధతి ద్వారా, ఆక్సీకరణ సంఖ్యా పద్ధతి ద్వారా తుల్యం చేసి, ఆక్సీకరణ కారకాన్ని, క్షయకరణ కారకాన్ని గుర్తించండి.
a) P4(ఘ) + OH–(జల) → PH3(వా) + HP\(\mathrm{O}_2^{-}\) (జల)
b) N2H4(ద్ర) + ClO3 (జల) → NO (వా) + Cl–(వా)
c) Cl2O7(వా) + H2O2 → CI\(\mathrm{O}_2^{-}\)(జల) + O2(వా) + H+
జవాబు:
a)
P4(ఘ) + OH– (జల) → PH3(వా) + H3P\(\mathrm{O}_2^{-}\) (జల)
అయాన్-ఎలక్ట్రాన్ పద్ధతి :
1వ దశ : ఆక్సీకరణ సంఖ్యలను గుర్తించుట.
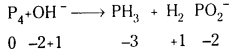
2వ దశ : P4 → PH3 క్షయకరణ అర్ధ చర్య
P4 → H2P\(\mathrm{O}_2^{-}\) ఆక్సీకరణ అర్ధ చర్య
3వ దశ : P పరమాణువులను తుల్యం చేయాలి.
P4 → 4PH3
P4 → 4H2P\(\mathrm{O}_2^{-}\)
4వ దశ : ఆక్సిజన్లను తుల్యం చేయాలి, ఆక్సిజన్ తక్కువగా ఉన్నవైపు H2O లు వ్రాయాలి.
P4 + 8H2O → 4H2P\(\mathrm{O}_2^{-}\)
5వ దశ : Hలను తుల్యం చేయాలి. చర్య క్షార యానకంలో జరుగుతున్నది కాబట్టి H2O మరియు OH– అయానులను కలపాలి. హైడ్రోజన్లు తక్కువగా ఉన్న వైపు ఎన్ని తక్కువగా ఉన్నాయో అన్ని H2O లను, వ్యతిరేక వైపు సమాన సంఖ్య
OH– లను కలపాలి.

1వ దశ : ఈ చర్యలో ఫాస్ఫరస్ ఆక్సీకరణం మరియు క్షయకరణం చెందుతుంది.
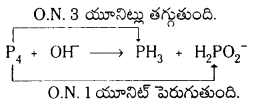
ఆక్సీకరణ సంఖ్యలో మార్పులను సమం చేయాలి.
P4 + OH– → PH3 + 3H2P\(\mathrm{O}_2^{-}\)
2వ దశ :
a) H, O లను తుల్యం చేయాలి. ఇందుకోసం హైడ్రోజన్ పరమాణువుల కొరత ఉన్న వైపు చర్య ఆమ్లయానకంలో జరిగినట్లైతే H+ అయాన్లని, క్షార యానకంలో జరిగినట్లయితే H2O ని తగిన సంఖ్యలో కలపాలి.
b) ఆక్సిజన్ పరమాణువుల కొరత ఉన్న వైపున చర్య ఆమ్ల యానకంలో జరిపితే H2O ని క్షారయానకంలో జరిగితే OH– ని తగిన సంఖ్యలో కలపాలి.
P4 + 3OH– + 3H2O → PH3 + 3H2P\(\mathrm{O}_2^{-}\)
తుల్య సమీకరణం P4 + 3OH– + 3H2O → PH3 + 3H2P\(\mathrm{O}_2^{-}\)
b) N2H2(ద్ర) + ClO (జల) → NO(వా) + Cl–(వా)
ఆక్సీకరణ అర్ధ చర్యను, క్షయకరణ అర్ధ చర్యను గుర్తించాలి.
1వ దశ :
N2H4(ద్ర) → NO(ద్ర) ఆక్సీకరణ అర్ధ చర్య
Cl\(\mathrm{O}_3^{-}\)(వా) → Cl–(వా)
2వ దశ : O, H నినహా మిగిలిన వాటిని తుల్యం చేయాలి.
N2H4(ద్ర) → 2NO
3వ దశ : చర్య క్షారయానకంలో జరుగుతున్నది. హైడ్రోజన్ తుల్యంచేయడానికి H2Oలను, OH– లను ఉపయోగించాలి. ముందుగా ఆక్సిజన్రను తుల్యం చేయాలి. అందుకోసం ఆక్సిజన్ తక్కువగా ఉన్నవైపు H2Oలను వ్రాయాలి.

ఆక్సీకరణ సంఖ్యా పద్ధతి : 1వ దశ : ఆక్సీకరణ సంఖ్యలో మార్పును గుర్తించాలి.
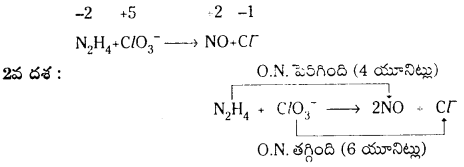
3వ దశ : ఆక్సీకరణ సంఖ్యలో పెరుగుదలను, తగ్గుదలను సమం చేయాలి. N2H4 ను 3 చేత, Cl\(\mathrm{O}_3^{-}\) ను 2చేత గుణించాలి.
3N2H4 + 4Cl\(\mathrm{O}_3^{-}\) → 6NO + 4Cl–
4వ దశ : H, O లు మిగిలిన పరమాణువులను తుల్యం చేయాలి. పై సమీకరణంలో అవి తుల్యం అయినవి.
5వ దశ : O, H లను తుల్యం చేయడానికి OH–, H2O లను వ్రాయాలి.
3N2H4 + 4Cl\(\mathrm{O}_3^{-}\) → 6NO + 4Cl– + 6H2O
c) Cl2O7(వా) + H2O2 → Cl\(\mathrm{O}_2^{-}\) (జల) + O2(వా) + H+ అయాన్ ఎలక్ట్రాన్ పద్ధతి లేదా అర్థ చర్యా పద్ధతి
1వ దశ :
Cl2O7 + H2O2 → Cl\(\mathrm{O}_2{ }^{-}\) + O2 + H+ ఆక్సీకరణ అర్ధ చర్యను, క్షయకరణ అర్ధ చర్యను విడివిడిగా వ్రాయాలి.
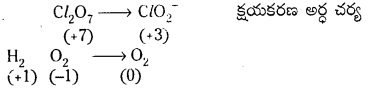
2వ దశ : పరమాణువులను (O, Hమినహా) తుల్యం చేయాలి.

ఆక్సీకరణ సంఖ్య పద్ధతి : ఆక్సీకరణ సంఖ్యలో పెరుగుదలను తగ్గుదలను గుర్తించాలి.
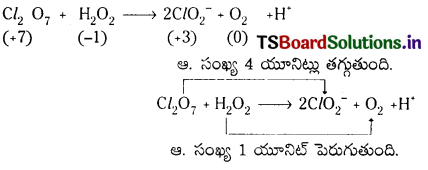
2వ దశ : ఆక్సీకరణ సంఖ్య పెరుగుదలను, తగ్గుదలను సమం చేయాలి. H2O2 ను 4 చే గుణించాలి.
Cl2O7 + 4H2O2 → 2Cl\(\mathrm{O}_2^{-}\) + O2 + H+
3వ దశ : O, H లను తుల్యం చేయాలి. దాగుడు మూతల పద్ధతిలో H2O2 OH– లను చేర్చాలి.
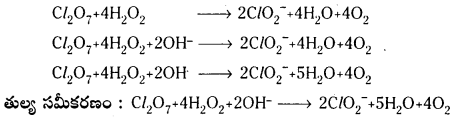

ప్రశ్న 63.
ఈ కింది చర్య ద్వారా ఏమి తెలుస్తోంది. (CN)2(వా) + 2OH–(జల) → CN–(జల) + CNO– (జల) + H2O(ద్ర)
జవాబు:
ఈ చర్యలో సయనోజన్ వాయువు క్షారయానకంలో అననుపాత చర్యకు లోనవుతోంది. ఈ చర్యలో CN ప్రాతిపదిక ఆక్సీకరణ సంఖ్య CN– ఏర్పడుటలో -1కి తగ్గుతుంది. CNO– లో +1 కి పెరుగుతుంది.
ప్రశ్న 64.
Mn3+ అయాన్ ద్రావణంలో అస్థిరంగా ఉండి, అననుపాతం చెంది Mn2+, MnO2, H+ అయాన్లను ఇస్తుంది. ఈ చర్యకు తుల్య అయానిక సమీకరణాన్ని రాయండి.
జవాబు:
Mn3+ + 2H2O → MnO2 + Mn++ + 4H+
2Mn3+ + 2H2O → MnO2 + Mn++ + 4H+
ప్రశ్న 65.
a) ఋణ ఆక్సీకరణస్థితిని మాత్రమే ప్రదర్శించే మూలకం ఏది ?
b) ధన అక్సీకరణస్థితిని మాత్రమే ప్రదర్శించే మూలకం ఏది ?
c) ధన, ఋణ ఆక్సీకరణ స్థితులు రెండింటినీ ప్రదర్శించే మూలకం ఏది ?
d) ధన, ఋణ అక్సీకరణ స్థితులలో దేనిని కూడా ప్రదర్శించని మూలకం ఏది ?
జవాబు:
a) ఫ్లోరిన్ F ఋణ ఆక్సీకరణస్థితిని మాత్రమే ప్రదర్శిస్తుంది. అది అధిక ఋణ విద్యుదాత్మకత గల మూలకం. ఫ్లోరిన్ కన్నా అధిక ఋణ విద్యుదాత్మకత కలిగిన మూలకము మరియొకటి లేదు. కనుక అది ఎల్లప్పుడు ఋణ ఆక్సీకరణస్థితి (-1) మాత్రమే చూపుతుంది.
b) CS అత్యధిక ధన విద్యుదాత్మకత గల మూలకము. అది ధన ఆక్సీకరణస్థితి (+1) ని మాత్రమే చూపుతుంది.
c) అయోడిన్ | ధన ఋణ ఆక్సీకరణ స్థితులను చూపగలదు. ఉదా : ICl3 లో I ఆక్సీకరణస్థితి HNal లో దాని అక్సీకరణ స్థితి -1.
d) నియాన్ Ne జడవాయువు. అది రసాయన చర్యలలో పాల్గొనదు. కనుక అది ధన లేదా ఋణ చూపదు.
ప్రశ్న66.
తాగునీటిని శుద్ధిచేయటానికి క్లోరినన్ను వాడతారు. అధిక క్లోరిన్ హానికరమైనది. అధికంగా ఉన్న క్లోరినన్ను సల్ఫర్ డై ఆక్సైడ్తో చర్య నొందించి తొలగిస్తారు. నీటిలో జరిగే ఈ ఆక్సీకరణ క్షయకరణ మార్పుకు తుల్య సమీకరణాన్నివ్వండి.
జవాబు:
SO2 + Cl2 + 2H2O → H2SO4 + 2HCl
ప్రశ్న67.
మీ పుస్తకంలో ఇచ్చిన ఆవర్తనపట్టికను పరిశీలించి, కింది ప్రశ్నలకు జవాబు ఇవ్వండి.
a) అననుపాత చర్యలను ప్రదర్శించే అలోహాలను ఎంపిక చేయండి.
b) అననుపాత చర్యలను ప్రదర్శించే మూడు లోహాలను ఎంపిక చేయండి.
జవాబు:
a) ఫాస్ఫరస్, సల్ఫర్, క్లోరిన్, బ్రోమిన్, అయోడిన్
b) క్రోమియం, మాంగనీస్, లెడ్
ప్రశ్న68.
ఆస్వాల్డ్ పద్ధతిలో నత్రికామ్లం తయారుచేసే చర్యల్లో మొదటి అంచెలో అమ్మోనియా ఆక్సిజన్తో ఆక్సీకరణం చెంది నైట్రిక్ ఆక్సైడ్, నీటి ఆవిరి వస్తాయి. చర్యను 10.0 గ్రా. అమ్మోనియా, 20.0 గ్రా. ఆక్సిజన్ జరిపితే గరిష్ఠంగా ఎంత నైట్రిక్ ఆక్సైడ్ వస్తుంది.
జవాబు:
ఆస్వార్డు పద్ధతిలో NH3 ఆక్సీకరణం చెంది నైట్రిక్ ఆక్సైడ్గా మారుతుంది.
4NH3 + 5O2 → 4NO + 6H2O
స్థాయికియోమెట్రీ
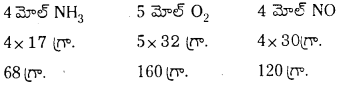
10 గ్రా అమ్మోనియాతో చర్యపొందే ఆక్సిజన్ భారం = \(\frac{10}{68}\) × 160 = 23.529 గ్రా
తగినంత ఆక్సిజన్ లేకపోవుట వలన 10గ్రా. అమ్మోనియా చర్య పొందలేదు. అందువల్ల 20 గ్రా. ఆక్సిజన్ మాత్రమే చర్యలో పాల్గొన్నప్పుడు NO ఏర్పడుతుంది.
160 గ్రా. ఆక్సిజన్ నుండి 120 గ్రా. NO ఏర్పడుతుంది.
20 గ్రా. ఆక్సిజన్ నుండి ?
NO భారం = \(\frac{20}{160}\) × 120 = 15 గ్రా.
[20 గ్రా. O2 తో చర్య పొందే అమ్మోనియా
160 గ్రా. O2 తో చర్య పొందే అమ్మోనియా 68 గ్రా.
20 గ్రా. ౦ తో చర్య పొందే అమ్మోనియా = \(\frac{20 \times 68}{160}\) = 8.5 గ్రా. NH3
68 గ్రా. అమ్మోనియా నుండి ఏర్పడే NO 120 గ్రా.
8.5 గ్రా. అమ్మోనియా నుండి ఏర్పడే NO = \(\frac{8.5}{68}\) × 120 = 15 గ్రా
∴ 10 గ్రా. అమ్మోనియా 20 గ్రా. ఆక్సిజన్తో చర్య పొందినపుడు 15 గ్రా. NO ఏర్పడుతుంది.
ప్రశ్న 69.
క్రింది లోహాలను వాటి లవణాల నుంచి ఒకదానితో ఒకటి స్థానభ్రంశం చెందించే క్రమంలో అమర్చండి.
Al, Cu, Fe, Mg, Zn.
జవాబు:
విద్యుత్ రసాయన శ్రేణిలో ఎక్కువ ఋణ క్షయకరణ పొటెన్షియల్ గల మూలకం దాని క్రింద నున్న మూలకాన్ని దాని లవణ ద్రావణం నుండి స్థానభ్రంశం చెందిస్తుంది.
ఉదా : CuSO4 + Zn → 2nSO4 + Cu
Zn++/Zn క్షయకరణ పొటెన్షియల్ -0.762 Cu++/Cu +0/337. జింక్కు ఎలక్ట్రానులను విడుదల చేసే స్వభావం ఎక్కువ. అందువల్ల Cu++ ను Cu గా క్షయకరణం చేస్తుంది.
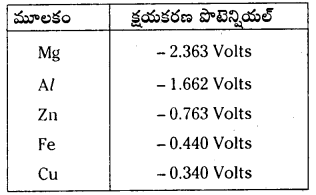
పై టేబుల్ నుండి స్థానభ్రంశ క్రమం క్రింది విధంగా ఉంటుంది.
Mg > Al > Zn > Fe > Cu
దీర్ఘ సమాధాన ప్రశ్నలు
ప్రశ్న 70.
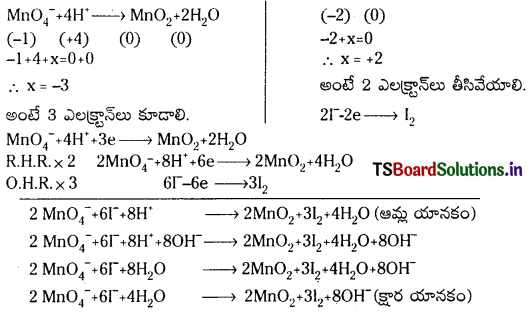
క్షార యానకంలో పర్మాంగనేట్ అయాన్, అయొడైడ్ (I–) అయానన్ను ఆక్సీకరణం చేసి, అయొడిన్ (I2), మాంగనీస్ డై ఆక్సైడ్ (MnO2) ఇచ్చే చర్యకు తుల్య అయానిక సమీకరణాన్ని రాయండి.
జవాబు:
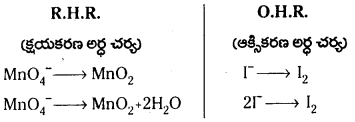
ప్రశ్న71.
ఆమ్ల యానకంలో పర్మాంగనేట్, సల్ఫైట్ అయాన్లను సల్ఫేట్ అయాన్లుగా ఆక్సీకరణ చేసే చర్యకు తుల్య సమీకరణాన్ని రాబట్టండి.
జవాబు:

ప్రశ్న72.
ఆమ్లయానకంలో ఆక్జాలిక్ ఆమ్లం, పర్మాంగనేట్ అయాన్తో Mn”tగా అక్సీకరించబడుతుంది. అయాన్ – ఎలక్ట్రాన్ పద్ధతిలో తుల్యం చేయండి.
జవాబు:
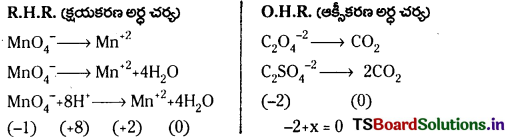

ప్రశ్న 73.
ఫాస్ఫరసు NaOH ద్రావణంలో వేడి చేస్తే ఫాస్ఫేన్ PH3, H2P\(\mathrm{O}_2^{-}\) లను ఇస్తుంది. తుల్య సమీకరణాన్ని వ్రాయండి.
జవాబు:


ప్రశ్న 74.
కింది సమీకరణాన్ని తుల్యం చేయండి.
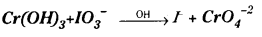
జవాబు:
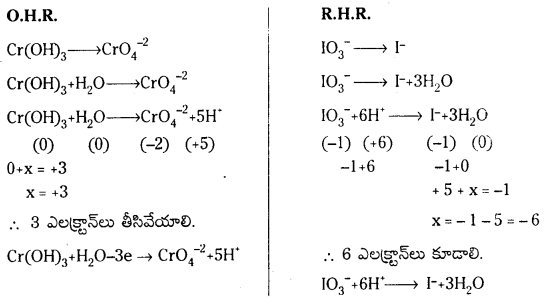
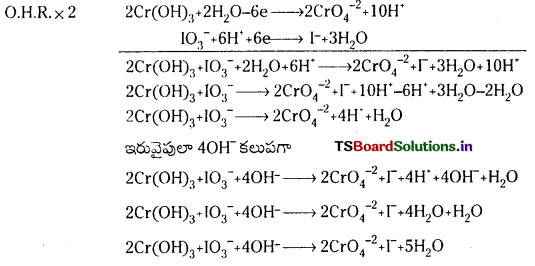
ప్రశ్న 75.
క్రింది సమీకరణాన్ని ఆక్సీకరణ సంఖ్య పద్ధతిలో తుల్యం చేయండి.
Mn\(\mathrm{O}_4^{-2}\) + Cl2 → Mn\(\mathrm{O}_4^{-}\) + Cl–
జవాబు:
మొదటిదశ : Mn\(\mathrm{O}_4^{-2}\) + Cl2 → Mn\(\mathrm{O}_4^{-}\) + Cl–
రెండవదశ : ఆక్సీకరణ సంఖ్యలలో మార్పులను గుర్తించాలి.
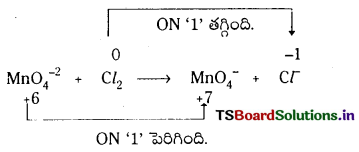
మూడవదశ : ఆక్సీకరణ సంఖ్యలో తగ్గుదల, పెరుగుదల సమానంగానే ఉన్నాయి.
నాల్గవదశ : O, H మినహా మిగిలిన పరమాణువులను తుల్యం చేయాలి.
Mn\(\mathrm{O}_4^{-2}\) + Cl2 → Mn\(\mathrm{O}_4^{-}\) + 2Cl–
ఐదవదశ : విద్యుదావేశాన్ని తుల్యం చేయాలి.
2Mn\(\mathrm{O}_4^{-2}\) + Cl2 → Mn\(\mathrm{O}_4^{-}\) + 2Cl–
ప్రశ్న 76.
వివిధ రకాల ఆక్సీకరణ, క్షయకరణ (రెడాక్స్) చర్యలను వివరించండి.
జవాబు:
ఆక్సీకరణం : ఒక కణం ఆక్సీకరణ సంఖ్య ఇచ్చిన చర్యలో పెరగడం ఆ కణం అక్సీకరణం అంటారు. క్షయకరణం : ఒక కణం ఆక్సీకరణ సంఖ్య ఇచ్చిన చర్యలో తగ్గడం ఆ కణం క్షయకరణం అంటారు.
ఆక్సీకరణ – క్షయకరణ చర్యలు : ఏక కాలంలో ఒక కణం ఆక్సీకరణం చెంది, వేరొక కణం క్షయకరణం చెందడం జరిగే రసాయన చర్యలను ఆక్సీకరణ-క్షయకరణ చర్యలు అంటారు. కాబట్టి పరస్పరం చర్య జరిపే కణాల అక్సీకరణ సంఖ్యలలో మార్పులను తీసుకువచ్చే చర్యలు ఆక్సీకరణ క్షయకరణ చర్యలు.
1. సంకలన చర్య : A + B → C
ఇందులో A గాని B గాని లేదా A, B లు రెండూ గాని మూలకస్థితిలో ఉంటే ఆక్సీకరణ క్షయకరణ చర్య జరుగుతుంది. ఇవన్నీ సంయోగచర్యలే.
ఉదా :
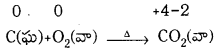
2. విఘటన చర్య :
సంకలన చర్యకు వ్యతిరేకంగా జరిగే చర్యను విఘటన చర్య అంటారు.
ఉదా :
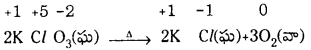
3. స్థానభ్రంశ చర్యలు : స్థానభ్రంశ చర్యలు 2 రకాలు. 1. లోహ స్థానభ్రంశ చర్యలు. 2. అలోహ స్థానభ్రంశ చర్యలు.
X + YZ → XZ + Y
1. లోహ స్థానభ్రంశ చర్యలు : సమ్మేళనంలోని లోహాన్ని వేరొక లోహంతో స్థానభ్రంశం చెందించవచ్చు. ఈ చర్యలలో క్షయకరణం చేసే లోహం క్షయీకృతం అయ్యే లోహంకంటే బలమైన క్షయకారిణి. దీనిని బట్టి క్షయకరణికి ఎలక్ట్రాన్లను వదులుకొనే శక్తి క్షయకరణం చెందే లోహం కంటే ఎక్కువ అని తెలుస్తుంది.
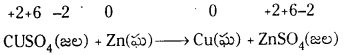
1. అలోహ స్థానభ్రంశ చర్యలు : అలోహాన్ని స్థానభ్రంశం చేసే చర్యలలో హైడ్రోజన్ స్థానభ్రంశం అరుదుగా జరిగే ఆక్సిజన్ స్థానభ్రంశం ఉంటాయి.
క్షార లోహాలన్నీ, కొన్ని క్షార మృత్తిక లోహాలు (Ca, Sr, Ba) చాలా బలమైన క్షయకరణులు. అవి చల్లని నీటి నుంచి హైడ్రోజన్ను స్థాన భ్రంశం చేస్తాయి.
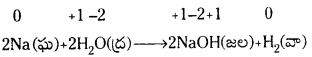
సాపేక్షంగా తక్కువ చర్యాశీలతగల లోహాలు (మెగ్నీషియమ్, ఐరన్ వంటివి) నీటి ఆవిరితో చర్యలో హైడ్రోజన్ని స్థానభ్రంశం చేస్తాయి.
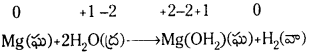
నీటి ఆవిరితో కూడా చర్య జరపని లోహాలు
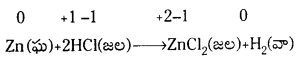
ఫ్లోరిన్ చాలా చురుకైన మూలకం. ద్రావణాల నుంచి క్లోరైడ్, బ్రోమైడ్, అయోడైడ్లు అయాన్లను స్థానభ్రంశం చేస్తుంది. వాస్తవానికి ఫ్లోరిన్ నీటి నుంచి ఆక్సిజనిని స్థానభ్రంశం చేయగలిగేటంత చర్యాశీలత గలది.
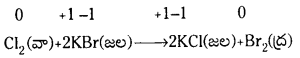
4. అసౌష్టవ విఘటన చర్యలు (అననుపాత చర్యలు) :
అసౌష్ఠవ విఘటన చర్యలలో నిర్ధిష్ట కణంలోని మూలకం ఒక ఆక్సీకరణ స్థితిలో ఉంటుంది. అది ఒకే సమయంలో ఆక్సీకరణం, క్షయకరణం కూడా చెందుతుంది. అననుపాతం చెందే క్రియా జనకాల్లో ఒకదాంట్లోని మూలకం ఒకటి కనీసం మూడు ఆక్సీకరణ స్థితులలో ఉండగలదు. క్రియాజన్యంలో ఆ మూలకం మూడు ఆక్సీకరణ స్థితులలోని మధ్యస్థ స్థితిలో ఉంటుంది. దానికి పై ఆక్సీకరణ స్థితి కింది ఆక్సీకరణ స్థితి ఉన్న క్రియాజన్యాలు ఏర్పడతాయి. ఈ విధమైన చర్యకు హైడ్రోజన్ పెరాక్సైడ్ విఘటనం మనకు పరిచయమైన ఉదాహరణ. ఇందులో ఆక్సిజన్ అసౌష్ఠవ విఘటనం
చెందుతుంది.
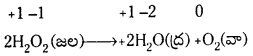
ఈ చర్యలో పెరాక్సైడ్లోని ఆక్సిజన్ -1 స్థితిలో ఉంటుంది. దాని స్థితి O2 లో సున్నా అక్సీకరణ స్థితికి పెరగడం, H2O లో -2 ఆక్సీకరణ స్థితికి తగ్గడం జరుగుతుంది.
ఫాస్ఫరస్, సల్ఫర్, కోర్లిన్లు క్షార యానకంలో ఈ అననుపాత చర్యలను జరుపుతాయి.
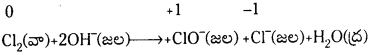
ప్రశ్న 77.
స్థిరానుపాత నియమాన్ని తెలపండి ఒక సమస్యను సాధనచేయడం ద్వారా ఈ నియమాన్ని విశదీకరించండి.
జవాబు:
జోసెఫ్ ప్రౌస్ట్ (Joseph Proust) అనే ఫ్రెంచి రసాయన శాస్త్రవేత్త ఈ నియమాన్ని చెప్పాడు. “ఒక నిర్దిష్ట సమ్మేళనంలో అవే మూలకాలు భారాత్మకంగా ఒకే నిష్పత్తిలో కలిసి ఉంటాయి.” అని చెప్పాడు.
ప్రౌస్ట్ రెండు నమూనాలు క్యూప్రక్ కార్బొనేట్తో పని చేశాడు. ఒక నమూనా సహజ సిద్ధమైంది. రెండోది కృత్రిమంగా తయారు చేయబడింది. ఈ రెండు నమూనాల సంఘటనం ఒక్కటిగానే ఉంటుంది.
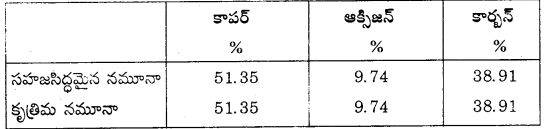
ఈ విధంగా ప్రాప్తి స్థానంతో సంబంధం లేకుండా ఒక నిర్దిష్ట సమ్మేళనంలో ఘటక మూలకాలు భారాత్మకంగా అదే నిష్పత్తిలో సంయోగం చెంది ఉంటాయి.
ప్రశ్న 78.
క్రింది చర్యల అంశమాపనంలో అంతిమ స్థానాలను ఎట్లా గుర్తిస్తారు.
(i) Mn\(\mathrm{O}_4{ }^{2-}\) తో Fe2+ ను ఆక్సీకరించుట.
(ii) Cr2\(\mathrm{O}_7^{2-}\) తో Fe+ ను ఆక్సీకరించుట.
(iii) Cu2+ తో I– ను ఆక్సీకరించుట.
జవాబు:
(i) 2Mn\(\mathrm{O}_4^{-}\) తో Fe2+ పర్మాంగనేటు ఫెర్రస్ను ఫెర్రిక్గా ఆమ్లయానకంలో ఆక్సీకరణం చేస్తుంది. ఈ చర్యలో పర్మాంగనేట్ వివర్ణం అవుతుంది. అందువల్ల అంతిమ స్థానం వద్ద చర్య పొందని పర్మాంగనేట్ వల్ల ద్రావణానికి కలిగే గులాబి రంగు ద్వారా అంతిమ స్థానాన్ని గుర్తించవచ్చు. ఈ చర్యలో పర్మాంగనేట్ స్వయం సూచిక. Fe++ అంతయూ F+++ గా మారిన తరువాత పర్మాంగనేట్ వల్ల ద్రావణానికి గులాబి రంగు కలుగుతుంది.
(ii) Cr2\(\mathrm{O}_7{ }^{2-}\) తో Fe++ ను ఆక్సీకరించుట : అంత్యస్థానము వద్ద స్వయం మార్పు ఖచ్చితంగా లేకపోతే అంత్యస్థానాన్ని తెలుసుకోవడం కోసం సూచికలను వాడతారు. Cr2\(\mathrm{O}_7^{2-}\) స్వయం సూచిక కాదు. కాని తుల్య స్థానం దాటిన వెంటనే డైఫినైల్ ఎమీన్ సూచికను శాశ్వతంగా ఆక్సీకరణం చేస్తుంది. ఫలితంగా ముదురు నీలిరంగు వస్తుంది. ఇది అంత్యస్థానాన్ని సూచిస్తుంది.
Cr2\(\mathrm{O}_7^{2-}\)తో Fe++ ను అంశమాపనం చేయడంలో డైఫినైల్ ఎమీన్ సూచికను వాడతారు. అంతిమస్థానం వద్ద ముదురు నీలిరంగు ఏర్పడుతుంది.
(iii) Cu++ తో I– ను ఆక్సీకరించుట : Cu++ అయాన్ను అయోడైడ్ అయానుతో జరిపే చర్యలో అయొడీన్ ను విడుదల చేస్తుంది. 2Cu++(జల) + 4l–(జల) → Cu2l2(ఘ) + I2(జల). ఈ అంశమాపనంలో విడుదలైన అయొడిన్ న్ను థయోసల్ఫేట్ అంశమాపనం చేస్తారు.
I2(జల) + 2S2\(\mathrm{O}_3{ }^{2-}\)(జల) → 21–(జల) + S4\(\mathrm{O}_6^{2-}\) (జల). ఇపుడు స్టార్చిని కలిపితే ముదురు నీలి రంగు వస్తుంది. అయొడిన్తో థయోసల్ఫేట్ అయానులు పూర్తిగా చర్య పొందినపుడు ఈ రంగు పోతుంది. ఈ విధంగా అంత్య స్థానాన్ని తేలికగా తెలుసుకోవచ్చు.
ప్రశ్న 79.
కింది చర్యలలో వెలువడే కార్బన్ డై ఆక్సైడ్ భారాన్ని లెక్కకట్టండి.
1. గాలిలో ‘ఒక మోల్ కార్బన్ను మండించినప్పుడు
2. 16 గ్రా. డైఆక్సిజన్లో 2 మోల్ల కార్బన్ను మండించినపుడు
జవాబు:
1.
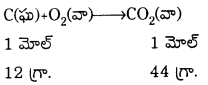
ఒక మోల్ కార్బన్ను మండించినపుడు 44 గ్రా. CO2 విడుదలవుతుంది.
2. 16 గ్రా. డైఆక్సిజన్లో 2 మోల్ల కార్బన్ను మండించినపుడు

64 గ్రా. ఆక్సిజన్లో మండే కార్బన్ 24 గ్రా.
16 గ్రా. ఆక్సిజన్లో మండే కార్బన్ ?
= \(\frac{16}{64}\) × 24 = 6గ్రా.
కనుక 6 గ్రా. కార్బన్ మాత్రమే చర్యపొంది CO2 ను ఇస్తుంది. 12 గ్రా. కార్బన్ 32 గ్రా. ఆక్సిజన్తో చర్య పొందుతుంది. కనుక 6 గ్రా. కార్బన్ 16 గ్రా. ఆక్సిజన్తో చర్య పొందుతుంది.
ప్రశ్న 80.
కింది రసాయన సమీకరణాన్ని అనుసరించి, డైనైట్రోజన్ డైహైడ్రోజన్ ఒకదానితో ఒకటి చర్య జరిపినప్పుడు అమ్మోనియా ఏర్పడుతుంది.
N2(వా) + 3H2(వా) + 2NH3(వా)
(i) 2.00 × 103గ్రా. డైనైట్రోజన్, 1.00 × 103 గ్రా. డై హైడ్రోజన్తో చర్య జరిపినప్పుడు ఏర్పడే అమ్మోనియా భారాన్ని లెక్కించండి.
(ii) రెండు క్రియాజనకాలలో ఏదైనా చర్య జరపకుండా మిగిలిపోతుందా?
(iii) అయితే ఏ క్రియాజనకం మిగిలిపోతుంది. దాని భారం ఎంత?
జవాబు:
(i) నైట్రోజన్ మోత్ల సంఖ్య = \(\frac{2 \times 10}{28}\) = 71.4 మోల్లు
హైడ్రోజన్ మోత్ల సంఖ్య = \(\frac{1 \times 10^3}{2}\) = 500 మోల్లు
సమీకరణం ప్రకారం

తగినంత హైడ్రోజన్ ఉన్నది కనుక 71.4 మోల్లు నైట్రోజన్ చర్య పొందుతుంది.
71.4 మోల్ నైట్రోజన్ 2 × 71.4 మోల్ల అమ్మోనియాను ఇస్తుంది.
∴ ఏర్పడే అమ్మోనియా భారం 2 × 71.4 × 17గ్రా. = 247.6 గ్రా.
ii) ఈ చర్యలో అధికంగా ఉన్న హైడ్రోజన్ మిగిలిపోతుంది.
iii) మిగిలిన ఆక్సిజన్ = 500 – 214.2 = 285.8 మోల్స్
ఆక్సిజన్ భారం = 285.8 × 2 గ్రా = 571.6 గ్రా.
ప్రశ్న 81.
కింది సమ్మేళనపు అణువులలో కింద గీతలో చూపించిన మూలకాల ఆక్సీకరణ సంఖ్యలను తెలపండి.
a) NaH2PO4
b) NaHSO4
c) H4P2O7
d) K2MnO4
e) CaO2
f) NaBH4
g) H2S2O7
h) KAl(SO4)2.12H2O
జవాబు:
(a) NaH2PO4
+1+2+x-8=.0
x-5 = 0 x=+5
ఫాస్పరస్ ఆక్సీకరణ సంఖ్య = +5
b) NaHSO4
1+1+x-8=0
x-6= 0 x=+6
సల్ఫర్ ఆక్సీకరణ సంఖ్య = +6
c) H4P2O7
+4+2x+-14 = 0
2x-10= 0 x = \(\frac{10}{2}\) = +5
H2P2O7 P ఆక్సీకరణ సంఖ్య = +5
d) K2MnO4
Mn ఆక్సీకరణ సంఖ్య = x అనుకొనుము.
+2+x-8 = 0
x-6 = 0
x=+6
K2MnO4 Mn ఆక్సీకరణ సంఖ్య = +6
e) CaO2
(Ca) క్షార మృత్తిక లోహాల ఆక్సీకరణ స్థితి = +2
‘O’ ఆక్సీకరణ స్థితి = X
+2+2x = 0 2x = -2 x = -1
CaO2 లో O ఆక్సీకరణ స్థితి = -1

f) NaBH4
+1 +x+-4 = 0
x-3= 0 x=+3
NaBH4 లో బోరాన్ ఆక్సీకరణ సంఖ్య = +3
g) H2S2O7
+2+2x-14 = 0
2x-12= 0 2x= +12 x=+6
H2S2O7 లో ‘S’ ఆక్సీకరణ సంఖ్య = +6
(h) KAI(SO4)2.12H2O
\(\mathrm{SO}_4^{–}\) లో ‘S’ ఆక్సీకరణ సంఖ్య ఇచ్చిన పదార్థంతో,
‘S’ ఆక్సీకరణ సంఖ్య = +6
x-8=-2 x=+6
ప్రశ్న 82.
కింది వాటిలో కింద గీత చూపించిన మూలకాల ఆక్సీకరణ సంఖ్యలు లెక్క కట్టండి. మీరు ఆ ఫలితాలను ఎలా సమర్థించుకుంటారు?
జవాబు:
a) H2S4O6
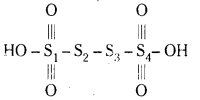
S1, S2ల ఆక్సీకరణ సంఖ్యలు సున్న
S1, S4 ల ఆక్సీకరణ సంఖ్యలు +5
సరాసరి విలువ = \(\frac{10}{4}\) = 2.5
b) Fe3O4
Fe3O4 లో FeO మరియు Fe3O4 ఉంటాయి.
FeO లో Fe ఆక్సీకరణ స్థితి = +2
Fe2O3 లో Fe ఆక్సీకరణ స్థితి = + 3
సరాసరి ఆక్సీకరణ స్థితి = \(\frac{+2+2(+3)}{3}\) = \(\frac{8}{3}\) = 2.67
c) CH3-CH2-OH
CH3 సమూహంలోని కార్బన్ ఆక్సీకరణ స్థితి = -3
CH2OH లో కార్బన్ ఆక్సీకరణ స్థితి = -1
d) CH3COOH
CH3 లో C ఆక్సీకరణ స్థితి -3
COOH లో C ఆక్సీకరణ స్థితి +3
అదనపు ప్రశ్నలు
ప్రశ్న 1.
16 గ్రా. మీథేన్ను మండిస్తే తయారయ్యే నీటి పరిమాణాన్ని గణించండి.
జవాబు:
మీథేన్ దహనక్రియకు తుల్య సమీకరణం
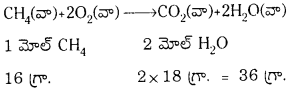
∴ 16 గ్రా. మీథేన్ ను మండిస్తే తుల్య సమీకరణాన్ని అనుసరించి, 36 గ్రా. నీరు ఏర్పడుతుంది.
ప్రశ్న 2.
దహన చర్యలో 22 గ్రా. CO2 ని ఏర్పరచడానికి ఎన్ని మోల్ల మీథేన్ కావాలి.
జవాబు:
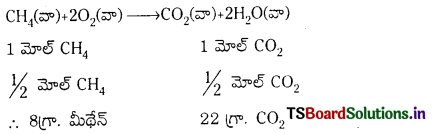
∴ 22 గ్రా. CO2 ను ఏర్పరచడానికి 8 గ్రా. మీథేన్ అనగా \(\frac{8}{16}\) గ్రా. = 0.5 గ్రా. మోల్ల మీథేన్ కావలెను.
ప్రశ్న 3.
పరిమిత కారకం అంటే ఏమిటి?
జవాబు:
సమతుల రసాయన చర్యకు ఉండవలసిన క్రియాజనకాల పరిమాణాల కంటే తక్కువ పరిమాణంలో కొన్ని క్రియాజనకాలు ఉన్నప్పుడు ఒక క్రియాజనకం మరొక క్రియాజనకం కన్నా అధికంగా ఉంటుంది. తక్కువగా ఉన్న క్రియాజనకం కొంత చర్య జరిగిన తరువాత పూర్తిగా ఖర్చు అయిపోతుంది. దాని తరువాత రెండో క్రియాజనకం ఎంత ప్రమాణంలో ఉన్నప్పటికి చర్య జరగదు. కాబట్టి ఖర్చు అయిపోయిన క్రియాజనకం ఏర్పడే క్రియాజన్యం పరిమాణాన్ని పరిమితం చేస్తుంది. అందువల్ల దానిని పరిమిత కారకం అంటారు.
ప్రశ్న 4.
50 కేజీల N2(వా), 10 కేజీల H2(వా) ని కలిపి NH3 (వా) ను తయారుచేస్తారు. ఏర్పడిన NH3(వా)ని లెక్కించండి. ఈ పరిస్థితులలో NH3(వా)ని తయారు చేయడానికి ఏదైనా పరిమిత కారకం ఉంటే దానిని గుర్తించండి.
జవాబు:
50 Kg ల N2 మోల్ సంఖ్య = \(\frac{50 \times 10^3}{28}\) = 17.86 × 102 మోల్.
10 Kg ల H2 మోల్ సంఖ్య = \(\frac{10 \times 10^3}{2.016}\) = 4.96 × 103 మోల్.
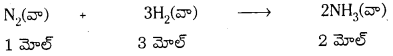
17.86 × 102 మోల్ 3 × 17.8 × 102 మోల్ 2 × 17.86 × 102 మోల్
17.86 × 102 మోల్ల N2 తో చర్య జరపడానికి అవసరమయ్యే H2 = 5.36 × 103 మోల్
కాని 4.96 × 103 మోల్ H2 మాత్రమే ఉంది.
కాబట్టి హైడ్రోజన్ పరిమిత కారకం అవుతుంది.
3 మోల్ల హైడ్రోజన్ – 2 మోల్ NH3 ను ఇస్తుంది.
4.96 × 103 మోల్ హైడ్రోజన్ నుండి ఏర్పడే NH3
= \(\frac{4.96 \times 10^3}{3}\) × 2 = 3.30 × 103 మోల్.
NH3 భారం గ్రాములలో = 3.30 × 103 × 17 గ్రా. = 56.1 × 103గ్రా. = 56.1 Kgలు.
ప్రశ్న 5.
2 గ్రా. ‘A’ ని 18 గ్రా. నీటిలో కలిపి ద్రావణాన్ని తయారుచేస్తారు. ద్రావితం ద్రవ్యరాశిని, శాతాన్ని లెక్కించండి.
జవాబు:
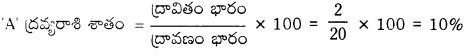
ప్రశ్న 6.
4 గ్రా. NaOH ని తగినంత నీటిలో కరిగించి 250 మి.లీ. ద్రావణం చేయగా దాని మొలారిటీని లెక్కించండి.
జవాబు:
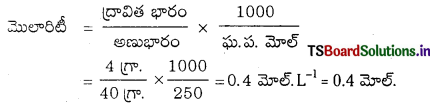
ప్రశ్న 7.
500 మి.లీ.ల ద్రావణంలో 6.3 గ్రా. H2C2O4. 2H2O ఉంటే దాని నార్మాలిటి ఎంత?
జవాబు:
ఆక్సాలిక్ ఆమ్లం H2C2O4.2H2O
అణుభారం = 126
తుల్యభారం = \(\frac{126}{2}\) = 63
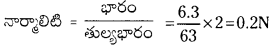

ప్రశ్న 8.
250 మోల్ల 0.5 N ద్రావణాన్ని తయారుచేయడానికి కావలసిన Na2CO3 ద్రవ్యరాశిని కనుక్కోండి.
జవాబు:
ద్రావణపు నార్మాలిటి = 0.5N
Na2CO3 తుల్యభారం = \(\frac{106}{2}\) = 53
ఘనపరిమాణం = 250mL = \(\frac{250}{1000}\)L
ద్రావిత భారం = నార్మాలిటి × ఘ.ఫ.లీ × గ్రాము. తుల్యభారం
= 0.5 × \(\frac{250}{1000}\) × 53 = \(\frac{53}{8}\) = 6.62 గ్రా.
ప్రశ్న 9.
ఇవ్వబడిన చర్యలలో ఆక్సీకరణం – క్షయకరణం చెందే పదార్థాలను గుర్తించండి.
(i) H2S(వా) + Cl2(వా) → 24Cl(వా) + S(ఘ)
(ii) 3Fe3O4(ఘ) + 8Al(ఘ) → 9Fe(ఘ) + 4Al2O2(ఘ)
(iii) 2Na(ఘ) + H2(వా) → 2NaH(ఘ)
జవాబు:
(i) H2S ఆక్సీకరణం చెందింది. అధిక ఋణ విద్యుదాత్మకత గల క్లోరిన్ని హైడ్రోజన్ సంకలనం చేయబడింది. క్లోరిన్ క్షయకరణం చెందింది. దాని ఆక్సీకరణస్థితి 0 నుండి (-1) కి తగ్గింది.
సల్ఫర్ ఆక్సీకరణస్థితి -2 నుండి 0 కు పెరుగుతుంది. అందువల్ల ‘S’ ఆక్సీకరణం చెందింది.
(ii) 3Fe3O4 + 8Al → 9Fe + 4Al2O3 Fe+++, Fe గా క్షయకరణం చెందింది. దాని ఆక్సీకరణస్థితి + 3 నుండి ‘0’కు తగ్గింది. Al ఆక్సీకరణ స్థితి 0 నుండి +3కు పెరిగింది. కనుక ఆక్సీకరణం చెందింది.
(iii) Na అక్సీకరణ స్థితి నుండి 0 నుండి +1 కు పెరిగింది. కనుక ఆక్సీకరణం. H ఆక్సీకరణ స్థితి 0 నుండి -1కి తగ్గింది. కనుక క్షయకరణం.

![]()
![]()

![]()



![]()



![]()


![]()





























































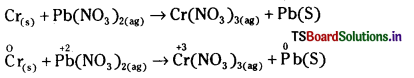
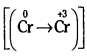 లో మార్పు 3 యూనిట్లు క్షయకరణ ప్రక్రియ [(pb+2 → Pb0)] లో మార్పు 2 యూనిట్లు. ఆక్సీకరణ ప్రక్రియలో ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పు, క్షయకరణ ప్రక్రియలో వచ్చిన ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పుకు సమానం చేయాలి. తగిన సంఖ్యలతో గుణించాలి.
లో మార్పు 3 యూనిట్లు క్షయకరణ ప్రక్రియ [(pb+2 → Pb0)] లో మార్పు 2 యూనిట్లు. ఆక్సీకరణ ప్రక్రియలో ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పు, క్షయకరణ ప్రక్రియలో వచ్చిన ఆక్సీకరణ సంఖ్య యూనిట్లలో మార్పుకు సమానం చేయాలి. తగిన సంఖ్యలతో గుణించాలి.