TS Inter 1st Year Maths 1B Maxima and Minima Important Questions

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Maxima and Minima Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Maxima and Minima Important Questions

Question 1.
Find two positive integers whose sum is 16 and the sum of whose square is minimum. [Mar. ’18 (AP); Mar. ’07; May ’03]
Solution:
Let x, y be the required positive integers.
Given that sum of two positive integers = 16
x + y = 16
y = 16 – x
Sum of the squares of the numbers = x² + y²
= x² + (16 – x)²
= x² + 256 + x² – 32x
= 2x² – 32x + 256
Let f(x) = 2x² – 32x + 256
Now, f(x) = 4x – 32
f”(x) = 4
for maxima or minima, f'(x) = 0
4x – 32 = 0
4x = 32
x = 8
x = 8 ⇒ f”(8) = 4 > 0
∴ f(x) has minima at x = 8
If x = 8, y = 16 – 8 = 8
∴ The required numbers are 8, 8.

Question 2.
From a rectangular sheet of dimensions 30 cm × 80 cm. Four equal squares of side x cm are removed at the corners and the sides are then turned up so as to form an open rectangular box. Find the value of x so that the volume of the box is the greatest. [Mar. ’16 (AP), ’14, ’09; Mar. ’18, May ’15 (TS)]
Solution:
Let l, b, h denote the length, breadth, and height of the box.
Since x cm are removed at the corners. Then
l = 80 – 2x; b = 30 – 2x; h = x

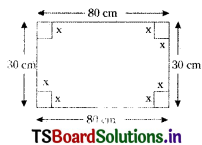
The volume of a box, V = lbh
= (80 – 2x) (30 – 2x) x
V = (80 – 2x) (30x – 2x²)
= 2400x – 160x² – 60x² + 4x³
= 4x³ – 220x² + 2400x
\(\frac{\mathrm{dV}}{\mathrm{dx}}\) = 12x² – 440x + 2400
\(\frac{\mathrm{d}^2 \mathrm{V}}{\mathrm{dx}^2}\) = 24x – 440
V has maxima or minima, \(\frac{\mathrm{dV}}{\mathrm{dx}}\) = 0
12x² – 440x + 2400 = 0
3x² – 110x + 600 = 0
3x² – 90x – 20 x + 600 = 0
3x(x – 30) – 20(x – 30) = 0
(x – 30)(3x – 20) = 0
x – 30 = 0 (or) 3x – 20 = 0
x = 30 (or) x = \(\frac{20}{3}\)
If x = \(\frac{20}{3}\), \(\left(\frac{\mathrm{d}^2 \mathrm{~V}}{\mathrm{dx^{2 }}}\right)_{\mathrm{x}=\frac{20}{3}}\)
= 24(\(\frac{20}{3}\)) – 440
= 160 – 440
= -280 < 0
∴ V has maxima at x = \(\frac{20}{3}\)
∴ x = \(\frac{20}{3}\) cm

Question 3.
A window is in the shape of a rectangle surmounted by a semicircle. If the perimeter of the window is 20 ft. Find the maximum area. [Mar. ’17, ’15 (TS); May ’12, ’09]
Solution:
Let r be the radius of the semi-circle
Let x be the one side of a rectangle.
Given that, the perimeter of the window = 20ft

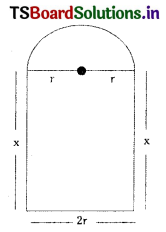
x + πr + x + 2r = 20
2x = 20 – πr – 2r ……..(1)
Area of window = Area of rectangle + Area of semi-circle
A = x(2r) + \(\frac{\pi r^2}{2}\)
A = r(20 – πr – 2r) + \(\frac{\pi r^2}{2}\)

Question 4.
If the curved surface of the right circular cylinder inscribed in a sphere of radius ‘r’ is maximum. Show that the height of the cylinder is √2r. [May ’15 (AP), ’13, ’11, ’10, ’04; Mar. ’13, ’08, ’04]
Solution:
Given r be the radius of the sphere.
Let R, h be the base radius and height of the cylinder.

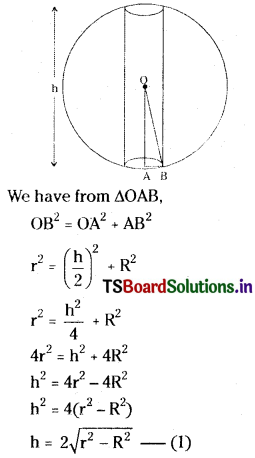
Question 5.
A wire of length l is cut into two parts which are bent respectively in the form of a square and a circle. What are the lengths of pieces of the wire respectively so that the sum of the areas is the least? [Mar. ’17 (AP), ’14; B.P.]
Solution:
Given that the total length of wire = l
Let x be the first part length and it is bent in the form of a square.
The remaining part l – x is made into a circle of radius ‘r’.
Let y be the side of the square.
The perimeter of a square = 4y

Question 6.
Find the absolute maximum value and absolute minimum value of the function f(x) = x + sin 2x on [0, π].
Solution:
Given f(x) = x + sin 2x
f'(x) = 1 + 2 cos 2x
and f”(x) = -4 sin 2x
For maximum or minimum we have

Question 7.
Find two positive integers x and y such that x + y = 60 and xy³ is maximum. [Mar. ’15 (AP); May ’14]
Solution:
Let x, y be the required positive integers
given that x + y = 60
y = 60 – x
given that xy³ is maximum
Let f(x) = x(60 – x)³
Now, f(x) = x . 3(60 – x)² (0 – 1) + (60 – x)³ . 1
= -3x(60 – x)² + (60 – x)³
= (60 – x)² (-3x + 60 – x)
= (60 – x)² (60 – 4x)
f”(x) = (60 – x)² (0 – 4) + (60 – 4x) . 2(60 – x) (0 – 1)
= -4(60 – x)² – 2(60 – 4x) (60 – x)
f(x) has maximum or minimum, f'(x) = 0
(60 – x)² (60 – 4x) = 0
(60 – x)² = 0 (or) 60 – 4x = 0
60 – x = 0 (or) 60 = 4x
x = 60 (or) x = 15
∴ x = 60, 15
If x = 60,
f”(60) = -4(60 – 60) – 2(60 – 4 . 60) (60 – 60)
= 0 – 0
= 0
f(x) has neither maximum nor minimum.
If x= 15,
f”(15) = -4(60 – 15)² – 2(60 – 4 . 15) (60 – 15)
= -4(45)² – 0
= -4(45)² < 0
∴ f(x) has maximum at x = 15
If x = 15, y = 60 – 15 = 45
∴ The required positive integers are 15, 45.

Some More Maths 1B Maxima and Minima Important Questions

Question 8.
Find the maximum area of the rectangle that can be formed with a fixed perimeter of 20. [Mar. ’19 (TS)]
Solution:
Let x and y denote the length and breadth of a rectangle respectively.
Given that the perimeter of the rectangle = 20
2(x + y) = 20
x + y = 10
y = 10 – x
The area of a rectangle, A = xy
A = x(10 – x) = 10x – x²

Question 9.
Prove that the radius of the right circular cylinder of the greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
Solution:
Let ‘O’ be the centre of the circular base of the cone & height be ‘h’.
Let ‘r’ be the radius of the circular base of the cone. Then AO = h, OC = r.
Let a cylinder with radius x(OS) be inscribed in the given cone.
let its height be u, i.e., PR = OD = QS = u.



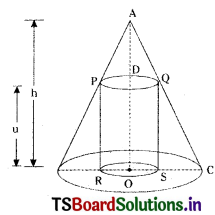
Hence the radius of the cylinder of the greatest curved surface which can be inscribed in a given cone is \(\frac{r}{2}\).

Question 10.
The profit function P(x) of a company selling x items per day is given by P(x) = (150 – x)x – 1000. Find the no.of items that the company should manufacture to get maximum profit. Also, find the maximum profit.
Solution:
Given P(x) = (150 – x)x – 1000
P(x) = 150x – x² – 1000
Now, P'(x) = 150 – 2x
For maximum or minimum, P'(x) = 0
150 – 2x = 0
2x = 150
x = 75
P”(x) = 0 – 2 . 1 = -2
If x = 75
P”(75) = -2 < 0
∴ P(x) has maximum at x = 75.
Maximum value P(75) = (150 – 75)75 – 1000 = 4625
∴ The required no.of items = 75
∴ Maximum profit = 4625.

Question 11.
Find the maxima or minima of f(x) = x³ – 6x² + 9x + 15, ∀ x ∈ R.
Solution:
Given, f(x) = x³ – 6x² + 9x + 15
Now, f'(x) = 3x² – 12x + 9
For, maxima or minima, f'(x) = 0
3x² – 12x + 9 = 0
3x² – 3x – 9x + 9 = 0
3x(x – 1) – 9(x – 1) = 0
(x – 1)(3x – 9) = 0
x – 1 = 0 or 3x – 9 = 0
x = 1 (or) x = 3
∴ x = 1, 3
f”(x) = 6x – 12
If x = 1, f”(1) = 6(1) – 12
= 6 – 12
= -6 < 0
f(x) has maxima at x = 1
maxima value = f(1) = (1)³ – 6(1)² + 9(1) + 15
= 1 – 6 + 9 + 15
= 19
If x = 3, f”(3) = 6 . 3 – 12
= 18 – 12
= 6 > 0
f(x) has minima at x = 3
minima value = f(3)
= (3)³ – 6(3)² + 9(3) + 15
= 27 – 54 + 27 + 15
= 15

Question 12.
Find the maxima or minima of f(x) = \(\frac{x}{2}+\frac{2}{x}\), ∀ x ∈ (0, ∞)
Solution:

Question 13.
Define the strictly increasing function and strictly decreasing function on an interval. [May ’14]
Solution:
Let f: A → R be a function. Then
(i) f is said to be strictly increasing on A if
x₁, x₂ ∈ A,
x₁ < x₂
⇒ f(x₁) < f(x₂)
(ii) f is said to be strictly decreasing on A if
x₁, x₂ ∈ A,
x₁ > x₂
⇒ f(x₁) > f(x₂)

Question 14.
Verify Rolle’s theorem for the function f(x) = log(x² + 2) – log 3 on [-1, 1]. [Mar. ’15 (AP)]
Solution:
f(x) = log(x² + 2) – log 3 is continuous on [-1, 1] and derivable on (-1, 1).
Now f'(x) = \(\frac{2 \mathrm{x}}{\mathrm{x}^2+2}\) ∀ x ∈ (-1, 1)
Further f(-1) = 0, f(l) = 0
f(-1) = f(1)
By Rolle’s theorem ∃ c ∈ (-1, 1) ∃ f'(c) = 0
\(\frac{2 c}{x^2+2}\) = 0
2c = 0
c = 0 ∈ (-1, 1)
∴ Rolle’s theorem is verified.

Question 15.
Determine the intervals in which f(x) = \(\frac{2}{x-1}\) + 18x ∀ x ∈ R / {0} is strictly increasing and decreasing. [Mar. ’15 (TS)]
Solution:

Question 16.
Find the absolute extremum of f(x) = x² defined on [-2, 2]. [Mar. ’19 (AP)]
Solution:
f(x) = x²
f'(x) = 2x, f”(x) = 2 > 0
f'(x) = 0 ⇒ x = 0
∴ f(x) has minimum value at x = 0
Minimum value = f(0) = 0
f(2) = 4 and f(-2) = 4
Absolute maximum = max{f(-2), f(2), f(0)}
= max {4, 4, 0}
= 4
Absolute minimum = min{f(-2), f(2), f(0)}
= min {4, 4, 0}
= 0

Question 17.
Find the points of local extrema and local extrema for the function f(x) = cos 4x defined on (0, \(\frac{\pi}{2}\)).
Solution:
f(x) = cos 4x
f'(x) = -4 sin 4x
f”(x) = -16 cos 4x
f'(x) = 0
-4 sin 4x = 0
4x = π
x = \(\frac{\pi}{4}\)
f”(\(\frac{\pi}{4}\)) = -16 cos π = 16 > 0
f(x) has minimum value at x = \(\frac{\pi}{4}\)
Minimum value = f(\(\frac{\pi}{4}\)) = cos π = -1