TS Inter 1st Year Maths 1B Tangent and Normal Important Questions

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Tangent and Normal Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Tangent and Normal Important Questions

Question 1.
Find the slope of the tangent to the curve y = 5x² at the point (-1, 5). [May ’04]
Solution:
Given, the equation of the curve is y = 5x²
Differentiating on both sides with respect to ‘x’
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 5(2x) = 10x
∴ Slope of the tangent at P(-1, 5) is m = \(\left(\frac{d y}{d x}\right)_P\)
= 10(-1)
= -10

Question 2.
Find the equations of the tangent and the normal to the curve y = 5x⁴ at the point (1, 5). [May ’15 (AP), ’10, ’07]
Solution:
Given, the equation of the curve is y = 5x⁴
Differentiating on both sides with respect to ‘x’
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 5 . 4x³ = 20x³
Slope of tangent at P(1, 5) is m = \(\left(\frac{d y}{d x}\right)_P\)
= 20(1)³
= 20
The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 5 = 20(x – 1)
y – 5 = 20x – 20
20x – y – 15 = 0
The equation of normal at P is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 5 = \(\frac{-1}{20}\) (x – 1)
20y – 100 = -x + 1
x + 20y – 101 = 0

Question 3.
Find the equations of the tangent and the normal to the curve y⁴ = ax³ at (a, a). [May ’13]
Solution:
Given the equation of the curve is y⁴ = ax³
Differentiating on both sides with respect to ‘x’

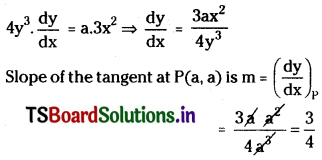
Equation of tangent at P(a, a) is y – y₁ = m(x – x₁)
y – a = \(\frac{3}{4}\)(x – a)
4y – 4a = 3x – 3a
3x – 4y + a = 0
Equation of normal at P (a, a) is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – a = \(\frac{-1}{\frac{3}{4}}\) (x – a)
3y – 3a = 4x + 4a
4x + 3y – 7a = 0

Question 4.
II Show that the tangent at any point ‘θ’ on the curve x = c sec θ, y = c tan θ is y sin θ = x – c cos θ. [Mar. ’19 (TS)]
Solution:
Given that x = c sec θ
Differentiating on both sides with respect to ‘θ’.
\(\frac{d x}{d \theta}\) = c sec θ tan θ
and y = c tan θ
Differentiating on both sides with respect to ‘θ’
\(\frac{d y}{d \theta}\) = c sec²θ
Now,


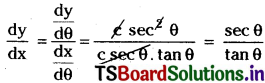
y sin θ cos θ – c sin²θ = x cos θ – c
y sin θ cos θ – c sin²θ + c = x cos θ
y sin θ cos θ + c(1 – sin²θ) = x cos θ
y sin θ cos θ + c cos²θ = x cos θ
y sin θ + c cos θ = x
y sin θ = x – c cos θ

Question 5.
Find the equations of tangent and the normal to the curve y = x² – 4x + 2 at the point (4, 2).
Solution:
Given equation of the curve is y = x² – 4x + 2 ……….(1)
Let given point be P(x, y) = (4, 2)
Differentiating (1) on both sides with respect to ‘x’
\(\frac{d y}{d x}\) = 2x – 4
Slope of the tangent at P is m = \(\left(\frac{\mathrm{d} y}{\mathrm{dx}}\right)_{\mathrm{P}}\)
m = 2(4) – 4 = 4
The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 2 = 4(x – 4)
y – 2 = 4x – 16
4x – y – 14 = 0
Equation of normal at P is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 2 = \(\frac{-1}{m}\) (x – 4)
4y – 8 = -x + 4
x + 4y – 12 = 0

Question 6.
Show that the length of the subnormal at any point on the curve y² = 4ax is a constant. [Mar. ’13 (Old), ’11, ’05; May ’09]
Solution:
Given, the equation of the curve is y² = 4ax
Differentiating on both sides with respect to ‘x’

∴ The length of the subnormal at any point (x, y) on the curve is a constant.

Question 7.
Show that the length of the subtangent at any point on the curve y = a^x (a > 0) is a constant.
Solution:
Given, the equation of the curve is y = a^x
Differentiating on both sides with respect to ‘x’
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a^x log a
The slope of the tangent at any point P(x, y) is

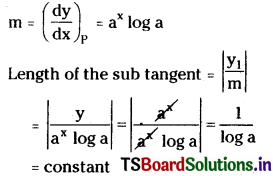
∴ The length of the subtangent at any point P(x, y) on the curve is a constant.

Question 8.
Show that the square of the length of sub tangent at any point on the curve by² = (x + a)³ (b ≠ 0) varies with the length of the subnormal at that point.
Solution:
Given, equation of the curve is by² = (x + a)³
Differentiating on both sides with respect to ‘x’


∴ (length of subtangent)² ∝ (length of the subnormal).

Question 9.
Find the lengths of sub tangent and subnormal at a point on the curve y = b sin(\(\frac{x}{a}\)). [Mar. ’16 (TS); May ’05]
Solution:
Given equation of the curve is y = b sin(\(\frac{x}{a}\))
Differentiating on both sides with respect to ‘x’

Question 10.
Show that at any point (x, y) on the curve y = \(b e^{x / a}\), the length of the subtangent is a constant and the length of the subnormal is \(\frac{\mathbf{y}^2}{a}\). [Mar. ’18 (TS); May ’12; Mar. ’10]
Solution:
Given equation of the curve is y = \(b e^{x / a}\)
Differentiating on both sides with respect to ‘x’

Question 11.
Find the lengths of normal and subnormal at a point on the curve y = \(\frac{a}{2}\left[e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right]\). [Mar. ’13]
Solution:
Given equation of the curve is y = \(\frac{a}{2}\left[e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right]\)
y = a cosh(\(\frac{x}{a}\))
Differentiating on both sides with respect to ‘x’

Question 12.
Show that the tangent at P(x₁, y₁) on the curve √x + √y = √a is \(\mathrm{y}_1 \mathrm{y}^{-1 / 2}+\mathrm{xx}_1^{-1 / 2}\) = \(a^{1 / 2}\). [May ’15 (AP), ’04]
Solution:
Given the equation of the curve is √x + √y = √a ……….(1)
Since the point P(x₁, y₁) lies on the curve (1) then √x₁ + √y₁ = √a ……….(2)
Differentiating (1) on both sides with respect to ‘x’


Which is a required equation of a tangent.

Question 13.
If the tangent at any point on the curve \(x^{2 / 3}+y^{2 / 3}=a^{2 / 3}\) intersects the coordinate axes in A and B, then show that the length AB is a constant. [Mar. ’19 (TS); Mar. ’15 (TS), ’14, ’13, ’08, ’07, ’05, ’03; May ’10]
Solution:
Given equation of the curve is \(x^{2 / 3}+y^{2 / 3}=a^{2 / 3}\)
Differentiating on both sides with respect to ‘x’


AB² = a²
⇒ AB = a (constant)
∴ The length AB is a constant.

Question 14.
If the tangent at any point P on the curve x^m yⁿ = a^m+n (mn ≠ 0) meets the coordinate axes in A, B, then show that AP : BP is a constant. [Mar. ’10; May ’08, ’06]
Solution:
Given the equation of the curve is x^m yⁿ = a^m+n
Differentiating on both sides with respect to ‘x’

Question 15.
At any point, ‘t’ on the curve x = a (t + sin t), y = a(1 – cos t), find the lengths of a tangent, normal, subtangent, and subnormal. [Mar. ’18 (AP)]
Solution:
Given that x = a(t + sin t)
Differentiating on both sides with respect to ‘t’

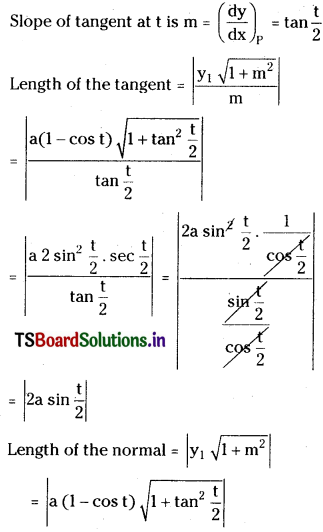
Question 16.
(i) Find the angle between the curves xy = 2 and x² + 4y = 0. [Mar. ’17 (AP); May ’13, ’11]
(ii) Define the angle between the curves. [May ’11]
Solution:
(i) Given, the equations of the curves are
xy = 2 …….(1)
x² + 4y = 0 ………(2)
From (1), y = \(\frac{2}{x}\)
Substituting in equation (2)


(ii) Angle between two curves: If two curves intersect at a point P and the tangents at P for both curves exists then the angle between the tangents at P is called the angle between the curves at P.

Question 17.
Show that the curves y² = 4(x + 1) and y² = 36(9 – x) intersect orthogonally. [Mar. ’13 (old), ’11, ’09, ’08, ’06, ’02; May ’15 (AP), ’05]
Solution:
Given curves are
y² = 4(x + 1) ………(1)
y² = 36(9 – x) ……..(2)
From (1) and (2)
4(x + 1) = 36(9 – x)
x + 1 = 81 – 9x
10x = 80
x = 8
If x = 8,
y² = 4(8 + 1) = 4(9) = 36
y = ±6
∴ Required points are P(8, 6), Q(8, -6)
Differentiating (1) on both sides with respect to ‘x’

Now, m₁m₂ = \(\frac{-1}{3}\)(3) = -1
∴ m₁m₂ = -1
Since, m₁m₂ = -1, the two curves cut each other orthogonally.

Question 18.
Find the angle between the curves y² = 4x and x² + y² = 5. [Mar. ’16 (AP), ’12; May ’07]
Solution:
Given, the equations of the curves are
y² = 4x ……..(1)
x² + y² = 5 ……..(2)
Substitute equation (1) with equation (2)
x² + 4x = 5
x² + 4x – 5 = 0
x² + 5x – x – 5 = 0
x(x + 5) – 1(x + 5) = 0
(x + 5) (x – 1) = 0
x + 5 = 0 (or) x – 1 = 0
x = -5 (or) x = +1
If x = -5, from (1)
y² = 4(-5)
y² = -20 ∉ R
If x = 1, from (1)
y² = 4(1)
y² = 4
y = √4 = ±2
∴ Required point are P(1, 2), Q(1, -2)

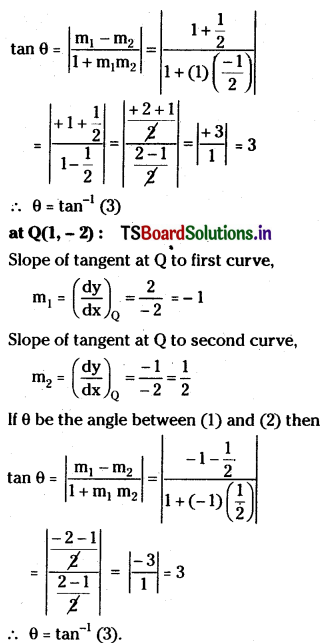
Question 19.
Find the angle between the curves x² + 3y = 3 and x² – y² + 25 = 0. [May ’03]
Solution:
Given, the equations of the curves are
x² + 3y = 3 …….(1)
x² – y² + 25 = 0 …….(2)
From (1),
x² + 3y = 3
x² = 3 – 3y
Substituting in equation (2)
3 – 3y – y² + 25 = 0
-y² – 3y + 28 = 0
y² + 3y – 28 = 0
y² + 7y – 4y – 28 = 0
y(y + 7) – 4(y + 7) = 0
(y + 7)(y – 4) = 0
y + 7 = 0 (or) y – 4 = 0
y = -7 (or) y = 4
If y = -7,
x² = 3 – 3(-7)
= 3 + 21
x² = 24
x = ±2√6
If y = 4,
x² = 3 – 3(4)
= 3 – 12
= -9 ∉ R
∴ Required points are P(2√6, -7), Q(-2√6, -7)
Differentiating (1) on both sides with respect to ‘x’

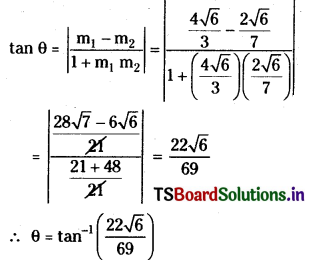
Question 20.
Find the angle between the curves 2y² – 9x = 0 and 3x² + 4y = 0 (in the 4th quadrant). [May ’09]
Solution:
Given, the equations of the curves are
2y² – 9x = 0 ……..(1)
3x² + 4y = 0 ………(2)
From (1), 2y² = 9x
x = \(\frac{2 y^2}{9}\)
Substituting in equation (2)

Question 21.
Find the angle between the curves y² = 8x and 4x² + y² = 32. [Mar. ’18 (AP); May ’12]
Solution:
Given, the equations of the curves are
y² = 8x ……..(1)
4x² + y² = 32 ………(2)
Substituting y² = 8x in equation (2)
4x² + 8x = 32
4x² + 8x – 32 = 0
x² + 2x – 8 = 0
x² + 4x – 2x – 8 = 0
x(x + 4) – 2(x + 4) = 0
(x + 4) (x – 2) = 0
x + 4 = 0 (or) x – 2 = 0
x = -4 (or) x = 2
If x = -4,
y² = 8(-4) = -32 ∉ R
If x = 2,
y² = 8(2) = 16
y = ±4
∴ Required point are P(2, 4), Q(2, -4).
Differentiating (1) on both sides with respect to ‘x’
2y . \(\frac{d y}{d x}\) = 8
y . \(\frac{d y}{d x}\) = 4
\(\frac{d y}{d x}=\frac{4}{y}\)
Differentiating (2) on both sides with respect to ‘x’
4(2x) + 2y . \(\frac{d y}{d x}\) = 0
8x + 2y . \(\frac{d y}{d x}\) = 0

Question 22.
Show that the curves 6x² – 5x + 2y = 0 and 4x² + 8y² = 3 touch each other at \(\left(\frac{1}{2}, \frac{1}{2}\right)\). [Mar. ’15 (AP), ’10; May ’13 (old)]
Solution:
Given, the equations of the curves are
6x² – 5x + 2y = 0 ……….(1)
4x² + 8y² = 3 ………(2)
Let the given point P = \(\left(\frac{1}{2}, \frac{1}{2}\right)\)
Differentiating (1) on both sides with respect to ‘x’


∴ m₁ = m₂
∴ The curves 6x² – 5x + 2y = 0, 4x² + 8y² = 3 touch each other.

Some More Maths 1B Tangent and Normal Important Questions

Question 23.
Find the equations of the tangents to the curve y = 3x² – x³, where it meets the X-axis.
Solution:
Given, equation of the curve is y = 3x² – x³ ………(1)
Given that the curve meets at X-axis then y = 0
∴ 3x² – x³ = 0
x²(3 – x) = 0
x² = 0 or 3 – x = 0
x = 0 or x = 3
∴ P(0, 0), Q(3, 0)
Differentiating (1) on both sides with respect to ‘x’.
\(\frac{d y}{d x}\) = 3(2x) – 3x² = 6x – 3x²
at P(0, 0):
Slope of the tangent at P(0, 0) is
m = \(\left(\frac{d y}{d x}\right)_P\)
= 6(0) – 3(0)²
= 0
Equation of tangent at P(0, 0) is y – y₁ = m(x – x₁)
y – 0 = 0(x – 0)
y = 0
at Q(3, 0):
Slope of tangent at Q(3, 0) is m = \(\left(\frac{d y}{d x}\right)_Q\)
= 6(3) – 3(3)²
= 18 – 27
= -9
∴ Equation of the tangent at Q(3, 0) is y – y₁ = m(x – x₁)
y – 0 = -9(x – 3)
y = -9x + 27
9x + y – 27 = 0
∴ The required equations of the tangents are y = 0, 9x + y – 27 = 0.

Question 24.
Show that the area of the triangle formed by the tangent at any point on the curve xy = c (c ≠ 0), with the coordinate axes is constant.
Solution:
Given, the equation of the curve is xy = c
Differentiating on both sides with respect to ‘x’

\(\frac{x}{2 x_1}+\frac{y}{2 y_1}\) = 1
∴ x-intercept, a = 2x₁, y-intercept, b = 2y₁
∴ The area of the triangle formed by this tangent and the coordinate axes = \(\frac{1}{2}\) |ab|
= \(\frac{1}{2}\) |2x₁ . 2y₁|
= 2|x₁y₁|
= 2c (constant) (∵ P(x₁, y₁) lies on curve, x₁y₁ = c)

Question 25.
Show that the equation of the tangent to the curve is \(\left(\frac{x}{a}\right)^n+\left(\frac{y}{b}\right)^n\) = 2 (a ≠ 0, b ≠ 0) at the point (a, b) is \(\frac{\mathbf{x}}{\mathbf{a}}+\frac{\mathbf{y}}{\mathbf{b}}\) = 2. [Mar. ’18 (TS)]
Solution:
Given, equation of the curve is \(\left(\frac{x}{a}\right)^n+\left(\frac{y}{b}\right)^n\) = 2
Differentiating on both sides with respect to ‘x’

∴ The equation of the tangent to the curve at the point (a, b) is y – y₁ = m(x – x₁)
y – b = \(\frac{-b}{a}\) (x – a)
ay – ab = -bx + ab
bx + ay = 2ab
\(\frac{b x}{a b}+\frac{a y}{a b}=2\)
\(\frac{x}{a}+\frac{y}{b}=2\)

Question 26.
Find the slope of the tangent to the curve y = \(\frac{x-1}{x-2}\) at x = 10.
Solution:
Given, equation of the curve is y = \(\frac{x-1}{x-2}\)
Differentiating on both sides with respect to ‘x’

Question 27.
Find the slope of the tangent to the curve y = x³ – x + 1 at the point whose x-coordinate is 2.
Solution:
Given, equation of curve is y = x³ – x + 1
Differentiating on both sides with respect to ‘x’
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dx}}\)(x³ – x + 1) = 3x² – 1
Slope of tangent at x = 2 is m = \(\left(\frac{d y}{d x}\right)_{x=2}\)
= 3(2)² – 1
= 12 – 1
= 11

Question 28.
Find the slope of the tangent to the curve y = x³ – 3x + 2 at the point whose x-coordinate is 3.
Solution:
Given, equation of curve is y = x³ – 3x + 2
Differentiating on both sides with respect to ‘x’
\(\frac{d y}{d x}=\frac{d}{d x}\left(x^3\right)-3 \frac{d}{d x}(x)+\frac{d}{d x}(2)\)
= 3x² – 3 + 0
= 3x² – 3
Slope of tangent at x = 3 is m = \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\mathrm{x}=3}\)
= 3(3)² – 3
= 27 – 3
= 24

Question 29.
Find the slope of the normal to the curve x = a cos³θ, y = a sin³θ at θ = \(\frac{\pi}{4}\).
Solution:
Given, x = a cos³θ
Differentiating on both sides with respect to ‘θ’

Question 30.
Find the point on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11.
Solution:
Given, the equation of the curve is y = x³ – 11x + 5
Differentiating on both sides with respect to ‘x’
\(\frac{d y}{d x}=\frac{d}{d x}\left(x^3\right)-11 \frac{d}{d x}(x)+\frac{d}{d x}(5)\) = 3x² – 11
The slope of the tangent at any point P(x, y) is m = \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\mathrm{P}}\) = 3x² – 11
Given the equation of the tangent is y = x – 11
Slope of the tangent is m = \(\frac{-\mathrm{a}}{\mathrm{b}}=\frac{-1}{-1}\) = 1
∴ 3x² – 11 = 1
3x² = 12
x² = 4
x = 2
If x = 2, y = 2 – 11 = -9
∴ The required point is (2, -9).

Question 31.
Find the equations of tangent and normal to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at the point (0, 5).
Solution:
Given, equation of the curve is y = x⁴ – 6x³ + 13x² – 10x + 5 ……..(1)
Let the given point P(x, y) = (0, 5)
Differentiating (1) on both sides with respect to ‘x’
\(\frac{d y}{d x}=\frac{d}{d x}\left(x^4\right)-6 \frac{d}{d x}\left(x^3\right)+13 \frac{d}{d x}\left(x^2\right)\) – \(10 \frac{d}{d x}(x)+\frac{d}{d x}(5)\)
= 4x³ – 18x² + 26x – 10
Slope of the tangent at P is m = \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\mathrm{P}}\)
= 4(0)³ – 18(0)² + 26(0) – 10
= -10
The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 5 = -10(x – 0)
y – 5 = -10x
10x + y – 5 = 0
The equation of the normal at P is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 5 = \(\frac{-1}{-10}\) (x – 10)
10y – 50 = x
x – 10y + 50 = 0

Question 32.
Find the equations of tangent and normal to the curve x = cos t, y = sin t at t = \(\frac{\pi}{4}\).
Solution:
Given, x = cos t
Differentiating on both sides with respect to ‘t’.
\(\frac{\mathrm{dx}}{\mathrm{dt}}\) = -sin t
Now, y = sin t
Differentiating on both sides with respect to ‘t’
\(\frac{\mathrm{dy}}{\mathrm{dt}}\) = cos t

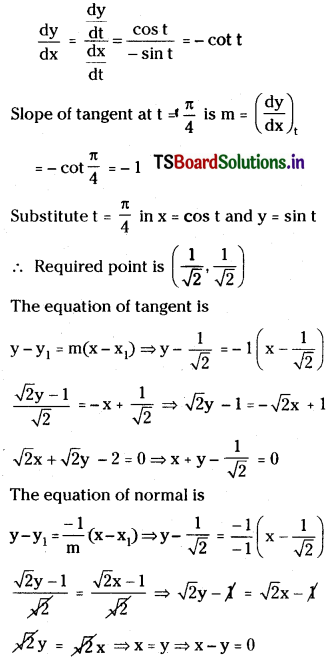
Question 33.
Find the equations of tangent and normal to the curve y = \(\frac{1}{1+x^2}\) at the point (0, 1).
Solution:
Given, equation of the curve is y = \(\frac{1}{1+x^2}\)
Differentiating on both sides with respect to ‘x’

The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 1 = 0(x – 0)
y – 1 = 0
Equation of normal at P is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 1 = \(\frac{-1}{-0}\) (x – 0)
0(y – 1) = -x + 0
0 = -x
x = 0

Question 34.
Find the equations of tangent and normal to the curve xy = 10 at (2, 5). [Mar. ’17 (AP)]
Solution:
Given, the equation of the curve is xy = 10
y = \(\frac{10}{x}\) …….(1)
Let given point be P(x₁, y₁) = (2, 5)
Differentiating on both sides with respect to ‘x’

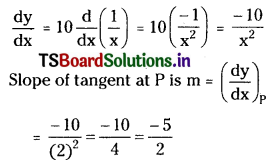
The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 5 = \(\frac{-5}{2}\) (x – 2)
2y – 10 = -5x + 10
5x + 2y – 20 = 0
Equation of normal at P is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 5= \(\frac{-1}{\frac{-5}{2}}(x-2)\)
y – 5 = \(\frac{2}{5}\) (x – 2)
5y – 25 = 2x – 4
2x – 5y + 21 = 0

Question 35.
Find the equations of tangent and normal to the curve y = x³ + 4x² at (-1, 3). [May ’15 (TS), ’14]
Solution:
Given, the equation of the curve is y = x³ + 4x² …….(1)
Let the given point P(x₁, y₁) = (-1, 3)
Differentiating (1) on both sides with respect to ‘x’
\(\frac{d y}{d x}\) = 3x² + 8x
Slope of tangent at P is m = \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\mathrm{P}}\)
= 3(-1)² + 8(-1)
= 3 – 8
= -5
The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 3 = -5(x + 1)
y – 3 = -5x – 5
5x + y + 2 = 0
Equation of normal at P is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 3 = \(\frac{-1}{-5}\) (x + 1)
5y – 15 = x + 1
x – 5y + 16 = 0

Question 36.
If the slope of the tangent to the curve y = x log x at a point on it is \(\frac{3}{2}\), then find the equations of tangent and normal at the point.
Solution:
Given, the equation of the curve is y = x log x
Differentiating on both sides with respect to ‘x’

Question 37.
Show that the curves x² + y² = 2 and 3x² + y² = 4x have a common tangent at the point (1, 1).
Solution:
Given the equation of the first curve is x² + y² = 2
Differentiating on both sides with respect to ‘x’
2x + 2y . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
x + y . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
y \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = -x
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{-\mathrm{x}}{\mathrm{y}}\)
Slope of the tangent at P(1, 1) is m = \(\left(\frac{d y}{d x}\right)_P=\frac{-1}{1}\) = -1
The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 1 = -1(x – 1)
y – 1 = -x + 1
x + y – 2 = 0
Given the equation of the second curve is 3x² + y² = 4x
Differentiating on both sides with respect to ‘x’

The equation of the tangent at P is y – y₁ = m(x – x₁)
y – 1 = -1(x – 1)
y – 1 = -x + 1
x + y – 2 = 0
∴ The curves x² + y² = 2 and 3x² + y² = 4x have a common tangent at the point (1, 1).

Question 38.
At a point (x₁, y₁) on the curve x³ + y³ = 3axy, show that the tangent is (\(x_1^2\) – ay₁)x + (\(y_1^2\) – ax₁)y = ax₁y₁. [Mar. ’17 (TS)]
Solution:
Given, equation of the curve is x³ + y³ = 3axy ……..(1)
Since P(x₁, y₁) lies on the curve (1). Then


Which is the required equation of tangent.

Question 39.
Show that the length of the subnormal at any point on the curve xy = a² varies as the cube of the ordinate of the point.
Solution:
Given the equation of the curve is xy = a²
Differentiating on both sides with respect to ‘x’
x . \(\frac{d y}{d x}\) + y . 1 = 0
x \(\frac{d y}{d x}\) = -y
\(\frac{d y}{d x} = \frac{-y}{x}\)
Let P(x, y) be any point on the curve.
The slope of the tangent at P is m = \(\left(\frac{d y}{d x}\right)_P=\frac{-y}{x}\)
Length of the sub-normal = |y₁m|

∴ Length of the sub-normal ∝ y³. (Cube of ordinate)

Question 40.
Find the value of k so that the length of the subnormal at any point on the curve xy^k = a^k+1 is a constant.
Solution:
Given the equation of the curve is xy^k = a^k+1
Differentiating on both sides with respect to ‘x’

∴ Length of the subnormal at any point is constant then k + 2 = 0
∴ k = -2.

Question 41.
Find the value of k, so that the length of the subnormal at any point on the curve y = a^1-k x^k is a constant.
Solution:
Given, the equation of the curve is y = a^1-k x^k
Differentiating on both sides with respect to ‘x’

The length of subnormal at any point is constant then 2k – 1 = 0
2k = 1
k = \(\frac{1}{2}\)

Question 42.
Find the lengths of sub tangent, and subnormal at a point ‘t’ on the curves x = a(cos t + t sin t), y = a(sin t – t cos t). [Mar. ’17 (TS); May ’15 (TS), ’14]
Solution:
Given that, x = a(cos t + t sin t)
Differentiating on both sides with respect to ‘t’
\(\frac{\mathrm{dx}}{\mathrm{dt}}\) = a[(-sin t) + t(cos t) + sin t (1)]
= a[-sin t + t cos t + sin t]
= at cos t
y = a(sin t – t cos t)
Differentiating on both sides with respect to ‘t’
\(\frac{\mathrm{dy}}{\mathrm{dt}}\) = a[cos t – (t(-sin t) + cos t (1)]
= a[cos t + t sin t – cos t]
= at sin t
\(\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{\not t \sin t}{\not t \cos t}=\tan t\)
Slope of tangent at any point t is m = \(\left(\frac{d y}{d x}\right)_t\) = tan t
Length of the sub tangent = \(\left|\frac{y_1}{m}\right|\)
= \(\left|\frac{\mathrm{a}(\sin \mathrm{t}-\mathrm{t} \cos \mathrm{t})}{\tan \mathrm{t}}\right|\)
= |a(sin t – t cos t) . cot t|
Length of the subnormal = |y₁ . m| = |a (sin t – t cos t) . tan t|

Question 43.
Show that the condition for the orthogonality of the curves ax² + by² = 1 and a₁x² + b₁y² = 1 is \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a_1}-\frac{1}{b_1}\). [Mar. ’19 (AP); Mar. ’16 (TS); May ’14]
Solution:
Given, curves are
ax² + by² = 1 ……..(1)
a₁x² + b₁y² = 1 ……….(2)
Let the curves intersect at P(x₁, y₁) then
\(\mathrm{ax}_1^2+\mathrm{by}_1^2=1, \mathrm{a}_1 \mathrm{x}_1{ }^2+\mathrm{b}_1 \mathrm{y}_1{ }^2=1\)
Differentiating (1) on both sides with respect to ‘x’

Question 44.
Find the angle between the curves x + y + 2 = 0 and x² + y² – 10y = 0. [Mar. ’14]
Solution:
Given equations of the curves are
x + y + 2 = 0 ………(1)
x² + y² – 10y = 0 ……….(2)
From (1), x = -y – 2
Substitute in (2)
(-y – 2) + y² – 10y = 0
y² + 4 + 4y + y² – 10y = 0
2y² – 6y + 4 = 0
y² – 3y + 2 = 0
y² – 2y – y + 2 = 0
y(y – 2) – 1(y – 2) = 0
(y – 2) (y – 1) = 0
y- 2 = 0 (or) y – 1 = 0
y = 2 (or) y = 1
If y = 2, x = -2 – 2 = -4
If y = 1, x = -1 – 2 = -3
Required points are P(-4, 2), Q(-3, 1)
Differentiating (1) on both sides with respect to ‘x’
1 + \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 0 = 0
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = -1
Differentiating (2) on both sides with respect to ‘x’

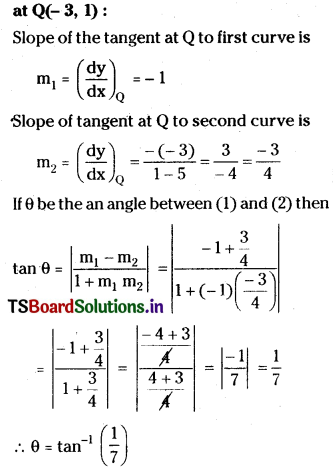
Question 45.
Find the equation of tangent and normal to the curve y = \(\text { 2. } \mathrm{e}^{-\mathrm{x} / 3}\) at the point where the curve meets the y-axis. [Mar. ’16 (TS)]
Solution:
Equation of the curve is y = \(\text { 2. } \mathrm{e}^{-\mathrm{x} / 3}\)
The equation of the y-axis is x = 0
y = 2
Required point = (0, 2)
Also \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{-2}{3} \cdot \mathrm{e}^{\frac{-\mathrm{x}}{3}}\)
and slope m = \(\frac{-2}{3} \cdot \mathrm{e}^{\frac{-0}{3}}=\frac{-2}{3}\)
Equation tangent at p(0, 2) is y – y₁ = m(x – x₁)
y – 2 = \(\frac{-2}{3}\)(x – 0)
3y – 6 = 2x
2x + 3y – 6 = 0
Equation of the normal is y – y₁ = \(\frac{-1}{m}\) (x – x₁)
y – 2 = \(\frac{3}{2}\) (x – 0)
2y – 4 = 3x
3x – 2y + 4 = 0