TS Inter 1st Year Maths 1A Solutions Chapter 3 Matrices Ex 3(d)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 3 Matrices Ex 3(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(d)

I.
Question 1.
Find the determinants of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & 1 \\
1 & -5
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{cc}
2 & 1 \\
1 & -5
\end{array}\right]\) then determinant A
= det A = |A| = 2(-5) – 1(1)
= -10 – 1
= -11

(ii) \(\left[\begin{array}{cc}
4 & 5 \\
-6 & 2
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{cc}
4 & 5 \\
-6 & 2
\end{array}\right]\) then
det A = 4(2) – 5(-6)
= 8 + 30 = 38

(iii) \(\left[\begin{array}{cc}
\mathrm{i} & 0 \\
0 & -\mathrm{i}
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{cc}
\mathrm{i} & 0 \\
0 & -\mathrm{i}
\end{array}\right]\) then
det A = i(-1) – 0 = -i² = 1 (∵ i² = -1)

(iv) \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\)
Answer:

(v) \(\left|\begin{array}{rrr}
1 & 4 & 2 \\
2 & -1 & 4 \\
-3 & 7 & 6
\end{array}\right|\)
Answer:
Let A = \(\left[\begin{array}{rrr}
1 & 4 & 2 \\
2 & -1 & 4 \\
-3 & 7 & 6
\end{array}\right]\)
Then det A = 1\(\left|\begin{array}{rr}
-1 & 4 \\
7 & 6
\end{array}\right|\) – 4\(\left|\begin{array}{ll}
-2 & 4 \\
-3 & 6
\end{array}\right|\) + 2\(\left|\begin{array}{rr}
2 & -1 \\
-3 & 7
\end{array}\right|\)
= 1(-6 – 28) – 4(12 + 12)+ 2(14 – 3)
= 1 (- 34) – 4(24) + 2(11)
= -34 – 96 + 22
= -108

(vi) \(\left[\begin{array}{rrr}
2 & -1 & 4 \\
4 & -3 & 1 \\
1 & 2 & 1
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{rrr}
2 & -1 & 4 \\
4 & -3 & 1 \\
1 & 2 & 1
\end{array}\right]\)
Then det A = 2\(\left|\begin{array}{rr}
-3 & 1 \\
2 & 1
\end{array}\right|\) + 1\(\left|\begin{array}{ll}
4 & 1 \\
1 & 1
\end{array}\right|\) + 4\(\left|\begin{array}{rr}
4 & -3 \\
1 & 2
\end{array}\right|\)
= 2(- 3 – 2)+ 1(4 – 1) + 4(8 + 3)
= 2(-5) + 3 + 4(11)
= – 10 + 3 + 44
= 37

(vii) \(\left[\begin{array}{rrr}
1 & 2 & -3 \\
4 & -1 & 7 \\
2 & 4 & -6
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{rrr}
1 & 2 & -3 \\
4 & -1 & 7 \\
2 & 4 & -6
\end{array}\right]\)
Then det A = 1\(\left|\begin{array}{rr}
-1 & 7 \\
4 & -6
\end{array}\right|\) – 2\(\left|\begin{array}{rr}
4 & 7 \\
2 & -6
\end{array}\right|\) – 3\(\left|\begin{array}{rr}
4 & -1 \\
2 & 4
\end{array}\right|\)
= 1(6 – 28) – 2(- 24 – 14) – 3(16 + 2)
= -22 + 76 – 54 = 0
[Note : Since R₁ and R₂ are proportional, we have det A = 0.]

(viii) \(\left[\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right]\)
Then det A = a\(\left|\begin{array}{ll}
b & f \\
f & c
\end{array}\right|\) – h\(\left|\begin{array}{ll}
\mathrm{h} & \mathrm{f} \\
\mathrm{g} & \mathrm{c}
\end{array}\right|\) – g\(\left|\begin{array}{ll}
h & b \\
g & f
\end{array}\right|\)
= a(bc – f²) – h(ch – fg) + g(fh – bg)
= abc – af² – ch² + fgh + fgh – bg²
= abc + 2fgh – af² – bg² – ch²

(ix) \(\left[\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right]\)
Then det A = 1\(\left|\begin{array}{ll}
c & a \\
a & b
\end{array}\right|\) – b\(\left|\begin{array}{ll}
b & a \\
c & b
\end{array}\right|\) – c\(\left|\begin{array}{ll}
b & \mathrm{c} \\
\mathrm{c} & \mathrm{a}
\end{array}\right|\)
= a(bc – a²) – b(b² – ac) + c(ab – c²)
= 3abc – a³ – b³ – c³

(x) \(\left[\begin{array}{ccc}
1^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{ccc}
1^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right]=\left[\begin{array}{ccc}
1 & 4 & 9 \\
4 & 9 & 16 \\
9 & 16 & 25
\end{array}\right]\)
Then det A = 1(225 – 256) – 4(100 – 144) + 9(64 – 81)
= -31 + 176 – 153 = -8

Question 2.
If A = \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\) and det A = 45 then find x.
Answer:
det A = 45
⇒ \(\left|\begin{array}{rrr}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right|\) = 45
⇒ 1(3x + 24) = 45
⇒ 3x = 21
⇒ x = 7

II.
Question 1.
Show that \(\left|\begin{array}{lll}
\mathrm{b c} & \mathrm{b}+\mathrm{c} & 1 \\
\mathrm{c a} & \mathrm{c}+\mathrm{a} & 1 \\
\mathrm{a b} & \mathrm{a}+\mathrm{b} & 1
\end{array}\right|\) = (a – b)(b – c)(c – a).
Answer:
Operating R₂ – R₁, R₃ – R₁, on the given determinant
LHS = \(\left|\begin{array}{ccc}
b c & b+c & 1 \\
c(a-b) & a-b & 0 \\
b(a-c) & a-c & 0
\end{array}\right|\)
= (a – b)(a – c)\(\left|\begin{array}{ccc}
b c & b+c & 1 \\
c & 1 & 0 \\
b & 1 & 0
\end{array}\right|\)
= (a – b)(a – c)(1)(c – b)
= (a – b)(b – c)(c – a) (exponding on 3rd column)
= RHS

Question 2.
Show that \(\left|\begin{array}{ccc}
b+c & c+a & a+b \\
a+b & b+c & c+a \\
a & b & c
\end{array}\right|\) = a² + b² + c² – 3abc (Mar. 2008; May 2007)
Answer:

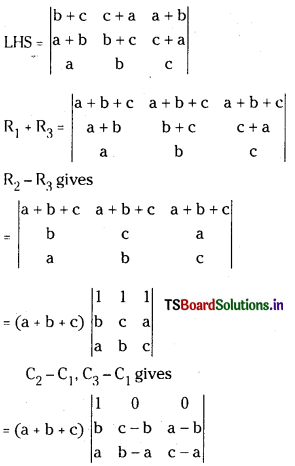
= (a + b + c) [(c – b) (c – a) – (a – b) (b – a)]
= (a + b + c) [c² – bc – ac + ab + a² – 2ab + b²]
= (a + b + c) [a² + b² + c² – ab – bc – ca]
= a² + b² + c² – 3abc

Question 3.
Show that \(\left|\begin{array}{ccc}
\mathrm{y}+\mathrm{z} & \mathrm{x} & \mathrm{x} \\
\mathrm{y} & \mathrm{z}+\mathrm{x} & \mathrm{y} \\
\mathrm{z} & \mathrm{z} & \mathrm{x}+\mathrm{y}
\end{array}\right|\) = 4xyz.
Answer:
R₁ – (R₂ + R₃) on the given determinant gives

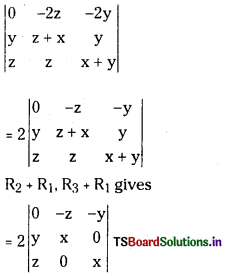
= 2[z(xy) – y(-xz)]
= 2[2xyz] = 4xyz = RHS

Question 4.
If \(\left|\begin{array}{ccc}
a & a^2 & 1+a^3 \\
b & b^2 & 1+b^3 \\
c & c^2 & 1+c^3
\end{array}\right|\) = 0 and \(\left|\begin{array}{ccc}
\mathrm{a} & \mathrm{a}^2 & 1 \\
\mathrm{b} & \mathrm{b}^2 & 1 \\
\mathrm{c} & \mathrm{c}^2 & 1
\end{array}\right|\) ≠ 0, then show that abc = -1. (Mar. ’14)
Answer:

⇒ abc + 1 = 0
⇒ abc = -1

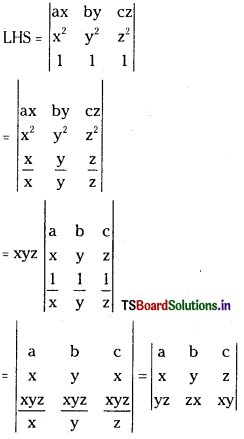
Question 5.
Without expanding the determinant, prove that
(i) \(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{a}^2 & \mathrm{b c} \\
\mathrm{b} & \mathrm{b}^2 & \mathrm{c a} \\
\mathrm{c} & \mathrm{c}^2 & \mathrm{a b}
\end{array}\right|=\left|\begin{array}{ccc}
1 & \mathrm{a}^2 & \mathrm{a}^3 \\
1 & \mathrm{b}^2 & \mathrm{b}^3 \\
1 & \mathrm{c}^2 & \mathrm{c}^3
\end{array}\right|\)
Answer:

(ii) \(\left|\begin{array}{ccc}
\mathrm{a x} & \mathrm{b y} & \mathrm{c z} \\
\mathrm{x}^2 & \mathrm{y}^2 & \mathrm{z}^2 \\
1 & 1 & 1
\end{array}\right|=\left|\begin{array}{ccc}
\mathrm{a} & \mathrm{b} & \mathrm{c} \\
\mathrm{x} & \mathrm{y} & \mathrm{z} \\
\mathrm{y z} & \mathrm{z x} & \mathrm{x y}
\end{array}\right|\)
Answer:

(iii) \(\left|\begin{array}{lll}
1 & b c & b+c \\
1 & c a & c+a \\
1 & a b & a+b
\end{array}\right|=\left|\begin{array}{lll}
1 & a & a^2 \\
1 & b & b^2 \\
1 & c & c^2
\end{array}\right|\) (Board Model Paper)
Answer:

(∵ R₂ – R₁; R₃ – R₁)
= (b – a) (c² – a²) – (c – a) (b² – a²)
= (b – a) (c – a) (c + a) – (c – a) (b – a) (b + a)
= (b – a) (c – a) (c + a – b – a)
= (b – a) (c – a) (c – b)
= (a – b) (b – c) (c – a)
LHS = RHS

Question 6.
If Δ₁ = \(\left|\begin{array}{ccc}
\mathrm{a}_1^2+\mathrm{b}_1+c_1 & \mathrm{a}_1 \mathrm{a}_2+\mathrm{b}_2+c_2 & \mathrm{a}_1 \mathrm{a}_3+\mathrm{b}_3+c_3 \\
\mathrm{b}_1 \mathrm{b}_2+c_1 & \mathrm{b}_2^2+\mathrm{c}_2 & \mathrm{b}_2 \mathrm{b}_3+\mathrm{c}_3 \\
\mathrm{c}_3 c_1 & \mathrm{c}_3 \mathrm{c}_2 & \mathrm{c}_3^2
\end{array}\right|\) and Δ₂ = \(\left|\begin{array}{lll}
\mathrm{a}_1 & \mathrm{b}_1 & \mathrm{c}_1 \\
\mathrm{a}_2 & \mathrm{b}_2 & \mathrm{c}_2 \\
\mathrm{a}_3 & \mathrm{b}_3 & \mathrm{c}_3
\end{array}\right|\), then find the value of \(\frac{\Delta_1}{\Delta_2}\).
Answer:

Question 7.
If Δ₁ = \(\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \gamma & 1
\end{array}\right|\) and Δ₂ = \(\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|\) and Δ₁ = Δ₂ then show that cos²α + cos²β + cos²γ = 1.
Answer:
Given \(\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \gamma & 1
\end{array}\right|\)
= (1 – cos²γ) – cos α (cos α – cos β cos γ) + cos β (cos α cos γ – cos β)
= 1 – cos²γ – cos²α + cos β cos α cos γ + cos α cos β cos γ – cos²β
= 1 – (cos²α + cos²β + cos²γ) + 2 cos α cos β cos γ

Δ₂ = \(\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|\)
= – cos α (0 – cos γ cos β) + cos β (cos α cos γ)
= cos α cos β cos γ + cos α cos β cos γ
= 2cos α cos β cos γ
Also given Δ₁ = Δ₂
⇒ 1 – (cos²α + cos²β + cos²γ) + 2 cos α cos β cos γ
= 2 cos α cos β cos γ
⇒ 1 – (cos²α + cos²β + cos²γ) = 0
∴ cos²α + cos²β + cos²γ = 1

III.
Question 1.
Show that
\(\left|\begin{array}{ccc}
a+b+2 c & a & b \\
c & b+c+2 a & b \\
c & a & c+a+2 b
\end{array}\right|\) = 2(a + b + c)³
Answer:

Question 2.
Show that \(\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|^2\) = \(\left|\begin{array}{ccc}
2 b c-a^2 & c^2 & b^2 \\
c^2 & 2 a c-b^2 & a^2 \\
b^2 & a^2 & 2 a b-c^2
\end{array}\right|\) = (a³ + b³ + c³ – 3abc)². (May 2014, Mar. 01′)
Answer:
Let Δ = \(\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|\) = a(bc – a²) – b(b² – ac) + c(ab – c²)
= abc – a³ – b³ + abc + abc – c³
= – (a³ + b³ + c³ – 3abc)
⇒ Δ² = (a³ + b³ + c³ – 3abc)² …………..(1)

From (1) and (2) the result is proved.

Question 3.
Show that \(\left|\begin{array}{ccc}
a^2+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|\) = (a – 1)³. (March 2007)
Answer:
Apply operations R₁ – R₂ and R₂ – R₃ we get

Question 4.
Show that \(\left|\begin{array}{ccc}
\mathrm{a} & \mathrm{b} & \mathrm{c} \\
\mathrm{a}^2 & \mathrm{b}^2 & \mathrm{c}^2 \\
\mathrm{a}^3 & \mathrm{b}^3 & \mathrm{c}^3
\end{array}\right|\) = abc(a – b)(b – c)(c – a)
Answer:
LHS = abc\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^2 & b^2 & c^2
\end{array}\right|\)
= abc\(\left|\begin{array}{ccc}
0 & 0 & 1 \\
a-b & b-c & c \\
a^2-b^2 & b^2-c^2 & c^2
\end{array}\right|\) (Use operations C₁ – C₂, C₂ – C₃)
= abc [(a – b) (b² – c²) – (b – c) (a² – b²)]
= abc [(a – b) (b – c) (b + c) – (b – c) (a – b) (a + b)]
= abc (a – b) (b – c) [b + c – a – b]
= abc (a – b) (b – c) (c – a)

Question 5.
Show that \(\left|\begin{array}{ccc}
-2 a & a+b & c+a \\
a+b & -2 b & b+c \\
c+a & c+b & -2 c
\end{array}\right|\) = 4(a + b)(b + c)(c + a)
Answer:

= 0 (∵ R₁ & R₃ are similar)
∴ (a + b) is a factor of Δ.
Similarly putting b + c = 0 and c + a = 0 we shall find that b + c and c + a are also factors of Δ.
∵ Δ is a 3rd degree expression in a, b, c.

Let Δ = k (a + b) (b + c) (c + a)
Where k ≠ 0 is a scalar.
Put a = 1, b = 1, c = 1 then
= k(1 + 1) (1 + 1) (1 + 1)
= 8k -2(4 – 4) – 2(-4 – 4) + 2(4 + 4)
= 8k
⇒ -16 + 16 = 8k ⇒ k = 4
Δ = 4(a + b) (b + c) (c + a)
Here \(\left|\begin{array}{ccc}
-2 a & a+b & c+a \\
a+b & -2 b & b+c \\
c+a & c+b & -2 c
\end{array}\right|\) = 4(a + b)(b + c)(c + a)

Question 6.
Show that \(\left|\begin{array}{lll}
\mathrm{a}-\mathrm{b} & \mathrm{b}-\mathrm{c} & \mathrm{c}-\mathrm{a} \\
\mathrm{b}-\mathrm{c} & \mathrm{c}-\mathrm{a} & \mathrm{a}-\mathrm{b} \\
\mathrm{c}-\mathrm{a} & \mathrm{a}-\mathrm{b} & \mathrm{b}-\mathrm{c}
\end{array}\right|\) = 0
Answer:
R₁ + (R₂ + R₃) given
\(\left|\begin{array}{ccc}
0 & 0 & 0 \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\)
= 0 (∵ If one row or column elements of a square matrix are zeroes then the value of the determinant of that matrix is equal to zero)
= RHS.

Question 7.
Show that \(\left|\begin{array}{lll}
1 & a & a^2-b c \\
1 & b & b^2-c a \\
1 & c & c^2-a b
\end{array}\right|\) = 0
Answer:
Make operations R₂ – R₁, R₃ – R₁ then the given determinant.

Question 8.
Show that \(\left|\begin{array}{lll}
x & a & a \\
a & x & a \\
a & a & x
\end{array}\right|\) = (x + 2a)(x – a)².
Answer: