TS Inter 1st Year Physics Study Material Chapter 7 కణాల వ్యవస్థలు, భ్రమణ గమనం

Telangana TSBIE TS Inter 1st Year Physics Study Material 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వ్యవస్థకైనా దాని ద్రవ్యరాశి కేంద్రం వద్ద ద్రవ్యరాశి తప్పక ఉండవలసిన అవసరం ఉందా ? (మే 2014)
జవాబు:
ఒక వస్తువు ద్రవ్యరాశి కేంద్రం వద్ద కొంత ద్రవ్యరాశి ఉండి తీరాలి అన్న నియమం లేదు) ఉదా : ఉంగరము లేదా గాజుల విషయంలో వాటి ద్రవ్యరాశి కేంద్రం వద్ద ఏ విధమైన ద్రవ్యరాశి లేదు.

ప్రశ్న 2.
ఒక అమ్మాయి బరువులున్న ఒక సంచిని ఒక చేతిలో పట్టుకొని నిలుచున్నది. ఇంకొక అమ్మాయి అంతే బరువు ఉన్న రెండు సంచులను తన రెండు చేతులతో పట్టుకొని నిలుచున్నది. ఆ అమ్మాయిల ద్రవ్యరాశి కేంద్ర స్థానాలలో మార్పులెలా ఉంటాయి ?
జవాబు:
a) అమ్మాయి బరువులు ఉన్న సంచిని ఒక చేతితో పట్టుకున్నపుడు ఆమె ద్రవ్యరాశి కేంద్రం బరువు ఉన్న చేతివైపు జరుగును.

b) అమ్మాయి రెండు చేతులతో సమానమైన బరువులు మోసినపుడు ఆమె ద్రవ్యరాశి కేంద్రస్థానము మారదు. అనగా బరువులు లేనపుడు ద్రవ్యరాశి కేంద్రం ఉన్న ప్రదేశంలోనే ఉంటుంది.

ప్రశ్న 3.
రెండు ద్రుఢ వస్తువుల జడత్వ భ్రామకాలు, వాటి సౌష్టవాక్షాల పరంగా సమానం. ఆ రెండింటిలో దేని గతిజ శక్తి అధికంగా ఉంటుంది ?
జవాబు:
ఒక వస్తువు భ్రమణ గతిశక్తి KE_rot మరియు కోణీయ ద్రవ్యవేగం (L) ల మధ్య సంబంధం KE_rot = \(\frac{\mathrm{L}^2}{2 \mathrm{I}}\)
ఇచ్చిన ప్రశ్నలో జడత్వ భ్రామకములు సమానం కావున KE_rot ∝ L²
ఎక్కువ కోణీయ ద్రవ్యవేగము గల వస్తువు ఎక్కువ భ్రమణ గతిశక్తి కల్గి ఉంటుంది.

ప్రశ్న 4.
సైకిల్ చక్రాలకు కమ్మీలు (spokes) ఎందుకు అమర్చుతారు ? (మే 2014)
జవాబు:
సైకిల్ చక్రాలకు కమ్మీలు (spokes) అమర్చడం వల్ల చక్రం బరువులో అధికభాగం భ్రమణాక్షం నుండి దూరంగా పంపిణీ చేయబడును. ఫలితంగా అంతే ద్రవ్యరాశి గల కమ్మీలు లేని చక్రం కన్నా కమ్మీలు గల చక్రం జడత్వ భ్రామకం చాలా ఎక్కువ. ఫలితంగా ఆ చక్రం ఎక్కువ జడత్వ భ్రామకం గల గతిపాలక చక్రం వలె పనిచేసి కుదుపులను తగ్గిస్తుంది. బాహ్య టార్క్న సున్న చేసినప్పటికి సమవేగంతో ఎక్కువ దూరం ప్రయాణిస్తుంది.

ప్రశ్న 5.
మడత బందుల (hinges) వద్ద బలాన్ని ప్రయోగించి ఒక తలుపును తెరవడం లేదా మూయడం సాధ్యంకాదు. ఎందువల్ల ?
జవాబు:
తలుపులు చలించే భ్రమణాక్షం మడత బందు గుండా పోతున్నది. కాబట్టి భ్రమణాక్షం నుండి బలానికి (\(\overline{\mathrm{F}}\)) గల
దూరము \(\overline{\mathrm{r}}\) = 0
తలుపులు తెరవడానికి అందించిన బలభ్రామకం
టార్క్, τ = \(\overline{\mathrm{r}}\) × \(\overline{\mathrm{F}}\) = |\(\overline{\mathrm{r}}\)| |\(\overline{\mathrm{F}}\)| sin θ = 0 ∵ sin 0 = 0
అందువల్ల \(\overline{\mathrm{r}}\) = 0 అయితే ఎంత ఎక్కువ బలం (F) వాడినప్పటికి టార్క్, τ = 0 కావడం వల్ల తలుపులు తెరవడం సాధ్యపడదు.

ప్రశ్న 6.
భుజం పొట్టిగా ఉన్న స్పానర్ (మరను తిప్పడానికి వాడే ఉపకరణం) కంటే భుజం పొడవుగా ఉన్న స్పానర్ను మనమెందుకు ఎక్కువగా ఎంచుకొంటాం ?
జవాబు:
టార్క్, τ = \(\overline{\mathrm{r}}\) × \(\overline{\mathrm{F}}\). స్పానర్ను వాడేటపుడు స్పానర్ పొడవు బలం నుండి ఆధారానికి గల దూరము \(\overline{\mathrm{r}}\) అవుతుంది. స్పానర్ పొడవు ఎక్కువ ఉంటే అదే బలము F కి టార్క్ ఎక్కువ. అందువలన అటువంటి స్పానర్లతో బోల్ట్ ను తేలికగా భ్రమణం చెందించవచ్చు.

ప్రశ్న 7.
టేబుల్ తలంపై ఒక గుడ్డును బొంగరంవలె తిప్పి అది ఉడికినదీ లేనిదీ ఎలా నిర్ధారించగలం ?
జవాబు:
గుడ్డును టేబుల్పై ఉంచి భ్రమణం చెందించితే అది ఉడికిన గుడ్డు అయితే మొత్తం ఘనపదార్థం వలె ఉంటుంది. కాబట్టి తేలికగా బల్లతోపాటు భ్రమణం చెందుతుంది.

ఉడకని గుడ్డు అయితే లోపల ద్రవాలు ఉంటాయి. దీనిని భ్రమణం చెందించేటప్పుడు ద్రవాలకు గల స్నిగ్ధతా బలాలవల్ల అవి భ్రమణవేగాన్ని అడ్డుకుంటాయి. అందువల్ల ఉడకని గుడ్డు భ్రమణ వేగం తక్కువ. ఈ విధంగా మనం గుడ్డు ఉడికిందీ, లేనిదీ తెలుసుకొనవచ్చు.
Note : ద్రవాలలో వివిధ పొరల మధ్య గల ఘర్షణబలమే స్నిగ్ధతా బలము.

ప్రశ్న 8.
ఒక హెలికాప్టర్కు ఎందుకు రెండు ప్రొపెల్లర్లు (propellers – ముందుకు నడిపే యంత్రం) తప్పక వుండి తీరాలి ?
జవాబు:
హెలికాప్టర్కు రెండు ప్రొపెల్లర్లు ఉండి తీరాలి. ఒకే ప్రొపెల్లర్ ఉంటే కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారము హెలికాప్టర్ వ్యతిరేక దిశలో ఆత్మభ్రమణం చెందుతుంది. స్థానాంతరణ గమనం సాధ్యపడదు. స్థానాంతరణ గమనం కోసం, హెలికాప్టర్ ఆత్మభ్రమణ నిరోధం కోసం హెలికాప్టర్లో రెండు ప్రొపెల్లర్లు వాడతారు.

ప్రశ్న 9.
భూగోళ ధ్రువాల వద్ద వున్న మంచు పూర్తిగా కరిగిపోతే ఒక రోజు కాలవ్యవధి ఏ విధంగా ప్రభావితమౌతుంది ?
జవాబు:
ధృవాల వద్ద ఉన్న మంచు పూర్తిగా కరిగిపోతే నీరు భూమధ్య రేఖ వద్దకు చేరుతుంది. అనగా భూమి భ్రమణాక్షం మీద ఉన్న మంచు, భ్రమణాక్షం నుండి ఎక్కువ దూరానికి జరగడం వల్ల భూమి జడత్వ భ్రామకం పెరిగి కోణీయ వేగం తగ్గును. కారణం I₁ω₁ + I₂ω₂ = 0 అన్న కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమము.

ఫలితంగా భూమి ఆత్మభ్రమణకాలం పెరుగుతుంది. అంటే ఒకరోజు కాలవ్యవధి పెరుగును.

ప్రశ్న 10.
కదిలే సైకిల్ను సులభంగా అటూ ఇటూ ఒరగకుండా నిలుపవచ్చు. ఎందుకు ?
జవాబు:
కదిలే సైకిల్ చక్రాలు భ్రమణ సమతాస్థితిలో ఉంటాయి. భ్రమణ సమతాస్థితి నియమాల నుండి భ్రమణాక్షానికి లంబంగా ఉండే టార్క్ అంశవల్ల వస్తువు భ్రమణాక్షపరంగా తిరుగుతుంది. బాహ్య టార్క్ లో భ్రమణాక్షానికి లంబంగా గల అంశ టార్క్ ప్రభావాన్ని శూన్యపరచే విధంగా ప్రతిబంధక బలాన్ని జడత్వ భ్రామకంలోని మార్పులు కలుగజేస్తాయి. ఫలితంగా గమనంలో ఉన్న సైకిల్ను సులభంగా పక్కకి ఒరగకుండా ఉంచవచ్చు.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఒక వ్యవస్థ ద్రవ్యరాశి కేంద్రం, గరిమనాభుల మధ్య భేదాలను గుర్తించండి. (మార్చి 2014)
జవాబు:
ద్రవ్యరాశి కేంద్రము, మధ్య తేడాలు :
ద్రవ్యరాశి కేంద్రము

1. వస్తువులోని ద్రవ్యరాశి అంతా దానిలో గల ఒక బిందువు వద్ద కేంద్రీకృతమైనట్లు ప్రవర్తిస్తుంది. ఈ బిందువునే ద్రవ్యరాశి కేంద్రము అంటారు.
2. క్రమాకారం కలిగిన చిన్న వస్తువుల విషయంలో ద్రవ్యరాశి కేంద్రం, గరిమనాభులు ఏకీభవిస్తాయి.
3. ద్రవ్యరాశి కేంద్రపరంగా వస్తువులో గల కణముల ద్రవ్యరాశుల భ్రామకాల బీజీయ మొత్తం సున్నాకి సమానము.
4. వస్తువు సంక్లిష్టచలనంలో ఉన్నపుడు దాని స్థానాంతరణ గమనాన్ని వివరించడానికి ద్రవ్యరాశి కేంద్రాన్ని ఉపయోగిస్తారు.

గరిమనాభి

1. వస్తువుపై పనిచేయు ‘మొత్తం గురుత్వాకర్షణ బలం దానిలో గల ఒక బిందువు వద్ద కేంద్రీకృతమైనట్లు ప్రవర్తిస్తుంది. ఈ బిందువును గరిమనాభి అంటారు.
2. వస్తు పరిమాణం చాలా పెద్దదిగా ఉండి, దానిలో ద్రవ్యరాశి పంపిణీ ఏకరీతిగా లేనపుడు, లేదా వస్తువు వ్యాప్తి చెందిన ప్రదేశంలో గురుత్వ త్వరణం స్థిరంగా లేనపుడు వాని ద్రవ్యరాశి కేంద్రం, గరిమనాభులు ఏకీభవించకపోవచ్చును.
3. గరిమనాభిపరంగా వస్తువులో గల కణముల భారముల భ్రామకాల బీజీయ మొత్తం సున్నాకి సమానము.
4. వస్తువుకు స్థిరత్వము కలిగించడానికి ఆధారమును కల్పించు ప్రక్రియలో గరిమనాభి అను భావనను వాడతారు.

ప్రశ్న 2.
బాహ్య బల ప్రభావానికి గురయిన ఒక కణవ్యవస్థ, ఆ బలం వ్యవస్థ ద్రవ్యరాశి కేంద్రం వద్ద ప్రయోగించినట్లుగా గమనంలో ఉంటుందని చూపండి.
జవాబు:
ఏదైనా వ్యవస్థలో గల m₁, m₂, m₃, ……… m_n అను కణాలు \(\overline{\mathrm{v}}_1, \overline{\mathrm{v}}_2, \overline{\mathrm{v}}_3, \ldots . . \overline{\mathrm{v}}_{\mathrm{n}}\) అను వేగాలతో చలించుచున్నాయను కొనుము.
ద్రవ్యరాశి కేంద్రవేగము \(\overline{v}_{\mathrm{cm}}=\frac{1}{M}\left\{\mathrm{~m}_1 \overline{v}_1+\mathrm{m}_2 \overline{v}_2+\mathrm{m}_3 \overline{\mathrm{v}}_3+\ldots . \mathrm{m}_{\mathrm{n}} \overline{\mathrm{v}}_{\mathrm{n}}\right\}\)
ఇందులో m₁ + m₁ + m₃ + ……….. + m_n = M వస్తువు మొత్తం ద్రవ్యరాశి

వ్యవస్థపై పనిచేయు మొత్తం బలము F = F₁ + F₂ + F₃ + ……… + F_n = F_cm
∴ వ్యవస్థపై పనిచేయు మొత్తం బలం ద్రవ్యరాశి కేంద్రం వద్ద పనిచేసే బలంలా ప్రవర్తించడం వల్ల అనేక కణవ్యవస్థలపై బాహ్య బల ప్రయోగం వల్ల కలిగే గమనం ద్రవ్యరాశి కేంద్రంపై అదే బలం ప్రయోగిస్తే కలిగే గమనాన్ని పోలి ఉంటుంది.

ప్రశ్న 3.
భూమి-చంద్రుడు వ్యవస్థ ద్రవ్యరాశి కేంద్రం పరంగా సూర్యుని చుట్టూ దాని భ్రమణాలను వివరించండి.
జవాబు:
భూమికి, చంద్రునికి మధ్య గల గురుత్వాకర్షణ బలాలు, భూమి మరియు చంద్రుని వ్యవస్థ ద్రవ్యరాశి కేంద్రంపై ప్రభావం చూపవు. ఎందుకనగా భూమి మరియు చంద్రుల మధ్య గల గురుత్వాకర్షణ బలాలు అంతర్గత బలాలు. ఇవి ద్రవ్యరాశి కేంద్రస్థానాన్ని మార్చజాలవు.

భూమి, చంద్రుల వ్యవస్థ ద్రవ్యరాశి కేంద్రంపై పనిచేసే బాహ్యబలము సూర్యునికి, భూమి చంద్రుల ద్రవ్యరాశి కేంద్రాల మధ్య గల బలము. ఈ బలం వల్ల భూమి చంద్రుల వ్యవస్థ సూర్యుని చుట్టూ చలిస్తుంది. కావున సూర్యుని చుట్టూ భూమి-చంద్రుల వ్యవస్థ యొక్క గమనము చంద్రుడు భూమి చుట్టూ పరిభ్రమించటం వల్ల ప్రభావితం కాదు.

ప్రశ్న 4.
సదిశాలబ్ధాన్ని నిర్వచించండి. సదిశా లబ్ధ ధర్మాలను రెండు ఉదాహరణలతో వివరించండి.
జవాబు:
సదిశల సదిశా లబ్ధము : రెండు సదిశలు \(\overline{\mathrm{a}}\) మరియు \(\overline{\mathrm{b}}\) లను మరల సదిశ ఏర్పడేవిధంగా గుణించడాన్ని సదిశల సదిశాలబ్ధము అంటారు.
\(\overline{\mathrm{a}}\) × \(\overline{\mathrm{b}}\) = |\(\overline{\mathrm{a}}\)||\(\overline{\mathrm{b}}\)| sin θ. \(\overline{\mathrm{n}}\). ఇందులో \(\overline{\mathrm{n}}\) ఇచ్చిన సదిశల తలానికి లంబదిశలో గల ప్రమాణ సదిశ.

సదిశా లబ్ధ ధర్మాలు :
1) రెండు సదిశల సదిశా లబ్ధము స్థిత్యంతర న్యాయాన్ని పాటించదు. \(\overline{\mathrm{a}} \times \overline{\mathrm{b}} \neq \overline{\mathrm{b}} \times \overline{\mathrm{a}}\) కాని \(\bar{a} \times \bar{b}=-(\bar{b} \times \bar{a})\) \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}\) = ab sin θ; \(\overline{b} \times \overline{a}\) = b a sin θ ఈ రెండూ పరిమాణంలో సమానమే కాని కుడిచేతి మర నిబంధన ననుసరించి a × \(a \times \overline{b}\) భ్రమణం \(\overline{\mathrm{a}}\) నుంచి \(\overline{\mathrm{b}}\) వైపు ఉంటుంది. \(\overline{\mathrm{b}} \times \overline{\mathrm{a}}\) లో భ్రమణం \(\overline{\mathrm{b}}\) నుంచి \(\overline{\mathrm{a}}\) వైపు ఉంటుంది. అనగా పరిమాణం సమానమైనా \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}\) మరియు \(\overline{\mathrm{b}} \times \overline{\mathrm{a}}\) ల దిశలు వ్యతిరేకము. అందువల్ల \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}=-(\overline{\mathrm{b}} \times \overline{\mathrm{a}})\) అని రాస్తారు. కావున \(\overline{\mathrm{a}} \times \overline{\mathrm{b}} \neq \overline{\mathrm{b}} \times \overline{\mathrm{a}}\)

2) సదిశా లబ్ధము సంకలనపరంగా విభాజక న్యాయాన్ని పాటిస్తుంది. అనగా \(\overline{\mathrm{a}} \times(\overline{\mathrm{b}}+\overline{\mathrm{c}})=\overline{\mathrm{a}} \times \overline{\mathrm{b}}+\overline{\mathrm{a}} \times \overline{\mathrm{c}}\)

ప్రశ్న 5.
కోణీయ వేగానికి నిర్వచనం తెలపండి. v = r ω లు రాబట్టండి. (మే 2014)
జవాబు:
కోణీయ స్థానభ్రంశము (θ) : భ్రమణ గమనంలో ఉన్న వస్తువు వృత్త కేంద్రం వద్ద చేసిన కోణాన్ని కోణీయ స్థానభ్రంశము ‘θ’ అంటారు. ప్రమాణము రేడియన్.
కోణీయ వేగము (ω) : కోణీయ స్థానభ్రంశంలోని మార్పు రేటును కోణీయవేగం అంటారు.
కోణీయ వేగములు = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) ప్రమాణము రేడియన్ / సెకను
ఏదైనా కణము ‘P’ వృత్తపరిధి వెంబడి V అను సమవడితో తిరుగుతున్నదను కొనుము. వృత్తవ్యాసార్ధం ‘r’ అనుకోనుము. మొదటగా P అను కణము ‘A’ అనే బిందువు వద్ద ఉన్నదనుకొనుము. B నుండి Cకు ప్రయాణించుటలో అది కేంద్రము వద్ద చేసిన కోణము ∆θ, మరియు పట్టిన కాలము ∆t అనుకొనుము.

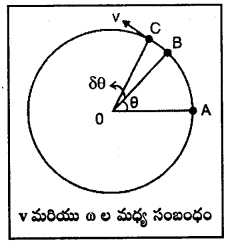
నిర్వచనము ప్రకారం కోణీయవేగం ω = \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta t}=\frac{d \theta}{d t}\)
కాని రేఖీయ వేగము V = \({Lt}_{\Delta t \rightarrow 0} \frac{B C}{\Delta t}\) ఇందులో BC = r dθ
కోణము dθ చిన్నదైనపుడు చాపము BC ని సరళరేఖ BC గా భావిస్తారు.
∴ V = r . \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) ( కాని \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) = ω ) ⇒ V = rω

ప్రశ్న 6.
కోణీయ త్వరణాన్ని, టార్క్ను నిర్వచించండి. ఈ రెండు రాశుల మధ్య సంబంధాన్ని తెలిపే సమాసాన్ని రాబట్టండి.
జవాబు:
కోణీయ త్వరణము : కోణీయ వేగంలో మార్పు రేటును కోణీయ త్వరణం అంటారు.
కోణీయ త్వరణము α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) ప్రమాణము రేడియన్ / సె² .
బలభ్రామకము లేదా టార్క్ (τ): మూలబిందువు (O) పరంగా \(\overline{\mathrm{r}}\) స్థానసదిశను కలిగిన ఒక వస్తువు లేదా కణంపై బలము \(\overline{\mathrm{F}}\) ను ప్రయోగిస్తే, \(\overline{\mathrm{r}}\) మరియు \(\overline{\mathrm{F}}\) ల వజ్రలబ్ధాన్ని టార్క్ నిర్వచించినారు.
టార్క్, τ = \(\overline{\mathrm{r}} \times \overline{\mathrm{F}}=|\overline{\mathrm{r}}||\overline{\mathrm{F}}| \sin \theta \overline{\mathrm{n}}\)
టార్క్ సదిశరాశి. దీని దిశ \(\overline{\mathrm{r}}\), \(\overline{\mathrm{F}}\)ల తలానికి లంబంగా ఉంటుంది.
టార్కు ప్రమాణము న్యూటన్ – మీటరు. D.F = ML²T^-2

కోణీయ త్వరణము a మరియు టార్క్ ల మధ్య సంబంధము : ఏదైనా వ్యవస్థపై కొంత టార్క్ ప్రయోగించడం వల్ల అది dθ అను కోణం స్థానభ్రంశం చెందితే జరిగిన పని dW = τdθ …………. (1)
సామర్థ్యము P = \(\frac{d W}{d t}=\tau \cdot \frac{d \theta}{d t}\) ………………. (2) కాని \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) = ω
∴ P = τω ………….. 3
సామర్థ్యము P = వ్యవస్థ భ్రమణ గతిజ శక్తిలోని మార్పు రేటు అని కూడా చెప్పవచ్చు.
P = \(\frac{\mathrm{d}}{\mathrm{dt}}\left(\frac{1}{2} \mathrm{I} \omega^2\right)=\frac{1}{2} \cdot 2 \mathrm{I} \omega \frac{\mathrm{d} \omega}{\mathrm{dt}}\) = Iωα ……………… 4
సమీకరణం 3, 4 ల నుండి τω = Iωα లేదా τ = Iα
టార్క్ τ, కోణీయ త్వరణాల మధ్య సంబంధము τ = Iα

ప్రశ్న 7.
ఒక స్థిర అక్షం పరంగా భ్రమణం చేస్తున్న కణం గమన సమీకరణాలను రాయండి.
జవాబు:
భ్రమణ గమనానికి గతిశాస్త్ర సమీకరణాలు
1) ω = ω₀ + αt
2) θ = ω₀t + \(\frac{1}{2}\) αt²
3) ω² – ω₀² = 2αθ
ఉత్పాదన : ఏదైనా వస్తువు స్థిర అక్షపరంగా కొంత కోణీయ త్వరణంతో చలిస్తున్నదనుకొనుము.
వస్తువు తొలికోణీయ వేగము = ω₀ ., తుది కోణీయ వేగము ω మరియు మార్పుకు పట్టిన కాలము t అనుకోండి.
1) ω = ω₀ + αt ఉత్పాదన
కోణీయ త్వరణము α = \(\frac{\omega-\omega_0}{t}\) ⇒ ω – ω₀ = αt లేదా ω = ω₀ + αt ……………. (1)

2) θ = ω₀t + \(\frac{1}{2}\) = αt² ఉత్పాదన
వస్తువు మొత్తం స్థానభ్రంశము θ = సగటు కోణీయ వేగము × కాలము

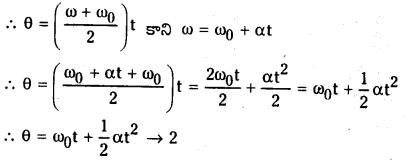
3) ω² – ω₀² = 2αθ ఉత్పాదన
వస్తువు మొత్తం కోణీయ స్థానభ్రంశము θ = సగటు కోణీయ వేగము × కాలము
సగటు కోణీయ వేగము = \(\frac{\omega+\omega_0}{2}\)
కాలము t = \(\frac{\omega-\omega_0}{2}\)
∴ θ = \(\frac{\left(\omega+\omega_0\right)}{2} \frac{\left(\omega-\omega_0\right)}{\alpha}=\frac{\omega^2-\omega_0^2}{2 \alpha}\)
∴ ω² – ω₀² = 2αθ …………….. 3

ప్రశ్న 8.
సమతలంపై నిశ్చల స్థితి నుంచి స్లిప్ కాకుండా దొర్లుతూ ఉన్న ఒక వస్తువు తుది వేగం, మొత్తం శక్తికి సమాసాలను రాబట్టండి.
జవాబు:
దొర్లుడు గమనము : దొర్లుడు గమనము అనేది స్థానాంతరణ గమనము మరియు భ్రమణ గమనముల సంయోగము.
దొర్లుడు గమనం గతిజశక్తి (R.K.E) : దొర్లుడు గమనంలో ఉన్న వస్తువుకు స్థానాంతరణ గమనం వల్ల గతిజశక్తి (1/2mv²) మరియు భ్రమణ గమనం వల్ల గతిజశక్తి (\(\frac{1}{2}\)Iω²) ఉంటాయి.
∴ దొర్లుడు గమనంలో వస్తువు గతిజశక్తి_K.E_R = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)Iω²
∴ K.E_R = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\) mk² \(\frac{v^2}{r^2}\) (∵ I = mk² మరియు v = rω)
∴ దొర్లే వస్తువు మొత్తం శక్తి E అనుకుంటే E = \(\frac{1}{2}\) mv² \(\left[1+\frac{\mathrm{k}^2}{\mathrm{r}^2}\right]\) …………….. (1)
లేదా v² = \(\frac{2 E}{m\left(1+\frac{k^2}{r^2}\right)}\)
వస్తువు వేగము V = \(\sqrt{\frac{2 \mathrm{E}}{\mathrm{m}\left[1+\frac{\mathrm{k}^2}{\mathrm{r}^2}\right]}}\) …………. (2)

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
(a)సమాంతరాక్షాల సిద్ధాంతాన్ని తెలిపి నిరూపించండి.
(b) పలుచని వృత్తాకార బిళ్ళకు, దాని వ్యాసం పరంగా భ్రమణ వ్యాసార్ధం k. పటంలో చూపినట్లు బిళ్ళను వ్యాసం AB వెంబడి రెండు ముక్కలుగా కత్తిరించినప్పుడు, AB పరంగా ప్రతి ముక్క భ్రమణ వ్యాసార్ధం కనుక్కోండి.

జవాబు:
సమాంతరాక్ష సిద్ధాంతము : ఏదైనా వస్తువులో ద్రవ్యరాశి కేంద్రంగుండా పోవు అక్షానికి సమాంతరంగాగల వేరొక అక్షం మీది జడత్వ భ్రామకం (I), ద్రవ్యరాశి కేంద్రంగుండా పోవు అక్షపరంగా గల జడత్వ భ్రామకము (I_G) మరియు వస్తువు ద్రవ్యరాశిని (M) అక్షముల మధ్యగల లంబదూరపు వర్గము (R²) చేత గుణించి కలుపగా వచ్చు మొత్తమునకు సమానము.
అనగా I = I_G + MR²
M ద్రవ్యరాశిగల ఒక సమతల పటలం యొక్క ద్రవ్యరాశి కేంద్రము ‘G’ అనుకొనుము. ద్రవ్యరాశి కేంద్రపరంగా వస్తువు జడత్వ భ్రామకము I_G అనుకొనుము. ద్రవ్యరాశి కేంద్రంగుండా పోవు అక్షానికి సమాంతరంగా గల వేరొక సమాంతరాక్షము పటతలంలోని మరొక బిందువు ” గుండా పోతున్నది అనుకొనుము.

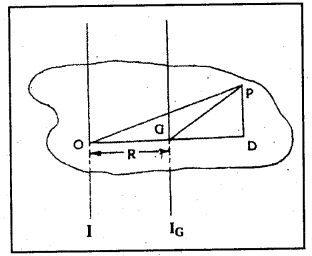
‘O’ గుండా పోవు కొత్త అక్షపరంగా జడత్వ భ్రామకము మరియు ‘O’, ‘G’ ల మధ్య దూరము OG = R అనుకొనుము.

ఇచ్చిన సమతలంలో ఏదైనా బిందువు ‘P’ ని తీసుకొనుము. OP మరియు GP లను కలుపుతూ సరళరేఖలు గీయుము. OG ని కలుపుతూ గీసిన రేఖను పొడిగించి P నుండి దానిపైకి లంబమును గీయుము. ఇది పటంలో చూపిన విధంగా ఉంటుంది.
ద్రవ్యరాశి కేంద్రము G పరంగా వస్తువు జడత్వ భ్రామకము I_G = ΣmOG² ……………. (1)
‘O’ బిందువుపరంగా వస్తువు జడత్వభ్రామకము I = ΣmOP² …………….. (2)
పటంలో OPD లంబకోణ త్రిభుజం నుండి OP² = OD² + PD²
కాని OD = OG + GD ……………. (3)
∴ I = ΣmOP² = Σm { (OG² + GD² + DP²} ……….. (4)
I = Σm {OG² + GD² + DP² + 2OG, GD} –
కాని లంబకోణ త్రిభుజము GPD నుండి GD² + DP² + GP²
∴ I = Σm {OG² + GP² + 2OG, GD}
∴ I = ΣmOG² + ΣmGP² + 2OG ΣmGD …………… (5)
కాని ΣmOG² = MR² (ఇందులో 2m = M వస్తువు మొత్తం ద్రవ్యరాశి, OG = R)
ΣmGP² = IG ద్రవ్యరాశి కేంద్రపరంగా వస్తువు జడత్వ భ్రామకము
2OG ΣmGD = 0 (ఇది ద్రవ్యరాశి కేంద్రపరంగా వస్తువు ద్రవ్యరాశుల భ్రామకముల బీజీయ మొత్తానికి సమానము. దీని విలువ సున్నాకు సమానము.)
ఈ విలువలను పై సమీకరణంలో వ్రాయగా I = I_G + MR² అనగా సమాంతరాక్ష సిద్ధాంతము నిరూపించబడినది.

b) M ద్రవ్యరాశి R వ్యాసార్ధము గల బిళ్ళ జడత్వ భ్రామకము I = \(\frac{\mathrm{MR}^2}{4}\)
భ్రమణ వ్యాసార్ధము k అనుకుంటే Mk² = \(\frac{\mathrm{MR}^2}{4}\) ⇒ k = R/2
బిళ్ళను రెండుముక్కలుగా విభజిస్తే దాని ద్రవ్యరాశి M₁ = \(\frac{\mathrm{M}}{2}\)
కొత్త జడత్వ భ్రామకము I’ = \(\frac{1}{4} \cdot \frac{\mathrm{M}}{2} \times \mathrm{R}^2=\frac{\mathrm{M}}{2} \mathrm{k}_1^2\)
∴ ప్రతిముక్క భ్రమణ వ్యాసార్ధము k₁ = \(\frac{\mathrm{R}}{2}\)

ప్రశ్న 2.
(a)లంబాక్షాల సిద్ధాంతాన్ని తెలిపి నిరూపించండి.
(b)ఒక సన్నని వృత్తాకార కంకణం, ఒక పలుచని చదునైన వృత్తాకార బిళ్ళలు సమాన ద్రవ్యరాశి, వాటి వాటి వ్యాసాల పరంగా సమాన జడత్వ భ్రామకాన్ని కలిగి ఉంటే వాటి వ్యాసార్థాల నిష్పత్తి కనుక్కోండి.
జవాబు:
లంబాక్ష సిద్ధాంతము : సమతల పటలానికి లంబంగా గల ఏదో ఒక బిందువు గుండా పోవు అక్షపరంగా గల జడత్వ భ్రామకము ఆ సమతల పటలంలో ఇచ్చిన బిందువు గుండా పోవు పరస్పర లంబ అక్షాల పరంగాగల విడి విడి జడత్వ భ్రామకముల మొత్తమునకు సమానము.
అనగా I_z = I_x + I_y
ఒక సమతల పటలంలో గల ఏదైనా బిందువు ” గుండా పోవు ఒక లంబాక్షము ‘Z’ ను తీసుకొనుము. అదే సమతల పటలంలో ‘O’ బిందువు గుండా పోవు మరొక రెండు పరస్పర లంబాక్షములు (x, y) లను తీసుకొనుము. XOY తలంలో గల ఏదైనా బిందువు P ని తీసుకొనుము. ఇది x-అక్షం నుండి ‘y’ దూరంలోను, y-అక్షం నుండి ‘x’ దూరంలోను కలదనుకొనుము.

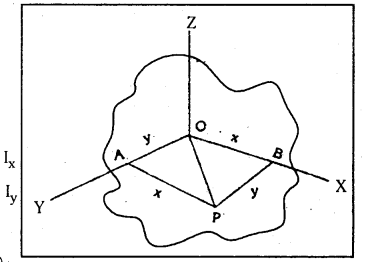
అప్పుడు X అక్షపరంగా వస్తువు జడత్వ భ్రామకము I_x = Σ my².
y అక్షపరంగా వస్తువు జడత్వ భ్రామకము I_y = Σmx²
z-అక్షపరంగా వస్తువు జడత్వ భ్రామకము I_z = ΣmOP²
కాని పటంలోని OAP త్రిభుజం నుండి
OP² = OA² + AD² = x² + y²
∴ I_z = Σm (x² + y²) = Σmx² + Σmy²
కాని Σ my² = x అక్షపరంగా వస్తువు జడత్వ భ్రామకము I_x
Σmx²
= y అక్షపరంగా వస్తువు జడత్వ భ్రామకము I_y
కావున I_z = I_x + I_y
అనగా x, y అక్షముల ఖండన బిందువు ‘0’ గుండా పోవు
అక్షపరంగా (z) గల జడత్వ భ్రామకము I_z = I_x + I_y అనగా లంబాక్ష సిద్ధాంతము నిరూపించబడినది.

b) వ్యాసము వెంబడి పలుచని రింగు జడత్వ భ్రామకము I₁ = m₁ R₁²
వ్యాసము వెంబడి వృత్తాకార బిళ్ళ జడత్వ భ్రామకము I₂ = \(\frac{\mathrm{m}_2 \mathrm{R}_2^2}{2}\)
రెంటికి జడత్వ భ్రామకాలు సమానము ⇒ I₁ = I₂
అనగా m₁ R₁² = m₂ \(\frac{\mathrm{R}_2^2}{2}\) కాని m₁ = m₂
∴ వ్యాసార్థాల నిష్పత్తి R₁² = \(\frac{\mathrm{R}_2^2}{2}\) లేదా R₁ = \(\frac{R_2}{\sqrt{2}}\)
∴ R₁ : R₂ = \({\sqrt{2}}\) : 1

ప్రశ్న 3.
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని తెలిపి నిరూపించండి. ఈ నియమాన్ని ఉదాహరణలతో వివరించండి.
జవాబు:
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమం : ఏదైనా వ్యవస్థపై బాహ్య టార్క్ పని చేయనంతవరకు ఆ వ్యవస్థకు గల కోణీయ ద్రవ్య వేగము స్థిరము. అనగా I₁ω₁ = I₂ω₂ (τ = 0 అయినపుడు )

వివరణ : భ్రమణ గమనంలో ఉన్న వస్తువు జడత్వ భ్రామకాలు I₁, I₂ మరియు దాని తొలి, తుది కోణీయ ద్రవ్యవేగాలు ω₁ మరియు ω₂ అనుకొనుము. బాహ్య టార్క్ పనిచేయనపుడు
అనగా τ = \(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}\) = 0 లేదా \(\mathrm{d} \overline{\mathrm{L}}\) = 0 అనగా కోణీయ ద్రవ్య వేగంలోని మార్పు \(\mathrm{d} \overline{\mathrm{L}}_2-\mathrm{d} \overline{\mathrm{L}}_1\) = 0
లేదా I₂ω₂ – I₁ω₁ = 0 అనగా I₁ω₁ = I₂ω₂

కోణీయ ద్రవ్య వేగ నిత్యత్వ నియమానికి ఉదాహరణలు :
1) నిలువు అక్షం చుట్టూ స్వేచ్ఛగా గుండ్రని బల్ల భ్రమణం చేస్తున్నది. దీనిపై ఒక బాలుడు రెండు చేతులతో రెండు భారాలు పట్టుకొని కాళ్ళు, చేతులు చాపుకొని నిల్చున్నాడు. అపుడు అతని జడత్వ భ్రామకం I₁. అతడి కోణీయ వేగం ω₁. అతడు చేతులను ముడుచుకొంటే అతడి జడత్వ భ్రామకం I₂ తగ్గిపోతుంది. కావున బల్ల వ్యవస్థ కోణీయ వేగం ω₂ పెరుగుతుంది.
బల్ల జడత్వ భ్రామకం I అనుకుంటే, (I + I₁)ω₁ = (I + I₂)ω₂
∴ ω₂ = \(\frac{\left(\mathrm{I}+\mathrm{I}_1\right) \omega_1}{\left(\mathrm{I}+\mathrm{I}_2\right)}\) కాని – (I + I₂) < (I + I₁) కనుక ω₂ + ω₁.

2) సూర్యుని చుట్టూ పరిభ్రమించే గ్రహం కోణీయ త్వరణం స్థిరంగా ఉంటుంది.
గ్రహం P వద్ద ఉన్నపుడు వేగం = v₁ ; సూర్యుని నుండి దూరం = r₁ ∴ కోణీయ ద్రవ్యవేగం = m v₁ r₁
అదే విధంగా Q వద్ద కోణీయ ద్రవ్యవేగం = m v₂ r₂ కాని m v₁ r₁ = m v₂ r₂ కాని v = rω
∴ m r₁ ω₁ r₁ = m r₂ ω₂ r₂ ⇒ I₁ω₁ = I₂ω₂ (∵ mr² = I)

లెక్కలు

ప్రశ్న 1.
a . (b × c) పరిమాణం a, b, c సదిశలు భుజాలుగా గల సమానాంతర చతుర్భుజ ఘనం (parallelepiped) ఘనపరిమాణానికి సమానం అని చూపండి.
సాధన:
సమాంతర చతుర్భుజ ఘనమును ఏర్పరచిన సదిశలు \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}\) ; \(\overline{\mathrm{OB}}=\overline{\mathrm{b}}\) మరియు \(\overline{\mathrm{OC}}=\overline{\mathrm{c}}\) అనుకోండి.

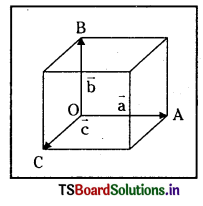
\(\overline{\mathrm{b}} \times \overline{\mathrm{c}}=|\overline{\mathrm{b}}||\overline{\mathrm{c}}| \sin \theta \overline{\mathrm{n}}=\mathrm{ab}(\overline{\mathrm{n}})\) (∵ θ = 90°)
ఇందులో \(\overline{\mathrm{n}}\) ప్రమాణ సదిశ. ఇది \(\overline{\mathrm{b}}, \overline{\mathrm{c}}\) ల తలానికి లంబంగా ఉంటుంది.
అనగా ఇది \(\overline{\mathrm{a}}\) కు సమాంతరంగా ఉంటుంది.
\(\overline{\mathrm{a}} \cdot(\overline{\mathrm{b}} \times \overline{\mathrm{c}})=\overline{\mathrm{a}} \cdot(\mathrm{bc}) \overline{\mathrm{n}}=\overline{\mathrm{a}} \cdot \overline{\mathrm{n}}(\mathrm{bc})\) cos θ = abc
ఇది సమాంతర చతుర్భుజ ఘనము ఘనపరిమాణానికి సమానము.

ప్రశ్న 2.
3 kg ద్రవ్యరాశి, 40 cm వ్యాసార్ధం ఉన్న ఒక బోలు స్థూపం చుట్టూ దాదాపు ద్రవ్యరాశి లేని ఒక తాడు చుట్టారు. 30 N బలంతో తాడును లాగితే స్థూపం ఎంత కోణీయ త్వరణాన్ని పొందుతుంది ? తాడు రేఖీయ త్వరణం ఎంత అవుతుంది? తాడు స్థూపంపై జారదు అని భావించండి.
సాధన:
ద్రవ్యరాశి M = 3 కి. గ్రా.
వ్యాసార్ధము R = 40 సెం.మీ. = 0.4 మీ.
బోలు స్థూపానికి అక్షం వెంబడి జడత్వ భ్రామకము
I = MR² = 3 (0.4)² = 0.48 kg . m²
బలము, F = 30 న్యూ; టార్క్, τ = F × R = 30 × 0.4 = 12 న్యూ
వస్తువులో త్వరణం ‘α’ అనుకుంటే α = \(\frac{\tau}{\mathrm{I}}=\frac{12}{0.48}\) = 25 రే/సె²
రేఖీయ త్వరణము a = r . α = 0.4 × 25 = 10 మీ/సె²

ప్రశ్న 3.
క్షితిజ తలంలో భ్రమణం చెందే తిరుగుడు బల్లపై దాని కేంద్రం నుండి 10 cm దూరంలో ఒక నాణాన్ని ఉంచారు. తిరుగుడు బల్ల, నాణాల మధ్య స్థితిక ఘర్షణ గుణకం 0.8 అయితే, నాణెం బల్లపై జారడం మొదలుపెట్టడానికి తిరుగుడు బల్ల భ్రమణ పౌనఃపున్యం ఎంత ఉండాలి ?
సాధన:
నాణెము ఉన్న దూరం r = 10 cm = 0.1 m. ; ఘర్షణ గుణకం μ = 0.8.
భ్రమణ పౌనఃపున్యము = 1 సెకనులో చేసిన భ్రమణాల సంఖ్య
నాణెము జారిపోకుండుటకు μmg = mrω² ⇒ ω = \(\sqrt{\frac{\mu \mathrm{g}}{\mathrm{r}}}\)
∴ ω = \(\sqrt{\frac{0.8 \times 9.8}{1}}=\sqrt{78.4}\) = 8.854 రే/సె.
సెకనుకు భ్రమణాల సంఖ్య = భ్రమణ పౌనఃపున్యం = \(\frac{\omega}{2 \pi}=\frac{8.854}{2 \pi}\) = 1.409 Rot/sec లేక 84.54 R.P.M.

ప్రశ్న 4.
ఒక మీటరు స్కేలుపై 1 cm, 2 cm, 3 cm, . 100 cm ల గుర్తుల వద్ద వరసగా 1g, 2g, 3g ….., 100g ద్రవ్యరాశు లు గల కణాలను ఉంచారు. మీటరు స్కేలు మధ్య లంబరేఖ పరంగా ఈ వ్యవస్థ జడత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
ఇచ్చిన ద్రవ్యరాశులు 1g, 2g, 3g….. 100 g స్కేలు మీద 1, 2, 3 …… 100 cm ల వద్ద ఉన్నవి.

iii) జడత్వ భ్రామకము = I = m₁r₁² +m₂r₂² + m₃r₃² + …+ m₁₀₀r₁₀₀²
∴ I = 1 × 1 × 1 + 2 × 2² + 3 × 3² + 100 × 100²
= 1 + 2³ + 3³ +……+ 100³ × 10^-7 Kg.m² ( ∵ 1 g = 10^-3 kg & 1 cm = 10^-2 m)
n సంఖ్యల ఘనముల మొత్తం S = \(\frac{n^2(n+1)^2}{4}\) ; ∴ I = \(\frac{100^2 \times(101)^2}{4}\) × 10^-7 = 2.550 Kg. m²
ద్రవ్యరాశి కేంద్రం ద్వారా పోయే అక్షం పరంగా జడత్వ భ్రామకం = I_G = I – MR²
= 2.550 × – 5.05 × 0.67 x 0.67 = 2.550 – 2.267 = 0.283 kg.m²

iv) లంబ సమద్విఖండన రేఖ 50 cm వద్ద ఉంటుంది.
x₁ = 50 cm నుండి x₂ = 67 cm కు ద్రవ్యరాశి కేంద్రం మారినపుడు
∴ అక్షముల మధ్యదూరం R = 67 – 50 – 17cm = 0.17 m
జడత్వ భ్రామకం I = I_G + MR² = 0.283 + 5.05 × 0.17 × 0.17
= 0.283 + 0.146 = 0.429 kgm²
∴ లంబ సమద్విఖండన రేఖ వలన జడత్వ భ్రామకం = 0.429 kg – m²

ప్రశ్న 5.
10 cm భుజం కలిగిన ఒక సమబాహు త్రిభుజ శీర్షాల వద్ద ప్రతిది 100g ద్రవ్యరాశి ఉన్న మూడు కణాలను ఉంచారు. ఆ త్రిభుజ కేంద్రాభం ద్వారా పోతూ, త్రిభుజ తలానికి లంబంగా ఉన్న అక్షం పరంగా ఈ వ్యవస్థ జడత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
ఒక్కొక్క కణం ద్రవ్యరాశి = 100 gm;
సమబాహు త్రిభుజం, భుజం పొడవు = 10 cm.
కోణ సమద్విఖండన రేఖ ఎత్తు CD : \(\frac{\sqrt{3}}{2}\)l
గురుత్వ కేంద్రం ఈ రేఖను 2 : 1 నిష్పత్తిలో ఖండిస్తుంది.

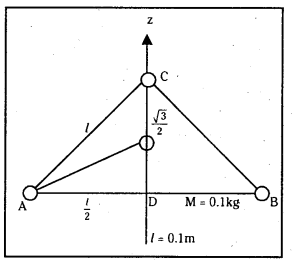
శీర్షము నుండి గురుత్వ కేంద్రం దూరం 2. \(\frac{\sqrt{3}}{2}\)l = \(\frac{1}{\sqrt{3}}\)l
వ్యవస్థ మొత్తం జడత్వ భ్రామకం I = m₁r₁² + m₂r₂² + m₃r₃²
∴ I = 0.1 × \(\left(\frac{\sqrt{3}}{3} \times 0.1\right)^2\) + 0.1 × \(\left(\frac{\sqrt{3}}{3} \times 0.1\right)^2\) + 0.1 × \(\left(\frac{\sqrt{3}}{3} \times 0.1\right)^2\)
= 3 × \(\frac{3}{2}\) × 0.1³ = 1 × 10^-3 kg. m³ = 10^-3 kg. m³

ప్రశ్న 6.
10 cm భుజం ఉన్న చతురస్ర శీర్షాల వద్ద ప్రతిది 100 g ద్రవ్యరాశి ఉన్న నాలుగు కణాలను ఉంచారు. చతురస్రం మధ్య బిందువు ద్వారా పోతూ, దాని తలానికి లంబంగా ఉన్న అక్షం పరంగా వ్యవస్థ జడత్వ భామ్రకాన్ని కనుక్కోండి. వ్యవస్థ భ్రమణ వ్యాసార్ధాన్ని కనుక్కోండి.
సాధన:
ఒక్కొక్క కణము ద్రవ్యరాశి m = 100 g = 0.1 kg.
చతురస్రము పొడవు a = 10 cm = 0.1 m
చతురస్ర కేంద్రం నుండి, చతురస్ర మూలలకు దూరం = \(\frac{1}{2}\) కర్ణం = \(\frac{a}{\sqrt{2}}\)

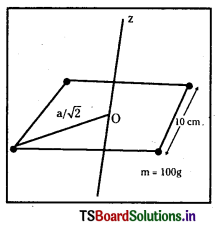
a) ∴ మొత్తం జడత్వ భ్రామకం I = m₁r₁² + m₂r₂² + m₃r₃² + m₄r₄² = 4mr²
∴ I = 4 × 0.1 \(\left(\frac{1}{\sqrt{2}} \times 0.1\right)^2\) = 4 × \(\frac{1}{2}\) × 0.13³ = 2 × 10^-3 Kg. m²

b) భ్రమణ వ్యాసార్ధము K = \(\sqrt{\frac{\mathrm{I}}{\mathrm{m}}}=\sqrt{\frac{2 \times 10^{-3}}{4 \times 10^{-1}}}=\sqrt{2} \times \frac{10^{-1}}{\sqrt{2}} 10^{-1}\)
= 0.7071 × 0.12 m or 7.071 cm. = 0.07071 m.

ప్రశ్న 7.
1 kg ద్రవ్యరాశి, 20 cm వ్యాసార్ధం ఉన్న రెండు ఏకరీతి వృత్తాకార దిమ్మెలు ఒకదానికొకటి స్పృశించుకునేటట్లుగా స్పర్శారేఖ (tangent) స్పర్శా బిందువు ద్వారా పోయేటట్లు అమర్చారు. స్పర్శా బిందువు ద్వారా పోయే స్పర్శారేఖ పరంగా ఈ వ్యవస్థ జడత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
బిళ్ళ ద్రవ్యరాశి = M = 1 kg.; బిళ్ళ వ్యాసార్ధం = 20 cm = 0.2 m అవి పటములో చూపినట్లుగా స్పర్శలో నున్నవి.

తలానికి లంబంగా స్పర్శరేఖ పరంగా జడత్వ భ్రామకం = \(\frac{5}{4}\) MR²
మొత్తం వ్యవస్థ జడత్వ భ్రామకం I = \(\frac{5}{4}\) MR² + \(\frac{5}{4}\) MR² = \(\frac{5}{2}\) MR²
∴ I = \(\frac{5}{2}\) × 1 × 0.2 × 0.2 = 5 × 1 × 0.1 × 0.2 = 0.1 kgm²

ప్రశ్న 8.
24 వ్యాసం, m ద్రవ్యరాశి ఉన్న నాలుగు గోళాల కేంద్రాలను b భుజంగా ఉన్న ఒక చతురస్ర నాలుగు శీర్షాల వద్ద ఉంచారు. ఒక భుజం భ్రమణ అక్షంగా ఈ వ్యవస్థ జడత్వ భ్రామకాన్ని లెక్కించండి.
సాధన:
గోళం వ్యాసం = 2a ⇒ వ్యాసార్ధం = a; చతురస్ర భుజం = b.
1, 2 గోళాలకు వ్యాసం పరంగా జడత్వ భ్రామకం \(\frac{2}{5}\) MR²
(M = m, R = aగా రాయగా)

∴ 1 మరియు 2 గోళాల జడత్వ భ్రామకం = I₁ + I₂
= \(\frac{2}{5}\) ma² + \(\frac{2}{5}\) ma² = \(\frac{4}{5}\) ma² …………… (1)
3,4 గోళాల జడత్వ భ్రామకం = \(\frac{2}{5}\) ma² + \(\frac{2}{5}\) ma² = \(\frac{4}{5}\) ma²
సమాంతర అక్ష సిద్ధాంతం ప్రకారం
∴ I₃ + I₄ = \(\frac{2}{5}\) ma² + mb² + \(\frac{2}{5}\) ma² + mb² = \(\frac{4}{5}\) ma² + 2 mb²
మొత్తం వ్యవస్థ జడత్వ భ్రామకం I = \(\frac{4}{5}\) ma² + \(\frac{4}{5}\) ma² + 2mb² ⇒ I = [\(\frac{8}{5}\) ma² + 2mb²]

ప్రశ్న 9.
ఒక యంత్రం భ్రమణ భాగానికి (rotor) 200 rad s^-1 ఏకరీతి కోణీయ వడిని సమకూర్చడానికి యంత్రం 180 Nm టార్క్ ను అందించవలసి ఉంది. యంత్రానికి అవసరమయ్యే సామర్థ్యం ఎంత ? (గమనిక : ఘర్షణ లేనప్పుడు సమకోణీయ వేగం కలిగి ఉండటమంటే టార్క్ శూన్యం అని అర్థం. వాస్తవానికి ప్రయోగించిన టార్క్ ఘర్షణ వల్ల కలిగే టార్క్న వ్యతిరేకిస్తుంది) యంత్రం 100% దక్షత కలిగి ఉన్నదని భావించండి.
సాధన:
కోణీయ వేగము, ω = 200 రేడియన్ / సె ;
ప్రయోగించిన టార్క్, τ = 180 నూ – మీ.
యంత్రం సామర్థ్యము, p = ? p = τω
∴ P = 180 × 200 = 36000 = 36 కి. వాట్

ప్రశ్న 10.
ఒక మీటర్ స్కేలును దాని కేంద్రం వద్ద కత్తిమొన ఉంచి తుల్య స్థితిలో నిలిపారు. ఒక్కొక్కటి 5g ద్రవ్యరాశి ఉన్న రెండు నాణాలను ఒకదానిపై ఒకటి అమరేటట్లుగా స్కేలుపై 12.0 cm విభాగం వద్ద ఉంచారు. అప్పుడు కత్తిమొన 45.0 cm విభాగం వద్ద ఉన్నప్పుడు స్కేలు తుల్య స్థితికి వచ్చింది. మీటర్ స్కేలు ద్రవ్యరాశి ఎంత ?
సాధన:
స్కేలు బరువు M. ఇది C వద్ద కేంద్రీకరింపబడినది అనుకోండి.
C’ బిందుపరంగా సమతాస్థితి ఉంది, C’ దూరము = 45 సెం.మీ.
రెండు నాణెముల బరువు = 10 గ్రా.; వాటి స్థానము = 12 సెం.మీ. వద్ద
∴ సమతాస్థితి వద్ద 10g (45 – 12) = mg (50 – 45)
∴ 10g × 33 = mg. 5 ⇒ m = \(\frac{10 \times 330}{5}\) = 66 గ్రా.

ప్రశ్న 11.
వృత్తపరిధిపై ఏదో ఒక బిందువు ద్వారా పోతూ, తలానికి లంబంగా ఉన్న అక్షం పరంగా 60 rpm వడితో భ్రమణం చెందే ఒక వృత్తాకార దిమ్మె గతిజ శక్తిని కనుక్కోండి. దిమ్మె ద్రవ్యరాశి 5 kg, వ్యాసార్ధం 1 m.
సాధన:
వృత్తాకార బిళ్ళ ద్రవ్యరాశి M = 5 kg, వ్యాసార్ధం R = 1 m. ; కోణీయ వేగం ω = 60 RPM = \(\frac{60 \times 2 \pi}{60}\) = 2π రే/సె.
వృత్తాకార బిళ్ళ అంచులోని బిందువు ద్వారా పోతూ తలానికి లంబంగా నున్న అక్షంపరంగా జడత్వ భ్రామకం
I’ = I_G + MR² కాని I_G = \(\frac{\mathrm{MR}^2}{2}\) (పై వస్తువు విషయంలో)
∴ I’ = \(\frac{\mathrm{MR}^2}{2}\) + MR² = \(\frac{3}{2}\) MR²
భ్రమణ గతిశక్తి = \(\frac{1}{2}\) Iω² = \(\frac{1}{2}\) . \(\frac{3}{2}\) MR² × (2π)² = \(\frac{3}{4}\) × 5 × 1 × 1 × 2 × 3.142 × 2 × 3.142
∴ భ్రమణ గతిశక్తి = 15 × 3.142 × 3.142 = 148.1 J.

ప్రశ్న 12.
ఒక్కొక్కటిm ద్రవ్యరాశి గల రెండు కణాలు, వ్యతిరేక దిశలో, d దూరంలో ఉన్న సమాంతర రేఖలపై U వడితో గమనంలో ఉన్నాయి. ఏ బిందువు పరంగా కోణీయ ద్రవ్యవేగాన్ని కొలిచినా, ఈ ద్వికణ వ్యవస్థ కోణీయ ద్రవ్యవేగ సదిశ సమానమని చూపండి.
సాధన:
కోణీయ ద్రవ్యవేగము L = mvr, ద్రవ్యరాశి = m, వడి = u
ఏదైనా అక్షము A పరంగా వస్తువుల దూరాలు L₁ మరియు L₂ అనుకోండి.
L = L₁ + L₂
మొత్తం కోణీయ ద్రవ్యవేగము L = muL₁ + muL₁ = mu (L₁ + L₁) = muL ………….. (1)

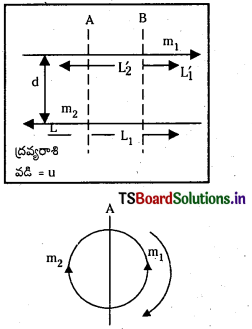
ఏదైనా కొత్తం అక్షం B పరంగా m, m, ద్రవ్యరాశుల దూరాలు
L’₁ మరియు L’₂ అనుకోండి.
అపుడు L = L’₁ + L’₂
కొత్త అక్షం B పరంగా కోణీయ ద్రవ్యవేగము L₁ = muL’₁ + muL’₂
L₁ = mu(L’₁ + L’₂) = muL → 1
1, 2 సమీకరణాల నుండి మొత్తం కోణీయ ద్రవ్యవేగము స్థిరమని తెలుస్తున్నది.

ప్రశ్న 13.
నిమిషానికి 300 భ్రమణాలు చేసే ఒక గతిపాలకచక్రం (flywheel) జడత్వ భ్రామకం 0.3 kgm². 20 సెకన్లలో దీన్ని నిశ్చల స్థితికి తీసుకురావడానికి అవసరమైన టార్క్ను కనుక్కోండి.
సాధన:
జడత్వ భ్రామకము I = 0.3 కి.గ్రా. మీ²
కాలము = 20 సె
ω₁ = 300 R.P.M. = \(\frac{300}{60}\) = 5 × 2π = 10π రేడియన్ / సె ;
ω₂ = 0 (ఆగిపోయింది కావున)
టార్క్, τ = Iα = I \(\left(\frac{\omega_2-\omega_1}{t}\right)\)
∴ τ = 0.33 \(\left(\frac{10 \pi-0}{20}\right)=\frac{3 \pi}{20}\) = 0.471 న్యూ.మీ.

ప్రశ్న 14.
ఒక గతిపాలకచక్రం (flywheel) పై 100 J పని జరిగినప్పుడు దాని కోణీయ వేగం 60 rpm నుంచి 180 rpm కి పెరిగింది. చక్రం జడత్వ భ్రామకాన్ని లెక్కించండి.
సాధన:
పని W = 100 J, ω₁ = 600 RPM = 1 R.P.S = 2π రేడియన్/సె
ω₂ = 180 R.P.M. = \(\frac{180}{60}\) R.P.S = 3 RPS = 3 × 2π = 6π రే/సె
కాని పని W = భ్రమణ గతిజశక్తిలోని భేదము = \(\frac{1}{2}\)I(ω₂² – ω₁²)
∴ 100 = \(\frac{1}{2}\) (36π² – 4π²) = \(\frac{1}{2}\) 32π² I
∴ జడత్వ భ్రామకము I = \(\frac{200}{32 \pi^2}\) = 0.6332 కి.గ్రా.మీ ² .

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
0.5 m భుజం ఉన్న ఒక సమబాహు త్రిభుజం శీర్షాల వద్ద ఉన్న మూడు కణాల ద్రవ్యరాశి కేంద్రాన్ని కనుక్కోండి. కణాల ద్రవ్యరాశులు వరసగా 100 g, 150 g, 200 g.
సాధన:

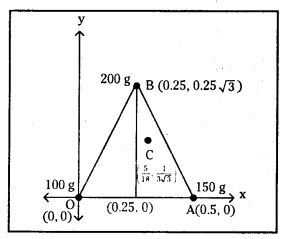
పటంలో చూపినట్లు X-, y- అక్షాలను ఎంచుకొంటే సమబాహు త్రిభుజాన్ని ఏర్పరచే బిందువులు O, A, B ల నిరూపకాలు వరసగా (0, 0), (0.5, 0), (0.25, 0.25 \(\sqrt{3}\)). 100 g, 150g, 200g ద్రవ్యరాశులు వరసగా O, A, B ల వద్ద ఉన్నాయనుకొంటే,

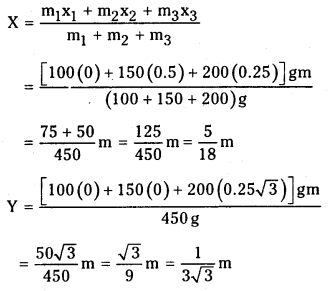
ప్రశ్న 2.
L-ఆకారంలో ఉన్న పల్చని ఏకరీతి పలక (పటలం) ద్రవ్యరాశి కేంద్రాన్ని కనుక్కోండి. దాని కొలతలు పటంలో చూపడమైంది. పలక ద్రవ్యరాశి 3 kg.
సాధన:
పటంలో చూపినట్లు X, Y అక్షాలను తీసుకొంటే Lఆకారం ఉన్న పటలం శీర్షాలు 000, 0), A(2, 0), B(2, 1), D(1, 1), E(1, 2), F(0, 2) అవుతాయి. ఈ పటలాన్ని 1 m భుజం ఉన్న మూడు చతురస్రాలుగా భావించవచ్చు. ఈ చతురస్రాల ద్రవ్యరాశి కేంద్రాలు C, C2, C3 లు, సౌష్ఠవం వల్ల, ఆయా చతురస్రాల జ్యామితీయ కేంద్రాలవుతాయి. వాటి నిరూపకాలు వరసగా (1/2, 1/2), (3/2, 1/2), (1/2, 3/2) అని తెలుసుకోవచ్చు. చతురస్రాల ద్రవ్యరాశులు ఈ బిందువుల వద్ద కేంద్రీకృతమైనట్లుగా మనం భావించవచ్చు. ఈ మూడు ద్రవ్యరాశి బిందువుల ద్రవ్యరాశి కేంద్రమే, మొత్తంగా L ఆకారం ఉన్న పటలం ద్రవ్యరాశి కేంద్రం (X, Y) అవుతుంది.

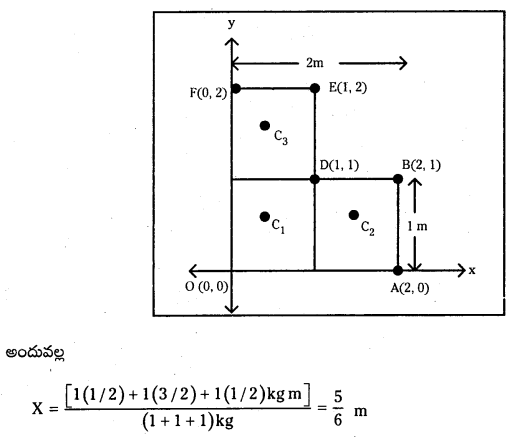
Y = \(\frac{[1(1 / 2)+1(1 / 2)+1(3 / 2)] \mathrm{kg} \mathrm{m}}{(1+1+1) \mathrm{kg}}=\frac{5}{6}\) m
∴ L-ఆకార పటలం ద్రవ్యరాశి కేంద్రం OD రేఖపై ఉంటుంది.

ప్రశ్న 3.
రెండు సదిశలు a = \((3 \hat{\mathrm{i}}-4 \hat{\mathrm{j}}+5 \hat{\mathrm{k}})\), b = \((-2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-3 \hat{\mathrm{k}})\) ల అదిశ, సదిశా లబ్ధాలను కనుక్కోండి. (3î – o
సాధన:
a · b = \((3 \hat{\mathrm{i}}-4 \hat{\mathrm{j}}+5 \hat{\mathrm{k}})\) . \((-2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-3 \hat{\mathrm{k}})\)
= -6 – 4 – 15
= – 25
a × b = \(\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\
3 & -4 & 5 \\
-2 & 1 & -3
\end{array}\right|=7 \hat{\mathrm{i}}-\hat{\mathrm{j}}-5 \hat{\mathrm{k}}\)
b × a = – \(7 \hat{\mathrm{i}}+\hat{\mathrm{j}}+5 \hat{\mathrm{k}}\) అని గుర్తించండి.

ప్రశ్న 4.
ఒక మోటారు చక్రం కోణీయ వడిని 1200 rpm నుంచి 3120 rpm కు 16 సెకన్లలో పెంచారు. (i) కోణీయ త్వరణం స్థిరమని భావించి, కోణీయ త్వరణాన్ని లెక్కించండి. (ii) ఈ సమయంలో ఇంజను ఎన్ని భ్రమణాలు చేస్తుంది ?
సాధన:
(i) తొలి కోణీయ వడి, ω₀ = 1200 R.P.M. 1200 × \(\frac{2 \pi}{60}\) = 40π రే/సె
తుది కోణీయ వడి, ω = 3120 RPM = 3120 × \(\frac{2 \pi}{60}\) = 104π రే/సె
కాలము t = 16 సె. కోణీయ త్వరణము α = ?
ω = ω₀ + αt నుండి α = \(\frac{\omega-\omega_0}{t}=\frac{(104-40) \pi}{16}\) = 4π రే/సె²

(ii) ఆగిపోవుటకు ముందు కోణీయ స్థానభ్రంశము θ = భ్రమణములలో
1 భ్రమణము = 2π రేడియన్
θ = \(\frac{\omega^2-\omega_0^2}{2 \alpha}\) భ్రమణాలలో ‘θ’ ను చెపితే θ = \(\frac{\omega^2-\omega_0^2}{2 \alpha \times 2 \pi}\)
= \(\frac{(104 \pi)^2-(40 \pi)^2}{2 \times 4 \pi \times 2 \pi}=\frac{(104+4.0)(104-40) \pi^2}{16 \pi^2}\) [a² – b² = (a + b)(a – b) నుండి]
= \(\frac{144 \times 64}{16}\) = 576 భ్రమణాలు

ప్రశ్న 5.
బలం \(\mathrm{7 i}+3 \hat{\mathrm{j}}-5 \hat{\mathrm{k}}\) వల్ల, మూలబిందువు పరంగా టార్క్ను కనుక్కోండి. బలం ప్రయోగించిన కణం స్థానసదిశ \(\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}\) (మార్చి 2014)
సాధన:
ఇక్కడ r = \(\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}\), F = \(\mathrm{7 i}+3 \hat{\mathrm{j}}-5 \hat{\mathrm{k}}\)
టార్క్ τ = r × F కనుక్కోవడానికి నిర్ధారక నియమాన్ని ఉపయోగిస్తాం..
τ = \(\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\
1 & -1 & 1 \\
7 & 3 & -5
\end{array}\right|=(5-3) \hat{\mathrm{i}}-(-5-7) \hat{\mathrm{j}}+3-(-7) \hat{\mathrm{k}}\)
లేదా τ = \(2 \hat{i}+12 \hat{j}+10 \hat{k}\)

ప్రశ్న 6.
M ద్రవ్యరాశి, l పొడవు ఉన్న కడ్డీకి లంబంగా, ఒక కొన ద్వారా పోయే అక్షం పరంగా జడత్వ భ్రామకం ఎంత ?
సాధన:
M ద్రవ్యరాశి, l పొడవు ఉన్న కడ్డీకి I = Ml² / 12. సమాంతరాక్ష సిద్ధాంతం ప్రకారం,
I’ = M\(\frac{l^2}{12}+\mathrm{M}\left(\frac{l}{2}\right)^2=\frac{\mathrm{M} l^2}{3}\)
2M ద్రవ్యరాశి, 2l పొడవు ఉన్న కడ్డీ మధ్య బిందువు నుంచి పోతూ, పొడవుకు లంబంగా ఉండే అక్షం పరంగా జడత్వ భ్రామకంలో సగం I’ అవ్వడం వల్ల ఈ ఫలితాన్ని స్వతంత్రంగానే సరిచూడవచ్చు.
I’ = 2M. \(\frac{4 l^2}{12} \times \frac{1}{2}=\frac{\mathrm{M} l^3}{3}\)

అదనపు లెక్కలు

ప్రశ్న 1.
ఏకరీతి సాంద్రత ఉన్న (i) గోళం, (ii) స్తూపం, (iii) కంకణం, (iv) ఘనాల ద్రవ్యరాశి కేంద్ర స్థానాన్ని గుర్తించండి. వస్తువు ద్రవ్యరాశి కేంద్రం తప్పక ఆ వస్తువులో ఉండి తీరాలా ?
సాధన:
(i) గోళానికి ద్రవ్యరాశి కేంద్రం, గోళ కేంద్రం వద్ద ఉంటుంది.

(ii) స్థూపానికి ద్రవ్యరాశి కేంద్రం దాని జ్యామితీయ కేంద్రం వద్ద ఉంటుంది. (స్థూపం పొడవు, r వ్యాసార్ధము అయితే దాని ద్రవ్యరాశి కేంద్రం స్థూల అక్షం మీద l/2 దూరంలో) ఉంటుంది.

(iii) కంకణం : కంకణానికి ద్రవ్యరాశి కేంద్రం, కంకణం కేంద్రం వద్ద ఉంటుంది.

(iv) ఘనానికి ద్రవ్యరాశి కేంద్రం దాని జ్యామితీయ కేంద్రం వద్ద ఉంటుంది.
ఘనము భుజము = a మరియు ఘనం ఒక మూలను మూలబిందువుగా తీసుకుంటే దాని ద్రవ్యరాశి కేంద్రం నిర్దేశకాలు x, y; 2 దిశలలో a/2, 2/2, a/2.
వస్తువు ద్రవ్యరాశి కేంద్రం వద్ద ద్రవ్యరాశి ఉండవలసిన అవసరం లేదు. ఉదా : కంకణం కేంద్రం వద్ద ద్రవ్యరాశి లేదు. కాని కంకణం ద్రవ్యరాశి కేంద్రం, కంకణ కేంద్రం వద్ద ఉంటుంది.

ప్రశ్న 2.
HCl అణువులో రెండు పరమాణువుల కేంద్రకాల మధ్య దూరం దాదాపు 1.27 Å (1Å = 10^-10 m). ఈ అణువు ద్రవ్యరాశి కేంద్ర స్థానాన్ని ఉజ్జాయింపుగా కనుక్కోండి. హైడ్రోజన్ పరమాణువుతో పోలిస్తే క్లోరిన్ పరమాణువు ద్రవ్యరాశి సుమారు 35.5 రెట్లు ఉంటుంది. పరమాణు ద్రవ్యరాశి అంతా కేంద్రకం వద్దనే కేంద్రీకృతమవుతుందని ఊహించండి.
సాధన:
హైడ్రోజన్ పరమాణు ద్రవ్యరాశి = m యూనిట్లు
క్లోరిన్ పరమాణు ద్రవ్యరాశి = 35.5 m యూనిట్లు
హైడ్రోజన్ పరమాణువులు నుండి x Å కు దూరము c.m అనుకొనుము.
∴ క్లోరిన్ పరమాణువు నుండి ద్రవ్యరాశి కేంద్రానికి దూరము – (1.27 – x)Å
ద్రవ్యరాశి కేంద్రాన్ని మూలబిందువు వద్ద తీసుకొంటే, m x + (1.27 – x) 35.5 m = 0
mx = – (1.27 – x) 35.5 m
c.m (ద్రవ్యరాశి కేంద్రం) (+) క్లోరిన్ పరమాణువు కుడివైపున ఉంటే, హైడ్రోజన్ పరమాణువు c. m కు ఎడమవైపున ఉంటుందని ఋణాత్మక గుర్తు సూచిస్తుంది.

కనుక ఋణాత్మక గుర్తును వదలివేస్తే,
x + 35.5 x = 1.27 × 35.5
i.e. 36.5 x = 45.085
= \(\frac{45.085}{36.5}\) = 1.235
x = 1.235 Å
∴ ద్రవ్యరాశి కేంద్రం హైడ్రోజన్, క్లోరిన్ పరమాణువుల కేంద్రకాలను కలిపే రేఖపై హైడ్రోజన్ నుండి 1.235 Å దూరంలో ఉండును.

ప్రశ్న 3.
నున్నని క్షితిజ సమాంతర నేలపై V వడితో సమరీతి గమనం కలిగిన ఒక ట్రాలీ (trolley – చక్రాలున్న పొడవైన బండి) మీద ఒక చివర ఒక బాలుడు నిశ్చలంగా కూర్చుని ఉన్నాడు. బాలుడు లేచి ట్రాలీపై ఏ విధంగా పరిగెత్తినా ట్రాలీ – బాలుడు వ్యవస్థ ద్రవ్యరాశి కేంద్రం వడి ఎంత ?
సాధన:
ట్రాలి, బాలుడి వ్యవస్థలో బాలుడు లేచి ఏ విధంగా పరిగెత్తినా ద్రవ్యరాశి కేంద్రం వడి మారదు. ఎందుకనగా ఈ చర్యలో ఇమిడి ఉన్న బలాలు అంతర్గత బలాలు. అంతర్గత బలాలు ద్రవ్యరాశి కేంద్రం గమనాన్ని మార్చజాలవు.

ప్రశ్న 4.
సదిశలు a, b లు భుజాలుగా కలిగి ఉన్న త్రిభుజ వైశాల్యం axb పరిమాణంలో సగం ఉంటుందని చూపండి.
సాధన:
\(\overline{\mathrm{a}}\) = OP మరియు \(\overline{\mathrm{b}}\) = OQ లను ఆసన్న భుజాలుగా తీసుకొని సమాంతర చతుర్భుజాన్ని (OPRQ) నిర్మించండి. ఈ సమాంతర చతుర్భుజ వైశాల్యము A = \(|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|\) = ab sin θ = OP . ON

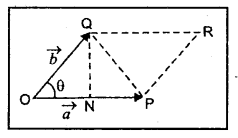
∆Oప్రశ్న నుండి sin θ = \(\frac{\mathrm{ప్రశ్న}}{\mathrm{OP}}\) ⇒ ప్రశ్న = \(\overline{\mathrm{b}}\) sin θ
కాని సమాంతర చతుర్భుజ వైశాల్యము
A = 2 త్రిభుజము Oప్రశ్న వైశాల్యము
∴ \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}\) = ab sin θ = 2 త్రిభుజము OPQ వైశాల్యము
∴ ∆OPQ వైశాల్యము = \(\frac{\overline{\mathrm{a}} \times \overline{\mathrm{b}}}{2}\) అని నిరూపించబడినది.

ప్రశ్న 5.
a · (b × c) పరిమాణం a, b, c సదిశలు భుజాలుగా గల సమానాంతర చతుర్భుజ ఘనం (parallelepiped) ఘనపరిమాణానికి సమానం అని చూపండి.
సాధన:
సమాంతర చతుర్భుజ ఘనమును ఏర్పరచిన సదిశలు \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}\) ; \(\overline{\mathrm{OB}}=\overline{\mathrm{b}}\) మరియు \(\overline{\mathrm{OC}}=\overline{\mathrm{c}}\) అనుకోండి.

\(\overline{\mathrm{b}} \times \overline{\mathrm{c}}=|\overline{\mathrm{b}}||\overline{\mathrm{c}}| \sin \theta \overline{\mathrm{n}}=\mathrm{ab}(\overline{\mathrm{n}})\) (∵ θ = 90°)
ఇందులో \(\overline{\mathrm{n}}\) ప్రమాణ సదిశ. ఇది \(\overline{\mathrm{b}}, \overline{\mathrm{c}}\) ల తలానికి లంబంగా ఉంటుంది.
అనగా ఇది \(\overline{\mathrm{a}}\) కు సమాంతరంగా ఉంటుంది.
\(\overline{\mathrm{a}} \cdot(\overline{\mathrm{b}} \times \overline{\mathrm{c}})=\overline{\mathrm{a}} \cdot(\mathrm{bc}) \overline{\mathrm{n}}=\overline{\mathrm{a}} \cdot \overline{\mathrm{n}}(\mathrm{bc})\) cos θ = abc
ఇది సమాంతర చతుర్భుజ ఘనము ఘనపరిమాణానికి సమానము.

ప్రశ్న 6.
ఒక కణం కోణీయ ద్రవ్యవేగం 1. x, y, z అక్షాల వెంబడి అంశాలను కనుక్కోండి. కణం స్థానసదిశ అంశాలు x, y, z లు, రేఖీయ ద్రవ్యవేగం p అంశాలు p_x, p_y, p_z ఒకవేళ కణం కేవలం x-y తలంలోనే గమనంలో ఉంటే కోణీయ ద్రవ్యవేగం zఅంశాన్ని మాత్రమే కలిగి ఉంటుందని చూపండి.
సాధన:

ప్రశ్న 7.
ఒక్కొక్కటి m ద్రవ్యరాశి గల రెండు కణాలు, వ్యతిరేక దిశలో, d దూరంలో ఉన్న సమాంతర రేఖలపై v వడితో గమనంలో ఉన్నాయి. ఏ బిందువు పరంగా కోణీయ ద్రవ్యవేగాన్ని కొలిచినా, ఈ ద్వికణ వ్యవస్థ కోణీయ ద్రవ్యవేగ సదిశ సమానమని చూపండి.
సాధన:
పటము నుండి X₁,Y₁, రేఖపై గల ఏదైనా బిందువు వద్ద కోణీయ ద్రవ్యవేగము \(\overrightarrow{\mathrm{L}}_{\mathrm{A}}=m \vec{v} \times 0+m \vec{v} \times d=m \vec{v} d\) ఇదే విధంగా X₂Y₂ రేఖపై గల B బిందువు వద్ద కోణీయ
ద్రవ్యవేగము \(\bar{L}_{\mathrm{B}}=m \overline{\mathrm{v}} \times \mathrm{d}+\mathrm{m} \overline{\mathrm{v}} \times 0=m \overline{v} d\)
AB రేఖపై గల ఏదైనా బిందువు C వద్ద AC = x అయితే BC = d – x

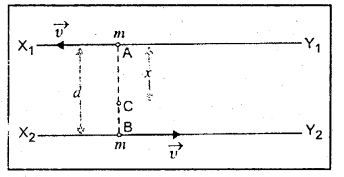
C బిందువు పరంగా రెండు కణముల వ్యవస్థ కోణీయ ద్రవ్యవేగము \(\overline{\mathrm{L}}_{\mathrm{c}}=m \overline{\mathrm{v}}(\mathrm{x})+\mathrm{m} \overline{\mathrm{v}}(\mathrm{d}-\mathrm{x})=\mathrm{m} \overline{\mathrm{v}} \mathrm{d}\)
అనగా \(\overline{\mathrm{L}}_{\mathrm{A}}=\overline{\mathrm{L}}_{\mathrm{B}}=\overline{\mathrm{L}}_{\mathrm{C}}\) అని నిరూపించబడినవి.

ప్రశ్న 8.
ఒక అసమరీతి, W భారం ఉన్న కడ్డీని ఉపేక్షించదగ్గ ద్రవ్యరాశి ఉన్న రెండు దారాలతో, పటంలో చూపినట్లు నిశ్చల స్థితిలో ఉండేటట్లు వేలాడదీశారు. క్షితిజ లంబరేఖతో దారాలు చేసే కోణాలు వరసగా 36.9°, 53.1°. కడ్డీ పొడవు 2m. కడ్డీ ఎడమ చివర నుంచి గరిమనాభి ఉండే దూరం d ని లెక్కించండి.

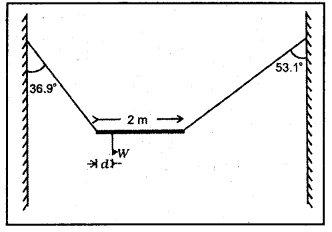
సాధన:
పటము నుండి θ₁ = 36.9° మరియు θ₂ = 53.1° .

కడ్డీ యొక్క ద్రవ్యరాశి కేంద్రము ‘C’ దూరము ఒక చివర నుండి ‘d’ అనుకోండి. అపుడు
T₁ cosθ₁ × d = T₂ cos θ₂ (2 – d) లేదా T₁ cos 36.9° × d = T₂ cos(53.1°)(2 – d)
∴ T₁ × 0.8366 d = T₂ × 0.6718(2 – d) ఇందులో
T₁ = 1.3523 T₂ ను వాడితే d = 0.745 మీ.

ప్రశ్న 9.
ఒక కారు 1800 kg బరువుంది. ముందు వెనకాల ఇరుసుల మధ్య దూరం 1.8 m. కారు గరిమనాభి, ముందు ఇరుసు వెనక 1.05 m దూరంలో ఉంది. సమతలంగా ఉన్న భూమి వల్ల ముందు వెనక గల చక్రాలొక్కొక్కటి పై ప్రయోగించే బలాన్ని కనుక్కోండి.
సాధన:
దత్తాంశం నుండి m = 1800 కి.గ్రా ; అక్షముల మధ్యదూరము = 1.8 మీ.
వెనక అక్షం నుండి ద్రవ్యరాశి కేంద్రదూరము = 1.05 మీ.
సమాంతరంగా ఉన్న నేల ముందువైపు, వెనుకవైపు గల చక్రాలపై అభిలంబచర్యలు R₁ మరియు R₂ అనుకుంటే
R₁ + R₂ = mg = 1800 × 9.8 → (i).
భ్రమణ సమతాస్థితి కోసం R₁ × 1.05 = R₂ (1.8 – 1.05) = 0.75R₂

ప్రశ్న 10.
a) ఘనగోళానికి స్పర్శరేఖ పరంగా దాని జడత్వ భ్రామకాన్ని కనుక్కోండి. గోళం వ్యాసంపరంగా జడత్వ భ్రామకం 2MR²/5 గా ఇచ్చారు. M గోళం ద్రవ్యరాశి, R దాని వ్యాసార్ధం.
b) M ద్రవ్యరాశి, R వ్యాసార్ధం ఉన్న వృత్తాకార దిమ్మె జడత్వ భ్రామకం, వ్యాసం పరంగా MR²/4, దిమ్మె ఒక అంచు నుంచి పోతూ దిమ్మె తలానికి లంబంగా ఉండే అక్షం పరంగా జడత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
a) ఏదైనా అక్షంపరంగా గోళం M.O.I = \(\frac{2}{5}\) MR²
సమాంతరాక్ష సిద్ధాంతం నుండి ఏదైనా స్పర్శరేఖ పరంగా M.O.I = \(\frac{2}{5}\) MR² + MR² = \(\frac{7}{5}\) MR²

b) వృత్తాకారపు బిళ్ళ వ్యాసము పరంగా M.O.I. = \(\frac{\mathrm{MR}^2}{4}\)
i) లంబాక్ష సిద్ధాంతం ప్రకారం తలానికి లంబంగా ఉండి బిళ్ళ కేంద్రం గుండా పోవు అక్షపరంగా
M.O.I = I_x + I₄ = \(\frac{\mathrm{MR}^2}{4}\) + \(\frac{\mathrm{MR}^2}{4}\) = \(\frac{\mathrm{MR}^2}{2}\)

ii) సమాంతరాక్ష సిద్ధాంతం నుండి అంచుకు లంబంగాగల ఏదైనా అక్షపరంగా
M.O.I = I_G + MR² = \(\frac{\mathrm{MR}^2}{2}\) + MR² = 3/2 MR²

ప్రశ్న 11.
సమాన ద్రవ్యరాశి, సమాన వ్యాసార్ధం ఉన్న ఒక బోలు స్తూపం, ఒక ఘనగోళంపై సమాన పరిమాణం ఉన్న టార్క్లను ప్రయోగించారు. స్తూపం దాని సౌష్టవాక్షం పరంగా స్వేచ్ఛగా భ్రమణం చేయగలుగుతుంది. గోళం దాని కేంద్రం ద్వారా పోయే అక్షం పరంగా స్వేచ్ఛగా భ్రమణం చేయగలుగుతుంది. వీటిల్లో, ఇచ్చిన కాలవ్యవధిలో, ఏది అధిక కోణీయ వేగాన్ని పొందుతుంది ?
సాధన:
బోలు స్థూపము మరియు ఘనగోళముల ద్రవ్యరాశి M మరియు వ్యాసార్ధము R అనుకోండి.
అక్షపరంగా బోలు స్థూపానికి M.O.I = I₁ = MR², గోళానికి I₂ = \(\frac{2}{5}\) MR²
కావలసిన టార్క్ τ = I₁α₁ = I₂α₂
∴ \(\frac{\alpha_2}{\alpha_1}=\frac{\mathrm{I}_1}{\mathrm{I}_2}=\frac{\mathrm{MR}^2}{\frac{2}{5} \mathrm{MR}^2}=\frac{5}{2}\)
∴ α₂ > α₁
ω = ω₀ + αt సమీకరణం నుండి ఇచ్చిన ω₀ మరియు t లకు ω₂ విలువ ω₁ కన్న ఎక్కువ అనగా ఘనగోళం కోణీయ వేగం బోలు స్థూపం కోణీయ వేగం కన్న ఎక్కువ.

ప్రశ్న 12.
20 kg ద్రవ్యరాశి ఉన్న ఒక ఘన స్తూపం దాని అక్షం పరంగా 100 rad s^-1 కోణీయ వడితో భ్రమణాలు చేస్తుంది. స్తూపం వ్యాసార్ధం 0.25 m. స్తూపం గతిజ శక్తి ఎంత ? స్తూపం అక్షంపరంగా కోణీయ ద్రవ్యవేగ పరిమాణం ఎంత?
సాధన:
దత్తాంశం నుండి M = 20 కి.గ్రా.; R = 0.25 మీ.; ω = 100 Rad/s
ఘనస్థూపానికి M.O.I = \(\frac{\mathrm{MR}^2}{2}=\frac{20 \times 0.25 \times 0.25}{2}\) = 0.65 కి. గ్రా. -మీ²
భ్రమణ గతిజశక్తి = \(\frac{1}{2}\) Iω² = \(\frac{1}{2}\) × 0.625 × 100 × 100 = 3125 J.
కోణీయ ద్రవ్యవేగము L = Iω = 0.625 × 100 = 62.5 Js.

ప్రశ్న 13.
(a)ఒక తిరుగుడు బల్ల కేంద్రం వద్ద ఒక బాలుడు తన చేతులను బయటకు చాచి నిలబడి ఉన్నాడు. తిరుగుడు బల్ల 40 భ్రమణాలు / నిమిషం కోణీయ వడితో భ్రమణంచేసేట్లు దాన్ని తిప్పారు. ఇలా తిరుగుతున్న బల్ల మీద బాలుడు తన చేతులను అతని జడత్వ భ్రామకం తొలి విలువకు 2/5 వంతులయ్యేట్లు ముడిస్తే అతని కోణీయ వడి ఎంత ? తిరుగుడు బల్ల ఘర్షణ లేకుండా భ్రమణాలు చేస్తుందని భావించండి.
(b)బాలుని కొత్త భ్రమణ గతిజశక్తి తొలి గతిజశక్తి కంటె ఎక్కువ అని చూపండి. అతని భ్రమణ గతిజశక్తి పెరుగుదలకు కారణాన్ని వివరించండి.
సాధన:
a) దత్తాంశం నుండి తొలి కోణీయ వడి
ω₁ = 40R.P.M
తుది M.O.I. I₂ = \(\frac{2}{5}\) I₁, ω₂ = ?
ఈ ప్రక్రియలో బాహ్య టార్క్ τ = 0;
∴ L = స్థిరరాశి కావున I₁ω₁ = I₂ω₂
∴ తుది కోణీయ వడి ω₂ = \(\frac{l_1}{\mathrm{l}_2} \omega_1=\frac{5}{2} \times 40\) = 100 R.P.M

b) తొలి భ్రమణ గతిజశక్తి E₁ = \(\frac{1}{2}\) I₁ω₁² ; తుది R.K.E. (E₂) = \(\frac{1}{2}\) I₂ω₂²
∴ \(\frac{\mathrm{E}_2}{\mathrm{E}_1}=\frac{\frac{1}{2} \mathrm{I}_2 \omega_2^2}{\frac{1}{2} \mathrm{l}_1 \omega_1^2}=\left(\frac{\mathrm{I}_2}{\mathrm{I}_1}\right)\left(\frac{\omega_2}{\omega_1}\right)^2=\frac{2}{5} \times \frac{100}{40} \times \frac{100}{4}=\frac{5}{2}\)
∴ E₂ = 2.5 E₁

ప్రశ్న 14.
3 kg ద్రవ్యరాశి, 40 cm వ్యాసార్ధం ఉన్న ఒక బోలు స్తూపం చుట్టూ దాదాపు ద్రవ్యరాశి లేని ఒక తాడు చుట్టారు. 30 N బలంతో తాడును లాగితే స్తూపం ఎంత కోణీయ త్వరణాన్ని పొందుతుంది ? తాడు రేఖీయ త్వరణం ఎంత అవుతుంది? తాడు స్థూపంపై స్లిప్కాదు అని భావించండి.
సాధన:
దత్తాంశం నుండి M = 3కి.గ్రా.; R = 40 సెం.మీ. = 0.4 మీ.
అక్షపరంగా బోలు స్థూపము M.O.I = I = MR² = 3 × 0.4 × 0.4 = 0.48 kg m².
బలము F = 30 N ∴ టార్క్ τ = F × R = 30 × 0.4 = 12 N-m.
కోణీయ త్వరణము α = \(\frac{\tau}{\mathrm{I}}\) (∵ τ = Iα)
∴ α = \(\frac{12}{0.48}\) = 25 Rad/s
రేఖీయ త్వరణము a = R α = 0.4 × 25 = 10 m/s²

ప్రశ్న 15.
ఒక యంత్రం భ్రమణ భాగానికి (rotor) 200 rad s^-1 ఏకరీతి కోణీయ వడిని సమకూర్చడానికి యంత్రం 180 Nm టార్క్న అందించవలసి ఉంది. యంత్రానికి అవసరమయ్యే సామర్థ్యం ఎంత ? (గమనిక : ఘర్షణ లేనప్పుడు సమకోణీయ వేగం కలిగి ఉండటమంటే టార్క్ శూన్యం అని అర్థం. వాస్తవానికి ప్రయోగించిన టార్క్ ఘర్షణ వల్ల కలిగే టార్క్్న వ్యతిరేకిస్తుంది.) యంత్రం 100% దక్షత కలిగి ఉన్నదని భావించండి.
సాధన:
దత్తాంశం నుండి (ω) = 200 Rad/s ; టార్క్ τ = 180 N – m
సామర్థ్యము P = τω = 180 × 200 = 36000 = 36 KW.

ప్రశ్న 16.
R వ్యాసార్ధం ఉన్న ఒక ఏకరీతి వృత్తాకార దిమ్మె నుంచి R/2 వ్యాసార్ధం గల వృత్తాకార ముక్కను వేరుచేసి రంధ్రాన్ని చేశారు. రంధ్రం కేంద్రం అసలు దిమ్మె కేంద్రం నుంచి R/2 దూరంలో ఉంది. ఫలితంగా ఏర్పడిన చదును వస్తువు గరిమనాభి స్థానాన్ని తెలపండి.
సాధన:
వృత్తాకార పలక ద్రవ్యరాశి కేంద్రం మూల బిందువు వద్ద కలదు.
చిన్న వృత్తాకార పలకను తొలగించకముందు, ద్రవ్యరాశి కేంద్రం = 0, 0
మొత్తం వృత్తాకార పలక ద్రవ్యరాశి = M = π (R)² = πR²ρ = M
ρ = ప్రమాణవైశాల్యానికి ద్రవ్యరాశి
చిన్న వృత్తాకార పలక వ్యాసార్ధం = \(\frac{\mathrm{R}}{2}\)
∴ ద్రవ్యరాశి M₂ = \(\frac{\pi \mathrm{R}^2}{4}\) ρ = \(\frac{\mathrm{M}}{4}\)

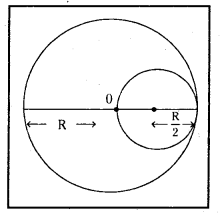
చిన్నపలక ద్రవ్యరాశి కేంద్రం దాని కేంద్రం వద్ద ఉండును. అనగా పెద్ద పలక కేంద్రం నుండి \(\frac{\mathrm{R}}{2}\) దూరంలో ఉండును.
ద్రవ్యరాశి కేంద్రం నిరూపకం \(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\) = 0 (చిన్నపలక తొలగించకముందు)
చిన్నపలకను తొలగించిన తరువాత ద్రవ్యరాశి M₁ = M – \(\frac{\mathrm{M}}{4}\) = \(\frac{\mathrm{3}}{4}\) M
∴ \(\frac{3}{4}\) M . x₁ + \(\frac{\mathrm{M}}{4}\) . \(\frac{\mathrm{R}}{2}\) = 0 ⇒ \(\frac{-3}{4}\) Mx₁ = \(\frac{\mathrm{M}}{4}\) \(\frac{\mathrm{R}}{2}\)
∴ x₁ = – \(\frac{\mathrm{R}}{6}\)
ద్రవ్యరాశి కేంద్రం వ్యతిరేక దిశలో కదులును అని ఋణ గుర్తు వలన తెలియును.

ప్రశ్న 17.
ఒక మీటర్ స్కేలును దాని కేంద్రం వద్ద కత్తిమొన ఉంచి తుల్య స్థితిలో నిలిపారు. ఒక్కొక్కటి 58 ద్రవ్యరాశి ఉన్న రెండు నాణాలను ఒకదానిపై ఒకటి అమరేట్లుగా స్కేలుపై 12.0 cm విభాగం వద్ద ఉంచారు. అప్పుడు కత్తిమొన 45.0 cm విభాగం వద్ద ఉన్నప్పుడు స్కేలు తుల్య స్థితికి వచ్చింది. మీటర్ స్కేలు ద్రవ్యరాశి ఎంత ?
సాధన:
స్కేలు బరువు M. ఇది C వద్ద కేంద్రీకరింపబడినది అనుకోండి.
C’ బిందుపరంగా సమతాస్థితి ఉంది, C’ దూరము = 45 సెం.మీ.
రెండు నాణెముల బరువు = 10 గ్రా.; వాటి స్థానము = 12 సెం.మీ. వద్ద
∴ సమతాస్థితి వద్ద 10g (45 – 12) = mg (50 – 45)
∴ 10g × 33 = mg. 5 ⇒ m = \(\frac{10 \times 330}{5}\) = 66 గ్రా.

ప్రశ్న 18.
ఒక ఘనగోళం, వరస క్రమంలో, సమాన ఎత్తులున్న రెండు భిన్న వాలు కోణాలున్న వాలుతలాలపై కిందికి
(a) ప్రతి వాలుతలంపై దొర్లుతూ అడుగుభాగానికి చేరినప్పుడు గోళం సమాన వడి కలిగి ఉంటుందా ?
b) ఒక వాలు తలంపై దొర్లడానికి తీసుకొనే కాలం, రెండవ దానిపై తీసుకొన్న కాలం కంటే ఎక్కువగా ఉంటుందా ? c) అలా అయితే ఏ వాలుతలంపై ఎక్కువ సమయం తీసుకొంటుంది ? ఎందుకు ?
సాధన:
a) వాలుతలం అడుగుభాగంలో ఘనగోళం వేగం ‘v’ అనుకోండి. శక్తినిత్యత్వ నియమం నుండి
\(\frac{1}{2}\) mv² + \(\frac{1}{2}\) Iω² = mgh కాని ఘనగోళం MOI = I = \(\frac{2}{5}\) MR²
∴ \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) \(\frac{2}{5}\) (mR)²ω² = mgh కాని v = rω
∴ \(\frac{1}{2}\) mv² + \(\frac{1}{5}\) mv² = mgh ⇒ v² = \(\frac{10}{7}\) gh ⇒ v = \(\sqrt{\frac{10}{7} \mathrm{gh}}\)
వాలుకోణం θ మారినప్పటికి తుదివేగం ” మారదు. అనగా గోళం వాలుతలం అడుగుభాగాన్ని తాకే వేగం వాలు కోణము ‘θ’ పై ఆధారపడదు.

b) కాని ప్రయాణించిన కాలము t ∝ \(\frac{1}{\sin \theta}\) అనగా వాలుకోణము ‘θ’ తగ్గితే కాలము t పెరుగును.

c) తక్కువ వాలుకోణము గల తలముపై గోళము ఎక్కువసేపు దొర్లుతుంది.

ప్రశ్న 19.
2 m వ్యాసార్ధం ఉన్న ఒక కంకణం 100 kg ల బరువు కలిగి ఉంది. అది ఒక క్షితిజ సమాంతర తలంపై, దాని ద్రవ్యరాశి కేంద్రం 20 cm/s వడితో గమనంలో ఉండేటట్లు దొర్లుతున్నది. దీన్ని నిశ్చలస్థితికి తేవడానికి ఎంతపని చేయవలసి ఉంటుంది ?
సాధన:
దత్తాంశం నుండి R = 2 మీ., M = 100 కి.గ్రా., v = 20 సెం.మీ/సె = 0.2 మీ/సె
కంకణం మొత్తం శక్తి E = \(\frac{1}{2}\) mV² + \(\frac{1}{2}\) Iω² = \(\frac{1}{2}\) mV² + \(\frac{1}{2}\) mR²ω²
= \(\frac{1}{2}\) mV² + \(\frac{1}{2}\) mR² \([\frac{\mathrm{V}^2}{\mathrm{R}^2}/latex] = [latex]\frac{1}{2}\) mV² + \(\frac{1}{2}\)mV² = mv² ( ∵ ω = \(\frac{\mathrm{V}}{\mathrm{R}}\))
కంకణాన్ని ఆపడానికి చేసిన పని W = కంకణంలోని మొత్తం శక్తి
⇒ W = mV² = 100 × 0.2 x 0.2 = 4 J

ప్రశ్న 20.
ఆక్సిజన్ అణువు ద్రవ్యరాశి 5.30 × 10^-26 kg. ఈ అణువులోని పరమాణువులను కలిపే రేఖకు గల మధ్య లంబరేఖ పరంగా దాని జడత్వ భ్రామకం 1.94 × 10^-46 kg m². ఇటువంటి అణువులున్న ఒక వాయువులో అణువు సగటు వడి పరంగా 500 m/s, అణువు భ్రమణ గతిజశక్తి దాని స్థానాంతరణ గతిజ శక్తిలో 2/3 వంతులు ఉన్నది అనుకొంటే అణువు సగటు కోణీయ వేగం ఎంత ?
సాధన:
దత్తాంశం నుండి m = 5.30 × 10^-26 kg,
I = 1.94 × 10^-46 kg m²,
v = 500m/s
ఒక్కొక్క ఆక్సిజన్ పరమాణువు ద్రవ్యరాశి = \(\frac{\mathrm{m}}{\mathrm{2}}\)
వాటి మధ్యదూరము d = 2r. పటము నుండి ఆక్సిజన్ అణువుల

కాని భ్రమణ గతిజశక్తి = \(\frac{2}{3}\) స్థానాంతరణ గతిజశక్తి
∴ \(\frac{1}{2}\) Iω² = \(\frac{2}{3}\) × \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) (mr²)ω² = \(\frac{1}{3}\) mv² ⇒ ω = \(\sqrt{\frac{2}{3}} \frac{\mathrm{v}}{\mathrm{r}}\)
∴ ω = \(\sqrt{\frac{2}{3}} \times \frac{500}{0.61 \times 10^{-10}}\) = 6.7 × 10¹² Rad/Sec.

ప్రశ్న 21.
ఒక ఘన స్తూపం 30° వాలు కోణం ఉన్న ఒక వాలు తలంపై కింది నుంచి పైకి దొర్లుతోంది. వాలుతలం కింది అంచువద్ద స్తూపం ద్రవ్యరాశి కేంద్ర వడి 5m/s.
(a)స్తూపం ఎంత దూరం వాలుతలం మీద పైకి దొర్లుతుంది ?
(b)మళ్ళీ అడుగుకు చేరడానికి ఎంత సమయం పడుతుంది ?
సాధన:
దత్తాంశం నుండి θ = 30°, v = 5 m/s
స్థూపము ‘h’ ఎత్తు వరకు వెళ్ళింది అని అనుకోండి.
శక్తి నిత్యత్వ నియమం నుండి \(\frac{1}{2}\) mV² + \(\frac{1}{2}\) Iω² = mgh