Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Errors and Approximations Important Questions to help strengthen their preparations for exams.
TS Inter 1st Year Maths 1B Errors and Approximations Important Questions
Question 1.
If y = x2 + 3x + 6, find ∆y and dy when x = 10, ∆x = 0.01. [Mar. ’15 (TS), ’14, ’11, ’05; May ’15 (AP)]
Solution:
Let y = f(x) = x2 + 3x + 6, x = 10, ∆x = 0.01
∆y = f(x + ∆x) – f(x)
= (x + ∆x)2 + 3(x + ∆x) + 6 – (x2 + 3x + 6)
= x2 + (∆x)2 + 2 . x . ∆x + 3x + 3(∆x) + 6 – x2 – 3x – 6
= (∆x)2 + 2 . x . ∆x + 3 . ∆x
= (2x + 3) ∆x + (∆x)2
= (2.10 + 3) (0.01) + (0. 01)2
= (23)(0.01) + 0.0001
= 0.23 + 0.0001
= 0.2301
dy = \(\frac{d y}{d x}\) × ∆x
= (2x + 3) ∆x
= (2.10 + 3)(0.01)
= 23(0.01)
= 0.23
![]()
Question 2.
Find ∆y and dy for the function y = ex + x when x = 5, ∆x = 0.02. [May ’13]
Solution:
Let y = f(x) = ex + x, x = 5, ∆x = 0.02
∆y = f(x + ∆x) – f(x)
= e(x+∆x) + (x + ∆x) – (ex + x)
= ex+∆x + x + ∆x – ex – x
= ex+∆x + ∆x – ex
= e5+0.02 + 0.02 – e5
dy = \(\frac{d y}{d x}\) × ∆x
= (ex + 1) × ∆x
= (e5 + 1) 0.02
Question 3.
Find the approximate value of √82. [Mar. ’13; May ’09]
Solution:
f(x) = √x, x = 81, ∆x = 1
∆f = df = \(\frac{d f}{d x}\) . ∆x
= \(\frac{1}{2 \sqrt{81}} \cdot 1\)
= \(\frac{1}{18}\)
= 0.05556
Now, √82 = f(x + ∆x) = ∆f + f(x)
= 0.05556 + 9
= 9.05556
Question 4.
Find the approximate value of \(\sqrt[3]{65}\).
Solution:
Let f(x) = \(\sqrt[3]{65}\), x = 64, ∆x = 1

f(x) = \(\sqrt[3]{x}\) = \(\sqrt[3]{64\) = 4
Now, \(\sqrt[3]{65}\) = f(x + ∆x) = ∆f + f(x)
= 4 + 0.02083
= 4.02083
![]()
Question 5.
If the increase in the side of a square is 2% then find the approximate percentage of increase in its area. [Mar. ’18 (TS); Mar. ’12, ’08; May ’05]
Solution:
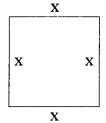
Let x be the side and A be the area of a square.
Given, that % error in x = 2
\(\frac{\Delta \mathrm{x}}{\mathrm{x}}\) × 100 = 2
The area of a square, A = x2

∴ % error in area = 4.
Question 6.
The diameter of a sphere is measured to be 40 cm. If an error of 0.02 cm is made in it, then find approximate errors in the volume and surface area of the sphere. [Mar. ’13(old), ’09; May ’03]
Solution:
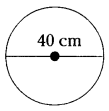
Let r, d, s, v be the radius, diameter, surface area, and volume of a sphere.
Given, diameter, d = 40 cm,
radius, r = 20 cm
error in diameter, ∆d = 0.02 cm
error in radius, ∆r = 0.01 cm
(i) Volume of a sphere, V = \(\frac{4}{3}\)πr3
error in V = ∆V = \(\frac{\mathrm{dV}}{\mathrm{dr}}\) . ∆r
= \(\frac{4}{3}\)π(3r2) . ∆r
= 4πr2 . ∆r
= 4π(20)2 (0.01)
= 16π cu. cm
(ii) Surface area of a sphere, s = 4πr2
error in surface area of a sphere ∆s = \(\frac{\mathrm{ds}}{\mathrm{dr}}\) ∆dr
= 4π(2r) . ∆r
= 8π(20)(0.01)
= 1.6π sq. cm
∴ Approximate error in the volume of sphere = 16π cu. cm.
∴ Approximate error in the area of sphere = 1.6π sq. cm.
Some More Maths 1B Errors and Approximations Important Questions
Question 7.
If y = 5x2 + 6x + 6, find ∆y and dy when x = 2, ∆x = 0.001.
Solution:
Let y = f(x) = 5x2 + 6x + 6, x = 2, ∆x = 0.001
∆y = f(x + ∆x) – f(x)
= 5(x + ∆x)2 + 6(x + ∆x) + 6 – (5x2 + 6x + 6)
= 5(x2 + (∆x)2 + 2 . x . ∆x) + 6x + 6(∆x) + 6 – 5x2 – 6x – 6
= 5x2 + 5(∆x)2 + 10 . x . ∆x + 6(∆x) – 5x2
= [5(∆x) + 10x + 6)] ∆x
= [5(0.001) + 10(2) + 6] (0.001)
= [0.005 + 20 + 6] 0.001
= 0.026005
dy = \(\frac{\mathrm{dy}}{\mathrm{dx}}\) × ∆x
= (5(2x) + 6) ∆x
= (10x + 6) ∆x
= (10 . 2 + 6) 0.001
= (26) 0.001
= 0.026
![]()
Question 8.
Find the approximate value of \(\sqrt{\mathbf{25.001}}\).
Solution:
Let f(x) = √x, x = 25, ∆x = 0.001

f(x) = √x = √25 = 5
Now, \(\sqrt{\mathbf{25.001}}\) = f(x + ∆x)
= ∆f + f(x)
= 0.0001 + 5
= 5.0001
Question 9.
If the increase in the side of a square is 4% then find the approximate percentage of increase in the area of the square.
Solution:
Let x be the side and A be the area of a square.
Given, that % error in the side = 4
∴ \(\frac{\Delta x}{x}\) × 100 = 4
Area of a square, A = x2
∆A = 2x . ∆x (∵ ∆A = \(\frac{\mathrm{dA}}{\mathrm{dx}}\) . ∆x)
Now, % error in area = \(\frac{\Delta \mathrm{A}}{\mathrm{A}}\) × 100
= \(\frac{2 \mathrm{x} \cdot \Delta \mathrm{x}}{\mathrm{x}^2}\) × 100
= \(\frac{2 \cdot \Delta x}{x}\) × 100
= 2 × 4
= 8
∴ % error in area = 8
Question 10.
Find dy and ∆y of y = f(x) = x2 + x, at x = 10 when ∆x = 0.1. [Mar. ’16 (TS), ’15 (AP); May ’15 (TS); Mar. ’17 (AP & TS)]
Solution:
Given, y = f(x) = x2 + x, x = 10, ∆x = 0.1
∆y = f(x + ∆x) – f(x)
= (x + ∆x)2 + x + ∆x – (x2 + x)
= x2 + (∆x)2 + 2 . x . ∆x + x + ∆x – x2 – x
= (∆x)2 + 2 . x . ∆x + ∆x
= (2x + 1) ∆x + (∆x)2
= (2 . 10 + 1) 0.1 + (0.1)2
= (21) (0.1) + 0.01
= 2.1 + 0.01
= 2.11
dy = \(\frac{\mathrm{dy}}{\mathrm{dx}}\) × ∆x
= (2x + 1) ∆x
= (2 . 10 + 1) 0.1
= (21) (0.1)
= 2.1
![]()
Question 11.
Find ∆y and dy of y = \(\frac{1}{x+2}\), x = 8 and ∆x = 0.02.
Solution:
Let y = f(x) = \(\frac{1}{x+2}\), x = 8, ∆x = 0.02
∆y = f(x + ∆x) – f(x)


Question 12.
Find ∆y and dy of y = cos x, x = 60°, and ∆x = 1°. [Mar. ’19 (TS)]
Solution:
Let y = f(x) = cos x, x = 60°,
∆x = 1° = 1(0.01745) = 0.01745
∆y = f(x + ∆x) – f(x)
= cos(x + ∆x) – cos x
= cos (60° + 1°) – cos 60°
= cos 61° – cos 60°
= 0.4848 – \(\frac{1}{2}\)
= 0.4848 – 0.5
= -0.0152
dy = \(\frac{\mathrm{dy}}{\mathrm{dx}}\) . ∆x
= -sin x . ∆x
= -sin 60° . (0.01745)
= \(\frac{-\sqrt{3}}{2}\) . (0.01745)
= -(0.8660)(0.01745)
= -0.015
Question 13.
Find the approximate value of \(\sqrt[3]{999}\). [Mar. ’19 (AP)]
Solution:

Question 14.
Find the approximate value of \(\sqrt[3]{7.8}\).
Solution:

Question 15.
Find the approximate value of sin 62°.
Solution:
Let y = f(x) = sin x, x = 60°,
∆x = 2° = 2(0.01745) = 0.03490
∆f = df = \(\frac{d f}{d x}\) . ∆x
= cos x . ∆x
= cos 60° (0.03490)
= \(\frac{0.03490}{2}\)
= 0.01745
f(x) = sin x = sin 60° = 0.8660
Now, sin 62° = f(x + ∆x) = f(x) + ∆f
= 0.8660 + 0.01745
= 0.88345
![]()
Question 16.
Find the approximate value of cos(60°5′).
Solution:
Let y = f(x) = cos x, x = 60°,
∆x = 5′ = \(\left(\frac{5}{60}\right)^{\circ}=\left(\frac{1}{12}\right)^{\circ}\)
= \(\frac{1}{12}\)(0.01745)
= 0.001454
∆f = df = \(\frac{\mathrm{df}}{\mathrm{dx}}\) . ∆x
= -sin x . ∆x
= -sin 60° . (0.001454)
= -0.8660 . (0.001454)
= -0.001259
f(x) = cos x = cos 60° = 0.5
Now, cos(60° 5′) = f(x + ∆x) = f(x) + ∆x
= 0.5 – 0.001259
= 0.498741
Question 17.
Find the approximate value of \(\sqrt[4]{17}\).
Solution:

Question 18.
The radius of a sphere is measured as 14 cm. Later it was found that there is an error of 0.02 cm in measuring the radius. Find the approximate error in the surface area of the sphere.
Solution:
Let r be the radius and s be the surface area of the sphere.
Given, radius, r = 14 cm
error in radius, ∆r = 0.02 cm
the surface area of a sphere, s = 4πr2
error in surface area of sphere = ∆s
= \(\frac{\mathrm{ds}}{\mathrm{dr}}\) . ∆r
= 4π(2r) . ∆r
= 8π(14)(0.02)
= 2.24π
= 2.24(3.14)
= 7.03356 or 7.04 sq.cm.
Question 19.
The side of a square is increased from 3 cm to 3.01 cm. Find the approximate increase in the area of the square.
Solution:
Let x be the side and A be the area of a square.
Given that x = 3, ∆x = 0.01
Area of a square, A = x2
error in area = ∆A = \(\frac{\mathrm{dA}}{\mathrm{dx}}\) . ∆x
= 2x . ∆x
= 2.3(0.01)
= 6(0.01)
= 0.06 sq. cm
![]()
Question 20.
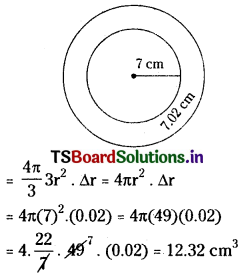
If the radius of a sphere is increased from 7 cm to 7.02 cm then find the approximate increase in the volume of the sphere.
Solution:
Ler r be the radius of a sphere and V be its volume.
Given that, radius r = 7 cm, ∆r = 0.02 cm
Volume of the sphere, V = \(\frac{4}{3} \pi r^3\)
error in volume = ∆V = \(\frac{\mathrm{dV}}{\mathrm{dr}}\) . ∆r
Question 21.
If y = f(x) = kxn then show that the approximate relative error (or increase) in y is n times the relative error (or increase) in x where n and k are constants.
Solution:
Given that y = f(x) = k . xn
error in y = ∆y = \(\frac{d y}{d x}\) . ∆x
= k . n . xn-1 . ∆x
relative error in y = \(\frac{\Delta \mathrm{y}}{\mathrm{y}}\)

∴ The relative error in y is n times the relative error in x.
Question 22.
The time t, of a complete oscillation of a simple pendulum of length l, is given by t = \(2 \pi \sqrt{\frac{l}{g}}\), where g is gravitational constant. Find the approximate percentage of error in ‘t’ when the percentage of error in l is 1%.
Solution:
