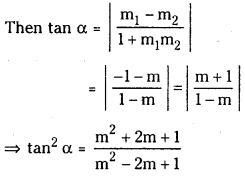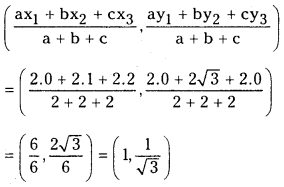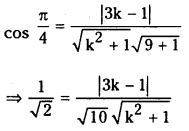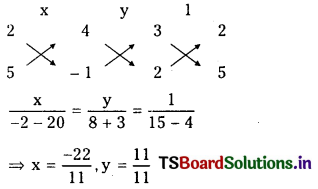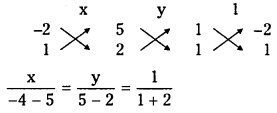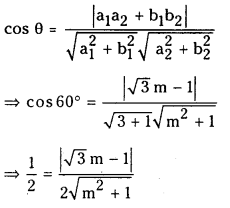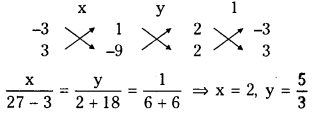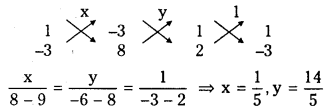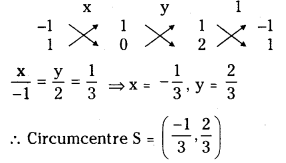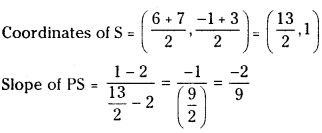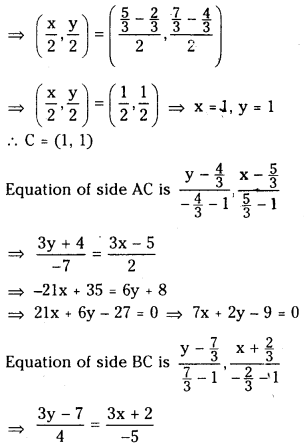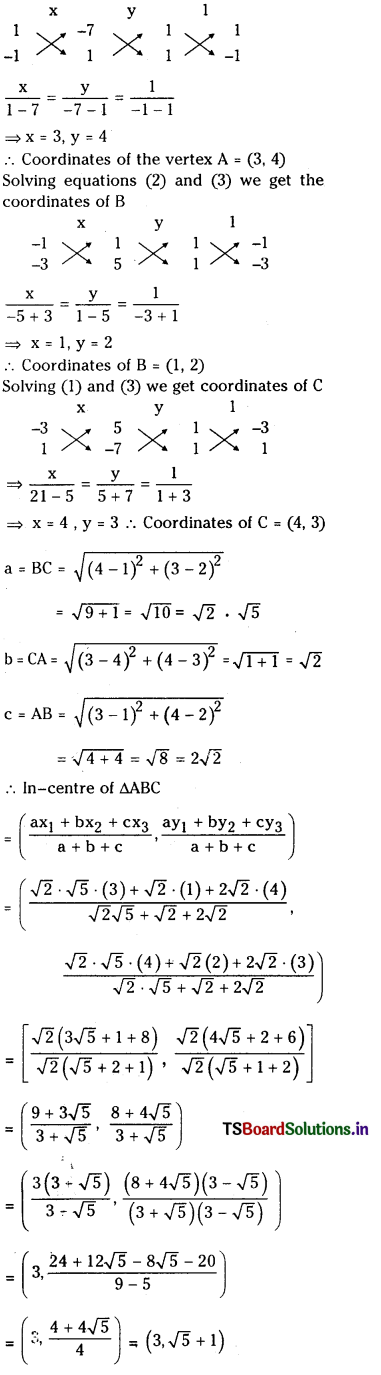Mahesh

Students must practice these TS Intermediate Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c)

I.
Question 1.
Find the equation of the lines joining the origin to the points of intersection of x² + y² = 1 and x + y = 1. (V.S.A.Q.)
Answer:
Given equations are
x² + y² = 1 ………………. (1)
and x + y = 1 ………………. (2)
Homogenising (1) with (2) we get
(x² + y²) = 1²
= (x + y)²
⇒ x² + y² = x² + y² + 2xy ⇒ xy = 0

Question 2.
Find the angle between the lines joining the origin to the points of intersection of y² = x and x + y = 1. (V.S.A.Q.)
Answer:
Given equations are
y² = x …………….. (1)
and x + y = 1 ……………… (2)
Homogenising (1) with (2) we get
y² = x (1)
= x (x + y) ⇒ x² + xy – y² = 0
Coefficient of x² + coefficient of y² = 1 – 1 = 0
∴ Angle between lines is 90°, lines being perpendicular.

II.

Question 1.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – √2 = 0 are mutually perpendicular. (S.A.Q.) (May, March ’12)
Answer:

The given equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 ………………… (1)
Equation of AB is x – y – √2 = 0
⇒ x – y = √2
⇒ \(\frac{x-y}{\sqrt{2}}\) = 1 …………………. (2)
Homogenising (1) using (2) we get
x² – xy + y² + (3x + 3y) (1) – 2 (1)² = 0

Question 2.
Find the values of k, if the lines joining the origin to the points of intersection of the curve 2×2 – 2xy + 3y2 + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular. (E.Q.) (Board New Model Paper)
Answer:
Given equation of the curve is
2x² – 2xy + 3y² + 2x – y – 1 = 0 ……………… (1)
and equation of the line is x + 2y = k
We have \(\frac{x+2 y}{k}\) = 1 ……………….. (2)
Homogenising equation (1) with equation (2) we get
2x² – 2xy + 3y² + 2x (1) – y (1) – (1)² = 0
⇒ 2×2 – 2xy + 3y2 + 2x\(\left(\frac{\mathrm{x}+2 \mathrm{y}}{\mathrm{k}}\right)\) – y\(\left(\frac{\mathrm{x}+2 \mathrm{y}}{\mathrm{k}}\right)\) – \(\left(\frac{x+2 y}{k}\right)^2\) = 0
⇒ 2k²x² – 2k²xy + 3k²y² + 2kx (x + 2y) – ky (x + 2y) – (x + 2y)² = 0
⇒ 2k²x² – 2k²xy + 3k²y² + 4kxy + 2kx² – kxy – 2ky² – (x² + 4xy + 4y²) = 0
⇒ (2k² + 2k – 1) x² + (- 2k² + 3k – 4) xy + (3k² – 2k – 4) y² = 0
Since the lines joining the origin to the points of intersection are mutually perpendicular, coefficient of x² + coefficient of y² = 0
⇒ (2k² + 2k – 1) + (3k² – 2k – 4) = 0
⇒ 5k² – 5 = 0 ⇒ k² = 1 ⇒ k = ± 1

Question 3.
Find the angle between the lines joining the origin to the points of intersection of the curve x² + 2xy + y² + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0 (E.Q.) (May 2014, 11, Mar.13, 07, June 04)
Answer:
Given equation of the curve is
x² + 2xy + y² + 2x + 2y – 5 = 0 …………….. (1)
Equation of the line is 3x – y + 1 = 0
⇒ y – 3x = 1 ……………….. (2)
Homogenising (1) with equation (2) we get the equation of lines joining the origin to the points of intersection of curve and the line.
∴ x² + 2xy + y² + 2x (1) + 2y (1) – 5 (1)² = 0
⇒ x² + 2xy + y² + 2x (y – 3x) + 2y (y – 3x) – 5 (y – 3x)² = 0
⇒ x² + 2xy + y² + 2xy – 6x² + 2y² – 6xy – 5(y² – 6xy + 9x²) = 0
⇒ – 5x² – 2xy + 3y² – 5y² – 45x² + 30xy = 0
⇒ – 50x² + 28xy – 2y² = 0
⇒ 25x² – 14xy + y² = 0
Let θ be the angle between lines then by the formula

III.
Question 1.
Find the condition for the chord lx + my = 1 of the circle x² + y² = a² (whose centre is the origin) to subtend a right angle at the origin. (Mar. 14) (SA.Q.)
Answer:

Equation of the circle is x² + y² = a² ………………. (1)
Equation of the line AB is lx + my = 1 ……………….. (2)
Homogenising (1) with equation (2) we get
x² + y² = a² (1)2
⇒ x² + y² = a²(lx + my)²
⇒ x² + y² = a² (l² x² + 2lmxy + m²y²)
⇒ (a²l² – 1)x² + 2a² lmxy + (a²m² – 1) y² = 0
Since OA, OB are perpendicular, we have coefficient of x² + coefficient of y² = 0
⇒ (a² l² – 1) + (a²m² – 1) = 0
⇒ a² (l² + m²) – 2 = 0
⇒ a² (l² + m²) = 2

Question 2.
Find the condition for the lines joining the origin to the points of intersection of the circle x2 + y2 = a2 and the line lx + my = 1 to coincide. (S.A.Q.)
Answer:
The given equation of the curve is
x² + y² = a² ……………. (1)
and the equation of line is
lx + my = 1 ………………… (2)
Homogenising (1) with equation (2) we get
x² + y² = a²(1)² = a² (lx + my)²
⇒ x² + y² = a² (l²x² + 2lmxy + m²y²)
⇒ x² (1 – a²l²) + y² (1 – a²m²) – 2 lma²xy = 0
This equation represents combined equation of lines joining the origin to the points of intersection of (1) and (2)
If the lines are coincident then h² = ab
l²m²a⁴ = (1 – a²m²) (1 – a²m²)
= 1 – a² (l² + m²) + a⁴l²m²
⇒ a² (l² + m²) = 1

Question 3.
Write down the equation of the pair of straight lines joining the origin to the points of intersection of the line 6x – y + 8 = 0 with the pair of straight lines 3x² + 4xy – 4y² – 11x + 2y + 6 = 0. Show that the lines so obtained make equal angles with the coordinate axes. (E.Q.)
Answer:
Given equation of pair of lines is
3x² + 4xy – 4y² – 11x + 2y + 6 = 0 ……………….. (1)
Given equation of line is 6x – y + 8 = 0 ………………. (2)
Homogenising (1) with equation (2)

⇒ 64 (3x² + 4xy – 4y²) – 8 [11xy – 66x² – 2y² + 12xy) + 6[y² + 36x² – 12xy] = 0
⇒ 936x² – 256xy + 256xy – 234y² = 0
⇒ 468x² – 117y² = 0
⇒ 4x² – y² = 0 …………………. (3)
This equation represents the combined equation of pair of lines joining the origin to the points of intersection of (1) and (2).
The equation of pair of angular bisectors of
(3) is h (x² – y²) – (a – b) xy = 0
⇒ 0(x² – y²) – (4 + 1) xy = 0
⇒xy = 0 ⇒ x = 0 or y = 0
Which are the equations of coordinate axes.
∴ The pair of lines are equally inclined to the coordinate axes.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 4 Preparation of Subsidiary Books to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 4 Preparation of Subsidiary Books

→ Subsidiary books are divided into 8 types. They are:

1. Purchase book
2. Sales book
3. Purchase returns book
4. Sales returns book
5. Cash book
6. Bills receivable book
7. Bills payable book
8. Journal proper.

→ Purchases book is the book in which only credit purchases of goods are recorded. Cash purchases of goods and assets are not recorded.

→ Sales book is a book of original entries in which transactions related to credit sales are recorded.

→ Purchase returns book is a book of original entries in which transactions related to the return of purchases of goods are recorded.

→ Sales returns book is a book in which transactions related to the return of sales of goods are recorded.

→ Journal proper is the Eighth Subsidiary book. This book is also called as “General Proper”.

→ Journal proper is used to record all those transactions which cannot be recorded in the other seven subsidiary books.

→ Some important items which are recorded in the journal proper are given below:

• Opening entry
• Closing entry
• Adjustment entry
• Rectification entry
• Transfer entry.

TS Inter 1st Year Accountancy Notes Chapter 4 సహాయక చిట్టాల తయారీ

→ సహాయక చిట్టాలు 8 రకాలు. అవి:

1. కొనుగోలు చిట్టా
2. అమ్మకాల చిట్టి
3. కొనుగోలు వాపసుల చిట్టా
4. అమ్మకాల వాపసుల చిట్టా
5. నగదు చిట్టా
6. వసూలు హుండీల చిట్టా
7. చెల్లింపు పొండీల చిట్టి
8. అసలు చిట్టా.

→ కొనుగోలు పుస్తకంలో అరువుపై కొనుగోలు చేసిన సరుకుల వివరాలు మాత్రమే నమోదు చేయాలి.

→ అమ్మకాల పుస్తకంలో అరువుపై అమ్మిన సరుకుల వివరాలు మాత్రమే నమోదు చేయాలి.

→ వ్యాపార సంస్థ కొనుగోలు చేసిన సరుకులను తిరిగి సరఫరాదారుకు వాపసు చేసిన వివరాలను కొనుగోలు వాపసుల పుస్తకంలో నమోదు చేయాలి.

→ వ్యాపార సంస్థ ఖాతాదారులకు సరుకు అమ్మిన తరువాత, కొనుగోలుదారుకు సరుకు వాపసు చేసినట్లయితే ఆ వివరాలను అమ్మకాల వాపసుల పుస్తకంలో నమోదు చేయాలి.

→ ఋణగ్రస్తుల నుండి రావలసిన బిల్లులను వసూలు హుండీల చిట్టాలో రాయాలి.

→ ఋణదాతలకు చెల్లింపు చేయవలసిన బిల్లులను చెల్లింపు హుండీల చిట్టాలో రాయాలి.

→ అసలు చిట్టా 8వ సహాయక పుస్తకం. మొదటి 7 సహాయక పుస్తకాలలో నమోదు చేయడానికి వీలుకాని వ్యాపార వ్యవహారాలను అసలు చిట్టాలో నమోదు చేస్తారు.

→ అసలు చిట్టాలో ఈ క్రింది వ్యవహారాలను నమోదు చేస్తారు.

1. ప్రారంభ పద్దులు
2. ఆస్తి అరువు కొనుగోలు పద్దులు
3. సవరణ పద్దులు
4. బదిలీ పద్దులు
5. ముగింపు పద్దులు
6. ఆస్తి అరువు అమ్మకాల పద్దులు
7. సర్దుబాటు పద్దులు
8. ఇతర పద్దులు.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 6 Bank Reconciliation Statement to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 6 Bank Reconciliation Statement

→ Bank Reconciliation Statement is a statement prepared to reconcile the difference between the balance as per the bank column of the cash book and pass book on any given date.

→ There are certain reasons for the difference in the pass book balance and the cash book balance.

→ Favourable balance means debit balance as per cash book and credit balance as per credit balance.

→ Unfavourable balance/overdraft balance means credit balance as per cash book and debit balance as per pass book.

TS Inter 1st Year Accountancy Notes Chapter 6 బ్యాంక్ నిల్వల సమన్వయ పట్టిక

→ నిర్ణీత తేదీన నగదు చిట్టి బ్యాంకు వరసల నిల్వ, పాస్బుక్ నిల్వలకు గల తేడాలను సమన్వయపరుస్తూ తయారుచేసే పట్టికను బ్యాంకు నిల్వల సమన్వయ పట్టిక అంటారు.

→ నగదు చిట్టాలోని నిల్వకు, పాస్బుక్లో లోని నిల్వకు గల తేడా చూపడానికి కొన్ని కారణాలున్నవి.

→ నగదు పుస్తకము డెబిట్ నిల్వను, పాస్బుక్ క్రెడిట్ నిల్వను చూపితే దానిని అనుకూల నిల్వ అంటారు.

→ నగదు పుస్తకము క్రెడిట్ నిల్వను, పాస్బుక్ డెబిట్ నిల్వను చూపితే దానిని ప్రతికూల నిల్వ అంటారు.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 5 Cash Book to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 5 Cash Book

→ Cash book is a very important subsidiary book. The object of the cash book is to keep a daily record of transactions relating to cash receipts and cash payments. Cash book acts as both journal and a ledger.

→ There are different kinds of cash books :

1. Simple cash book.
2. Two-column cash book with cash and discount columns.
3. Two-column cash books with Bank and discount columns.
4. Three-column cash book.
5. Petty cash book.

→ The entry which appears on both sides of the three-column cash book is known as a contra entry. It is required for transactions relating to cash or cheques deposited into the bank and cash withdrawn for office use.

→ All small payments are recorded in a separate cash book known as the Analytical Petty cash book.

TS Inter 1st Year Accountancy Notes Chapter 5 నగదు పుస్తకము

→ నగదు పుస్తకము చాలా ముఖ్యమైన సహాయక చిట్టా. రోజువారీ నగదు వసూళ్ళు చెల్లింపు వ్యవహారములు నమోదు చేయడమే నగదు పుస్తకము ముఖ్య ఉద్దేశ్యము.

→ నగదు పుస్తకములో దిగువ రకాలు ఉన్నవి;

1. సాధారణ నగదు చిట్టా,
2. నగదు, డిస్కౌంటు వరుసలు గల నగదు చిట్టి,
3. బాంకు, డిస్కౌంటు వరుసలు గల నగదు చిట్టా,
4. మూడు వరుసలు గల నగదు చిట్టా,
5. చిల్లర నగదు చిట్టా.

→ ఒక చిట్టాపద్దును మూడు వరుసలు గల నగదు చిట్టాలో రెండు వైపులా నమోదు చేస్తే దానిని ఎదురు వద్దు అంటారు. ఎదురు పద్దును దిగువ సందర్భాలలో రాయాలి.

• నగదు లేదా చెక్కులను బాంకులో జమ చేసినపుడు,
• ఆఫీసు అవసరాలకై బాంకు నుంచి నగదు తీసినపుడు.

→ వివిధ రకాల చిల్లర ఖర్చులను నమోదు చేయడానికి తయారుచేసే ప్రత్యేక నగదు పుస్తకాన్ని చిల్లర నగదు చిట్టా అంటారు.

Students must practice these TS Intermediate Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(a)

Question 1.
Find the acute angle between the pair of lines represented by the following equations. (V.S.A.Q.)
(i) x² – 7xy + 12y² = 0
Answer:
x² – 7xy + 12y² = 0
Comparing with ax² + 2hxy + by²
We get a = 1, b = 12, h = \(\frac{-7}{2}\)

(ii) y² – xy – 6x² = 0
Answer:
y² – xy – 6x² = 0
a = – 6, h = – \(\frac{1}{2}\), b = 1

(iii) (x cos α – y sin α)² = (x² + y²) sin² α
Answer:
(x cos α – y sin α)² = (x² + y²) sin2 α
x² cos² α + y² sin² α – 2xy cos α sin α
= x² sin² α + y² sin² α
= x² (cos² α – sin² α) – 2xy cos α sin α = 0
⇒ x² cos 2α – xy sin 2α = 0
Here a = cos 2α, b = 0, h = –\(\frac{1}{2}\) sin 2α
∴ tan θ = \(\left|\frac{2 \sqrt{h^2-a b}}{a+b}\right|\) = \(\left|\frac{2 \sqrt{\frac{1}{4} \sin ^2 2 \alpha}}{\cos 2 \alpha}\right|\)
= tan 2α
∴ θ = 2α

(iv) x² + 2xy cot α – y² = 0
Answer:
x² + 2xy cot α – y² = 0
Here a = 1, b = – 1, h = cot α
tan θ = \(\left|\frac{2 \sqrt{h^2-a b}}{a+b}\right|\) = \(\left|\frac{2 \sqrt{\cot ^2 \alpha+1}}{0}\right|\) = ∞
∴ θ = \(\frac{\pi}{2}\)

II.
Question 1.
Show that the following pairs of straight lines have the same set of angular bisectors (that is they are equally inclined to each other) (S.A.Q.)
(i) 2x² + 6xy + y² = 0
4x² + 18xy + y² = 0
(ii) a²x² + 2h(a + b)xy + b²y² = 0
ax² + 2hxy + by² = 0, a + b ≠ 0
(iii) ax² + 2hxy + by² + λ(x² + y²) = 0 (λ ∈ R)
ax² + 2hxy + by² = 0
Answer:

(i) Given equation 2x² + 6xy + y² = 0 represents combined equation of OA and OB.
Equation of pair of bisectors is
3(x² – y²) = (2 – 1)xy
⇒ 3(x² – y²) = xy ………………. (1)
Combined equation of OP and OQ is
4x² + 18xy + y² = 0
Equation to the pair of bisectors is
9(x² – y²) = (4 – 1)xy
⇒ 9(x² – y²) = 3xy
⇒ 3(x² – y²) = xy ………………… (2)
(1) and (2) denote the same lines.
∴ OA, OB and OP, OQ are inclined to each other. OR and OT are angular bisectors.

(ii) Given equation is a²x² + 2h(a + b)xy + b²y² = 0
represents combined equation of OA, OB.
∴ Equation to the pair of bisectors is
h(a + b) (x² – y²) = (a² – b²) xy
⇒ h(a + b) (x² – y²) = (a – b) (a + b) xy
⇒ h(x² – y²) = (a – b)xy …………………. (1)
Combined equation of OP, OQ is
ax² + 2hxy + by² = 0
Equation to the pair of bisectors is
\(\frac{x^2-y^2}{a-b}=\frac{x y}{h}\)
⇒ h(x² – y²) = (a – b)xy ………………….. (2)
(1), (2) represent the same equation.
Hence the pairs of lines have the same set of angular bisectors.

(iii) Equation to the pair of bisectors of the equation
ax² + 2hxy + by² + λ(x² + y²) = 0
⇒ x²(a + λ) + 2hxy + y²(b + λ) = 0 is

⇒ h(x² – y²) – xy(a – b) = 0 ………………. (1)
Equation to the pair of bisectors of
ax² + 2hxy + by² = 0 is \(\frac{x^2-y^2}{a-b}=\frac{x y}{h}\)
⇒ h(x² – y²) – xy(a – b) = 0
(1), (2) represent the same equation.
Hence the pairs of lines have the same set of angular bisectors.

Question 2.
Find the value of h, if the slopes of the lines represented by 6x² + 2hxy + y² = 0 are in the ratio 1 : 2. (S.A.Q.)
Answer:
Combined equation of the lines is
6x² + 2hxy + y² = 0
Suppose the slopes of two lines represented by the above equation be m₁ and m₂.
Then m₁ + m₁ = \(\frac{-2 h}{1}\), m₁m₂ = 6
Given that m₁ : m₂ = 1 : 2 ⇒ \(\frac{\mathrm{m}_1}{\mathrm{~m}_2}=\frac{1}{2}\)
⇒ m₂ = 2m₁
∴ 3m₁ = – 2h; 2m₁² = 6

Question 3.
If ax² + 2hxy + by² = 0 represents two straight lines such that the slope of one line is twice the slope of the other. Prove that 8h² = 9ab. (S.A.Q.)
Answer:
Combined equation of the lines is
ax² + 2hxy + by² = 0 ……………… (1)
Suppose y = m₁x and y = m₂x are the lines represented by (1).

Question 4.
Show that the equation of the pair of straight lines passing through the origin and making an angle of 30° with the line 3x – y – 1 = 0 is 13x² + 12xy – 3y² = 0. (S.A.Q.)
Answer:

Given equation of the straight line is
3x – y – 1 = 0 ………………….. (1)
Let the slope of (1) be m₁. Then m₁ = 3 Suppose the slope of the line passing through the origin making an angle 30° be ‘m’.
∴ Equation of the line passing through the origin with slope ’m’ is y = mx and
m = \(\frac{\mathrm{y}}{\mathrm{x}}\) …………………… (2)
Suppose angle between lines (1) and (2) be θ then tan θ =

⇒ 9m² + 6m + 1 = 3m² – 18m + 27
⇒ 6m² + 24m – 26 = 0
⇒ 3m² + 12m – 13 = 0
⇒ \(3\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^2+12\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\) – 13 = 0 [∵ From (2)]
⇒ 3y² + 12xy – 13x² = 0
⇒ 13x² – 12xy – 3y² = 0

Question 5.
Find the equation to the pair of straight lines passing through the origin and making an acute angle a with the straight line x + y + 5 = 0. (SA.Q.)
Answer:
Given equation of the line is x + y + 5 = 0 ………………… (1)

Let the slope of the given line be m₁ then m₁ = – 1. If m is the slope of the line making angle a with the line (1), then the equation of the line passing through the origin is
y = mx ⇒ m = \(\frac{y}{x}\) ………………….. (2)
If α is the angle between the lines (1) ans (2)

⇒ (m² – 2m + 1)tan² α = m² + 2m + 1
⇒ m²(1 – tan² α) + 2m(1 + tan² α) + (1 – tan²α)= 0 ……………… (3)
From (2) we have
\(\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^2\) (1 – tan² α) + 2\(\frac{y}{x}\)(1 + tan² α)
+ (1 – tan² α) = 0
⇒ (1 – tan² α)y² + 2xy(1 + tan² α) + x²(1 – tan² α) = 0 …………….. (4)

Case (i): If α = \(\frac{\pi}{4}\) then from (4)
2xy (1 + 1) = 0
⇒ 4xy = 0 ⇒ xy = 0

Case (ii): If α ≠ \(\frac{\pi}{4}\) then
x²+ 2xy\(\left(\frac{1+\tan ^2 \alpha}{1-\tan ^2 \alpha}\right)\) + y² = 0
⇒ x²+ 2xy\(\frac{1}{\cos 2 \alpha}\) + y² = 0
⇒ x²+ 2xy sec 2α + y² = 0
So if α ≠ \(\frac{\pi}{4}\) then the combined equation of lines is x² + 2xy sec 2α + y² = 0 and if α = \(\frac{\pi}{4}\) then the equation is xy = 0.

Question 6.
Show that the straight lines represented by (x + 2a)² – 3y² = 0 and x = a form an equilateral triangle. (S.A.Q.)
Answer:

Given equation of pair of lines is
(x + 2a)² – 3y² = 0
⇒ (x + 2a + √3 y) (x + 2a – √3y) = 0
Equation of OA is x + √3 y + 2a = 0 ………………. (1)
Equation of OB is x – √3y + 2a = 0 ………………. (2)
Equation of AB is x – a = 0 ………………… (3)
Use the formula for
cos θ = \(\left|\frac{a_1 a_2+b_1 b_2}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\right|\)
Between (1) and (3) lines
cos ∠OAB = \(\frac{|1+0|}{\sqrt{1+3} \sqrt{1}}=\frac{1}{2}\) = cos 60°
∴ ∠OAB = 60°
Similarly angle between (2) and (3) is
cos ∠OBA = \(\frac{|1+0|}{\sqrt{1+3} \sqrt{1}}=\frac{1}{2}\) = cos 60°
∴ ∠OBA = 60°
∴ ∠AOB = 180° – (∠OBA + ∠OAB)
= 180° – (60° + 60°) = 60°
∴ ∆ AOB is an equilateral triangle.

Question 7.
Show that the pair of bisectors of the angles between the straight lines (ax + by)2 = c (bx – ay)2, c > 0 are parallel and perpen¬dicular to the line ax + by + k = 0.(S.A.Q.)
Answer:
Combined equation of the given lines is
(ax + by)² = c(bx – ay)²
⇒ a²x² + 2abxy + b²y²
= c(b²x² – 2abxy + a²y²)
⇒ (a² – cb²)x² + 2ab(1 + c) xy + (b² – ca²)y² = 0 ……………… (1)
Using the standard equation of bisectors,
(x² – y²)h = xy(a – b)
Equation of bisectors of angles between the lines (1) is
(x² – y²) ab (1 + c) = (a² – cb² – b² + ca²)xy
= [a² – b² + c(a² – b²)]xy
= (a² – b²) (1 + c) xy
⇒ ab(x² – y²) = (a² – b²)xy
⇒ ab(x² – y²) – (a² – b²)xy = 0
⇒ abx² – aby² – a²xy + b²xy = 0
⇒ ax(bx – ay) + by (bx – ay) = 0
⇒ (ax + by) (bx – ay) = 0
Hence the equation of bisectors represented by (1) are ax + by = 0 ………………. (2)
bx – ay = 0 ………………….. (3)
Given equation of the line is
ax + by + k = 0 …………………… (4)
ax + by = 0 is parallel to ax + by + k = 0 and bx – ay = 0 is perpendicular to ax + by + k = 0.

Question 8.
The adjacent sides of a parallelogram are 2x² – 5xy + 3y² = 0 and one diagonal is x + y + 2 = 0. Find the vertices and the other diagonal. (S.A.Q.)
Answer:

The given equation is
2x² – 5xy + 3y² = 0 ……………… (1)
Which represent lines OA and OB respectively in the figure.
Equation of AB is x + y + 2 = 0
⇒ y = – (x + 2) ………………. (2)
∴ From (1)
⇒ 2x² + 5x(x + 2) + 3(x + 2)² = 0
⇒ 2x² + 5x² + 10x + 3(x² + 4x + 4) = 0
⇒ 10x² + 22x +12 = 0
⇒ 5x² + 11x + 6 = 0
⇒ 5x² + 5x + 6x + 6 = 0
⇒ 5x(x + 1) + 6(x + 1) = 0
⇒ (x + 1) (5x + 6) = 0
⇒ x = – 1 or x = \(\frac{-6}{5}\)
Also from (2), y = -(x + 2)
x = -1 ⇒ y = – 1

Question 9.
Find the centroid and the area of the triangle formed by the following lines.
(i) 2y² – xy – 6x² = 0, x + y + 4 = 0
(ii) 3x² – 4xy + y² = 0, 2x – y = 6 (S.A.Q.)
Answer:
(i)

The equation 2y² – xy – 6x² = 0
represents combined equation of OA and OB and equation of AB is x + y + 4 = 0
⇒ y = – (x + 4) …………….. (2)
From (1) 2(x + 4)² + x(x + 4) – 6x² = 0
⇒ 2(x² + 8x + 16) + x² + 4x – 6x² = 0
⇒ 3x² – 20x – 32 = 0
⇒ 3x² – 20x – 32 = 0
⇒ (3x + 4) (x – 8) = 0
⇒ x = – \(\frac{4}{3}\)

Case (i): x = – \(\frac{4}{3}\)
∴ y = – (x + 4)
= – \(\left(-\frac{4}{3}+4\right)\) = – \(\frac{8}{3}\)
∴ Co-ordinates of A = \(\left(-\frac{4}{3},-\frac{8}{3}\right)\)

Case (ii): x = 8 ⇒ y = – (8 + 4) = – 12
∴ Co-ordinates of B = (8, -12)
Let G be the centroid of ∆OAB

(ii) The equation 3x² – 4xy + y² = 0 ……………… (1)
represents pair of lines OA and OB.
Equation of AB is 2x – y = 6
⇒ y = 2x – 6 ……………. (2)
From (1) 3x² – 4x(2x – 6) + (2x – 6)² = 0
⇒ 3×2² – 8x² + 24x + 4x² – 24x + 36 = 0
⇒ – x² + 36 = 0 ⇒ x² – 36 = 0
⇒ (x + 6) (x – 6) = 0 ⇒ x = 6 or – 6
If x = 6 ⇒ y = 12 – 6 = 6
∴ Co-ordinates of A = (6, 6)
x = – 6 ⇒ y = -12 – 6 = -18
∴ Co-ordinates of B = (-6, -18)
∴ Co-ordinates of G = \(\left(\frac{0+6-6}{3}, \frac{0+6-18}{3}\right)\)
= (0, -4)
∴ Area of ∆OAB = \(\frac{1}{2}\) |₁y₂ – x₂yi I
= \(\frac{1}{2}\) |6 (- 18) – (- 6)6|
= \(\frac{1}{2}\) |- 108 + 36| = \(\frac{1}{2}\) (72) = 36 sq. units.

Question 10.
Find the equation of the pair of lines intersecting at (2, -1) and (S.A.Q.)
(i) Perpendicular to the pair 6x² – 13xy – 5y² = 0 and
(ii) Parallel to the pair 6x² – 13xy – 5y² = 0
Answer:
Given equation 6x² – 13xy – 5y² = 0 represents lines OA and OB.
(i) Equation of the pair of lines through
(x₁, y₁) and perpendicular to ax² + 2hxy + by² = 0 is b(x – x₁)²] a(y – y₁)² = 0
⇒ -5(x – 2)² + 13 (x – 2) (y + 1) + 6(y + 1)² = 0
⇒ -5(x² – 4x + 4) + 13 (xy + x – 2y – 2) + 6(y² + 2y + 1) = 0
⇒ -5x² + 20x – 20 + 13xy + 13x – 26y – 26 + 6y² + 12y + 6 = 0
⇒ 5x² – 13xy – 6y² – 33x + 14y + 40 = 0

(ii) Equation of the pair of lines through (x₁, y₁) and parallel to ax² + 2hxy + by² = 0 is
a(x – x₁)² + 2h (x – x₁) (y – y₁) + b(y – y₁)² = 0
⇒ 6(x – 2)² – 13 (x – 2) (y + 1) – 5(y + 1)² = 0
⇒ 6(x² – 4x + 4) – 13 (xy – 2y + x – 2) – 5(y² + 2y + 1) = 0
⇒ 6x² – 13xy – 5y² – 37x + 16y + 45 = 0

Question 11.
Find the equation of the bisector of the acute angle between the lines (S.A.Q.)
3x – 4y + 7 = 0 and 12x + 5y – 2 = 0.
Answer:
Given equations of lines are
3x – 4y + 7 = 0 ……………….. (1)
12x + 5y – 2 = 0 ………………… (2)
The equation of bisectors of angles between

⇒ 13(3x – 4y + 7) ± 5(12x + 5y – 2) = 0
⇒ (39x – 52y + 91) ± (60x + 25y – 10) = 0
∴ (39x – 52y + 91) + (60x + 25y – 10) = 0
⇒ 99x – 27y + 81 = 0
⇒ 11x – 3y + 9 = 0 ………………….. (3)
Also (39x – 52y + 91) – (60x + 25y – 10) = 0
⇒ – 21x – 77y + 101 = 0
⇒ 21x + 77y – 101 = 0 ………………….. (4)
Let θ be the angle between (1) and (4) then

∴ (4) is an obtuse angled bisector then (3) will be the acute angled bisector.
∴ 11x – 3y + 9 = 0 is the acute angled bisector.

Question 12.
Find the equation of the bisector of the obtuse angle between the lines x + y – 5 = 0 and x – 7y + 7 = 0 (S.A.Q.)
Answer:
Given equations of lines are
x + y – 5 = 0 ………………. (1)
and x – 7y + 7 = 0 ………………….. (2)
The equation of bisectors of angles between (1) and (2) is

⇒ 5x + 5y – 25 ± (x – 7y + 7) = 0
(i) (5x + 5y – 25) + (x – 7y + 7) = 0
⇒ 6x – 2y – 18 = 0
⇒ 3x – y – 9 = 0 …………………. (3)
(ii) (5x + 5y – 25) – (x – 7y + 7) = 0
⇒ 4x + 12y – 32 = 0
⇒ x + 3y – 8 = 0 ……………… (4)
Let θ be the angle between (1) and (4)
Then

∴ (4) is an acute angle bisector and hence (3) is an obtuse angle bisector.
∴ 3x – y – 9 = 0 is the obtuse angle bisector.

III.
Question 1.
Show that the lines represented by (lx + my)² – 3 (mx – ly)² = 0 and lx + my + n = 0 form an equilateral triangle with area \(\frac{n^2}{\sqrt{3}\left(l^2+m^2\right)}\). (S.A.Q.)
Answer:
The equation (lx + my)² – 3(mx – ly)² = 0 represents combined equation of lines OA and OB.
∴ (l²x² + m²y² + 2lmxy) – 3(m²x² – 2lmxy + l²y²) = 0
⇒ x²(l² – 3m²) + 8lmxy + (m² – 3l²)y² = 0 ……………….. (1)
Angle between lines represented by (1) by the formula cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^2+4 h^2}}\)

∴ θ = 60° which is the angle between OA and OB,
∴ ∠AOB = 60°
Combined equation of the bisectors of OA
and OB is h(x² – y²) = (a – b)xy
⇒ 4lm(x² – y²) = (l² – 3m² – m² + 3l²) xy
⇒ 4lm(x² – y²) = 4 (l² – m²) xy
⇒ lmx² – (l² – m²) xy – lmy² = 0
⇒ (lx + my) (mx – ly) = 0
⇒ lx + my = 0 and mx – ly = 0
∴ The bisector mx – ly = 0 is perpendicular to AB whose equation is lx + my + n = 0
∴ ∠OBA = 60°
∴ OAB is an equilateral triangle,
p = length of the perpendicular from O to AB.
= \(\frac{|\mathrm{n}|}{\sqrt{l^2+\mathrm{m}^2}}\)
∴ Area of ∆OAB = \(\frac{\mathrm{p}^2}{\sqrt{3}}=\frac{\mathrm{n}^2}{\sqrt{3}\left(l^2+\mathrm{m}^2\right)}\) sq.units

Question 2.
Show that the straight lines represented by 3x² + 48xy + 23y² = 0 and 3x – 2y + 13 = 0 form an equilateral triangle of area \(\frac{13}{\sqrt{3}}\) = sq.units. (E.Q.)
Answer:
The equation 3x² + 48xy + 23y² = 0 ……………… (1)
represents lines OA, OB.
Equation of AB is 3x – 2y + 13 = 0 — (2)
From (1) we.can express the equation as
(9x² – 12xy + 4y²) – 3 (4x² + 9y² + 12xy) = 0
⇒ (3x – 2y)² – 3 (2x + 3y)² = 0
⇒ [(3x – 2y) + √3 (2x + 3y)] [(3x – 2y) – √3 (2x + 3y)] = 0
⇒ [(3 + 2√3)x + (3√3 – 2) y] [(3 – 2√3 ) x – (3√3 + 2) y] = 0
∴ Equation of OA is
(3 – 2√3 ) x + (3√3 – 2) y = 0 ………………… (3)
Equation of OB is
(3 – 2√3) x – (3√3 + 2) y = 0 ……………… (4)
Angle between (2) and (3) is cos θ

Question 3.
Show that the equation of the pair of lines bisecting the angles between the pair of bisectors of the angles between the pair of lines ax² + 2hxy + by² = 0 is (a – b) (x² – y²) + 4hxy = 0. (S.A.Q.)
Answer:
Equation of the given lines is
ax² + 2hxy + by² = 0
Equation of the pair of bisectors is
(x² – y²) h = (a – b) xy — (1)
hx² – hy² – (a – b) xy = 0
Equation to the pair of bisectors of (1) is
– \(\frac{(a-b)}{2}\) (x² – y²) = (h + h)xy
⇒ (a – b) (x² – y²) + 4hxy = 0
∴ Equation of the pair of bisectors of the pair of bisectors of lines ax² + 2hxy + by² = 0 is (a – b) (x² – y²) + 4hxy = 0

Question 4.
If one line of the pair of lines ax² + 2hxy + by² = 0 bisects the angle be-tween the coordinate axes, prove that (a + b)² = 4h². (S.A.Q.) (June ’04)
Answer:
The angular bisectors of the coordinate axes are y = x and y = – x
Case (i) : When y = x is one of the lines of
ax² + 2hxy + by² = 0 then
ax² + 2hx (x) + bx² = 0
⇒ a + 2h + b = 0 …………………. (1)
Case (ii) : When y = – x is the other line of
ax² + 2hxy + by² = 0 then
ax² + 2hx(-x) + bx² = 0
⇒ a – 2h + b = 0 ………………… (2)
From (1) and (2)
[(a + b) + 2h] [(a + b) – 2h] = 0
⇒ (a + b)² – 4h² = 0
⇒ (a + b)² = 4h²

Question 5.
If (α, β) is the centroid of the triangle formed by the lines ax² + 2hxy + by² = 0 and lx + my = 1, prove that (E.Q.)
\(\frac{\alpha}{b l-h m}=\frac{\beta}{a m-h l}=\frac{2}{3\left(b l^2-2 h l m+a m^2\right)}\)
Answer:

Combined equation of OA and OB is
ax² + 2hxy + by² = 0 …………………. (1)
Equation of AB is lx + my = 1 ……………………. (2)
⇒ my = 1 – lx
⇒ y = \(\frac{1-l \mathrm{x}}{\mathrm{m}}\) ……………………… (3)
From (1) ax² + 2hx \(\left(\frac{1-l x}{m}\right)\) + b\(\left(\frac{1-l x}{m}\right)^2\) = 0
⇒ am²x² + 2hmx (1 – lx) + b (1 – lx)² = 0
⇒ (am² – 2hml + bl²) x² + 2hmx – 2blx + b = 0
⇒ (am² – 2hml + bl²) x² + 2x (hm – bl) + b = 0
Let the coordinates of point of intersection of lines (1) with (2) be A (x₁, y₁) and B (x₂, y₂).
Then x₁ + x₂ = \(\frac{-2(\mathrm{hm}-\mathrm{b} l)}{\mathrm{am}^2-2 \mathrm{hm} l+\mathrm{b} l^2}\)
= \(\frac{2(\mathrm{~b} l-\mathrm{hm})}{\mathrm{am}^2-2 \mathrm{~h} / \mathrm{m}+\mathrm{b} l^2}\) …………………… (4)
A(x₁, y₁) and B(x₂, y₂) lies on (2)
∴ lx₁ + my₁ = 1
lx₂ + my₂ = 1
⇒ l(x₁ + x₂) + m (y₁ + y₂) = 2
⇒ m (y₁ + y₂) = 2 – l(x₁ + x₂)

Question 6.
Prove that the distance from the origin to the orthocentre of the triangle formed by the lines \(\frac{x}{\alpha}+\frac{y}{\beta}\) = 1 and ax² + 2hxy + by² = 0 is (α² + β²)^1/2 \(\left|\frac{(a+b) \alpha \beta}{a \alpha^2-2 h \alpha \beta+b \beta^2}\right|\).
Answer:

Let OA and OB be the lines through the origin denoted by ax² + 2hxy + by² = 0 given by
l₁x + m₁y = 0 ………………. (1)
l₂x + m₂y = 0 ……………… (2)
∴ (l₁x + m₁y) (l₂x + m₂y) = ax² + 2hxy + by²
∴ l₁l₂ = a, m₁m₂ = b, l₁m₂ + l₂m₁ = 2h
Given line is \(\frac{1}{\alpha}\) x + \(\frac{1}{\beta}\) y = 1
Solving (1) and (3) we get the coordinates of A

Let B be the point of intersection of (2) and (3) Let P be the orthocentre of ∆AOB.

⇒ l₂y (l₁α – m₁β) + αβl₁l₂
= m₂x (l₁α – m₁β) + αβm₁m₂
= m₂x (l₁α – m₁β) – l₂y (l₁α – m₁β)
= – αβl₁l₂ – αβm₁m₂

Question 7.
The straight line lx + my + n = 0 bisects an angle between the pair of lines of which one is px + qy + r = 0. Show that the other line is (px + qy + r) (l² + m²) – 2 (lp + mq) (lx + my + n) = 0. (E.Q.)
Answer:
Let (α, β) be any point on the bisector
lx + my + n = 0 and lα + mβ + n = 0 ……………… (1)
The other line passes through the intersection of px + qy + r = 0 and lx + my + n = 0. This will be of the form p + λq = 0.
⇒ (px + qy + r) + λ(lx + my + n) = 0 ………………. (2)
Given px + qy + r = 0 ………………….. (3)
is one of the lines in pair of lines. If (α, β) is a point on the bisector then its perpendicular distance from lines (2) and (3) are same.

Simplifying and squaring on both sides,
(p + λl)² + (q + λm)² = p² + q²
⇒ (p² + 2pλl + λ²l²) + (q² + 2q λm + λ²m²) = p² + q²
⇒ 2 λ (pi + qm) + λ² (l² + m²) = 0
∴ 2λ (pl + qm) = – λ² (l² + m²)
⇒ λ = – 2 \(\left(\frac{\mathrm{p} l+\mathrm{qm}}{l^2+\mathrm{m}^2}\right)\)
∴ From equation (2), the equation of other line is (px + qy + r) – \(\frac{2(\mathrm{p} l+\mathrm{qm})}{l^2+\mathrm{m}^2}\) (lx + my + n) = 0
⇒ (px + qy + r) (l² + m²) – 2 (lp + qm) (lx + my + n) = 0

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Differentiation Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Differentiation Important Questions Short Answer Type

Question 1.
Find the derivative of x³ from the first principle. [Mar. ’15 (TS), ’98]
Solution:
Let f(x) = x³ then f(x + h) = (x + h)³

Question 2.
Find the derivative of \(\sqrt{x+1}\) from the first principle. [Mar. ’12, ’05]
Solution:

Question 3.
Find the derivative of sin 2x from the first principle. [B.P. May ’15 (TS), ’10, ’91; Mar. ’02; Mar. ’18 (AP)]
Solution:
Let f(x) = sin 2x
f(x + h) = sin 2(x + h) = sin 2x + 2h

Question 4.
Find the derivative of cos ax from the first principle. [May ’14; Mar. ’13 (old), ’13, ’11, ’09]
Solution:
Let f(x) = cos ax
f(x + h) = cos a(x + h) = cos(ax + ah)

Question 5.
Find the derivative of tan 2x from the first principle. [Mar. ’14, ’13 (old). ’05; May ’13. ’11; May ’15 (AP)]
Solution:
Let f(x) = tan 2x
f(x + h) = tan 2(x + h) = tan (2x + 2h)

Question 6.
Find the derivative of sec 3x from the first principle. [Mar. ’16 (AP), ’12, ’08]
Solution:
Let f(x) = sec 3x
f(x + h) = sec 3(x + h) = sec (3x + 3h)

Question 7.
Find the derivative of x sin x from the first principle. [Mar. ’18, ’15 (AP), ’10; May ’09]
Solution:
Let f(x) = x sin x
f(x + h) = (x + h) sin (x + h)

Question 8.
Find the derivative of cos²x from the first principle. [Mar. ’19 (TS); May ’08, ’04]
Solution:

Question 9.
Find the derivative of log x from the first principle. [Mar. ’03]
Solution:
Given, f(x) = log x
Now, f(x + h) = log (x + h)

∴ f is differentiable at x and f'(x) = \(\frac{1}{x}\)

Question 10.
Prove that \(\frac{d}{d x} \mathbf{u v}=\mathbf{u} \frac{d v}{d x}+v \frac{d u}{d x}\). [May ’97]
(Or)
If f, g are two differentiable functions at x then fg is differentiable at x. then show that (fg)’ (x) = f(x) g'(x) + g(x) f'(x).
Solution:
Since f and g are two differentiable functions at x, f'(x) and g'(x) exist.


= f(x + 0) . g'(x) + g(x) . f'(x)
= f(x) . g'(x) + g(x) . f'(x)
∴ fg is differentiable at x and (fg)’ (x) = f(x) g'(x) + g(x) f'(x).

Question 11.
Prove that \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\). [May ’04, ’98]
(Or)
If f, g are two differentiable functions at x and g(x) ≠ 0 then \(\frac{f}{g}\) is differentiable at x, then show that \(\left(\frac{f}{g}\right)^{\prime}(x)=\frac{g(x) f^{\prime}(x)-f(x) g^{\prime}(x)}{[g(x)]^2}\)
Solution:
Since f, g are differentiable at x and f'(x), g'(x) exists.

Question 12.
Find the derivative of \(\cos ^{-1}\left(\frac{b+a \cos x}{a+b \cos x}\right)\), (a > 0, b > 0). [May ’09]
Solution:
Let y = \(\cos ^{-1}\left(\frac{b+a \cos x}{a+b \cos x}\right)\)
Differentiating on both sides with respect to ‘r’ to ‘x’

Question 13.
If xy = ex-y, then show that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)^2}\). [Mar. ’08, ’07, ’96, ’88; May ’00, ’95]
Solution:
Given, x^y = e^x-y
Taking logarithms on both sides,
log(x^y) = log(e^x-y)
y log x = (x – y) log e
y log x = x – y
y + y log x = x
y(1 + log x) = x
y = \(\frac{x}{1+\log x}\)
Differentiating on both sides with respect to ‘x’

Question 14.
If sin y = x sin (a + y), then show that \(\frac{d y}{d x}=\frac{\sin ^2(a+y)}{\sin a}\). [Mar. ’95, May ’87]
Solution:
Given, sin y = x sin (a + y)
x = \(\frac{\sin y}{\sin (a+y)}\)
Differentiating on both sides with respect to ‘x’.

Question 15.
Differentiate \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\) with respect to \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\). [Mar. ’13 (Old); May ’04, ’95]
Solution:

Question 16.
Find the derivative of tan^-1(sec x + tan x). [May ’97]
Solution:

Question 17.
If x = a (cos t + t sin t), y = a (sin t – t cos t) then find \(\frac{d \mathbf{y}}{d \mathbf{x}}\). [Mar. ’16 (TS), May ’08, ’00, ’93]
Solution:
Given that x = a(cos t + t sin t)
Differentiating on both sides with respect to ‘t’.

Question 18.
If x = a(t – sin t), y = a(1 + cos t) then find \(\frac{d^2 \mathbf{y}}{\mathbf{d x}^2}\). [May ’02]
Solution:
Given, x = a(t – sin t)
Differentiating on both sides with respect to ‘x’.
\(\frac{\mathrm{dx}}{\mathrm{dt}}\) = a(1 – cos t)
y = a(1 + cos t)
Differentiating on both sides with respect to ‘x’.
\(\frac{\mathrm{dy}}{\mathrm{dt}}\) = a(0 – sin t) = -a sin t

Question 19.
Find the second order derivative of \(\tan ^{-1}\left(\frac{1+x}{1-x}\right)\). [May ’12]
Solution:
Given, f(x) = \(\tan ^{-1}\left(\frac{1+x}{1-x}\right)\)
Differentiating on both sides with respect to ‘x’.

Again differentiating on both sides with respect to ‘x’.
f”(x) = \(-\frac{1}{\left(1+x^2\right)^2}(0+2 x)=\frac{-2 x}{\left(1+x^2\right)^2}\)

Question 20.
If y = ae^nx + be^-nx, then prove that y” = n2y. [Mar. ’15 (AP); May ’14]
Solution:
Given y = ae^nx + be^-nx ………(1)
Differentiating on both sides with respect to ‘x’.
y’ = ae^nx (n) + be^-nx (-n)
y’ = n ae^nx – n be^-nx
again differentiating on both sides with respect to ‘x’
y” = na . e^nx (n) – n be^-nx (-n)
= n² ae^xnx + n2be^-nx
= n² (ae^nx + be^-nx)
= n²y (∵ from 1)
∴ y” = n²y

Question 21.
If y = axⁿ⁺¹ + bx^-n then prove that x²y¹¹ = n(n + 1)y. [May ’10; Mar. ’06]
Solution:
Given, y = axⁿ⁺¹ + bx^-n …….(1)
Differentiating on both sides with respect to ‘x’.
y¹ = a . (n + 1) x^n+1-1 + b(-n) x^-n-1
= a(n + 1)xⁿ – bn . x^-n-1
Again differentiating on both sides with respect to ‘x’.

Question 22.
If y = a cos x + (b + 2x) sin x, then prove that y¹¹ + y = 4 cos x. [May ’07]
Solution:
Given, y = a cos x + (b + 2x) sin x ………(1)
Differentiating on both sides with respect to ‘x’.
y¹ = a(-sin x) + (b + 2x) cos x + sin x (0 + 2 . 1)
y¹ = -a sin x + (b + 2x) cos x + 2 sin x
Again differentiating of both sides with respect to ‘x’.
y¹¹ = -a cos x + (b + 2x) (-sin x) + cos x (0 + 2 . 1) + 2 cos x
= -a cos x – (b + 2x) sin x + 2 cos x + 2 cos x
= -a cos x – (b + 2x) sin x + 4 cos x
= -[a cos x + (b + 2x) sin x] + 4 cos x
y¹¹ = -y + 4 cos x [∵ from (1)]
y¹¹ + y = 4 cos x

Question 23.
If ax² + 2hxy + by² = 1 then prove that \(\frac{d^2 y}{d x^2}=\frac{h^2-a b}{(h x+b y)^3}\). [Mar. ’08; May ’97]
Solution:
Given, ax² + 2hxy + by² = 1 ……..(1)
Differentiating on both sides with respect to ‘x’.

Question 24.
Find the derivative of cot x from the first principle. [Mar. ’19, ’17 (AP)]
Solution:

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 3 Subsidiary Books to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 3 Subsidiary Books

→ Recording transactions of ‘similar nature in separate and special books are known as subsidiary books.

→ Types of subsidiary books are 1. Purchases Book. 2. Purchase Returns Book. 3. Sales Book 4. Sales Return Book. 5. Cash Book 6. Bills Receivable Book 7. Bills Payable Book 8. Journal Proper.

→ Advantages of subsidiary books are :

1. Saving of time
2. Division of work
3. Easy and fast recording
4. Improves efficiency
5. Detection of errors.

TS Inter 1st Year Accountancy Notes Chapter 3 సహాయక చిట్టాలు

→ ఒకే స్వభావము కల వ్యవహారాలను రాయడానికి ఉపయోగించే ప్రత్యేక పుస్తకాలను సహాయక చిట్టాలు అంటారు.

→ సహాయక చిట్టాలు ముఖ్యముగా 8 రకాలు

1. కొనుగోలు చిట్టి
2. కొనుగోలు వాపసుల చిట్టా
3. అమ్మకాల చిట్టా
4. అమ్మకాల వాపసుల చిట్టా
5. నగదు చిట్టి
6. వసూలు హుండీల చిట్టా
7. చెల్లింపు హుండీల చిట్టి
8. అసలు చిట్టా

→ సహాయక చిట్టాల వలన ఉపయోగాలు 1. కాలం ఆదా 2 శ్రమ విభజన 3. సులభముగా నమోదు చేయడం 4. తప్పుల పట్టివేత 5. త్వరితముగా నైపుణ్యాలతో నమోదు చేయుట.

→ అసలుచిట్టా 8వ సహాయకచిట్టి. మొదటి 7 సహాయక చిట్టాలలో రాయడానికి వీలుకాని వ్యాపార వ్యవహారములను అసలు చిట్టాలో వ్రాస్తారు.

→ అసలు చిట్టి సాధారణ చిట్టాను పోలి ఉంటుంది. వ్యవహారాలను చిట్టాపద్దుల రూపములో వ్రాస్తారు.

→ అసలు వ్రాసే ప్రధాన వ్యవహారాలు, ముఖ్యముగా

• ప్రారంభ పద్దులు
• అరువుపై ఆస్తుల కొనుగోలు
• అరువుపై ఆస్తుల అమ్మకము
• సవరణ పద్దులు
• సర్దుబాటు పద్దులు
• ముగింపు పద్దులు
• బదిలీ పద్దులు
• ఇతర పద్దులు

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(e)

Question 1.
Find the in-centre of the triangle whose vertices are ( 1, √3), ( 2, 0) and (0, 0). (S.A.Q.)
Answer:
Let 0(0, 0), A (1, √3) and B (2, 0) are the vertices of ∆ABC

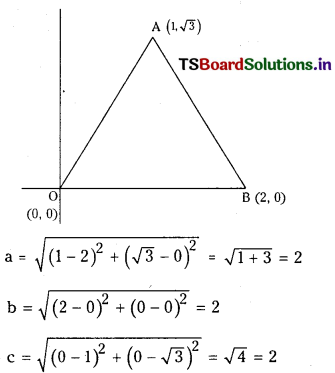
∴ ABC is an equilateral triangle.
Coordinates of in-centre are

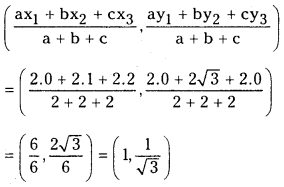
Question 2.
Find the orthocentre of the triangle whose sides are given by x + y + 10 = 0, x – y – 2 = 0 and 2x + y – 7 = 0
Answer:

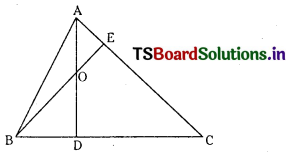
Equation of AB is x + y + 10 = 0 ………………. (1)
Equation of BC is x – y – 2 = 0 ………………. (2)
Equation of CA is 2x + y – 7 = 0 ………………… (3)
Solving (1) and (2) Coordinates of B are (-4, -6)
Solving (1) and (3) Coordinates of A are (17, -27)
Equation of BC is 2x – y – 2 = 0
AD is perpendicular to BC
Equation of AD is x + y + k = 0
AD passes through A (17, -27)
∴ 17 – 27 + k = 0 ⇒ k = 10
∴ Equation of AB is x + y + 10 = 0 ……………… (1)
Equation of AC is 2x + y – 7 = 0
BE is perpendicular to AC
Equation of DE can be taken as x – 2y = k
BE passes through D(-4 -6); – 4 + 12 = k ⇒ k = 8
Equation of BE is x – 2y = 8 ………………. (2)
x + y = – 10 ……………….. (1)
Solving (1) & (2)
– 3y = 18 ⇒ y = – 6
x + y + 10 = 0 ⇒ x – 6 + 10 = 0 ⇒ x = – 4
∴ Orthocentre of AABC is (- 4, – 6)

Question 3.
Find the orthocentre of the triangle whose sides are given by 4x – 7y + 14 = 0, x + y = 5 and 7x + 4y = 15 (V.S.A.Q.)
Answer:
Equation of sides AB and BC of a ∆ABC are
given by 4x – 7y + 10 = 0 ……………….. (1)
x + y = 5 ……………… (2)
and equation of side AC is
7x + 4y – 15 = 0 ………………. (3)
AB and AC are perpendicular and ∠A = 90°

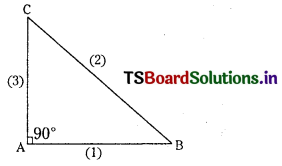
∴ ABC is a right angle triangle with ∠A = 90°and A is the orthocentre.
Solving (1) and (3)

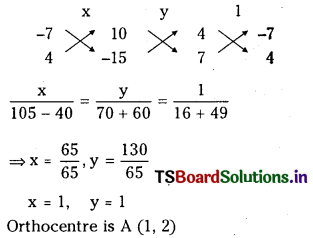
Question 4.
Find the circumcentre of the triangle whose sides are x = 1, y = 1 and x + y = 1 (V.S.A.Q.)
Answer:

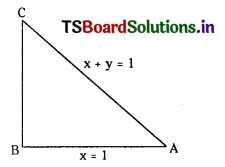
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1
AB and BC are perpendicular.
∴ ABC is a right angled triangle ∠B = 90°
Mid point of AC is the circumcentre.
Coordinates of A are (1, 0) and C are (0, 1).
∴ Circumcentre = \(\left(\frac{1}{2}, \frac{1}{2}\right)\)

Question 5.
Find the in-centre of the triangle formed by the lines x = 1, y = 1 and x + y = 1. (V.S.A.Q.)
Answer:
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1
Solving these equations we get vertices as
A(1, 0), B(1, 1), C(0, 1)

Question 6.
Find the circumcentre of the triangle whose vertices are (1, 0), (-1, 2) and (3, 2).(E.Q.) (March 2012)
Answer:

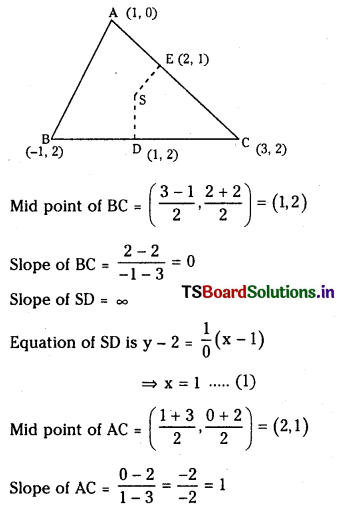
Slope of SE = – 1
Equation of SE is y – 1 = – l(x – 2)
⇒ y – 1 = – x + 2
⇒ x + y – 3 = 0 ………….. (2)
Solving (1) and (2) we get y – 2 = 0 ⇒ y = 2
⇒ Circumcentre S = (1, 2).

Question 7.
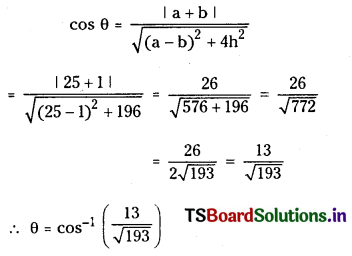
Find the values of k, if the angle between the straight lines kx + y + 9 = 0 and 3x – y + 4 = 0 is \(\frac{\pi}{4}\). (S.A.Q.)
Answer:
Equations of the given lines are
kx + y + 9 = 0
3x – y + 4 = 0

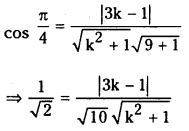
⇒ (k² + 1) 10 = 2 (3k – 1)²
⇒ 10k² + 10 = 2(9k² – 6k + 1)
⇒ 8k² – 12k – 8 = 0
⇒ 4k² – 6k – 4 = 0
⇒ 2k² – 3k – 2 = 0
⇒ (k – 2) (2k + 1) = 0 – 1
⇒ k = 2 or \(\frac{-1}{2}\)

Question 8.
Find the equation of the straight line passing through the origin and also through the point of intersection of lines 2x – y + 5 = 0 and x + y + 1 = 0. (V.S.A.Q.)
Answer:
Equations of given lines are
L₁ = 2x – y + 5 = 0 and L₂ = x + y + 1= 0
Equation of any line passing through A is
L₁ + k L₂ = 0
⇒ (2x – y + 5) + k(x + y + 1) = 0 (1)
This line passes through (0, 0) then
5 + k = 0 ⇒ k = – 5
Substituting in (1) equation of OA is
(2x – y + 5) – 5(x + y + 1) = 0
⇒ – 3x – 6y = 0
⇒ x + 2y = 0

Question 9.
Find the equation of the straight line parallel to the line 3x + 4y = 7 and passing through the point of intersection of the lines x – 2y – 3 = 0 and x + 3y – 6 = 0. (S.A.Q.)
Answer:
Let L₁ = x + 3y – 6 = 0 and L₂ = x – 2y – 3 = 0 be the given lines.
Equation of any line passing through the intersection is L₁ + KL₂ = 0
⇒ (x + 3y – 6) + k (x – 2y – 3) = 0 ….. (1)
⇒ x(1 + k) + y (3 – 2k) – (6 + 3k) = 0
This is parallel to 3x + 4y = 7
a₁b₂ = a₂b₁
⇒ 4(1 + k) = 3 (3 – 2k)
⇒ 4 + 4k = 9 – 6k
⇒ 10k = 5 ⇒ k = \(\frac{1}{2}\)
∴ From (1) (x + 3y – 6) + \(\frac{1}{2}\) (x – 2y – 3) = 0
⇒ 3x + 4y – 15 = 0
Equation of the required line is 3x + 4y – 15 = 0

Question 10.
Find the equation of the straight line perpendicular to the line 2x + 3y = 0 and passing through the point of intersection of lines x + 3y – 1 = 0 and x – 2y + 4 = 0. (S.A.Q.)
Answer:
Let L₁ = x + 3y – 1 = 0
and L₂ = x – 2y + 4 = 0
Equation of any line passing through the
point of intersection of L₁ = 0, L₂ = 0 is L₁ + kL₂ = 0
⇒ (x + 3y – 1) + k (x – 2y + 4) = 0 (1)
⇒ x(1 + k) + y (3 – 2k) – (1 – 4k) = 0
Slope of the line is –\(\left(\frac{1+\mathrm{k}}{3-2 \mathrm{k}}\right)\)
Slope of the given line 2x + 3y = 0 is \(\frac{-2}{3}\)
∴ Since the lines are perpendicular
\(\left(\frac{1+\mathrm{k}}{3-2 \mathrm{k}}\right)\left(\frac{2}{3}\right)\) = – 1
⇒ 2 + 2k = – 3 (3 – 2k)
= – 9 + 6k
⇒ 4k = 11 ⇒ k = \(\frac{11}{4}\)
Substituting in (1) equation of required line is
(x + 3y – 1) + \(\frac{11}{4}\)(x – 2y + 4) = 0
⇒ 4x + 12y – 4 + 11x – 22y + 44 = 0
⇒ 15x – 10y + 40 = 0
⇒ 3x – 2y + 8 = 0

Question 11.
Find the equation of the straight line making non-zero equal intercepts on the coordinate axes and passing through the point of intersection of the lines 2x – 5y + 1 = 0 and x – 3y – 4 = 0. (S.A.Q.)
Answer:
Equations of the given lines are
L₁ = 2x – 5y + 1 = 0
and L₂ = x – 3y – 4 = 0
Equation of any line passing through the point of intersection of L₁ = 0, L₂ = 0 is
L₁ + kL₂ = 0
⇒ (2x – 5y + 1) + k (x – 3y – 4) = 0 …. (1)
⇒ (2 + k) x – (5 + 3k) y + (1 – 4k) = 0
Intercepts on coordinate axes are equal.
⇒ 2 + k = – 5 – 3k
⇒ 4k = -7 ⇒ k = \(\frac{-7}{4}\)
∴ From (1) (2x – 5y + 1) – \(\frac{-7}{4}\) (x – 3y – 4) = 0
⇒ x + y + 32 = 0

Question 12.
Find the length of the perpendicular drawn from the point of intersection of the lines 3x + 2y + 4 = 0 and 2x + 5y – 1 = 0 to the straight line 7x + 24y – 15 = 0. (S.A.Q.)
Answer:
Equation of the given lines
3x + 2y + 4 = 0
2x + 5y – 1 = 0
Solving

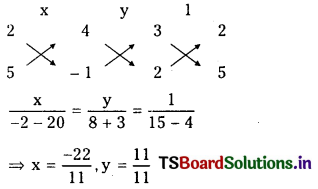
⇒ x = – 2, y = 1
Coordinates of point of intersection are (-2, 1)
Equation of the given line is 7x + 24y -15 = 0
∴ Length of the perpendicular from (-2, 1) to 7x + 24y – 15 = 0 is
\(\left|\frac{-14+24-15}{\sqrt{49+576}}\right|=\frac{5}{25}=\frac{1}{5}\)

Question 13.
Find the value of ‘a’ if the distances of the points (2, 3) and (-4, a) from the straight line 3x + 4y – 8 = 0 are equal. (S.A.Q.)
Answer:
Let A (2, 3) and B (-4, a) be the two points.
The distance from (2, 3) to the line 3x + 4y – 8 = 0 is
= \(\left|\frac{3(2)+4(3)-8}{\sqrt{3^2+4^2}}\right|\) = \(\frac{10}{5}\) = 2.
The distance from B(- 4, a) to the line 3x + 4y – 8 = 0
= \(\left|\frac{3(-4)+4 a-8}{\sqrt{3^2+4^2}}\right|\) = \(\frac{|4 a-20|}{5}\)
∴ 2 = \(\frac{|4 a-20|}{5}\)
⇒ |4a – 20| = 10 ⇒ 4a – 20 = ±10
⇒ 4a = 30 or 4a = 10
⇒ a = \(\frac{15}{2}\) or a = \(\frac{5}{2}\)

Question 14.
Find the circumcentre of the triangle formed by the straight lines x + y = 0, 2x + y + 5 = 0 and x – y = 2. (E.Q.)
Answer:

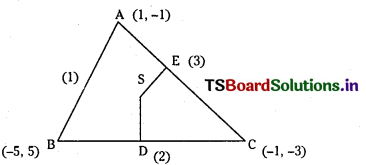
Equation of AB is x + y = 0, …………………. (1)
Equation of BC is 2x + y + 5 = 0 ……………………… (2 )
Equation of CA is x – y = 2 ………………………… (3)
Solving (1) and (2), Coordinates of B are (-5, 5)
Solving (2) and (3), Coordinates of C are (-1, -3)
Solving (1) and (3), Coordinates of A are (1, -1)

Equation of SE is y + 2 = – 1 (x)
⇒ x + y + 2 = 0 ………………. ( 5 )
Solving (4) and (5) we get coordinates of circumcentre S

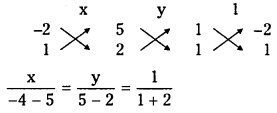
⇒ x = – 3, y = 1
∴ Coordinates of circumcentre S = (- 3, 1)

Question 15.
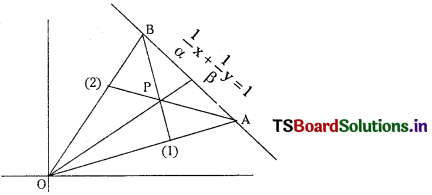
If θ is the angle between the lines \(\frac{x}{a}+\frac{y}{b}\) = 1 and \(\frac{x}{b}+\frac{y}{a}\) = 1, find the value of sin θ when a > b. (S.A.Q.)
Answer:
Equation of given lines \(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ bx + ay – ab = 0 ……………….. (1)

II.
Question 1.
Find the equation of straight lines passing through the point (- 10, 4) and making an angle 0 with the line x – 2y = 10 such that tan θ = 2. (E.Q.)
Answer:
Equation of BC is x – 2y – 10 = 0
Suppose slope of AB is’m’. AB passes through A (-10, 4)

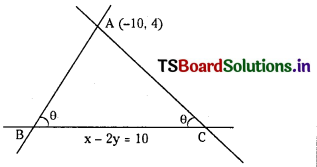
Equation of AB is y – 4 = m(x + 10) = mx + 10m
⇒ mx – y + (10m + 4) = 0 ………………… (1)

⇒ (m² + 1) = (m + 2)² = m² + 4m + 4
⇒ 4m + 3 = 0 ⇒ m = -3/4

Case (i): Coefficient of m² = 0
⇒ one of the roots is ∞.
Hence AC is a vertical line
∴ Equation of AC is x + 10 = 0;
(∵ y – 4 = \(\frac{1}{0}\) (x + 10))

Case (ii) : m = \(\frac{-3}{4}\)
From (1) equation of AB is
\(\frac{-3}{4}\) – y + (latex]\frac{-30}{4}[/latex] + 4) = 0
⇒ \(\frac{-3 x-4 y-14}{4}\) = 0
⇒ 3x + 4y + 14 = 0

Question 2.
Find the equations of the straight lines passing through the point (1,2) and making an angle of 60° with the line √3 x + y + 2 = 0. (Board Model Paper) (E.Q.)
Answer:

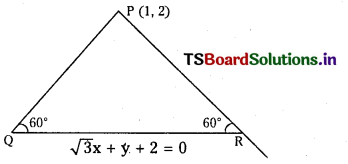
PQ, PR are two lines passing through P(1, 2) and makes an angle of 60° with QR.
Let slope of PQ is m
Equation of PQ is y – 2 = m (x – 1) = mx – m
∴ mx – y + (2 – m) = 0 …………….. ( 1 )

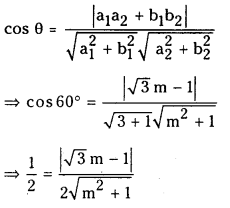
⇒ m² + 1 = (√3m – 1)² = 3m² + 1 – 2√3 m
⇒ 2m² – 2 √3 m = 0
⇒ 2m (m – √3) = 0 ⇒ m = 0 or √3

Case (i): m = 0
Equation of PQ is – y + 2 = 0 or y – 2 = 0

Case (ii): m = √3
Equation of PQ is √3x – y + (2 – √3) = 0

Question 3.
The base of an equilateral triangle is x + y – 2 = 0 and the opposite vertex is (2, -1). Find the equations of the remaining sides. (E.Q.)
Answer:

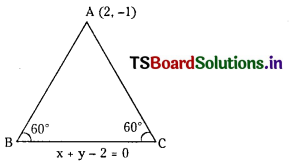
Equation of BC is x + y – 2 = 0
AB passes through A (2, -1)
Suppose slope of AB is’m’
Equation of AB is y + 1 = m (x – 2) = mx – 2m
⇒ mx – y – (2m + 1) = 0 …………………. (1)
cos 60° = \(\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
⇒ \(\frac{1}{2}=\frac{|m-1|}{\sqrt{1+1} \sqrt{m^2+1}}\)
⇒ (m² + 1) (2) = 4(m – 1)²
⇒ 2m² + 2 = 4(m² – 2m + 1)
⇒ 2m² – 8m + 2 = 0
⇒ m² – 4m + 1 = 0
⇒ m = \(\frac{4 \pm \sqrt{16-4}}{2}\) = \(\frac{4 \pm \sqrt{12}}{2}\) = \(\frac{4 \pm 2 \sqrt{3}}{2}\) = 2 ± √3
Substituting in (1)
Equation of AB is y + 1 = (2 + √3) (x – 2)
Equation of AC is y + 1 = (2 – √3) (x – 2)

Question 4.
Find the orthocentre of the triangle with the following vertices (E.Q.)
(i) (- 2, – 1), (6, – 1) and (2, 5) (March ’07)
(ii) ( 5, – 2 ), ( – 1, 2 ) and ( 1, 4 ) (March ’12)
Answer:
(i) Let A( – 2, – 1), B( 6, – 1), C( 2, 5 ) are the vertices of ∆ABC

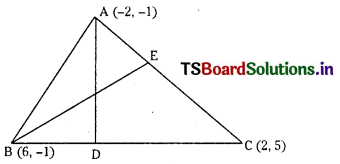
Slope of BC = \(\frac{5+1}{2-6}=\frac{6}{-4}=\frac{-3}{2}\)
AD is perpendicular to BC
Slope of AD = \(\frac{2}{3}\)
Equation of AD is y + 1 = \(\frac{2}{3}\) (x + 2)
⇒ 2x – 3y + 1 = 0 ………. (1)
Slope of AC = \(\frac{5+1}{2+2}=\frac{6}{4}=\frac{3}{2}\) = 2
BE is perpendicular to AC
Slope of BE = \(\frac{-2}{3}\)
Equation of BE is
y + 1 = \(\frac{-2}{3}\) (x – 6)
⇒ 2x + 3y – 9 = 0 ……………… (2)
Solving (1) and (2)

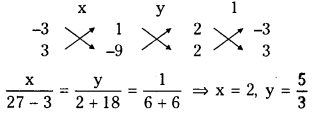
Coordinates of the orthocentre O are \(\left(2, \frac{5}{3}\right)\)

(ii) (5, – 2), (- 1, 2) and (1, 4)
Answer:

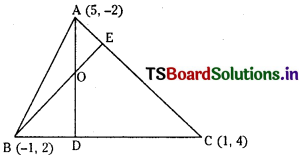
Let A(5, -2), B (-1, 2) and C(1, 4) be the vertices of ∆ABC.
Slope of BC =\(\frac{2-4}{-1-1}=\frac{-2}{-2}\) = 1
Slope of AD = – 1
Equation of AD is y + 2 = – 1 (x – 5)
⇒ x + y – 3 = 0 …………… (1)
Slope of AC = \(\frac{-2-4}{5-1}=\frac{-6}{4}=\frac{-3}{2}\)
∴ Slope of BE = \(\frac{2}{3}\)
∴ Equation of BE is y – 2 = \(\frac{2}{3}\) (x + 1)
⇒ 3y – 6 = 2x + 2
⇒ 2x – 3y + 8 = 0 ………………. (2)
Solving (1) and (2) we get the coordinates of the orthocentre ‘O’

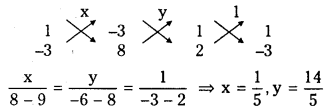
∴ Coordinates of orthocentre O are \(\left(\frac{1}{5}, \frac{14}{5}\right)\)

Question 5.
Find the circumcentre of the triangle whose vertices are given below.
(i) (-2, 3), (2, -1) and (4, 0) (March 2011)
(ii) (1, 3), (0, – 2) and (- 3, 1) (May 2006) (E.Q.)
Answer:
(i) (-2, 3), (2, -1) and (4, 0)

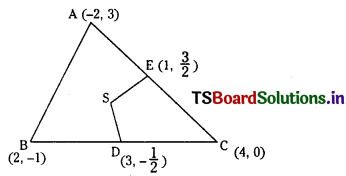
Let A(-2, 3), B(2, -1) and C(4, 0) be the vertices of ∆ ABC.
Mid point of side BC; D = \(\left(\frac{4+2}{2}, \frac{-1+0}{2}\right)\)
= \(\left(3,-\frac{1}{2}\right)\)
Slope of BC = \(\frac{-1-0}{2-4}=\frac{1}{2}\)
∴ Slope of SD is – 2.
Equation of SD is y + \(\frac{1}{2}\) = – 2(x – 3)
⇒ 2y + 1 = – 4 (x – 3)
⇒ 4x + 2y – 11 = 0 ……. (2)
E is the mid point of AC Coordinates of E are
⇒ x = \(\frac{12}{8}\) = \(\frac{3}{2}\) and 4\(\left(\frac{3}{2}\right)\) – 2y – 1 = 0
⇒ – 2y + 5 = 0 ⇒ y = \(\frac{5}{2}\)
∴ Coordinates of circumcentre S = \(\left(\frac{3}{2}, \frac{5}{2}\right)\)

(ii) (1, 3), (0, – 2) and (- 3, 1)

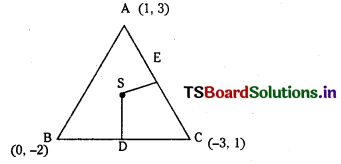
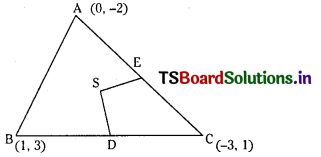
Let A(1, 3), B(0, -2) and C(-3, 1) be the vertices of ∆ABC. D is the mid point of BC.

SE is perpendicular to CA
Slope of SE is -2
Equation of SE is y – 2 = – 2 (x + 1)
⇒ 2x + y = 0 (2)
Solving (1) and (2)

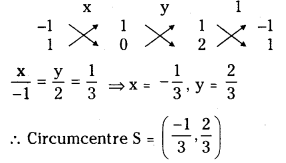
Question 6.
Let \(\overline{\text { PS }}\) be the median of the triangle with vertices P( 2, 2 ), Q ( 6, – 1 ) and R ( 7, 3 ). Find the equation of the straight line passing through ( 1, – 1) and parallel to the median PS. (E.Q.)
Answer:

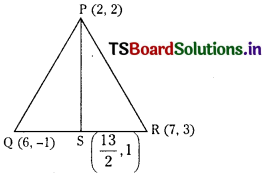
Let P (2, 2), Q (6, -1) and R (7, 3) be the vertices of ∆ABC.
S is the mid point of QR.

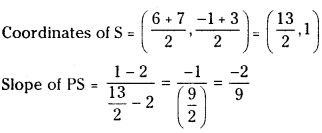
AB is parallel to PS and passes through A(1, – 1)
Equation of AB is y + 1 = \(\frac{-2}{9}\) (x – 1)
⇒ 9y + 9 = – 2x + 2
⇒ 2x + 9y + 7 = 0

III.
Question 1.
Find the orthocentre of the triangle formed by the lines x + 2y = 0, 4x + 3y – 5 = 0 and 3x + y = 0 (E.Q.)
Answer:

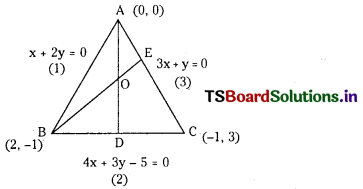
Equation of AB is x + 2y = 0 …………… (1)
Equation of BC is 4x + 3y – 5 = 0 …………… (2)
Equation of AC is 3x + y = 0 …………………. (3)
Solving (1) and (3) coordinates of A are (0,0)
Solving (1) and (2) we get the coordinates of C

Coordinates of C = (-1. 3)
Slope of BC = \(\frac{-1-3}{2+1}\) = \(\frac{-4}{3}\)
∴ Slope of AD = \(\frac{3}{4}\)
∴ Equation of AD is y – 0 = \(\frac{3}{4}\) (x – 0)
⇒ 3x – 4y = 0 ……… (4)
Slope of AC = \(\frac{0-3}{0+1}\) = – 3
∴ Slope of BE = \(\frac{1}{3}\)
∴ Equation of BE is y + 1 = \(\frac{1}{3}\) (x – 2)
⇒ 3y + 3 = x- 2
⇒ x – 3y – 5 = 0 ……………….. (5)
Solving (4) and (5) we get the coordinates of orthocentre.

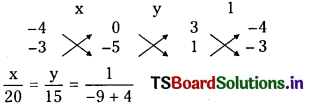
⇒ x = -4, y = -3
∴ Coordinates of orthocentre of ∆ABC is 0(- 4, -3)

Question 2.
Find the circumcentre of the triangle whose sides are given by x + y + 2 = 0; 5x – y – 2 = 0 and x – 2y + 5 = 0 (E.Q.)
Answer:
Given lines are x + y + 2 = 0 ………………….. ( 1 )
5x – y – 2 = 0 ………………….. (2)
x – 2y + 5 = 0 ………………….. (3)
Point of intersection of lines (1) and (2) is A = (0, -2)
Point of intersection of lines (2) and (3) is B = (1, 3)

Point of intersection of lines (1) and (3) is C(-3, 1)
D is the mid point of BC;
∴ Coordinates of D = \(\left(\frac{1-3}{2}, \frac{3+1}{2}\right)\)
= (-1, 2)
Slope of BC = \(\frac{3-1}{1+3}=\frac{2}{4}=\frac{1}{2}\)
Slope of SD = -2
Equation of SD is y – 2 = -2 (x + 1)
⇒ 2x + y = 0 …
E is the mid point of AC
(0-3 -2 + 0
∴ Coordinates of E = \(\left(\frac{0-3}{2}, \frac{-2+1}{2}\right)\)
= \(\left(\frac{-3}{2}, \frac{-1}{2}\right)\)
Slope of AC is \(\frac{-2-1}{0+3}\) = – 1
∴ Slope of SE = 1
∴ Equation of SE is y + \(\frac{1}{2}\) = 1 \(\left(x+\frac{3}{2}\right)\)
⇒ 2y + 1 = 2x + 3
⇒ 2x – 2y + 2 = 0
⇒ x – y + 1 = 0 ……………… (5)
Solving (4) and (5) we get the coordinates of circumcentre ‘S’.

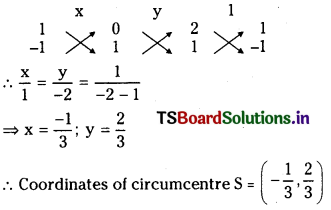
Question 3.
Find the equation of the straight lines passing through (1, 1) and which are at a distance of 3 units from (- 2, 3). (E.Q.)
Answer:
Let the line passing through A(l, 1) has slope’m’ then equation of the line is y – 1 = m(x – 1)
⇒ mx – y + (1 – m) = 0 …………… (1)
Distance from (-2, 3) to the line = 3
∴ \(\frac{|m(-2)-3+(1-m)|}{\sqrt{m^2+1}}\) = 3
⇒ (3m + 2)² = 9(m² + 1)
9m² + 12m + 4 = 9m² + 9
⇒ 12m = 5 ⇒ m = \(\frac{5}{12}\)
Coefficient of m² = 0 ⇒ m = ∞
(i) m = ∞
Equation of the line is y – 1 = \(\frac{1}{0}\) (x – 1)
⇒ x = 1

(ii) m = \(\frac{5}{12}\)
Substitute in (1)
Equation of the line is y – 1 = \(\frac{5}{12}\) (x – 1)
⇒ 12y – 12 = 5x – 5
⇒ 5x – 12y + 7 = 0

Question 4.
If p and q are the lengths of the perpendiculars from the origin to the straight lines x sec α + y cosec α = a and x cos α – y sin α = a cos 2α. Prove that 4p² + q² = a² (E.Q.)
Answer:
Equation of the line is x sec α + y cosec α = α
⇒ \(\frac{x}{\cos \alpha}+\frac{y}{\sin \alpha}\) = a
⇒ x sin α + y cos α = a sin α cos α
⇒ x sin α + y cos α – a sin α, cos α = 0 …….. (1)
p = length of the perpendicular from 0 on the line (1)
= \(\left|\frac{0+0-a \sin \alpha \cos \alpha}{\sqrt{\sin ^2 \alpha+\cos ^2 \alpha}}\right|\)
⇒ a sin α + cos α = p
⇒ 2p = a sin 2 α
Equation of the other given line is
x cos α – y sin α = a cos 2α ………………. ( 2 )
q = length of the perpendicular from 0 on the line (2)
∴ q = \(\left|\frac{a \cos 2 \alpha}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\right|\)
⇒ a² cos² 2α = q²
∴ 4p² + q² = a² sin² 2α + a² cos² 2α
= a² (sin² 2α + cos² 2α) = a² (1) = a²

Question 5.
Two adjacent sides of a Parallelogram are given by 4x + 5y = 0 and 7x + 2y = 0 and one diagonal is 1 lx + 7y = 9. Find the equation of the remaining sides and the other diagonal. (E.Q.)
Answer:

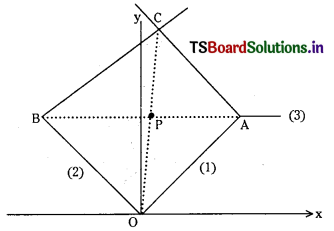
Let 4x + 5y = 0 ……………….. (1) and
7x + 2y = 0 …………….. (2) respectively
denote the sides \(\overrightarrow{O A}\) and \(\overrightarrow{O B}\) of the parallelogram OABC
Equation of the diagonal AB is 1 lx + 7y -9 =0 .
Solving (1) and (2) we get O = (0, 0)
Solving (1) and (3) we get


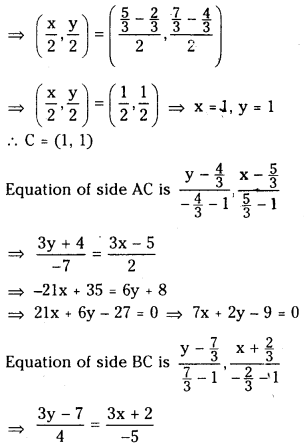
⇒ – 15y + 35 = 12x + 8
⇒ 12x + 15y – 27 = 0
⇒ 4x + 5y – 9 = 0

Question 6.
Find the in – centre of the triangle formed by the following straight lines. (E.Q.)
(i) x + 1= 0, 3x – 4y = 5 and 5x + 12y = 27
(ii) x + y – 7 = 0, x – y + 1 = 0 and x – 3y + 5 = 0
Answer:
(i)x + 1 = 0, 3x – 4y = 5 and 5x + 12y = 27
x + 1 = 0 …………….. (1)
3x – 4y = 5 …………………. (2)
5x + 12y = 27 ………………. (3) are the given equations of lines.
Point of intersection of (1) and (2) is A = (-1,-2)
Point of intersection of (2) and (3) is

(ii) x + y – 7 = 0, x – y + 1 = 0 and x – 3y + 5 = 0
Answer:
x + y – 7 = 0 …………….. (1)
x – y + 1 = 0 …………….. (2)
x – 3y + 5 = 0 …………….. (3)
Solving (1) and (2) we get

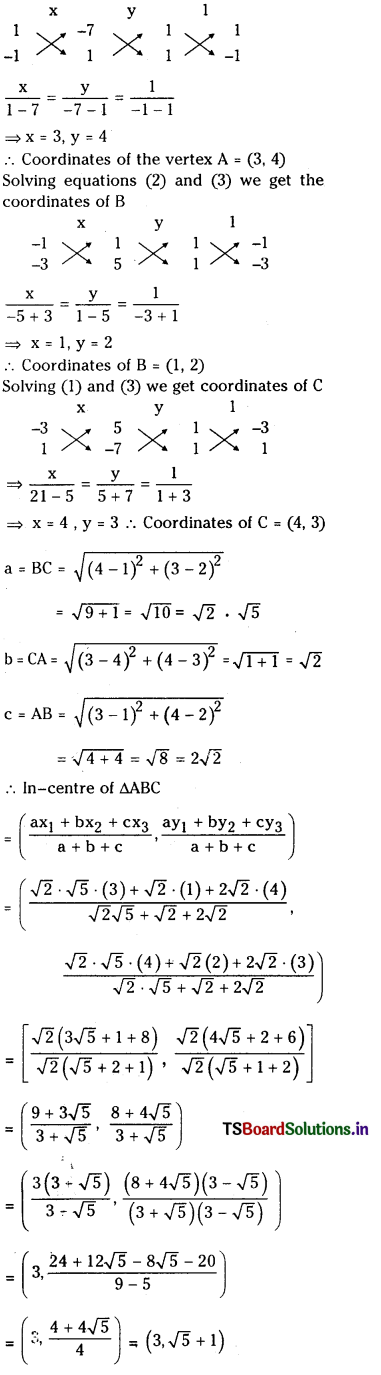
∴ In-center of the triangle formed by the sides x + y – 7 = 0, x – y + 1 = 0 and x – 3y + 5 = 0 is (3√5 + 1)

Question 7.
A triangle is formed by the lines ax + by + c = 0, lx + my + n = 0 and px + qy + r = 0. Given that the triangle is not right angled, show that the straight line \(\frac{a x+b y+c}{a p+b q}\) = \(\frac{l \mathbf{x}+\mathbf{m y}+\mathbf{n}}{l \mathbf{p}+\mathbf{m q}}\) passes through the orthocentre of the triangle. (E.Q.)
Answer:
Given equations of lines are
ax + by + c = 0 ……………… (1)
lx + my + n = 0 ……………. (2)
px + qy + r = 0 ……………… (3)
Equation of the line passing through the point of intersection of (1) and (2) is
(ax + by + c) + k (/x + my + n) = 0 (4)
⇒ (a + kl) x + (b + km) y + (c + nk) = 0
It is perpendicular to (3) then
p(a + kl) + q (b + km) = 0
⇒ k = – \(\left(\frac{\mathrm{ap}+\mathrm{bq}}{l \mathrm{p}+\mathrm{mq}}\right)\)
Substitute in (4) we get
(ax + by + c) – \(\left(\frac{\mathrm{ap}+\mathrm{bq}}{l \mathrm{p}+\mathrm{mq}}\right)\) (lx + my + n) = 0
⇒ \(\frac{\mathrm{ax}+\mathrm{by}+\mathrm{c}}{\mathrm{ap}+\mathrm{bq}}=\frac{l \mathrm{x}+\mathrm{my}+\mathrm{n}}{l \mathrm{p}+\mathrm{mq}}\)
is the required equation of the line line passing through the orthocentre of triangle which represents the altitude through A.

Question 8.
The Cartesian equations of the sides
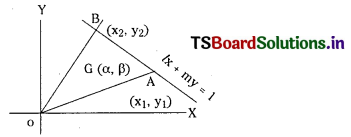
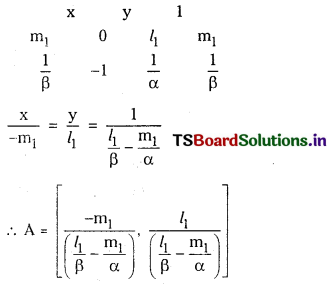
\(\overleftrightarrow{\mathbf{B C}}, \overleftrightarrow{\mathbf{C A}}\) and \(\overleftrightarrow{\mathbf{A B}}\) 0f a triangle are respectively u_r = a_rx + b_ry + c_r = 0, r = 1, 2, 3. Show that the equation of the straight line passing through A and bisecting the side \(\overline{\mathbf{B C}}\) is
\(\frac{u_3}{a_3 b_1-a_1 b_3}=\frac{u_2}{a_1 b_2-a_2 b_1}\) (E.Q.)
Answer:
A is a point of intersection of lines u₂ = 0 and u₃ = 0
Equation of the line passing through A is u₂ + λu₃ = 0
⇒ (a₂x + b₂y + c₂) + λ(a₃x + b₃y + c₃) = 0 …….(1)
⇒ (a₂ + λa₃)x + (b₂ + λb₃)y + (c₂ + λc₃) = 0
If this is parallel to a₁x + b₁y + c₁ = 0 we get

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 2 Recording of Business Transactions to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 2 Recording of Business Transactions

→ Voucher is a source document which is base for recording transactions in the books of Accounts.

→ A voucher may be in the form of cash memo, invoice, bill, debit note, credit note etc. Every transaction brings change in the financial position of business. This can be ex¬pressed in accounting equation, i.e., total assets are equal to capital plus liabilities.

→ For recording the business transactions, a firm follows single entry or double entry systems and cash system of accounting or mercantile system.

→ Accounts are classified into personal accounts, real accounts and nominal accounts. Each one of them have a rule of the account to be debited and credited.

→ Journal is a prime book in which we record the transactions. It is also called as “original entry”.

→ The process of recording transactions in the Journal is called “Journalising”. The entries made in the Journal are called “Journal Entries”.

→ The collection of all the accounts in book is called “Ledger” and recording of an entry in an account is called as “Posting”.

→ Ledger is also called as “Secondary Entry”.

TS Inter 1st Year Accountancy Notes Chapter 2 వ్యాపార వ్యవహారాలను నమోదు చేయటం

→ వోచర్ అనేది మూలస్తుతం. దీని ఆధారంగానే వ్యవహారాలను ఖాతా పుస్తకాలలో నమోదు చేస్తారు.

→ ఈ వోచర్ నగదు మెమో, ఇన్వాయిస్, బిల్లు, డెబిట్ నోట్స్, కెడిట్ నోట్ మొదలైన రూపాలలో ఉంటుంది. వీటిని ఖాతాల తనిఖీ చేసే నిమిత్తం భ్రదపరచాలి.

→ ప్రతి వ్యవహారం, వ్యాపార ఆర్థికస్థితి గతులను ప్రభావితం చేస్తుంది. దీనినే అకౌంటింగ్ సమీకరణం రూపంలో వ్యక్తపరచవచ్చును. అంటే ఒక నిర్థిష్ట సమయంలో ఆస్తుల మొత్తం విలువ సంస్థ యొక్క అప్పులు మరియు మూలధనానికి సమానంగా ఉంటుంది.

→ వ్యాపార వ్యవహారాలను నమోదు చేయుటకు, సంస్థలు, ఒంటి పద్దు విధానం లేదా జంట పద్దు విధానం కాని, నగదు పద్ధతి లేదా సముపార్జన పద్ధతిని పాటించవచ్చు.

→ ఖాతాలను వ్యక్తిగత, వాస్తవిక, నామమాత్రపు ఖాతాలుగా వర్గీకరించవచ్చు ఈ ఖాతాలకు సంబంధించిన డెబిట్స్, కెడిట్ సూత్రాలను రూపొందించటం జరిగింది.

→ చిట్టి అంటే రోజువారి వ్యాపార వ్యవహారాలను నమోదు చేసే పుస్తకం. దీనిలో వ్యాపార వ్యవహారాలు జరిగిన వెంటనే ప్రప్రధమంగా నమోదు చేస్తారు. అందువల్లే చిట్టాను “తొలిపద్దు” లేదా “అసలుపద్దు” పుస్తకం అని కూడా పిలుస్తారు.

→ చిట్టాలో వ్యవహారాలు రాయటాన్ని “చిట్టిపద్దులు” అంటారు.

→ ఆవర్జాలో వివిధ ఖాతాలలో నమోదు అయిన వ్యవహారాల నికర ఫలితాలకు సంబంధించిన సమాచారం ఉంటుంది. దీనిలో అన్ని ఖాతాలు అనగా వాస్తవిక నామమాత్రపు, వ్యక్తిగత ఖాతాలకు సంబంధించిన మొత్తం సమాచారాన్ని ఒక చోట కూర్చి ఖాతాలను నమోదు చేస్తారు.

→ ఆవర్షాను “మలిపద్దు పుస్తకం” అని కూడా వ్యవహరిస్తారు.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 1 Book Keeping and Accounting to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 1 Book Keeping and Accounting

→ Accounting is called as the “language of business”. Accounting helps in communicating financial information to various parties interested in it.

→ Bookkeeping is the branch of knowledge that is concerned with the recording of business transactions.

→ An accounting cycle is a complete sequence of accounting processes that begins with the recording of business transactions and ends with the preparation of final statements.

→ Generally Accepted Accounting Principles (GAAP) may be defined as those rules of action which are derived from experience and practice.

→ The accounting principles are general accounting procedures practices that guide the accountant in the preparation of accounting records.

→ Accounting principles can be broadly classified into Accounting concepts and accounting conventions.

→ Some of accounting concepts are :

1. Business entity concept
2. Money measurement concept
3. Cost concept
4. Duel concept
5. Going concern concept
6. Matching concept etc.

→ Consistency, disclosure, conservation and materiality are Accounting conventions.

→ Accounting standard is a principle that guides and standardizes accounting practices.

→ “International Financial Reporting Standards (IFRS) are the standards issued by IFRS Foundation and International Accounting Standards Board (IASB).

TS Inter 1st Year Accountancy Notes Chapter 1 బుక్ కీపింగ్

1. వ్యాపార వ్యవహారములను క్రమ పద్ధతిలో, కాలానుక్రమముగా నమోదు చేసే ప్రక్రియను బుక్ కీపింగ్ అంటారు. అన్ని వ్యాపార వ్యవహారాలకు సంబంధించిన శాశ్వతమైన రికార్డు రూపొందించడానికి బుక్ కీపింగ్ సహాయపడుతుంది.

2. పూర్తిగా గాని కొంతమేరకు ఆర్థిక సంబంధము గల వ్యవహారాలను శాస్త్రీయ పద్ధతిలో నమోదు చేసి, వర్గీకరించి, సంక్షిప్తపరచి వాటి ఫలితాలను నివేదికల ద్వారా యజమానులకు వివరించే కళే గణకశాస్త్రము.

3. వ్యాపార వ్యవహారాలను రికార్డు చేయడం, వర్గీకరించడం, సంక్షిప్తపరచడము, విశ్లేషించడం వంటి దశలు అకౌంటింగ్లో ఉంటాయి.

4. అకౌంటింగ్ ప్రక్రియ వ్యాపార వ్యవహారాల నమోదుతో ప్రారంభమై, ముగింపు లెక్కల తయారీతో ముగుస్తుంది.

5. ఖాతా పుస్తకాల తయారీకి సహాయపడే సాధారణ అకౌంటింగ్ ప్రక్రియల పద్ధతులను గణకసూత్రాలు అంటారు. వీటిని స్థూలముగా అకౌంటింగ్ భావాలు, అకౌంటింగ్ సంప్రదాయాలుగా విభజిస్తారు.

6. గణక భావనలు అకౌంటింగ్కు మూల సూత్రాలు. ఆర్థిక నివేదికలపై ఆసక్తి ఉన్న వ్యక్తులకు ఆర్థిక సమాచారము అందించడానికి ఖాతా పుస్తకాల తయారీకి ఈ భావనలు అభివృద్ధిపరచడం జరిగినది. ముఖ్యమైన అకౌంటింగ్ భావనలు వ్యాపార అస్తిత్వ భావన, ద్వంద రూప భావన, గతిశీల సంస్థ భావన, ద్రవ్య కొలమాన భావన, వ్యయ భావన, అకౌంటింగ్ కాల భావన, జతపరిచే భావన మొదలైనవి.

7. గణక సంప్రదాయాలు సంస్థల ఆర్థిక నివేదికలను తయారుచేసేటప్పుడు అకౌంటెంట్కు మార్గాన్ని చూపే ఆచారాలు లేదా కట్టుబాట్లు వెల్లడి చేసే సంప్రదాయం, ప్రాధాన్యత సంప్రదాయం, అనురూప సంప్రదాయం, మితవాద సంప్రదాయం మొదలైనవి ముఖ్యమైన గణక సంప్రదాయాలు.

8. అకౌంటింగ్ పద్ధతులను నిర్దేశించడానికి, ప్రమాణీకరించడానికి తోడ్పడే సూత్రాలను గణక ప్రమాణాలు అంటారు.

9. జంటపద్దు విధానాన్ని ఇటలీ దేశస్తుడు “లుకాస్ పాసియోలి” ప్రవేశపెట్టాడు. ప్రతి వ్యాపార వ్యవహారములో రెండు అంశాలు రెండు ఖాతాలను ప్రభావితం చేస్తాయి. వ్యాపార వ్యవహారములలో వచ్చే అంశాన్ని ఇచ్చే అంశాన్ని నమోదు చేసే విధానము జంటపద్దు విధానము.

10. ఈ విధానము డెబిట్, క్రెడిట్ అంశాలను రికార్డు చేస్తుంది. ప్రతి డెబిట్కు క్రెడిట్ ఉంటుంది. ప్రతి క్రెడిట్కు డెబిట్ ఉంటుంది. డెబిట్ మొత్తము క్రెడిట్ మొత్తముతో సమానముగా ఉండటమే జంటపద్దు విధానపు ముఖ్య లక్షణము.

Here students can locate TS Inter 1st Year Commerce Notes Chapter 12 Emerging Trends in Business to prepare for their exam.

TS Inter 1st Year Commerce Notes Chapter 12 Emerging Trends in Business

→ E-business refers to the integration of business fools based on ICT to improve the functioning of the company.

→ E-commerce refers to the use of online support for the relationship between the company and the clients.

→ E-business can be divided into three areas within the organization; business-to-business; business-to-customers.

→ The 21st-century business is opening up many opportunities for entrepreneurs.

→ Business enterprises in India have been facing many challenges in changing business.

TS Inter 1st Year Commerce Notes Chapter 12 వ్యాపారంలో ప్రస్తుత ధోరణులు

→ e – వ్యాపారము ICT పై ఆధారపడి, సంస్థ పనితీరును మెరుగుపరచడానికి వ్యాపార పద్ధతులను సమైక్య పరచటం. e – వాణిజ్యాన్ని e – వ్యాపారములో ఒక అంశముగా ఉండి ఆన్లైన్ సహాయముతో కంపెనీకి, ఖాతాదారుల మధ్య సంబంధాలను ఏర్పరుస్తుంది.

→ e- వ్యాపారము యొక్క ధ్యేయమేమిటంటే కంపెనీ, దాని అంతర్గత నిర్వహణ పద్ధతుల మధ్య సమాచార వ్యవస్థను ఏర్పరచి, కంపెనీ యొక్క అంతర్గత, బహిర్గత అంశాలను సమర్థవంతంగా నిర్వర్తించడం.

→ నేడు ఆర్థిక సరళీకరణ కారణముగా ఇంట్రానెట్, ఇంటర్ నెట్ల వేగం ఆపాదించడం వలన e – వ్యాపారం యొక్కఅవగాహన పెరుగుతున్నది. e- వ్యాపారాన్ని మూడు భాగాలుగా విభజించవచ్చు అవి: 1. సంస్థలో అంతర్గతంగా 2 వ్యాపారము నుంచి వ్యాపార వ్యవహారాలు 3. వ్యాపారము నుంచి వినియోగదారుల లావాదేవీలు,

→ 21వ శతాబ్దపు వ్యాపారము, వ్యాపార వేత్తలకు అనేక అవకాశాలను, సవాళ్ళను సృష్టిస్తున్నది.