TS Inter 1st Year Maths 1B Solutions Chapter 3 Straight Lines Ex 3(e)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(e)

Question 1.
Find the in-centre of the triangle whose vertices are ( 1, √3), ( 2, 0) and (0, 0). (S.A.Q.)
Answer:
Let 0(0, 0), A (1, √3) and B (2, 0) are the vertices of ∆ABC

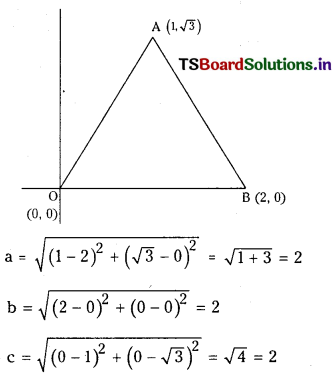
∴ ABC is an equilateral triangle.
Coordinates of in-centre are

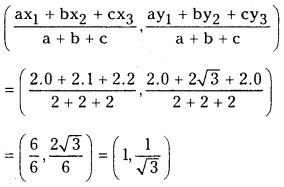
Question 2.
Find the orthocentre of the triangle whose sides are given by x + y + 10 = 0, x – y – 2 = 0 and 2x + y – 7 = 0
Answer:

Equation of AB is x + y + 10 = 0 ………………. (1)
Equation of BC is x – y – 2 = 0 ………………. (2)
Equation of CA is 2x + y – 7 = 0 ………………… (3)
Solving (1) and (2) Coordinates of B are (-4, -6)
Solving (1) and (3) Coordinates of A are (17, -27)
Equation of BC is 2x – y – 2 = 0
AD is perpendicular to BC
Equation of AD is x + y + k = 0
AD passes through A (17, -27)
∴ 17 – 27 + k = 0 ⇒ k = 10
∴ Equation of AB is x + y + 10 = 0 ……………… (1)
Equation of AC is 2x + y – 7 = 0
BE is perpendicular to AC
Equation of DE can be taken as x – 2y = k
BE passes through D(-4 -6); – 4 + 12 = k ⇒ k = 8
Equation of BE is x – 2y = 8 ………………. (2)
x + y = – 10 ……………….. (1)
Solving (1) & (2)
– 3y = 18 ⇒ y = – 6
x + y + 10 = 0 ⇒ x – 6 + 10 = 0 ⇒ x = – 4
∴ Orthocentre of AABC is (- 4, – 6)

Question 3.
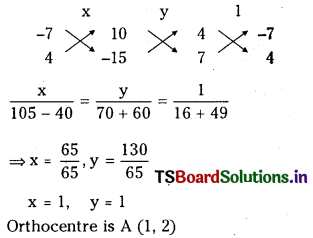
Find the orthocentre of the triangle whose sides are given by 4x – 7y + 14 = 0, x + y = 5 and 7x + 4y = 15 (V.S.A.Q.)
Answer:
Equation of sides AB and BC of a ∆ABC are
given by 4x – 7y + 10 = 0 ……………….. (1)
x + y = 5 ……………… (2)
and equation of side AC is
7x + 4y – 15 = 0 ………………. (3)
AB and AC are perpendicular and ∠A = 90°

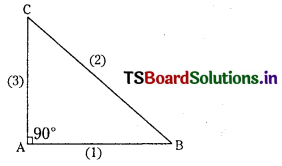
∴ ABC is a right angle triangle with ∠A = 90°and A is the orthocentre.
Solving (1) and (3)

Question 4.
Find the circumcentre of the triangle whose sides are x = 1, y = 1 and x + y = 1 (V.S.A.Q.)
Answer:

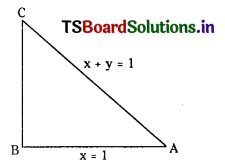
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1
AB and BC are perpendicular.
∴ ABC is a right angled triangle ∠B = 90°
Mid point of AC is the circumcentre.
Coordinates of A are (1, 0) and C are (0, 1).
∴ Circumcentre = \(\left(\frac{1}{2}, \frac{1}{2}\right)\)

Question 5.
Find the in-centre of the triangle formed by the lines x = 1, y = 1 and x + y = 1. (V.S.A.Q.)
Answer:
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1
Solving these equations we get vertices as
A(1, 0), B(1, 1), C(0, 1)

Question 6.
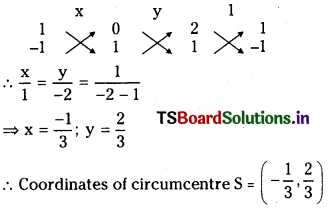
Find the circumcentre of the triangle whose vertices are (1, 0), (-1, 2) and (3, 2).(E.Q.) (March 2012)
Answer:

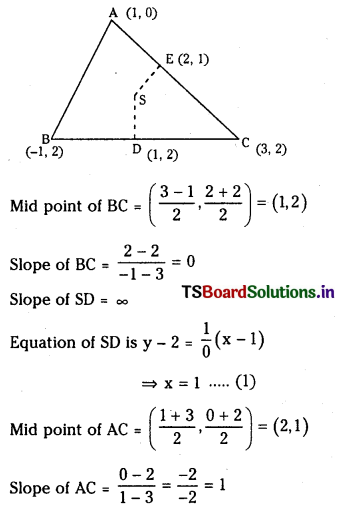
Slope of SE = – 1
Equation of SE is y – 1 = – l(x – 2)
⇒ y – 1 = – x + 2
⇒ x + y – 3 = 0 ………….. (2)
Solving (1) and (2) we get y – 2 = 0 ⇒ y = 2
⇒ Circumcentre S = (1, 2).

Question 7.
Find the values of k, if the angle between the straight lines kx + y + 9 = 0 and 3x – y + 4 = 0 is \(\frac{\pi}{4}\). (S.A.Q.)
Answer:
Equations of the given lines are
kx + y + 9 = 0
3x – y + 4 = 0

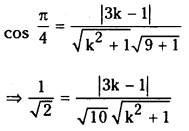
⇒ (k² + 1) 10 = 2 (3k – 1)²
⇒ 10k² + 10 = 2(9k² – 6k + 1)
⇒ 8k² – 12k – 8 = 0
⇒ 4k² – 6k – 4 = 0
⇒ 2k² – 3k – 2 = 0
⇒ (k – 2) (2k + 1) = 0 – 1
⇒ k = 2 or \(\frac{-1}{2}\)

Question 8.
Find the equation of the straight line passing through the origin and also through the point of intersection of lines 2x – y + 5 = 0 and x + y + 1 = 0. (V.S.A.Q.)
Answer:
Equations of given lines are
L₁ = 2x – y + 5 = 0 and L₂ = x + y + 1= 0
Equation of any line passing through A is
L₁ + k L₂ = 0
⇒ (2x – y + 5) + k(x + y + 1) = 0 (1)
This line passes through (0, 0) then
5 + k = 0 ⇒ k = – 5
Substituting in (1) equation of OA is
(2x – y + 5) – 5(x + y + 1) = 0
⇒ – 3x – 6y = 0
⇒ x + 2y = 0

Question 9.
Find the equation of the straight line parallel to the line 3x + 4y = 7 and passing through the point of intersection of the lines x – 2y – 3 = 0 and x + 3y – 6 = 0. (S.A.Q.)
Answer:
Let L₁ = x + 3y – 6 = 0 and L₂ = x – 2y – 3 = 0 be the given lines.
Equation of any line passing through the intersection is L₁ + KL₂ = 0
⇒ (x + 3y – 6) + k (x – 2y – 3) = 0 ….. (1)
⇒ x(1 + k) + y (3 – 2k) – (6 + 3k) = 0
This is parallel to 3x + 4y = 7
a₁b₂ = a₂b₁
⇒ 4(1 + k) = 3 (3 – 2k)
⇒ 4 + 4k = 9 – 6k
⇒ 10k = 5 ⇒ k = \(\frac{1}{2}\)
∴ From (1) (x + 3y – 6) + \(\frac{1}{2}\) (x – 2y – 3) = 0
⇒ 3x + 4y – 15 = 0
Equation of the required line is 3x + 4y – 15 = 0

Question 10.
Find the equation of the straight line perpendicular to the line 2x + 3y = 0 and passing through the point of intersection of lines x + 3y – 1 = 0 and x – 2y + 4 = 0. (S.A.Q.)
Answer:
Let L₁ = x + 3y – 1 = 0
and L₂ = x – 2y + 4 = 0
Equation of any line passing through the
point of intersection of L₁ = 0, L₂ = 0 is L₁ + kL₂ = 0
⇒ (x + 3y – 1) + k (x – 2y + 4) = 0 (1)
⇒ x(1 + k) + y (3 – 2k) – (1 – 4k) = 0
Slope of the line is –\(\left(\frac{1+\mathrm{k}}{3-2 \mathrm{k}}\right)\)
Slope of the given line 2x + 3y = 0 is \(\frac{-2}{3}\)
∴ Since the lines are perpendicular
\(\left(\frac{1+\mathrm{k}}{3-2 \mathrm{k}}\right)\left(\frac{2}{3}\right)\) = – 1
⇒ 2 + 2k = – 3 (3 – 2k)
= – 9 + 6k
⇒ 4k = 11 ⇒ k = \(\frac{11}{4}\)
Substituting in (1) equation of required line is
(x + 3y – 1) + \(\frac{11}{4}\)(x – 2y + 4) = 0
⇒ 4x + 12y – 4 + 11x – 22y + 44 = 0
⇒ 15x – 10y + 40 = 0
⇒ 3x – 2y + 8 = 0

Question 11.
Find the equation of the straight line making non-zero equal intercepts on the coordinate axes and passing through the point of intersection of the lines 2x – 5y + 1 = 0 and x – 3y – 4 = 0. (S.A.Q.)
Answer:
Equations of the given lines are
L₁ = 2x – 5y + 1 = 0
and L₂ = x – 3y – 4 = 0
Equation of any line passing through the point of intersection of L₁ = 0, L₂ = 0 is
L₁ + kL₂ = 0
⇒ (2x – 5y + 1) + k (x – 3y – 4) = 0 …. (1)
⇒ (2 + k) x – (5 + 3k) y + (1 – 4k) = 0
Intercepts on coordinate axes are equal.
⇒ 2 + k = – 5 – 3k
⇒ 4k = -7 ⇒ k = \(\frac{-7}{4}\)
∴ From (1) (2x – 5y + 1) – \(\frac{-7}{4}\) (x – 3y – 4) = 0
⇒ x + y + 32 = 0

Question 12.
Find the length of the perpendicular drawn from the point of intersection of the lines 3x + 2y + 4 = 0 and 2x + 5y – 1 = 0 to the straight line 7x + 24y – 15 = 0. (S.A.Q.)
Answer:
Equation of the given lines
3x + 2y + 4 = 0
2x + 5y – 1 = 0
Solving

⇒ x = – 2, y = 1
Coordinates of point of intersection are (-2, 1)
Equation of the given line is 7x + 24y -15 = 0
∴ Length of the perpendicular from (-2, 1) to 7x + 24y – 15 = 0 is
\(\left|\frac{-14+24-15}{\sqrt{49+576}}\right|=\frac{5}{25}=\frac{1}{5}\)

Question 13.
Find the value of ‘a’ if the distances of the points (2, 3) and (-4, a) from the straight line 3x + 4y – 8 = 0 are equal. (S.A.Q.)
Answer:
Let A (2, 3) and B (-4, a) be the two points.
The distance from (2, 3) to the line 3x + 4y – 8 = 0 is
= \(\left|\frac{3(2)+4(3)-8}{\sqrt{3^2+4^2}}\right|\) = \(\frac{10}{5}\) = 2.
The distance from B(- 4, a) to the line 3x + 4y – 8 = 0
= \(\left|\frac{3(-4)+4 a-8}{\sqrt{3^2+4^2}}\right|\) = \(\frac{|4 a-20|}{5}\)
∴ 2 = \(\frac{|4 a-20|}{5}\)
⇒ |4a – 20| = 10 ⇒ 4a – 20 = ±10
⇒ 4a = 30 or 4a = 10
⇒ a = \(\frac{15}{2}\) or a = \(\frac{5}{2}\)

Question 14.
Find the circumcentre of the triangle formed by the straight lines x + y = 0, 2x + y + 5 = 0 and x – y = 2. (E.Q.)
Answer:

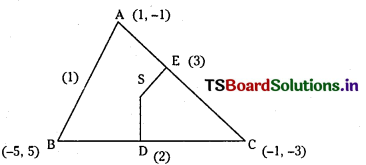
Equation of AB is x + y = 0, …………………. (1)
Equation of BC is 2x + y + 5 = 0 ……………………… (2 )
Equation of CA is x – y = 2 ………………………… (3)
Solving (1) and (2), Coordinates of B are (-5, 5)
Solving (2) and (3), Coordinates of C are (-1, -3)
Solving (1) and (3), Coordinates of A are (1, -1)

Equation of SE is y + 2 = – 1 (x)
⇒ x + y + 2 = 0 ………………. ( 5 )
Solving (4) and (5) we get coordinates of circumcentre S

⇒ x = – 3, y = 1
∴ Coordinates of circumcentre S = (- 3, 1)

Question 15.
If θ is the angle between the lines \(\frac{x}{a}+\frac{y}{b}\) = 1 and \(\frac{x}{b}+\frac{y}{a}\) = 1, find the value of sin θ when a > b. (S.A.Q.)
Answer:
Equation of given lines \(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ bx + ay – ab = 0 ……………….. (1)

II.
Question 1.
Find the equation of straight lines passing through the point (- 10, 4) and making an angle 0 with the line x – 2y = 10 such that tan θ = 2. (E.Q.)
Answer:
Equation of BC is x – 2y – 10 = 0
Suppose slope of AB is’m’. AB passes through A (-10, 4)

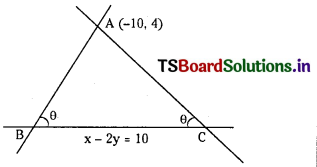
Equation of AB is y – 4 = m(x + 10) = mx + 10m
⇒ mx – y + (10m + 4) = 0 ………………… (1)

⇒ (m² + 1) = (m + 2)² = m² + 4m + 4
⇒ 4m + 3 = 0 ⇒ m = -3/4

Case (i): Coefficient of m² = 0
⇒ one of the roots is ∞.
Hence AC is a vertical line
∴ Equation of AC is x + 10 = 0;
(∵ y – 4 = \(\frac{1}{0}\) (x + 10))

Case (ii) : m = \(\frac{-3}{4}\)
From (1) equation of AB is
\(\frac{-3}{4}\) – y + (latex]\frac{-30}{4}[/latex] + 4) = 0
⇒ \(\frac{-3 x-4 y-14}{4}\) = 0
⇒ 3x + 4y + 14 = 0

Question 2.
Find the equations of the straight lines passing through the point (1,2) and making an angle of 60° with the line √3 x + y + 2 = 0. (Board Model Paper) (E.Q.)
Answer:

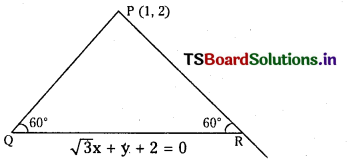
PQ, PR are two lines passing through P(1, 2) and makes an angle of 60° with QR.
Let slope of PQ is m
Equation of PQ is y – 2 = m (x – 1) = mx – m
∴ mx – y + (2 – m) = 0 …………….. ( 1 )

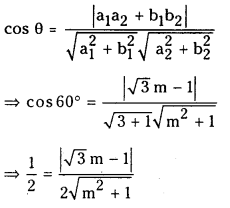
⇒ m² + 1 = (√3m – 1)² = 3m² + 1 – 2√3 m
⇒ 2m² – 2 √3 m = 0
⇒ 2m (m – √3) = 0 ⇒ m = 0 or √3

Case (i): m = 0
Equation of PQ is – y + 2 = 0 or y – 2 = 0

Case (ii): m = √3
Equation of PQ is √3x – y + (2 – √3) = 0

Question 3.
The base of an equilateral triangle is x + y – 2 = 0 and the opposite vertex is (2, -1). Find the equations of the remaining sides. (E.Q.)
Answer:

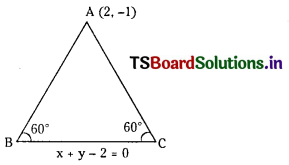
Equation of BC is x + y – 2 = 0
AB passes through A (2, -1)
Suppose slope of AB is’m’
Equation of AB is y + 1 = m (x – 2) = mx – 2m
⇒ mx – y – (2m + 1) = 0 …………………. (1)
cos 60° = \(\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
⇒ \(\frac{1}{2}=\frac{|m-1|}{\sqrt{1+1} \sqrt{m^2+1}}\)
⇒ (m² + 1) (2) = 4(m – 1)²
⇒ 2m² + 2 = 4(m² – 2m + 1)
⇒ 2m² – 8m + 2 = 0
⇒ m² – 4m + 1 = 0
⇒ m = \(\frac{4 \pm \sqrt{16-4}}{2}\) = \(\frac{4 \pm \sqrt{12}}{2}\) = \(\frac{4 \pm 2 \sqrt{3}}{2}\) = 2 ± √3
Substituting in (1)
Equation of AB is y + 1 = (2 + √3) (x – 2)
Equation of AC is y + 1 = (2 – √3) (x – 2)

Question 4.
Find the orthocentre of the triangle with the following vertices (E.Q.)
(i) (- 2, – 1), (6, – 1) and (2, 5) (March ’07)
(ii) ( 5, – 2 ), ( – 1, 2 ) and ( 1, 4 ) (March ’12)
Answer:
(i) Let A( – 2, – 1), B( 6, – 1), C( 2, 5 ) are the vertices of ∆ABC

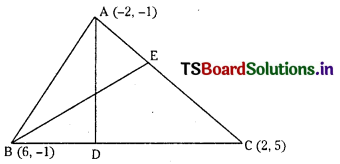
Slope of BC = \(\frac{5+1}{2-6}=\frac{6}{-4}=\frac{-3}{2}\)
AD is perpendicular to BC
Slope of AD = \(\frac{2}{3}\)
Equation of AD is y + 1 = \(\frac{2}{3}\) (x + 2)
⇒ 2x – 3y + 1 = 0 ………. (1)
Slope of AC = \(\frac{5+1}{2+2}=\frac{6}{4}=\frac{3}{2}\) = 2
BE is perpendicular to AC
Slope of BE = \(\frac{-2}{3}\)
Equation of BE is
y + 1 = \(\frac{-2}{3}\) (x – 6)
⇒ 2x + 3y – 9 = 0 ……………… (2)
Solving (1) and (2)

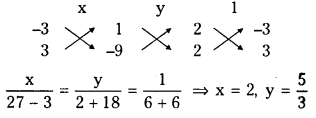
Coordinates of the orthocentre O are \(\left(2, \frac{5}{3}\right)\)

(ii) (5, – 2), (- 1, 2) and (1, 4)
Answer:

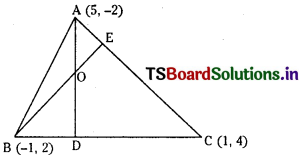
Let A(5, -2), B (-1, 2) and C(1, 4) be the vertices of ∆ABC.
Slope of BC =\(\frac{2-4}{-1-1}=\frac{-2}{-2}\) = 1
Slope of AD = – 1
Equation of AD is y + 2 = – 1 (x – 5)
⇒ x + y – 3 = 0 …………… (1)
Slope of AC = \(\frac{-2-4}{5-1}=\frac{-6}{4}=\frac{-3}{2}\)
∴ Slope of BE = \(\frac{2}{3}\)
∴ Equation of BE is y – 2 = \(\frac{2}{3}\) (x + 1)
⇒ 3y – 6 = 2x + 2
⇒ 2x – 3y + 8 = 0 ………………. (2)
Solving (1) and (2) we get the coordinates of the orthocentre ‘O’

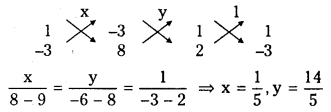
∴ Coordinates of orthocentre O are \(\left(\frac{1}{5}, \frac{14}{5}\right)\)

Question 5.
Find the circumcentre of the triangle whose vertices are given below.
(i) (-2, 3), (2, -1) and (4, 0) (March 2011)
(ii) (1, 3), (0, – 2) and (- 3, 1) (May 2006) (E.Q.)
Answer:
(i) (-2, 3), (2, -1) and (4, 0)

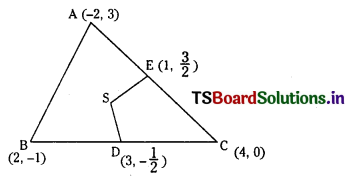
Let A(-2, 3), B(2, -1) and C(4, 0) be the vertices of ∆ ABC.
Mid point of side BC; D = \(\left(\frac{4+2}{2}, \frac{-1+0}{2}\right)\)
= \(\left(3,-\frac{1}{2}\right)\)
Slope of BC = \(\frac{-1-0}{2-4}=\frac{1}{2}\)
∴ Slope of SD is – 2.
Equation of SD is y + \(\frac{1}{2}\) = – 2(x – 3)
⇒ 2y + 1 = – 4 (x – 3)
⇒ 4x + 2y – 11 = 0 ……. (2)
E is the mid point of AC Coordinates of E are
⇒ x = \(\frac{12}{8}\) = \(\frac{3}{2}\) and 4\(\left(\frac{3}{2}\right)\) – 2y – 1 = 0
⇒ – 2y + 5 = 0 ⇒ y = \(\frac{5}{2}\)
∴ Coordinates of circumcentre S = \(\left(\frac{3}{2}, \frac{5}{2}\right)\)

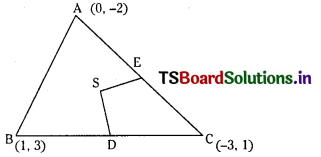
(ii) (1, 3), (0, – 2) and (- 3, 1)

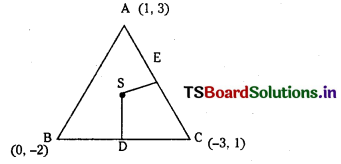
Let A(1, 3), B(0, -2) and C(-3, 1) be the vertices of ∆ABC. D is the mid point of BC.

SE is perpendicular to CA
Slope of SE is -2
Equation of SE is y – 2 = – 2 (x + 1)
⇒ 2x + y = 0 (2)
Solving (1) and (2)

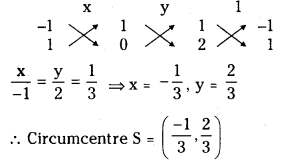
Question 6.
Let \(\overline{\text { PS }}\) be the median of the triangle with vertices P( 2, 2 ), Q ( 6, – 1 ) and R ( 7, 3 ). Find the equation of the straight line passing through ( 1, – 1) and parallel to the median PS. (E.Q.)
Answer:

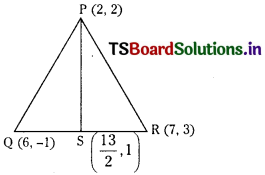
Let P (2, 2), Q (6, -1) and R (7, 3) be the vertices of ∆ABC.
S is the mid point of QR.

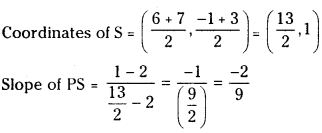
AB is parallel to PS and passes through A(1, – 1)
Equation of AB is y + 1 = \(\frac{-2}{9}\) (x – 1)
⇒ 9y + 9 = – 2x + 2
⇒ 2x + 9y + 7 = 0

III.
Question 1.
Find the orthocentre of the triangle formed by the lines x + 2y = 0, 4x + 3y – 5 = 0 and 3x + y = 0 (E.Q.)
Answer:

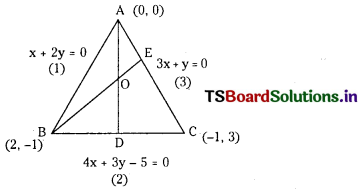
Equation of AB is x + 2y = 0 …………… (1)
Equation of BC is 4x + 3y – 5 = 0 …………… (2)
Equation of AC is 3x + y = 0 …………………. (3)
Solving (1) and (3) coordinates of A are (0,0)
Solving (1) and (2) we get the coordinates of C

Coordinates of C = (-1. 3)
Slope of BC = \(\frac{-1-3}{2+1}\) = \(\frac{-4}{3}\)
∴ Slope of AD = \(\frac{3}{4}\)
∴ Equation of AD is y – 0 = \(\frac{3}{4}\) (x – 0)
⇒ 3x – 4y = 0 ……… (4)
Slope of AC = \(\frac{0-3}{0+1}\) = – 3
∴ Slope of BE = \(\frac{1}{3}\)
∴ Equation of BE is y + 1 = \(\frac{1}{3}\) (x – 2)
⇒ 3y + 3 = x- 2
⇒ x – 3y – 5 = 0 ……………….. (5)
Solving (4) and (5) we get the coordinates of orthocentre.

⇒ x = -4, y = -3
∴ Coordinates of orthocentre of ∆ABC is 0(- 4, -3)

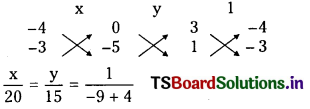
Question 2.
Find the circumcentre of the triangle whose sides are given by x + y + 2 = 0; 5x – y – 2 = 0 and x – 2y + 5 = 0 (E.Q.)
Answer:
Given lines are x + y + 2 = 0 ………………….. ( 1 )
5x – y – 2 = 0 ………………….. (2)
x – 2y + 5 = 0 ………………….. (3)
Point of intersection of lines (1) and (2) is A = (0, -2)
Point of intersection of lines (2) and (3) is B = (1, 3)

Point of intersection of lines (1) and (3) is C(-3, 1)
D is the mid point of BC;
∴ Coordinates of D = \(\left(\frac{1-3}{2}, \frac{3+1}{2}\right)\)
= (-1, 2)
Slope of BC = \(\frac{3-1}{1+3}=\frac{2}{4}=\frac{1}{2}\)
Slope of SD = -2
Equation of SD is y – 2 = -2 (x + 1)
⇒ 2x + y = 0 …
E is the mid point of AC
(0-3 -2 + 0
∴ Coordinates of E = \(\left(\frac{0-3}{2}, \frac{-2+1}{2}\right)\)
= \(\left(\frac{-3}{2}, \frac{-1}{2}\right)\)
Slope of AC is \(\frac{-2-1}{0+3}\) = – 1
∴ Slope of SE = 1
∴ Equation of SE is y + \(\frac{1}{2}\) = 1 \(\left(x+\frac{3}{2}\right)\)
⇒ 2y + 1 = 2x + 3
⇒ 2x – 2y + 2 = 0
⇒ x – y + 1 = 0 ……………… (5)
Solving (4) and (5) we get the coordinates of circumcentre ‘S’.

Question 3.
Find the equation of the straight lines passing through (1, 1) and which are at a distance of 3 units from (- 2, 3). (E.Q.)
Answer:
Let the line passing through A(l, 1) has slope’m’ then equation of the line is y – 1 = m(x – 1)
⇒ mx – y + (1 – m) = 0 …………… (1)
Distance from (-2, 3) to the line = 3
∴ \(\frac{|m(-2)-3+(1-m)|}{\sqrt{m^2+1}}\) = 3
⇒ (3m + 2)² = 9(m² + 1)
9m² + 12m + 4 = 9m² + 9
⇒ 12m = 5 ⇒ m = \(\frac{5}{12}\)
Coefficient of m² = 0 ⇒ m = ∞
(i) m = ∞
Equation of the line is y – 1 = \(\frac{1}{0}\) (x – 1)
⇒ x = 1

(ii) m = \(\frac{5}{12}\)
Substitute in (1)
Equation of the line is y – 1 = \(\frac{5}{12}\) (x – 1)
⇒ 12y – 12 = 5x – 5
⇒ 5x – 12y + 7 = 0

Question 4.
If p and q are the lengths of the perpendiculars from the origin to the straight lines x sec α + y cosec α = a and x cos α – y sin α = a cos 2α. Prove that 4p² + q² = a² (E.Q.)
Answer:
Equation of the line is x sec α + y cosec α = α
⇒ \(\frac{x}{\cos \alpha}+\frac{y}{\sin \alpha}\) = a
⇒ x sin α + y cos α = a sin α cos α
⇒ x sin α + y cos α – a sin α, cos α = 0 …….. (1)
p = length of the perpendicular from 0 on the line (1)
= \(\left|\frac{0+0-a \sin \alpha \cos \alpha}{\sqrt{\sin ^2 \alpha+\cos ^2 \alpha}}\right|\)
⇒ a sin α + cos α = p
⇒ 2p = a sin 2 α
Equation of the other given line is
x cos α – y sin α = a cos 2α ………………. ( 2 )
q = length of the perpendicular from 0 on the line (2)
∴ q = \(\left|\frac{a \cos 2 \alpha}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\right|\)
⇒ a² cos² 2α = q²
∴ 4p² + q² = a² sin² 2α + a² cos² 2α
= a² (sin² 2α + cos² 2α) = a² (1) = a²

Question 5.
Two adjacent sides of a Parallelogram are given by 4x + 5y = 0 and 7x + 2y = 0 and one diagonal is 1 lx + 7y = 9. Find the equation of the remaining sides and the other diagonal. (E.Q.)
Answer:

Let 4x + 5y = 0 ……………….. (1) and
7x + 2y = 0 …………….. (2) respectively
denote the sides \(\overrightarrow{O A}\) and \(\overrightarrow{O B}\) of the parallelogram OABC
Equation of the diagonal AB is 1 lx + 7y -9 =0 .
Solving (1) and (2) we get O = (0, 0)
Solving (1) and (3) we get


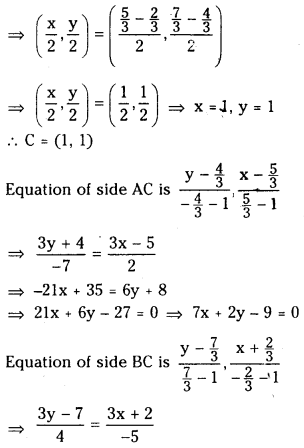
⇒ – 15y + 35 = 12x + 8
⇒ 12x + 15y – 27 = 0
⇒ 4x + 5y – 9 = 0

Question 6.
Find the in – centre of the triangle formed by the following straight lines. (E.Q.)
(i) x + 1= 0, 3x – 4y = 5 and 5x + 12y = 27
(ii) x + y – 7 = 0, x – y + 1 = 0 and x – 3y + 5 = 0
Answer:
(i)x + 1 = 0, 3x – 4y = 5 and 5x + 12y = 27
x + 1 = 0 …………….. (1)
3x – 4y = 5 …………………. (2)
5x + 12y = 27 ………………. (3) are the given equations of lines.
Point of intersection of (1) and (2) is A = (-1,-2)
Point of intersection of (2) and (3) is

(ii) x + y – 7 = 0, x – y + 1 = 0 and x – 3y + 5 = 0
Answer:
x + y – 7 = 0 …………….. (1)
x – y + 1 = 0 …………….. (2)
x – 3y + 5 = 0 …………….. (3)
Solving (1) and (2) we get

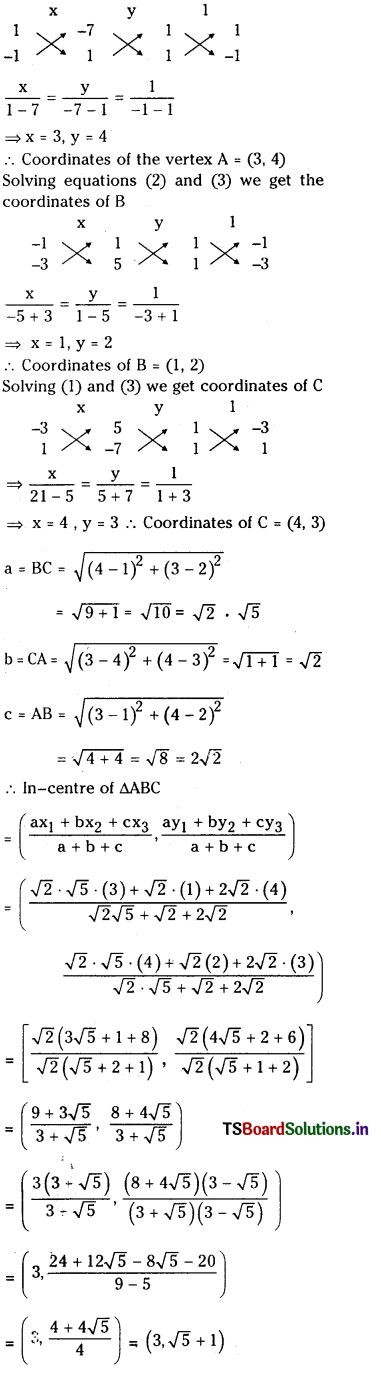
∴ In-center of the triangle formed by the sides x + y – 7 = 0, x – y + 1 = 0 and x – 3y + 5 = 0 is (3√5 + 1)

Question 7.
A triangle is formed by the lines ax + by + c = 0, lx + my + n = 0 and px + qy + r = 0. Given that the triangle is not right angled, show that the straight line \(\frac{a x+b y+c}{a p+b q}\) = \(\frac{l \mathbf{x}+\mathbf{m y}+\mathbf{n}}{l \mathbf{p}+\mathbf{m q}}\) passes through the orthocentre of the triangle. (E.Q.)
Answer:
Given equations of lines are
ax + by + c = 0 ……………… (1)
lx + my + n = 0 ……………. (2)
px + qy + r = 0 ……………… (3)
Equation of the line passing through the point of intersection of (1) and (2) is
(ax + by + c) + k (/x + my + n) = 0 (4)
⇒ (a + kl) x + (b + km) y + (c + nk) = 0
It is perpendicular to (3) then
p(a + kl) + q (b + km) = 0
⇒ k = – \(\left(\frac{\mathrm{ap}+\mathrm{bq}}{l \mathrm{p}+\mathrm{mq}}\right)\)
Substitute in (4) we get
(ax + by + c) – \(\left(\frac{\mathrm{ap}+\mathrm{bq}}{l \mathrm{p}+\mathrm{mq}}\right)\) (lx + my + n) = 0
⇒ \(\frac{\mathrm{ax}+\mathrm{by}+\mathrm{c}}{\mathrm{ap}+\mathrm{bq}}=\frac{l \mathrm{x}+\mathrm{my}+\mathrm{n}}{l \mathrm{p}+\mathrm{mq}}\)
is the required equation of the line line passing through the orthocentre of triangle which represents the altitude through A.

Question 8.
The Cartesian equations of the sides
\(\overleftrightarrow{\mathbf{B C}}, \overleftrightarrow{\mathbf{C A}}\) and \(\overleftrightarrow{\mathbf{A B}}\) 0f a triangle are respectively u_r = a_rx + b_ry + c_r = 0, r = 1, 2, 3. Show that the equation of the straight line passing through A and bisecting the side \(\overline{\mathbf{B C}}\) is
\(\frac{u_3}{a_3 b_1-a_1 b_3}=\frac{u_2}{a_1 b_2-a_2 b_1}\) (E.Q.)
Answer:
A is a point of intersection of lines u₂ = 0 and u₃ = 0
Equation of the line passing through A is u₂ + λu₃ = 0
⇒ (a₂x + b₂y + c₂) + λ(a₃x + b₃y + c₃) = 0 …….(1)
⇒ (a₂ + λa₃)x + (b₂ + λb₃)y + (c₂ + λc₃) = 0
If this is parallel to a₁x + b₁y + c₁ = 0 we get