TS Inter 1st Year Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(c)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c)

I.
Question 1.
Find the equation of the lines joining the origin to the points of intersection of x² + y² = 1 and x + y = 1. (V.S.A.Q.)
Answer:
Given equations are
x² + y² = 1 ………………. (1)
and x + y = 1 ………………. (2)
Homogenising (1) with (2) we get
(x² + y²) = 1²
= (x + y)²
⇒ x² + y² = x² + y² + 2xy ⇒ xy = 0

Question 2.
Find the angle between the lines joining the origin to the points of intersection of y² = x and x + y = 1. (V.S.A.Q.)
Answer:
Given equations are
y² = x …………….. (1)
and x + y = 1 ……………… (2)
Homogenising (1) with (2) we get
y² = x (1)
= x (x + y) ⇒ x² + xy – y² = 0
Coefficient of x² + coefficient of y² = 1 – 1 = 0
∴ Angle between lines is 90°, lines being perpendicular.

II.

Question 1.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – √2 = 0 are mutually perpendicular. (S.A.Q.) (May, March ’12)
Answer:

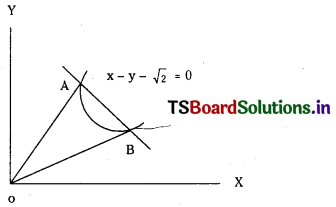
The given equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 ………………… (1)
Equation of AB is x – y – √2 = 0
⇒ x – y = √2
⇒ \(\frac{x-y}{\sqrt{2}}\) = 1 …………………. (2)
Homogenising (1) using (2) we get
x² – xy + y² + (3x + 3y) (1) – 2 (1)² = 0

Question 2.
Find the values of k, if the lines joining the origin to the points of intersection of the curve 2×2 – 2xy + 3y2 + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular. (E.Q.) (Board New Model Paper)
Answer:
Given equation of the curve is
2x² – 2xy + 3y² + 2x – y – 1 = 0 ……………… (1)
and equation of the line is x + 2y = k
We have \(\frac{x+2 y}{k}\) = 1 ……………….. (2)
Homogenising equation (1) with equation (2) we get
2x² – 2xy + 3y² + 2x (1) – y (1) – (1)² = 0
⇒ 2×2 – 2xy + 3y2 + 2x\(\left(\frac{\mathrm{x}+2 \mathrm{y}}{\mathrm{k}}\right)\) – y\(\left(\frac{\mathrm{x}+2 \mathrm{y}}{\mathrm{k}}\right)\) – \(\left(\frac{x+2 y}{k}\right)^2\) = 0
⇒ 2k²x² – 2k²xy + 3k²y² + 2kx (x + 2y) – ky (x + 2y) – (x + 2y)² = 0
⇒ 2k²x² – 2k²xy + 3k²y² + 4kxy + 2kx² – kxy – 2ky² – (x² + 4xy + 4y²) = 0
⇒ (2k² + 2k – 1) x² + (- 2k² + 3k – 4) xy + (3k² – 2k – 4) y² = 0
Since the lines joining the origin to the points of intersection are mutually perpendicular, coefficient of x² + coefficient of y² = 0
⇒ (2k² + 2k – 1) + (3k² – 2k – 4) = 0
⇒ 5k² – 5 = 0 ⇒ k² = 1 ⇒ k = ± 1

Question 3.
Find the angle between the lines joining the origin to the points of intersection of the curve x² + 2xy + y² + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0 (E.Q.) (May 2014, 11, Mar.13, 07, June 04)
Answer:
Given equation of the curve is
x² + 2xy + y² + 2x + 2y – 5 = 0 …………….. (1)
Equation of the line is 3x – y + 1 = 0
⇒ y – 3x = 1 ……………….. (2)
Homogenising (1) with equation (2) we get the equation of lines joining the origin to the points of intersection of curve and the line.
∴ x² + 2xy + y² + 2x (1) + 2y (1) – 5 (1)² = 0
⇒ x² + 2xy + y² + 2x (y – 3x) + 2y (y – 3x) – 5 (y – 3x)² = 0
⇒ x² + 2xy + y² + 2xy – 6x² + 2y² – 6xy – 5(y² – 6xy + 9x²) = 0
⇒ – 5x² – 2xy + 3y² – 5y² – 45x² + 30xy = 0
⇒ – 50x² + 28xy – 2y² = 0
⇒ 25x² – 14xy + y² = 0
Let θ be the angle between lines then by the formula

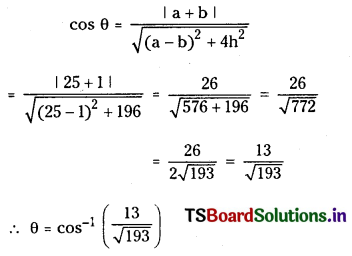
III.
Question 1.
Find the condition for the chord lx + my = 1 of the circle x² + y² = a² (whose centre is the origin) to subtend a right angle at the origin. (Mar. 14) (SA.Q.)
Answer:

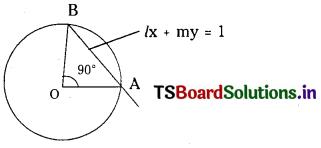
Equation of the circle is x² + y² = a² ………………. (1)
Equation of the line AB is lx + my = 1 ……………….. (2)
Homogenising (1) with equation (2) we get
x² + y² = a² (1)2
⇒ x² + y² = a²(lx + my)²
⇒ x² + y² = a² (l² x² + 2lmxy + m²y²)
⇒ (a²l² – 1)x² + 2a² lmxy + (a²m² – 1) y² = 0
Since OA, OB are perpendicular, we have coefficient of x² + coefficient of y² = 0
⇒ (a² l² – 1) + (a²m² – 1) = 0
⇒ a² (l² + m²) – 2 = 0
⇒ a² (l² + m²) = 2

Question 2.
Find the condition for the lines joining the origin to the points of intersection of the circle x2 + y2 = a2 and the line lx + my = 1 to coincide. (S.A.Q.)
Answer:
The given equation of the curve is
x² + y² = a² ……………. (1)
and the equation of line is
lx + my = 1 ………………… (2)
Homogenising (1) with equation (2) we get
x² + y² = a²(1)² = a² (lx + my)²
⇒ x² + y² = a² (l²x² + 2lmxy + m²y²)
⇒ x² (1 – a²l²) + y² (1 – a²m²) – 2 lma²xy = 0
This equation represents combined equation of lines joining the origin to the points of intersection of (1) and (2)
If the lines are coincident then h² = ab
l²m²a⁴ = (1 – a²m²) (1 – a²m²)
= 1 – a² (l² + m²) + a⁴l²m²
⇒ a² (l² + m²) = 1

Question 3.
Write down the equation of the pair of straight lines joining the origin to the points of intersection of the line 6x – y + 8 = 0 with the pair of straight lines 3x² + 4xy – 4y² – 11x + 2y + 6 = 0. Show that the lines so obtained make equal angles with the coordinate axes. (E.Q.)
Answer:
Given equation of pair of lines is
3x² + 4xy – 4y² – 11x + 2y + 6 = 0 ……………….. (1)
Given equation of line is 6x – y + 8 = 0 ………………. (2)
Homogenising (1) with equation (2)

⇒ 64 (3x² + 4xy – 4y²) – 8 [11xy – 66x² – 2y² + 12xy) + 6[y² + 36x² – 12xy] = 0
⇒ 936x² – 256xy + 256xy – 234y² = 0
⇒ 468x² – 117y² = 0
⇒ 4x² – y² = 0 …………………. (3)
This equation represents the combined equation of pair of lines joining the origin to the points of intersection of (1) and (2).
The equation of pair of angular bisectors of
(3) is h (x² – y²) – (a – b) xy = 0
⇒ 0(x² – y²) – (4 + 1) xy = 0
⇒xy = 0 ⇒ x = 0 or y = 0
Which are the equations of coordinate axes.
∴ The pair of lines are equally inclined to the coordinate axes.