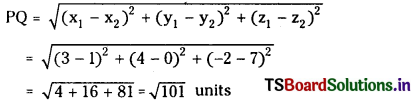TS Inter 1st Year

Students must practice these TS Intermediate Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates 5(b)

I.
Question 1.
Find the ratio in which the XZ – plane divides the line joining A (-2, 3, 4) and B(l, 2, 3). (V.S.A.Q.)
Answer:
Ratio in which XZ – plane divides the AB
= – y₁ : y₂
= – 3 : 2

Question 2.
Find the coordinates of the vertex C of ∆ABC if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively. (V.S.A.Q.)
Answer:
Given A (1,1,1) and B (-2, 4, 1) as two vertices of a ∆ABC and suppose C (x, y, z) is the third vertex. Given O(0, 0, 0) is the centroid.
Then 0 = \(\frac{x+1-2}{3}\) ⇒ x – 1 = 0 ⇒ x = 1
o = \(\frac{y+1+4}{3}\) ⇒ y = -5
0 = \(\frac{z+1+1}{3}\) ⇒ z = -2
∴ Coordinates of third vertex C = (1, – 5, – 2)

Question 3.
If (3, 2, -1), (4, 1, 1) and (6, 2, 5) are the three vertices and (4, 2, 2) is the centroid of a tetrahedron, find the fourth vertex. (V.S.A.Q.) (May 2011, 2005)
Answer:
Let A (3, 2, -1), B (4, 1, 1), C (6, 2, 5) and D (x, y, z) be the coordinates of vertices of a tetrahedron.
Given G = (4, 2, 2) is the centroid. Then

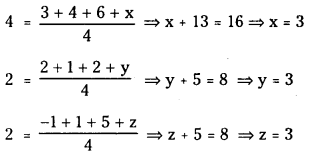
∴ Coordinates of fourth vertex D = (3, 3, 3)

Question 4.
Find the distance between the mid point of the line segment \(\overline{\mathrm{AB}}\) and the point (3, -1, 2) where A (6,3, -4) and B (-2, -1,2). (V.S.A.Q.)
Answer:
Mid point of the line AB where A (6, 3, -4) and B (-2, -1, 2) is
P = \(\left(\frac{6-2}{2}, \frac{3-1}{2}, \frac{-4+2}{2}\right)\)
= (2, 1,-1)
Suppose Q (3, -1, 2) then
PQ = \(\sqrt{(3-2)^2+(-1-1)^2+(2+1)^2}\)
= \(\sqrt{1+4+9}\) = √14 units.

II.
Question 1.
Show that the points (5, 4, 2), (6, 2, -1) and (8, -2, -7) are collinear. (V.S.A.Q.)
Answer:
Let A (5,4, 2), B (6, 2, -1) and C (8, -2, -7) be the given points.

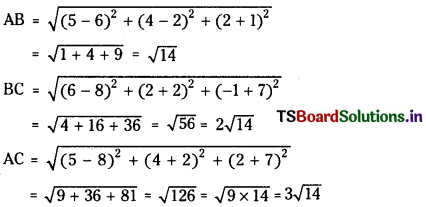
Since AB + BC = AC, the points A, B,.C are collinear.

Question 2.
Show that the points A (3, 2, -4), B( 5, 4, -6) and C (9, 8, -10) are collinear and find the ratio in which B divides \(\overline{\mathbf{A C}}\). (S.A.Q.)
Answer:
Given A (3, 2, -4), B (5, 4, -6), C (9, 8, -10) and

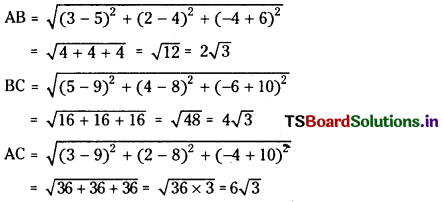
Since AB + BC = 2√3 + 4√3 = 6√3 = AC
We have the points A, B, C are collinear.
The ratio in which B divides AC is
AB : BC = 2√3 : 4√3 = 2 : 4 = 1 : 2

III.
Question 1.
If A (4, 8, 12), B (2, 4, 6), C (3, 5, 4) and D (5, 8, 5) are four points. Show that the lines \(\overleftrightarrow{\mathbf{A B}}\) and \(\overleftrightarrow{\mathbf{CD}}\) intersect. (E.Q.)
Answer:
Given A (4, 8, 12), B (2, 4, 6), C (3, 5, 4) and D (5, 8, 5) are the given points.
Coordinates of the points dividing AB in the ratio λ : 1 is
= \(\left(\frac{2 \lambda+4}{\lambda+1}, \frac{4 \lambda+8}{\lambda+1}, \frac{6 \lambda+12}{\lambda+1}\right)\) …………………….. (1)
Coordinates of the point dividing CD in the ratio μ : 1 is
= \(\left(\frac{5 \mu+3}{\mu+1}, \frac{8 \mu+5}{\mu+1}, \frac{5 \mu+4}{\mu+1}\right)\) …………………….. (2)
If the given lines intersect then these two points are same
∴ \(\frac{2 \lambda+4}{\lambda+1}=\frac{5 \mu+3}{\mu+1}\) …………………….. (3)
⇒ (2λ + 4) (μ + 1) = (5μ + 3) (λ + 1)
⇒ 2λμ + 4μ + 2λ + 4 = 5λμ + 3λ + 5μ + 3
⇒ 3λμ + λ + μ – 1 = 0
⇒ λ = – (3μ + 1) = – (μ – 1)
⇒ λ = – \(\left(\frac{\mu-1}{3 \mu+1}\right)\) ………………….. (4)
Also \(\frac{4 \lambda+8}{\lambda+1}=\frac{8 \mu+5}{\mu+1}\)
⇒ (4λ + 8) (μ + 1) = (8μ + 5) (λ + 1)
⇒ 4λμ + 8μ + 4λ + 8 = 8λμ + 5λ + 8μ + 5
⇒ 4λμ + λ – 3 = 0
⇒ (4μ + 1)λ = 3
⇒ (4μ + 1)\(\left(\frac{-(\mu-1)}{3 \mu+1}\right)\) = 3 (∵ from (4))
⇒ 4μ² – 4μ + μ – 1 = – 9μ – 3
⇒ 4μ² + 6μ + 2 = 0
⇒ 2μ² + 3μ + 1 = 0
⇒ (2μ + 1) (μ + 1) = 0
⇒ μ = – \(\frac{1}{2}\) (or) μ = – 1
μ = – 1 is not admissible
∴ μ = – \(\frac{1}{2}\)
Hence from (2)

Since the two points coincide, the given lines intersect.

Question 2.
Find the point of intersection of the lines \(\overleftrightarrow{\mathbf{A B}}\) and \(\overleftrightarrow{\mathbf{C D}}\) where
A = (7, -6, 1), B = (17, -18, -3)
C = (1, 4, -5) and D = (3, -4, 11) (E.Q.)
Answer:
Given A = (7, -6, 1), B = (17, -18, -3), C = (1, 4, -5) and D = (3, -4, 11)
Coordinates of the point dividing AB in the ratio λ : 1 are
= \(\left(\frac{17 \lambda+7}{\lambda+1}, \frac{-18 \lambda-6}{\lambda+1}, \frac{-3 \lambda+1}{\lambda+1}\right)\) …………………. (1)
Coordinates of the point dividing CD in the ratio μ : 1 are
= \(\left(\frac{3 \mu+1}{\mu+1}, \frac{-4 \mu+4}{\mu+1}, \frac{11 \mu-5}{\mu+1}\right)\) …………………. (2)
∴ \(\frac{17 \lambda+7}{\lambda+1}=\frac{3 \mu+1}{\mu+1}\)
⇒ (17λ + 4) (μ + 1) = (3μ + 1) (λ + 1)
⇒ 17λμ + 17λ + 7μ + 7 = 3λμ + 3μ + λ + 1
⇒ 14λμ + 16λ + 4μ + 6 = 0 …………………. (3)
Also \(\frac{-18 \lambda-6}{\lambda+1}=\frac{-4 \mu+4}{\mu+1}\)
⇒ – 18λμ – 6μ – 18λ – 6 = – 4λμ + 4λ – 4μ + 4
⇒ 14λμ + 22λ + 2μ + 10 = 0 ………………….. (4)
From (3) and (4)
– 6λ + 2μ – 4 = 0
⇒ 2μ = 6λ + 4 = 0
⇒ μ = 3λ + 2 ……………………… (5)
Substituting in (3) we get
⇒ 14λ (3λ + 2) + 16λ + 4(3λ + 2) + 6 = 0
⇒ 42λ² + 28λ + 16λ + 12λ + 8 + 6 = 0
⇒ 42λ² + 56λ + 14 = 0
⇒ 3λ² + 4λ + 1 = 0
⇒ (λ + 1) (3λ + 1) = 0
⇒ λ = – 1 or λ = – \(\frac{1}{3}\)
(λ = – 1 is not admissible)
∴ λ = – \(\frac{1}{3}\)

∴ These two points coincide
∴ The given lines \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) intersect
∴ Point of intersection = (2, 0, 3)

Question 3.
A (3, 2, 0), B(5, 3, 0, C (- 9, 6, – 3) are the vertices of a triangle. \(\overline{\mathbf{A D}}\), the bisector of ∠BAC meets \(\overline{\mathbf{B C}}\) at D. Find the coordinates of D. (E.Q.)
Answer:

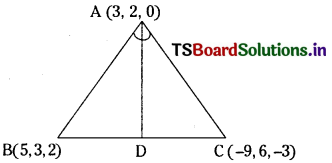
Given A = (3, 2, 0), B = (5, 3, 2), C = (-9, 6, -3) are the vertices of ∆ABC

Question 4.
Show that the points O (0, 0, 0), A (2, -3, 3), B (-2, 3, -3) are collinear. Find the ratio in which each point divides the segment joining the other two. (S.A.Q.)
Answer:
Given points are O(0, 0, 0), A (2, -3, 3) B (-2, 3, -3)

Since OA + OB = AB, the points O, A, B are collinear. Ratio in which O divides AB =
OA : OB = √22 : √22 = 1 : 1
Ratio in which A divides OB
= OA : AB = -√22 : 2√22 = – 1 : 2
Ratio in which B divides OA = AB : BO
= – 2√22 : √22 = -2 : 1
∴ A and B divide externally.

Students must practice these TS Intermediate Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates 5(a)

I.
Question 1.
Find the distance of P (3, -2, 4) from the origin. (V.S.A.Q.)
Answer:
OP = \(\sqrt{x^2+y^2+z^2}\)
= \(\sqrt{9+4+16}\) = √29 units

Question 2.
Find the distance of the points (3, 4, -2) and (1, 0, 7). (V.S.A.Q.)
Answer:
Let P = (3, 4, -2) and Q (1, 0, 7) then

II.
Question 1.
Find x if the distance between (5,-1,7) and (x, 5, 1) is 9 units. (V.S.A.Q.)
Answer:
Let P = (5, -1, 7) and Q (x, 5, 1)
and PQ = 9 ⇒ PQ² = 81
⇒ (x – 5)² + (5 + 1)² + (1 – 7)² = 81
⇒ x² – 10x + 25 + 36 + 36 = 81
⇒ x² – 10x + 25 = 9
⇒ (x – 5)² = 3²
⇒ x – 5 = ±3 ⇒ x = 2 or 8

Question 2.
Show that the points (2, 3, 5), (-1, 5, -1) and (4, -3, 2) form a right angled isosceles triangle. (V.S.A.Q.)
Answer:
Let A = (2, 3, 5), B = (-1, 5, -1) and C = (4, -3, 2) are the given points.
∴ AB² = (2 + 1)² + (3 – 5)² + (5 + 1)² = 9 + 4 + 36 = 49
BC² = (- 1 – 4)² + (5 + 3)² + (- 1 – 2)²
= 25 + 64 + 9 = 98
CA² = (4 – 2)² + (- 3 – 3)²+ (2 – 5)2²
= 4 + 36 + 9 = 49
∴ AB² = CA²
AB² + CA² = 49 + 49 = 98 = BC²
∆ABC is a right angled isosceles triangle.

Question 3.
Show that the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) form an equilateral triangle. (V.S.A.Q.) (Board New Model Paper)
Answer:
Let A (1, 2, 3), B (2, 3, 1) and C (3, 1, 2) are the given points.
AB² = (1 – 2)² + (2 – 3)² + (3 – 1)² = 1 + 1 + 4 = 6
BC² = (2 – 3)² + (3 – 1)² + (1 – 2)² = 1 + 4 + 1 = 6
AC² = (1 – 3)² + (2 – 1)² + (3 – 2)² = 4 + 1 + 1 =6
∴ AB² = BC² = AC² ⇒ AB = BC = AC
∴ ABC is an equilateral triangle.

Question 4.
P is a variable point which moves such that 3PA = 2PB. If A (-2, 2, 3) and B (13, -3,13) prove that P satisfies the equation x² + y² + z² + 28x – 12y +10z – 247 = 0. (S.A.Q.)
Answer:
Given A (-2, 2, 3) and B (13, -3, 13) and suppose P = (x, y, z) then
3PA = 2PB ⇒ 9PA² = 4PB²
⇒ 9 [(x + 2)² + (y – 2)² + (z – 3)²]
= 4 [(x – 13)² + (y + 3)² + (z – 13)²]
⇒ 9 [x² + 4x + 4 + y² – 4y + 4 + z² – 6z + 9]
= 4 [x² – 26x +169 + y² + 6y + 9 + z² – 26z +169]
⇒ 9x² + 9y² + 9z² + 36x – 36y – 54z + 153
= 4x² + 4y² + 4z² – 104x + 24y – 104z + 1388
⇒ 5x² + 5y² + 5z² + 140x – 60y + 50z – 1235 = 0
⇒ x² + y² + z² + 28x – 12y + 10z – 247 = 0

Question 5.
Show that the points (1, 2, 3), (7, 0, 1) and (-2, 3, 4) are collinear. (V.S.A.Q.) (March 2007)
Answer:
Let A (1, 2, 3), B (7, 0, 1), C (-2, 3, 4) be the given points.

∴ BC = AB + AC
∴ A, B, C are collinear.

Question 6.
Show that ABCD is a square where A,B,C,D are the points (0, 4, 1), (2, 3, -1), (4, 5, 0) and (2, 6, 2) respectively. (S.A.Q.)
Answer:
Let A (0, 4, 1), B (2, 3, -1), C (4, 5, 0) and D (2, 6, 2) be the given points.
AB² = (0 – 2)² + (4 – 3)² + (1 + 1)² = 4 + 1 + 4 = 9
BC² = ( 2 – 4)² + (3 – 5)² + (- 1 – 0)² = 4 + 4 + 1 = 9
CD² = (4 – 2)² + (5 – 6)² + (0 – 2)² = 4 + 1 +4 = 9
AD² = (0 – 2)² + (4 – 6)² + (1 – 2)² = 4 + 4 + 1 = 9
∴ AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA
AC² = (0 – 4)² + (4 – 5)² + (1 – 0)² = 16 + 1 + 1 = 18
BD² = (2 – 2)² + (3 – 6)² + (- 1 – 2)² = 9 + 9= 18
∴ AC² = BD² ⇒ AC = BD
AB² + BC² = 9 + 9 = 18 = AC²
∴ ∠ABC = 90°
∴ ABCD is a square.

Students must practice these TS Intermediate Maths 1B SoIutons Chapter 10 Applications of Derivatives Ex 10(g) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(g)

I.
Question 1.
(i) Without using the derivative, show that the function f(x) = 3x + 7 is strictly increasing on ℛ . (V.S.A.Q.)
Answer:
Let x₁ < x₂ ∈ℛ with x₁ < x₂
Then 3x₁ < 3x₁ ;
Adding 7 on both sides,
7 + 3x₁ < 7 + 3x₂ ⇒ f (x₁) < f(x₂)
x₁ < x₂ ⇒ f (x₁) < f(x₂) v x₁, x₂ ∈ ℛ
Hence the given function is strictly increasing on ℛ

(ii) The function f(x) = \(\left(\frac{1}{2}\right)^x\) is strictly decreasing on ℛ.
Answer:
f(x) = \(\left(\frac{1}{2}\right)^x\)
Let x₁, x₂ ∈ ℛ such that x₁ < x₂
⇒ \(\left(\frac{1}{2}\right)^{x_1}>\left(\frac{1}{2}\right)^{x_2}\)
⇒ f(x₁) > f(x₂)
f(x) is strictly decreasing on ℛ.

(iii) The function f(x) = e^3x is strictly increasing on ℛ.
Answer:
f(x) = e^3x
Let x₁, x₂ ∈ ℛ such that x₁ < x₂
We have that if a > b then e^a > e^b
e^3x₁ < e^3x₁ ⇒ f(x₁) < f(x₂)
So the function f is strictly increasing on ℛ.

Question 2.
Show that the function f(x) = sin x defined on ℛ is neither increasing nor decreasing on (0, π). (V.S.A.Q.)
Answer:
Given f(x) = sin x
since 0 < x < π and for 0 < x ⇒ f(0) < f(x)
⇒ sin 0 < sin x => 0 < sin x (1)
for x < π ⇒ f(x) < f(π)
⇒ sin x < sin π ⇒ 0 > sin x (2)
From (1) and (2) f(x) is neither increasing nor decreasing.

II.
Question 1.
Find the interval in which the following functions are stjpctly increasing strictIy decreasing. 1 (S.A.Q.)
(i) x² + 2x – 5
Answer:
Let f(x) = x² + 2x – 5
Then f'(x) = 2x + 2
f(x) is increasing if f'(x) > 0
⇒ 2x + 2 > 0
⇒ x + 1 > 0
⇒ x > – 1
f (x) increases in (- 1, ∞)
f (x) is decreasing if f’ (x) < 0
⇒ 2x + 2 < 0
⇒ x + 1 < 0
⇒ x < – 1
f is decreasing in (- ∞, -1)

(ii) 6 – 9x – x²
Answer:
Let f(x) = 6 – 9x – x²
Then f’ (x) = – 9 – 2x
f(x) is increasing if f’ (x) > 0
⇒ – 9 – 2x > 0 ⇒ 9 + 2x < 0
⇒ x < \(\frac{-9}{2}\)
∴ f(x) is increasing in (-∞, \(\frac{-9}{2}\))
f(x) is decreasing if f'(x) < 0 ⇒ 9 + 2x > 0
⇒ 2x > – 9
⇒ x > \(\frac{-9}{2}\)
∴ f is decreasing in (\(\frac{-9}{2}\), ∞)

(iii) (x + 1)³(x – 1)³
Answer:
Let f(x) = (x + 1)³ (x – 1)³ = (x² – 1)³
= x⁶ – 1 – 3x⁴ 3x²
∴ f'(x) = 6x⁵ – 12x³ + 6x
= 6x(x⁴ – 2x² + 1)
∴ f'(x) = 6x⁵ – 12x³ + 6x
= 6x(x⁴ – 2x² + 1)
= 6x(x² – 1)²
f(x) increases for f'(x) > 0
⇒ 6x(x² – 1) > 0
⇒ x² – 1 > 0, x > 0
∴ f is increasing in (0, 1) ∪ (1, ∞)
f(x) decreases for f'(x) < 0
∴ f is decreasing in (-∞, – 1) ∪ (-1, 0)

(iv) x³(x – 2)²
Answer:
Let f(x) = x³(x – 2)²
Then f(x) = x³. 2 (x – 2) + (x – 2)² 3x²
= x² (x – 2) [2x + 3 (x – 2)]
= x²(x – 2) (5x – 6) ∀ x ∈ R, x² > 0
f is increasing, f'(x) > 0
⇒ x² (x – 2) (5x – 6) > 0
⇒ x ∈(-∞, \(\frac{6}{5}\)) ∪ (2, ∞)
f is decreasing if f'(x) < 0
⇒ x²(x – 2)(5x – 6) < 0
⇒ x ∈ (\(\frac{6}{5}\), 2)

(v) xe^x
Answer:
Let f(x) = xe^x
Then f'(x) = xe^x + e^x = e^x(x + 1) ∀ x ∈ ℛ, e^x > 0
f'(x) > 0 ⇒ e^x(x + 1) > 0
⇒ x + 1 > 0 ⇒ x < – 1
Hence f is increasing in (-1, ∞)
Also f'(x) < 0 ⇒ e^x(1 + x) < 0
⇒ 1 + x < 0 ⇒ x < -1
Hence f is decreasing in (-∞, -1)

(vi) \(\sqrt{25-4 x^2}\)
Answer:
Suppose f(x) = \(\sqrt{25-4 x^2}\)
If f is real then 25 – 4x² ≥ 0
⇒ -(4x² – 25) ≥ 0
⇒ -(2x + 5)(2x – 5) ≥ 0
∴ x ∈ \(\left(\frac{-5}{2}, \frac{5}{2}\right)\)
Domain of f = \(\left(\frac{-5}{2}, \frac{5}{2}\right)\)
i.e., x < 0
f(x) is increasing when x ∈ (\(-\frac{5}{2}\), 0)
f(x) is decreasing when f'(x) < 0
⇒ \(-\frac{4 \mathrm{x}}{\sqrt{25-4 \mathrm{x}^2}}\) < 0 ∴ x > 0 and f(x) is decreasing when x ∈ (0, \(\frac{5}{2}\))

(vii) log (log x), x > 1
Answer:
f(x) = log (log x)
f'(x) = \(\frac{1}{x \log x}\)
f(x) is increasing when f ’(x) > 0
⇒ \(\frac{1}{x \log x}\) > 0 ⇒ x log x > 0
When x > 0, we have x is real and if x > 0 then log x is real.
log x > 0 = log 1 ⇒ x > 1
Function f is increasing in (1, ∞)
If f’ (x) < 0, then f is decreasing
⇒ x log x < 0 ⇒ log x > 0 and x < 1
∴ Function f is decreasing in (0, 1)

(viii) x³ + 3x² – 6x + 12
Answer:
f(x) = x³ + 3x² – 6x + 12
f’ (x) = 3x² + 6x – 6 = 3 (x² + 2x – 2)
= 3 [(x + 1)² – 3]
= 3 [ (x + 1) + √3 ] [ (x + 1) – √3 ]
= 3[x + (1 + √3)][x + (1 – √3)]
If f'(x) > 0 then
[x + (1+ √3)][x + (1 – √3)]>0
⇒ x ∈ [(-∞ , -1 – √3 ) u (√3 – 1 > ∞) ]
Hence f is increasing in above interval.
f'(x) < 0 ⇒ [x + (1 + √3)] [x + (1 – √3)] < 0
⇒ x ∈ [(-1 – √3), (-1 + √3)] f is decreasing in above interval.

Question 2.
Show that f(x) = cos²x is strictly increasing on (0, \(\frac{\pi}{2}\)). (S.A.Q)
Answer:
f(x) = cos2x
f'(x) = 2cosx (- sin x) = – sin 2x
Since 0 < x < \(\frac{\pi}{2}\)
⇒ 0 < 2x < π Since sin x > 0 between 0 and π
We have f'(x) is negative.
f’ (x) < 0 ⇒ f(x) is strictly decreasing.

Question 3.
Show that x + \(\frac{1}{x}\) is increasing on [1, ∞). (S.A.Q.)
Answer:

∴ f'(x) > 0 and f(x) is increasing.

Question 4.
Show that \(\frac{\mathbf{x}}{1+x}\) < log(1 + x) < x ∀ x > 0
Answer:

If x > 0 then f’ (x) > 0 When x > 0 f is increasing
⇒ f(x) > f(0)
f(0) = log 1 – 0 = log 1 = 0
f(x) > 0 ⇒ fog (1 + x) > \(\frac{x}{1+x}\)
Similarly suppose g(x) = x – log (1 + x) ………..(3)
g'(x) = 1 – \(\frac{1}{1+x}=\frac{x}{(1+x)}\) > 0
∴ When x > 0, g(x) is also increasing.
∴ g(x) > g(0) ⇒ g(x) > 0
⇒ x – log (1 + x) > 0 (4)
⇒ x > log (1 + x)
Hence from (2) and (4)
\(\frac{x}{1+x}\) < log(1 + x) < x ∀ x > 0

III.
Question 1.
Show that \(\frac{x}{1+x^2}\) < tan^-1x < x when x > 0. (S.A.Q)
Answer:
Let f(x) = tan^-1x – \(\frac{x}{1+x^2}\)

∴ When x > 0, f is increasing means f(x) > f(0) and f(0) = 0
∴ f(x) > 0 ⇒ tan^-1x – \(\frac{x}{1+x^2}\) > 0
⇒ tan^-1x > \(\frac{x}{1+x^2}\) ………..(1)
Similarly let g(x) = x – tan^-1x
Then g'(x) = 1 – \(\frac{1}{1+x^2}=\frac{x^2}{1+x^2}\) > 0 ∀ x > 0
∴ g is increasing when x > 0
⇒ g(x) = 0
But g(0) = 0
∴ g(x) < 0 ⇒ x – tan^-1x
⇒ x > tan^-1x ………….(2)
∴ From (1) and (2), \(\frac{x}{1+x^2}\) < tan^-1x < x ∀ x > 0

Question 2.
Show that tan x > x for all x ∈ [0, \(\frac{\pi}{2}\)). (S.A.Q)
Answer:
Let f(x) = tan x – x
Then f’ (x) = sec² x -1 > 0 for every x e
f(x) increases ∀ x ∈ [0, \(\frac{\pi}{2}\))
∴ f(x) > f(0) and f(0) = 0
⇒ f(x) > 0 ⇒ tan x – x > 0
⇒ tan x > x; ∀ x ∈ [0, \(\frac{\pi}{2}\))

Question 3.
If x ∈ (0, \(\frac{\pi}{2}\)), then show that \(\frac{2 \mathrm{x}}{\pi}\) < sin x < x. (EQ.) Answer: Let f(x) = sin x – \(\frac{2 \mathrm{x}}{\pi}\) and f’(x) = cos x – \(\frac{2}{\pi}\) > 0; ∀ x ∈ (0, \(\frac{\pi}{2}\))
∵ f’(x) > 0, f is increasing and f(x) > f(0);
Since f(0) = 0 we have f(x) > 0
⇒ sin x – \(\frac{2 \mathrm{x}}{\pi}\) > 0 ⇒ sin x > \(\frac{2 \mathrm{x}}{\pi}\) …………..(1)
Let g(x) = x – sin x
Then g'(x) = 1 – cos x > 0 ∀ x ∈ (0, \(\frac{\pi}{2}\))
∴ g(x) is an increasing function in
But g(0) = 0 – sin 0 = 0 g(x) >0
⇒ x – sin x > 0 x > sin x
⇒ sin x < x ……..(2)
∴ From (1) and (2);
\(\frac{2 \mathrm{x}}{\pi}\) < sin x < x ∀ x ∈ (0, \(\frac{\pi}{2}\))

Question 4.
If x ∈ (0, 1) then show that 2x < log\(\left[\frac{1+x}{1-x}\right]\) < 2x[1 + \(\frac{x^2}{2\left(1-x^2\right)}\)] (E.Q.)
Answer:

Hence ‘g’ is an increasing function in (0, 1) g(x) > g(0) ∀ x ∈ (0, 1)
But g(0) = 0
∴ g(x) > 0 ∀ x ∈ (0, 1)
⇒ 2x[1 + \(\frac{x^2}{2\left(1-x^2\right)}\)] > log\(\left(\frac{1+x}{1-x}\right)\) ………..(2)
From (1) and (2)
2x < log\(\left(\frac{1+x}{1-x}\right)\) < 2x[1 + \(\frac{x^2}{2\left(1-x^2\right)}\)] ∀ x ∈ (0, 1)

Question 5.
At what points the slopes of the tangents y = \(\frac{x^3}{6}-\frac{3 x^2}{2}+\frac{11 x}{2}\) + 12 increases? (E.Q.)
Answer:
Equation of the curve is
y = \(\frac{x^3}{6}-\frac{3 x^2}{2}+\frac{11 x}{2}\) + 12
\(\frac{d y}{d x}=\frac{3 x^2}{6}-\frac{6 x}{2}+\frac{11}{2}\)
Slope m = \(\frac{x^2}{2}\) – 3x + \(\frac{11}{2}\)
\(\frac{\mathrm{dm}}{\mathrm{dx}}\) = x – 3 > 0 (∵ Slope increases)
⇒ x > 3
Slope increases in ( 3, ∞)

Question 6.
Show that the functions \(\frac{\log (1+x)}{x}\) and \(\frac{x}{(1+x) \log (1+x)}\) are decreasing in (0, ∞). (E.Q.)
Answer:

Question 7.
Find the intervals in which the function f(x) = x³ – 3x² + 4 is strictly increasing for all x ∈ ℛ.
Answer:
f(x) = x³ – 3x² + 4
f'(x) = 3x² – 6x
f(x) is strictly increasing if f’ (x) > 0
3x² – 6x > 0
⇒ 3x (x – 2) > 0
⇒ x (x – 2) > 0
f(x) is strictly increasing if x ∈ (2, ∞)

Question 8.
Find the intervals in which the function
f(x) = sin⁴x + cos⁴ x ∀ x ∈ [0, \(\frac{\pi}{2}\)] is increasing and decreasing.
Answer:
Given f(x) = sin⁴x + cos⁴ x ∀ x ∈ [0, \(\frac{\pi}{2}\)]
= (sin²x + cos²x)² – 2 sin²x cos²x
= 1 – 2 sin²x cos²x
= 1 – \(\frac{1}{2}\)sin²2x

f'(x) = \(\frac{1}{2}\)(2 sin 2x)(cos 2x)(2)
= -sin 4x
f'(x) > 0 ⇒ -sin 4x > 0 ⇒ sin 4x < 0
⇒ π < 4x < 2π ⇒ \(\frac{\pi}{4}\) < x < \(\frac{\pi}{2}\)
∴ f is increasing when \(\frac{\pi}{4}\) < x < \(\frac{\pi}{2}\)
Now f'(x) < 0
– sin 4x < 0 ⇒ sin 4x > 0
⇒ 0 < 4x < π ⇒ 0 < x < \(\frac{\pi}{4}\)

∴ Function ‘f’ is decreasing when 0 < x < \(\frac{\pi}{4}\)
∴ f is decreasing in [0, \(\frac{\pi}{4}\)] and
f is increasing in \(\left(\frac{\pi}{4}, \frac{\pi}{2}\right)\)

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 9 Final Accounts of Sole Trading Concerns to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 9 Final Accounts of Sole Trading Concerns

→ To know the business results and financial position at the end of the period, the business prepares various statements which are called as final accounts.

→ Final accounts consist of two accounts and a balance sheet. The two accounts are

1. Trading account
2. Profit and Loss account

→ The expenses and incomes are three types :

1. Capital nature
2. Revenue nature
3. Deferred nature.

Revenue expenses and income appear in either trading account of profit and loss a/c. The capital nature appears in the balance sheet. The revenue part of the deferred part appears in Trading and Profit and Loss a/c, where he as the capital part of deferred nature expenditure and incomes appear in the Balance Sheet.

→ Trading account reveals either gross profit or gross loss. This is transferred to the profit and loss account.

→ Profit and loss account reveals either net profit or a net loss.

→ Balance Sheet is divided into two sides namely the assets side and the liabilities side. Assets are current assets, fixed assets, closing stock etc.

→ Liabilities are creditors, bank loans, bills payable, and net capital.

TS Inter 1st Year Accountancy Notes Chapter 9 సొంతవ్యాపార సంస్థల ముగింపు లెక్కలు

→ సంవత్సరాంతానికి వ్యాపార సంస్థ ఫలితాలు, ఆర్థిక పరిస్థితిని తెలుసుకోవడానికి తయారుచేసే నివేదికలను ముగింపు లెక్కలు అంటారు.

→ ముగింపు లెక్కలు రెండు ఖాతాలు మరియు ఆస్తి – అప్పుల పట్టీ సమూహము. ఆ రెండు ఖాతాలు

1. వర్తకపు ఖాతా
2. లాభనష్టాల ఖాతా

→ వ్యయాలను, ఆదాయాలను మూడు రకాలుగా విభజించవచ్చును.

1. మూలధన స్వభావము గలవి
2. రాబడి స్వభావము గలవి
3. విలంబిత స్వభావము గలవి

రాబడి వ్యయాలు, ఆదాయాలు, వర్తకపు లాభనష్టాల ఖాతాలలోను, మూలధన స్వభావము గలవి, ఆస్తి అప్పుల పట్టీలో చూపాలి. విలంబిత అంశాలు రాబడి స్వభావము గలవి, వర్తక లాభనష్టాల ఖాతాకు, మూలధన స్వభావము గల దానిని ఆస్తి – అప్పుల పట్టీలోను నమోదు చేయాలి.

→ వర్తకపు ఖాతా స్థూల లాభాన్ని లేదా స్థూల నష్టాన్ని సూచిస్తుంది. దీనిని లాభనష్టాల ఖాతాకు మళ్ళించాలి.

→ లాభనష్టాల ఖాతా నికర లాభము లేదా నికర నష్టమును తెలుపుతుంది.

→ ఆస్తి – అప్పుల పట్టీని రెండు భాగాలుగా విభజన చేసి అప్పులను ఎడమవైపు, ఆస్తులను కుడివైపు చూపాలి. ఆస్తులు, చరాస్తులు, స్థిరాస్తులు, ముగింపు సరుకు మొ||నవి. అప్పులు, ఋణదాతలు, బాంకు అప్పు, చెల్లింపు బిల్లులు మొ||నవి.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 8 Rectification of Errors to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 8 Rectification of Errors

→ దోషము అనగా తప్పు మరియు సవరణ అనగా జరిగిన తప్పును సరిచేయుట.

→ దోషాలను రెండు రకాలుగా విభజించవచ్చును.

• సిద్ధాంతపు దోషాలు
• రాతపూర్వక దోషాలు

→ రాతపూర్వక దోషాలు మరల దిగువ విధముగా వర్గీకరించవచ్చును.

• ఆకృత దోషాలు
• అకార్యాకరణ దోషాలు
• సరిపెట్టే దోషాలు

→ తప్పులను మరల రెండు రకాలుగా విభజించవచ్చును.

• అంకూ ద్వారా వెల్లడి అయ్యే తప్పులు
• అంకణా ద్వారా వెల్లడి కాని తప్పులు

→ అనామతు ఖాతా ఒక ఊహాజనిత ఖాతా మరియు తాత్కాలికమైనది. అంకజా సమానత్వము సాధించడానికి దీనిని తెరుస్తారు.

TS Inter 1st Year Accountancy Notes Chapter 8 తప్పుల సవరణ

→ An error is a mistake and rectification means correcting the mistake that has occured.

→ Errors are classified into two types.

1. Error of principle
2. Clerical errors.

→ Clerical errors are again classified into

• Error of omission
• Error of commission
• Compensating errors.

→ Errors are again classified as

1. Errors disclosed by trial balance
2. Errors not disclosed by trial balance.

→ Suspense account is an imaginary account opened temporarily for the purpose of tallying the trial balance.

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Differentiation Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Differentiation Important Questions Long Answer Type

Question 1.
If y = \(\tan ^{-1}\left[\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right]\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’18 (TS); Mar. ’16 (AP), ’12, ’10, ’09, ’04; May ’15 (AP & TS), ’12, ’97]
Solution:

Question 2.
If y = x^{tan x} + (sin x)^{cos x}, then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’14, ’13 (Old), ’11, ’08, ’07; May ’13, ’06; Mar. ’18 (AP)]
Solution:
Given y = x^{tan x} + (sin x)^{cos x}
Differentiating on both sides with respect to ‘x’.
Let u = x^{tan x}
v = sin x^{cos x}
y = u + v
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{u}+\mathrm{v})\)
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……(1)
Now, u = x^{tan x}
Taking logarithms on both sides,
log u = log x^{tan x}
log u = tan x log x
Differentiating on both sides with respect to ‘x’.

Now, v = (sin x)^{cos x}
Taking logarithms on both sides,
log v = log (sin x)^{cos x}
log v = cos x log(sin x)
Differentiating on both sides with respect to ‘x’.

Question 3.
If x = \(\frac{3 a t}{1+t^3}\), y = \(\frac{3 \mathrm{at}^2}{1+\mathrm{t}^3}\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [B.P.]
Solution:
Given that x = \(\frac{3 a t}{1+t^3}\)
Differentiating on both sides with respect to ‘t’.

Question 4.
If \(\sqrt{1-x^2}+\sqrt{1-y^2}\) = a(x – y) then show that \(\frac{d y}{d x}=\sqrt{\frac{1-y^2}{1-x^2}}\). [Mar. ’17 (TS), ’08, ’05; May ’14, ’13 (Old), ’11, ’97]
Solution:
Given that \(\sqrt{1-x^2}+\sqrt{1-y^2}\) = a(x – y)
Put x = sin α ⇒ α = sin^-1x
y = sin β ⇒ β = sin^-1y
Now, \(\sqrt{1-\sin ^2 \alpha}+\sqrt{1-\sin ^2 \beta}\) = a(sin α – sin β)
\(\sqrt{\cos ^2 \alpha}+\sqrt{\cos ^2 \beta}\) = a(sin α – sin β)
cos α + cos β = a(sin α – sin β)

Question 5.
If y = \(\mathbf{x} \sqrt{\mathbf{a}^2+x^2}+a^2 \log \left(x+\sqrt{a^2+x^2}\right)\) then show that \(\frac{d y}{d x}=2 \sqrt{a^2+x^2}\). [Mar. ’19, ’15 (AP). ’09, ’02; May ’08]
Solution:
Given, that y = \(\mathbf{x} \sqrt{\mathbf{a}^2+x^2}+a^2 \log \left(x+\sqrt{a^2+x^2}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 6.
If y = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)+\tan ^{-1}\left(\frac{3 x-x^3}{1-3 x^2}\right)\) – \(\tan ^{-1}\left(\frac{4 x-4 x^3}{1-6 x^2+x^4}\right)\) then show that \(\frac{\mathbf{d y}}{\mathbf{d x}}=\frac{1}{1+x^2}\). [May ’07]
Solution:
Given that

y = 2θ + 3θ – 4θ = θ
y = tan^-1x
Differentiating on both sides with respect to x.
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dx}} \tan ^{-1} \mathrm{x}\)
∴ \(\frac{d y}{d x}=\frac{1}{1+x^2}\)

Question 7.
If y = \(\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [May ’10]
Solution:

Question 8.
If y = (sin x)^{log x} + x^{sin x} then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’17 (AP), ’15 (TS), ’13]
Solution:
Given that, let y = (sin x)^{log x} + x^{sin x}
Let, u = (sin x)^{log x} , v = x^{sin x} then y = u + v
Differentiating on both sides with respect to x.
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) …….(1)
Now, u = (sin x)^{log x}
Taking logarithms on both sides
log u = log (sin x)^{log x}
log u = log x . log (sin x)
Differentiating on both sides with respect to ‘x’.

Now, v = x^{sin x}
Taking logarithms on both sides
log v = log x^{sin x}
log v = sin x log x
Differentiating on both sides with respect to ‘x’.

Question 9.
If x^y + y^x = a^b then show that \(\frac{d y}{d x}=-\left[\frac{y x^{y-1}+y^x \log y}{x^y \log x+x y^{x-1}}\right]\). [Mar. ’03; Mar. ’16 (TS)]
Solution:
Given that, x^y + y^x = a^b
Let, x^y = u, y^x = v then, u + v = a^b
Differentiating on both sides with respect to x.
\(\frac{\mathrm{du}}{\mathrm{dx}}+\frac{\mathrm{dv}}{\mathrm{dx}}=0\) ……(1)
Now, u = x^y
Taking logarithms on both sides
log u = log x^y
log u = y log x
Differentiating on both sides with respect to ‘x’.

Now, v = y^x
Taking logarithms on both sides
log v = log y^x
log v = x log y
Differentiating on both sides with respect to ‘x’.

Question 10.
If f(x) = \(\sin ^{-1} \sqrt{\frac{x-\beta}{\alpha-\beta}}\) and g(x) = \(\tan ^{-1} \sqrt{\frac{x-\beta}{\alpha-x}}\) then show that f'(x) = g'(x), (β < x < α).
Solution:

Some More Maths 1B Differentiation Important Questions Long Answer Type

Question 11.
Find the derivative of 20^{log(tan x)}.
Solution:
Let y = 20^{log(tan x)}
Differentiating on both sides with respect to ‘x’.

Question 12.
If f(x) = e^2x log x (x > 0), then find f'(x).
Solution:
f(x) = e^2x (log x)
Let y = e^2x (log x)
Differentiating with respect to ‘x’ on both sides,

Question 13.
If y = \(\frac{\mathbf{a}-\mathbf{x}}{\mathbf{a}+\mathbf{x}}\), find \(\frac{\mathbf{d y}}{\mathbf{d x}}\).
Solution:
Given y = \(\frac{\mathbf{a}-\mathbf{x}}{\mathbf{a}+\mathbf{x}}\)
Differentiating with respect to x on both sides.

Question 14.
If y = sin^-1(cos x) then find \(\frac{d y}{d x}\).
Solution:
Let y = sin^-1(cos x)
Differentiating on both sides with respect to ‘x’.

Question 15.
If x⁴ + y⁴ – a²xy = 0, find \(\frac{\mathbf{d y}}{\mathbf{d x}}\).
Solution:
Given that x⁴ + y⁴ – a²xy = 0
Differentiating on both sides with respect to ‘x’.

Question 16.
Find the derivative of cos^-1(4x³ – 3x) with respect to ‘x’.
Solution:
Let y = cos^-1(4x³ – 3x)
Put x = cos θ
⇒ θ = cos^-1x
Now, y = cos^-1(4 cos³θ – 3 cos θ)
= cos^-1(cos 3θ)
= 3θ
y = 3 cos^-1x
Differentiating on both sides with respect to ‘x’.

Question 17.
Find the derivative of sec x from the first principle.
Solution:
Given, f(x) = sec x
Now, f(x + h) = sec (x + h)

Question 18.
Find the derivative of \(\sin ^{-1}\left(\frac{b+a \sin x}{a+b \sin x}\right)\).
Solution:
Let y = \(\sin ^{-1}\left(\frac{b+a \sin x}{a+b \sin x}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 19.
Find the derivative of \(\tan ^{-1}\left(\frac{\cos x}{1+\cos x}\right)\)
Solution:
Let y = \(\tan ^{-1}\left(\frac{\cos x}{1+\cos x}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 20.
Find the derivative of \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\) with respect to tan^-1x. [May ’09]
Solution:

Question 21.
If f(x) = x e^x sin x, then find f'(x).
Solution:
f(x) = x . e^x . sin x
Let y = x . e^x . sin x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{d}{d x}\) (x . e^x . sin x)
= x . e^x . \(\frac{d}{d x}\) (sin x) + x . sin x . \(\frac{d}{d x}\) (e^x) + sin x . e^x . \(\frac{d}{d x}\) (x)
= x . e^x . cos x + x . sin x . e^x + sin x . e^x (1)
= e^x (x cos x + x sin x + sin x)
∴ f'(x) = e^x (x cos x + x sin x + sin x)

Question 22.
If f(x) = sin(log x), (x > 0), then find f'(x). [Mar. ’18 (AP)]
Solution:
f(x) = sin(log x)
Let y = sin(log x)

Question 23.
If f(x) = (x³ + 6x² + 12x – 13)¹⁰⁰, then find f'(x).
Solution:
Given that, f(x) = (x³ + 6x² + 12x – 13)¹⁰⁰
Let y = (x³ + 6x² + 12x – 13)¹⁰⁰
Differentiating with respect to x on both sides.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{d}{d x}\) (x³ + 6x² + 12x – 13)¹⁰⁰
= 100(x³ + 6x² + 12x – 13)^100-1 \(\frac{d}{d x}\)(x³ + 6x² + 12x – 13)
= 100(x³ + 6x² + 12x – 13)⁹⁹ (3x² + 6(2x) + 12(1) – 0)
= 100(x³ + 6x² + 12x – 13)⁹⁹ (3x² + 12x + 12)
= 100(x³ + 6x² + 12x – 13)⁹⁹ 3(x² + 4x + 4)
= 300(x + 2)² (x³ + 6x² + 12x – 13)⁹⁹
∴ f'(x) = 300(x + 2)² . (x³ + 6x² + 12x – 13)⁹⁹

Question 24.
Find the derivative of (ax + b)ⁿ (cx + d)^m.
Solution:
Given, f(x) = (ax + b)ⁿ (cx + d)^m
Let y = (ax + b)ⁿ (cx + d)^m
Differentiating with respect to ‘x’ on both sides.

Question 25.
Find the derivative of \(\frac{\mathbf{p} \mathbf{x}^2+\mathbf{q x}+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\).
Solution:
Given, f(x) = \(\frac{\mathbf{p} \mathbf{x}^2+\mathbf{q x}+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\)
Let y = \(\frac{\mathbf{p} \mathbf{x}^2+\mathbf{q x}+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\)
Differentiating with respect to ‘x’ on both sides.

Question 26.
Find the derivative of \(\log _7(\log x)\).
Solution:
Given that, f(x) = \(\log _7(\log x)\)
Let y = \(\log _7(\log x)\)
Differentiating with respect to ‘x’ on both sides.

Question 27.
Find the derivative of the function f(x) = (x² – 3)(4x³ + 1). [May ’15 (AP)]
Solution:

Question 28.
Find the derivative of tan^-1(log x). [Mar. ’19 (AP); May ’15 (TS)]
Solution:

Question 29.
If f(x) = 2x³ + 3x – 5, then prove that f'(0) + 3 . f'(-1) = 0. [Mar. ’16 (AP)]
Solution:
Given f(x) = 2x² + 3x – 5
Now f'(x) = 2(2x) + 3(1) – 0 = 4x + 3
f'(0) = 4(0) + 3 = 3
f(-1) = 4(-1) + 3 = -4 + 3 = -1
LHS = f'(0) + 3. f'(-1)
= 3 + 3(-1)
= 3 – 3
= 0
∴ f'(0) + 3 . f'(-1) = 0

Question 30.
If 2x² – 3xy + y² + x + 2y – 8 = 0, then find \(\frac{d \mathbf{y}}{\mathbf{d x}}\). [Mar. ’16 (TS)]
Solution:
Given 2x² – 3xy + y² + 2y – 8 = 0
differentiating on both sides with respect to ‘x’.

Question 31.
If ay⁴ = (x + b)⁵ then 5yy¹¹ = (y¹)². [Mar. ’17 (TS)]
Solution:

Question 32.
If y = x⁴ + tan x then find y¹¹. [Mar. ’18 (AP)]
Solution:
Given that y = x⁴ + tan x
y¹ = \(\frac{\mathrm{d}}{\mathrm{dx}}\)(x⁴ + tan x) = 4x³ + sec²x
y¹¹ = \(\frac{\mathrm{d}}{\mathrm{dx}}\)(4x³ + sec²x)
= 4(3x²) + 2 sec x \(\frac{\mathrm{d}}{\mathrm{dx}}\)(sec x)
= 12x² + 2 sec x (sec x tan x)
∴ y¹¹ = 12x² + 2 sec²x tan x

Question 33.
If y = \(\frac{2 x+3}{4 x+5}\), then find y”.
Solution:
y = \(\frac{2 x+3}{4 x+5}\)

Question 34.
If f(x) = log(tan e^x), then find f'(x). [Mar. ’19 (TS)]
Solution:

Question 35.
Evaluate \({Lim}_{x \rightarrow 0} \frac{\log _e(1+5 x)}{x}\). [Mar. ’19 (TS)]
Solution:

Question 36.
If x^{log y} = log x, then show that \(\frac{d y}{d x}=\frac{y}{x}\left(\frac{1-\log x \log y}{(\log x)^2}\right)\). [Mar. ’19 (TS)]
Solution:

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 7 Trial Balance to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 7 Trial Balance

→ Trial balance may be defined as a statement of balances of accounts of a business and it is prepared mainly to check the arithmetical accuracy of accounts.

→ Trial balance is a statement but not an account. It contains a summary of the accounts and helps in the preparation of final accounts.

→ Trial balance can be prepared by two methods

• Total Balances method
• Net balances method.

→ Accounts pertaining to assets, expenses and losses appear on the debit side and accounts related capital, liabilities incomes and gains appear on the credit side.

TS Inter 1st Year Accountancy Notes Chapter 7 అంకణా

→ జంటపద్దు విధానములోని ఖాతాలు లేదా ఖాతా నిల్వల అంకగణిత ఖచ్చితాన్ని ఋజువు చేసే నిమిత్తము తయారు చేసే నివేదికయే అంకణా.

→ అంకళా నివేదికయే కాని ఖాతా కాదు. దీనిలో ఖాతాల సంక్షిప్త సమాచారము ఉండి ముగింపు లెక్కలు తయారు చేయడానికి దోహదము చేస్తుంది.

→ అంకణాను రెండు పద్ధతులలో తయారు చేయవచ్చు.

• మొత్తాల పద్ధతి
• నిల్వల పద్ధతి

→ ఆస్తులు, ఖర్చులు, నష్టాలకు సంబంధించిన ఖాతాలు డెబిట్ నిల్వను, మూలధనము, అప్పులు, ఆదాయాలు, లాభాలకు సంబంధించిన ఖాతాలు క్రెడిట్ నిల్వను చూపుతాయి.

Students must practice these TS Intermediate Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c)

I.
Question 1.
Find the equation of the lines joining the origin to the points of intersection of x² + y² = 1 and x + y = 1. (V.S.A.Q.)
Answer:
Given equations are
x² + y² = 1 ………………. (1)
and x + y = 1 ………………. (2)
Homogenising (1) with (2) we get
(x² + y²) = 1²
= (x + y)²
⇒ x² + y² = x² + y² + 2xy ⇒ xy = 0

Question 2.
Find the angle between the lines joining the origin to the points of intersection of y² = x and x + y = 1. (V.S.A.Q.)
Answer:
Given equations are
y² = x …………….. (1)
and x + y = 1 ……………… (2)
Homogenising (1) with (2) we get
y² = x (1)
= x (x + y) ⇒ x² + xy – y² = 0
Coefficient of x² + coefficient of y² = 1 – 1 = 0
∴ Angle between lines is 90°, lines being perpendicular.

II.

Question 1.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – √2 = 0 are mutually perpendicular. (S.A.Q.) (May, March ’12)
Answer:

The given equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 ………………… (1)
Equation of AB is x – y – √2 = 0
⇒ x – y = √2
⇒ \(\frac{x-y}{\sqrt{2}}\) = 1 …………………. (2)
Homogenising (1) using (2) we get
x² – xy + y² + (3x + 3y) (1) – 2 (1)² = 0

Question 2.
Find the values of k, if the lines joining the origin to the points of intersection of the curve 2×2 – 2xy + 3y2 + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular. (E.Q.) (Board New Model Paper)
Answer:
Given equation of the curve is
2x² – 2xy + 3y² + 2x – y – 1 = 0 ……………… (1)
and equation of the line is x + 2y = k
We have \(\frac{x+2 y}{k}\) = 1 ……………….. (2)
Homogenising equation (1) with equation (2) we get
2x² – 2xy + 3y² + 2x (1) – y (1) – (1)² = 0
⇒ 2×2 – 2xy + 3y2 + 2x\(\left(\frac{\mathrm{x}+2 \mathrm{y}}{\mathrm{k}}\right)\) – y\(\left(\frac{\mathrm{x}+2 \mathrm{y}}{\mathrm{k}}\right)\) – \(\left(\frac{x+2 y}{k}\right)^2\) = 0
⇒ 2k²x² – 2k²xy + 3k²y² + 2kx (x + 2y) – ky (x + 2y) – (x + 2y)² = 0
⇒ 2k²x² – 2k²xy + 3k²y² + 4kxy + 2kx² – kxy – 2ky² – (x² + 4xy + 4y²) = 0
⇒ (2k² + 2k – 1) x² + (- 2k² + 3k – 4) xy + (3k² – 2k – 4) y² = 0
Since the lines joining the origin to the points of intersection are mutually perpendicular, coefficient of x² + coefficient of y² = 0
⇒ (2k² + 2k – 1) + (3k² – 2k – 4) = 0
⇒ 5k² – 5 = 0 ⇒ k² = 1 ⇒ k = ± 1

Question 3.
Find the angle between the lines joining the origin to the points of intersection of the curve x² + 2xy + y² + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0 (E.Q.) (May 2014, 11, Mar.13, 07, June 04)
Answer:
Given equation of the curve is
x² + 2xy + y² + 2x + 2y – 5 = 0 …………….. (1)
Equation of the line is 3x – y + 1 = 0
⇒ y – 3x = 1 ……………….. (2)
Homogenising (1) with equation (2) we get the equation of lines joining the origin to the points of intersection of curve and the line.
∴ x² + 2xy + y² + 2x (1) + 2y (1) – 5 (1)² = 0
⇒ x² + 2xy + y² + 2x (y – 3x) + 2y (y – 3x) – 5 (y – 3x)² = 0
⇒ x² + 2xy + y² + 2xy – 6x² + 2y² – 6xy – 5(y² – 6xy + 9x²) = 0
⇒ – 5x² – 2xy + 3y² – 5y² – 45x² + 30xy = 0
⇒ – 50x² + 28xy – 2y² = 0
⇒ 25x² – 14xy + y² = 0
Let θ be the angle between lines then by the formula

III.
Question 1.
Find the condition for the chord lx + my = 1 of the circle x² + y² = a² (whose centre is the origin) to subtend a right angle at the origin. (Mar. 14) (SA.Q.)
Answer:

Equation of the circle is x² + y² = a² ………………. (1)
Equation of the line AB is lx + my = 1 ……………….. (2)
Homogenising (1) with equation (2) we get
x² + y² = a² (1)2
⇒ x² + y² = a²(lx + my)²
⇒ x² + y² = a² (l² x² + 2lmxy + m²y²)
⇒ (a²l² – 1)x² + 2a² lmxy + (a²m² – 1) y² = 0
Since OA, OB are perpendicular, we have coefficient of x² + coefficient of y² = 0
⇒ (a² l² – 1) + (a²m² – 1) = 0
⇒ a² (l² + m²) – 2 = 0
⇒ a² (l² + m²) = 2

Question 2.
Find the condition for the lines joining the origin to the points of intersection of the circle x2 + y2 = a2 and the line lx + my = 1 to coincide. (S.A.Q.)
Answer:
The given equation of the curve is
x² + y² = a² ……………. (1)
and the equation of line is
lx + my = 1 ………………… (2)
Homogenising (1) with equation (2) we get
x² + y² = a²(1)² = a² (lx + my)²
⇒ x² + y² = a² (l²x² + 2lmxy + m²y²)
⇒ x² (1 – a²l²) + y² (1 – a²m²) – 2 lma²xy = 0
This equation represents combined equation of lines joining the origin to the points of intersection of (1) and (2)
If the lines are coincident then h² = ab
l²m²a⁴ = (1 – a²m²) (1 – a²m²)
= 1 – a² (l² + m²) + a⁴l²m²
⇒ a² (l² + m²) = 1

Question 3.
Write down the equation of the pair of straight lines joining the origin to the points of intersection of the line 6x – y + 8 = 0 with the pair of straight lines 3x² + 4xy – 4y² – 11x + 2y + 6 = 0. Show that the lines so obtained make equal angles with the coordinate axes. (E.Q.)
Answer:
Given equation of pair of lines is
3x² + 4xy – 4y² – 11x + 2y + 6 = 0 ……………….. (1)
Given equation of line is 6x – y + 8 = 0 ………………. (2)
Homogenising (1) with equation (2)

⇒ 64 (3x² + 4xy – 4y²) – 8 [11xy – 66x² – 2y² + 12xy) + 6[y² + 36x² – 12xy] = 0
⇒ 936x² – 256xy + 256xy – 234y² = 0
⇒ 468x² – 117y² = 0
⇒ 4x² – y² = 0 …………………. (3)
This equation represents the combined equation of pair of lines joining the origin to the points of intersection of (1) and (2).
The equation of pair of angular bisectors of
(3) is h (x² – y²) – (a – b) xy = 0
⇒ 0(x² – y²) – (4 + 1) xy = 0
⇒xy = 0 ⇒ x = 0 or y = 0
Which are the equations of coordinate axes.
∴ The pair of lines are equally inclined to the coordinate axes.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 4 Preparation of Subsidiary Books to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 4 Preparation of Subsidiary Books

→ Subsidiary books are divided into 8 types. They are:

1. Purchase book
2. Sales book
3. Purchase returns book
4. Sales returns book
5. Cash book
6. Bills receivable book
7. Bills payable book
8. Journal proper.

→ Purchases book is the book in which only credit purchases of goods are recorded. Cash purchases of goods and assets are not recorded.

→ Sales book is a book of original entries in which transactions related to credit sales are recorded.

→ Purchase returns book is a book of original entries in which transactions related to the return of purchases of goods are recorded.

→ Sales returns book is a book in which transactions related to the return of sales of goods are recorded.

→ Journal proper is the Eighth Subsidiary book. This book is also called as “General Proper”.

→ Journal proper is used to record all those transactions which cannot be recorded in the other seven subsidiary books.

→ Some important items which are recorded in the journal proper are given below:

• Opening entry
• Closing entry
• Adjustment entry
• Rectification entry
• Transfer entry.

TS Inter 1st Year Accountancy Notes Chapter 4 సహాయక చిట్టాల తయారీ

→ సహాయక చిట్టాలు 8 రకాలు. అవి:

1. కొనుగోలు చిట్టా
2. అమ్మకాల చిట్టి
3. కొనుగోలు వాపసుల చిట్టా
4. అమ్మకాల వాపసుల చిట్టా
5. నగదు చిట్టా
6. వసూలు హుండీల చిట్టా
7. చెల్లింపు పొండీల చిట్టి
8. అసలు చిట్టా.

→ కొనుగోలు పుస్తకంలో అరువుపై కొనుగోలు చేసిన సరుకుల వివరాలు మాత్రమే నమోదు చేయాలి.

→ అమ్మకాల పుస్తకంలో అరువుపై అమ్మిన సరుకుల వివరాలు మాత్రమే నమోదు చేయాలి.

→ వ్యాపార సంస్థ కొనుగోలు చేసిన సరుకులను తిరిగి సరఫరాదారుకు వాపసు చేసిన వివరాలను కొనుగోలు వాపసుల పుస్తకంలో నమోదు చేయాలి.

→ వ్యాపార సంస్థ ఖాతాదారులకు సరుకు అమ్మిన తరువాత, కొనుగోలుదారుకు సరుకు వాపసు చేసినట్లయితే ఆ వివరాలను అమ్మకాల వాపసుల పుస్తకంలో నమోదు చేయాలి.

→ ఋణగ్రస్తుల నుండి రావలసిన బిల్లులను వసూలు హుండీల చిట్టాలో రాయాలి.

→ ఋణదాతలకు చెల్లింపు చేయవలసిన బిల్లులను చెల్లింపు హుండీల చిట్టాలో రాయాలి.

→ అసలు చిట్టా 8వ సహాయక పుస్తకం. మొదటి 7 సహాయక పుస్తకాలలో నమోదు చేయడానికి వీలుకాని వ్యాపార వ్యవహారాలను అసలు చిట్టాలో నమోదు చేస్తారు.

→ అసలు చిట్టాలో ఈ క్రింది వ్యవహారాలను నమోదు చేస్తారు.

1. ప్రారంభ పద్దులు
2. ఆస్తి అరువు కొనుగోలు పద్దులు
3. సవరణ పద్దులు
4. బదిలీ పద్దులు
5. ముగింపు పద్దులు
6. ఆస్తి అరువు అమ్మకాల పద్దులు
7. సర్దుబాటు పద్దులు
8. ఇతర పద్దులు.

Here students can locate TS Inter 1st Year Physics Notes 8th Lesson డోలనాలు to prepare for their exam.

TS Inter 1st Year Physics Notes 8th Lesson డోలనాలు

→ ఆవర్తన చలనము : నిర్ణీత కాలవ్యవధులలో పునరావృతమయ్యే చలనాలను ఆవర్తన చలనాలు అంటారు.

→ ఆవర్తన చలనాన్ని ప్రత్యేకంగా డోలన చలనాన్ని వివరించేందుకు కాలం, పౌనఃపున్యము, స్థానభ్రంశము, కంపన పరిమితి, దశ లేక ప్రావస్థ వంటి ప్రాథమిక భావనలు అవసరము.

→ సరళహరాత్మక చలనం : డోలన చలనం యొక్క సరళమైన రూపాన్ని సరళ హరాత్మక చలనం అంటారు. ఈ చలనం కాల ప్రమేయము (f(t)) తో ఆవర్తనంగా ఉంటుంది.

→ సరళ హరాత్మక చలనాన్ని f(t) = A cos ωt లేదా A sin ωt వంటి అతిసరళమైన సమీకరణంతో సూచిస్తారు. నోట్:

• వస్తువు పౌనఃపున్యము (v) తక్కువగా ఉంటే వాటిని డోలన చలనము అని, పౌనఃపున్యము ఎక్కువగా ఉంటే దానిని కంపన చలనమని అంటారు.
• ప్రతి డోలన చలనం ఆవర్తన చలనమే కాని, ప్రతి ఆవర్తన చలనము డోలన చలనం కావలసిన అవసరం లేదు.

→ ఆవర్తన కాలము (T) : ఆవర్తన చలనంలో ఏ స్వల్ప కాలవ్యవధి తరువాత చలనం పునరావృతమవుతుందో కాలాన్ని ఇచ్చిన ఆవర్తన చలనము యొక్క ఆవర్తన కాలము అంటారు.
ఆవర్తన కాలము T = \(\frac{2 \pi}{\omega}\), ω = కోణీయ వేగము

→ పౌనఃపున్యము (v) : ఏకాంక కాలంలో జరిగే ఆవర్తనాలు లేదా చలనంలోని పునరావృతాలను ఆవర్తన చలనం పౌనఃపున్యము (v) అంటారు.
పౌనఃపున్యము (v) ఆవర్తన కాలము (T) విలోమానికి సమానము.

ప్రమాణము : డోలనము/సెకను లేదా హెర్జ్ (Hz)

→ స్థానభ్రంశము : ఆవర్తన చలనంలో కాలంతో పాటు మార్పును కలిగిన ఏదైనా భౌతిక ధర్మంలో వచ్చే మార్పును స్థానభ్రంశం సూచిస్తుంది.
ఉదా :

• సరళ హరాత్మక చలనంలో రేఖీయ గమనంలో ఉన్న ఒక బంతి ఆరంభ బిందువు నుంచి దాని దూరాన్ని కాలప్రమేయంగా తీసుకుంటే, వస్తువు స్థానం బట్టి మూలబిందువు ఎంపికను బట్టి స్థానభ్రంశ పరిమాణం ఉంటుంది.
• ఏకాంతర విద్యుత్ ప్రవాహ వలయంలో కెపాసిటర్ పలకల మధ్య కాలంతో పాటు మారే వోల్టేజిని కూడా స్థానభ్రంశ చలరాశిగా భావించవచ్చు.

→ ఫోరియర్ సిద్ధాంతము : ఏ ఆవర్తన ప్రమేయాన్ని అయినా వివిధ డోలనా వర్తన కాలాలు (T), వాటికి అనుగుణమైన గుణకాలు కలిగి ఉండే sine మరియు cosine ల ప్రమేయాల అధ్యారోపణంగా రాయవచ్చు. ఉదా :

• Y = sin ωt + cos ωt
• Y = sin ωt + cos 2 ωt + sin 4 ωt
• Y = e^-ωt
• Y = log (ωf) వంటి ప్రమేయాలు ఆవర్తన చలనాన్ని సూచించటానికి వాడవచ్చు.

→ సరళ హరాత్మక చలన సమీకరణ వివరణ : కాలంతో పాటు స్థానభ్రంశం జ్యా వక్రీయ ప్రమేయం (sinusodial)గా ఉన్న ఆవర్తన చలనాన్ని సరళ హరాత్మక చలనంగా తీసుకుంటారు. ఇటువంటి చలనంలో కణ స్థానభ్రంశం ‘X’ కాలంతో పాటు (t) మారే విధానాన్ని x(t) = A cos (ωt + Φ) తో సూచిస్తారు. ఇందులో A కణం పొందే గరిష్ఠ స్థానభ్రంశ పరిమాణము. దీనిని కంపన పరిమితి అంటారు. sine, cosine ప్రమేయాలకు దీని విలువ – 1 నుండి 1 వరకు మారును. ut ని ఆర్గ్యుమెంట్ అంటారు. ఇది కాలంతో పాటు మారే స్థానభ్రంశ పరిమాణాన్ని సూచిస్తుంది. ఈ ప్రమేయం ఆవర్తన కాలము T = అవుతుంది.

→ ప్రావస్థ లేక దశ (Φ) : ఆవర్తన చలన ప్రారంభంలో t = 0 వద్ద ωt + Φ = 0 అవుతుంది. t = 0 వద్ద గల స్థానభ్రంశాన్ని ప్రావస్థ లేదా దశ ” అంటారు.

→ కోణీయ వేగము లేదా కోణీయ పౌనఃపున్యము (ω) : ఆవర్తన చలనాన్ని కోసైన్ (cosine) లేదా సైన్ (sine)ల ఆవర్తన ప్రమేయంగా చూపితే, ఆవర్తన కాలం ‘T’ లో ఆర్గ్యుమెంట్ (కణ కోణీయ స్థానభ్రంశం)లో మార్పు 2π అయితే దాని స్థానభ్రంశం పునరావృతమవుతుంది. అనగా కోణీయ వేగము ω = \(\frac{2 \pi}{T}\). దీనినే వస్తువు కోణీయ పౌనఃపున్యము అని కూడా అంటారు.

→ నివేశ వృత్తము : ఒక వృత్త వ్యాసంపై ఏకరీతి వృత్తాకార చలనం యొక్క విక్షేపం (projection) సరళ హరాత్మక చలనము వృత్త వ్యాసంపై ఏకరీతి చలనం చేసే కణాన్ని (p) నిర్దేశకం అని, ఈ కణం ఏ వృత్తంపై తిరుగుతుందో దానిని నివేశ వృత్తము అని అంటారు.

→ సరళ హరాత్మక చలనంలో ఉన్న వస్తువు వేగము : ఏకరీతి వృత్తాకార చలనంలో కణం గరిష్ఠ వడి అనేది కోణీయ వేగం మరియు వృత్త వ్యాసార్థాల లబ్ధానికి సమానము. V = ωA. S.H.M లో గల వస్తు సమీకరణం x(t) = = A cos (ωt + d) అయితే కణం వడి υ = \(\frac{d}{d x}\)[x(t)] = \(\frac{d}{d x}\) [A cos (ωt + d)] = – A ω sin (ωt + d) = ω\(\sqrt{A^2-x^2}\) – గుర్తు U దిశ ధన X – అక్షానికి వ్యతిరేకము. గరిష్ఠ వడి X = 0 వద్ద ఉంటుంది .υ = ωA అనగా S.H.M లో స్థానభ్రంశం x = 0 అయితే కణం వడి గరిష్ఠము.

→ త్వరణము : S.H.M లో గల వస్తువు తాక్షణిక త్వరణము a(t) = \(\frac{\mathrm{d}}{\mathrm{dt}}\)
a(t) = \(\frac{d}{d t}\)[- Aω sin (ωt + Φ)] = -Aω² cos (ωt + Φ) = -ω². x(t)
గరిష్ఠ త్వరణము a = -ω²A ఇది X = A బిందువు వద్ద ఉంటుంది. అనగా స్థానభ్రంశము గరిష్ఠమైతే S.H.M లో వస్తువు త్వరణము గరిష్ఠము ఈ త్వరణము ఎల్లప్పుడూ మాధ్యమిక బిందువు వైపు ఉంటుంది.

→ సరళ హరాత్మక చలనం చేసే వస్తువు పై బలము : m ద్రవ్యరాశి గల S.H.M ఉన్న వస్తువు పై బలం కూడా కాలం ప్రమేయంగా మారుతుంది. F(t) = ma = – mω²x(t) లేదా F(t) = – K x(1) ఇందులో K = -mω² S.H.M లో గల వస్తువుపై పనిచేసే బలం ఎల్లప్పుడూ ఆ చలనంలో గల మాధ్యమిక బిందువు వైపు ఉంటుంది.

→ S.H.M లో గల వస్తువు శక్తి : సరళ హరాత్మక చలనం చేసే కణం యొక్క స్థితిజశక్తి, గతిజశక్తి విలువలు సున్న నుండి గరిష్ఠ విలువ మధ్య మారుతుంటాయి.
కణం గతిజశక్తి K.E = \(\frac{1}{2}\)mω² = \(\frac{1}{2}\)mω²A² sin² (ωt + Φ) = = K. A² sin² (ωt + Φ) లేదా KE = \(\frac{1}{2}\) mω² (A² – x²) = \(\frac{1}{2}\) K (A² – x²)
x = స్థానభ్రంశము; A – కంపన పరిమితి
S.H.M లో కణం స్థితి శక్తి : S.HM లో కణం స్థితిశక్తి U = \(\frac{1}{2}\) mω² A² cos (ωt + Φ)
U = P.E = \(\frac{1}{2}\)mω² A² cos² (ωt + Φ) = \(\frac{1}{2}\)KAx²
S.H.M లో గల వస్తువు లేదా కణం మొత్తం శక్తి E = \(\frac{1}{2}\)m² A² = \(\frac{1}{2}\)K A²

→ స్ప్రింగ్లలో డోలనాలు : స్ప్రింగ్లలో స్ప్రింగ్ పొడవుతో పోలిస్తే స్థానభ్రంశం తక్కువగా ఉన్నపుడు మాత్రమే హుక్ నియమం వర్తిస్తుంది.
స్ప్రింగ్ స్థిరాంకము

గుర్తు పునఃస్థాపక బలాలు వ్యతిరేక దిశలో పనిచేస్తాయి అని చెపుతుంది.
గట్టి స్ప్రింగ్లకు K విలువ ఎక్కువ, మెత్తటి స్ప్రింగ్లకు K విలువ తక్కువ.
స్ప్రింగ్లలో కోణీయ వేగం లేదా కోణీయ పౌనఃపున్యము ω = \(\sqrt{\frac{\mathrm{K}}{\mathrm{m}}}\)
స్ప్రింగ్ అవర్తన డోలనాకాలము T = \(\frac{2 \pi}{\omega}\) = 2π\(\sqrt{\frac{m}{K}}\)

→ లఘు లోలకము : సాగదీయడానికి వీలులేని, ద్రవ్యరాశి లేనటువంటి ఓ పొడవు గల దారానికి ఒక చిన్న లోహపు గుండును తగిలించి దృఢమైన ఆధారానికి కడితే దానిని లఘు లోలకము అంటారు.

→ కంపన పరిమితి తక్కువగా గల లఘు లోలకం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.

→ లోలకం పొడవు వెంబడి నికర వ్యాసార్ధియ బలం mg cos θ. ఇది దారంతో తన్యత T ని తుల్యం చేస్తుంది.

→ లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ T ను స్పర్శియ బలం ng sin θ ఇస్తుంది.

→ లోలకం డోలనాలకు కావలసిన టార్క్ τ = – L mg sin θ

→ లోలకం కోణీయ త్వరణము α = \(\frac{-\mathrm{mgL}}{\mathrm{I}}\)θ

→ లోలకం జడత్వ భ్రామకం I = mL²
లోలకం ఆవర్తన కాలము T = 2π\(\sqrt{\frac{1}{\mathrm{mgL}}}\) = 2π\(\sqrt{\frac{L}{g}}\)

→ సెకండ్ల లోలకం : డోలనావర్తన కాలం రెండు సెకనులు గల లోలకాన్ని సెకండ్ల లోలకం అంటారు.
సెకన్ల లోలకం ఆవర్తన కాలము T = 2 సెకనులు.

→ అవరుద్ధ దోలనాలు : అవరుద్ధ డోలనాలలో వ్యవస్థ శక్తి అవిచ్ఛిన్నంగా వ్యర్థమవుతుంది. అవరోధం అల్పంగా ఉండే సందర్భంలో డోలనాలు దాదాపు ఆవర్తన చలనాన్ని కలిగి ఉంటాయి.

గమనిక :
అవరోధబలం పరిమాణం యానకం స్వభావంపై ఆధారపడి ఉంటుంది. అవరోధబలం పెరిగితే కంపించే వ్యవస్థ తొందరగా శక్తిని కోల్పోయి వ్యవస్థ కంపనాలు లేదా డోలనాలు తొందరగా ఆగిపోతాయి.
అవరోధబలానికి గురైన వస్తువు ఆవృత చలనాన్ని m\(\frac{d^2 x}{d t^2}\) + b\(\frac{\mathrm{dx}}{\mathrm{dt}}\) + Kx = 0 అన్న సమీకరణంతో సూచిస్తారు.
ఇటువంటి వ్యవస్థ కోణీయత = \(\sqrt{\frac{K}{m}-\frac{b^2}{4 m^2}}\)
ఇందులో K = స్ప్రింగ్ స్థిరాంకము, b = అవరోధ స్థిరాంకము

→ స్వేచ్ఛా కంపనాలు లేదా స్వేచ్ఛా డోలనాలు : వస్తువును మాధ్యమిక స్థానం నుంచి స్థానభ్రంశం చెందించి వదలివేస్తే ఆ వస్తువు చేసే కంపనాలను స్వేచ్ఛా కంపనాలు అంటారు.

→ బలాత్కృత లేదా చోదిత డోలనాలు : ఏదైనా వ్యవస్థ తన సహజ పౌనఃపున్యం వద్ద కాక బాహ్య కారకం పౌనఃపున్యంతో చలిస్తే అటువంటి డోలనాలను బలాత్కృత డోలనాలు అంటారు. బలాత్కృత డోలనాలన్నీ అవరుద్ధ డోలనాలే.

→ అనునాదము : ఏదైనా వస్తువుపై చోదకబలం పౌనఃపున్యము వస్తువు సహజ పౌనఃపున్యానికి సమానమైనపుడు డోలకం కంపన పరిమితిలో పెరుగుదల కలిగించే దృగ్విషయాన్ని అనునాదము అంటారు.
గమనిక : వస్తువు సహజ పౌనఃపున్యం చోదకబలం పౌనఃపున్యానికి చాలా దగ్గరగా ఉంటే కూడా అనునాదం సంభవించవచ్చు. ఈ కారణం వల్ల భూకంపం వచ్చినపుడు భూప్రకంపనల పౌనఃపున్యానికి సమీప సహజ పౌనఃపున్యం గల భవనాలు తొందరగా నేల కూలతాయి.

→ సరళహరాత్మక చలనములో ఉన్న వస్తువు స్థానభ్రంశ సమీకరణములు
Y = A sin (ωt ± Φ) లేదా Y = A cos (ωt ± Φ)

→ స.హ.చ. లో ఉన్న వస్తువు వేగము : V = \(\frac{\mathrm{dy}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\)(A cos ωt)
∴ V = -Aω sin ωt
లేదా V = \(\sqrt{A^2-Y^2}\); గరిష్ఠవేగము V_{గరిష్ఠ} = Aω

→ స.హ.చ. లో ఉన్న వస్తువు త్వరణము :
a = -ω² A sin ωt లేదా a = -ω²Y (ఇక్కడడ Y = A sin ωt)
(– ఋణగుర్తు త్వరణము మరియు స్థానభ్రంశములు వ్యతిరేకదిశలలో ఉండుటను సూచించును.) గరిష్ఠ త్వరణము a_max = ω²A.

→ స.హ.చ.లో ఉన్న వస్తువు కోణీయ వేగము ‘ω’ : స.హ.చ.లో త్వరణము ∝ స్థానభ్రంశము a ∝ – Y లేదా a = -ω²y ( ఋణగుర్తు a మరియు y లు వ్యతిరేకదిశలలో ఉండుటను సూచించును.)

ఇందులో ω స.హ.చ.లో ఉన్న వస్తువు కోణీయ వేగము.

→ స.హ.చ.లో ఉన్న వస్తువు ఆవర్తన కాలము: ఒక పూర్తి కంపనమునకు పట్టుకాలమును దాని ఆవర్తనకాలము

పౌనఃపున్యము υ = \(\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{a}{Y}}\) లేదా υ = \(\frac{\omega}{2 \pi}\) లేదా ω = 2πυ

→ స్ప్రింగ్లు :
1) స్ప్రింగ్ స్థిరాంకము

2) వస్తువు త్వరణము a = \(\frac{K}{m}\). Y (m స్ప్రింగ్ కు వ్రేలాడదీసిన దిమ్మ ద్రవ్యరాశి)
3) దిమ్మ యొక్క కోణీయ వేగము ω = \(\sqrt{\frac{K}{m}}\) [∵ a = -ω²Y కాని స్ప్రింగ్లో a = \(\frac{K}{m}\). Y ∴ ω = \(\sqrt{\frac{K}{m}}\)
4) ఆవర్తన కాలము T = \(\frac{2 n}{\omega}=2 \pi \sqrt{\frac{m}{K}}\)
5) T₁ = \(2 \pi \frac{\sqrt{\left(m+\frac{m_1}{3}\right)}}{K}\) (నిజస్ప్రింగ్లందు)
6) కంపన పౌనఃపున్యము n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{m}}\), నిజ స్ప్రింగ్లందు n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{\left(m+\frac{m_1}{3}\right)}}\)
7) ఏ స్థానము వద్దనైనా స్థితిశక్తి P.E. = \(\frac{1}{2}\)Kx² ణి మరియు గతిశక్తి K.E. = \(\frac{1}{2}\)K(A² – x²)
8) మొత్తము శక్తి T.E. = స్థితిశక్తి + గతిశక్తి = \(\frac{1}{2}\)KA²
9) k స్థిరాంకము గల స్ప్రింగ్ను ‘n’ సమానభాగములుగా కత్తిరించిన ఒక్కొక్క భాగము స్ప్రింగ్ స్థిరాంకము k¹ = nk n = భాగముల సంఖ్య మరియు k = మొదటి స్ప్రింగ్ స్థిరాంకము

→ స.హ.చ.లో ఉన్న వస్తువు యొక్క శక్తి :

• ఏ బిందువు వద్దనైనా స్థితిశక్తి P.E. = \(\frac{1}{2}\)mω²x²; PE_max = \(\frac{1}{2}\)mω²A²
• ఏ బిందువు వద్దనైనా K.E. = \(\frac{1}{2}\)mω²(A² – x²); గరిష్ట గతిశక్తి = \(\frac{1}{2}\)mω²A² (x = ‘0’ వద్ద)
• పౌనఃపున్యము ‘U’ లో సమీకరణాలు వ్రాసినపుడు
  స్థితిశక్తి P.E. = 2mπ²v²x² గతిశక్తి K.E. = 2mπ²v² (A² – x²)
  మొత్తము శక్తి T. E. = P.E. + K.E. = 2mπ²v²A²

→ లఘు లోలకము:

• లఘులోలకములో భారము యొక్క అంశము mg sin θ. ఇది డోలనాలు చేయుటకు కావలసిన బలమును సమకూర్చును. F = mg.sin θ. లోలకం పై టార్క్ τ = L. mg sin θ,
• డోలనావర్తన కాలము T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{mgL}}}\) = 2π\(\sqrt{\frac{l}{g}}\) లేదా g = 4π²\(\frac{l}{\mathrm{~T}^2}\)
• లోలకము M.O.I = I = mL² ; కోణీయ త్వరణము α = –\(\frac{\mathrm{mgL}}{\mathrm{I}}\).θ
• లిఫ్ట్ ‘a’ త్వరణముతో పైకి వెళుతున్న దానిలోని లోలకము ఆవర్తనకాలము తగ్గును T = 2π\(\sqrt{\frac{l}{g+a}}\)
• లఘులోలకమును ‘a’ త్వరణముతో క్రిందికి వెళ్ళుతున్న లిఫ్ట్ లో ఉంచిన దాని ఆవర్తనకాలము పెరుగును
  T = 2π\(\sqrt{\frac{l}{g-a}}\)
• సెకనుల లోలకము డోలనావర్తన కాలము T = 2 సె.; పొడవు = 100 సెం.మీ. = 1మీ. (సుమారుగా)

Telangana TSBIE TS Inter 1st Year Hindi Study Material उपवाचक 6th Lesson सफलता की कुंजी : टीम वर्क Textbook Questions and Answers.

TS Inter 1st Year Hindi उपवाचक 6th Lesson सफलता की कुंजी : टीम वर्क

अभ्यास

अ. निम्न लिखित प्रश्नों के उत्तर तीन चार वाक्यों में दीजिए ।

प्रश्न 1.
ए. पी. जे. अब्दुल कलाम का संक्षिप्त परिचय लिखिए ।
उत्तर:
ए.पी.जे अब्दुल कलाम को भारत के ग्यारहवें राष्ट्रपति के तौर पर अधिक जाना जाता है, जो साल 2002 से लेकर साल 2007 तक भारत के राष्ट्रपति के पद पर रहे। इस से पहले कलाम विज्ञान क्षेत्र में सक्रिय थे । कलाम ने तमिलनाडु के रामेश्वरम में जन्म लिया और वही पर उनका पालन पोषण भी हुआ ।

शिक्षा के लिहाज से उन्होंने अन्तरिक्ष विज्ञान और भौतिक विज्ञान की पढ़ाई की । अपने करियर के अगले करीब चालीस सालों तक, वह भारतीय रक्षा अनुसन्धान और विकास संगठन यानि संक्षेप में कहें तो डी.आर.डी.ओ. और भारतीय अन्तरिक्ष अनुसन्धान संगठन यानि इसरो में वैज्ञानिक और इंजिनियर के पद पर रहे । इन्हें लोगों के दिल में बहुत सम्मान प्राप्त है ।

प्रश्न 2.
“सफलता अकेले आगे बढने में नहीं है, बल्कि दूसरों को भी साथ लेकर बढने में है ।” इस कथन का समर्थन करते हुए अपने विचार लिखिए ?
उत्तर:
किसी भी संस्था के परिणामों को बेहतर बनाने केलिए टीम वर्क की अहमियत को समझना बेहद जरुरी है। संकटपूर्ण स्थितियों में टीम भावना से किया काम सफलता को सुनिश्चित करता है । यह वह स्थिति होती है, जिसमें सभी की जीत होती है । पारस्परिक मधुर संबंध टीम की सफलता केलिए जरुरी होते है । सदस्यों के बीच भरोसा मजबूत होना चाहिए। टीम वर्क से कोई भी काम कम वक्त में पूरा हो जाता है ।

जब कई लोग किसी एक समस्या का समाधान ढूंढने का कोशिश करते है तो बेहतर विचार सामने आते हैं। टीम वर्क में गलती की संभावनाएं कम होती हैं, क्यों कि एक व्यक्ति का काम दूसरे से जुड़ा होता है, इसलिए प्रत्येक स्तर पर काम की जांच होती रहती है। अच्छा टीम वर्क किसी संगठन को कम समय में बेहतर नतीचे तक पहुंचाता है । सफलता एक व्यक्ति का न होकर समस्त व्यक्तियों के होते तो उसका मजा ही और है । हम उस आनंद बातों में नहीं बता सकते ।

सफलता की कुंजी : टीम वर्क Summary in Hindi

लेखक परिचय

‘भारतरत्न’ अबुल पकीर जैनुलाबदीन अब्दुल कलाम का जन्म सन् 1931 में धनुषकोडी, रामेश्वरम, तमिलनाडु राज्य में एक मध्यम वर्गीय मुस्लिम परिवार में हुआ था । कलाम सात भाई – बहनों में से एक थे । उनके पिता का नाम जैनुलाबश्रान और माता का नाम आशियाम्मा था । कलाम ने तिरुचीरापल्ली के सेंट जोसेफ कॉलेज से अपनी बारहवी की परीक्षा उत्तीर्ण की। तत्पश्चात वें एयरोनॉटीकल इंजीनियरिंग की पढ़ाई के लिए मद्रास इंस्टिटयूट ऑफ टेक्नोलॉजी आ गए ।

कलाम ने सन् 1958 में रक्षा अनुसंधान और विकास संगठन (डीआरडीओ) के साथ अपनी नौकरी शुरु की। तत्पश्चात वें भारतीय अंतरिक्ष अनुसंधान संगठन (इसरो) में स्थानांतरित हो गए। वहां उन्होंने एसएलवी – 3 ( उपग्रह प्रक्षेपण वाहन – 3) की मदद से रोहिणी – 1 उपग्रह को निम्न- पृथ्वी कक्षा में स्थापित किया । उनके नेतृत्व में कम दूरी और मध्यम दूरी की बैलेस्टिक मिसाइल पृथ्वी और अग्नि भारत के मिसाइल शस्त्रागार में शामिल हुई। सन् 1998 में कलाम ने भारत के पोखरण परमाणु परीक्षण में एक निर्णायक, संगठनात्मक, तकनीकी और राजनीतिक भूमिका निभाई ।

स्वयं एक गरीब परीवार से आये थे इसलिए सुनहरे भविष्य निर्माण मे शिक्षा की शक्ति के योगदान को अच्छी तरह से जानते थे। कलाम को बच्चों से विशेष लगाव था ।

कलाम को वैसे तो अनगिनत पुरस्कार व सम्मान मिले, किंतु भारतरत्न का सम्मान उनके लिए विशेष था । उन्हें जब कभी समय मिलता लेखन कार्य में जुट जाते । ‘इग्नाइटेड माइंड्स’, ‘इंडिया माय ड्रीम’ उनकी चिंतनपरक रपनाएँ थी, वहीं दूसरी ओर ‘विंग्स ऑफ फायर’ और ‘साइंटिस्ट टू प्रेसिडेंट’ उनकी आत्मकथात्मक पुस्तकें हैं । इन पुस्तकों को पढने के पश्चात पता चलता है कि हौंसला हो तो कुछ भी असंभव नहीं है । इसका उदाहरण स्वयं अब्दुल कलाम हैं जो समाचार पत्र बेचने से लेकर राष्ट्रपति पद तक पहुँचे । महान व्यक्तित्व के धनी कलाम जी का 27 जुलाई 2015 को शिलांग में निधन हो गया ।

प्रस्तुत अंश ए. पी. जी. अब्दुल कलाम की आत्मकथा ‘विंग्स’ ऑफ फायर से लिया गया हैं । इसका हिंदी अनुवाद श्री अरुण तिवारी ने ‘अग्नि की उड़ान’ शीर्षक से किया है। इसमें कलाम जी सामूहिक कार्य के महत्व का विश्लेषण करते हैं ।

‘भारतरत्न’ अबुल पकीर जैनुलाबदीन अब्दुल कलाम का जन्म सन् 1931 में तलिलनाडु में एक मध्यम वर्गीय मुस्लिम परिवार में हुआ था । आप महान वैज्ञानिक थे । सन् 1998 में कलाम ने भारत के पोखरण परमाणु परीक्षण में निर्णायक, संगठनात्मक, तकनीकी और राजनीतिक भूमिका निभाई ।

सारांश

भारत में आज भी ज्यादातर लागों के लिए टेक्नोलॉजी शब्द का अर्थ धुआँ उगलते स्टील कारखानों या झनझनाती मशीनोंवाले कारखाने से हैं । टेक्नोलॉजी शब्द की जो सही – सही अवधारणा है। वह उससे बिलकुल अलग है। टेक्नालॉजी में तकनोकियाँ शामिल होती हैं – ठीक वैसे ही जैसे मशीने, जिन्हें इस्तेमाल करना जरुरी हो भी सकता है और नहीं भी । तकनी हमें यह कभी नहीं भूलवा चाहिए कि टेक्नोलॉजी खुद ही अपनी पोषक होती है। दरअसल टेक्नोलॉजी विकास के तीन चरण मुख्य होते हैं। जो आपस में एक दुसरे से जुड़े हैं। पहला चरण सृजन का होता है। जिसमें उपयुक्त विचार था। फिर यह अपने व्यावहारिक प्रयोग से वास्तविक में इसका अंत हो जाता है। यह प्रक्रिया तब पूरी हो जाती है जब यह टेक्नोलॉजी नए – नए सृजनात्मक विचारों को पैदा करती है ।

टेक्नोलॉजी विज्ञान से भिन्न एक सामुहिक गतिविधि है । यह किसी एक व्यक्ति की बुध्दि या समझ पर आधारित नहीं होती बल्कि कई व्यक्तियों की आपसी बोध्दिक प्रतिभा पर आधारित होती है । एकीकृत गाइडेड मिसाइल विकास कार्यक्रम (आई.जी. एम. डी. पी) Integrated Guided Missile Development Programme की सबसे बड़ी सफलता का तथ्य यह नहीं है कि देश ने रिकॉर्ड समय के भीतर पांच मिसाइल प्रणालियाँ विकसित कर लेने की क्षमता हासिल कर ली, बल्कि तथ्य यह है कि इसके माध्यम से वैज्ञानिकों एवं इंजीनियरों की कुछ सर्वश्रेष्ठ टीमें तैयार हो गई । अगर कोई मुझसे भारतीय रॉकेट विज्ञान में मेरी व्यक्तिगत उपलब्दि के बारे में पूछता है तो मैं बताऊँगा कि मैं ने नौजवानों की टीमों के लिए एक ऐसा माहोल तैयार किया जिसमें वे अपने दिल और आत्मा का संघर्ष अपने मिशन में लगा सकें ।

अपने निर्माण के दौर में टीमें बच्चों की तरह ही होती हैं । वे एकदम उत्तेजनशील, ओजस्विता, उत्साह एवा उत्सुक्ता से भरपूर और अपने को विशिष्ट दिखाने की इच्छा लिये होती हैं। अपनी टीमों को हमेशा ऐसा माहौल देना सुनिश्चित किया जिसमें वे कुछ नया कर सकें और जोखिम उठा सकें ।

एस.एल.वी – 3 परियोजना और बाद में एकीकृत गाइडेड मिसाइल विकास कार्यक्रम (आइ.जी.एम.डी.पी.) Integrated Guided Missile Development Programme (I.G.M.D.P) के दौरा न हमने पहले परियोजना टीमें बनानी शुरु कीं तो इन टीमों में काम कर रहे लोगों ने अपने पंक्ति में पाया । चूँकि इन टीमों में एक तरह से मनोवैज्ञानिक निवेश किया गया था, इसलिए वे बहुत ही सुस्पष्ट और अति संवेदनशील बन गई । सामूहिक यश लेने के लिए ने एक – दूसरे से व्यक्तिगत रुप. से विषमानुपात में काम करने की उम्मीद करते ।

जब आप एक परियोजना टीम के रूप में काम करते हैं तो आपको सफलता की कसौटी के लिए मिली जुली दृष्टि विकसित करनी होगी। हर टीम के काम में हमेशा बहुविधि और विरोधाव्यासी उम्मीदें बनी रहती हैं। अच्छी परियोजना टीमें उस मूल तत्व और उन मुख्य लोगों को फौरन पहचात लेने में समर्थ होती हैं, जिनसे सफलता की कसौटी तय कर ली जानी चाहिए। टीम के नेता की भूमिका का एक निर्णायक पक्ष ऐसे मुख्य लोगों से उनकी जरुरतों के बारे में बातचीत कर लेने तथा उनको प्रभावित करने का होता है और टीम नेता को यह भी सुनिश्चित करना होता है कि जैसे जैसे परिस्थियाँ विकसित हों या बदलें, तत्व पर नज़र जमी रहे, मुख्य लोगों और अन्य लोगों के बीच संवाद नियमित रुप से जारी रहे ।

टीम ने स्वयं ही आंतरिक सफलता की कसौटी विकसित की थी स्वयं ही अपने स्पष्ट मानदंड उम्मीदें और लक्ष्य निर्धारित किए थे ।

किस भी टीम में सफलता की कसौटी तक पहुँचने की प्रक्रिया बहुत ही जटिल एवं कौशलयुक्त होती है, क्यों कि एक ही छत के नीचे काफी कुछ घटित होता है ।

दुसरे स्तर पर परियोजना नेता को टीमों एवं कार्य केंद्रों के बीच संबंध को बढ़ावा देने तथा विकसित करने का काम करना चाहिए । दोनों ही पक्षों को अपनी आपसी समझ के बारे में बहुत ही स्पष्ट होना चाहिए और दोनों को ही परियोजना में बराबर का पूर्णरूप से साझेदार होना चाहिए ।

अब्राहम मैसलो पहले व्यक्ति थे, जिन्होंने स्व कार्यान्वयत के नए मनोविज्ञान को अवधारणा के स्तर पर बहस के लिए प्रस्तुत किया । युरोप में रुडोल्फ स्टेनर और रेग रेवांस ने इस अवधारणा को व्यक्तिगत शिक्ष की प्रणाली तभा संगठनात्मक नवीनीकरण के रूप में विकसित किया ।

डाँ. होमी जहाँगीर भाभा और प्रा. विक्रम साराभाई ने परमाणु उर्जा पर आधारित उच्च टेक्नोलॉजी एवं अंतरिक्ष कार्यक्रमों की शुरुआत की और साथ ही संपूर्णता व प्रवाह के प्राकृतिक नियमों पर स्पष्ट जोर दिया । डॉ. वर्गीज कुरियन ने सहकारिता आंदोलन को सशक्त बनाकर डेयरी उद्योग में एक नई क्रांति ला दी। प्रो. सतीश धवन ने अंतरिक्ष शोध में मिरान प्रबंधन की अवधारणाओं को विकसित किया ।

तकनीकी प्रबंधन वृक्ष तभी फैलता है जब सफल रुप में जरुरतों, नवीनीकरण, अंतर्निर्भरता और प्राकृतिक प्रवाह का स्व कार्यान्वयन होता है । विकास के प्रतिरुप ही विकास की प्रक्रिया के लक्षण होते हैं । जिनका मतलब यह होता है कि चीजें धीमे परिवर्तन और अचानक रुपांतरण के मिले-जुले रूप में चलती हैं।

हर रुपांतरण या तो एक नई छलंग को जन्म देता है जिससे सोच, ज्ञान अभवा क्षमता के एक और विकसित पटल का प्रादुर्भाव होता है या फिर पुराने किसी पटल पर जा गिरता है । अच्छा प्रबंध ऊपर उठाने तभा पीछे गिराने की प्रक्रिया को इस प्रकार अनवरत जारी रखता है कि ऊपर उठने की आवृत्ति और उसका तान्विक आकार पीछे गिरने की अपरिहार्यता को सदा न सिर्फ संभाले रहे बल्कि निरस्त भी करता चले ।

विशेषताएँ :

1. आधुनिक भारत के उन विज्ञान प्रतिष्ठानों की सफलताओं एवं असफलताओं के बारे में बताया है, जो तकनीकी मोरचे पर अपने को स्थापित करने केलिए संघर्ष कर रहे हैं ।
2. जितना भी परियोजनाएँ भारत के वैज्ञानिक और इंजनीयर्स ने किया उन सब की सफलता का मंत्र एक ही है – टीमवर्क.
3. टीम वर्क सफल होने केलिए बहुत जरुरी है । आज हम चाहे परिवार में देखे, किसी संस्था में (Organisation) देखें या समाज में देखे कही न कही हम एक टीम के रूप में काम कर रहे है । लेकिन सबकी सफलता एक अच्छी और सफल टीम पर निर्भर करती है ।
4. टीम वर्क काम करनेवाले लोग जबरदस्त लक्ष्य प्राप्त कर सकते है ।

सफलता की कुंजी : टीम वर्क Summary in Telugu

సారాంశము

ప్రస్తుత అంశం ‘सफलता की कुंजी : टीम वर्क’ అబ్దుల్ కలాం యొక్క ఆత్మకథ ‘వింగ్స్ ఆఫ్’ ఫయర్’ నుండి తీసుకోబడినది. దీనిని అరుణ తివారి గారు హిందీలో ‘అగ్నికీ ఉడాన్’ అను పేరుతో అనువదించారు. ఇందులో కలాంగారు సామూహిక కార్యం యొక్క గొప్పతనాన్ని గూర్చి వివరించారు.

ఏ వ్యక్తి అయిన ఏ రంగంలోనైనా సామూహికంగా కలిసి ఉంటే ఎంత కష్టతరమైన పనిని అయిన తేలికగా చేయవచ్చు అని వివరించారు. అబ్దుల్ కలాం గారు మనకు కొన్ని విషయాలను తెలియచేశారు. భారతదేశంలో ఇప్పటికి చాలా మందికి టెక్నాలజీ అనే శబ్దం యొక్క అర్థం తెలియదు.

వారు టెక్నాలజీ అంటే ఫ్యాక్టరీల నుండి వచ్చే పొగ లేక పెద్ద పెద్ద శబ్దాలు వచ్చే మెషీనులు, కర్మాగారాలు అని అంటారు. టెక్నాలజీ శబ్దం అర్థం ఎన్నో రకాలైన టెక్నిక్స్ కూడుకుని ఉండటం. అనగా రసాయన పదార్థాల వాడకం, రోగులకు చికిత్స చేయడం, చరిత్ర చదవడం, యుద్ధ సమయంలో ఎలా ఉండటం, ఎలా పోరాడటం, ఎలా తప్పించుకోవడం వంటి చాలా విషయాలు ఉంటాయి.

టెక్నాలజీకి తనకంటూ ప్రత్యేకమైన వస్త్రధారణ ఉండదు. టెక్నాలజీకి ముఖ్యంగా కొన్ని అభివృద్ధి పద్ధతులు ఉన్నాయి. ముఖ్యంగా 3 పద్ధతులు కలవు. అవి ఒక దానితో ఒకటి ముడిపడి ఉంటాయి. మొదటిది Creation క్రియేషన్ క్రియేటివిటీ అనేది ఒక వ్యక్తితో కాక ఒక సామూహిక కార్యంవలె పనిచేస్తే ఆ క్రియేషన్ చాలా అద్భుతంగా బయటకు వస్తుంది.

ప్రజల ఆదరణ కూడా పొందుతుంది. ఒక వ్యక్తి అభివృద్ధి వెనుక ఏ రంగంలోనైన అనేక సమూహాల పని దాగి ఉంటుంది. ఉదాహరణకు I.G.M.D.P. మిసైల్ గూర్చి తెలుసుకుందాం. ఈ కార్యక్రమం అభివృద్ధి వెనుక ఎంతో మంది శాస్త్రవేత్తలు మరియు ఇంజనీర్లు ఉన్నారు. వారందరి సహాయ సహకారాలతోనే ఈ మిసైల్ వృద్ధి చెందింది.

ఎవరైన భారతీయ రాకెట్ విజ్ఞానం గురించి నన్ను ప్రశ్నిస్తే ఒకే సమాధానం చెబుతాను. నాకు తోడుగా, నా వెంట ఎంతో మంది నవయువకులు ఉన్నారు. వారి సంఘీభావం, సమిష్టి కృషి వలన నేను గొప్పవాడిని కాగలిగాను. నాతో పనిచేసే నవయువకులను టీమ్స్ గా చేసి వారి మనసుకు నచ్చిన విధంగా వారి అభిప్రాయాలను తెలియచేయమని కోరతాను. వారు సంతోషంతో వారిలోని తెలివితేటలను, ఉత్సాహాన్ని, ఉత్తేజాన్ని పూర్తిగా పనిపై నిమగ్నం చేసి గొప్ప విషయాలు సృష్టిస్తారు. ఏ టీక్కైన ఎటువంటి వాతావరణం కల్పించాలంటే వారు ఏ కొత్త విషయాన్నైనా భయపడకుండా చెప్పగలగాలి.

S.L.V – 3 ప్రాజెక్టు మరియు తరువాత I.G.M.D.P ప్రాజెక్టులలో మా అభివృద్ధి, సఫలతకు కారణం టీమ్ వర్క్ ప్రతి ప్రాజెక్టులో ప్రతి శాస్త్రవేత్త తన అభిప్రాయాలు టీమ్ లోని ప్రతి ఒక్కరితో చర్చించేవారు. అందరి ఆమోదం తరువాత కార్యాచరణ చేసేవారు. ప్రతి టీమ్కి ఒక నాయకుడు ఉండేవారు తన టీమ్ పనిచేసే వ్యక్తుల అభిప్రాయాలు తప్పనిసరిగా తెలుసుకునేవారు. మీరు కూడా ఏ పని చేసిన కొన్ని టీమ్స్ కొందరిని విభజించి పనిచేసి చూడండి. ఆ టీమ్స్్క నాయకుడిని ఇచ్చి వారి ద్వారా పనిచేయిస్తే ఏ పని అయినా త్వరగా అయిపోతుంది. ప్రతి టీమ్ వారికి కొన్ని ఆశయాలు, లక్ష్యాలు, అభిప్రాయాలు ఉంటాయి.

టీమ్ సఫలత రావడం లేదు అంటే ఆ టీమ్ లీడరు వ్యక్తులను పరిశీ లించాలి. కొన్ని ప్రక్రియలలో కొందరు కష్టపడతారు. వ్యక్తులకు వ్యక్తులకు మధ్య సంఘీభావం కల్పించాలి. అబ్రహామ్ మైసలో, యూరప్ రూడోల్ఫ్ సంఘటనాత్మక గూర్చి గొప్పగా తెలియచేశారు. నీ విజయానికి అడ్డుకునేది నీలోని ప్రతికూడా ఆలోచనలే.

క్రింద పడ్డామని ప్రయత్నం ఆపితే చేసే పనిలో ఎన్నటికి విజయం సాధించలేం, నైపుణ్యం ఒక నిరంతర సాధనా ఫలితం అది ఆకస్మాత్తుగా వచ్చేది కాదు. నైపుణ్యం కలిగిన వ్యక్తులు సమూహంగా ఏర్పడి చేసే పని ఒక అద్భుత కార్యంగా చరిత్రలో నిలిచిపోతుంది.

“నీ ధ్యేయంలో నువ్వు నెగ్గాలంటే నీకు ఏకాగ్ర చిత్తంతో కూడిన అంకిత భావం కావాలి”.