TS Inter 1st Year Maths 1B Solutions Chapter 10 Applications of Derivatives Ex 10(g)

Students must practice these TS Intermediate Maths 1B SoIutons Chapter 10 Applications of Derivatives Ex 10(g) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(g)

I.
Question 1.
(i) Without using the derivative, show that the function f(x) = 3x + 7 is strictly increasing on ℛ . (V.S.A.Q.)
Answer:
Let x₁ < x₂ ∈ℛ with x₁ < x₂
Then 3x₁ < 3x₁ ;
Adding 7 on both sides,
7 + 3x₁ < 7 + 3x₂ ⇒ f (x₁) < f(x₂)
x₁ < x₂ ⇒ f (x₁) < f(x₂) v x₁, x₂ ∈ ℛ
Hence the given function is strictly increasing on ℛ

(ii) The function f(x) = \(\left(\frac{1}{2}\right)^x\) is strictly decreasing on ℛ.
Answer:
f(x) = \(\left(\frac{1}{2}\right)^x\)
Let x₁, x₂ ∈ ℛ such that x₁ < x₂
⇒ \(\left(\frac{1}{2}\right)^{x_1}>\left(\frac{1}{2}\right)^{x_2}\)
⇒ f(x₁) > f(x₂)
f(x) is strictly decreasing on ℛ.

(iii) The function f(x) = e^3x is strictly increasing on ℛ.
Answer:
f(x) = e^3x
Let x₁, x₂ ∈ ℛ such that x₁ < x₂
We have that if a > b then e^a > e^b
e^3x₁ < e^3x₁ ⇒ f(x₁) < f(x₂)
So the function f is strictly increasing on ℛ.

Question 2.
Show that the function f(x) = sin x defined on ℛ is neither increasing nor decreasing on (0, π). (V.S.A.Q.)
Answer:
Given f(x) = sin x
since 0 < x < π and for 0 < x ⇒ f(0) < f(x)
⇒ sin 0 < sin x => 0 < sin x (1)
for x < π ⇒ f(x) < f(π)
⇒ sin x < sin π ⇒ 0 > sin x (2)
From (1) and (2) f(x) is neither increasing nor decreasing.

II.
Question 1.
Find the interval in which the following functions are stjpctly increasing strictIy decreasing. 1 (S.A.Q.)
(i) x² + 2x – 5
Answer:
Let f(x) = x² + 2x – 5
Then f'(x) = 2x + 2
f(x) is increasing if f'(x) > 0
⇒ 2x + 2 > 0
⇒ x + 1 > 0
⇒ x > – 1
f (x) increases in (- 1, ∞)
f (x) is decreasing if f’ (x) < 0
⇒ 2x + 2 < 0
⇒ x + 1 < 0
⇒ x < – 1
f is decreasing in (- ∞, -1)

(ii) 6 – 9x – x²
Answer:
Let f(x) = 6 – 9x – x²
Then f’ (x) = – 9 – 2x
f(x) is increasing if f’ (x) > 0
⇒ – 9 – 2x > 0 ⇒ 9 + 2x < 0
⇒ x < \(\frac{-9}{2}\)
∴ f(x) is increasing in (-∞, \(\frac{-9}{2}\))
f(x) is decreasing if f'(x) < 0 ⇒ 9 + 2x > 0
⇒ 2x > – 9
⇒ x > \(\frac{-9}{2}\)
∴ f is decreasing in (\(\frac{-9}{2}\), ∞)

(iii) (x + 1)³(x – 1)³
Answer:
Let f(x) = (x + 1)³ (x – 1)³ = (x² – 1)³
= x⁶ – 1 – 3x⁴ 3x²
∴ f'(x) = 6x⁵ – 12x³ + 6x
= 6x(x⁴ – 2x² + 1)
∴ f'(x) = 6x⁵ – 12x³ + 6x
= 6x(x⁴ – 2x² + 1)
= 6x(x² – 1)²
f(x) increases for f'(x) > 0
⇒ 6x(x² – 1) > 0
⇒ x² – 1 > 0, x > 0
∴ f is increasing in (0, 1) ∪ (1, ∞)
f(x) decreases for f'(x) < 0
∴ f is decreasing in (-∞, – 1) ∪ (-1, 0)

(iv) x³(x – 2)²
Answer:
Let f(x) = x³(x – 2)²
Then f(x) = x³. 2 (x – 2) + (x – 2)² 3x²
= x² (x – 2) [2x + 3 (x – 2)]
= x²(x – 2) (5x – 6) ∀ x ∈ R, x² > 0
f is increasing, f'(x) > 0
⇒ x² (x – 2) (5x – 6) > 0
⇒ x ∈(-∞, \(\frac{6}{5}\)) ∪ (2, ∞)
f is decreasing if f'(x) < 0
⇒ x²(x – 2)(5x – 6) < 0
⇒ x ∈ (\(\frac{6}{5}\), 2)

(v) xe^x
Answer:
Let f(x) = xe^x
Then f'(x) = xe^x + e^x = e^x(x + 1) ∀ x ∈ ℛ, e^x > 0
f'(x) > 0 ⇒ e^x(x + 1) > 0
⇒ x + 1 > 0 ⇒ x < – 1
Hence f is increasing in (-1, ∞)
Also f'(x) < 0 ⇒ e^x(1 + x) < 0
⇒ 1 + x < 0 ⇒ x < -1
Hence f is decreasing in (-∞, -1)

(vi) \(\sqrt{25-4 x^2}\)
Answer:
Suppose f(x) = \(\sqrt{25-4 x^2}\)
If f is real then 25 – 4x² ≥ 0
⇒ -(4x² – 25) ≥ 0
⇒ -(2x + 5)(2x – 5) ≥ 0
∴ x ∈ \(\left(\frac{-5}{2}, \frac{5}{2}\right)\)
Domain of f = \(\left(\frac{-5}{2}, \frac{5}{2}\right)\)
i.e., x < 0
f(x) is increasing when x ∈ (\(-\frac{5}{2}\), 0)
f(x) is decreasing when f'(x) < 0
⇒ \(-\frac{4 \mathrm{x}}{\sqrt{25-4 \mathrm{x}^2}}\) < 0 ∴ x > 0 and f(x) is decreasing when x ∈ (0, \(\frac{5}{2}\))

(vii) log (log x), x > 1
Answer:
f(x) = log (log x)
f'(x) = \(\frac{1}{x \log x}\)
f(x) is increasing when f ’(x) > 0
⇒ \(\frac{1}{x \log x}\) > 0 ⇒ x log x > 0
When x > 0, we have x is real and if x > 0 then log x is real.
log x > 0 = log 1 ⇒ x > 1
Function f is increasing in (1, ∞)
If f’ (x) < 0, then f is decreasing
⇒ x log x < 0 ⇒ log x > 0 and x < 1
∴ Function f is decreasing in (0, 1)

(viii) x³ + 3x² – 6x + 12
Answer:
f(x) = x³ + 3x² – 6x + 12
f’ (x) = 3x² + 6x – 6 = 3 (x² + 2x – 2)
= 3 [(x + 1)² – 3]
= 3 [ (x + 1) + √3 ] [ (x + 1) – √3 ]
= 3[x + (1 + √3)][x + (1 – √3)]
If f'(x) > 0 then
[x + (1+ √3)][x + (1 – √3)]>0
⇒ x ∈ [(-∞ , -1 – √3 ) u (√3 – 1 > ∞) ]
Hence f is increasing in above interval.
f'(x) < 0 ⇒ [x + (1 + √3)] [x + (1 – √3)] < 0
⇒ x ∈ [(-1 – √3), (-1 + √3)] f is decreasing in above interval.

Question 2.
Show that f(x) = cos²x is strictly increasing on (0, \(\frac{\pi}{2}\)). (S.A.Q)
Answer:
f(x) = cos2x
f'(x) = 2cosx (- sin x) = – sin 2x
Since 0 < x < \(\frac{\pi}{2}\)
⇒ 0 < 2x < π Since sin x > 0 between 0 and π
We have f'(x) is negative.
f’ (x) < 0 ⇒ f(x) is strictly decreasing.

Question 3.
Show that x + \(\frac{1}{x}\) is increasing on [1, ∞). (S.A.Q.)
Answer:

∴ f'(x) > 0 and f(x) is increasing.

Question 4.
Show that \(\frac{\mathbf{x}}{1+x}\) < log(1 + x) < x ∀ x > 0
Answer:

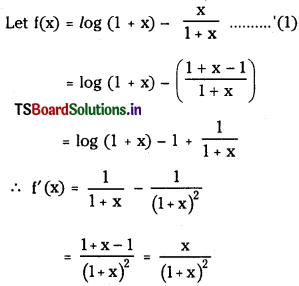
If x > 0 then f’ (x) > 0 When x > 0 f is increasing
⇒ f(x) > f(0)
f(0) = log 1 – 0 = log 1 = 0
f(x) > 0 ⇒ fog (1 + x) > \(\frac{x}{1+x}\)
Similarly suppose g(x) = x – log (1 + x) ………..(3)
g'(x) = 1 – \(\frac{1}{1+x}=\frac{x}{(1+x)}\) > 0
∴ When x > 0, g(x) is also increasing.
∴ g(x) > g(0) ⇒ g(x) > 0
⇒ x – log (1 + x) > 0 (4)
⇒ x > log (1 + x)
Hence from (2) and (4)
\(\frac{x}{1+x}\) < log(1 + x) < x ∀ x > 0

III.
Question 1.
Show that \(\frac{x}{1+x^2}\) < tan^-1x < x when x > 0. (S.A.Q)
Answer:
Let f(x) = tan^-1x – \(\frac{x}{1+x^2}\)

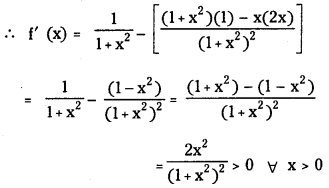
∴ When x > 0, f is increasing means f(x) > f(0) and f(0) = 0
∴ f(x) > 0 ⇒ tan^-1x – \(\frac{x}{1+x^2}\) > 0
⇒ tan^-1x > \(\frac{x}{1+x^2}\) ………..(1)
Similarly let g(x) = x – tan^-1x
Then g'(x) = 1 – \(\frac{1}{1+x^2}=\frac{x^2}{1+x^2}\) > 0 ∀ x > 0
∴ g is increasing when x > 0
⇒ g(x) = 0
But g(0) = 0
∴ g(x) < 0 ⇒ x – tan^-1x
⇒ x > tan^-1x ………….(2)
∴ From (1) and (2), \(\frac{x}{1+x^2}\) < tan^-1x < x ∀ x > 0

Question 2.
Show that tan x > x for all x ∈ [0, \(\frac{\pi}{2}\)). (S.A.Q)
Answer:
Let f(x) = tan x – x
Then f’ (x) = sec² x -1 > 0 for every x e
f(x) increases ∀ x ∈ [0, \(\frac{\pi}{2}\))
∴ f(x) > f(0) and f(0) = 0
⇒ f(x) > 0 ⇒ tan x – x > 0
⇒ tan x > x; ∀ x ∈ [0, \(\frac{\pi}{2}\))

Question 3.
If x ∈ (0, \(\frac{\pi}{2}\)), then show that \(\frac{2 \mathrm{x}}{\pi}\) < sin x < x. (EQ.) Answer: Let f(x) = sin x – \(\frac{2 \mathrm{x}}{\pi}\) and f’(x) = cos x – \(\frac{2}{\pi}\) > 0; ∀ x ∈ (0, \(\frac{\pi}{2}\))
∵ f’(x) > 0, f is increasing and f(x) > f(0);
Since f(0) = 0 we have f(x) > 0
⇒ sin x – \(\frac{2 \mathrm{x}}{\pi}\) > 0 ⇒ sin x > \(\frac{2 \mathrm{x}}{\pi}\) …………..(1)
Let g(x) = x – sin x
Then g'(x) = 1 – cos x > 0 ∀ x ∈ (0, \(\frac{\pi}{2}\))
∴ g(x) is an increasing function in
But g(0) = 0 – sin 0 = 0 g(x) >0
⇒ x – sin x > 0 x > sin x
⇒ sin x < x ……..(2)
∴ From (1) and (2);
\(\frac{2 \mathrm{x}}{\pi}\) < sin x < x ∀ x ∈ (0, \(\frac{\pi}{2}\))

Question 4.
If x ∈ (0, 1) then show that 2x < log\(\left[\frac{1+x}{1-x}\right]\) < 2x[1 + \(\frac{x^2}{2\left(1-x^2\right)}\)] (E.Q.)
Answer:

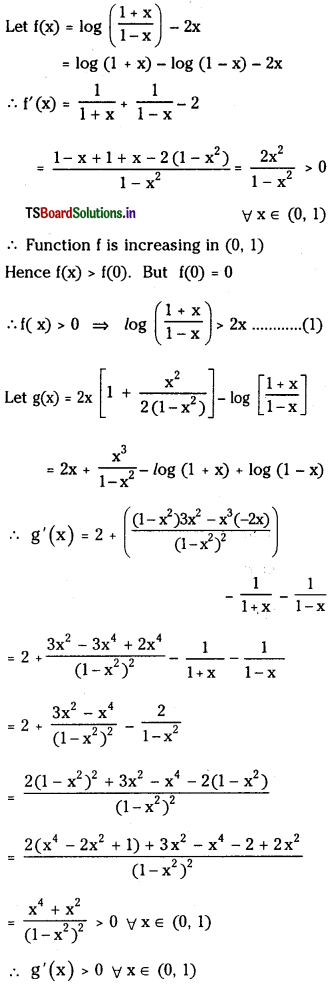
Hence ‘g’ is an increasing function in (0, 1) g(x) > g(0) ∀ x ∈ (0, 1)
But g(0) = 0
∴ g(x) > 0 ∀ x ∈ (0, 1)
⇒ 2x[1 + \(\frac{x^2}{2\left(1-x^2\right)}\)] > log\(\left(\frac{1+x}{1-x}\right)\) ………..(2)
From (1) and (2)
2x < log\(\left(\frac{1+x}{1-x}\right)\) < 2x[1 + \(\frac{x^2}{2\left(1-x^2\right)}\)] ∀ x ∈ (0, 1)

Question 5.
At what points the slopes of the tangents y = \(\frac{x^3}{6}-\frac{3 x^2}{2}+\frac{11 x}{2}\) + 12 increases? (E.Q.)
Answer:
Equation of the curve is
y = \(\frac{x^3}{6}-\frac{3 x^2}{2}+\frac{11 x}{2}\) + 12
\(\frac{d y}{d x}=\frac{3 x^2}{6}-\frac{6 x}{2}+\frac{11}{2}\)
Slope m = \(\frac{x^2}{2}\) – 3x + \(\frac{11}{2}\)
\(\frac{\mathrm{dm}}{\mathrm{dx}}\) = x – 3 > 0 (∵ Slope increases)
⇒ x > 3
Slope increases in ( 3, ∞)

Question 6.
Show that the functions \(\frac{\log (1+x)}{x}\) and \(\frac{x}{(1+x) \log (1+x)}\) are decreasing in (0, ∞). (E.Q.)
Answer:

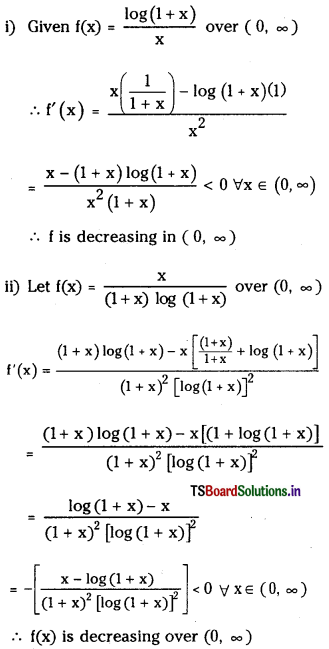
Question 7.
Find the intervals in which the function f(x) = x³ – 3x² + 4 is strictly increasing for all x ∈ ℛ.
Answer:
f(x) = x³ – 3x² + 4
f'(x) = 3x² – 6x
f(x) is strictly increasing if f’ (x) > 0
3x² – 6x > 0
⇒ 3x (x – 2) > 0
⇒ x (x – 2) > 0
f(x) is strictly increasing if x ∈ (2, ∞)

Question 8.
Find the intervals in which the function
f(x) = sin⁴x + cos⁴ x ∀ x ∈ [0, \(\frac{\pi}{2}\)] is increasing and decreasing.
Answer:
Given f(x) = sin⁴x + cos⁴ x ∀ x ∈ [0, \(\frac{\pi}{2}\)]
= (sin²x + cos²x)² – 2 sin²x cos²x
= 1 – 2 sin²x cos²x
= 1 – \(\frac{1}{2}\)sin²2x

f'(x) = \(\frac{1}{2}\)(2 sin 2x)(cos 2x)(2)
= -sin 4x
f'(x) > 0 ⇒ -sin 4x > 0 ⇒ sin 4x < 0
⇒ π < 4x < 2π ⇒ \(\frac{\pi}{4}\) < x < \(\frac{\pi}{2}\)
∴ f is increasing when \(\frac{\pi}{4}\) < x < \(\frac{\pi}{2}\)
Now f'(x) < 0
– sin 4x < 0 ⇒ sin 4x > 0
⇒ 0 < 4x < π ⇒ 0 < x < \(\frac{\pi}{4}\)

∴ Function ‘f’ is decreasing when 0 < x < \(\frac{\pi}{4}\)
∴ f is decreasing in [0, \(\frac{\pi}{4}\)] and
f is increasing in \(\left(\frac{\pi}{4}, \frac{\pi}{2}\right)\)