TS Inter 1st Year Physics Notes Chapter 8 డోలనాలు

Here students can locate TS Inter 1st Year Physics Notes 8th Lesson డోలనాలు to prepare for their exam.

TS Inter 1st Year Physics Notes 8th Lesson డోలనాలు

→ ఆవర్తన చలనము : నిర్ణీత కాలవ్యవధులలో పునరావృతమయ్యే చలనాలను ఆవర్తన చలనాలు అంటారు.

→ ఆవర్తన చలనాన్ని ప్రత్యేకంగా డోలన చలనాన్ని వివరించేందుకు కాలం, పౌనఃపున్యము, స్థానభ్రంశము, కంపన పరిమితి, దశ లేక ప్రావస్థ వంటి ప్రాథమిక భావనలు అవసరము.

→ సరళహరాత్మక చలనం : డోలన చలనం యొక్క సరళమైన రూపాన్ని సరళ హరాత్మక చలనం అంటారు. ఈ చలనం కాల ప్రమేయము (f(t)) తో ఆవర్తనంగా ఉంటుంది.

→ సరళ హరాత్మక చలనాన్ని f(t) = A cos ωt లేదా A sin ωt వంటి అతిసరళమైన సమీకరణంతో సూచిస్తారు. నోట్:

• వస్తువు పౌనఃపున్యము (v) తక్కువగా ఉంటే వాటిని డోలన చలనము అని, పౌనఃపున్యము ఎక్కువగా ఉంటే దానిని కంపన చలనమని అంటారు.
• ప్రతి డోలన చలనం ఆవర్తన చలనమే కాని, ప్రతి ఆవర్తన చలనము డోలన చలనం కావలసిన అవసరం లేదు.

→ ఆవర్తన కాలము (T) : ఆవర్తన చలనంలో ఏ స్వల్ప కాలవ్యవధి తరువాత చలనం పునరావృతమవుతుందో కాలాన్ని ఇచ్చిన ఆవర్తన చలనము యొక్క ఆవర్తన కాలము అంటారు.
ఆవర్తన కాలము T = \(\frac{2 \pi}{\omega}\), ω = కోణీయ వేగము

→ పౌనఃపున్యము (v) : ఏకాంక కాలంలో జరిగే ఆవర్తనాలు లేదా చలనంలోని పునరావృతాలను ఆవర్తన చలనం పౌనఃపున్యము (v) అంటారు.
పౌనఃపున్యము (v) ఆవర్తన కాలము (T) విలోమానికి సమానము.

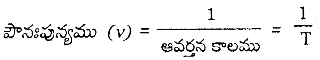
ప్రమాణము : డోలనము/సెకను లేదా హెర్జ్ (Hz)

→ స్థానభ్రంశము : ఆవర్తన చలనంలో కాలంతో పాటు మార్పును కలిగిన ఏదైనా భౌతిక ధర్మంలో వచ్చే మార్పును స్థానభ్రంశం సూచిస్తుంది.
ఉదా :

• సరళ హరాత్మక చలనంలో రేఖీయ గమనంలో ఉన్న ఒక బంతి ఆరంభ బిందువు నుంచి దాని దూరాన్ని కాలప్రమేయంగా తీసుకుంటే, వస్తువు స్థానం బట్టి మూలబిందువు ఎంపికను బట్టి స్థానభ్రంశ పరిమాణం ఉంటుంది.
• ఏకాంతర విద్యుత్ ప్రవాహ వలయంలో కెపాసిటర్ పలకల మధ్య కాలంతో పాటు మారే వోల్టేజిని కూడా స్థానభ్రంశ చలరాశిగా భావించవచ్చు.

→ ఫోరియర్ సిద్ధాంతము : ఏ ఆవర్తన ప్రమేయాన్ని అయినా వివిధ డోలనా వర్తన కాలాలు (T), వాటికి అనుగుణమైన గుణకాలు కలిగి ఉండే sine మరియు cosine ల ప్రమేయాల అధ్యారోపణంగా రాయవచ్చు. ఉదా :

• Y = sin ωt + cos ωt
• Y = sin ωt + cos 2 ωt + sin 4 ωt
• Y = e^-ωt
• Y = log (ωf) వంటి ప్రమేయాలు ఆవర్తన చలనాన్ని సూచించటానికి వాడవచ్చు.

→ సరళ హరాత్మక చలన సమీకరణ వివరణ : కాలంతో పాటు స్థానభ్రంశం జ్యా వక్రీయ ప్రమేయం (sinusodial)గా ఉన్న ఆవర్తన చలనాన్ని సరళ హరాత్మక చలనంగా తీసుకుంటారు. ఇటువంటి చలనంలో కణ స్థానభ్రంశం ‘X’ కాలంతో పాటు (t) మారే విధానాన్ని x(t) = A cos (ωt + Φ) తో సూచిస్తారు. ఇందులో A కణం పొందే గరిష్ఠ స్థానభ్రంశ పరిమాణము. దీనిని కంపన పరిమితి అంటారు. sine, cosine ప్రమేయాలకు దీని విలువ – 1 నుండి 1 వరకు మారును. ut ని ఆర్గ్యుమెంట్ అంటారు. ఇది కాలంతో పాటు మారే స్థానభ్రంశ పరిమాణాన్ని సూచిస్తుంది. ఈ ప్రమేయం ఆవర్తన కాలము T = అవుతుంది.

→ ప్రావస్థ లేక దశ (Φ) : ఆవర్తన చలన ప్రారంభంలో t = 0 వద్ద ωt + Φ = 0 అవుతుంది. t = 0 వద్ద గల స్థానభ్రంశాన్ని ప్రావస్థ లేదా దశ ” అంటారు.

→ కోణీయ వేగము లేదా కోణీయ పౌనఃపున్యము (ω) : ఆవర్తన చలనాన్ని కోసైన్ (cosine) లేదా సైన్ (sine)ల ఆవర్తన ప్రమేయంగా చూపితే, ఆవర్తన కాలం ‘T’ లో ఆర్గ్యుమెంట్ (కణ కోణీయ స్థానభ్రంశం)లో మార్పు 2π అయితే దాని స్థానభ్రంశం పునరావృతమవుతుంది. అనగా కోణీయ వేగము ω = \(\frac{2 \pi}{T}\). దీనినే వస్తువు కోణీయ పౌనఃపున్యము అని కూడా అంటారు.

→ నివేశ వృత్తము : ఒక వృత్త వ్యాసంపై ఏకరీతి వృత్తాకార చలనం యొక్క విక్షేపం (projection) సరళ హరాత్మక చలనము వృత్త వ్యాసంపై ఏకరీతి చలనం చేసే కణాన్ని (p) నిర్దేశకం అని, ఈ కణం ఏ వృత్తంపై తిరుగుతుందో దానిని నివేశ వృత్తము అని అంటారు.

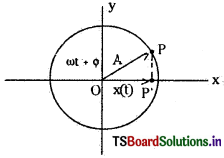
→ సరళ హరాత్మక చలనంలో ఉన్న వస్తువు వేగము : ఏకరీతి వృత్తాకార చలనంలో కణం గరిష్ఠ వడి అనేది కోణీయ వేగం మరియు వృత్త వ్యాసార్థాల లబ్ధానికి సమానము. V = ωA. S.H.M లో గల వస్తు సమీకరణం x(t) = = A cos (ωt + d) అయితే కణం వడి υ = \(\frac{d}{d x}\)[x(t)] = \(\frac{d}{d x}\) [A cos (ωt + d)] = – A ω sin (ωt + d) = ω\(\sqrt{A^2-x^2}\) – గుర్తు U దిశ ధన X – అక్షానికి వ్యతిరేకము. గరిష్ఠ వడి X = 0 వద్ద ఉంటుంది .υ = ωA అనగా S.H.M లో స్థానభ్రంశం x = 0 అయితే కణం వడి గరిష్ఠము.

→ త్వరణము : S.H.M లో గల వస్తువు తాక్షణిక త్వరణము a(t) = \(\frac{\mathrm{d}}{\mathrm{dt}}\)
a(t) = \(\frac{d}{d t}\)[- Aω sin (ωt + Φ)] = -Aω² cos (ωt + Φ) = -ω². x(t)
గరిష్ఠ త్వరణము a = -ω²A ఇది X = A బిందువు వద్ద ఉంటుంది. అనగా స్థానభ్రంశము గరిష్ఠమైతే S.H.M లో వస్తువు త్వరణము గరిష్ఠము ఈ త్వరణము ఎల్లప్పుడూ మాధ్యమిక బిందువు వైపు ఉంటుంది.

→ సరళ హరాత్మక చలనం చేసే వస్తువు పై బలము : m ద్రవ్యరాశి గల S.H.M ఉన్న వస్తువు పై బలం కూడా కాలం ప్రమేయంగా మారుతుంది. F(t) = ma = – mω²x(t) లేదా F(t) = – K x(1) ఇందులో K = -mω² S.H.M లో గల వస్తువుపై పనిచేసే బలం ఎల్లప్పుడూ ఆ చలనంలో గల మాధ్యమిక బిందువు వైపు ఉంటుంది.

→ S.H.M లో గల వస్తువు శక్తి : సరళ హరాత్మక చలనం చేసే కణం యొక్క స్థితిజశక్తి, గతిజశక్తి విలువలు సున్న నుండి గరిష్ఠ విలువ మధ్య మారుతుంటాయి.
కణం గతిజశక్తి K.E = \(\frac{1}{2}\)mω² = \(\frac{1}{2}\)mω²A² sin² (ωt + Φ) = = K. A² sin² (ωt + Φ) లేదా KE = \(\frac{1}{2}\) mω² (A² – x²) = \(\frac{1}{2}\) K (A² – x²)
x = స్థానభ్రంశము; A – కంపన పరిమితి
S.H.M లో కణం స్థితి శక్తి : S.HM లో కణం స్థితిశక్తి U = \(\frac{1}{2}\) mω² A² cos (ωt + Φ)
U = P.E = \(\frac{1}{2}\)mω² A² cos² (ωt + Φ) = \(\frac{1}{2}\)KAx²
S.H.M లో గల వస్తువు లేదా కణం మొత్తం శక్తి E = \(\frac{1}{2}\)m² A² = \(\frac{1}{2}\)K A²

→ స్ప్రింగ్లలో డోలనాలు : స్ప్రింగ్లలో స్ప్రింగ్ పొడవుతో పోలిస్తే స్థానభ్రంశం తక్కువగా ఉన్నపుడు మాత్రమే హుక్ నియమం వర్తిస్తుంది.
స్ప్రింగ్ స్థిరాంకము

గుర్తు పునఃస్థాపక బలాలు వ్యతిరేక దిశలో పనిచేస్తాయి అని చెపుతుంది.
గట్టి స్ప్రింగ్లకు K విలువ ఎక్కువ, మెత్తటి స్ప్రింగ్లకు K విలువ తక్కువ.
స్ప్రింగ్లలో కోణీయ వేగం లేదా కోణీయ పౌనఃపున్యము ω = \(\sqrt{\frac{\mathrm{K}}{\mathrm{m}}}\)
స్ప్రింగ్ అవర్తన డోలనాకాలము T = \(\frac{2 \pi}{\omega}\) = 2π\(\sqrt{\frac{m}{K}}\)

→ లఘు లోలకము : సాగదీయడానికి వీలులేని, ద్రవ్యరాశి లేనటువంటి ఓ పొడవు గల దారానికి ఒక చిన్న లోహపు గుండును తగిలించి దృఢమైన ఆధారానికి కడితే దానిని లఘు లోలకము అంటారు.

→ కంపన పరిమితి తక్కువగా గల లఘు లోలకం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.

→ లోలకం పొడవు వెంబడి నికర వ్యాసార్ధియ బలం mg cos θ. ఇది దారంతో తన్యత T ని తుల్యం చేస్తుంది.

→ లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ T ను స్పర్శియ బలం ng sin θ ఇస్తుంది.

→ లోలకం డోలనాలకు కావలసిన టార్క్ τ = – L mg sin θ

→ లోలకం కోణీయ త్వరణము α = \(\frac{-\mathrm{mgL}}{\mathrm{I}}\)θ

→ లోలకం జడత్వ భ్రామకం I = mL²
లోలకం ఆవర్తన కాలము T = 2π\(\sqrt{\frac{1}{\mathrm{mgL}}}\) = 2π\(\sqrt{\frac{L}{g}}\)

→ సెకండ్ల లోలకం : డోలనావర్తన కాలం రెండు సెకనులు గల లోలకాన్ని సెకండ్ల లోలకం అంటారు.
సెకన్ల లోలకం ఆవర్తన కాలము T = 2 సెకనులు.

→ అవరుద్ధ దోలనాలు : అవరుద్ధ డోలనాలలో వ్యవస్థ శక్తి అవిచ్ఛిన్నంగా వ్యర్థమవుతుంది. అవరోధం అల్పంగా ఉండే సందర్భంలో డోలనాలు దాదాపు ఆవర్తన చలనాన్ని కలిగి ఉంటాయి.

గమనిక :
అవరోధబలం పరిమాణం యానకం స్వభావంపై ఆధారపడి ఉంటుంది. అవరోధబలం పెరిగితే కంపించే వ్యవస్థ తొందరగా శక్తిని కోల్పోయి వ్యవస్థ కంపనాలు లేదా డోలనాలు తొందరగా ఆగిపోతాయి.
అవరోధబలానికి గురైన వస్తువు ఆవృత చలనాన్ని m\(\frac{d^2 x}{d t^2}\) + b\(\frac{\mathrm{dx}}{\mathrm{dt}}\) + Kx = 0 అన్న సమీకరణంతో సూచిస్తారు.
ఇటువంటి వ్యవస్థ కోణీయత = \(\sqrt{\frac{K}{m}-\frac{b^2}{4 m^2}}\)
ఇందులో K = స్ప్రింగ్ స్థిరాంకము, b = అవరోధ స్థిరాంకము

→ స్వేచ్ఛా కంపనాలు లేదా స్వేచ్ఛా డోలనాలు : వస్తువును మాధ్యమిక స్థానం నుంచి స్థానభ్రంశం చెందించి వదలివేస్తే ఆ వస్తువు చేసే కంపనాలను స్వేచ్ఛా కంపనాలు అంటారు.

→ బలాత్కృత లేదా చోదిత డోలనాలు : ఏదైనా వ్యవస్థ తన సహజ పౌనఃపున్యం వద్ద కాక బాహ్య కారకం పౌనఃపున్యంతో చలిస్తే అటువంటి డోలనాలను బలాత్కృత డోలనాలు అంటారు. బలాత్కృత డోలనాలన్నీ అవరుద్ధ డోలనాలే.

→ అనునాదము : ఏదైనా వస్తువుపై చోదకబలం పౌనఃపున్యము వస్తువు సహజ పౌనఃపున్యానికి సమానమైనపుడు డోలకం కంపన పరిమితిలో పెరుగుదల కలిగించే దృగ్విషయాన్ని అనునాదము అంటారు.
గమనిక : వస్తువు సహజ పౌనఃపున్యం చోదకబలం పౌనఃపున్యానికి చాలా దగ్గరగా ఉంటే కూడా అనునాదం సంభవించవచ్చు. ఈ కారణం వల్ల భూకంపం వచ్చినపుడు భూప్రకంపనల పౌనఃపున్యానికి సమీప సహజ పౌనఃపున్యం గల భవనాలు తొందరగా నేల కూలతాయి.

→ సరళహరాత్మక చలనములో ఉన్న వస్తువు స్థానభ్రంశ సమీకరణములు
Y = A sin (ωt ± Φ) లేదా Y = A cos (ωt ± Φ)

→ స.హ.చ. లో ఉన్న వస్తువు వేగము : V = \(\frac{\mathrm{dy}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\)(A cos ωt)
∴ V = -Aω sin ωt
లేదా V = \(\sqrt{A^2-Y^2}\); గరిష్ఠవేగము V_{గరిష్ఠ} = Aω

→ స.హ.చ. లో ఉన్న వస్తువు త్వరణము :
a = -ω² A sin ωt లేదా a = -ω²Y (ఇక్కడడ Y = A sin ωt)
(– ఋణగుర్తు త్వరణము మరియు స్థానభ్రంశములు వ్యతిరేకదిశలలో ఉండుటను సూచించును.) గరిష్ఠ త్వరణము a_max = ω²A.

→ స.హ.చ.లో ఉన్న వస్తువు కోణీయ వేగము ‘ω’ : స.హ.చ.లో త్వరణము ∝ స్థానభ్రంశము a ∝ – Y లేదా a = -ω²y ( ఋణగుర్తు a మరియు y లు వ్యతిరేకదిశలలో ఉండుటను సూచించును.)

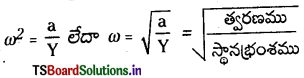
ఇందులో ω స.హ.చ.లో ఉన్న వస్తువు కోణీయ వేగము.

→ స.హ.చ.లో ఉన్న వస్తువు ఆవర్తన కాలము: ఒక పూర్తి కంపనమునకు పట్టుకాలమును దాని ఆవర్తనకాలము

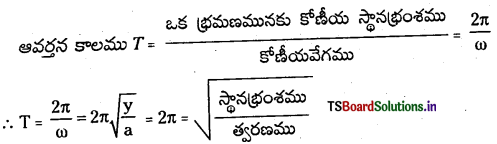
పౌనఃపున్యము υ = \(\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{a}{Y}}\) లేదా υ = \(\frac{\omega}{2 \pi}\) లేదా ω = 2πυ

→ స్ప్రింగ్లు :
1) స్ప్రింగ్ స్థిరాంకము

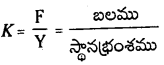
2) వస్తువు త్వరణము a = \(\frac{K}{m}\). Y (m స్ప్రింగ్ కు వ్రేలాడదీసిన దిమ్మ ద్రవ్యరాశి)
3) దిమ్మ యొక్క కోణీయ వేగము ω = \(\sqrt{\frac{K}{m}}\) [∵ a = -ω²Y కాని స్ప్రింగ్లో a = \(\frac{K}{m}\). Y ∴ ω = \(\sqrt{\frac{K}{m}}\)
4) ఆవర్తన కాలము T = \(\frac{2 n}{\omega}=2 \pi \sqrt{\frac{m}{K}}\)
5) T₁ = \(2 \pi \frac{\sqrt{\left(m+\frac{m_1}{3}\right)}}{K}\) (నిజస్ప్రింగ్లందు)
6) కంపన పౌనఃపున్యము n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{m}}\), నిజ స్ప్రింగ్లందు n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{\left(m+\frac{m_1}{3}\right)}}\)
7) ఏ స్థానము వద్దనైనా స్థితిశక్తి P.E. = \(\frac{1}{2}\)Kx² ణి మరియు గతిశక్తి K.E. = \(\frac{1}{2}\)K(A² – x²)
8) మొత్తము శక్తి T.E. = స్థితిశక్తి + గతిశక్తి = \(\frac{1}{2}\)KA²
9) k స్థిరాంకము గల స్ప్రింగ్ను ‘n’ సమానభాగములుగా కత్తిరించిన ఒక్కొక్క భాగము స్ప్రింగ్ స్థిరాంకము k¹ = nk n = భాగముల సంఖ్య మరియు k = మొదటి స్ప్రింగ్ స్థిరాంకము

→ స.హ.చ.లో ఉన్న వస్తువు యొక్క శక్తి :

• ఏ బిందువు వద్దనైనా స్థితిశక్తి P.E. = \(\frac{1}{2}\)mω²x²; PE_max = \(\frac{1}{2}\)mω²A²
• ఏ బిందువు వద్దనైనా K.E. = \(\frac{1}{2}\)mω²(A² – x²); గరిష్ట గతిశక్తి = \(\frac{1}{2}\)mω²A² (x = ‘0’ వద్ద)
• పౌనఃపున్యము ‘U’ లో సమీకరణాలు వ్రాసినపుడు
  స్థితిశక్తి P.E. = 2mπ²v²x² గతిశక్తి K.E. = 2mπ²v² (A² – x²)
  మొత్తము శక్తి T. E. = P.E. + K.E. = 2mπ²v²A²

→ లఘు లోలకము:

• లఘులోలకములో భారము యొక్క అంశము mg sin θ. ఇది డోలనాలు చేయుటకు కావలసిన బలమును సమకూర్చును. F = mg.sin θ. లోలకం పై టార్క్ τ = L. mg sin θ,
• డోలనావర్తన కాలము T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{mgL}}}\) = 2π\(\sqrt{\frac{l}{g}}\) లేదా g = 4π²\(\frac{l}{\mathrm{~T}^2}\)
• లోలకము M.O.I = I = mL² ; కోణీయ త్వరణము α = –\(\frac{\mathrm{mgL}}{\mathrm{I}}\).θ
• లిఫ్ట్ ‘a’ త్వరణముతో పైకి వెళుతున్న దానిలోని లోలకము ఆవర్తనకాలము తగ్గును T = 2π\(\sqrt{\frac{l}{g+a}}\)
• లఘులోలకమును ‘a’ త్వరణముతో క్రిందికి వెళ్ళుతున్న లిఫ్ట్ లో ఉంచిన దాని ఆవర్తనకాలము పెరుగును
  T = 2π\(\sqrt{\frac{l}{g-a}}\)
• సెకనుల లోలకము డోలనావర్తన కాలము T = 2 సె.; పొడవు = 100 సెం.మీ. = 1మీ. (సుమారుగా)