TS Inter 1st Year Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a)

by

Students must practice these TS Intermediate Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates 5(a)

I.
Question 1.
Find the distance of P (3, -2, 4) from the origin. (V.S.A.Q.)
Answer:
OP = \(\sqrt{x^2+y^2+z^2}\)
= \(\sqrt{9+4+16}\) = √29 units

TS Inter 1st Year Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a)

Question 2.
Find the distance of the points (3, 4, -2) and (1, 0, 7). (V.S.A.Q.)
Answer:
Let P = (3, 4, -2) and Q (1, 0, 7) then
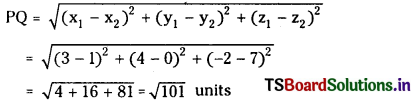
TS Inter 1st Year Maths 1B Solutions Chapter 5 Three-Dimensional Coordinates Ex 5(a) 1

II.
Question 1.
Find x if the distance between (5,-1,7) and (x, 5, 1) is 9 units. (V.S.A.Q.)
Answer:
Let P = (5, -1, 7) and Q (x, 5, 1)
and PQ = 9 ⇒ PQ2 = 81
⇒ (x – 5)2 + (5 + 1)2 + (1 – 7)2 = 81
⇒ x2 – 10x + 25 + 36 + 36 = 81
⇒ x2 – 10x + 25 = 9
⇒ (x – 5)2 = 32
⇒ x – 5 = ±3 ⇒ x = 2 or 8

Question 2.
Show that the points (2, 3, 5), (-1, 5, -1) and (4, -3, 2) form a right angled isosceles triangle. (V.S.A.Q.)
Answer:
Let A = (2, 3, 5), B = (-1, 5, -1) and C = (4, -3, 2) are the given points.
∴ AB2 = (2 + 1)2 + (3 – 5)2 + (5 + 1)2 = 9 + 4 + 36 = 49
BC2 = (- 1 – 4)2 + (5 + 3)2 + (- 1 – 2)2
= 25 + 64 + 9 = 98
CA2 = (4 – 2)2 + (- 3 – 3)2+ (2 – 5)22
= 4 + 36 + 9 = 49
∴ AB2 = CA2
AB2 + CA2 = 49 + 49 = 98 = BC2
∆ABC is a right angled isosceles triangle.

Question 3.
Show that the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) form an equilateral triangle. (V.S.A.Q.) (Board New Model Paper)
Answer:
Let A (1, 2, 3), B (2, 3, 1) and C (3, 1, 2) are the given points.
AB2 = (1 – 2)2 + (2 – 3)2 + (3 – 1)2 = 1 + 1 + 4 = 6
BC2 = (2 – 3)2 + (3 – 1)2 + (1 – 2)2 = 1 + 4 + 1 = 6
AC2 = (1 – 3)2 + (2 – 1)2 + (3 – 2)2 = 4 + 1 + 1 =6
∴ AB2 = BC2 = AC2 ⇒ AB = BC = AC
∴ ABC is an equilateral triangle.

TS Inter 1st Year Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a)

Question 4.
P is a variable point which moves such that 3PA = 2PB. If A (-2, 2, 3) and B (13, -3,13) prove that P satisfies the equation x2 + y2 + z2 + 28x – 12y +10z – 247 = 0. (S.A.Q.)
Answer:
Given A (-2, 2, 3) and B (13, -3, 13) and suppose P = (x, y, z) then
3PA = 2PB ⇒ 9PA2 = 4PB2
⇒ 9 [(x + 2)2 + (y – 2)2 + (z – 3)2]
= 4 [(x – 13)2 + (y + 3)2 + (z – 13)2]
⇒ 9 [x2 + 4x + 4 + y2 – 4y + 4 + z2 – 6z + 9]
= 4 [x2 – 26x +169 + y2 + 6y + 9 + z2 – 26z +169]
⇒ 9x2 + 9y2 + 9z2 + 36x – 36y – 54z + 153
= 4x2 + 4y2 + 4z2 – 104x + 24y – 104z + 1388
⇒ 5x2 + 5y2 + 5z2 + 140x – 60y + 50z – 1235 = 0
⇒ x2 + y2 + z2 + 28x – 12y + 10z – 247 = 0

Question 5.
Show that the points (1, 2, 3), (7, 0, 1) and (-2, 3, 4) are collinear. (V.S.A.Q.) (March 2007)
Answer:
Let A (1, 2, 3), B (7, 0, 1), C (-2, 3, 4) be the given points.
TS Inter 1st Year Maths 1B Solutions Chapter 5 Three-Dimensional Coordinates Ex 5(a) 2
∴ BC = AB + AC
∴ A, B, C are collinear.

TS Inter 1st Year Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a)

Question 6.
Show that ABCD is a square where A,B,C,D are the points (0, 4, 1), (2, 3, -1), (4, 5, 0) and (2, 6, 2) respectively. (S.A.Q.)
Answer:
Let A (0, 4, 1), B (2, 3, -1), C (4, 5, 0) and D (2, 6, 2) be the given points.
AB2 = (0 – 2)2 + (4 – 3)2 + (1 + 1)2 = 4 + 1 + 4 = 9
BC2 = ( 2 – 4)2 + (3 – 5)2 + (- 1 – 0)2 = 4 + 4 + 1 = 9
CD2 = (4 – 2)2 + (5 – 6)2 + (0 – 2)2 = 4 + 1 +4 = 9
AD2 = (0 – 2)2 + (4 – 6)2 + (1 – 2)2 = 4 + 4 + 1 = 9
∴ AB2 = BC2 = CD2 = DA2
⇒ AB = BC = CD = DA
AC2 = (0 – 4)2 + (4 – 5)2 + (1 – 0)2 = 16 + 1 + 1 = 18
BD2 = (2 – 2)2 + (3 – 6)2 + (- 1 – 2)2 = 9 + 9= 18
∴ AC2 = BD2 ⇒ AC = BD
AB2 + BC2 = 9 + 9 = 18 = AC2
∴ ∠ABC = 90°
∴ ABCD is a square.

Leave a Comment