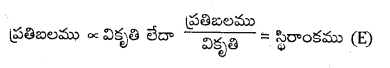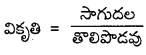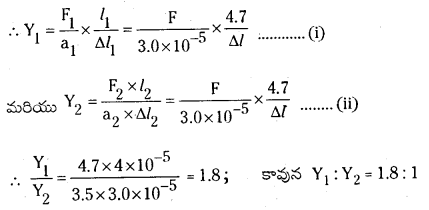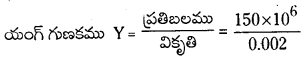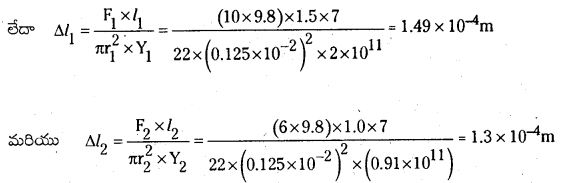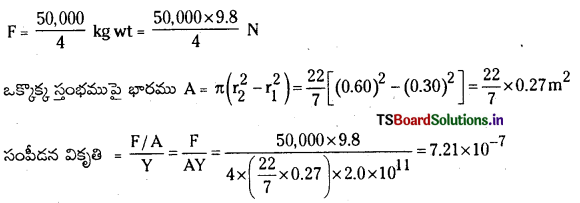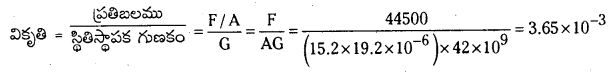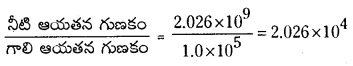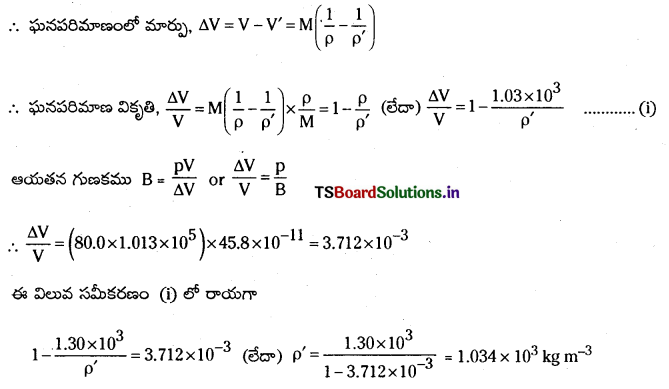Telangana TSBIE TS Inter 1st Year Physics Study Material 10th Lesson ఘనపదార్ధాల యాంత్రిక ధర్మాలు Textbook Questions and Answers.
TS Inter 1st Year Physics Study Material 10th Lesson ఘనపదార్ధాల యాంత్రిక ధర్మాలు
అతిస్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
స్థితిస్థాపకతలో హుక్ నియమాన్ని తెలపండి.
జవాబు:
స్థితిస్థాపక అవధిలో ప్రతిబలము వికృతికి అనులోమానుపాతంలో ఉండును.
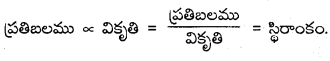
ఈ స్థిరాంకమును స్థితిస్థాపకతా గుణకము అందురు.
ప్రశ్న 2.
ప్రతిబలానికి మితులు, ప్రమాణాలు తెలపండి.
జవాబు:
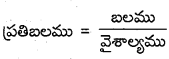
S.I. పద్ధతిలో ప్రమాణము : న్యూ/మీ2 లేదా పాస్కల్. మితిఫార్ములా : ML-1T-2
ప్రశ్న 3.
స్థితిస్థాపక గుణకానికి ప్రమాణాలు, మితులను తెలపండి.
జవాబు:
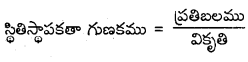
S.I. ప్రమాణము : న్యూ/మీ2 లేదా పాస్కల్. మితిఫార్ములా : ML-1T-2

ప్రశ్న 4.
యంగ్ గుణకం ప్రమాణాలు, మితులను తెలపండి.
జవాబు:
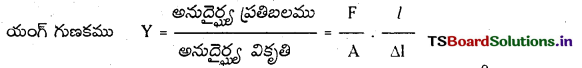
మితిఫార్ములా : ML-1T-2
ప్రమాణము : న్యూటన్/మీ2 లేదా పాస్కల్
ప్రశ్న 5.
దృఢతా గుణకం ప్రమాణాలు, మితులను తెలపండి.
జవాబు:
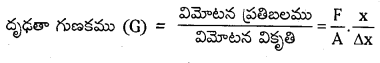
మితిఫార్ములా : ML-1T-2
ప్రమాణము : న్యూటన్/మీ2 లేదా పాస్కల్
ప్రశ్న 6.
ఆయత గుణకం ప్రమాణాలు, మితులను తెలపండి.
జవాబు:
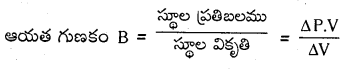
మితిఫార్ములా : ML-1T-2
ప్రమాణము : న్యూటన్/మీ2 లేదా పాస్కల్

ప్రశ్న 7.
సంపూర్ణ స్థితిస్థాపక, ప్లాస్టిక్ కు సమీపంగా ఉండే వస్తువులకు ఉదాహరణలు ఇవ్వండి.
జవాబు:
సమ సర్పిలాకార స్ప్రింగు సంపూర్ణ స్థితిస్థాపక వస్తువులకు ఉదాహరణ. పిండి లేదా మట్టి ముద్ద ప్లాస్టిక్ వస్తువులకు ఉదాహరణ.
స్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
హుక్ నియమం, అనుపాత అవధి, శాశ్వత స్థితి, విచ్ఛేదన ప్రతిబలం పదాలను నిర్వచించండి.
జవాబు:
హుక్ నియమము : స్థితిస్థాపక అవధులలో ప్రతిబలము వికృతికి అనులోమానుపాతంలో ఉంటుంది.
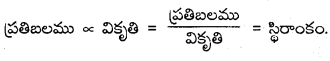
ఈ స్థిరాంకమును స్థితిస్థాపక గుణకము అంటారు.
అనుపాత అవధి : ప్రతిబలము – వికృతి వక్రరేఖపై OA బిందువుల మధ్య భాగం సరళరేఖ ఈ ప్రాంతంలో ప్రతిబలం వికృతికి అనులోమానుపాతంలో ఉంటుంది. బాహ్య బలం తొలగించగానే వస్తువు సంపూర్ణంగా యథాస్థితి పొందుతుంది. అందువల్ల ‘A’ బిందువును అనుపాత అవధి అంటారు.
శాశ్వత స్థితి : ప్రతిబలం – వికృతి వక్రంలో బాహ్యబలాన్ని ‘C’ బిందువు వరకు పెంచి తొలగిస్తే వస్తువు తన పూర్వ స్థితిని సంపూర్ణంగా పొందలేదు. వస్తువులో కొంత వికృతి శాశ్వతంగా మిగిలిపోతుంది. అందువల్ల ‘C’ బిందువును శాశ్వత స్థితి బిందువు అంటారు.
విచ్ఛేదన ప్రతిబలము : ప్రతిబలం-వికృతి వక్రంలో వస్తువుపై ప్రతిబలాన్ని ఈగే బిందువు దాటి ప్రయోగిస్తే (E బిందువు వరకు) ప్రతిబలంలో స్వల్ప మార్పుకే వికృతి విపరీతంగా పెరిగి E అను బిందువు వద్ద తీగ సన్నబడి తెగిపోతుంది. తీగ తెగిపోవడానికి అవసరమైన E బిందువు వద్ద గల ప్రతిబలాన్ని విచ్ఛేదన ప్రతిబలం అంటారు.

ప్రశ్న 2.
స్థితిస్థాపక గుణకం, ప్రతిబలం, వికృతి, స్వాజూన్ నిష్పత్తులను నిర్వచించండి.
జవాబు:
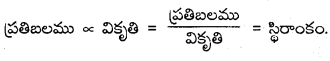
ఈ స్థిరాంకమును స్థితిస్థాపక గుణకము అంటారు.
ప్రతిబలము (σ) : ఏకాంక వైశాల్యంపై పనిచేసే పునఃస్థాపక బలాన్ని ప్రతిబలం అంటారు.
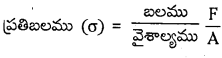
ప్రమాణము Nm-2 లేదా పాస్కల్ మితి ఫార్ములా = ML-1T-2
వికృతి : ప్రమాణ పరిమాణం గల వస్తువు ఆకారంలో వచ్చిన మార్పును వికృతి అంటారు.

ఇది నిష్పత్తి. కావున ప్రమాణాలు, మితులు లేవు.
ప్వాజూన్ నిష్పత్తి (σ) : సాగదీసిన తీగలో పార్శ వికృతి మరియు అనుదైర్ఘ్య వికృతుల నిష్పత్తిని ప్వాజూన్ నిష్పత్తి అంటారు.
ప్వాజూన్ నిష్పత్తి (σ) = \(\frac{\Delta \mathrm{d} / \mathrm{d}}{\Delta l / l}\) దీనికి మితులు, ప్రమాణాలు లేవు.
ప్రశ్న 3.
యంగ్ గుణకం, ఆయత గుణకం, ద్రుఢతా గుణకాలను నిర్వచించండి.
జవాబు:
యంగ్ గుణకము : అనుదైర్ఘ్య ప్రతిబలము, అనుదైర్ఘ్య వికృతిల నిష్పత్తిని యంగ్ గుణకమందురు.
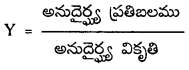
అనుదైర్ఘ్య ప్రతిబలము = \(\frac{\mathrm{F}}{\mathrm{A}}\); అనుదైర్ఘ్య వికృతి = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\)
∴ Y = \(\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{F}}{\mathrm{A}} \frac{\mathrm{l}}{\Delta \mathrm{L}}\)
ఆయత గుణకము (B) : ఘనపరిమాణాత్మక ప్రతిబలము మరియు ఘనపరిమాణాత్మక వికృతిల నిష్పత్తిని ఆయత గుణకము అందురు.
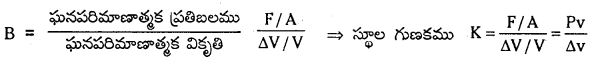
విమోటనా గుణకము లేదా దృఢతా గుణకము (G) :
స్పర్శీయ ప్రతిబలము మరియు విరూపణా వికృతిలో నిష్పత్తిని విమోటనా గుణకము అందురు.


ప్రశ్న 4.
ప్రతిబలం నిర్వచనం తెలిపి వివిధ రకాల ప్రతిబలాలను వివరించండి.
జవాబు:
ప్రతిబలము (σ) : ఏకాంక వైశాల్యంపై పనిచేసే పునఃస్థాపక బలాన్ని ప్రతిబలం అంటారు.
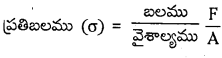
ప్రమాణము Nm-2 లేదా
పాస్కల్ మితి ఫార్ములా = ML-1T-2
ప్రతిబలమునందలి రకాలు : 1) అనుదైర్ఘ్య ప్రతిబలము 2) స్పర్శియ ప్రతిబలము 3) ఘనపరిమాణాత్మక ప్రతిబలము
అనుదైర్ఘ్య ప్రతిబలము లేదా తన్యజ ప్రతిబలం : వస్తువుపై దాని పొడవు పెరుగునట్లు బలమును ప్రయోగించిన ప్రమాణ వైశాల్యములోని పునఃస్థాపక బలమును అనుదైర్ఘ్య ప్రతిబలము అంటారు.
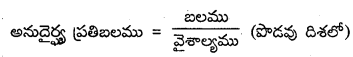
స్పర్శీయ లేదా విమోటన ప్రతిబలము : తలానికి సమాంతరముగా దాని ఉపరితల పొరలో స్థానభ్రంశము కలుగునట్లు బలమును ప్రయోగించిన ప్రమాణ వైశాల్యములోని పునఃస్థాపక బలమును స్పర్శియ ప్రతిబలము అందురు.
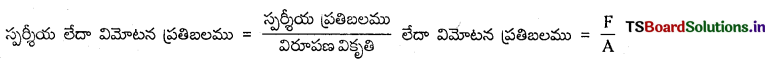
ఘనపరిమాణాత్మక ప్రతిబలము : ఒక వస్తువుపై అన్ని వైపులా లేదా వస్తువు ఘనపరిమాణమంతటా బలమును ప్రయోగించిన ప్రమాణ. వైశాల్యములోని పునఃస్థాపక బలమును ఘనపరిమాణాత్మక ప్రతిబలము అందురు.
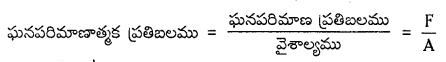
ప్రశ్న 5.
వికృతిని నిర్వచించి, వివిధ రకాల వికృతులను వివరించండి.
జవాబు:
వికృతి : ప్రమాణ పరిమాణం గల వస్తువు ఆకారంలో వచ్చిన మార్పును వికృతి అంటారు.
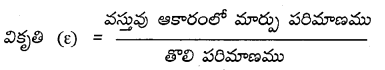
ఇది నిష్పత్తి. కావున ప్రమాణాలు, మితులు లేవు.
వికృతి నందలి రకాలు : వికృతి మూడు రకములు.
1) అనుదైర్ఘ్య వికృతి 2) స్పర్శీయ లేదా విరూపణ వికృతి 3) ఘనపరిమాణ వికృతి.
1) అనుదైర్ఘ్య వికృతి (ε) : వస్తువు పొడవులో మార్పు (∆l) మరియు తొలి పొడవు (l) లకు గల నిష్పత్తిని అనుదైర్ఘ్య వికృతి అంటారు.
అనుదైర్ఘ్య వికృతి (ε) = \(\frac{\Delta l}{l}\)
2) విరూపణ వికృతి : ఒక వస్తువు తలముపై స్పర్శరేఖ దిశలో బలమును ప్రయోగించిన, దాని ఉపరితలము పొందిన స్థానభ్రంశపు మరియు మొదటి లంబ తలముల మధ్య గల కోణమును విరూపణ వికృతి అంటారు.
విరూపణ వికృతి = θ = \(\left(\frac{\Delta l}{l}\right)\) = tan θ (కోణము చిన్న విలువలకు tan θ = θ)
3) ఘనపరిమాణాత్మక వికృతి : వస్తువు ఘనపరిమాణంలో మార్పు కలుగునట్లు బలమును ప్రయోగించిన ఘనపరిమాణంలో మార్పుకు తొలి ఘనపరిమాణ మార్పుకు గల నిష్పత్తిని ఘనపరిమాణాత్మక వికృతి అందురు.
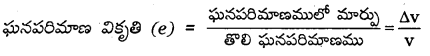

ప్రశ్న 6.
వికృతి శక్తి అంటే ఏమిటో తెలిపి, దానికి సమీకరణాన్ని ఉత్పాదించండి. (మార్చి 2014, మే 2014)
జవాబు:
వికృతిశక్తి : తీగలో వికృతి కలుగునట్లు బలమును ప్రయోగించినపుడు జరిగిన పని తీగలో స్థితిశక్తిగా నిల్వయుండును. దీనిని వికృతిశక్తి అందురు.
తీగపై ప్రయోగించిన విరూపణ బలమును తొలగించిన వికృతిశక్తి ఉష్ణశక్తిగా మారును.
సమీకరణ ఉత్పాదన : L పొడవు గల ఏకరీతి తీగ ఒక చివరను స్థిర ఆధారము నుండి వ్రేలాడదీసి దానిపై F బలమును . ప్రయోగించిన దానిలో సాగుదల dl అనుకొనుము.
∴ జరిగిన పని = dW = Fdl
తీగను దాని పొడవులో మార్పు ‘0’ నుండి / ను పొందుటలో జరిగిన పని
W = \(\int\) dW కాని \(\int_o^l \mathrm{Fd} l=\int_0^l \frac{\mathrm{YA} l}{\mathrm{~L}}=\frac{\mathrm{YA}}{\mathrm{L}}\left(\frac{l^2}{2}\right)_0^l \mathrm{~d} l\)
∴ \(\frac{\mathrm{YA}}{\mathrm{L}}\left(\frac{l^2}{2}\right)=\frac{\mathrm{YA}}{\mathrm{L}}\left(\frac{l^2}{2}\right) \frac{1}{2} \frac{\mathrm{Ya} l}{\mathrm{~L}} \cdot l\)
W = \(\frac{1}{2}\) × బలము × సాగుదల. ఈ పని తీగలో వికృతిశక్తికి సమానము.
∴ వికృతి శక్తి = \(\frac{1}{2}\) × బలము × సాగుదల.
ప్రమాణ ఘనపరిమాణంలో వికృతి శక్తి
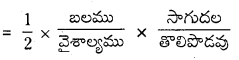
ప్రమాణ ఘనపరిమాణంలో శక్తి = \(\frac{1}{2}\) × ప్రతిబలము × వికృతి
ప్రశ్న 7.
భారీ పని యంత్రాలలోనూ, నిర్మాణరంగ రూపకల్పనలోనూ రాగి, ఇత్తడి, అల్యూమినియంతో పోల్చితే ఉక్కును ఎందుకు వాడతారు ?
జవాబు:
ఉక్కుకు యంగ్ గుణకము మరియు దృఢతా గుణకములు రాగి, ఇత్తడి మరియు అల్యూమినియంల కన్న చాలా ఎక్కువ. అందువల్ల ఉక్కు కడ్డీలను సాగదీయడానికి మరియు వంచడానికి చాలా ఎక్కువ ప్రతిబలం కావాలి.
సుమారు 0.1 సెం.మీ2 వైశాల్యం గల ఉక్కు తీగను 0.1% సాగదీయటానికి సుమారు 2000 న్యూటన్ల బలం అవసరము. ఇదే సాగుదలకు అల్యూమినియంకు 690 న్యూ, రాగికి 900 న్యూ మరియు ఇత్తడికి 1100 న్యూటన్ల బలం అవసరము. అంటే ఉక్కు స్థితిస్థాపక గుణకము అల్యూమినియం, రాగి, ఇత్తడిల కన్నా ఎక్కువ కాబట్టి ఉక్కుతో కట్టిన కట్టడాలు ఎక్కువ బరువును మోయగల సామర్థ్యాన్ని, దృఢత్వాన్ని కలిగి ఉండటం వల్ల భవన నిర్మాణంలో, భారీ కట్టడాలు కట్టడంలోను ఉక్కును వాడతారు.

ప్రశ్న 8.
క్రమంగా భారం పెంచుతూ పోయినప్పుడు తీగ ప్రవర్తన ఏ విధంగా ఉంటుందో విశదీకరించండి.
జవాబు:
ఏకరీతి అడ్డుకోత వైశాల్యము గల తీగ ఒక చివరను స్థిరమైన ఆధారానికి బిగించి రెండవ చివర భారమును క్రమంగా పెంచినామనుకొనుము. వస్తువుపై ప్రయోగించిన ప్రతిబలము మరియు వస్తువులోని వికృతికి రేఖాపటం గీయగా అది పటంలో చూపినట్లు ఉంటుంది. ఈ రేఖాపటం నుండి తీగ ప్రవర్తనను వివిధ బిందువుల వద్ద వివరించవచ్చు.
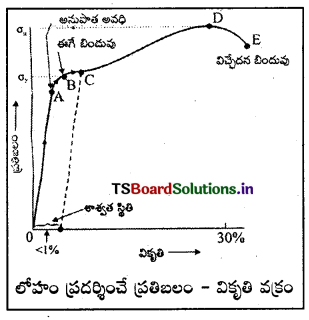
అనుపాత అవధి : ప్రతిబలము వికృతి వక్రరేఖపై OA బిందువుల మధ్య భాగం సరళరేఖ ఈ ప్రాంతంలో ప్రతిబలం వికృతికి అనులోమానుపాతంలో ఉంటుంది. బాహ్య బలం తొలగించగానే వస్తువు సంపూర్ణంగా యథాస్థితి పొందుతుంది. అందువల్ల ‘A’ బిందువును అనుపాత అవధి అంటారు.
స్థితిస్థాపక అవధి : ప్రతిబలము – వికృతి వక్రంలోని AB ప్రాంతము వక్రరేఖ. ఈ ప్రాంతంలో ప్రతిబలము, వికృతికి రేఖీయ సంబంధం కలిగి ఉండదు. కాని బాహ్యబలాన్ని తొలగించగానే వస్తువు తన యథాస్థితిని సంపూర్ణంగా పొందుతుంది. అందువల్ల B బిందువును ఈగే బిందువు లేదా స్థితిస్థాపక అవధి అంటారు.
ఈగే బిందువును చేరడానికి ప్రయోగించిన బాహ్యబలాన్ని ఈగుడుబలం అంటారు.
శాశ్వత స్థితి : ప్రతిబలం – వికృతి వక్రంలో బాహ్యబలాన్ని ‘C’ బిందువు వరకు పెంచి తొలగిస్తే వస్తువు తన పూర్వ స్థితిని సంపూర్ణంగా పొందలేదు. వస్తువులో కొంత వికృతి శాశ్వతంగా మిగిలిపోతుంది. అందువల్ల ‘C’ బిందువును శాశ్వత స్థితి బిందువు అంటారు.
విచ్ఛేదన ప్రతిబలము : ప్రతిబలం-వికృతి వక్రంలో వస్తువుపై ప్రతిబలాన్ని ఈగే బిందువు దాటి ప్రయోగిస్తే (E బిందువు వరకు) ప్రతిబలంలో స్వల్ప మార్పుకే వికృతి విపరీతంగా పెరిగి E అను బిందువు వద్ద తీగ సన్నబడి తెగిపోతుంది. తీగ తెగిపోవడానికి అవసరమైన E బిందువు వద్ద గల ప్రతిబలాన్ని విచ్ఛేదన ప్రతిబలం అంటారు.
ప్రశ్న 9.
ఏనుగు దంతంతో, బంక మట్టితో చేసిన రెండు సర్వసమాన బంతులను కొంత ఎత్తు నుంచి కిందికి వేసినారు. నేలను తాకిన తరువాత రెండింటిలో ఏది ఎక్కువ ఎత్తుకు లేస్తుంది ? ఎందువల్ల ?
జవాబు:
ఏనుగు దంతంతోను మరియు బంకమట్టితోను తయారుచేసిన రెండు సర్వసమానమైన బంతులను ఒకే ఎత్తు నుంచి జారవిడిచితే ఏనుగు దంతంతో చేసిన బంతి ఎక్కువ ఎత్తుకు లేస్తుంది.
వివరణ : 1) బంకమట్టి ప్లాస్టిక్ పదార్థము. అనగా దీని మీద బాహ్యబలం ప్రయోగిస్తే దాని ఆకారం మారుతుంది. పైనుండి క్రింద పడి నేలను తాకగానే వస్తువుకు గల శక్తి దానిలో విరూపణ కలిగించడానికి సరిపోవడం వల్ల బంకమట్టి ముద్ద దాదాపు సంపూర్ణ అస్థితిస్థాపక అభిఘాతానికి లోనుగావడం వల్ల పైకి లేవదు.
2) ఏనుగు దంతము దృఢమైన నిర్మాణం గల పదార్థంతో చేయబడటం వల్ల ఎక్కువ స్థితిస్థాపకతను కలిగి ఉంటుంది. ఫలితంగా నేలను తాకినపుడు దాని ఆకారంలో విరూపణ అతిస్వల్పంగా ఉండి దంతపు బంతి స్థితిస్థాపక అభిఘాతానికి లోనై ఎక్కువ ఎత్తు పైకి లేస్తుంది.

ప్రశ్న 10.
వంతెనలు, భవనాల నిర్మాణంలో భారం వితరణ చెందని స్తంభాల కంటే వితరిత స్తంభాలను వాడతారు. ఎందుకు ?
జవాబు:
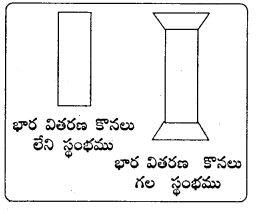
భవనాలు, వంతెనలు వంటి కట్టడాలకు ఆధారంగా ఉండవలసిన దూలాలవంటివి నిర్మించేటపుడు నిర్మాణంలో వాడిన పదార్థాల స్థితిస్థాపక ధర్మాలతో పాటు నిర్మాణపు ఆకారం వల్ల కూడా దృఢత్వం సంతరించు కుంటుంది. స్థంభాలు లేదా కాలమ్స్ విషయంలో కొనలు ఉన్న స్తంభాలు (వితరిత స్తంభాలు), కొనలు లేని (వితరితం చెందని) స్థంభాల కన్నా ఎక్కువ భారం మోయగలుగుతాయి. అందువల్ల పెద్ద పెద్ద నిర్మాణాలలో భార వితరిత కొనలు ఉన్న స్థంభాలను ఎక్కువగా వాడతారు.
ప్రశ్న 11.
భూమిపై పర్వతాల గరిష్ఠ ఎత్తు సుమారు 10 కి.మీ. మాత్రమే ఎందుకు ఉంటుందో వివరించండి.
జవాబు:
రాళ్ళ స్థితి స్థాపక ధర్మాలను పరిగణనలోకి తీసుకొని భూమిపై పర్వతాల గరిష్ఠ ఎత్తు సుమారు 10 కి.మీ. దాటదు అని వివరించవచ్చు.
రాయి స్థితిస్థాపక అవధి సుమారు 30 × 107 న్యూ/మీ3 మరియు రాయి తయారుచేయబడిన పదార్థ సాంద్రత ρ = 3 × 103 కి.గ్రా./మీ3.
కావున h ఎత్తు గల రాళ్ళ పర్వతాల వల్ల పర్వతం అడుగున ఉన్న రాయిపై ప్రతిబలము ప్రతిబలము = hρg న్యూ/మీ2. ఈ ప్రతిబలము రాయి స్థితిస్థాపక హద్దులలో గల ప్రతిబలము దాటరాదు. ఒకవేళ దాటితే రాయి స్థితిస్థాపక ధర్మాలు కోల్పోయి పూర్తిగా విరూపణం చెందే అవకాశం ఎక్కువ.
∴ 30 × 107 = hpg లేదా 30 × 107 = h . 3 × 103 × 10
∴ h = 104 = 10 కి.మీ.
అందువల్ల భూమిపై పర్వతాల ఎత్తు గరిష్ఠంగా 10 కి.మీ.కు మించదు.

ప్రశ్న 12.
సాగదీసిన తీగలో స్థితిస్థాపక స్థితిజశక్తి భావనను వివరించి దానికి సమాసాన్ని రాబట్టండి.
జవాబు:
తీగపై తన్యజ ప్రతిబలం పనిచేసినపుడు అంతరపరమాణు బలాలకు వ్యతిరేకంగా పని జరుగుతుంది. ఈ పని తీగలో స్థితిస్థాపక స్థితిజశక్తిగా మిగిలిపోతుంది.
‘l’ పొడవు గల, A మధ్యచ్ఛేద వైశాల్యం గల తీగపై F బలం ప్రయోగించామనుకోండి. తీగ యంగ్ గుణకము Y అనుకొనుము.
Y = \(\frac{\mathrm{F} / \mathrm{A}}{l / \mathrm{L}}\) సమీకరణం నుండి F = \(\frac{\text { YAl }}{\text { L }}\)
తీగలో ∆l పొడవులో వృద్ధి కలిగించడానికి చేసిన పని ∆W అనుకుంటే తీగను ‘l’ పొడవు సాగదీయడానికి చేసిన పని
∴ W = \(\int \mathrm{dw}=\int_0^l \mathrm{~F} \cdot \Delta l=\int_0^l \frac{\mathrm{YA} l}{\mathrm{~L}} \mathrm{~d} l=\frac{1}{2} \mathrm{YA} \frac{l^2}{\mathrm{~L}}\)
∴ W = \(\frac{1}{2}\) Y . AL . \(\frac{l^2}{\mathrm{~L}}\) = \(\frac{1}{2}\) × యంగ్ గుణకము × తీగ ఘ.ప. × (వికృతి)2 ……………. (1)
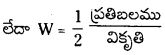 × ఘ.ప. × (వికృతి)2 = \(\frac{1}{2}\) ప్రతిబలము × వికృతి × ఘ.ప.
× ఘ.ప. × (వికృతి)2 = \(\frac{1}{2}\) ప్రతిబలము × వికృతి × ఘ.ప.
ప్రమాణ ఘనపరిమాణానికి వికృతి శక్తి = W/ఘ.ప. = \(\frac{1}{2}\) ప్రతిబలము (σ) × వికృతి (ε) …………. (2)
పై సమీకరణాలలో తీగను సాగదీయడానికి జరిపిన పని W వస్తువులో గల స్థితిస్థాపక శక్తికి సమానము.
దీర్ఘ సమాధాన ప్రశ్నలు
ప్రశ్న 1.
స్థితిస్థాపకతలోని హుక్ నియమాన్ని నిర్వచించి, తీగ పదార్థపు యంగ్ గుణకాన్ని కనుక్కొనే ప్రయోగాన్ని వివరించండి.
జవాబు:
హుక్ సూత్రము :
స్థితిస్థాపక అవధిలో ప్రతిబలము వికృతికి అనులోమానుపాతంలో ఉండును.
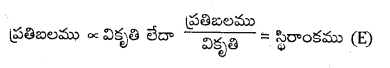
E అనుపాత స్థిరాంకము. దీనిని పదార్థము యొక్క స్థితిస్థాపకతా గుణకము అందురు.
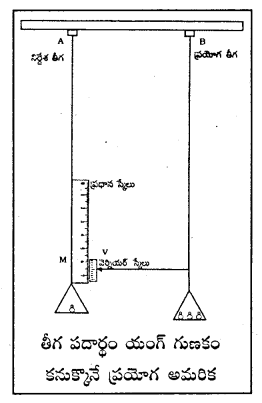
పరికరం వర్ణన : యంగ్ గుణకాన్ని కనుగొనే ప్రయోగం అమరికలో సమాన పొడవు, వ్యాసార్థం గల రెండు తీగలను (A, B) దృఢమైన ఆధారం నుండి వ్రేలాడదీసి వాటి చివర ఒక వెర్నియర్ మాపకాన్ని కలుపుతారు. తీగ A ను మాపకం ప్రధాన స్కేలు (M) కు కలిపి దాని క్రింద భాగంలో ఒక స్థిరమైన బరువును కలిపి తీగ A లో నొక్కులు లేకుండా స్థిరంగా ఉండేటట్లు చేస్తారు. తీగ B ని వెర్నియర్ స్కేలుకు కలుపుతారు.. ఈ తీగకు గల పళ్ళెంలో కావలసిన విధంగా బరువులను మార్చవచ్చు. ఈ ప్రయోగంలో ప్రతిసారి ప్రధాన స్కేలు రీడింగు (M.S.R.) మరియు వెర్నియర్ స్కేలు రీడింగు (V.S.R.) లను కొలుస్తారు.
చేయు విధానము : ప్రయోగపు తీగ నొక్కులు లేకుండా ఉండటానికి తగినంత బరువును కొంకి తీగకు తగిలిస్తారు. వెర్నియర్ మాపకం రీడింగులు కొలుస్తారు. కొంకి బరువులను ప్రతిసారి 1/2 కిలో చొప్పున పెంచుతూ సుమారు 3 కి.గ్రా. వరకు బరువు పెంచుతారు. బరువు పెంచేటప్పుడు ప్రతిసారి ప్రధాన స్కేలు రీడింగు (M.S.R) మరియు వెర్నియర్ స్కేలు రీడింగు (V.S.R) లను కొలుస్తారు.
బరువు 3 కి.గ్రా. వరకు పెంచిన తరువాత క్రమంగా ప్రతిసారి 1/2 కి.గ్రా. చొప్పున తగ్గిస్తారు. బరువు తగ్గించిన ప్రతిసారి ప్రధాన స్కేలు (M.S.R.) మరియు వెర్నియర్ స్కేలు (V.S.R.) రీడింగులు కొలుస్తారు. ఈ విలువలు పట్టికలో పొందుపరుస్తారు.
మొదటి రీడింగును (M1 మరియు e1) లను ఆధారంగా తీసుకొని ప్రతి విలువ (M2, M3 మరియు e2, e3 వంటివి) నుండి తొలి విలువ (M1, e1) లను తీసివేయడం ద్వారా ద్రవ్యరాశిలో మార్పు ‘m’ మరియు దానికి సంబంధించిన సాగుదల ‘e’ లను లెక్కగడతారు.
ద్రవ్యరాశిలో మార్పు m = m2 – m1; తీగలో సాగుదల e = e2 – e1
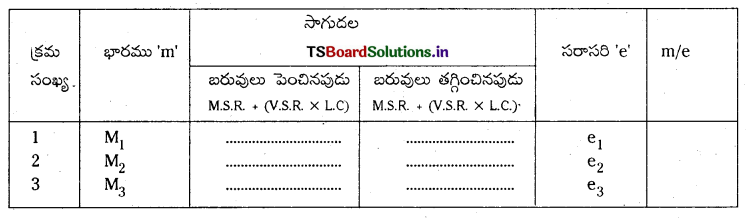
సరాసరి = m/e; తీగపై బలము = mg
తీగ అడ్డుకోత వైశాల్యము = πr2
r = తీగ వ్యాసార్ధము
సాగుదల = e,
తీగ తొలి పొడవు = l
ప్రతిబలము = \(\left(\frac{\mathrm{F}}{\mathrm{a}}\right)=\frac{\mathrm{mg}}{\pi r^2}\)
వికృతి = \(\left(\frac{\mathrm{e}}{l}\right)\)
యంగ్ గుణకము Y = \(\left(\frac{g l}{\pi r^2}\right)\left(\frac{m}{e}\right)\)
ప్రయోగపూర్వకంగా కనుగొనిన విలువలు l, r, e, m లను ఈ సమీకరణంలో ప్రతిక్షేపించి Y విలువ కనుగొంటారు.
జాగ్రత్తలు :
- వ్రేలాడదీయు బరువులు స్థితిస్థాపక అవధి కన్న చాలా తక్కువగా ఉండవలెను.
- ఏకీభవించు వెర్నియర్ స్థానమును పారలాక్సు దోషము లేకుండా కొలవవలెను.

లెక్కలు
ప్రశ్న 1.
1 mmవ్యాసం ఉన్న రాగి తీగను 10 N బలం అనువర్తించి సాగదీశారు. ఆ తీగలోని ప్రతిబలం కనుక్కోండి.
సాధన:
వ్యాసము d = 1 mm;
బలము F = 10N;
∴ వ్యాసార్ధము r = 0.5 mm = = 0.5 × 10-3 m
∴ ప్రతిబలము = \(\frac{\mathrm{F}}{\pi \mathrm{r}^2}=\frac{10}{3.141 \times 0.5 \times 0.5 \times 10^{-6}}=\frac{40 \times 10^6}{3.141}\) = 1.273 × 107 Pa
ప్రశ్న 2.
20 cm పొడవు వున్న టంగ్స్టన్ తీగను 0.1 cm అదనంగా సాగదీశారు. తీగలోని వికృతిని కనుక్కోండి.
సాధన:
తీగ పొడవు l = 20cm = 0.2m;
సాగుదల e = 0.1cm = 1 × 10-3 m
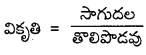
= \(\frac{1 \times 10^{-3}}{0.2}\) = 5 × 10-3 = 0.005
ప్రశ్న 3.
ఇనుప తీగను 1% సాగదీసినట్లయితే దానిలో వచ్చిన వికృతి ఎంత ?
సాధన:
పొడవులో పెరుగుదల = e = 1% = \(\frac{1}{100}\) l
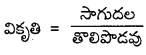
= \(\frac{\mathrm{e}}{l}=\frac{1}{100 \times l}=\frac{1}{100}\) = 0.01

ప్రశ్న 4.
1 mm వ్యాసం, 2m పొడవు ఉన్న ఇత్తడి తీగపై 20 N బలం ప్రయోగించి సాగదీశారు. పొడవులో పెరుగుదల 0.51 mm అయితే, 1) తీగ ప్రతిబలం, 2) వికృతి, 3) యంగ్ గుణకాలను కనుక్కోండి.
సాధన:
తీగ పొడవు l = 2m;
బలము F = 20N;
వ్యాసము d = 1mm = 10-3 m
పొడవులో పెరుగుదల e = 0.51mm = 0.51 × 10-3 m

ప్రశ్న 5.
రాగి, అల్యూమినియం తీగల పొడవుల నిష్పత్తి 3: 2, వ్యాసాల నిష్పత్తి 2: 3, వీటిపై అనువర్తిత బలాల నిష్పత్తి 4:5గా ఉన్నాయి. రెండు తీగల పొడవుల పెరుగుదల నిష్పత్తిని కనుక్కోండి. (YCu = 1.1 × 1011 Nm-2, YAl = 0.7 × 1011 Nm-2)
సాధన:
పొడవుల నిష్పత్తి l1 : l2 = 3 : 2 ;
వ్యాసముల నిష్పత్తి d1 : d2 = 2 : 3
బలాల నిష్పత్తి F1 : F2 = 4:5
Y1 = రాగి యంగ్ గుణకము : 1.1 × 1011
Y2 = అల్యూమినియం యంగ్ గుణకము = 0.7 × 1011
సాగుదల నిష్పత్తి e1 : e2 = ?
e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}=\frac{4 \mathrm{~F} l}{\pi \mathrm{d}^2 \mathrm{Y}}\)
∴ \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{4 \mathrm{~F}_1 l_1}{\pi \mathrm{d}_1^2 \mathrm{Y}_1} \times \frac{\pi \mathrm{d}_2^2 \mathrm{Y}_2}{4 \mathrm{~F}_2 l_2}\)
⇒ \(\frac{\mathrm{e}_1}{\mathrm{e}_2}=\frac{\mathrm{F}_1 l_1 \mathrm{~d}_2^2 \mathrm{Y}_2}{\mathrm{~F}_2 l_2 \mathrm{~d}_1^2 \mathrm{Y}_1}=\frac{4 \times 3 \times 3^2 \times 0.7 \times 10^{11}}{5 \times 2 \times 2^2 \times 1.1 \times 10^{11}}=\frac{189}{110}\)
∴ e1 : e2 = 189 : 110
ప్రశ్న 6.
2 mm2 మధ్యచ్ఛేద వైశాల్యం ఉన్న ఇత్తడి తీగ ఒక కొనను ద్రుఢ ఆధారానికి బిగించి రెండో కొనకు 100 cm3 ఘనపరిమాణం ఉన్న వస్తువును కట్టారు. వస్తువును నీటిలో పూర్తిగా ముంచినప్పుడు తీగ పొడవు 0.11 mm తగ్గింది. తీగ సహజ పొడవును కనుక్కోండి. (Yఇత్తడి : 0.91 × 1011 Nm-2, ρనీరు = 103 kg m-3)
సాధన:
అడ్డుకోత వైశాల్యము A = 2mm2 = 2 × 10-6 m2
వస్తువు ఘనపరిమాణము V = 100cc = 100 × 10-6 m3
పొడవులో తగ్గుదల e’ = 0.11mm = 0.11 × 10-3 m
ఇత్తడి యంగ్ గుణకము Y = 0.91 × 1011 N/m2
నీరు సాంద్రత ρ = 1000 kg / m3; వికృతి e’ = \(\frac{\mathrm{V} \rho \mathrm{g} l}{\mathrm{AY}}\) ని ఉపయోగించగా
తీగ సహజ పొడవు l = \(\frac{\mathrm{e}^{\prime} \mathrm{AY}}{\mathrm{V} \rho \mathrm{g}}=\frac{0.11 \times 10^{-3} \times 2 \times 10^{-6} \times 0.91 \times 10^{11}}{100 \times 10^{-6} \times 1000 \times 9.8}\)
∴ l = \(\frac{0.2002 \times 10^2}{9.8}=\frac{20.02}{9.8}\) = 2.043 m

ప్రశ్న 7.
ఒకే పదార్థంతో చేసిన రెండు తీగల వ్యాసార్ధాల, పొడవుల నిష్పత్తులు ఒకే విధంగా ఉన్నాయి. ఆ నిష్పత్తి 1 : 2 రెండింటిలోనూ వచ్చిన దైర్ఘ్యవృద్ధి సమంగా ఉంటే, వాటిపై వేసిన భారాల నిష్పత్తి ఎంత ?
సాధన:
పొడవుల నిష్పత్తి l1 : l2 = 1 : 2; .
తీగలలో సాగుదలలు సమానము ⇒ e1 = e2;
వ్యాసార్ధముల నిష్పత్తి r1 : r2 = 1 : 2
రెండు తీగలు ఒకే పదార్థముతో చేయబడినవి ⇒ Y1 = Y2
వ్రేలాడదీసిన ద్రవ్యరాశుల నిష్పత్తి m1 : m2 = ?
Y = \(\frac{\mathrm{mg}}{\pi \mathrm{r}^2} \frac{\mathrm{l}}{\mathrm{e}}\) ని ఉపయోగించగా
\(\frac{\mathrm{m}_1}{\mathrm{~m}_2}=\frac{\mathrm{Y}_1 \mathrm{r}_1^2 l_2}{l_1 \mathrm{Y}_2 \mathrm{r}_2^2}=\frac{1 \times 2}{1 \times 2^2}=\frac{1}{2}\)
∴ m1 : m2 = 1 : 2
ప్రశ్న 8.
వేరు వేరు పదార్థాలతో చేసిన రెండు తీగలు ఒకే పొడవు, మధ్యచ్ఛేదాన్ని కలిగి ఉన్నాయి. వీటిపై సమానమైన బలాలను అనువర్తించినప్పుడు రెండింటి పొడవుల పెరుగుదల నిష్పత్తి ఎంత ?
(Y1 = 0.9 × 1011 Nm-2, Y2 = 3.60 × 1011 Nm-2)
సాధన:
రెండు తీగల పొడవులు సమానము ⇒ l1 = l2; తీగల అడ్డుకోత వైశాల్యములు సమానము A1 = A2
Y1 = 0.9 × 1011 Nm-2
Y2 = 3.60 × 1011 Nm-2
సాగుదల e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}\)
∴ \(\frac{e_1}{e_2}=\frac{F_1 l_1}{A_1 Y_1} \cdot \frac{A_2 Y_2}{F_2 l_2}\) (∵ ఇందులో F, I మరియు A లు సమానము)
∴ \(\frac{e_1}{e_2}=\frac{Y_2}{Y_1}\)
∴ \(\frac{e_1}{e_2}=\frac{3.60 \times 10^{11}}{0.9 \times 10^{11}}=\frac{4}{1}\) (లేదా) e1 : e2 = 4 : 1

ప్రశ్న 9.
2.5 m పొడవు, 1.5 × 106 m2 మధ్యచ్ఛేద వైశాల్యం ఉన్న లోహతీగను 2 mm సాగదీశారు. తీగ యంగ్ గుణకం 1.25 × 1011 Nm-2 అయితే దానిలో ఉండే తన్యతను కనుక్కోండి.
సాధన:
తీగ పొడవు l = 2.5m
సాగుదల e = 2 m.m = 2 × 10-3 m
అడ్డుకోత వైశాల్యము A = 1.5 × 10-6 m2
Y = 1.25 × 1022 N/m2
తన్యత T = mg = F = ?
Y = \(\frac{\mathrm{Fl}}{\mathrm{Ae}}\) ⇒ F = \(\frac{\mathrm{YAe}}{l}\)
∴ T = \(\frac{1.25 \times 10^{11} \times 1.5 \times 10^{-6} \times 2 \times 10^{-3}}{2.5}\) = \(\frac{3.75 \times 10^2}{2.5}\) = 150 N
ప్రశ్న 10.
ఒకే పొడవు, మధ్యచ్ఛేదం ఉన్న అల్యూమినియం, ఉక్కు తీగల కొనలను కలిపారు. ఈ మిశ్రమ తీగ ఒక కొనను ద్రుఢ ఆధారానికి బిగించి రెండో కొనకు భారాన్ని వేలాడదీశారు. మిశ్రమ తీగ పొడవులో పెరుగుదల 1.35mm ఉంటే 1) రెండు తీగలపై పనిచేసే ప్రతిబలాల 2) రెండు తీగలలో వచ్చే వికృతుల నిష్పత్తులను కనుక్కోండి.
(YAL = 0.7 × 1011 Nm-2, Ysteel = 2 × 1011 Nm-2)
సాధన:
i) రెండు తీగల పొడవులు సమానము ⇒ l1 = l2 ;
అడ్డుకోత వైశాల్యములు సమానము ⇒ A1 = A2
సంయోగ తీగలో రెండు తీగలపై ఒకే బలము పనిచేయును;
∴ ప్రతిబలాల నిష్పత్తి = 1 : 1
ii) మొత్తము సాగుదల e = 1.35mm = eAl + es
అల్యూమినియం యంగ్ గుణకము 7 × 1011 N/m2,
స్టీలు తీగ యంగ్ గుణకము, Y = 2 × 1011 N/m2
సాగుదల e = \(\frac{\mathrm{Fl}}{\mathrm{AY}}\) కాని F, I మరియు A లు సమానము.
∴ e ∝ \(\frac{1}{\mathrm{Y}}\) లేదా \(\frac{\mathrm{e}_{\mathrm{A} l}}{\mathrm{e}_{\mathrm{S}}}=\frac{\mathrm{Y}_{\mathrm{S}}}{\mathrm{Y}_{\mathrm{A} l}}=\frac{20 \times 10^{10}}{7 \times 10^{10}}=\frac{20}{7}\) లేదా 20 : 7
∴ తీగలలో వికృతిల నిష్పత్తి 20 : 7.
ప్రశ్న 11.
ఒక పదార్థంతో చేసిన 2 cm భుజం కలిగిన ఘనంపై ప్రయోగించిన 0.3 N స్పర్శాబలం దాని పై తలాన్ని 0.15 cm స్థానభ్రంశం చెందించింది. ఘనం కింది తలాన్ని స్థిరంగా ఉంచారు. పదార్థం విమోటన గుణకం కనుక్కోండి.
జవాబు:
ఘనము యొక్క ఒక భుజము పొడవు a = 2.0cm = 2 × 102 m
∴ ఘనము యొక్క ఒక తలము వైశాల్యము A = 4 × 10-4 m2
ఉపరితల పొర స్థాన భ్రంశం = 0.15cm = 0.15 × 10-2m
స్పర్శీయ బలము F = 0.30N
విమోటనా గుణకము η = \(\frac{\mathrm{F}}{\mathrm{A}} \cdot \frac{\mathrm{x}}{\Delta \mathrm{x}}=\frac{0.30}{4 \times 10^{-4}} \frac{2 \times 10^{-2}}{0.15 \times 10^{-2}}\)
∴ η = \(\frac{0.60 \times 10^4}{0.60}\) = 1 × 104 N/m2

ప్రశ్న 12.
1000 cm3 ఘనపరిమాణం ఉన్న గోళాకార బంతిపై 10 atm పీడనాన్ని ప్రయోగించారు. ఘనపరిమాణంలో వచ్చిన మార్పు 10-2 cm3. బంతిని ఇనుముతో తయారుచేసినట్లైతే దాని యంగ్ గుణకాన్ని కనుక్కోండి. (1 atm = 1 × 105 Nm-2)
సాధన:
గోళాకార బంతి ఘనపరిమాణము V = 1000 cm3 = 10-3 m3 (∵ 1M3 = 106 cm3)
పీడనము P = 10 అట్మాస్పియర్లు = 10 × 105 పాస్కల్ ( ∵ 1 atm = 105 cm)
ఘనపరిమాణములో మార్పు ∆V = 10-8 cm3 స్థూల గుణకము K ?
K = \(\frac{\mathrm{PV}}{\Delta \mathrm{V}}=\frac{10^6 \times 10^{-3}}{10^{-8}}\) = 1 × 1011 N/m2
ప్రశ్న 13.
1 cm భుజం ఉన్న రాగి ఘనాన్ని 100 atm పీడనానికి గురిచేశారు. రాగి ఆయత గుణకం 1.4 × 1011 Nm-2 అయితే ఘనపరిమాణంలో వచ్చే మార్పును కనుక్కోండి. (1 atm = 1 × 105 Nm-2)
సాధన:
ఒక రాగి ఘనము ఒక్కొక్క భుజము పొడవు ‘a’ 1 సెం.మీ. = 10-2 m
∴ ఘనము ఘనపరిమాణము = 10-6m
పీడనము P = 100 అట్మాస్పియర్లు = 100 × 105 = 107 పాస్కల్లు
స్థూల గుణకము K = 1.4 × 1011 N/m2;
ఘనపరిమాణములో మార్పు ∆V = \(\frac{P . V}{K}=\frac{10^7 \times 10^{-6}}{1.4 \times 10^{11}}=\frac{10^{-10}}{1.4}\)
= 0.7143 × 10-10 m3
ప్రశ్న 14.
ఇచ్చిన నీటి ఘనపరిమాణాన్ని 2% తగ్గించడానికి ఎంత పీడనం అవసరమవుతుంది ? నీటి ఆయత గుణకం 2.2 × 109 Nm-2.
సాధన:
స్థూల వికృతి = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) = 2% ⇒ ∆V = \(\frac{2}{100}\) V
స్థూల గుణకము _ K = 2.2 × 109 Nm-2
∴ కావలసిన పీడనము P = \(\frac{\mathrm{K} \Delta \mathrm{V}}{\mathrm{V}}=\frac{2.2 \times 10^9 \times 2 \mathrm{~V}}{\mathrm{~V} \times 100}\) = 4.4 × 107 పాస్కల్

ప్రశ్న 15.
20 cm పొడవు ఉన్న ఉక్కు తీగను సాగదీసి దాని పొడవును 0.2 cm పెంచారు. ఉక్కు ప్వాజూన్ నిష్పత్తి 0.19 అయితే, తీగలో వచ్చే పార్శ్వ వికృతి ఎంత ?
సాధన:
తీగ పొడవు l = 20cm = 0.20m, ప్వాజూన్ నిష్పత్తి σ = 0.19
పొడవులో సాగుదల ∆l = 0.2cm = 2 × 103 m;
పార్శ్వీయ వికృతి = ?
పార్శ్వ వికృతి = σ × అనుదైర్ఘ్య వికృతి ‘e’;
కాని e = \(\)
∴ పార్శ్వీయ వికృతి = σ \(\frac{\Delta l}{l}\) = \(\frac{0.19 \times 2 \times 10^{-3}}{0.20}\) = 1.9 × 10-3 = 0.0019m.
ముఖ్యమైన అదనపు లెక్కలు
ప్రశ్న 1.
4.7 m పొడవు, 3.0 × 10-5 m2 మధ్యచ్ఛేద వైశాల్యం ఉన్న ఉక్కు తీగ, 3.5 m పొడవు, 4.0 × 10-5 m2 తీగ రెండూ ఇచ్చిన భారం వల్ల సమానంగా సాగాయి. ఉక్కు రాగి యంగ్ గుణకాల మధ్యచ్ఛేద వైశాల్యం ఉన్న రాగి నిష్పత్తి ఎంత ?
సాధన:
ఉక్కు తీగకు a1 = 3.0 × 10-5 m2; l1 = 4.7 m; ∆l1 = ∆l ; F1 = F
రాగి తీగకు a2 = 4.0 × 10-5 m2; l2 = 3.5 m; ∆l2 = ∆l ; F2 = F
Y1, Y2 లను వరుసగా ఉక్కు, కాపర్ల యంగ్ గుణకాలు అనుకొనుము.
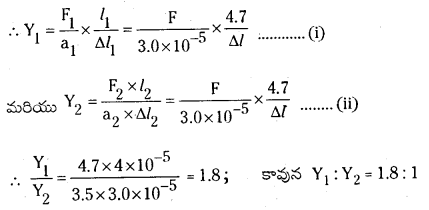

ప్రశ్న 2.
పటంలో ఒక పదార్థం వికృతి-ప్రతిబలం వక్రం చూపించడమైనది. ఈ పదార్థం ఎ) యంగ్ గుణకం, బి) ఉజ్జాయింపు ఈగే సామర్థ్యం ఎంత ?
సాధన:
ఎ) గ్రాఫ్ నుండి ప్రతిబలము = 150 × 106 Nm-2,
వికృతి = 0.002
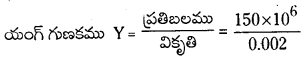
= 7.5 × 1010 Nm-2
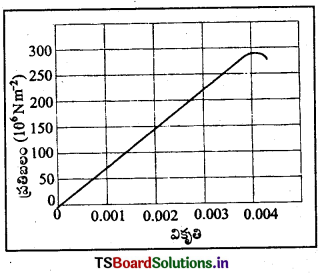
బి) ఉజ్జాయింపుగా ఊగే సామర్థ్యము అది భరించగల అత్యధిక ప్రతిబలానికి సమానము.
∴ ఉజ్జాయింపుగా ఊగే సామర్థ్యము
= 300 × 106 Nm-2 = 3 × 108 Nm-2
ప్రశ్న 3.
రెండు పదార్థాలు A, B ప్రతిబలం – వికృతి వక్రాలను పటంలో ఇవ్వడమైంది. రెండు వక్రాలను ఒకే స్కేలు ప్రకారం గీశారు.
ఎ) రెండు పదార్థాల్లో ఏ పదార్థం యంగ్ గుణకం ఎక్కువ ?
బి) రెండు పదార్థాల్లో ఏది బలమైనది ?
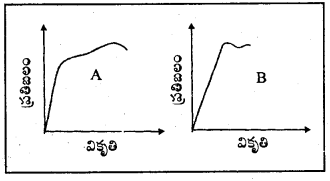
సాధన:
ఎ) ఇచ్చిన రెండు ప్రతిబలము – వికృతి రేఖాపటాలలో A గ్రాఫ్ ప్రతిబలము B కన్న ఎక్కువ కావున A కి యంగ్ గుణకము ఎక్కువ. (Y = ప్రతిబలము/వికృతి కావున)
బి) ఒక వస్తువు యొక్క దృఢత్వము దానిని తెంపటానికి కావలసిన ప్రతిబలంపై ఆధారపడును. A కి ప్రతిబలం ఎక్కువ కావున కన్న A దృఢమైనది.
ప్రశ్న 4.
కింద ఇచ్చిన రెండు ప్రవచనాలను జాగ్రత్తగా చదివి అది తప్పా, ఒప్పా కారణాలతో వివరించండి.
ఎ) రబ్బరు యంగ్ గుణకం ఉక్కు కంటే ఎక్కువ.
బి) తీగ చుట్ట సాగుదలను దాని విమోటన గుణకం ఆధారంగా నిర్ణయించవచ్చు.
సాధన:
ఎ) ఈ వాక్యము అబద్ధము. ఒకే ప్రతిబలానికి స్టీలు కన్న రబ్బరుకు వికృతి ఎక్కువ. స్థితిస్థాపక గుణకము వికృతికి విలోమానుపాతంలో ఉండును. yo : 1/వికృతి
బి) ఈ వాక్యము నిజము. స్ప్రింగ్ను సాగదీస్తే మనం వాడిన బలం తీగ పొడవు మారకుండా స్ప్రింగ్ ఆకారాన్ని మారుస్తుంది. అందువల్ల ఈ ప్రక్రియలో దృఢతా గుణకము లెక్కలోనికి వస్తుంది.

ప్రశ్న 5.
పటంలో చూపించినట్లు 0.25 cm వ్యాసం ఉన్న ఉక్కు, ఇత్తడి తీగలను భారయుతం చేశారు. భారరహిత స్థితిలో ఉక్కుతీగ పొడవు 1.5 m, ఇత్తడి తీగ పొడవు 1.0 m. ఉక్కు, ఇత్తడి తీగలలో వచ్చే దైర్ఘ్యవృద్ధి లెక్కించండి.
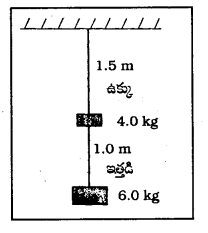
సాధన:
ఉక్కుతీగకు, ఉక్కు తీగపై మొత్తం బలము
F1 = 4 + 6 = 10 kg f = 10 × 9.8 N;
l1 = 1.5 m, ∆l1 = ?; 2r1 = 0.25 cm
లేదా r1 = (0.25/2) cm = 0.125 × 10-2 m;
Y1 = 2.0 × 1011 Pa
ఇత్తడి తీగకు F2 = 6.0 kg, f = 6 × 9.8 N; 2r2 = 0.25 cm
లేదా r2 = (0.25/2) cm = 0.125 × 10-2 m;
Y2 = 0.91 × 1011 Pa, l2 = 1.0 m, ∆l2= ?
Y1 = \(\frac{\mathrm{F}_1 \times l_1}{\mathrm{a}_1 \times \Delta l_1}=\frac{\mathrm{F}_1 \times l_1}{\pi \mathrm{r}_1^2 \times \Delta l_1}\)
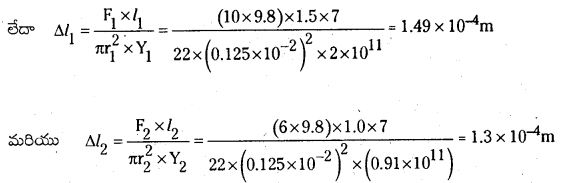
ప్రశ్న 6.
అల్యూమినియం ఘనం అంచు పొడవు 10 cm. ఘనం ఒక తలాన్ని నిలువు గోడకు గట్టిగా బిగించారు. ఘనం ఎదురు తలానికి 100 kg ద్రవ్యరాశిని తగిలించారు. అల్యూమినియం విమోటన గుణకం 25 GPa. ఈ తలం నిట్టనిలువు అపవర్తనం ఎంత ?
సాధన:
A = 0.10 × 0.10 = 10-2 m2; F = mg = 100 × 10 N
విమోటన వికృతి = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\) = \(\frac{(\mathrm{F} / \mathrm{A})}{\mathrm{G}}\) or ∆L = \(\frac{\mathrm{FL}}{\mathrm{AG}}\) = \(\frac{(100 \times 10) \times 0.10}{10^{-2} \times\left(25 \times 10^9\right)}\) = 4 × 10-7 m.

ప్రశ్న 7.
50,000 kg ద్రవ్యరాశి ఉన్న భారీ కట్టడానికి ఆధారంగా నాలుగు బోలు స్థూపాకార, మృదు ఉక్కుస్తంభాలు ఉన్నాయి. ప్రతీ స్తంభం లోపలి, బాహ్య వాసార్ధాలు వరుసగా 30, 60 cm గా ఉన్నాయి. భార వితరణ ఏకరీతిగా ఉన్నదనుకొని ప్రతీ స్తంభంలో వచ్చే సంపీడన వికృతిని కనుక్కోండి.
సాధన:
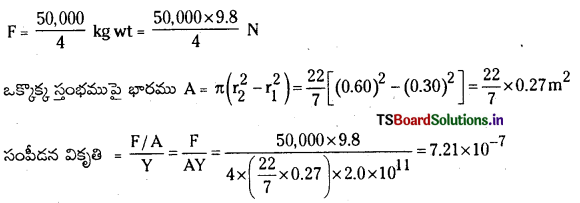
ప్రశ్న 8.
15.2 mm × 19.1 mm కొలతలు ఉన్న దీర్ఘచతురస్రాకార రాగి ముక్కను 44,500 N తన్యత బలంతో కేవలం స్థితిస్థాపక విరూపణ కలిగే విధంగా లాగారు. దాని మూలంగా కలిగే ఫలిత వికృతిని గణించండి.
సాధన:
దత్తాంశం నుండి A = 15.2 × 19.2 × 10-6 m2; F = 44,500 N; G = 42 × 109 Nm-2
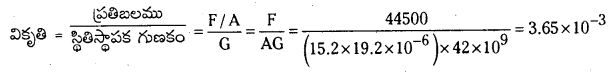
ప్రశ్న 9.
స్కీయింగ్ ప్రాంతంలో ఉన్న చైర్ లిఫ్ట్ను మోసే ఉక్కు కేబుల్ వ్యాసార్ధం 1.5cm. గరిష్ట ప్రతిబలం విలువ 108 Nm-2 ను దాటకూడదు. అంటే, కేబుల్ గరిష్ఠంగా ఎంత బరువును మోయగలదు ?
సాధన:
గరిష్ఠ భారము = గరిష్ఠ ప్రతిబలము × అడ్డుకోత వైశాల్యము
= 108 × πr2 = 108 × (22/7) × (1.5 × 10-2)2 = 7.07 × 104 N
ప్రశ్న 10.
15 kg ద్రవ్యరాశి ఉన్న ద్రుఢమైన కడ్డీని సౌష్ఠవంగా అమర్చి ఉన్న మూడు తీగలు మోస్తున్నాయి. ప్రతి తీగ పొడవు 2.0 m. రెండు చివరల ఉన్న తీగలు రాగికి కాగా, మధ్యలో తీగ ఇనుముతో తయారయింది. అన్ని సమాన తన్యతను కలిగి ఉండాలంటే, వాటి వ్యాసాల నిష్పత్తులు ఎలా ఉండాలి ?
సాధన:
ప్రతీ తీగ ఒకే తన్యత 1 ను కల్గి ఉన్నందున, అవి ద్రుఢమైన కడ్డీ ద్రవ్యరాశి కారణంగా ఒకే విధమైన సాగుదలను కలిగి ఉంటాయి. ప్రతీ తీగ ఒకే పొడవు కలిగి ఉన్నందున వాటికి సమాన వికృతి ఉంటుంది. తీగ వ్యాసం D అయితే
Y = \(\frac{4 \mathrm{~F} / \pi \mathrm{D}^2}{\text { వికృతి }}\) (లేదా) D2 ∝ 1/Y
∴ \(\frac{D_{\mathrm{cu}}}{\mathrm{D}_{\mathrm{iron}}}\) = \(\sqrt{\frac{Y_{\text {iron }}}{Y_{\mathrm{Cu}}}}\) = \(\sqrt{\frac{190 \times 10^9}{110 \times 10^9}}\) = \(\sqrt{\frac{19}{11}}\) = 1.31

ప్రశ్న 11.
1.0 m సహజ పొడవు ఉన్న ఉక్కు తీగ ఒక చివర 14.5 kg ద్రవ్యరాశిని కట్టి నిలువు తలంలో వృత్తాకారంగా తిప్పారు. దాని కనిష్ఠ బిందువు వద్ద కోణీయ వేగం 2 reu/s. తీగ మధ్యచ్ఛేద వైశాల్యం 0.065 cm2. ద్రవ్యరాశి వృత్తాకార పథంలో కనిష్ఠ బిందువు వద్ద ఉన్నప్పుడు తీగలో వచ్చే దైర్ఘ్యవృద్ధిని లెక్కించండి.
సాధన:
దత్తాంశం నుండి m = 14.5 kg; l = r = 1 m; v = 2 rps; A = 0.065 × 10-4 m2
నిలువు వృత్తంలో కనిష్ఠ బిందువు వద్ద మొత్తము బలము
F = mg + mr ω2 = mg + mr 4 π2 v2 = 14.5 × 9.8 + 14.5 × 1 × 4 × (22/7)2 × 22
= 142.1+ 2291.6 = 2433.7 N
Y =\(\frac{\mathrm{F}}{\mathrm{A}} \times \frac{l}{\Delta l}\) or ∆l = \(\frac{\mathrm{Fl}}{\mathrm{AY}}=\frac{2433.7 \times 1}{\left(0.065 \times 10^{-4}\right) \times\left(2 \times 10^{11}\right)}\) = 1.87 × 10-3 m = 1.87mm
ప్రశ్న 12.
క్రింద ఇచ్చిన దత్తాంశం సహాయంతో నీటి ఆయత గుణకాన్ని కనుక్కోండి. తొలి ఘనపరిమాణం = 100.0 litre, పీడనం పెరుగుదల = 100.0 atm (1 atm = 1,013 × 105 Pa), తుది ఘనపరిమాణం = 100,5 litre. నీటి ఆయతన గుణకాన్ని గాలి (స్థిర ఉష్ణోగ్రత వద్ద) ఆయత గుణకంతో పోల్చండి. ఈ నిష్పత్తి ఎందుకు చాలా అధికంగా ఉంటుందో సులభరీతిలో వివరించండి.
సాధన:
దత్తాంశం నుండి V = 100 litre = 100 × 10-3 m3; p = 100 atm = 100 × 1.013 105 Pa.
V + ∆V = 100.5 లీటర్లు (లేదా) ∆V = (V + ∆V) – V = 100.5 – 100 = 0.5 litre = 0.5 ×10-3 m3.
ఆయతన గుణకము, B = \(\frac{\mathrm{pV}}{\Delta \mathrm{V}}\) = \(\frac{100 \times 1.013 \times 10^5 \times 100 \times 10^{-3}}{0.5 \times 10^{-3}}\) = 2.026 × 109 Pa
గాలి ఆయతన గుణకము 1.0 × 105 Pa
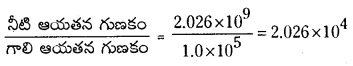
వాయువులలో అణువుల మధ్య దూరము చాలా ఎక్కువ. వాటి మధ్య గల బంధాలు చాలా బలహీనమైనవి. అందువల్ల ద్రవాల కన్నా వాయువుల ఆయతన గుణకం చాలా తక్కువ.

ప్రశ్న 13.
ఉపరితలంపై నీటి సాంద్రత 1.03 × 103 kg m-3 గా ఉన్నట్లయితే, 80.00 atm పీడనం ఉండే లోతులో నీటి సాంద్రత ఎంత ఉంటుంది ?
సాధన:
దత్తాంశం నుండి_p = 80.00 atm = 80.0 × 1.013 × 105 Pa; సంపీడ్యత \(\frac{1}{B}\) = 45.8 × 10-11 Pa-1
ఉపరితలం వద్ద నీటి సాంద్రత ρ = 1.03 × 103 kg m-3
M ద్రవ్యరాశి గల నీటికి ఉపరితలం వద్ద మరియు ఇచ్చిన లోతు వద్ద నీటి ఘనపరిమాణాలు
V = \(\frac{M}{\rho}\) మరియు V’ = \(\frac{\mathrm{M}}{\rho^{\prime}}\)
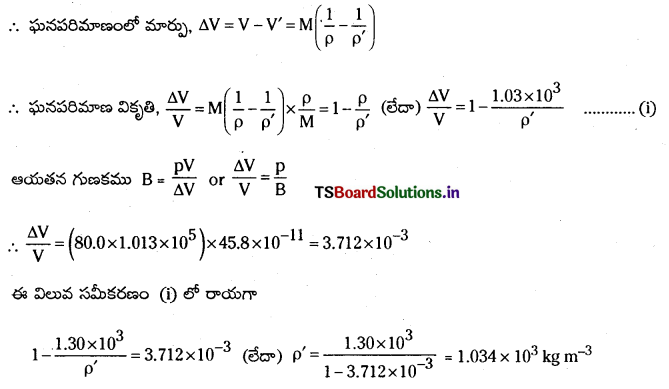
ప్రశ్న 14.
10 atm హైడ్రాలిక్ పీడనానికి గురిచేసిన గాజు పలక ఘనపరిమాణంలో వచ్చే అంశిక మార్పు కనుక్కోండి.
సాధన:
దత్తాంశం నుండి p = 10 atm = 10 × 1.013 × 105 Pa; B = 37 × 109 Nm-2
ఘనపరిమాణ వికృతి = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{\mathrm{p}}{\mathrm{B}}=\frac{10 \times 1.013 \times 10^5}{37 \times 10^9}\) = 2.74 × 10-5
∴ ఘనపరిమాణంలో అంశిక మార్పు = \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) = 2.74 × 10-5
ప్రశ్న 15.
7.0 × 106 Pa హైడ్రాలిక్ పీడనానికి గురయిన 10 cm భుజం ఉన్న ఘన రాగి ఘనం ఏర్పడే ఘనపరిమాణ సంకోచాన్ని నిర్ణయించండి.
సాధన:
దత్తాంశం నుండి L = 10 cm = 0.10 m; p = 7 × 106 Pa; B = 140 GPa = 140 × 109 Pa
B = \(\frac{\mathrm{pV}}{\Delta \mathrm{V}}=\frac{\mathrm{p} L^3}{\Delta \mathrm{V}}\) or ∆V = \(\frac{\mathrm{pL}^3}{\mathrm{~B}}=\frac{\left(7 \times 10^6\right) \times(0.10)^3}{140 \times 10^9}\) = 5 × 10-8; m3 = 5 × 10-2 mm3

ప్రశ్న 16.
ఒక లీటరు నీటిని 0.10% సంపీడనం చెందించడానికి ఎంత పీడనం అవసరం ?
సాధన:
దత్తాంశం నుండి V = 1 లీటరు = 10-3 m3; ∆V/V = 0.10/100 = 10-3
B = \(\frac{\mathrm{pV}}{\Delta \mathrm{V}}\) (లేదా) p = B\(\frac{\Delta V}{V}\) = (2.2 × 109) × 10-3 = 2.2 × 106 Pa
ప్రశ్న 17.
అధిక పీడనాల వద్ద పదార్థాల ప్రవర్తనను తెలుసుకోవడానికి పటంలో చూపిన ఆకృతిలో ఉన్న ఏక స్పటిక వజ్రం (స్వర్ణకారులు వాడేది) దాగిలి (Anvil) ని వాడతారు. సన్నకొన వద్ద ఉండే సమతలం వ్యాసం 0.50mm. వెడల్పు కొనను 50,000 N సంపీడ్యత బలానికి గురిచేశారు. దాగిలి మొన (tip) పై పనిచేసే పీడనం ఎంత ?
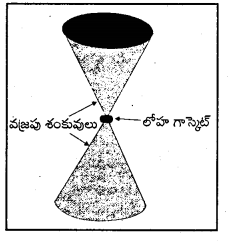
సాధన:
దత్తాంశం నుండి D = 0.5 mm = 0.5 × 10-3 m = 5 × 10-4 m
F = 50,000 N = 5 × 104 N
దాగిలి మొనపై పీడనము, P = \(\frac{\mathrm{F}}{\pi \mathrm{D}^2 / 4}=\frac{4 \mathrm{~F}}{\pi \mathrm{D}^2}\)
∴ P = \(\frac{4 \times\left(5 \times 10^4\right)}{(22 / 7) \times\left(5 \times 10^{-4}\right)^2}\) = 2.5 × 1011 Pa
ప్రశ్న 18.
రెండు లోహ పలకలను ఒకదానితో ఒకటి చివరల నాలుగు రివెట్లనుపయోగించి బిగించారు. ప్రతి రివెట్ వ్యాసం 6.0 mm. ప్రతి రివెట్పై విమోటన బలం 6.9 × 107 Pa దాటకూడదు. రివెట్లు కట్టిన లోహ పలకల వల్ల కలిగే గరిష్ఠ తన్యత ఎంత ? ప్రతి రివెట్ భారంలో నాలుగో వంతును భరిస్తుందనుకోండి.
సాధన:
దత్తాంశం నుండి = : 6/2 = 3 mm = 3 × 10-3 m; గరిష్ఠ ప్రతిబలము = 6.9 × 107 Pa;
రివెట్ పై గరిష్ఠ భారము = గరిష్ఠ ప్రతిబలము × అడ్డుకోత వైశాల్యము = 6.9 × 107 × (22/7) × (3 × 10-3)2
∴ గరిష్ఠ తన్యత = 4[6.9 × 107 × \(\frac{22}{7}\) × 9 × 10-6] = 7.8 × 103 N

ప్రశ్న 19.
పసిఫిక్ మహాసముద్రంలో ఉన్న మరీనా అగాధం లోతు ఒక చోట ఉపరితలం నుంచి 11 km ఉంటుంది. అగాధం అడుగు భాగంలో ద్రవ పీడనం సుమారు 1.1 × 108 Pa గా ఉంటుంది. సముద్రంలో 0.32 m3 తొలి ఘనపరిమాణం ఉన్న ఉక్కు బంతిని వదిలినప్పుడు అది అగాధం అడుగుకు చేరుకొంది. అక్కడ బంతి ఘనపరిమాణంలో వచ్చే మార్పు ఎంత ?
సాధన:
దత్తాంశం నుండి p = 1.1 × 108 pa; V = 0.32 m3; B = 1.6 × 1011 Pa
∆V = \(\frac{\mathrm{pV}}{\mathrm{B}}\) = \(\frac{\left(1.1 \times 10^8\right) \times 0.32}{1.6 \times 10^{11}}\) = 2.2 × 10-4 m3.
![]()

![]()

![]()


![]()



![]()
![]()
![]()

![]()


![]()
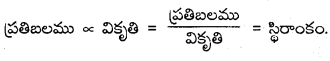
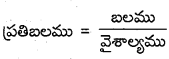
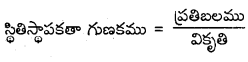
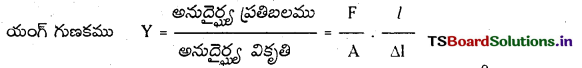
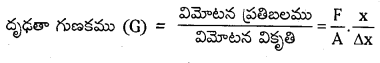
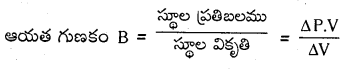
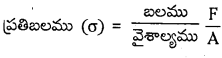

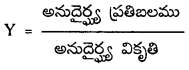
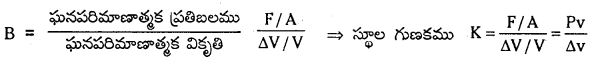

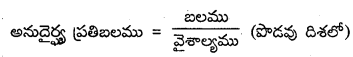
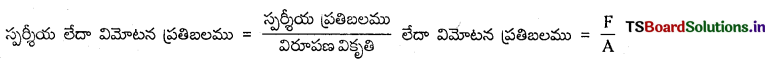
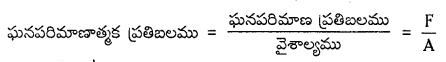
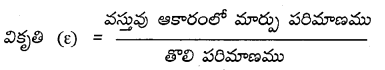
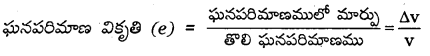
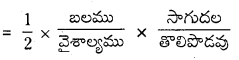


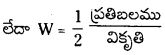 × ఘ.ప. × (వికృతి)2 = \(\frac{1}{2}\) ప్రతిబలము × వికృతి × ఘ.ప.
× ఘ.ప. × (వికృతి)2 = \(\frac{1}{2}\) ప్రతిబలము × వికృతి × ఘ.ప.