TS Inter 1st Year Maths 1A Solutions Chapter 10 Properties of Triangles Ex 10(a)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 10 Properties of Triangles Ex 10(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(a)

(Note : All problems in this exercise refer to ∆ABC)

I.
Question 1.
Show that Σa (sin B – sin C) = 0
Answer:
L.H.S. = Σa (sin B – sin C)
= Σa \(\left(\frac{b}{2 R}-\frac{c}{2 R}\right)\) (∵ a = 2R sin A, b = 2R sin B, c = 2R sin C)
= \(\frac{1}{2 R}\) Σa(b – c)
= \(\frac{1}{2 R}\) [a(b – c) + b(c – a) + c(a – b)]
= 0 = R.H.S.

Question 2.
If a = √3 + 1 cm, ∠B = 30°, ∠C = 45°, then find c.
Answer:
Given ∠B = 30°, ∠C = 45°, a = √3 + 1, we have ∠A = 180° – (30 + 45) = 180° – 75° = 105°

Question 3.
If a = 2 cm, b = 3 cm, c = 4 cm, then find cos A.
Answer:
Given a = 2cm, b = 3 cm, c = 4 cm.
cos A = \(\frac{b^2+c^2-a^2}{2 b c}\)
= \(\frac{9+16-4}{2(3)(4)}=\frac{21}{24}=\frac{7}{8}\)

Question 4.
If a = 26 cm, b = 30 cm and cos C = \(\frac{63}{65}\) then find c. (Mar. 2011)
Answer:
By the formula c² = a² + b² – 2ab cos C
c2² = (26)² + (30)² – 2 (26) (30)
= 676 + 900 – 1512
= 1576 – 1512 = 64
c = 8 cm

Question 5.
If the angles are in the ratio 1:5:6, then find the ratio of its sides. (May 2007)
Answer:
Given A : B : C = 1 : 5 : 6
∴ \(\frac{\mathrm{A}}{1}=\frac{\mathrm{B}}{5}=\frac{\mathrm{C}}{6}\) = B = C 1 “ 5 “ 6
A + B + C = 180° ;
⇒ A + 5A + 6A = 180°
⇒ 12 A = 180° ⇒ A = 15°
Ratio of sides = a : b : c
= sin A : sin B : sin C
= sin 15° : sin 75° : sin 90°
= \(\frac{\sqrt{3}-1}{2 \sqrt{2}}: \frac{\sqrt{3}+1}{2 \sqrt{2}}\) : 1
= √3 – 1 : √3 + 1 : 2√2

Question 6.
Prove that 2(bc cos A + ca cos B + ab cos C) = a² + b² + c². (Mar. 2005)
Answer:
L.H.S. = Σ 2bc cos A
= Σ 2bc \(\left(\frac{b^2+c^2-a^2}{2 b c}\right)\)
= Σ (b² + c² – a²)
= b² + c² – a² + c² + a²
= a² + b² + c²
= R.H.S.

Question 7.
Prove that \(\frac{a^2+b^2-c^2}{c^2+a^2-b^2}=\frac{\tan B}{\tan C}\)
Answer:
Use c² = a² + b² – 2ab cos C and
b² = c² + a² – 2ca cos B in L.H.S. then

Question 8.
Prove that (b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c.
Answer:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + a cos B) + (c cos A + a cos C) + (b cos C + c cos B)
= c + b + a = a + b + c = R.H.S. (Use projection formula)

Question 9.
Prove that (b – a cos C) sin A = a cos A sin C. (Mar. 2006)
Answer:
L.H.S. = (b – a cos C) sin A
= (a cos C + c cos A – a cos C) sin A
= c cos A sin A
= 2R sin C cos A sin A
= (2R sin A) cos A sin C
= a cos A sin C = R.H.S.

Question 10.
If 4, 5 are two sides of a triangle and the included angle is 60°, find its area.
Answer:
Let a = 4, b = 5 both sides and angle between them be C = 60° then area of ∆ABC,
∆ = \(\frac{1}{2}\) ab sin C
= \(\frac{1}{2}\) (4) (5) sin 60°
= 10 \(\left(\frac{\sqrt{3}}{2}\right)\) = 5√3 sq. cm.

Question 11.
Show that b cos² \(\frac{C}{2}\) + c cos² \(\frac{B}{2}\) = s.
Answer:

Question 12.
If \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\), then show that ∆ABC is equilateral.
Answer:

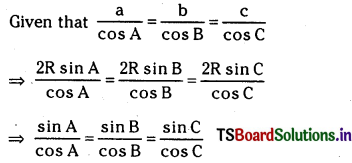
⇒ tan A = tan B = tan C
⇒ A = B = C
⇒ ∆ ABC is an equilateral triangle.

II.
Question 1.
Prove that a cos A + b cos B + c cos C = 4R sin A sin B sin C.
Answer:
L.H.S. = a cos A + b cos B + c cos C
= Σ a cos A
= Σ 2R sin A cos A
= R Σ sin 2A
= R [sin 2A + sin 2B + sin 2C]
= R [sin 2A + 2 sin (B + C) cos (B – C)]
= R [2 sinA cosA + 2 sin A cos(B – C)]
(∵ A + B + C = 180° ⇒ sin (B + C) = sin A)
= 2R sin A [cos A + cos (B – C)]
= 2R sin A[- cos(B + C) + cos(B – C)]
= 2R sin A [cos (B – C) – cos (B + C)]
= 2R sin A (2 sin B sin C)
= 4R sin A sin B sin C = R.H.S.

Question 2.
Prove that Σa³ sin (B – C) = 0.
Answer:
L.H.S. = Σa³ sin (B – C)
= Σa². a sin (B – C)
= Σa² (2R sin A) sin (B – C)
= 2R Σa² sin A sin (B – C)
= R Σa² 2 sin (B + C) . sin (B – C)
(∵ A + B + C = π, sin (B + C) = sin A)
= R Σa² 2(sin²B – sin²C)

Question 3.
Prove that
\(\frac{a \sin (B-C)}{b^2-c^2}=\frac{b \sin (C-A)}{c^2-a^2}=\frac{c \sin (A-B)}{a^2-b^2}\)
Answer:

Question 4.
Prove that Σa² \(\frac{\sin (B-C)}{\sin B+\sin C}\) = 0
Answer:

= Σ a(b – c)
= a(b – c) + b(c – a) + c(a – b)
= 0 = R.H.S.

Question 5.
Prove that
\(\frac{a}{b c}+\frac{\cos A}{a}=\frac{b}{c a}+\frac{\cos B}{b}=\frac{c}{a b}+\frac{\cos C}{c}\)
Answer:

Question 6.
Prove that
\(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^2+b^2}{a^2+c^2}\)
Answer:

Question 7.
If C = 60°, then show that
(i) \(\frac{a}{b+c}+\frac{b}{c+a}\) = 1
(ii) \(\frac{b}{c^2-a^2}+\frac{a}{c^2-b^2}\) = 0
Answer:
C = 60° ⇒ c² = a² + b² – 2ab cos C
= a² + b² – 2ab (cos 60°)
= a² + b² – 2ab (½)
= a² + b² – ab ……………….. (1)

(i)

(ii)

Question 8.
If a : b : c = 7 : 8 : 9, find cos A : cos B : cos C.
Answer:

Question 9.
Show that
\(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^2+b^2+c^2}{2 a b c}\)
Answer:

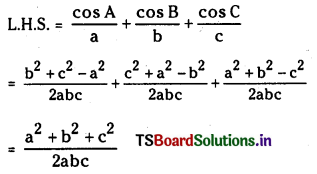
Question 10.
Prove that (b – a) cos C + c (cos B – cos A)
= c sin \(\left(\frac{A-B}{2}\right)\) cosec \(\left(\frac{A+B}{2}\right)\)
Answer:
L.H.S. = (b – a) cos C + c (cos B – cos A)
= b cos C – a cos C + c cos B – c cos A
= (b cos C + c cos B) – (a cos C + c cos A)
= a – b
= 2R (sin A – sin B)
(using Projection and sine rule)

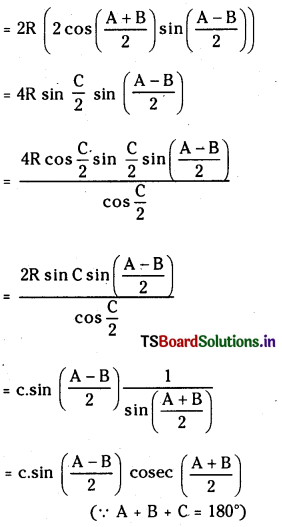
Question 11.
Express a sin²\(\frac{C}{2}\) + c sin² \(\frac{A}{2}\) in terms of s, a, b, c.
Answer:

Question 12.
If b + c = 3a, then find the value of cot \(\frac{B}{2}\) cot \(\frac{C}{2}\).
Answer:
2s = a + b + c = a + 3a = 4a ⇒ s = 2a

Question 13.
Prove that
(b + c) cos \(\left(\frac{B+C}{2}\right)\) = a cos \(\left(\frac{B-C}{2}\right)\).
Answer:

Question 14.
In a ∆ABC show that \(\frac{b^2-c^2}{a^2}=\frac{\sin (B-C)}{\sin (B+C)}\)
Answer:

III.
Question 1.
Prove that
(i) cot \(\frac{A}{2}\) + cot \(\frac{B}{2}\) + cot \(\frac{C}{2}\) = \(\frac{s^2}{\Delta}\)
Answer:
Using the formulae

(ii) tan\(\frac{A}{2}\) + tan \(\frac{B}{2}\) + tan\(\frac{C}{2}\) = \(\frac{b c+c a+a b-s^2}{\Delta}\)
Answer:

(iii)

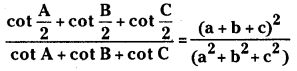
Answer:

Question 2.
Show that
(i) Σ(a + b) tan\(\left(\frac{A-B}{2}\right)\) = 0.
Answer:
We have Napler’s analogy as

(ii) \(\frac{b-c}{b+c}\) cot \(\frac{A}{2}\) + \(\frac{b+c}{b-c}\) tan \(\frac{A}{2}\) = 2 cosec (B – C).
Answer:
We have using Napler’s rule

Question 3.
(i) If sin θ = \(\frac{a}{b+c}\), then show that cos θ = \(\frac{2 \sqrt{b c}}{b+c}\) cos \(\frac{A}{2}\). (May 2014, Mar.12)
Answer:
We have cos²θ = 1 – sin²θ
= 1 – \(\frac{a^2}{(b+c)^2}\)

(ii) If a = (b + c) cos θ, then prove that sin θ = \(\frac{2 \sqrt{b c}}{b+c}\) cos \(\frac{A}{2}\).
Answer:

(iii) For any angle θ, show that
a cos θ = b cos (C + θ) + c cos (B – θ).
Sol.
R.HS. = b cos (C + θ) + c cos (B – θ)
= b (cos C cos θ – sin C sin θ) + c(cos B cos θ + sin B sin θ)
= (b cos C + C cos B) cos θ – sin θ(- c sin B – b sin C)
= a cos θ + sin θ(- b sin C + c sin B)
= a cos θ +(- 2R sin B sin θ sin C + 2R sin B sin C sin θ)
= a cos θ (∵ a = b cos C + c cos B)

Question 4.
If the angles of ∆ ABC are in A.P. and b : c = √3 : √2 , then show that A = 75°.
Answer:
Given A, B, C are in A.P
⇒ 2B = A + C
∴ A + B + C = π ⇒ 3B = π ⇒ B = 60°
Also b : c = √3 : √2

Question 5.
If \(\frac{a^2+b^2}{a^2-b^2}\) = \(\frac{\sin C}{\sin (A-B)}\), prove that ∆ABC is either isosceles or right angled.
Answer:

⇒ 2R sin A cos A = 2R sin B cos B
⇒ R sin 2A = R sin 2B
⇒ sin 2A – sin 2B = 0
∴ ∆ ABC is isosceles.
(or) 2A = 180° – 2B ⇒ A + B = 90°
Hence A ≠ B
⇒ ∆ABC is a right angled triangle.
∴ ∆ ABC is either isosceles or right angled.

Question 6.
If cos A + cos B + cos C = \(\frac{3}{2}\), then show that the triangle is equilateral.
Answer:

Question 7.
If cos² A + cos² B + cos² C = 1, then show that ∆ ABC is right angled.
Answer:
Given cos² A + cos² B + cos² C = 1 ……………. (1)
∴ cos² A + cos² B + cos² C
= cos² A + cos² B + 1 – sin² C
= 1 + cos² A + cos (B + C) cos (B – C).
= 1 + cos² A – cos A cos (B – C)
= 1 + cos A [cos (A) – cos (B – C)]
= 1 – cos A [cos (B + C) + cos (B – C)]
= 1 – 2 cos A cos B cos C
(∵ A + B + C = π, cos (B + C) = – cos A)
∴ 1 – 2 cos A cos B cos C = 1
⇒ 2 cos A cos B cos C = 0
⇒ A = 90° or B = 90° or C = 90°
⇒ ∆ ABC is right angled.

Question 8.
If a² + b² + c² = 8R², then prove that the triangle is right angled. (June 2001)
Answer:
Given a² + b² + c² = 8R²
⇒ 4R² (sin² A + sin² B + sin² C) = 8R²
⇒ sin² A + sin² B + sin² C = 2 ………………. (1)
Consider sin² A + sin² B + sin² C
= sin² A + sin² B + 1 – cos² C
= 1 + sin² A + sin² B – cos² C
= 1 + sin² A – (cos² C – sin² B)
= 1 + sin² A – cos (B + C) cos (B – C)
= 1 + sin² A + cos A cos (B – C)
(∵ cos (B + C) = cos (180 – A)° = – cos A)
= 1 + 1 – cos² A + cos A cos (B – C)
= 2 + cos A [cos (B – C) – cos A]
= 2 + cos A [cos (B – C) + cos (B + C)]
= 2 + 2 cos A cos B cos C ……………… (2)
∴ From (1) we have
2 + 2 cos A cos B cos C = 2
⇒ 2 cos A cos B cos C = 0
⇒ cos A = 0 or cos B = 0 or cos C = 0
⇒ A = \(\frac{\pi}{2}\) or B = \(\frac{\pi}{2}\) or C = \(\frac{\pi}{2}\)
∴ ∆ ABC is right angled.

Question 9.
If cot \(\frac{A}{2}\), cot \(\frac{B}{2}\), cot \(\frac{C}{2}\) are in A.P., then prove that a, b, c are in A.P.
Answer:
cot \(\frac{A}{2}\), cot \(\frac{B}{2}\), cot \(\frac{C}{2}\) are in A.P.
⇒ \(\frac{s(s-a)}{\Delta}, \frac{s(s-b)}{\Delta}, \frac{s(s-c)}{\Delta}\) are in A.P.
⇒ (s – a), (s – b), (s – c) are in A.P.
⇒ – a, – b, – c are in A.P.
⇒ a, b, c are in A.P.

Question 10.
If sin²\(\frac{A}{2}\), sin²\(\), sin²\(\) are in H.P., then show that a, d, c are in H.P.
Answer:

Question 11.
If C = 90°, then prove that
\(\frac{a^2+b^2}{a^2-b^2}\) sin (A – B) = 1.
Answer:
Given C = 90° and c² = a² + b² – 2ab cos C.
⇒ c² = a² + b²

Question 12.
Show that \(\frac{a^2}{4}\) sin 2C + \(\frac{a^2}{4}\) sin 2A = ∆.
Answer:

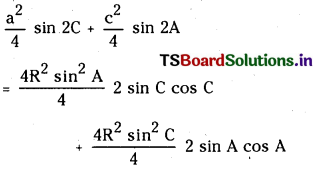
= 2R² sin² A sin C cos C + 2R² sin² C sin A cos A
= 2R² sin A sin C (sin A cos C + cos A sin C)
= 2R² sin A sin C sin (A + C)
= 2R² sin A sin C sin B
(∵ A + B + C = π ⇒ sin (A + C) = sin B)
= ∆ = R.H.S.

Question 13.
A lamp post is situated at the middle point M of the side AC of a triangular plot ABC with BC = 7 m, CA = 8 m and AB = 9 m. Lamp post subtends an angle 15° at the point B. Find the height of the lamp post.
Answer:

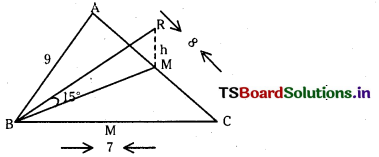
Let MR = h be the height of the lamp post and MR = h.
From ∆BMR, tan 15° = \(\frac{\mathrm{h}}{\mathrm{BM}}\)
∴ h = (2 – √3) BM ……………… (1)

Question 14.
Two ships leave a port at the same time. One goes 24 km per hour in the direction N 45° E and other travel 32 kms per hour in the direction S 75° E. Find the distance between the ships at the end of 3 hours.
Answer:

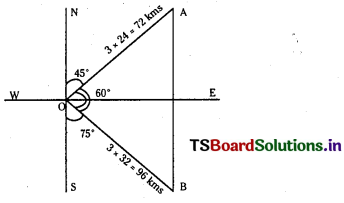
The first ship goes 24 km/hr.
∴ After 3 hrs. first ship goes 72 kms.
The second ship goes 32 km/hr.
∴ After 3 hrs. second ship goes 96 kms.
Let AB = x be the distance between the ships.
From the geometry of the figure ∠AOB = 60°
Using cosine rule in ∆AOB we have
cos 60° = \(\frac{(72)^2+(96)^2-x^2}{2(72)+(96)}\)
⇒ \(\frac{1}{2}\) = \(\frac{5184+9216-x^2}{13824}\)
⇒ 13824 = 28800 – 2x²
⇒ 2x² = 14976
⇒ x² = 7488
⇒ x = 86.4 (approximate)
At the end of 3 hours the difference between the ships is 86.4 kms.

Question 15.
A tree stands vertically on the slant of the hill. From a point A on the ground 35 metres down the hill from the base of the tree, the angle of elevation of the top of the tree is 60°. If the angle of elevation of the foot of the tree from A is 15°, then find the height of the tree.
Answer:

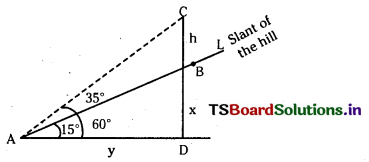
Let BC = h be the height of the tree. AL is the slant of hill.
Let BD = x and AD = y and given AB = 35 m
∴ From ∆ADB, sin 15° = \(\frac{x}{35}\)
⇒ x = 35\(\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)\)
Also cos 15° = \(\frac{\mathrm{y}}{35}\)

Question 16.
The upper 3/4^th portion of a vertical pole subtends an angle tan^-13/5 at a point in the horizontal plane through its foot and at a distance of 40 m from the foot. Given that the vertical pole is at a height less than 100 m from the ground, find its height.
Answer:

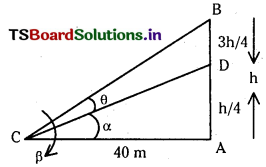
From the figure AB is the vertical pole of height ‘h’.
∠BCD = θ, suppose ∠DCA = α and ∠BCA = β.
Also AC = 40 m ; given tan θ = 3/5

Question 17.
AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7 m. From D, the angle of elevation of the point A is 45°. Find the height of the pole.
Answer:

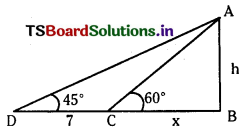
Let AB = ‘h’ be the height of the pole.
Given CD = 7
∠ACB = 60°, ∠ADB = 45° and line BC = x.

Question 18.
Let an object be placed at some height h cm and let P and Q be two points of observation which are at a distance of 10 cm apart on a line inclined at angle 15° to the horizontal. If the angles of elevation of the object from P and Q are 30° and 60° respectively then find h.
Answer:

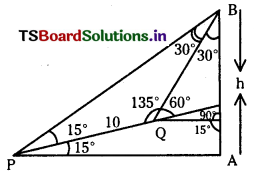
Let AB = h cm be the height of the tower P and Q are points of observations.
From the geometry of the figure ∠BPA = 30° given ∠BPQ = 15°. Also ∠PQB = 135°.
∴ ∠PBQ = 30°, PQ = 10 cm (given).
In the ∆PQB, applying sine rule.