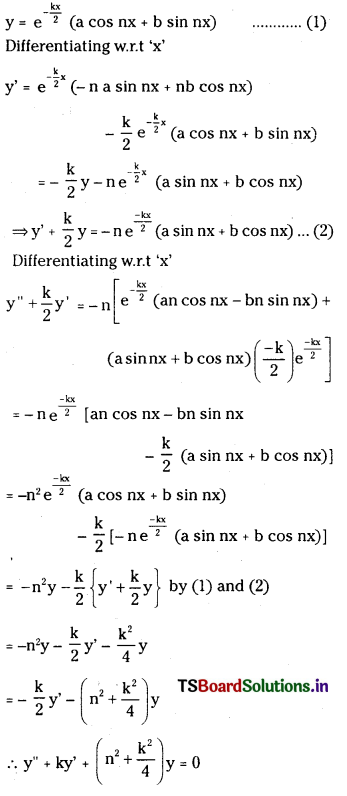TS Inter 1st Year Maths 1B Solutions Chapter 9 Differentiation Ex 9(d)

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 9 Differentiation Ex 9(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Differentiation 9(d)

I.
Question 1.
If y = \(\frac{2 x+3}{4 x+5}\) then find y”. (V.S.A.Q.)
Answer:

Question 2.
If y = ae^nx + be^-nx then prove that y” = n²y. (May 2014) (V.S.A.Q.)
Answer:
y’ = ane^nx – bne^-nx
y” = an²e^nx + bn²e^-nx
= n²(ae^nx + be^{– nx}) = n²y
∴ y” = n²y

II.
Question 1.
Find the second order derivatives of the following functions f(x). (S.A.Q.)
(i) cos³x
Answer:
Let y = cos³x = \(\frac{1}{4}\)[cos 3x + 3 cos x]
y’ = \(\frac{1}{4}\) [- 3 sin x – 3 sin x]
y” = \(\frac{1}{4}\) [- 9 cos 3x – 3 cos x]
= – \(\frac{3}{4}\) (3 cos 3x + cos x)

(ii) sin⁴x
Answer:
Let y = sin⁴x sin³x sin x

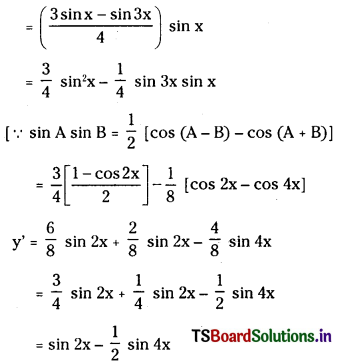
y” = 2 cos 2x – 2 cos 4x
= 2 (cos 2x – cos 4x)

(iii) log (4x² – 9)
Answer:
Let y = log (4x² – 9)
= log [(2x – 3) (2x + 3)]
= log (2x + 3) + log (2x + 3)

(iv) e^-2x sin³x
Answer:
Let y = e^-2x sin³x
y ‘ = e^-2x (3 sin²x cos x) + sin³x (-2) e^-2x
= e^-2x [ 3 sin²x cos x – 2 sin³x]
y” = e^-2x [3 sin²x (- sin x) + cos x (6 sin x cos x) – 6 sin²x cos x] – 2e^-2x [ 3 sin²x cos x – 2 sin³x]
= – e^-2x [6 sin x cos²x – 6 sin²x cos x – 3 sin³x – 6 sin²x cos x + 4 sin³x]
= e^-2x [sin³x – 12 sin²x cos x + 6 sin x cos²x]

(v) e^x sin x cos 2x
Answer:
Let y = e^x sin x cos 2x
= e^x \(\frac{1}{2}\) [sin 3x – sin x]
y’ = \(\frac{1}{2}\)[e^x (3 cos 3x – cos x) + e^x (sin 3x – sin x)]
y” = \(\frac{1}{2}\)[e^x (- 9 sin 3x + sin x) + e^x (3 cos 3x – cos x) + e^x (3 cos 3x – cos x) + (sin 3x – sin x)e^x]
= \(\frac{1}{2}\) e^x [6 cos 3x – 8 sin 3x – 2 cos x]
= e^x [3 cos 3x – 4 sin 3x – cos x]

(vi) tan^-1 \(\left(\frac{1+x}{1-x}\right)\)
Answer:

(vii) tan^-1\(\left(\frac{3 x-x^3}{1-3 x^2}\right)\)
Answer:

Question 2.
Prove the following. (S.A.Q.)
(i) If y = ax^{n + 1} + bx^-n then x²y” = n(n + 1) y.
Answer:
y = ax^{n + 1} + bx^-n
y’ = (n + 1) ax^-n – nbx^{– n – 1}
y” = an (n + 1) x^{n + 1} + bn (n + 1) x^-n-2
x²y” = an(n + 1) x^{n + 1} + b(n + 1)n x^{– n}
= n(n + 1) [ax^{n + 1} + bx^{– n}]
= n(n + 1) y

(ii) If y = a cos x + (b + 2x) sin x then y” + y = 4 cos x.
Answer:
y = a cos x + (b + 2x) sin x
y’ = – a sin x + (b + 2x) cos x + 2 sin x
y” = – a cos x + (b + 2x) (- sin x) + 2 cos x + 2 cos x
= – a cos x + 4 cos x – (b + 2x) sin x
= -[a cos x + (b + 2x) sin x] + 4 cos x
= – y + 4 cos x
∴ y” + y = 4 cos x

(iii) If y = 6 (x + 1) + (a + bx) e^3x then y” – 6y’ + 9y = 54x + 18
Answer:
y = 6 (x + 1) + (a + bx) e^3x
∴ y’ = 6 + (a + bx) 3e^3x + be^3x
y” = (a + bx) 9e^3x + 3e^3x(b) + 3be^3x
∴ L.H.S. = y” – 6y’ + 9y
= (a + bx) 9e^3x + 6be^3x – 6 [6 + (a + bx) 3e^3x + be^3x] + 9 [ 6 (x + 1) + (a + bx) e^3x]
= (a + bx) 9e^3x + ebe^3x – 36 – 18e^3x (a + bx) – 6be^3x+ 54 (x + 1) + 9 (a + bx) e^3x
= 54x+ 18

(iv) If ay⁴ = (x + b)⁵ then 5yy” = (y’)²
Answer:

(v) If y = a cos (sin x) + b sin (sin x) then y” + (tan x)y’ + y cos²x = 0
Answer:
Given y = a cos (sin x) + b sin (sin x) then
y’ = -a sin (sin x) cos x + b cos (sin x) cos x
= cos x [-a sin (sin x) + b cos (sin x)]
y” = cos x [- a cos (sin x) cos x – b sin (sin x) (cos x)] – sin x [- a sin (sin x) + b cos (sin x)]
= – sin x \(\frac{y^{\prime}}{\cos x}\) – cos² x . y
∴ y” + (tan x) y’ + y cos²x = 0

III.
Question 1.
(i) If y = 128 sin³ x cos⁴x then find y”. (E.Q.)
Answer:
Given y = 128 sin³x cos⁴x
∴ y’ = 128 [sin³x 4 cos³x (- sin x) + cos⁴x (3 sin²x) cos x]
= 128 [3 sin²x cos⁵x – 4 sin⁴x cos³x]
y” = 128[3 sin²x (5 cos⁴x) (- sin x) + cos⁵x (6 sin x cos x) – 4 [sin⁴x (3 cos²x) (- sin x) + c0s³x 4 sin³x cos x]]
= 128 [- 15 sin³ x cos⁴x + 6 cos⁶x sin x + 12 sin⁵x cos²x – 16 cos⁴x sin³x]
= 128 [6 sin x cos⁶x + 12 sin⁵x cos²x – 31 cos⁴x sin³x]
= 128 sin x cos²x (12 sin⁴x – 31 sin²x cos²x + 6 cos⁴x)

(ii) If y = sin 2x sin 3x sin 4x then find y”. (E.Q.)
Answer:
y = sin 2x \(\frac{1}{2}\) [2sin 3x sin 4x]
= sin 2x \(\frac{1}{2}\) [cos x – cos 7x]
= \(\frac{1}{2}\) sin 2x cos x – \(\frac{1}{2}\) sin 2x cos 7x
= \(\frac{1}{4}\) [sin 3x + sin x – sin 9x + sin 5x]
= \(\frac{1}{4}\) [- sin 9x + sin 5x + sin 3x + sin x]
y’ = \(\frac{1}{4}\) [- 9 cos 9x + 5 cos 5x + 3 cos 3x + cos x] 1
y” = \(\frac{1}{4}\) [81 sin 9x – 25 sin 5x – 9 sin 3x – sin x]

(iii) If ax² + 2hxy + by² = 1 then prove that \(\frac{d^2 y}{d x^2}=\frac{h^2-a b}{(h x+b y)^3}\) (E.Q.)
Answer:
Differentiating ax² + 2hxy + by² = 1 with respect to x on both sides we get

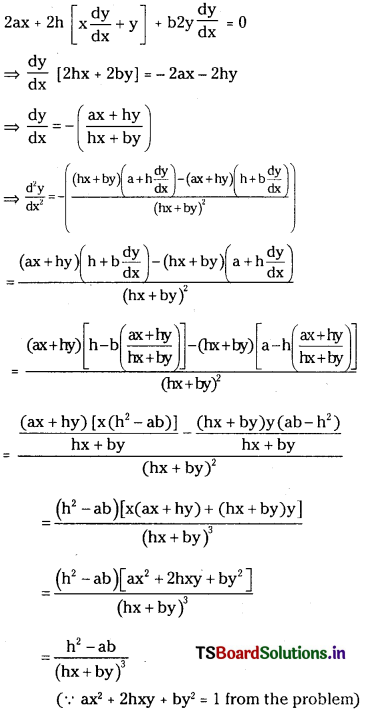
(iv) If y = ae^-bx cos (cx + d) then prove that y” + 2by’ + (b² + c²)y = 0 (E.Q.)
Answer:
Given y = ae^-bx cos (cx + d)
Differentiating w.r.t ‘x’ then
y’ = a[e^-bx(-c sin (cx + d)) – cos(cx + d) be^-bx]
= ae^-bx [- c sin(cx + d) – bcos(cx + d)]
= – ace^-bx sin (cx + d) – by
∴ y’ + by = -ace^-bx sin(cx + d)
Differentiating again w.r.t ‘x’
∴ y” + by’ = -ac [e^-bx c cos (cx + d) – be^-bx sin (cx + d)]
= – ac e^-bx [c cos (cx + d) – b sin(cx + d)]
= abce^-bx sin (cx + d) – ac²e^-bxcos (cx + d)
= – b (y’ + by) – c²y
∴ y” + 2by’ + (b² + c²)y = 0

(v) If y = e^{–\(\frac{\mathbf{k}}{2}\)x} (a cos nx + b sin nx) then prove that y” + ky’ + (n² + \(\frac{k^2}{4}\)) y = 0 (E.Q.)
Answer: