TS Inter 1st Year Maths 1A Solutions Chapter 10 Properties of Triangles Ex 10(b)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 10 Properties of Triangles Ex 10(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(b)

(Note : All problems in this exercise have reference to ∆ABC)

I.
Question 1.
Express Σ r₁ cot \(\frac{\mathrm{A}}{2}\) in terms of s. (Mar. 2006)
Answer:
We have r₁ = s tan \(\frac{\mathrm{A}}{2}\)
∴ Σ r₁ cot\(\left(\frac{\mathrm{A}}{2}\right)\)
= Σ s tan\(\left(\frac{\mathrm{A}}{2}\right)\) cot\(\frac{\mathrm{A}}{2}\)
= Σs = s + s + s = 3s

Question 2.
Show that Σ a cot A = 2 (R + r).
Answer:
L.H.S. = Σ a cot A
= Σ 2R sin A \(\frac{\cos A}{\sin A}\)
= Σ 2R cos A
= 2R Σ cos A
= 2R (cos A + cos B + cos C)

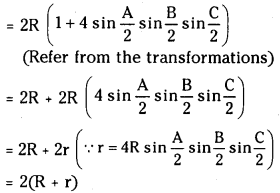
Question 3.
In ∆ ABC, prove that
r₁ + r₂ + r₃ – r = 4R (Mar. 2006)
Answer:

Question 4.
In ∆ ABC, prove that
r + r₁ + r₂ – r₃ = 4R cos C. (May 2006)
Answer:

Question 5.
If r + r₁ + r₂ = r₃, then show that C = 90°
Answer:
Given r + r₁ + r₂ = r₃
We have given that r₁ + r₂ = r₃ – r
r₁ + r₂ = 4R sin\(\frac{\mathrm{A}}{2}\) cos\(\frac{\mathrm{B}}{2}\) cos\(\frac{\mathrm{C}}{2}\) + 4R sin\(\frac{B}{2}\) cos\(\frac{C}{2}\) cos\(\frac{A}{2}\)

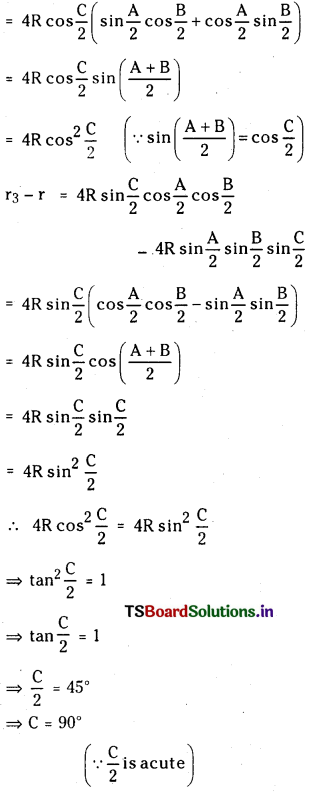
II.
Question 1.
Prove that
4 (r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)²
Answer:
r₁r₂ + r₂r₃ + r₃r₁

Question 2.
Prove that
\(\left(\frac{1}{r}-\frac{1}{r_1}\right)\left(\frac{1}{r}-\frac{1}{r_2}\right)\left(\frac{1}{r}-\frac{1}{r_3}\right)=\frac{a b c}{\Delta^3}=\frac{4 R}{r^2 s^2}\)
Answer:

Question 3.
Prove that r(r₁ + r₂ + r₃) = ab + bc + ca – s² – s²
Answer:
L.H.S. = r(r₁ + r₂ + r₃)

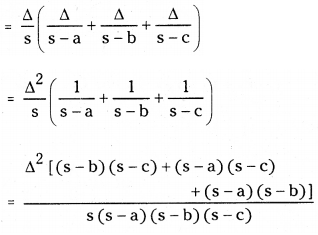
= \(\frac{\Delta^2}{\Delta^2}\) [(s² + s² + s²) – s(b + c) – s(a + c) – s (a + b) + bc + ca + ab]
= [3s² – 2s (a + b + c) + bc + ca + ab]
= 3s² – 2s (2s) + ab + bc + ca
= ab + bc + ca – s²
= R.H.S.

Question 4.
Show that \(\Sigma \frac{r_1}{(s-b)(s-c)}=\frac{3}{r}\).
Answer:

Question 5.
Show that
(r₁ + r₂) tan\(\frac{C}{2}\) = (r₃ – r)cot\(\frac{C}{2}\) = c.
Answer:

Question 6.
Show that
r₁ r₂ r₃ = r₃ cot²\(\frac{A}{2}\) cot²\(\frac{B}{2}\) cot²\(\frac{C}{2}\)
Answer:

III.
Question 1.
Show that cos A + cos B + cos C = 1 + \(\frac{\mathbf{r}}{\mathbf{R}}\)
Answer:

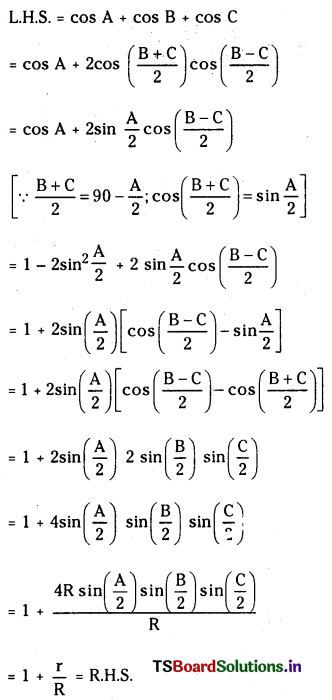
Question 2.
Show that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) + cos²\(\frac{C}{2}\) = 2 + \(\frac{\mathbf{r}}{2 R}\). (Mar. 2005)
Answer:

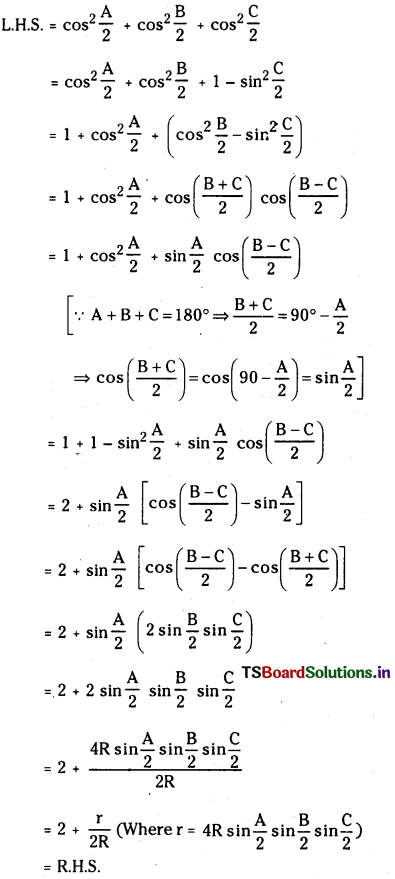
Question 3.
Show that
sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + sin²\(\frac{C}{2}\) = 1 – \(\frac{r}{2 R}\)
Answer:

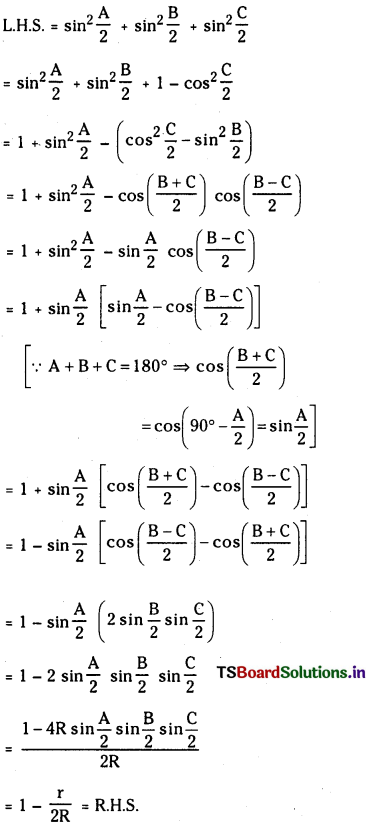
Question 4.
Show that
(i) a = (r₂ + r₃) \(\sqrt{\frac{r r_1}{r_2 r_3}}\)
Answer:

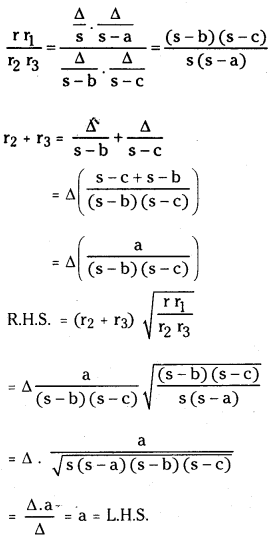
(ii) ∆ = r₁r₂\(\sqrt{\frac{4 R-r_1-r_2}{r_1+r_2}}\)
Answer:

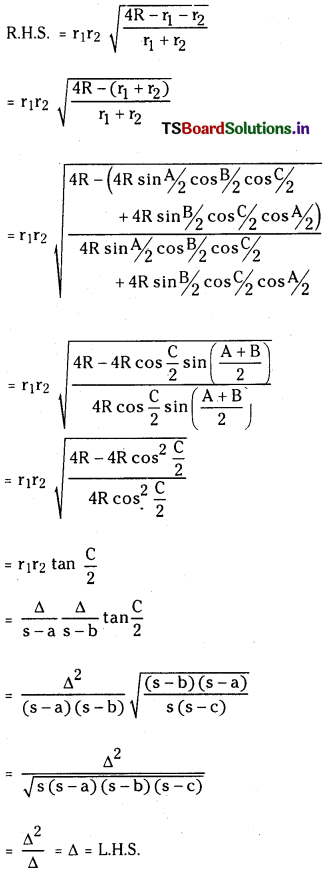
Question 5.
Prove that
r₁² + r₂² + r₃² + r² = 16R² – (a² + b² + c²).
Answer:
(r₁ + r₂ + r₃ – r)² = [(r₁ + r₂ + r₃ – r]²
= (r₁ + r₂ + r₃)² – 2r(r₁ + r₂ + r₃)r + r²
= (r₁² + r₂² + r₃² + r²) – 2r(r₁ + r₂ + r₃) + 2(r₁ r₂ + r₂ r₃ + r₃ r₁)
But using results r₁ + r₂ + r₃ – r = 4R and
r₁ r₂ + r₂r₃ + r₃r₁ = s²
We have 16R² = (r₁² + r₂² + r₃² + r²) – 2r(r₁ + r₂ + r₃) + 2s² …………………….. (1)
Now 2r(r₁ + r₂ + r₃)

= 2 (ab + bc + ca) – 2s²
= 2(ab + bc + ca – s²) ……………….. (2)
∴ From (1)
r₁² + r₂² + r₃² + r² = 16R² + 2(ab + bc + ca – s²) – 2s²
= 16R² + 2(ab + bc + ca) – 4s²
= 16R² = [4s² – 2 (ab + bc + ca)]
= 16R² – {(a + b + c)² – 2(ab + bc + ca)}
= 16R² – (a² + b²+ c²)

Question 6.
If P₁, P₂, P₃ are altitudes drawn from vertices A, B, C to the opposite sides of a triangle respectively, then show that
(i) \(\frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}=\frac{1}{r}\)
(ii) \(\frac{1}{p_1}+\frac{1}{p_2}-\frac{1}{p_3}=\frac{1}{r_3}\) and
(iii) P₁.P₂.p₃ = \(\frac{(a b c)^2}{8 R^3}=\frac{8 \Delta^3}{a b c}\) (Mar.2010)
Answer:

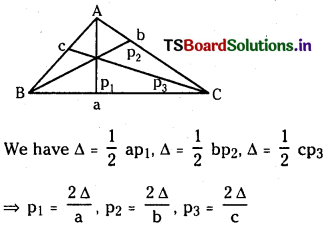
(i)

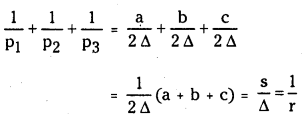
(ii)

(iii)

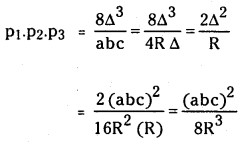
Question 7.
If a = 13, b = 14, c = 15 show that R = \(\frac{65}{8}\) r = 4, r₁ = \(\frac{21}{2}\), r₂ = 12 and r₃ = 14. (Mar. 14) (Board New Model Paper) (March 2015-A.P)
Answer:
Given a = 13, b = 14, c = 15
We have s = \(\frac{a+b+c}{2}\) = \(\frac{13+14+15}{2}\) = 21
s – a = 21 – 13 = 8; s – b = 21 – 14 = 7;
s – c = 21 – 15 = 6

∴ The values are R = \(\frac{65}{8}\), r = 4, r₁ = \(\frac{21}{2}\), r₂ = 12 and r₃ = 14.

Question 8.
If r₁ = 2, r₂ = 3, r₃ = 6 and r = 1, Prove that a = 3, b = 4 and c = 5. (March 2015-T.s) (Mar. 09, Oct. 97)
Answer:
We have given r = 1, r₁ = 2, r₂ = 3 and r₃ = 6 and ∆² = r . r₁.r₂.r₃ = (1) (2) (3) (6) = 36
⇒ ∆ = 6
Now r = \(\frac{\Delta}{s}\) ⇒ s = \(\frac{\Delta}{r}\) = 6
r₁ = \(\frac{\Delta}{s-a}\) ⇒ 2 = \(\frac{6}{s-a}\)
⇒ s – a = 3 ⇒ 6 – a = 3 ⇒ a = 3
r₁ = \(\frac{\Delta}{s-b}\) ⇒ 2 = \(\frac{6}{s-b}\)
⇒ s – b = 2
⇒ b = 4
r₁ = \(\frac{\Delta}{s-c}\) ⇒ 2 = \(\frac{6}{s-c}\)
⇒ s – c = 1
⇒ c= 5
∴ a= 3, b = 4, c = 5.