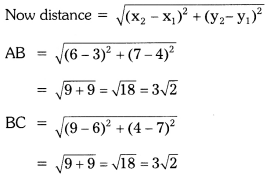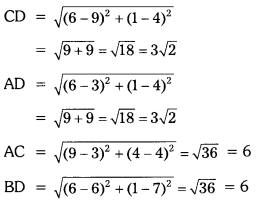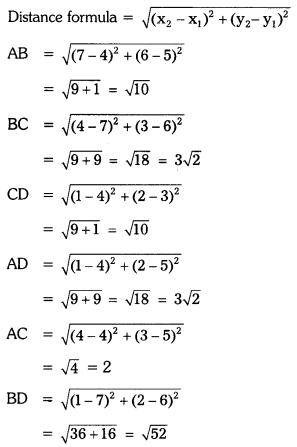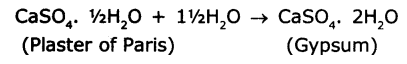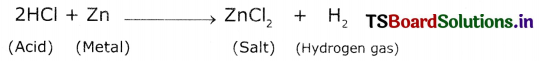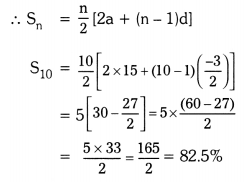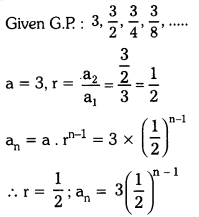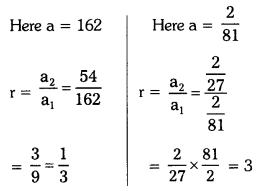Class 10

We are offering TS 10th Class Maths Notes Chapter 12 Applications of Trigonometry to learn maths more effectively.

TS 10th Class Maths Notes Chapter 12 Applications of Trigonometry

→ Trigonometry is widely used in our daily life, geography and in navigation also.

→ If a person is looking at an object then the imaginary line joining the object and the eye of the observer is called the line of sight or ray of view.

→ An imaginary line parallel to earth surface and passing through the point of observation is called the horizontal.

→ If the line of sight is above the horizontal then the angle between them is called “angle of elevation”.

→ If the line of sight is below the horizontal then the angle between them is called the angle of depression.

→ Useful hints to solve the problems :

• Draw a neat diagram of a right triangle or a combination of right triangles if necessary.
• Represent the data given on the triangle.
• Find the relation between known values and unknown values.
• Choose appropriate trigonometric ratio and solve for the unknown.

→ The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.

→ To use this application of trigonometry, we should know the following terms.

→ The terms are Horizontal line, Line of Sight, Angle of Elevation and Angle of Depression.

→ Horizontal line : A line which is parallel to earth from observation point to object is called “horizontal line”.

→ Line of sight: It is the line drawn from the eye of an observer to the object viewed.

→ Angle of elevation : It is the angle formed by the line of sight with the horizontal, when the object viewed is above the horizontal level. In this case, we have to raise our head to look at the object.

→ Angle of depression : It is the angle formed by the line of sight with the horizontal when the object viewed is below the horizontal level. In this case, we have to lower our head to look at the object.
The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.

→ Trigonometric ratios in a right triangle:

→ Trigonometric ratios of some specific angles :

Solving Procedure :
When we want to solve the problems of height and distances, we should consider the following :

• All the object such as tower, trees, buildings, ships mountains etc. shall be considered as linear for mathematical convenience.
• The angle of elevation or angle of depression is considered with referece to the horizontal line.
• The height of the observer is neglected, if it is not given in the problem.
• To find heights and distances, we need to draw figures and with the help of these figures we can solve the problems.

Leonard Euler:

• Euler is a Swiss Mathematical genius.
• Euler’s famous formula is F + C = E + 2.
• Euler’s equation is e’q = cos q + i sin q.
• He introduced the notations like S, f(x) etc.

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.4

Question 1.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals. (AS₂)
Solution:
ABCD is a rhombus. Let its diagonals AC and BD meet at ‘O’.

In ∆AOD, ∠AOD = 90°
∴ By Pythagoras theorem,
AD² = OA² + OD² …………… (1)
In ∆COD, ∠COD = 90°
∴ CD² = OC² + OD² …………… (2)
In ∆ AOB, ∠AOB = 90°
∴ AB² = OA² + OB² ……………… (3)
In ∆BOC, ∠BOC = 90°
∴ BC² = OB² + OC² ……………… (4)
Adding (1), (2), (3) & (4), we get
AD² + CD² + AB² + BC² = OA² + OD² + OC² + OD² + OA² + OB² + OB² + OC²
= OA² + OA² + OC² + OC² + OB² + OB² + OD² + OD²
= OA² + OA² + OA² + OA² + OB² + OB² + OB² + OB² (∵ OC = OA & OD = OB)
= 4OA² + 4OB²
= (2OA² + 2OB²) (∵ 2OA = AC & 2OB = BD)

Question 2.
ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively.
Prove that AE² + CD² = AC² + DE². (AS₂)

Solution:
In ∆ABE, ∠B = 90°
By Pythagoras Theorem,
AE² = AB² + BE² …………… (1)
In ∆CBD, ∠CBD = 90°
By Pythagoras Theorem,
CD² = BD² + BC² ……………. (2)
Adding (1) & (2), we get AE² + CD² = AB² + BE² + BD² + BC²
= (AB² + BC²) + (BE² + BD²)
= AC² + DE² (∵ In ∆ABC, ∠B = 90°)
(∴ AB² + BC² = AC² and In ∆DBE, ∠B = 90° ∴ BD² + BE² = DE²)

Question 3.
Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude. (AS₂)
Solution:
ABC is an equilateral triangle,

(∵ AD ⊥ BC)
(i.e„) AB = BC = CA, AD ⊥ BC
In ∆^les ADB and ADC
∠ADB = ∠ADC = 90°
Hyp. AB = Hyp. AC
AD is common.
∴ ∆ ADB = ∆ADC
∴ BD = DC
In ∆ADB, ∠ADB = 90°
By Pythagoras Theorem,
AB² = AD² + BD²
= AD² + \(\left(\frac{\mathrm{BC}}{2}\right)^2\) (∵ BD = CD)
= AD² + \(\frac{\mathrm{BC}^2}{4}\) = \(\frac{4 \mathrm{AD}^2+\mathrm{BC}^2}{4}\)
= \(\frac{4 \mathrm{AD}^2+\mathrm{AB}^2}{4}\) (∵ BC = AB)
⇒ 4AB² = 4AD² + AB²
⇒ 4AB² – AB² = 4AD²
⇒ 3AB² = 4AD²

Question 4.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥QR. Show that PM² = QM . MR (AS₂)
Solution:
∆PRM and ∆PQM are right angled triangles.

∴ PR² = PM² + RM² ……………. (1)
and PQ² = PM² + QM² …………… (2)
Adding (1) & (2), we get
PR² + PQ² = PM² + RM² + PM² + QM²
⇒ QR² = 2PM² + RM² + QM²
(∵ In ∆PQR, ∠P = 90° ∴ QR² = PR² + PQ²)
⇒ (QM + MR)² = 2PM² + RM² + QM²
⇒ QM² + RM² + 2QM. MR = 2PM² + RM² + QM²
⇒ 2QM. MR = 2PM²
⇒ PM² = QM. MR

Question 5.
ABD is a triangle right angled at A and AC ⊥ BD. Show that (AS₂)
(i) AB² = BC. BD
(ii) AC² = BC . DC
(iii) AD² = BD . CD

Solution:
(i) In ∆^les BAD and BCA,
∠BAD = ∠BCA = 90°
∠B is common.
∴ ∆BAD ~ ∆BCA

Hence, their corresponding sides are in proportion.
⇒ \(\frac{\mathrm{BD}}{\mathrm{AB}}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ AB² = BC . BD ……………. (1)

(ii) In ∆^les ACB and DCA,
∠ACB = ∠DCA = 90°
∠A is common.
∴ ∆ ACB ~ ∆DCA

Hence, their corresponding sides are in pro-portion.
⇒ \(\frac{\mathrm{AC}}{\mathrm{DC}}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ AC² = BC . DC ……………. (2)

iii) In ∆^les DAB and DCA,
∠DAB = ∠DCA = 90°
∠D is common.
∴ ∆DAB ~ ∆DCA

Hence, their corresponding sides are in proportion.
⇒ \(\frac{\mathrm{BD}}{\mathrm{AD}}\) = \(\frac{\mathrm{AD}}{\mathrm{CD}}\)
⇒ AD² = BD . CD ……………. (3)

Question 6.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC². (AS₂)
Solution:
In ∆ABC, ∠ACB = 90°

∴ AB is the hypotenuse, since it is an isosceles triangle, AC = BC
By Pythagoras Theorem,
AB² = AC² + BC²
= AC² + (AC)² (∵ BC = AC)
= AC² + AC² = 2AC²

Question 7.
‘O’ is any point in the interior of a triangle ABC. OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
ii) AF² + BD² + CE² = AE² + CD² + BF². (AS₂)

Solution:
In ∆ABC, OD, OE and OF are drawn perpendicular to BC, CA and AB respectively. Join OB, OC and OA.
i) In ∆AFO, ∠AFO = 90°
∴ By Pythagoras Theorem,
OA² = AF² + OF² …………….. (1)
In ABDO, ∠BDO = 90°
∴ OB² = OD² + BD² ………………. (2)
In ACEO, ∠CEO = 90°
∴ OC² = OE² + CE² ……………….. (3)

Adding (1), (2) & (3), we get
OA² + OB² + OC² = AF² + OF² + OD² + BD² + OE² + CE²
⇒ OA² + OB² + OC² – OD² – OE² – OF²
= AF² + BD² + CE² …………….. (4)

ii) From (4), we get
AF² + BD² + CE² = (OA² – OE²) + (OB² – OF²) + (OC² – OD²)
= AE² + BF² + CD² (∵ In the right triangle AEO,
∠AEO = 90° ∴ OA² = OE² + AE²
⇒ OA² – OE² = AE²
Similarly, in the right triangle OFB,
∠OFB = 90°; ∴ OB² = OF² + BF²
⇒ OB² – OF² = BF²
Lastly, in the right triangle ODC,
∠ODC = 90°,
OC² = OD² + CD²
⇒ O² – OD² = CD²

Question 8.
A wire attached to a vertical pole of height 18m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut ? (AS₄)
Solution:
In triangle ABC, ∠B = 90°
AB stands for the vertical pole AC represents the wire ‘B’ denotes ‘base’ and C denotes ‘stake’.

By Pythagoras Theorem,
AC² = AB² + BC²
⇒ BC² = AC² – AB²
= (24)² – (18)²
= 576 – 324 = 252
∴ BC = \(\sqrt{252}\)
= \(\sqrt{252}\) = \(\sqrt{2 2 3 3 7}\)
= \(\sqrt{2^2 \times 3^2}\) × 7
= 2 × 3 × \(\sqrt{7}\) = 6\(\sqrt{7}\) Therefore, the stake should be driven 6 \(\sqrt{7}\) meters for the base of the pole so that the wire will be taut.

Question 9.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance be¬tween the feet of the poles is 12m find the distance between their tops. (AS₄)
Solution:
AB and CD represent two poles of heights 11m and 6m respectively. BC represents the distance between their feet. BC = 12m
Draw DE || CB intersecting AB at E. Join AD.

ED = BC = 12m.
EB = DC = 6m
AE = AB – CD = 11 – 6 = 5m
In ∆AED, ∠AED = 90°
∴ By Pythagoras theorem,
AD² = AE² + DE²
= 5² + 12² = 25 + 144 = 169
∴ AD = \(\sqrt{169}\) = 13m
∴ The distance between the tops of the poles = 13 meters.

Question 10.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\) BC. Prove that 9AD² = 7 AB². (AS₂)
Solution:
ABC is an equilateral triangle.
∴ AB = BC = CA
D is a point on BC, such that
BD = \(\frac{1}{3}\) BC; Draw AE ⊥ BC.

∴ E bisects BC.
⇒ BE = CE
In ∆ABD, ∠ADB is obtuse.
∴ AB² = AD² + BD² + 2 BD . DE
⇒ AD² = AB² – BD² – 2BD. DE

Question 11.
In the given figure, ABC Is a triangle right angled at B. D and E are points on BC trisect it. Prove that 8AE² = 3AC² + 5AD². (AS₂)

Solution:
In ∆ADC, ∠ADC is obtuse.
∠B = 90° and BD = DE = EC.
Let BD = DE = EC = x
AC² = AD² + DC² + 2 DC. DB
= AD² + (2x)² + 2. 2x. x
= AD² + 4x² + 4x²
= AD² + 8x² ………………… (1)
In ∆ABD, ∠B = 90°
∴ AD² = AB² + BD² (By Pythagoras Theorem)
⇒ AB² = AD² – BD² = AD² – x² …………. (2)
In ∆ABE = ∠B = 90°
∴ AE² = AB² + BE² = AB² + (2x)² = AB² + 4x²
∴ AB² = AE² – 4x² ……………. (3)
From (2) & (3), we get
AE² – 4x² = AD² – x²
AE² – 4x² = AD² – x² + 4x² = AD² + 3x²
8AE² = 8(AD² + 3x²)
= 8AD² + 24x² ………………. (4)
From (1),
3AC² + 5 AD²
= 3 (AD² + 8x²) + 5 AD²
= 3 AD² + 24x² + 5AD²
= 8AD² + 24x² ……………….. (5)
From (4) & (5), we have,
8AE² = 3AC² + 5 AD²

Question 12.
ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ∆ABE and ∆ACD.

Solution:
In ∆ABC, ∠B = 90°
Let AB = BC = x

∴ By Pythagoras theorem,
AC² = AB² + BC² = x² + x² = 2x²
∴ AC = \(\sqrt{2 \mathrm{x}^2}\) = \(\sqrt{2}\)x
By problem ∆ACD ~ ∆ABE,
Therefore, \(\frac{\text { area of }(\triangle \mathrm{ABE})}{\text { area of }(\triangle \mathrm{ACD})}\) = \(\frac{\mathrm{AB}^2}{\mathrm{AC}^2}\)
= \(\frac{(x)^2}{(\sqrt{2} x)^2}\) (∵ AB = x and AC = \(\sqrt{2}\)x )
= \(\frac{x^2}{2 x^2}\) = \(\frac{1}{2}\)
Hence, the ratio between the areas of ∆ABE and ∆ACD = 1 : 2

Students can practice TS Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.1

Question 1.
Find the distance between the following pair of points.

i) (2, 3) and (4, 1)
Solution:

ii) (-5, 7) and (-1, 3)
Solution:

iii) (-2, -3) and (3, 2)
Solution:

iv) (a, b) and (-a, -b)
Solution:

Question 2.
Find the distance between the points (0, 0) and (36, 15)
Solution:
Given : origin O(0, 0) and a point P(36, 15)
Distance between any point and origin = \(\sqrt{x^2+y^2}\)

Question 3.
Verify whether the points (1, 5),(2, 3) and (-2, -1) are colleniar or not.
Solution:
Given : A(1, 5) B(2, 3) and C(-2, -1)

Here the sum of no two line segments is equal to third segment
Hence the points are not collinear.
slope of AB, m₁ = \(\frac{3-5}{2-1}\) = -2
slope of BC, m₂ = \(\frac{-1-3}{-2-2}\) = -2
m₁ ≠ m₂
Hence A, B, C are not collinear.

Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an Isosceles triangle.
Solution:
Let A = (5, -2); B = (6, 4) and C = (7, -2)

Now we have AB = BC.
∴ Δ ABC is an isosceles triangle.
i.e., given points are the vertices of an isosceles triangle.

Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in figure. Jarina and Phani walk into the class and after observing for a few minutes Jarina asks Phani ‘Don’t you think ABCD ¡s a square ?“ Phani disagrees. Using distance formula. find which of them is correct. Why?

Solution:
Given : Four friends are seated at A, B, C and D where A(3, 4), B(6, 7), C(9, 4) and D(6, 1)


Hence in ABCD four sides are equal.
i.e., AB = BC = CD = DA = 3\(\sqrt{2}\) units.and two diagonals are equal.
ie., AC = BD = 6 units.
∴ ABCD forms a square
i.e., Jarina is correct.

Question 6.
Show that the following points form an equilateral triangle A(a, 0), B(-a, 0), C(0, a\(\sqrt{3}\)).
Solution:

Now AB = BC = CA.
∴ Δ ABC is an equilateral triangle.

Question 7.
Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram and find its area.
(A.P. Mar. ’15)
Solution:
Diagram

Given : A(-7, -3), B(5, 10), C(15, 8) and D(3, -5)

In ABCD, both pairs of opposite sides (AB, CD) and (BC, AD) are equal.
Hence the given points form a parallelogram.
Area of ABCD = 2 × ΔABC

Question 8.
Show that the points (-4, -7), (-1, 2), (8, 5) and (5, -4) taken in order are the vertices of a rhombus.
Hint : Area of rhombus = \(\frac{1}{2}\) × product (A.P. June ‘is’)
Solution:
Given in ABCD, A (-4, -7), B(-1, 2), C(8, 5) and D(5, -4)
Distance formula = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

∴ In ABCD, AB = BC = CD = AD [from sides are equal]
Hence ABCD is a rhombus.
Area of a rhombus = \(\frac{1}{2}\)d₁d₂
= \(\frac{1}{2}\) × 12\(\sqrt{2}\) × 6\(\sqrt{2}\)
= 72 sq. units.

Question 9.
Name the type of quadrilateral formed, if any, by the following points and give reasons for your answer.

i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
Solution:
Let A(-1, -2), B(1, 0), C(-1, 2), D(-3, 0) be the given points.

AC = \(\sqrt{(-1+1)^2+(2+2)^2}\)
= \(\sqrt{16}\) = 4 units.
BD = \(\sqrt{(-3-1)^2+(0-0)^2}\)
= \(\sqrt{16}\) = 4 units.
In ABCD, AB = BC = CD = AD four sides are equal.
AC = BD → diagonals are equal.
Hence, the given points form a square.

ii) (-3, 5), (3, 1), (1, -3), (-1, -4)
Solution:
Let A(-3, 5), B(3, 1), C(1, -3) and D(-1, -4) be the given points.

∴ Opposite sides are not equal.

∴ Its diagonal are not equal.
In ABCD, AB ≠ CD, BC ≠ AD and AC ≠ BD
Hence ABCD is not a parallelogram
∴ The given points can’t be form a parallelogram.

iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
Let A(4, 5), B(7, 6), C(4, 3) and D(1, 2) be the given points.

In ABCD, AB = CD and BC = AD (i.e., both pairs of opposite sides are equal) and AC ≠ BD
Hence ABCD is a parallelogram, i.e., the given points form a parallelogram.

Question 10.
Find the point on the X-axis which is equidistant from (2, -5) and (-2, 9).
Solution:
Given points, A(2, -5), B(-2, 9)
Let P(x, 0) be the point on x-axis.
Which is equidistant from A and B i.e., PA = PB.

But PA = PB
⇒ \(\sqrt{x^2-4 x+29}\) = \(\sqrt{x^2+4 x+85}\)
squaring on both sides, we get
x² – 4x + 29 = x² + 4x + 85
-4x – 4x = 85 – 29
-8x = 56
∴ (x, 0) = (-8, 0) is the point which is equidis¬tant from the given points.

Question 11.
If the distance between two points (x, 7) and (1, 15) is 10, find the value of x.
Solution:
Given = A(x, 7), B(1, 15) and AB = 10.
Distance formula

squaring on both sides, we get.
\(\left[\sqrt{x^2-2 x+65}\right]^2\) = 10²
⇒ x² – 2x + 65 = 100
x² – 2x – 35 = 0
⇒ x² – 7x + 5x – 35 = 0
x(x- 7) + 5(x – 7) = 0
(x – 7) (x + 5) = 0
(x – 7) = 0 or x + 5 = 0
x = 7 or x = -5
∴ x = 7 or – 5

Question 12.
Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Solution:
Given : P(2, -3), Q(10, y) and \(\overline{\mathrm{PQ}}\) = 10
Distance formula

squaring on both sides we get,
\(\left[\sqrt{y^2+6 y+73}\right]^2\) = 10²
⇒ y² + 6y + 73 = 100
⇒ y² + 9y – 3y – 27 = 0
⇒ y(y + 9) – 3 (y + 9) = 0
⇒ (y + 9) (y – 3) = 0
⇒ y + 9 = 0 or y – 3 = 0
⇒ y = – 9 or y = 3
⇒ y = – 9 or 3

Question 13.
Find the radius of the circle whose centre is (3, 2) and passes through (-5, 6).
Solution:

Given : A circle with centre A(3, 2) passing through B(-5, 6).
Radius = AB
[∵ Distance of a point from the centre of the circle.]
Distance formula
\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
Radius r = \(\sqrt{(-5-3)^2+(6-2)^2}\)
= \(\sqrt{64+16}\) = \(\sqrt{80}\) = 4\(\sqrt{5}\) units.

Question 14.
Can you draw a triangle with vertices (1, 5), (5, 8) and (13, 14) ? Give reason.
Solution:
Let A(1, 5), B(5, 8) and C(13, 14) be the given points.
Distance formula

Here, AC = AB + BC
∴ Δ ABC can’t be formed with the given vertices.
[∵ sum of the any two sides of a triangle must be greater than the third side],

Question 15.
Find a relation between x and y such that the point (x, y) is equidistant from the points (-2, 8) and (-3, -5).
Solution:
Let A(-2, 8), B(-3, -5) and P(x, y)
If P is equidistant from A, B then PA = PB
Distance formula

Now PA = PB
⇒ \(\sqrt{x^2+y^2+4 x-16 y+68}\)
⇒ \(\sqrt{x^2+y^2+6 x+10 y+34}\)
squaring on both sides we get,
⇒ 4x – 16y – 6x – 10y = 34 – 68
⇒ – 2x – 26y = – 34
⇒ x + 13y = 17 is the required condition.

Telangana SCERT TS 10th Class Physical Science Study Material Pdf 3rd Lesson Acids, Bases and Salts Textbook Questions and Answers.

TS 10th Class Physical Science 3rd Lesson Questions and Answers Acids, Bases and Salts

Improve Your Learning
I. Reflections on concepts

Question 6.
An acid or a base is mixed with water. Is this process exothermic or endothermic one?
Answer:
When acid or base is mixed with water heat is liberated. So, this process is exothermic.

Question 2.
Distilled water does not conduct electricity. Why?
Answer:

1. Water consists of H₃O⁺ and OH^– ions.
2. In distilled water, the concentration of both H₃O⁺ and OH^– is same. Hence they do not form as ions, so distilled water can be treated as a neutral solution.
3. As there is no flow of ions, distilled water does not conduct electricity.
4. On the other hand, while falling to earth through the atmosphere rainwater dissolves some acidic gases like CO₂, SO₂, and N₂O and forms acids such as H₂CO₃, H₂SO₃, HNO₃.
5. These acids produce Ions. Due to presence of Ions, rainwater conducts electricity.

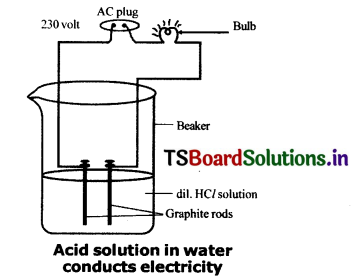
Question 3.
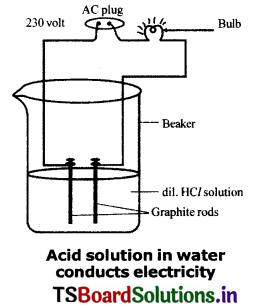
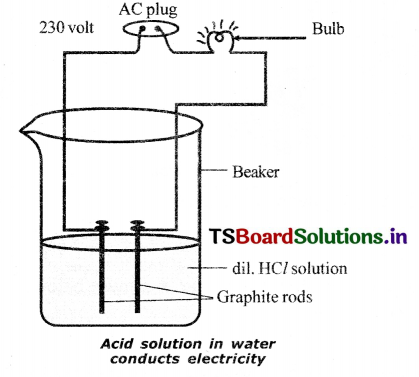
Draw a neat diagram for showing acid solution In water conducting electricity.
Answer:

Question 4.
Why the flow of acid rain Into a river make the survival of aquatic lite in a river difficult?
Answer:

• When pH value of rainwater is less than 5.6, it is called acid rain.
• When acid rain flows into the rivers, it lowers the pH of the river water.
• Living organisms can survive only in a narrow range of pli change.
• So flow of acid rainwater into rivers Is dangerous to the survival of aquatic “ life. These acids have free ions that conduct electric current.

Question 5.
What Is baking powder? How does It make the cake soft and spongy?
Answer:
Baking powder s a mixture of baking soda and mild edible acid such as tartaric acid.

1. The chemical name of baking powder is sodium hydrogen carbonate (NaHCO₃).
2. It is added to the dough while making cake because on heating It Is converted to sodium carbonate with release of carbon dioxide.
   NaHCO₃ + H⁺ → CO₂ + H₂O + Sodium salt of acid
3. While baking the cake the CO₂ released by baking powder causes the cake or bread to rise making them soft and spongy.

Question 6.
What is a neutralization reaction? Give two examples.
Answer:
Neutralization reaction: The reaction between an acid and a base to give a salt and water is known as a neutralization reaction.

Examples:
(i) When diluted NaOH solution reacts with HCl solution, NaCl (Sodium chloride) salt and water are formed.
NaOH (aq) + HCl (aq) → NaCl (aq) +H₂O

(ii) When diluted KOH solution reacts with Nitric acid solution, KNO₃ (Potassium nitrate) salt and water are formed.
KOH (aq) + HNO₃ (aq) → KNO₃ (aq) + H₂O

Question 7.
Dry hydrogen chloride gas does not turn blue litmus to red whereas aqueous hydrogen chloric acid does. Why?
Answer:

1. Dry hydrogen chloride gas does not dissociate in the absence of water. Hence it does not turn blue litmus to red. So dry hydrogen chloride gas is not acidic.
2. The HCl (hydrochloric acid) dissociates in the presence of water. Hence it turns blue litmus to red. So. HC (Hydrochloric acid) is acidic.
   The dissociation wIll be as follows:
   HCl + H₂O → H₃O⁺ + Cl^–

Question 8.
Give two important uses for each of washing soda and baking soda.
Answer:
Uses of Washing soda (Na₂CO₃):

• Washing soda (sodium carbonate) is used in glass, soap and paper industries.
• It is used In the manufacture of sodium compounds such as borax.
• Sodium carbonate can be used as a cleaning agent for domestic purposes.
• It is used for removing permanent hardness of water.

Uses of Baking soda (NaHCO₃):

1. Baking soda (Sodium hydrogen carbonate) is used for faster cooking.
2. Baking powder (a mixture of baking soda and a mild acid) is used in preparation of cakes.
3. Sodium hydrogen carbonate Is also an ingredient in antacids.
4. It is also used in soda-acid, fire extinguishers.
5. It acts as a mild antiseptic.

Application Of Concepts

Question 1.
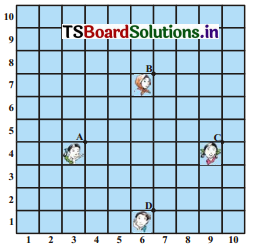
Five solutions A, B, C, D and E when tested with universal indicator showed pH as 4, 1, 11, 7 and 9 respectively. Classify the solutions given below.
(a) neutral
(b) strongly alkaline
(c) strongly acidic
(d) weakly acidic
(e) weakly alkaline

Order of pH is In increasing order of hydrogen Ion co4centratIon, higher the hydrogen ion concentration lower is the pH value.
11<9< 7<4< 1
C<E<D<A<B

Question 2.
Why does tooth decay start when the pH of mouth is lower than 5.5?
(or)
What value of pH in the mouth leads to tooth decay? Why?
Answer:

1. Tooth decay starts when the pH of the mouth is lower than 5.5.
2. Tooth enamel, made up of calcium phosphate is the hardest substance in the body.
3. It does not dissolve ¡n water but is corroded when the pH in the mouth is below 5.5 due to acids.
4. Bacteria present In the mouth produce free acids whose pH is lower than 5.5, due to degradation of sugar and food particles present in the mouth. Due to this the pH of the mouth falls.

Question 3.
A milkman adds a very small amount of baking soda to fresh milk.
(a) Why does he shift the pH of the fresh milk from 6to slightly alkaline?
(b) Why does this milk take a long time to set as curd?
Answer:
(a) There is a shift In p’ of fresh milk from 6 to slightly alkaline when a little of baking soda is added to It is because the W ion concentration has been decreased and so the nature of solution has become slightly alkaline.

(b) Lactic acid which was formed initially, reduce the basic nature of the baking soda. Then more lactic acid is needed to convert milk Into curd. That is why it takes time to produce more lactic acid and hence the milk take a long time to set as curd.

Question 4.
Plaster of Parts should be stored in a moisture-proof container. Explain why.
Answer:

• Plaster of Paris means calcium sulphate hemihydrate (CaSO₄. ½H₂O).
• Plaster of París on mixing with water, sets into hard solid mass due to the formation of gypsum (CaSO₄. 2H₂O)

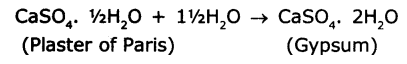
Because of the above reason Plaster of Pans should be stored in a moisture-proof container so that it won’t turn into gypsum.

Question 5.
Equal lengths of magnesium ribbons are taken in test tubes A and B. Hydrochloric acid is added to test tube A, while acetic acid Is added to test tube B. The valances and concentration of both the acids Is same. In which test tube will the fizzing occur more vigorously and why?
Answer:

1. The fizzing occur more vigorously In test tube A.
2. Hydrochloric acid contains more H₃O⁺ ions and it is a strong acid. Hence the reaction will be faster in test tube A.
3. Acetic acid contains fewer H₃O⁺ ions and it is a weak acid. Hence the reaction will be slower.

Higher Order Thinking Questions

Question 1.
Fresh milk has a pH of 6.6 Explain why the pH changes as it turns into curd?
Answer:

• pH value of milk decreases as milk turns to curd.
• Lactobacillus bacteria turn milk to curd by releasing lactic acid.
• That means curd contains lactic acid. So its pH decreases than 6, so. curd Is acidic in nature.

Question 2.
How do you prepare an indicator, using beetroot? Explain.
Answer:
Aim: To prepare own indicator.
Materials required:

1. Beetroot corms -2 or 3,
2. Knife,
3. Bowls,
4. Water,
5. Spoon,
6. Mixy,
7. Orange juice

Procedure:

• Take the beetroots and peel them with the help of a knife. (At first, wash them).
• Chop them into pieces.
• Put those pieces into a mixie jar and make a paste.
• Add some water to the paste. Now filter this and collect only juice from this.

Observation & Result:

1. Now add 5 to 6 drops of this juice (beetroot juice (indicator)) to orange juice (5 to 6 drops) and mix it.
2. We can see the colour change. This indicates the presence of acidic nature in orange Juice.

IV. Multiple choices questions

Question 1.
The colour of methyl orange indicator in acidic medium is ………………….. ( )
(A) yellow
(B) green
(C) orange
(D) red
Answer:
(D) red

Question 2.
The colour of phenolphthalein Indicator in basic solution is ………………….. ( )
(A) yellow
(B) green
(C) pink
(D) orange
Answer:
(C) pink

Question 3.
Colour of methyl orange In alkali conditions ……………………………. ( )
(A) orange
(B) yellow
(C) red
(D) blue
Answer:
(B) yellow

Question 4.
A solution turns red litmus blue, its pH is likely to be …………………………….. ( )
(A) 1
(B) 4
(C) 5
(D) 10
Answer:
(D) 10

Question 5.
One of the following solutions reacts with crushed egg shells to give a gas that turns lime-water milky, the solution is of …………………………….. ( )
(A) NaCl
(B) HCl
(C) LiCl
(D) KCl
Answer:
(B) HCl

Question 6.
If a base dissolves in water, by what name is it better known’ ……………………….. ( )
(A) neutral
(B) base
(C) acid
(D) alkali
Answer:
(D) alkali

Question 7.
Which of the following substances when mixed together will produce table salt? ( )
(A) Sodium thiosulphate and sulphur dioxide
(B) Hydrochloric acid and sodium hydroxide
(C) Chlorine and oxygen
(D) Nitric acid and sodium hydrogen carbonate
Answer:
(B) Hydrochloric acid and sodium hydroxide

Question 8.
What colour would hydrochloric acid (pH=1) turn universal indicator? ()
(A) orange
(B) purple
(C) yellow
(D) red
Answer:
(D) red

Question 9.
Which one of the following types of medicines is used for treating Indigestion? ()
(A) antibiotic
(B) analgesic
(C) antacid
(D) antiseptic
Answer:
(C) antacid

Question 10.
What gas is produced when magnesium is made to react with hydrochloric acid? ()
(A) hydrogen
(b) oxygen
(C) carbon dioxide
(D) no gas is produced
Answer:
(A) hydrogen

Suggested Experiments

Question 1.
Compounds such as alcohol and glucose contain hydrogen but are not categorized as acids. Describe an activity to prove It.
Answer:

1. Prepare solutions of glucose, alcohol, hydrochloric acid and sulphuric acid etc.
2. Connect two different coloured electrical wires to graphite rods separately in a 100 ml beaker as shown In the figure.
3. Connect free ends of the wire to 230 V AC plug and complete the circuit, by connecting a bulb to one of the wires.
4. Now pour some dilute H in the beaker and switch on the current.
5. We observe that the bulb glows.
6. Repeat the activity with dilute sulphuric acid, glucose and alcohol.
7. We observe that the bulb glows only in sulphuric acid solution, but not in glucose and alcohol solutions.
8. Glowing of bulb indicates that there Is a flow of electric current through the solution.
9. Acid solutions have ions and the moment of these ions in solution helps for flow of electric current through the solution.
10. 10) The positive Ion present In HCl solution is H⁺. This suggests that acids produce hydrogen ions (H⁺) in solution, which are responsible for their acidic properties.
11. In glucose and alcohol solution, the bulb does not glow indicating the absence of H+ Ions, though they contain hydrogen.
12. Hence glucose and alcohol are not categorized as acids.

Question 2.
What is meant by “water of crystallization” of a substance? Describe an activity to show the water of crystallization.
Answer:
Water of Crystallization: Water of crystallizatIon Is the fixed number of water molecules present in one formula unit of a salt in its crystalline form.
Eg: CuSO₄. 5H₂O.
It means that five water molecules are present in one formula unit of copper sulphate.

Activity to show the water of crystallization:

1. Take a few crystals of copper sulphate In a dry test tube and heat the test tube.
2. We observed water droplets on the walls of the test tube and sat turns white.
3. Add 2 – 3 drops of water on the sample of copper sulphate obtained after heating
4. We observe the blue colour of copper sulphate crystals is restored.

Suggested Projects

Question 1.
How do you select a good place to plant a tree in your school/at home? lest the soil and investigate and write a report on it.
Answer:
You have to select a good place to plant a tree in your school at home which satisfies following requirements.
(1) Water: Close, easy access to a water source essential. The water must be from a potable source. The water source must also be nearly because it will be used almost daily.

2) sunlight: A minimum of six flours of direct sunlight per day is necessary to grow most vegetables and flowers, Watch out for shading from nearby trees, buildings, hills and so on.

(3) Access: The site should be dose to classrooms/house and easily accessible. if the garden too For away, it will be difficult to get and keep the plants checking daily.

(4) Secured: the site should be secured from animals and birds. So s should have fencing to protect the plants from, animals and birds.

(5) Healthy sell: The soil where you want to plant it shouid be healthy and safe. the sod should not have more acidic nature or more basic nature which prevents the healthy growth of s plant. To confirm that the soil is safe, conduct a soil test

Procedure:
Put about 2 gm. of soil in a test tube and add 5 mi water to It. shake the contents of the test tube. Filter the contents and coiled the filtrate in test tube. Check the pH of this filtrate with the help of universal indicator paper.

Observations :

1. If the soil is too acidic (having low pH ) then it is treated with materials like quick lime (Calcium Oxide) or slaked lime (calcium hydroxide) or chalk (calcium carbonate).
2. If the soil Is too basic leaving a high pH its alkalinity can be reduced by adding decaying organic matter (manure or compost) which contains acidic materials.

Conclusions: Plants require a specific pH range for their healthy growth. Chemicals can be added to soil to adjust its pH and make it suitable for growing plants.

Question 2.
Do all vegetables are acids? To find this Investigate with pH paper and tabulate the values and write a report on It?
Answer:
Yes, most of the vegetables are slightly acidic cut a small piece of the following vegetables and test it with universal pH paper and note the values In the table given below :

Question 3.
Collect Information about the Importance of the pH value In daily life to human beings as well as plants.
Answer:
The pH plays on important role Is many activities of our everyday life.
1. pH is our Digestive system:
Our stomach produces hydrochloric acid (of pH about 1.4) which helps in digesting our food without harming the stomach excess acid is produced in the stomach due to various reasons causes is digestion which produces pain and Irritation. order to cure Indigestion and get rid of pain, we can take bases called ‘antacids’ which neutralise the excess acid produced in the stomach and gives relief to the person.

2. pH change as the cause of tooth decay:
When we eat food containing sugar, then the bacteria present in our mouth break down the sugar to form acids which lowers the pH In the mouth. Tooth decay starts when the pH of acid formed in the mouth falls below 5.5. The best way to present tooth decay is to clear, the mouth thoroughly with toothpaste (pH is about 8.0) being a base it neutralizes the excess acid In the mouth.

3. Plants and Animals are sensitive to pH changes:
(a) Soil pH and Plant Growth: Most of the plants grow best when the pH of the soil is close to 7. If the soil is too acidic or too basic, the plants grow at all. Chemicals can be added to soil to adjust Its pH and make it suitable for growing plants.

(b) pH change and survival of Animlals: The pH plays an important role in the survival of animals, including human beings. Our body works well within a narrow pH range of 7.0 to 7.8. If due to some reason, this pH range gets disturbed in the body of a person, then many ailments can occur. The aquatic animals can survive in the lake or river water within a narrow range of pH change.

4. Self defince by animals and plants through chemical warfare:
Many animals and plants protect themselves from their enemines by injecting painful and Irritating acids and bases into their skin. For example, Bee sting leaves an acid which causes pain and irritation. Rubbing with mild base like baking soda on the stung area gives relief. Stringing hair of leaves of nettle pant, inject methanoic acid causing burning pain. In rubbing the area with the leaf of dock plant which is basic gives relief from pain.

TS 10th Class Physical Science Acids, Bases and Salts Intext Questions

Page 33

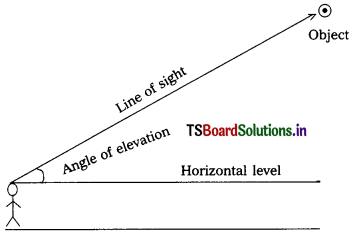
Question 1.
What chemical reaction takes place?
Answer:
The antacid tonic or chewing tablet contains base which neutralises the action of acid in the stomach. So the reaction takes place is called neutralisation reaction.

Page 34

Question 2.
What do you conclude from the observations noted in table – 1?
Answer:
From the table given, I conclude that solutions of HCl, H₂SO₄, HNO₃, CH₃COOH change blue litmus into red colour, phenolphthalein solution colourless and methyl orange to red. The solutions of NaOH, KOH, Mg(OH)₂ NH₄OH and Ca(OH)₂ change red litmus to blue colour, phenolphthalein to pink colour and methyl orange to yellow colour.

Page 35

Question 3.
What do you conclude from thIs activity?
Answer:
Chopped onions, clove oil and vanilla essence can also be used as Indicators because we observe a change In the odour of these substances In acid medium and basic medium.

Question 4.
Can you give example for use of olfactory indicators in daily life?
Answer:
We use olfactory Indicators in cooking curries which are stale to eat and have disagreeable smell and change them to give agreeable and pleasant smell. Eg. Onions and cloves.

Question 5.
Why pickles and sour substances are not stored in brass and copper vessels?
Answer:
Pickles and sour substances contain acids. These acids react with copper and brass vessels to form blue scales and corrode the vessels, These blue scales are harmful to our health. So pickles and sour substances should not be kept In brass and copper vessels.

Page 37

Question 6.
What do you observe by adding dilute HCl to sodium carbonate and sodium hydrogen carbonate?
Answer:
When dilute HCl is added to sodium carbonate carbon dioxide gas which turns lime water milky is obtained. The reaction is as follows :
NaCO_3(s) + 2HCl_(aq) → 2NaCl_(aq) + H₂O_(l) + CO_2(g)
When dilute HCl reacts with sodium hydrogen carbonate CO₂ and NaCl are formed.
The reaction is as follows :
NaHCO_3(s) + HCl_(aq) → NaCl_(aq) + H₂O_(l) + CO_2(g)

Page 38

Question 7.
Why did the colour of the solution change after adding the HCI solution?
Answer:
The pink colour of the solution of NaOH to which phenolphthalein is added becomes colourless after adding dilute HCl because HCl Is an acid and phenolphthalein becomes colourless in acid medium.

Question 8.
Does the Pink colour reappear?
Answer:
The pink colour reappears on adding NaOH.

Question 9.
Do you guess the reason for reappearance of pink colour?
Answer:
The reaction occurring between acid and base In the above activity can be written as :
NaOH_(aq) + HCl_(aq) → NaCl_(aq) + H₂O_(l) .
The reason for reappearance of pink colour is the presence of acid in excess.

Page 39

Question 10.
What do you observe in the above reaction?
Answer:
We observe copper oxide present in the beaker dissolves in dilute HCl and the colour of the solution becomes bluish-green due to formation of cupric chloride.

Question 11.
What do you conclude from the activity 5 and 6?
Answer:
By observing both activities 5 and 6, 1 conclude that carbon dioxide which is a non-metallic oxide Is acidic In nature.

Question 12.
What do acids have in common?
Answer:
We find that hydrogen is common in all acids.

Page 40

Question 13.
What do you notice?
Answer:
When dilute HCl or dilute H₂SO₄ is poured In the beaker, the electricity is conducted through these solutions.

Question 14.
What do you observe?
Answer:
Acid solutions have ions and the movement of these Ions in solution helps for flow of electric current through solution.

Question 15.
Doesthebulbglowinallcases?
Answer:
No. Bulb glows only when hydrochloric acid or sulphuric acid is taken in the beaker.

Question 16.
What do bases have In common?
Answer:
Bases have (OH^–) ions in common.

Question 17.
Does the bulb glow?
Answer:
Yes, the bulb glows when current is passed through sodium hydroxide, calcium hydroxide solutions etc.

Question 18.
What do you conclude from the results of this activity?
Answer:
Aqueous solutions of acids as well as bases conduct electricity, because of the presence of ions.

Page 41

Question 19.
Do acids produce ions only in aqueous solution? (AS1) (1 Mark)
Answer:
Yes, Acids produce Ions only in aqueous solutions. For example HCl produces W ions in aqueous solutions and shows acidic properties.
But when H gas is dissolved in benzene It does not produce H’ Ions and does not show any acidic properties.

Question 20.
What do you observe? Is there a gas coming out of the delivery tube?
Answer:
I observe a gas coming out of delivery tube. It changes wet blue litmus paper into red colour.

Question 21.
What do you Infer from the above observation?
Answer:
We conclude that dry HCl gas (hydrogen chloride) is not an acid because we notice no change in colour of dry litmus paper but HCl aqueous solution is an acid because wet blue litmus paper turns to red.

Page 42

Question 22.
What do you feel?
Answer:
we feel the test tube has become hot.

Question 23.
Is ¡tan exothermic or endothermic process?
Answer:
It is an exothermic process.

Page 43

Question 24.
What do you observe?
Answer:
We observe that the bulb glows brightly in HCI solution while the glowing intensity of the bulb Is low In acetic acid solution.

Question 25.
Can you guess the reason for the changes you observed?
Answer:
There are more W ions in HO solution and fewer W ions in acetic acid solution.

Page 44

Question 26.
What is the nature of each substance on the basis of your observations?
Answer:
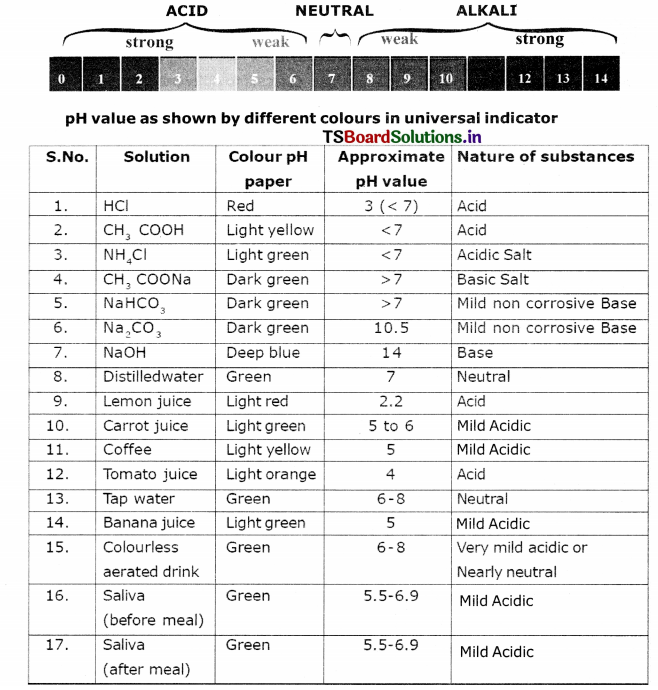
On the basis of our observations, as PH gradually increases from 1 to 6 the acid becomes weaker and weaker.
As the P^H increases from 8 to 14 the basic nature grows stronger and stronger.  If the PH is exactly ”7” the solution is neutral.

Page 47

Question 27.
What is the reason for change In colour of solution? (AS 1) (1 Mark)
Answer:
When we add methyl orange indicator to diluted HCI., the colour of methyl orange turns to red. But on adding antacid tablet powder it slightly becomes yellow. The reason is antacid contains a mild base, namely Mg(OH)₂ or Al(OH)₃.

Question 28.
Can you write the chemical equation for this reaction?
Answer:
3HCI+Al(OH)₃ → AlCl₃+3H₂O

Question 29.
What can you conclude about the Ideal soil PH for the growth of plants In your region?
Answer:

1. My region Is nearer to the sea coast of Bay of Bengal. So it is a little basic in nature.
2. So fertilizers of acidic nature are to be used in our soil to improve yield of crops in our region.

Question 30.
Under what soil conditions a farmer would treat the soil of his fields with quicklime (Callum hydroxide) or calcium carbonate?
Answer:
If the soil Is acidic In nature the farmer would treat the soil of his fields with quick lime (calcium hydroxide) or calcium carbonate to neutralize the acidic nature of soil.

Page 48

Question 31.
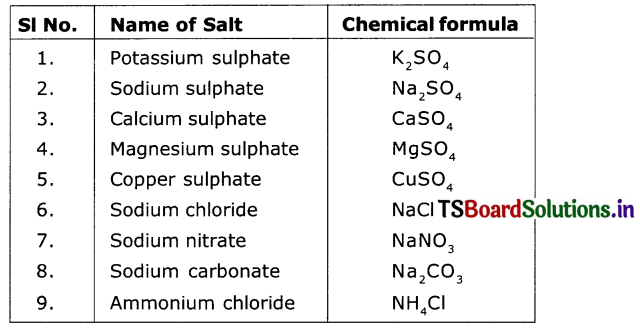
Write the formulae of the following salts.
Answer:
(Salts are mentioned in the following table and answers are given against each)

Question 32.
How many families can you Identity among the salts given above?
Answer:
I can identify: Sodium family, Sulphate family, Chloride family.

Page 49

Question 33.
What do you say about salts of both weak acid and weak base?
Answer:
In such case, the P^H depends on the relative strengths of acid and base. Further, the formation of salts does not occur as the heat of neutralization is lost to a large extent to ionize the weak acid and the weak base.

Page 52

Question 34.
What does 10H₂O signify?
Answer:
10H₂O signifies 10 molecules of water.

Question 35.
Does it make Na₂CO₃ wet?
Answer:
10 molecules of water do not wet NaCO₃. They are chemically added to form solid crystals. These molecules of water are called water of crystallization.

Question 36.
Did you notice water droplets on sides of the test tube? Where did they came from?
Answer:
Yes. They came from crystals of copper sulphate.

Question 37.
What do you observe? Is the blue colour of copper sulphate restored?
Answer:
Yes, To anhydrous copper sulphate if 2-3 drops of water is added the blue colour of copper sulphate ¡s restored.

Page 53

Question 38.
How can you get half a water molecule?
Answer:
It is written as CaSO₄. 1/2H₂O (Plaster of Paris) because two formula units of CaSO₄ share one molecule of water.

Think And Discuss

Question 1.
Is the substance present in antacid tablet acidic or basic?
Answer:
One of the substance present in antacid tablet Is sodium hydrogen carbonate. It is an alkali.

Question 2.
What type of reaction takes place In stomach when an antacid tablet is consumed?
Answer:
During lndigestion, the stomach produces too much acid and this causes pain and irritation. When we use an antacid, being an alkali it neutralizes the excess acid in the stomach and provides relief. It is a neutralization reaction.

Question 3.
Which gas is usually liberated when an acid reacts with a metal? How will you test for the presence of this gas?
Answer:

1. When acid reacts with metal, hydrogen gas is evolved.
2. When we bring a burning match stick or candle to the mouth of the delivery tube, it turns off with a pop Sound.

Question 4.
A compound of a calcium reacts with dilute hydrochloric acid to produce effervescence. The gas evolved extinguishes a burning candle; turns -lime water milky. Write a balanced chemical equation for the reaction If one of the compounds formed is calcium chloride.
Answer:
CaCO₃ + 2HCl → CaCl₂ + CO₂ + H₂O

Question 5.
Why do HCl, HNO₃ etc, show acidic characters In aqueous solutions while solutions of compounds like alcohol and glucose do not show acidic character?
Answer:
HCl, HNO₃ etc., show acidic characters in aqueous solutions because they release H⁺ ions in water solutions.
But alcohol and glucose do not show acidic character because they do not release H⁺ ions in aqueous solutions.

Question 6.
While diluting an acid, why is It recommended that the acid should be added to water and not water to acid?
Answer:

1. The process of diluting an acid or a base in water is exothermic process.
2. If water is added to concentrated acid, the heat generated may cause the mixture to splash out and cause burns on the skin.
3. So acid must always be added to water slowly with constant stirring.

Question 7.
What will happen if the pH value In our body Increases?
Answer:
Bacteria present in the mouth produce acids by degradation of sugar and food particles in the mouth. The acidic nature of chemicals in our body increases and causes irritation in the digestive system and finally leads to ulcers in the stomach and intestines.

Question 8.
Why do living organisms have narrow pH range?
Answer:
Our body carries metabolic activities with the pH range of 7.0 to 7.8. Living organisms can survive only in a narrow range of pH range. If the PH range exceeds this limit, acids form in the body and cause irritation in the stomach and throat and develop acidity which corrodes the membrane in the digestive
system and finally it leads to ulcers and cancer.

TS 10th Class Physical Science Acids, Bases and Salts Activities

Activity 1

Question 1.
Testing the acids and bases with indicators viz.. Red litmus, blue litmus, phenolphthalein solution and methyl orange solution.
Answer:

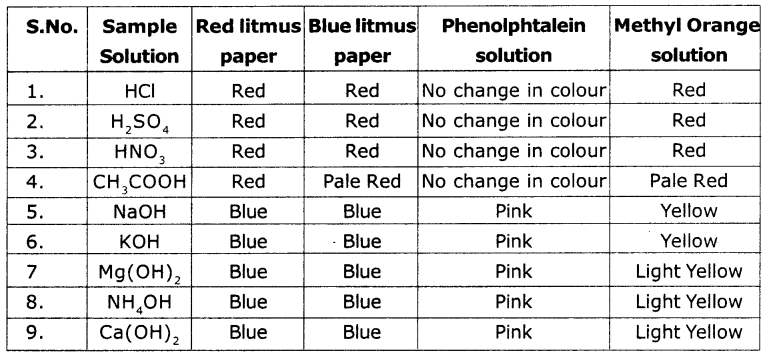
From the above table, we conclude that the acids and bases change the colour of indicators.

Activity 2

Question 2.
What are Olfactory indicators? Write an activity to prove them.
Answer:
Olfactory Indicators: There are some substances whose odour changes in acidic or basic media. These are called olfactory indicators.
Aim: To check the olfactory indicator.
Required materials :

1. Onions
2. Knife
3. Plastic bag
4. Clean clothes.

Procedure:

1. Take some onions and finely chop them.
2. Put the chopped onions in a plastic bag with some clean cloth.
3. Tie up the bag tightly and keep It overnight in the fridge.

Observation: Check the odour of the cloth strips.
Result: It is used as the acid indicator.

Lab Activity 1

Question 3.
Show that acids produce hydrogen gas when react with mals.
Answer:
Aim: To show that acid produces hydrogen gas when react with metals.
Materials required: Test tube, delivery tube, grass trough, candle, soap water, dii HCl, zinc granules and cork

Procedure:

1. Set the apparatus as shown In figure.

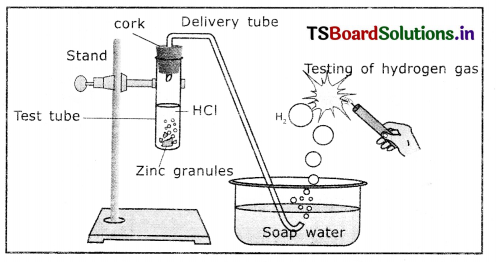
Reaction of zinc granules with dil.HCl and testing of hydrogen gas by a burning matchstick
2. Take about 10 ml of dilute MCI In a test tube and add a few zinc granules to It.
3. We observe a gas evolving from the test tube
4. Pass the gas released by through the soap water.
5. We observe some bubbles formed in the soap solution.
6. Bring a burning matchstick near the gas-filled bubble.
7. The burning matchstick is put out with a pop sound.
8. The pop sound indicates that the gas evolved is H₂.

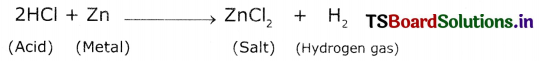
9. Repeat this experiment with H₂SO₄, HNO₃ etc.
From the above experiment, we conclude that hydrogen gas is produced when an acid reacts with metals.

Activity 3

Question 4.
Show that the reaction of metal with a base produces hydrogen gas.
Answer:

1. Place a few granules of zinc in a test tube and add 10 ml of sodium hydroxide (NaOH) solution and warm the contents of the test tube.
2. Pass the gas being evolved through the soap water.
3. Some bubbles are observed In the test tube.
4. Bring a burning candle near the gas filled bubble.
5. The candle is put out with a pop sound.
6. The pop sound indicates that the gas produced is hydrogen.
7. In this activity we also notice that evolved gas is hydrogen and salt formed is sodium zincate.
   2NaOH +Zn → Na₂ZnO₂ + H₂

But these reactions are not possible with all metals.

Activity 4

Question 5.
Show that the reaction of acids with carbonates and metal hydrogen carbonates produce carbon dioxide gas.
Answer:

1. Take two test tubes, label them as A dnd B.
2. Take about 0.5 gm of sodium carbonate (Na₂CO₃, in test tube A and about 0.5 gm of sodium hydrogen carbonate (NaHCO₃) in test tube B.
3. Add about 2 ml. of dilute HCl to both the test tubes.
4. Pass the gas produced In each case through lime water and record your observation.
5. We observe that the lime water turns to milky white colour.
6. The reactions are
   Na₂CO₃ + 2HCl → 2NaCI + H₂O + CO₂
   NaHCO₃+ HCl → NaCl + H₂O + CO₂

Reactions when the gas Is passed through lime water.
Ca(OH)₂ + CO₂ → CaCO₃ ↓+ H₂O
On passing excess of carbondioxide, the following reaction takes place.

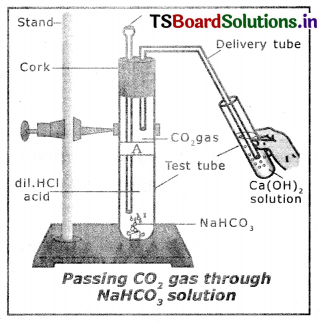
CaCO₃ + H₂O+ CO₂ → Ca(HCO₃)₂
Thus from the above activity we can conclude that the reaction of metal carbonates and hydrogen carbonates with acids give a corresponding salt, carbondioxide and water.

Activity 5

Question 6.
What Is neutralization? Explain an activity to demonstrate neutralization.
Answer:
Neutralization: The reaction of an acid with a base to give a salt and water is known as a neutralization reaction.
Base + Acid → Salt + Water

Activity:

1. Take about 2 ml of dilute NaOH solution in a test tube and add one drop of phenolphthalein indicator. The solution turns to pink.
2. Add dilute HCI solution to the above solution drop by drop. The pink colour disappears.
3. Now add one or two drops of NaOH to the above mixture.
4. Now the pink colour reappears.
5. In the above reaction first the pink colour disappears on adding HCl because NaOH Is completely reacted with HCl The effect of base Is nullified by an acid.
6. Pink colour reappears on adding a drop of NaOH because the solution becomes basic once again. The reaction occu ring between acid and base in this activity

can be written as :
NaOH + HCI → NaCl + H₂O
This is neutralization reaction.

Activity 6

Question 7.
Show that the metal oxides are basIc In nature through an actIvity.
(OR)
Describe an activity to observe the reaction of acids with metal oxides. What do you observe?
Answer:

1. Take a small amount of copper oxide In a beaker and slowly add dilute HCl acid while stirring.
2. We will notice that the copper oxide present in the beaker dissolves In dilute HCl and the colour of the solution becomes bluish-green.
3. The reason for this change is the formation of copper chloride in the reaction.
4. The general reaction is : Metal oxide + Acid → Salt + Water.
5. In this reaction, metal oxide reacts with acid to give salt and water. This reaction is similar to the neutralization reaction.
6. In this reaction metal oxide gives salt and water when it reacts with acid. Thus we can conclude that metal oxides are basic in nature.

Activity 7

Question 8.
Write an activity to show that whether all compounds containing hydrogen are acids or not.
(or)
Write an activity which proves acids are good conductors of electricity.
Answer:
Procedure:

1. Prepare glucose, alcohol, hydrochloric acid and sulphuric acid solutions.
2. Fix two iron graphite rods on a rubber cork and place the cork in a lOOmI beaker.
3. Connect two different coloured electrical wires to graphite rods separately as shown In figure.
4. Connect free ends of the wire to 230 volts AC plug.
5. Complete the circuit as shown in the figure by connecting a bulb to one of the wires.
6. Now pour some dilute HCl in the beaker and switch on the current.

Observation: The bulb starts glowing.
Repetition: Repeat activity with dilute sulphuric acid, glucose and alcohol solutions separately.

Observation :

• We will notice that the bulb glows only In acid solutions.
• But the bulb does not glow in glucose and alcohol solutions.

Result:

1. GlowIng of bulb indicates that there Is flow of electric current through the solution.
2. Acid solutions have ions and the movement of these ions in solution helps for flow of electric current through the solution.

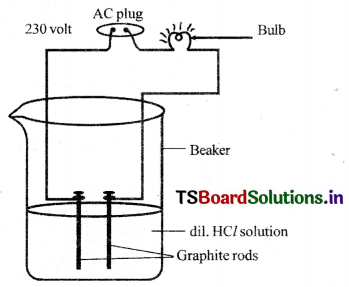
Conclusion:

1. The positive ion (cation) present in HCl solution is W.
2. This suggests that acids produce hydrogen ions W in solution, which are responsible for their acidic properties.
3. In glucose and alcohol solution the bulb did not glow Indicating the absence of W ions in these solutions. .
4. The acidity of acids is attributed to the W ions produced by them in solutions.

Activity 8

Question 9.
Do acids produce ions only in aqueous solution? Explain an activity to observe this.
Answer:
1. Take about 1.0 gm of solid NaCl in a clean and dry test tube.
2. Add some concentrated sulphuric acid to the test tube.
3. We observe a gas is liberated.
4. The reaction is 2NaCl + H₂SO₄ → 2HCl + Na₂SO₄
5. Test the gas evolved successively with dry and wet blue litmus paper.
6. We observe that there is no change in the colour of dry litmus paper, because dry HCl is not an acid. But aqueous solution of HCl Is an acid because wet blue litmus paper turned into red.

The HCl gas evolved from delivery tube dissociates in presence of water to produce hydrogen ions. In the absence of water, dissociation of HCl molecules does not occur.
7. The dissociation of HCI In water is shown below.
HCl + H₂O → H₃O⁺+ Cl^–
Hence acids give H₃O⁺ ions in water.

Question 10.
What happens when a base is dissolved in water?
Answer:
1. Take some bases like NaOH, KOH, Mg(OH)₂ in different test tubes and add water to them.

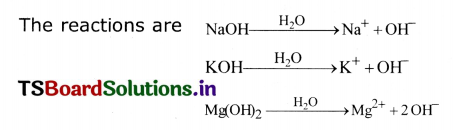
2. Bases in water produce hydroxide (OH^–)ions.

Activity 9

Question 11.
Write an activity to show that dissolving of an acid in water is an exothermic process (or) endothermic process.
Answer:
Experiment:

1. Take 10 ml water in a beaker.
2. Add a few drops of concentrated H₂SO₄ to it and swirl the beaker slowly.
3. Touch the base of the beaker.
4. The base of beaker is hot.

Result:
This is an exothermic process called as dilution.

Activity 10

Question 12.
Explain a test to know whether the acid (or base) is strong or weak.
Answer:
1. Take two beakers A and B.
2. Fill the beaker A with dil. CH₃COOH and beaker B with dii. HCI.
3. Arrange the apparatus as shown in the figure and pass electricity through the solutions in separate beakers.
4. We notice that the bulb glows brightly in HCl solution while the intensity of the bulb is low in acetic acid solution.
5. This indicates that there are more ions in HCl solutions and fewer ions are than is In acetic acid solution.
6. But in H solution means more H₃O⁺ ions. Therefore it is a strong acid. But acetic add has fewer H₃O⁺ ions and hence it is weak acid.

7. Carry out the same experiment by taking bases like dii. NaOH and dil. NH₄OH instead of acids.
8. We observe that NaOH is a strong base and NH₄OH is a weak base.

Activity 11

Question 13.
Test the pH value of solution given in table. Record your observations. What s the nature of each substance on the basis of your observations?
Answer:

Activity 12

Question 14.
Check the action of antacid tablet with acid.
Answer:

1. Take dii. HCl in a beaker and add two to three drops of methyl orange indicator. The solution turns to red.
2. Mix antacid tablet powder to the above solution in the beaker. Now the solution becomes normai i.e., the red colour disappears.
3. We can conclude that the antacid tablet neutralizes the acid.

Activity 13

Question 15.
How can we test the pH value of the soil?
Answer:

1. Collect the soil samples from various places Into different bags.
2. Put about 2g of soil In a test tube and add 5 ml water to it. Shake the contents of the test tube. Fitter the contents and collect the filtrate In a test tube.
3. Check the pH of this filtrate with the help of universal indicator paper.
4. The colour of universal indicator paper shows the pH of the soil as per the colour code.

Activity 14

Question 16.
Write the formulae of the following salts and classify them as families based on radicals.
Potassium sulphate, sodium sulphate, calcium sulphate, magnesium sulphate, copper sulphate, sodium, chloride, sodium nitrate, sodium carbonate and ammonium chloride.
Answer:
Potassium sulphate → K₂SO₄ Sodium sulphate → Na₂SO₄
Calcium sulphate → CaSO₄ Magnesium sulphate → MgSO₄
Copper sulphate → CuSO₄ Sodium chloride → NaCl
Sodium nitrate → NaNO₃ Sodium Carbonate → Na₂CO₃
Ammonium chloride → NH₄Cl
Sodium family:Na₂SO₄, NaCl, NaNO1, Na,Co etc.
Family of chloride salts : NaCl, NH₄Cl. etc.
Family of sulphate salts: K₂SO₄, Na₂SO₄, CaSO₄, MgSO₄, CuSO₄ etc.
Family of carbonate salts: Na₂CO₃, MgCO₃, CaCO₃ etc.

Activity 15

Question 17.
Collect the salt samples like sodium chloride, aluminium chloride, copper sulphate, sodium acetate, ammonium chloride, sodium hydrogen carbonate and sodium carbonate. Dissolve them in distilled water. Check the action of these solutions with litmus papers. Find the pH using pH paper. Classify them into acidic, basic or neutral salts. Identify the acid & base used to form the above salts. Record your observations in table.
Answer:

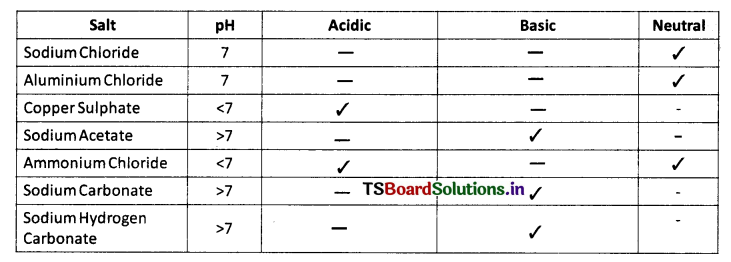
Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.2

Question 1.
In the given figure, ∠ADE = ∠B
i) Show that ∆ABC ~ ∆ADE
ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm. Find DE. (AS₁, AS₂)

Solution:
In ∆^les ADE and ABC, we have
i) ∠ADE = ∠ABC (Given)
∠A = ∠A (Common)
∴ ∠AED = ∠ACB
Hence, ∆ADE ~ ∆ABC Therefore, their corresponding sides are proportional.
⇒ \(\frac{\mathrm{AB}}{\mathrm{AD}}\) = \(\frac{\mathrm{BC}}{\mathrm{AD}}\) = \(\frac{\mathrm{AC}}{\mathrm{AE}}\)

ii) Given that AD = 3.8 cm; AE = 3.6 cm; BE = 2.1 cm; BC = 4.2 cm; DE = ?

∴ DE = 2.8 cm

Question 2.
The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm., determine the corresponding side of the second triangle. (AS₁)
Solution:
Let ∆ABC and ∆DEF be two similar triangle of perimeters 30 cm and 20 cm.

The ratio of the perimeters = 30 : 20 = 3 : 2
Let AB = 12 cm
We have \(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{BC}}{\mathrm{EF}}\) = \(\frac{\mathrm{AC}}{\mathrm{DF}}\)
We know that the ratio of corresponding sides of similar triangles is equal to the ratio of their perimeters.
∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{3}{2}\)
⇒ \(\frac{12}{\mathrm{DE}}\) = \(\frac{3}{2}\)
⇒ 3 × DE = 12 × 2
⇒ DE = \(\frac{12 \times 2}{3}\) = \(\frac{24}{3}\) = 8 cm
Hence, the corresponding side of the triangle = 8 cm.

Question 3.
A girl of height 90 cm is walking away from the base of a lamp post at a speed of 1.2m/sec. If the lamp post is 3.6m above the ground, find the length of her shadow after 4 seconds. (AS₄)
Solution:
In the adjacent figure, AB represents the height of the lamp post, DE, the height of the girl. EC represents the length of girls shadow let EC = x.
The distance between the foot of the lamp post and the girl = 1.2 × 4 = 4.8 meters = 480 cm
DE = 90 cm = 0.9 meters
AB = 3.6 meters
∆ABC ~ ∆DEC
∴ The corresponding sides are proportional.

⇒ 3.6 × x = (4.8 × 0.9) + (0.9 × x)
⇒ 3.6x = 4.32 + 0.9x
⇒ 3.6x – 0.9x = 4.32
⇒ 2.7x = 4.32
⇒ x = \(\frac{4.32}{2.7}\) = \(\frac{432}{100}\) × \(\frac{10}{27}\) = \(\frac{16}{10}\) = 1.6
∴ The length of the girl’s shadow = 1.6 meters.

Question 4.
Given that ∆ABC ~ ∆PQR, CM and RN are respectively the medians of similar triangles ∆ABC and ∆PQR. Prove that (AS₂)
i) ∆AMC ~ ∆PNR (AS₂)
ii) \(\frac{\mathrm{CM}}{\mathrm{RN}}\) = \(\frac{\mathrm{AB}}{\mathrm{PQ}}\)
iii) ∆CMB ~ ∆RNQ

Solution:
i) ∆ABC ~ ∆PQR (Given)
∴ \(\frac{\mathrm{AB}}{\mathrm{PQ}}\) = \(\frac{\mathrm{BC}}{\mathrm{QR}}\) = \(\frac{\mathrm{CA}}{\mathrm{RP}}\) ………………. (1)
(Corresponding sides are proportional)
And ∠A = ∠P; ∠B = ∠Q; ∠C = ∠R ……………… (2)
(Corresponding angles are equal)
AB = 2AM and PQ = 2PN (∵ CM and RN are medians)
From (1) we have

∴ ∆CMB ~ ∆RNQ

Question 5.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point ‘O’. Using the criterion of similarity for two triangles, show that \(\frac{\mathrm{OA}}{\mathrm{OC}}\) = \(\frac{\mathrm{OB}}{\mathrm{OD}}\). (AS₂)
Solution:
ABCD is a trapezium in which AB || DC.
The diagonals AC and BD intersect at ‘O’.

AB || CD and AC is a transversal
∴ ∠DCA = ∠CAB (Alternate angles)
⇒ ∠DCO = ∠OAB
Lines AC and BD intersect at ‘O’.
∴ ∠AOB = ∠COD (Vertically opposite angles)
Now is triangles COD and AOD, we have
∠DCO = ∠OAB
∠AOB = ∠COD
∴ ∠CDO = ∠ABO
Hence, ∆AOB ~ ∆COD
Therefore, their corresponding sides are proportional.
∴ \(\frac{\mathrm{OA}}{\mathrm{OC}}\) = \(\frac{\mathrm{OB}}{\mathrm{OD}}\)

Question 6.
AB, CD, PQ are perpendicular to BD. AB = x, CD = y and PQ = ∠. Prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\) (A.P. Mar. ’15)

Solution:
In ∆ABD, PQ || AB.
∴ \(\frac{\mathrm{PQ}}{\mathrm{AB}}\) = \(\frac{\mathrm{DQ}}{\mathrm{DB}}\)
⇒ \(\frac{\mathrm{z}}{\mathrm{x}}\) = \(\frac{\mathrm{DQ}}{\mathrm{DB}}\) …………. (1)
In ∆BDC, PQ || CD.

Question 7.
A flag pole 4m tall casts a 6m., shadow. At the same time, a nearby building casts a shadow of 24m. How tall is the building ? (AS₄)
Solution:
∆ABC ~ ∆DEF

∴ Their corresponding sides are proportional.
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{BC}}{\mathrm{EF}}\)
⇒ \(\frac{\mathrm{4}}{\mathrm{x}}\) = \(\frac{6}{24}\)
⇒ x × 6 = 4 × 24
⇒ x = \(\frac{4 \times 24}{6}\) = 16
∴ The height of the building = 16 meters

Question 8.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆FEG respectively. If ∆ABC ~ ∆FEG then show that G
i) \(\frac{\mathrm{CD}}{\mathrm{GH}}\) = \(\frac{\mathrm{AC}}{\mathrm{FG}}\)
ii) ∆DCB ~ ∆HGE
iii) ∆DCA ~ ∆HGF (AS₂)
Solution:
Given that ∆ABC ~ ∆FEG
∴ Corresponding angles are equal.

∠CAB = ∠GFE ⇒ ∠CAD = ∠GFH
∠ACB = ∠FGE ⇒ \(\frac{1}{2}\) ∠ACB = \(\frac{1}{2}\) ∠FGE
∠ACD = ∠FGH
(∵ CD and GH are bisectors of ∠C and ∠G respectively)
Now in ∆ACD and ∆FGH,
∠CAD = ∠GFH
∠ACD = ∠FGH
∴ ∆ACD ~ ∆FGH (A. A similarity criterion)
\(\frac{\mathrm{CD}}{\mathrm{GH}}\) = \(\frac{\mathrm{AC}}{\mathrm{FG}}\) (Corresponding sides are in proportion)
Since, ∆ABC ~ ∆FEG, ∠ACB = ∠FGE
⇒ \(\frac{1}{2}\) ∠ACB = \(\frac{1}{2}\) ∠FGE
⇒ ∠DCB = ∠HGE
(∵ CD and GH are the bisectors of ∠C and ∠G respectively)
Moreover, ∠CBA = ∠GEH
⇒ ∠CBD = ∠GEH
Now in ∆^les DCB and HGE, we have
∠DCB = ∠HGE
∠CBD = ∠GEH
∴ ∆ DCB ~ ∆ HGE (A. A similarity criterion)

Question 9.
AX and DY are altitudes of two similar triangles ∆ABC and ∆DEF. Prove that AX : DY = AB : DE. (AS₂)
Solution:

∆ABC ~ ∆DEF
∠B = ∠E; ∠C = ∠F and ∠A = ∠D
In ∆^les ABX and DEY,
∠B = ∠E
∠AXB = ∠DYE = 90°
∠AXJ-BC = ∠DY ⊥ EF
∴ ∆ABX ~ ∆DEY
Hence, their corresponding sides are proportional.
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{AX}}{\mathrm{DY}}\) = \(\frac{\mathrm{BX}}{\mathrm{EY}}\)
⇒ AB : DE = AX : DY
⇒ AX : DY = AB : DE

Question 10.
Construct a triangle shadow similar to the given ∆ABC, with its sides equal to \(\frac{5}{3}\) of the corresponding sides of the triangle ABC. (AS₅)
Solution:

Construction :

1. Draw ∆ ABC
2. Make an acute angle CBX with BC.
3. Locate the points B₁, B₂, B₃, B₄ and B₅ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅.
4. Join B₃C. Draw B₅ C’ parallel to B₃C to meet BC produced at C’.
5. Draw CA’ parallel to CA to meet BA produced at A’.
6. Now BCA’ is required triangle.

Question 11.
Construct a triangle of sides 4 cm, 5 cm and 6 cm. Then, construct a triangle similar to it. Whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle. (AS₅)
Solution:
Construction :

1. Draw the triangle ABC in which BC = 6 cm, CA = 5 cm, AB = 4 cm.
2. Draw a ray \(\overrightarrow{\mathrm{BX}}\), making an acute angle with BC on the side opposite to vertex A.
3. Locate 3 points B₁, B₂ and B₃ on BX such that BB₁ = B₁ B₂ = B₂ B₃.
4. Join B₃C and draw a line from B₂ to C’ which is parallel to B₂C and intersecting BC atC’.
5. Draw a line through C’ parallel to CA to intersect AB at A’.
6. Now ∆A’ BC is the required triangle.

Question 12.
Construct an Isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another triangle whose sides are 1 \(\frac{1}{2}\) times the corresponding sides of the isosceles triangle. (AS₅)
Solution:

Construction :

1. Draw a line segment BC = 8 cm.
2. Draw the perpendicular bisector PQ of BC intersecting BC at ‘O’.
3. Mark a point A’ on PQ such that OA = 4 cm.
4. Join AB and AC to get the isosceles triangle ABC.
5. Extend BC on either side so that BC = 1 \(\frac{1}{2}\) times, BC = \(\frac{3}{2}\) × 8 = 12 cm
6. Similarly extend OA so that OA’ = 1\(\frac{1}{2}\) times, A = \(\frac{4 \times 3}{2}\) = 6 cm.
7. Join A’B’ and AC’.
8. Now, A’B’C’ is the required triangle.

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.3 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.3

Question 1.
Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
Solution:
We have to prove that area of ∆ABN + area of ∆BCL = area of ∆ACM
∆ABN and ∆ACM are equilateral triangles.
In an equilateral triangles each angle is equal to 60°.
In ∆ABN, ∠A = ∠B = ∠N = 60°
In ∆ACM, ∠A = ∠C = ∠M = 60°
∴ ∆ABN ~ ∆ACM (A.A.A criterion)

Adding (1) & (2), we get

Question 2.
Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.
Solution:
We have to prove that ar (∆BQC) = \(\frac{1}{2}\) ar (∆APC)
∆APC ~ ∆BQC (∵ ∆APC and ∆BQC are equiangular)
∴ \(\frac{{ar}(\triangle \mathrm{APC})}{{ar}(\triangle \mathrm{BQC})}\) = \(\left(\frac{\mathrm{AC}}{\mathrm{BC}}\right)^2\)
(∵ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.)
= \(\frac{\mathrm{AC}^2}{\mathrm{BC}^2}\) = \(\frac{(\sqrt{2} \mathrm{BC})^2}{\mathrm{BC}^2}\)
[Since ABCD is a square, its diagonal.
AC = \(\sqrt{42}\) × side
= \(\sqrt{42}\) × BC]

= 2 \(\frac{\mathrm{BC}^2}{\mathrm{BC}^2}\) = 2
\(\frac{{ar}(\triangle \mathrm{APC})}{{ar}(\triangle \mathrm{BQC})}\) = \(\frac{2}{1}\)
2 ar (∆BQC) = ar(∆APC)
∴ ar(∆BQC) = \(\frac{1}{2}\) ar(∆APC)

Question 3.
D,E,F are mid points of sides BC, CA, AB of ∆ABC. Find the ratio of areas of ∆DEF and ∆ABC. (AS₁, AS₄)
Solution:
We have to find the ratio of area ∆DEF and area ∆ABC.
E E are the mid points of AB and AC respectively. In ∆ABC,
∴ FE || BC ⇒ FE|| BD

Similarly D, F are the mid points of BC and AB respectively.
In ∴ ∆ ABC.
DF || AC ⇒ DF || AE
Similarly DE || AB ⇒ DE || AF
FEDB is a parallelogram.
(∵ FB || ED and BD || FE)
∴ ∠FED = ∠B
(Opposite angles of a ▱^gm are equal)
FDEA is a parallelogram
(∵ FD || AE and DE || FA)
∴ ∠FDE = ∠A
(Opposite angles of a ▱^gm are equal)
In ∆^les ABC and DEE
∠FED = ∠B
∠FDE = ∠A
∴ ∠EFD = ∠C
∴ ∆ABC ~ ∆DEF
∴ \(\frac{{area}(\triangle \mathrm{DEF})}{{area}(\triangle \mathrm{ABC})}\) = \(\frac{\mathrm{DE}^2}{\mathrm{AB}^2}\) = \(\frac{\left[\frac{1}{2} \mathrm{AB}\right]^2}{\mathrm{AB}^2}\)
= \(\frac{\frac{1}{4} \mathrm{AB}^2}{\mathrm{AB}^2}\) = \(\frac{1}{4}\) (∵ DE = \(\frac{1}{2}\) AB)
∴ area (∆DEF) : area (∆ABC) = 1 : 4

Question 4.
In ∆ABC, XY || AC and XY divides the triangle into two parts of equal area. Find the ratio of \(\frac{\mathrm{A X}}{\mathrm{A B}}\). (AS₁, AS₄)
Solution:
In ∆ABC, XY || AC. We have to find the ratio \(\frac{\mathrm{A X}}{\mathrm{A B}}\)
Given that XY divides the triangle ABC into 2 parts of equal area.
In ∆ABC, since XY || AC, BA and BC are transversals.
∠BXY = ∠A (Corresponding angles)
∠BYX = ∠C (Corresponding angles)
∠B is common.
∆BXY ~ ∆BAC
area of ∆BXY = area of trapezium XYCA
area of ∆BXY + ar. of ∆BXY = area of trapezium XYCA + ar. ABXY
2 ar. ∆BXY = ar. ∆BAC
Since, ∆BXY ~ ∆BAC,

⇒ \(\frac{1}{2}\) = \(\left[\frac{\mathrm{BX}}{\mathrm{BA}}\right]^2\)
⇒ \(\frac{2}{1}\) = \(\frac{\mathrm{BA}^2}{\mathrm{BX}^2}\)
⇒ BA² = 2BX²
⇒ BA = \(\sqrt{2}\) . BX = \(\sqrt{2}\) (BA – AX)
⇒ (\(\sqrt{2}\) – 1)BA = \(\sqrt{2}\) AX
⇒ \(\frac{\mathrm{AX}}{\mathrm{AB}}\) = \(\frac{\sqrt{2}-1}{\sqrt{2}}\)

Question 5.
Prove that the ratio of areas of two simi¬lar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
∆ABC ~ ∆DEF
AP is the median drawn from A to BC.
DQ is the median drawn from D to EH
We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.

In ∆^les ∆PB and DQE, we have

Question 6.
∆ABC ~ ∆DEF, BC = 3 cm, EF = 4cm and area of ∆ABC = 54 cm². Determine the area of ∆DEF. (AS₁)
Solution:
∆ABC ~ ∆DEF
area of ∆ABC = 54 cm²
Given that BC = 3 cm and EF = 4 cm
We know that the areas of two similar triangles are in the ratio of the squares of the corresponding sides.

⇒ area (∆DEF) × 9 = 54 × 16
⇒ area (∆DEF) = \(\frac{54 \times 16}{9}\)
∴ area (∆DEF) = 96 cm²

Question 7.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm. and BP = 3 cm., AQ =1.5 cm., CQ = 4.5 cm. Prove that (area of ∆APQ) = \(\frac{1}{2}\) (area of ∆ABC). (AS₂)
Solution:
In ∆ABC,
AP = 1 cm, PB = 3 cm,
AQ = 1.5 cm, QC = 4.5 cm

\(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{1}{3}\)
\(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{1.5}{4.5}\) = \(\frac{1}{3}\)
Since \(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{1.5}{4.5}\), PQ // BC.
Now in ∆^les ∆APQ and ABC
∠A = ∠A (Common)
∠APQ = ∠ABC (∵ PQ // BC, APB is a transversal.)
∴ ∠APQ = ∠ABC (Corresponding sides)
∴ ∠AQP = ∠ACB
Hence, ∆APQ ~ ∆ABC.
We know that the ratio of the areas of two similar triangles are equal to the ratio of the squares of any two corresponding sides.
AP and AB are corresponding sides.
AP = 1 cm,
AB = AP + PB = 1 + 3 = 4 cm
So, \(\frac{{area}(\Delta \mathrm{APB})}{{area}(\Delta \mathrm{ABC})}\) = \(\frac{(1)^2}{(4)^2}\)
\(\frac{{area}(\Delta \mathrm{APB})}{{area}(\Delta \mathrm{ABC})}\) = \(\frac{1}{16}\)
⇒ 16 × area (∆APB) = area (∆ABC)
⇒ area (∆APB) = \(\frac{1}{16}\) area (∆ABC)

Question 8.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. If the altitude of the bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle. (AS₁, AS₄)
Solution:
Areas of the two similar triangles are 81 cm² and 49 cm². Altitude of the bigger triangle = 4.5 cm
Let the corresponding altitude of the smaller triangle be x. We know that the areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.


Length of the corresponding altitude of smaller triangle = 3.5 cm

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions InText Questions

Try This

Question 1.
i) Which of these are arithmetic progressions and why ? (P.No. 128)

a) 2, 3, 5, 7, 8, 10, 15, …
Solution:
2, 3, 5, 7, 8, 10, 15, ……. is not an A.P
∵ a₂ – a₁ = 3 – 2 = 1
a₃ – a₂ = 3 – 2 = 1
a₄ – a₃ = 7 – 5 = 1
i.e., The difference between any two successive terms is not same throughout the series.
(or)
Every number is not formed by adding a fixed number to its preceding term.

b) 2, 5, 7, 10, 12, 15, ….
Solution:
The given list does not form an A.R, since each term is not obtained by adding a fixed number to its preceding term.

c) -1, – 3, – 5, -7
-1, – 3, – 5, – 7, … is an A.P.
∵ a₂ – a₁ = -3-(-1) = -3 + 1 = -2
a₃ – a₂ = -5 – (-3) = -5 + 3 = -2
a₄ – a₃ = -7 – (-5) = -7 + 3 = -2
Every number is formed by adding a fixed number to its preceding term.

ii) Write 3 more Arithmetic Progressions.
a) a = -7; d = – 3 and
A.P. is -7, -10, -13, -16, ….
b) a = 15; d = 4 and
A.P. is 15, 19, 23, 27, 31, ….
c) a = 100; d = 50 and
A.P. is 100, 150, 200, 250, ….

Think – Discuss

Question 1.
Think how each of the list given, form an A.P. Discuss with your friends. (Page No. 129)

a) Heights (in cm) of some students of a school standing in a queue in the morning assembly are 147,148,149,…., 157.
Solution:
The given list forms an A.P. since each term starting from the second is obtained by adding a fixed number +1 to its preceding term.

b) Minimum temperatures (in °C) recorded for a week, in the month of January in a city, arranged in ascending order are – 3.1, – 3.0, – 2.9, – 2.8, – 2.7, – 2.6, – 2.5
Solution:
The given list forms an A.R, since every term starting from the second is obtained by adding a fixed number +0.1 to its preceding term.

c) The balance money (in Rs.) after paying 5% of the total loan of Rs. 1000 every month is 950, 900, 850, 800, … , 50.
Solution:
The given list forms an A.P., since each term starting from the second is obtained by adding a fixed number (-50) to its preceding term.

d) Cash prizes (in Rs.) given by a school to the toppers of Classes I to XII are 200, 250, 300, 350, …., 750 respectively.
Solution:
The given list forms an A.P., since each term starting from the second is obtained by adding a fixed number 50 to its preceding term.

e) Total savings (in Rs.) after every month for 10 months when Rs. 50 are saved each month are 50, 100, 150, 200, 250, 300, 350, 400, 450, 500.
Solution:
The given list forms an A.P., since every term starting from the second term is obtained by adding a fixed number 50 to its preceding term.

Question 2.
Find the common difference of each of the above lists. Think when is it positive. (Page No. 129)
Solution:
Common difference d = a₂ – a₁
a) 148 -147 = 1
b) -3.0 – (-3.1) = 0.1
c) 900 – 950 = – 50
d) 250 – 200 = 50
e) 100 – 50 = 50
Common difference is positive when a₂ > a₁

Question 3.
Make a positive Arithmetic progression in which the common difference is a small positive quantity. (Page No. 129)
Solution:
a = 50; d = 0.5 then A.P is 50, 50.5, 51, 51.5, 52, …

Question 4.
Make an A.P. in which the common difference is negative. (Page No. 129)
Solution:
a = 100, d = 1000 then A.P. is 100, 1100, 2100, 3100, 4100, ….

Question 5.
Make an A.P. in which the common difference is negative. (Page No. 129)
Solution:
a = 80, d = -7 then A.P is 80, 73, 66, 59, 52,…….

Do This

Question 1.
Write three examples for finite A.P. and three for infinite A.P. (Page No. 130)
Solution:
Examples for finite A.P.
i) 3, 5, 7, 9, 11 where a = 3; d = 2.

ii) x, x + a, x + 2a, x + 3a, x + 4a, x + 5a
where a = x; d = a.

iii) \(\frac{1}{9}\), \(\frac{2}{9}\), \(\frac{3}{9}\), \(\frac{4}{9}\), \(\frac{5}{9}\), \(\frac{6}{9}\), \(\frac{7}{9}\)
where a = \(\frac{1}{9}\); d = \(\frac{1}{9}\).
Examples for infinite A.P

i) 10, 20, 30, 40,…
where a = 10, d = 10.
ii) 5.5, 6.6, 7,7, 8.8, 9.9,……..
where a = 5.5; d = 1.1.
iii) -100, -95, -90, -85,………
where a = -100, d = 5.

Question 2.
Take any Arithmetic Progression. (Page No. 131)
Solution:
4, 7, 10, 13, 16,……………

Question 3.
Add a fixed number to each and every term of A.P. Write the resulting numbers as a list. Check whether the resulting lists are AP. In each case. (Page No. 131)
Solution:
4, 7, 10, 13, 16, …
Adding 5’ to each term of the above A.P we get
4 + 5, 7 + 5, 10 + 5, 13 + 5, 16 + 5,……..
9, 12, 15, 18, 21,………
In the list obtained the first term
a₁ = 9; a₂ = 12, a₃ = 15,…………
Also a₂ – a₁ = 12 – 9 = 3
a₃ – a₂ = 15 – 12 = 3
a₄ – a₃ = 18 – 15 = 3
……………………
i.e., d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = …… = 3
∴ The resulting list forms an AP

Question 4.
Similarly subtract a fixed number from each and every term of A.P. Write the resulting numbers as a list. Check whether the resulting lists are A.P. in each case. (Page No. 131)
Solution:
4, 7, 10, 13, 16,………….
Subtracting ‘2’ from the each term of A.P. in given series, we get

In the list obtained, the first term
a₁ = 2, a₂ = 5, a₃ = 8, a₄ = 11, ……….
Also a₂ – a₁ = 5 – 2 = 3
a₃ – a₂ = 8 – 5 = 3
a₄ – a₃ = 11 – 8 = 3
…………………………….
i.e., d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ …… = 3
∴ The resulting list forms an A:P

Question 5.
Multiply and divide each term of A.P by a fixed number and write the resulting numbers as a list.
Check whether the resulting lists are A.P in each case. (Page No. 131)
Solution:
4, 7, 10, 13, 16,………….
Multiplying each term by 3. we get

In the list obtained, the first term
a₁ = 12 and a₂ = 21, a₃ = 30………
Also a₂ – a₁ = a₃ – a₂ = ……… = 9
∴ The resulting list also forms an A.P.
Now divide every term by 7, we get
\(\frac{4}{7}\), \(\frac{7}{7}\), \(\frac{10}{7}\), \(\frac{13}{7}\), \(\frac{16}{7}\),……….. is the resulting list.

Question 6.
Check whether the resulting lists are A.P in each case.
Solution:
The first term
a₁ = \(\frac{4}{7}\), a₂ = \(\frac{7}{7}\), a₃ = \(\frac{10}{7}\), a₄ = \(\frac{13}{7}\),………
Also, a₂ – a₁ = \(\frac{7}{7}\) – \(\frac{4}{7}\) = \(\frac{3}{7}\),
a₃ – a₂ = \(\frac{10}{7}\) – \(\frac{7}{7}\) = \(\frac{3}{7}\),
a₄ – a₃ = \(\frac{13}{7}\) – \(\frac{10}{7}\) = \(\frac{3}{7}\),
∴ d = a₂ – a₁= a₃ – a₂ = a₄ – a₃ = … = \(\frac{3}{7}\) and the above list forms an A.P

Question 7.
What is your conclusion? (Page No. 131)
Solution:
If a₁, a₂, a₃, … are in A.P, then
a₁ ± k, a₂ ± k, a₃ ± k, a₄ ± k. ….. are also inA.P
a₁k, a₂k, a₃k,………. are also in A.P
\(\frac{a_1}{\mathrm{k}}\), \(\frac{a_2}{\mathrm{k}}\), \(\frac{a_3}{\mathrm{k}}\) ,…….. are also in A.P.
i.e.. “If each term of an A.P is added/multiplied/divided by a fixed number,the resulting terms also form an A.P” and fixed term is subtraded from each term of an A.P, then the resulting terms also form an A.P

Do This

Question 1.
Find the sum of Indicated number of terms in each of the following A.Ps. (Page No. 143)

i) 16, 11, 6,……… 23 terms.
Solution:
Given: 16, 11, 6,……. S₂₃
t₁ = a = 16; t₂ = 11; t₃ = 6
d = t₂ – t₁ = 11 – 16 = -5
S_n = \(\frac{\mathrm{n}}{2}\)[2a + (n-1)d]
S₂₃ = \(\frac{23}{2}\)[2 × 16 + (23 – 1) × (-5)]
= \(\frac{23}{2}\)[32 + (22) × (-5)]
= \(\frac{23}{2}\)[32 – 110]
= \(\frac{23 \times(-78)}{2}\)
= -23 × 39 = -897

ii) -0.5, -1.0, -1.5,………. 10 terms.
Solution:
Given: -0.5, -1.0, -1.5, …….. S₁₀
a = -0.5
d = t₂ – t₁ = (-1.0) – (-0.5)
= -1.0 + 0.5 = -0.5
S_n = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d]
S₁₀ = \(\frac{10}{2}\) [ 2 × (-0.5) + (10 – 1)(-0.5)]
= 5[-1.0 + 9 × (-0.5)]
= 5[-1.0-4.5]
= 5 × (-5.5) = -27.5

iii) -1, \(\frac{1}{4}\), \(\frac{3}{2}\),……… 10 terms
Solution:
Given -1, \(\frac{1}{4}\), \(\frac{3}{2}\),……… S₁₀
a = -1

Do This

Question 1.
Find which of the following are not GP.? (Page No. 149)

Question 1.
6, 12, 24, 48,……..
Solution:
Given : 6, 12, 24, 48,……..
a₁ = a = 6; a₂ = 12; a₃ = 24
\(\frac{\mathrm{a}_2}{\mathrm{a}_1}\) = \(\frac{12}{6}\) = 2 ; \(\frac{a_3}{a_2}\) = \(\frac{24}{12}\) = 2 ;
\(\frac{a_4}{a_3}\) = \(\frac{48}{24}\) = 2
i.e., r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = \(\frac{a_4}{a_3}\) = …….. = 2
The given list is of the form
a, ar, ar², ar³,………..
∴ The given numbers are in G.P.

Question 2.
1, 4, 9, 16,………….
Solution:
Given: 1, 4, 9, 16,………
a₁ = a = 1
a₂ = 4; a₃ = 9, a₄ = 16

∴ The given numbers do not form a G.P.

Question 3.
1, -1, 1, -1,……….
Solution:

Question 4.
-4, -20, -100, -500,………
Solution:
Given, -4, -20, -100, -500,……….
a₁ = a = -4, a₂ = -20,
a₃ = -100, a₄ = -500,……….

∴ The given list forms a G.P

Think – Discuss

Question 1.
Explain why each of the lists given is a G.P. (Page No. 149)

i) 1, 4, 16, 64, 256,…………
Here
a = 1 = a₁ ; a₂ = 4; a₃ = 16; a₄ = 64;….
\(\frac{a_2}{a_1}\) = \(\frac{4}{1}\) ; \(\frac{a_3}{a_2}\) = \(\frac{16}{4}\) ; \(\frac{a_4}{a_3}\) = \(\frac{64}{16}\) = 4
i.e., Common ratio r = 4.

ii) 550, 605, 665.5,………..
Solution:
The given series is in G.P Since every term can be obtained by multiplying its preceding term by a fixed number ‘1.1’.
(\(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = ……. = 1.1 = r)

iii) 256, 128, 64, 32,………….
Solution:
The given series forms a G.P Since every term, starting from the second can be obtained by multiplying its preceding term by a fixed number \(\frac{1}{2}\).
[∵ r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = ………. = \(\frac{1}{2}\)]

iv) 18, 16.2, 14.58, 13.122,……….
Solution:
The given list forms a G.P
Since each term, starting from the second can be obtained by multiplying its preceding term by a fixed number 0.9.
here r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = \(\frac{a_4}{a_3}\) = …………. = 0.9

Question 2.
To know about a G.P. what is minimum information that we need ? (Page No. 149)
Solution:
To know whether a number pattern forms a G.P or not, we should check that the ratio between the successive terms is equal or not.

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions Optional Exercise

Question 1.
Which term of the AP:
121, 117, 113,…, is the first negative term?
[Hint: Find n for a_n < 0]
Solution:
Given A.P. : 121, 117, 113,……….
a = 121 and d = a₂ – a₁
= 117 – 121 = -4
Let the n^th term be the first negative term of the given G.P
Then, a_n = 0
⇒ a_n + (n – 1)d < 0
⇒ 121 + (n – 1)(-4) < 0
⇒ 121 – 4n + 4 < 0
⇒ 121 – 4n < 0
⇒ -4n < -125 ⇒ 4n > 125
⇒ n > \(\frac{125}{4}\)
n > 31.25
∴ When n = 32, the term becomes negative, (or) 32^nd term is the first negative term of the given A.P.

Question 2.
The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of theAP. ?
Solution:
Given in an A.P : t₃ + t₇ = 6
t₃ + t₇ = 8
a_n = t_n = a + (n – 1) d
Let the terms of the A.R be
(a – 4d), (a – 3d), (a – 2d), (a – d), a(a + d), (a + 2d), (a + 3d),….
Then a₃ = a – 2d; a₇ = a + 2d
So a₃ + a₇ = a – 2d + a + 2d = 6
⇒ 2a = 6 (or) a = 3
Also, a₃ . a₇ = (a – 2d) (a + 2d)
⇒ a² – 4d² = 8
⇒ 3² – 4d² = 8
⇒ 9 – 4d² = 8
⇒ 4d² = 9 – 8
⇒ d² = \(\frac{1}{4}\)
∴ d = ± \(\frac{1}{2}\)
Taking d = \(\frac{1}{2}\)

Question 3.
A ladder has rungs 25 cm apart. The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are 2\(\frac{1}{2}\) m apart, what is the length of the wood required for the rungs ?
[Hint : Number of rungs = \(\frac{250}{25}\) + 1]

Solution:
Given : A ladder with rungs separated by a distance between the rungs = 2\(\frac{1}{2}\)m = 250 cm
∴ Number of rungs = \(\frac{250}{25}\) + 1
= 10 + 1 = 11
Length of the bottom and top rungs = 45 cm and 25 cm
where a = 45; last term l = a₁₁ = 25 and d = 2 cm
∴ S_n = (a + l) = \(\frac{11}{2}\)(45 + 25)
= \(\frac{11}{2}\) × 70
= 35 × 11 = 385 cm
∴ Length of wood required for total rungs = 385 cm.

Question 4.
The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the
numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. And find this value of x.
[Hint : S_x-1 = S₄₉ – S_x]
Solution:
Given: Houses with numbers from 1 to 49.
x is a number x such that,
S_x-1 = S₄₉ – S_x
We know that, S_x = \(\frac{x}{2}\)[2a + (x – 1)d]
Where a = 1; d = a₂ – a₁ = 2 – 1 = 1

⇒ x(x – 1) + x(x + 1) = 2 × 1225
⇒ x + x² + x = 2450
⇒ 2x² = 2450
x² = \(\frac{2450}{2}\) = 1225
⇒ x = \(\sqrt{1225}\) = ±35
⇒ x = 35
(∵ x is a counting number)

Question 5.
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete.
Each step has a rise of \(\frac{1}{4}\)m and a tread of \(\frac{1}{2}\) m. (See Fig.). Calculate the total volume of concrete required to build the terrace.
[Hint : Volume of concrete required to build the first step = \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m³]

Solution:
Given No. of steps = 15
i.e., n = 15
Volume of concrete required to build the second step = (\(\frac{1}{4}\) + \(\frac{1}{4}\)) × \(\frac{1}{2}\) × 50
= \(\frac{1}{2}\) × \(\frac{1}{2}\) × 50
= \(\frac{25}{2}\) m³

∴ Total volume of the concrete required
= 750 m³

Question 6.
150 workers were engaged to finish a piece of work in a certain number of days. Four workers dropped from the work in the second day. Four workers dropped in third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed.
[Let the no.of days to finish the work is ‘x’ then
150x = \(\frac{x+8}{2}\)[2 × 150 + (x + 8 – 1)(-4)]
Solution:
Let the number of days to finish the work is x.
No. of workers engaged = 150
Given four workers dropped from the work in the second day.
Four workers dropped in the third day and so on.
∴ Common difference d = -4
8 more days to finish the work
n = x + 8
a = 150
S_n = 150x
\(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d] = 150x
\(\left(\frac{x+8}{2}\right)\)[2 × 150 + (x + 8 – 1)(-4)] = 150x
(x + 8)[150 + (x + 7)(-2)] = 150x
(x + 8) [150 – 2x – 14] = 150x
(x + 8)(136 – 2x) = 150x
136x – 2x² + 1088 – 16x = 150x
-2x² + 120x + 1088 – 150x = 0
-2x² – 30x + 1088 = 0
2x² + 30x – 1088 = 0
x² + 15x – 544 = 0
x² – 17x + 32x – 544 = 0
x(x – 17) + 32(x – 17) = 0
(x – 17) (x + 32) = 0
Either x – 17 = 0 or x + 32 = 0
x = 17 (or) x = -32
Number of days can’t be negative.
∴ x = 17
∴ Number of days to complete the work is
17 + 8 = 25

Question 7.
A machine costs ₹ 5,00,000. If the value depreciates 15% in the first year, 13\(\frac{1}{2}\) % in the second year, 12% in the third year and so on. What will be its value at the end of 10 years, when all the percent ages will be applied to the original cost?
Solution:
Given : Cost price of a machine = ₹ 5,00,000
Depreciation during the years

Sum of the depreciations =
15 + 13\(\frac{1}{2}\) +12+……..+10 terms
a = 15; d = a₂ – a₁
= 13\(\frac{1}{2}\) – 15 = -1\(\frac{1}{2}\) = –\(\frac{3}{2}\)

∴ Cost after 10 years = (100 – 82.5)% of 5,00,000
= 17.5% of 5,00,000
= \(\frac{17.5 \times 500000}{100}\)
= Rs. 87,500
∴ The value at the end of 10 years will be Rs. 87,500.

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions Ex 6.5 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions Exercise 6.5

Question 1.
For each geometric progression find the common ratio ‘r’, and then find a_n.

i) 3, \(\frac{3}{2}\), \(\frac{3}{4}\), \(\frac{3}{8}\),………..
Solution:

ii) 2, -6, 18, -54,…………
Solution:
Given
G.P. 2, -6, 18, -54,…………
a = 2, r = \(\frac{a_2}{a_1}\) = \(\frac{-6}{2}\) = -3
a_n = a. r^n-1 = 2 × (-3)^n-1
∴ r = -3; a_n = 2(-3)^n-1

iii) -1, -3, -9, -27,………..
Solution:
Given G.P. = – 1, – 3, – 9, – 27, ….
a = -1, r = \(\frac{a_2}{a_1}\) = \(\frac{-3}{-1}\) = 3
a_n = a . r^n-1 = (-1) × 3^n-1
∴ r = 3, a_n = (-1) × 3^n-1

iv) 5, 2, \(\frac{4}{5}\), \(\frac{8}{25}\),……….
Solution:
Given G.P: 5, 2, \(\frac{4}{5}\), \(\frac{8}{25}\),…………
a = 5, r = \(\frac{\mathrm{a}_2}{\mathrm{a}_1}\) = \(=\frac{2}{5}\)
a_n = a . r^n-1 = 5 × \(\left(\frac{2}{5}\right)^{\mathrm{n}-1}\)
∴ r = \(\frac{2}{5}\) ; a_n = 5\(\left(\frac{2}{5}\right)^{\mathrm{n}-1}\)

Question 2.
Find the 10^th and n^th term of G.P.:
5, 25, 125,……..
Solution:
Given G.P. = 5, 25, 125,……….
a = 5, r = \(\frac{a_2}{a_1}\) = \(\frac{25}{5}\) = 5
a_n = a. r^n-1 = 5 × 5^n-1 = 5^1+n-1 = 5ⁿ
∴ a₁₀ = a . r⁹ = 5 × 5⁹ = 5¹⁰
∴ a₁₀ = 5¹⁰; a_n = 5ⁿ

Question 3.
Find the indicated term of each geometric progression.

i) a₁ = 9 ; r = \(\frac{1}{3}\) ; find a₇.
Solution:
a_n = a . r^n-1
a₇ = 9 × \(\left(\frac{1}{3}\right)^{7-1}\) = 3² \(\left(\frac{1}{3}\right)^6\) = \(\frac{3^2}{3^6}\) = \(\frac{1}{3^4}\)
∴ a₇ = \(\frac{1}{3^4}\)

ii) a₁ = -12 ; r = \(\frac{1}{3}\) ; find a₆.
Solution:
a_n = a. r^n-1
a₆ = (-12) × \(\left(\frac{1}{3}\right)^{6-1}\)
= (-12) × \(\frac{1}{3^5}\) = \(\frac{-4 \times 3}{3^5}\) = \(\frac{-4}{3^4}\)
∴ a₆ = \(\frac{-4}{3^4}\)

Question 4.
Which term of the G.P.

i) 2, 8, 32,………. is 512?
Solution:
Given GP. :2, 8, 32,………. is 512
a = 2; r = \(\frac{a_2}{a_1}\) = \(\frac{8}{2}\) = 4
Let the n^th term of G.P. be 512
a_n = a . r^n-1
512 = 2 × (4)^n-1
2⁹ = 2 × (2²)^n-1
2⁹ = 2¹ × 2^2(n-1)
2⁹ = 2^2n-2+1
2⁹ = 2^2n-1
[∵ bases are equal, exponents are also equal]
∴ 2n = 9 + 1
n = \(\frac{10}{2}\) = 5
∴ 512 is the 5^th term of the given G.P

ii) \(\sqrt{3}\), 3, 3\(\sqrt{3}\),……. is 729?
Solution:

[∵ bases are equal, exponents are also equal]
\(\frac{1}{2}\)(n-1) = 6 – 1
⇒ n – 1 = 5 × 2
⇒ n = 10 + 1 = 11
∴ 729 is the 11^th term of the given G.P

iii) \(\frac{1}{3}\), \(\frac{1}{9}\), \(\frac{1}{27}\),……….. is \(\frac{1}{2187}\) ?
Solution:
Given

[∵ bases are equal, exponents are also equal]
∴ 7^th term of GP is \(\frac{1}{2187}\)

Question 5.
Find the 12^th term of a G.P whose 8^th term is 192 and the common ratio is 2.
Solution:
Given a G.P such that a₈ = 192 and
r = 2
a_n = a . r^n-1
∴ a₈ = a(2)^8-1 = 192
a.2⁷ = 192
⇒ a = \(\frac{192}{2^7}\) = \(\frac{192}{128}\) = \(\frac{12}{8}\) = \(\frac{3}{2}\)
∴ a₁₂ = a. r¹¹ = \(\frac{3}{2}\) × (2)¹¹
= 3 × 2¹⁰ = 3 × 1024 = 3072.

Question 6.
The 4^th term of a geometric progressions is \(\frac{2}{3}\) and the seventh term is \(\frac{16}{81}\). Find the geometric series.

Now substituting r = \(\frac{2}{3}\) in equation (1) we get,
a\(\left(\frac{2}{3}\right)^3\) = \(\frac{2}{3}\) ⇒ a = \(\frac{2}{3}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) = \(\frac{9}{4}\) ×
∴ The G.P is a, ar, ar², ar³,…………..
\(\frac{9}{4}\), \(\frac{9}{4}\) × \(\frac{2}{3}\) ; \(\frac{9}{4}\) × \(\left(\frac{2}{3}\right)^2\) …….. = \(\frac{9}{4}\), \(\frac{3}{2}\), 1,……..

Question 7.
If the geometric progressions 162, 54, 18 …. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),……….. have their n^th term equal, find the value of n.?
Solution:
Given G.P. :
162, 54, 18,…….. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),………

Given that n^th terms are equal
a_n = a. r^n-1
⇒ 162 × \(\left(\frac{1}{3}\right)^{\mathrm{n}-1}\) = \(\frac{2}{81}\) × (3)^n-1
⇒ 3^n-1 × 3^n-1 = 162 × \(\frac{81}{2}\)
⇒ 3^n-1+n-1 = 81 × 81
⇒ 3^2n-2 = 3⁸ [a^m . aⁿ = a^m+n]
⇒ 2n – 2 = 8
[∵ bases are equal, exponents are also equal]
2n = 8 + 2
∴ n = \(\frac{10}{2}\) = 5
The 5^th terms of the two G.Ps are equal.

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.1

Question 1.
In ∆PQR, ST is a line such that \(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{\mathrm{PT}}{\mathrm{TR}}\) and also ∠PST = ∠PRQ.
Prove that ∆PQR is an isosceles triangle. (AS₂)

Solution:
In ∆PQR. ST divides PQ and PR in the same ratio.
\(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{\mathrm{PT}}{\mathrm{TR}}\) (given)
∴ ST // QR
It is also given
that ∠PST = ∠PRQ …………… (1)
Since ST // QR and PQ is a transversal.
∠PST = ∠PQR (Corresponding angles) ………….. (2)
From (1) and (2) we have
∠PRQ = ∠PQR
In ∆PQR, ∠PRQ = ∠PQR
∴ PQ = PR
∴ ∆PQR is an isosceles triangle.

Question 2.
In the given figure, LM // CB and LN // CD, prove that \(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AN}}{\mathrm{AD}}\). (AS₂)

Solution:
In the figure, it is given that LM // CB and LN // CD.
In ∆ABC, ML // BC.
(By basic Proportionality Theorem,)
\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (1)
In ∆ADC, LN // CD
(By Basic Proportionality Theorem,)
\(\frac{\mathrm{AN}}{\mathrm{AD}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (2)
From (1) and (2) we have
\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AN}}{\mathrm{AD}}\)
Alter :
In ∆ABC, ML // BC, AC is a transversal.
∠ALM = ∠ACB (Corresponding angles)
ML // BC, AB is a transversal.
∠AML = ∠ABC (Coressponding angles)
Now in ∆^les AML and ABC,
∠ALM = ∠ACB;
∠AML = ∠ABC;
∠A is common.
∴ ∆AML ~ ∆ABC
∴ Their corresponding sides are proportional.
(i.e.,)\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (1)
Similarity in ∆ADC, LN // CD.
So we can prove that
\(\frac{\mathrm{AN}}{\mathrm{AD}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (2)
Hence from (1) & (2), we get
\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AN}}{\mathrm{AD}}\)

Question 3.
In the given figure, DE // AC and DF // AE prove that \(\frac{\mathrm{BF}}{\mathrm{FE}}\) = \(\frac{\mathrm{BE}}{\mathrm{EC}}\). (AS₂)

Solution:
In ∆ABC, DE // AC.
(∴ By Basic Proportionality Theorem,)
In ∆ABE, DF // AE
(∴ By Basic Proportionality Theorem,)

Hence proved.

Question 4.
Prove that a line drawn through the midpoint of one side of a triangle parallel to another side bisects the third side (Using basic proportionality theorem). (AS₂)
Solution:
In ∆ABC, P is the mid-point of AB.
PQ is drawn parallel to BC, intersecting AC in Q.
By Basic Proportionality theorem,

Since P is the mid-point of AB, we have
AP = PB
∴ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{\mathrm{AP}}{\mathrm{PB}}\)
⇒ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) \(\frac{\mathrm{AP}}{\mathrm{AP}}\) (∵ PB = AP)
⇒ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{1}{1}\)
⇒ AQ = QC
Since AQ = QC, Q bisects AC.

Question 5.
Prove that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem). (AS₂)
Solution:
In ∆ABC, D and E are the mid-points of the sides AB and AC respectively.

In ∆ABC, DE divides the sides.
AB and AC in the same ratio.
∴ DE||BC (Basic Proportionality Theorem)

Question 6.
In the given figure, DE || OQ and DF || OR. Show that EF || QR. (AS₂)

Solution:
In the given figure,
DE || OQ and DF || OR
In ∆PQO, DE || OQ
∴ \(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PD}}{\mathrm{DO}}\) (Basic Proportionality Theorem) ………….. (1)
Similarly in ∆PRO, DF || OR.
∴ \(\frac{\mathrm{PF}}{\mathrm{FR}}\) = \(\frac{\mathrm{PD}}{\mathrm{DO}}\) (Basic Proportionality Theorem) ………….. (2)
From (1) & (2), we have
\(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PF}}{\mathrm{FR}}\)
Now, in ∆PQR, we get that \(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF || QR (By converse of basic proportionality theorem).

Question 7.
In the adjacent figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR. (AS₂)

Solution:
In ∆ OPQ, A and B are the points on
OP and OQ such that AB || PQ.
So, in ∆ OPQ, AB || PQ.
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}\) = \(\frac{\mathrm{OB}}{\mathrm{BQ}}\) (Basic proportionality theorem) …………… (1)
In ∆ OPR, A and C are the points on OP and OR such that AC || PR.
So, in ∆ OPR, AC || PR.
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}\) = \(\frac{\mathrm{OC}}{\mathrm{CR}}\) (Basic proportionality theorem) …………… (2)
From (1) & (2), we get \(\frac{\mathrm{OB}}{\mathrm{BQ}}\) = \(\frac{\mathrm{OC}}{\mathrm{CR}}\)
Now, in ∆ OQR, we get that \(\frac{\mathrm{OB}}{\mathrm{BQ}}\) = \(\frac{\mathrm{OC}}{\mathrm{CR}}\)
Therefore, BC || QR (Converse of the Basic proportionality theorem).

Question 8.
ABCD is a trapezium in which AB ||DC and its diagonals intersect each other at point ‘O’. Show that \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\) (AS₂)
Solution:
ABCD is a trapezium. AB || DC.
The diagonals AC and BD intersect in ‘O’.
Draw a line through ‘O’ parallel to AB, meeting AD in E and BC in F.

Question 9.
Draw a line segment of length 7.2 cm and divide it in the ratio 5:3. Measure the two parts. (AS₃, AS₅)
Solution:

Construction :
Draw a line segment AB = 7.2 cm. Make an angle BAX. Mark A₁, A₂, A₃, A₄, A₅, A₆, A₇ on AX such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈. Mark D on AX such that AD = 5 equal parts and DC = 3 equal parts. Join BC. From D, draw DE || BC. E divides AB in the ratio 5:3. The parts are measured. AE = 4.2 cm on and EB = 2.7 cm.

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions Ex 6.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions Exercise 6.4

Question 1.
In which of the following situations, does the list of numbers involved in form a G.P. ?

i) Salary of Sharmila, when her salary is Rs. 5,00,000 for the first year and expected to receive yearly increase of 10%.
Solution:
Given : Sharmila’s yearly salary = Rs. 5,00,000
Rate of annual increment = 10%

Here, a = a₁ = 5,00,000

Every term starting from the second can be obtained by multiplying its preceding term by a fixed number \(\frac{11}{10}\).
∴ r = common ratio = \(\frac{11}{10}\)
Hence the situation forms a G.R

ii) Number of bricks needed to make each step, if the stair case has total 30 steps. Bottom step needs 100 bricks and each successive step needs 2 bricks less than the previous step.
Solution:
Given : Bricks needed for the bottom step = 100.
Each successive step needs 2 bricks less than the previous step.
∴ Second step from the bottom needs = 100 – 2 = 98 bricks.
Third step from the bottom needs = 98 – 2 = 96 bricks
Fourth step from the bottom needs = 96 – 2 = 94 bricks.
Here the numbers are
100, 98, 96, 94, ………….
Clearly this is an A.P. but not G.R

iii) Perimeter of the each triangle, when the mid-points of sides of an equilateral triangle whose side is 24 cm are joined to form another triangle, whose mid-points in turn are joined to form still another triangle and the process continues indefinitely.

Solution:
Perimeter of the 1^st equilateral triangle = 3 × 24 = 72 cm
Perimeter of the 2^nd equilateral triangle = 3 × 12 = 36 cm
Perimeter of the 3^rd equilateral triangle = 3 × 6 = 18 cm
Successive terms are obtained by dividing with 2 the preceding term except first term.
∴ The above situation is a G.P.

Question 2.
Write three terms of the G.P. when the first term ‘a’ and the common ratio ‘r’ are given.

i) a = 4; r = 3.
Solution:
The terms are a, ar, ar², ar³.
∴ 4, 4 × 3, 4 × 3², 4 × 3³
∴ 4, 12, 36, 108,…………

ii) a = \(\sqrt{5}\); r = \(\frac{1}{5}\)
Solution:
The terms of a G.P are:
a, ar, ar², ar³,……….

iii) a = 81; r = \(-\frac{1}{3}\).
Solution:
The terms of a G.P are:
a, ar, ar²,…………
⇒ 81, 81 × \(\left(\frac{-1}{3}\right)\), 81 × \(\left(\frac{-1}{3}\right)^2\)
⇒ 81, -27, 9,…………

iv) a = \(\frac{1}{64}\), r = 2.
Solution:
Given: a = \(\frac{1}{64}\) ; r = 2
a₁ = a = \(\frac{1}{64}\)
a₂ = ar = \(\frac{1}{64}\) × 2 = \(\frac{1}{32}\)
a₃ = ar² = \(\frac{1}{64}\) × 2² = \(\frac{1}{64}\) × 4 = \(\frac{1}{16}\)
∴ The G.P. is \(\frac{1}{16}\), \(\frac{1}{32}\), \(\frac{1}{16}\),………….

Question 3.
Which of the following are G.P.? If they are G.P, write three more terms.

i) 4, 8, 16,………….
Solution:
Given : 4, 8, 16,………….
where, a₁ = 4; a₂ = 8; a₃ = 16,………….
\(\frac{a_2}{a_1}\) = \(\frac{8}{4}\) = 2
\(\frac{\mathrm{a}_3}{\mathrm{a}_2}\) = \(\frac{16}{8}\) = 2
∴ r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = 2
Hence 4,8,16,……… is a G.P
where a = 4 and r = 2
a⁴ = a. r³ = 4 × 2³ = 4 × 8 = 32
a⁵ = a.r⁴ = 4 × 2⁴ = 4 × 16 = 64
a⁶ = a. r⁵ = 4 × 2⁵ = 4 × 32 = 128

ii) \(\frac{1}{3}\), \(\frac{-1}{6}\), \(\frac{1}{12}\)………, (x ≠ 0)
Solution:
Given: t₁= \(\frac{1}{3}\); t₂ = \(\frac{-1}{6}\): t₃ = \(\frac{1}{12}\),………….

Hence the ratio is common between any two successive terms.
∴ \(\frac{1}{3}\), \(\frac{-1}{6}\), \(\frac{1}{12}\),………. is a G.P.

iii) 5, 55, 555,………….
Solution:
Given: t₁ = 5, t₂ = 55, t₃ = 555
\(\frac{\mathrm{t}_2}{\mathrm{t}_1}\) = \(\frac{55}{5}\) = 11
\(\frac{\mathrm{t}_3}{\mathrm{t}_2}\) = \(\frac{555}{55}\) = \(\frac{111}{11}\)
∴ \(\frac{t_2}{t_1}\) ≠ \(\frac{t_3}{t_2}\)

iv) -2, -6, -18,…………..
Solution:
Given : t₁ = -2; t₂ = -6; t₃ = -18
\(\frac{\mathrm{t}_2}{\mathrm{t}_1}\) = \(\frac{-6}{-2}\) = 3; \(\frac{t_3}{t_2}\) = \(\frac{-18}{-6}\) = 3
∴ r = \(\frac{t_2}{t_1}\) = \(\frac{t_3}{t_2}\) = …….. = 3
∴ -2, -6, -18,……….. is a G.P.
where a = -2 and r = 3
a_n =a.r^n-1
a₄ = ar³ = (-2) × 3³ = -2 × 27 = -54
a₅ = ar⁴ = (-2) × 3⁴ = – 2 × 81 = -162
a₆ = a.r⁵ = (-2) × 3⁵ = -2 × 243 = -486

v) \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), …………..
Solution:
Given: t₁ = \(\frac{1}{2}\), t₂ = \(\frac{1}{4}\), t₃ = \(\frac{1}{6}\)
\(\frac{t_2}{t_1}\) = \(\frac{\frac{1}{4}}{\frac{1}{2}}\) = \(\frac{1}{4}\) × \(\frac{2}{1}\) = \(\frac{1}{2}\)
\(\frac{t_3}{t_2}\) = \(\frac{\frac{1}{6}}{\frac{1}{4}}\) = \(\frac{1}{6}\) × \(\frac{4}{1}\) = \(\frac{2}{3}\)
∴ \(\frac{\mathrm{t}_2}{\mathrm{t}_1}\) ≠ \(\frac{t_3}{t_2}\)
i.e., \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\),………… is not a G.P.

vi) 3, -3², 3³,…………
Solution:
Given : t₁ = 3; t₂ = -3², t₃ = 3³,….
\(\frac{t_2}{t_1}\) = \(\frac{-3^2}{3}\) = -3
\(\frac{\mathrm{t}_3}{\mathrm{t}_2}\) = \(\frac{3^3}{-3^2}\) = -3
∴ r = \(\frac{t_2}{t_1}\) = \(\frac{t_3}{t_2}\) = …….. = -3
i.e., every term is obtained by multiplying its preceding term by a fixed number -3.
3, -3², 3³, ……… forms a G.P
where a = 3; r = -3
aⁿ = a.r^n-1
∴ a₄ = 3 × (-3)^4-1 = 3 × (-3)³ = -81
a₅ = 3 × (-3)⁴ = 3 × 81 = 243
a₆ = 3 × (-3)⁵ = 3 × (-243) = -729

vii) x, 1, \(\frac{1}{x}\),……… (x ≠ 0)
Solution:
Given:

viii) \(\frac{1}{\sqrt{2}}\), -2, \(\frac{8}{\sqrt{2}}\),………..
Solution:
Given :

Given terms are not in G.P.

ix) 0.4, 0.04, 0.004,………
Solution:
Given : t₁ = 0.4; t₂ = 0.04; t₃ = 0.004,…………..

Question 4.
Find x so that x, x + 2, x + 6 are consecutive terms of a geometric progression.
Solution:
Given x, x + 2 and x + 6 are in G.P but read it as x, x + 2 and x + 6.
∴ r = \(\frac{t_2}{t_1}\) = \(\frac{t_3}{t_2}\)
⇒ \(\frac{x+2}{x}\) = \(\frac{x+3}{x+2}\)
⇒ (x + 2)² = x(x + 6)
⇒ x² + 4x + 4 = x² + 6x
⇒ 4x – 6x = -4 ⇒ -2x = -4
∴ x = 2