TS 10th Class Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1

Students can practice TS Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.1

Question 1.
Find the distance between the following pair of points.

i) (2, 3) and (4, 1)
Solution:

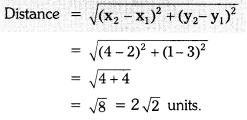
ii) (-5, 7) and (-1, 3)
Solution:

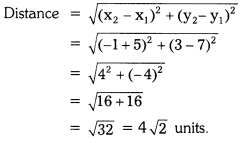
iii) (-2, -3) and (3, 2)
Solution:

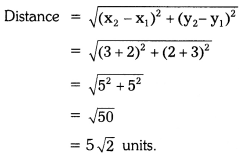
iv) (a, b) and (-a, -b)
Solution:

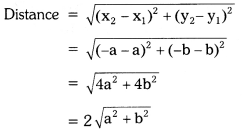
Question 2.
Find the distance between the points (0, 0) and (36, 15)
Solution:
Given : origin O(0, 0) and a point P(36, 15)
Distance between any point and origin = \(\sqrt{x^2+y^2}\)

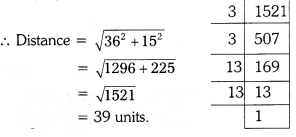
Question 3.
Verify whether the points (1, 5),(2, 3) and (-2, -1) are colleniar or not.
Solution:
Given : A(1, 5) B(2, 3) and C(-2, -1)

Here the sum of no two line segments is equal to third segment
Hence the points are not collinear.
slope of AB, m₁ = \(\frac{3-5}{2-1}\) = -2
slope of BC, m₂ = \(\frac{-1-3}{-2-2}\) = -2
m₁ ≠ m₂
Hence A, B, C are not collinear.

Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an Isosceles triangle.
Solution:
Let A = (5, -2); B = (6, 4) and C = (7, -2)

Now we have AB = BC.
∴ Δ ABC is an isosceles triangle.
i.e., given points are the vertices of an isosceles triangle.

Question 5.
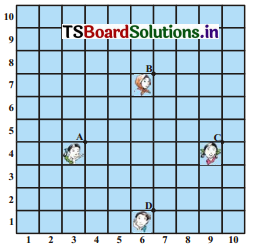
In a classroom, 4 friends are seated at the points A, B, C and D as shown in figure. Jarina and Phani walk into the class and after observing for a few minutes Jarina asks Phani ‘Don’t you think ABCD ¡s a square ?“ Phani disagrees. Using distance formula. find which of them is correct. Why?

Solution:
Given : Four friends are seated at A, B, C and D where A(3, 4), B(6, 7), C(9, 4) and D(6, 1)


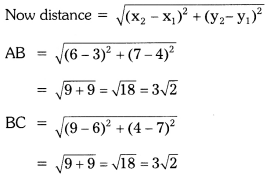
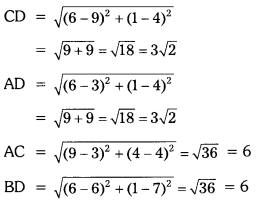
Hence in ABCD four sides are equal.
i.e., AB = BC = CD = DA = 3\(\sqrt{2}\) units.and two diagonals are equal.
ie., AC = BD = 6 units.
∴ ABCD forms a square
i.e., Jarina is correct.

Question 6.
Show that the following points form an equilateral triangle A(a, 0), B(-a, 0), C(0, a\(\sqrt{3}\)).
Solution:

Now AB = BC = CA.
∴ Δ ABC is an equilateral triangle.

Question 7.
Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram and find its area.
(A.P. Mar. ’15)
Solution:
Diagram

Given : A(-7, -3), B(5, 10), C(15, 8) and D(3, -5)

In ABCD, both pairs of opposite sides (AB, CD) and (BC, AD) are equal.
Hence the given points form a parallelogram.
Area of ABCD = 2 × ΔABC

Question 8.
Show that the points (-4, -7), (-1, 2), (8, 5) and (5, -4) taken in order are the vertices of a rhombus.
Hint : Area of rhombus = \(\frac{1}{2}\) × product (A.P. June ‘is’)
Solution:
Given in ABCD, A (-4, -7), B(-1, 2), C(8, 5) and D(5, -4)
Distance formula = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

∴ In ABCD, AB = BC = CD = AD [from sides are equal]
Hence ABCD is a rhombus.
Area of a rhombus = \(\frac{1}{2}\)d₁d₂
= \(\frac{1}{2}\) × 12\(\sqrt{2}\) × 6\(\sqrt{2}\)
= 72 sq. units.

Question 9.
Name the type of quadrilateral formed, if any, by the following points and give reasons for your answer.

i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
Solution:
Let A(-1, -2), B(1, 0), C(-1, 2), D(-3, 0) be the given points.

AC = \(\sqrt{(-1+1)^2+(2+2)^2}\)
= \(\sqrt{16}\) = 4 units.
BD = \(\sqrt{(-3-1)^2+(0-0)^2}\)
= \(\sqrt{16}\) = 4 units.
In ABCD, AB = BC = CD = AD four sides are equal.
AC = BD → diagonals are equal.
Hence, the given points form a square.

ii) (-3, 5), (3, 1), (1, -3), (-1, -4)
Solution:
Let A(-3, 5), B(3, 1), C(1, -3) and D(-1, -4) be the given points.

∴ Opposite sides are not equal.

∴ Its diagonal are not equal.
In ABCD, AB ≠ CD, BC ≠ AD and AC ≠ BD
Hence ABCD is not a parallelogram
∴ The given points can’t be form a parallelogram.

iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
Let A(4, 5), B(7, 6), C(4, 3) and D(1, 2) be the given points.

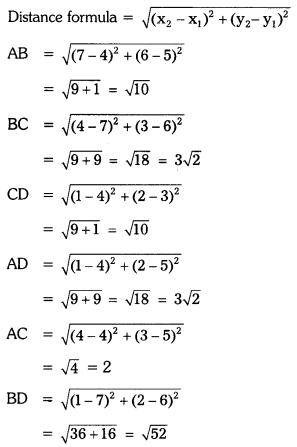
In ABCD, AB = CD and BC = AD (i.e., both pairs of opposite sides are equal) and AC ≠ BD
Hence ABCD is a parallelogram, i.e., the given points form a parallelogram.

Question 10.
Find the point on the X-axis which is equidistant from (2, -5) and (-2, 9).
Solution:
Given points, A(2, -5), B(-2, 9)
Let P(x, 0) be the point on x-axis.
Which is equidistant from A and B i.e., PA = PB.

But PA = PB
⇒ \(\sqrt{x^2-4 x+29}\) = \(\sqrt{x^2+4 x+85}\)
squaring on both sides, we get
x² – 4x + 29 = x² + 4x + 85
-4x – 4x = 85 – 29
-8x = 56
∴ (x, 0) = (-8, 0) is the point which is equidis¬tant from the given points.

Question 11.
If the distance between two points (x, 7) and (1, 15) is 10, find the value of x.
Solution:
Given = A(x, 7), B(1, 15) and AB = 10.
Distance formula

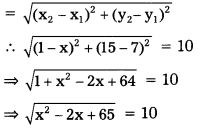
squaring on both sides, we get.
\(\left[\sqrt{x^2-2 x+65}\right]^2\) = 10²
⇒ x² – 2x + 65 = 100
x² – 2x – 35 = 0
⇒ x² – 7x + 5x – 35 = 0
x(x- 7) + 5(x – 7) = 0
(x – 7) (x + 5) = 0
(x – 7) = 0 or x + 5 = 0
x = 7 or x = -5
∴ x = 7 or – 5

Question 12.
Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Solution:
Given : P(2, -3), Q(10, y) and \(\overline{\mathrm{PQ}}\) = 10
Distance formula

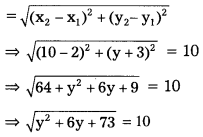
squaring on both sides we get,
\(\left[\sqrt{y^2+6 y+73}\right]^2\) = 10²
⇒ y² + 6y + 73 = 100
⇒ y² + 9y – 3y – 27 = 0
⇒ y(y + 9) – 3 (y + 9) = 0
⇒ (y + 9) (y – 3) = 0
⇒ y + 9 = 0 or y – 3 = 0
⇒ y = – 9 or y = 3
⇒ y = – 9 or 3

Question 13.
Find the radius of the circle whose centre is (3, 2) and passes through (-5, 6).
Solution:

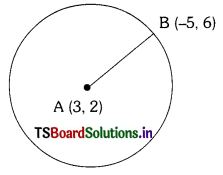
Given : A circle with centre A(3, 2) passing through B(-5, 6).
Radius = AB
[∵ Distance of a point from the centre of the circle.]
Distance formula
\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
Radius r = \(\sqrt{(-5-3)^2+(6-2)^2}\)
= \(\sqrt{64+16}\) = \(\sqrt{80}\) = 4\(\sqrt{5}\) units.

Question 14.
Can you draw a triangle with vertices (1, 5), (5, 8) and (13, 14) ? Give reason.
Solution:
Let A(1, 5), B(5, 8) and C(13, 14) be the given points.
Distance formula

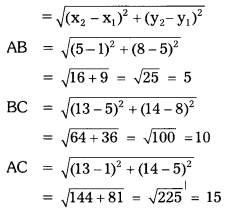
Here, AC = AB + BC
∴ Δ ABC can’t be formed with the given vertices.
[∵ sum of the any two sides of a triangle must be greater than the third side],

Question 15.
Find a relation between x and y such that the point (x, y) is equidistant from the points (-2, 8) and (-3, -5).
Solution:
Let A(-2, 8), B(-3, -5) and P(x, y)
If P is equidistant from A, B then PA = PB
Distance formula

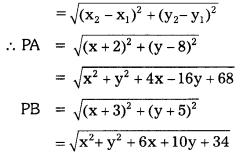
Now PA = PB
⇒ \(\sqrt{x^2+y^2+4 x-16 y+68}\)
⇒ \(\sqrt{x^2+y^2+6 x+10 y+34}\)
squaring on both sides we get,
⇒ 4x – 16y – 6x – 10y = 34 – 68
⇒ – 2x – 26y = – 34
⇒ x + 13y = 17 is the required condition.