TS 10th Class Maths Solutions Chapter 8 Similar Triangles Ex 8.1

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.1

Question 1.
In ∆PQR, ST is a line such that \(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{\mathrm{PT}}{\mathrm{TR}}\) and also ∠PST = ∠PRQ.
Prove that ∆PQR is an isosceles triangle. (AS₂)

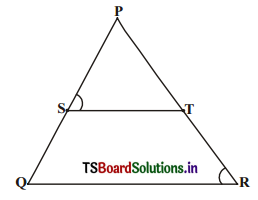
Solution:
In ∆PQR. ST divides PQ and PR in the same ratio.
\(\frac{\mathrm{PS}}{\mathrm{SQ}}\) = \(\frac{\mathrm{PT}}{\mathrm{TR}}\) (given)
∴ ST // QR
It is also given
that ∠PST = ∠PRQ …………… (1)
Since ST // QR and PQ is a transversal.
∠PST = ∠PQR (Corresponding angles) ………….. (2)
From (1) and (2) we have
∠PRQ = ∠PQR
In ∆PQR, ∠PRQ = ∠PQR
∴ PQ = PR
∴ ∆PQR is an isosceles triangle.

Question 2.
In the given figure, LM // CB and LN // CD, prove that \(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AN}}{\mathrm{AD}}\). (AS₂)

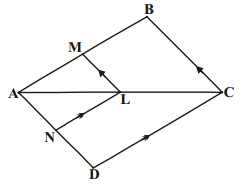
Solution:
In the figure, it is given that LM // CB and LN // CD.
In ∆ABC, ML // BC.
(By basic Proportionality Theorem,)
\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (1)
In ∆ADC, LN // CD
(By Basic Proportionality Theorem,)
\(\frac{\mathrm{AN}}{\mathrm{AD}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (2)
From (1) and (2) we have
\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AN}}{\mathrm{AD}}\)
Alter :
In ∆ABC, ML // BC, AC is a transversal.
∠ALM = ∠ACB (Corresponding angles)
ML // BC, AB is a transversal.
∠AML = ∠ABC (Coressponding angles)
Now in ∆^les AML and ABC,
∠ALM = ∠ACB;
∠AML = ∠ABC;
∠A is common.
∴ ∆AML ~ ∆ABC
∴ Their corresponding sides are proportional.
(i.e.,)\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (1)
Similarity in ∆ADC, LN // CD.
So we can prove that
\(\frac{\mathrm{AN}}{\mathrm{AD}}\) = \(\frac{\mathrm{AL}}{\mathrm{AC}}\) ……….. (2)
Hence from (1) & (2), we get
\(\frac{\mathrm{AM}}{\mathrm{AB}}\) = \(\frac{\mathrm{AN}}{\mathrm{AD}}\)

Question 3.
In the given figure, DE // AC and DF // AE prove that \(\frac{\mathrm{BF}}{\mathrm{FE}}\) = \(\frac{\mathrm{BE}}{\mathrm{EC}}\). (AS₂)

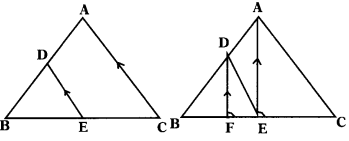
Solution:
In ∆ABC, DE // AC.
(∴ By Basic Proportionality Theorem,)
In ∆ABE, DF // AE
(∴ By Basic Proportionality Theorem,)

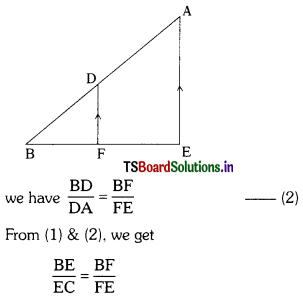
Hence proved.

Question 4.
Prove that a line drawn through the midpoint of one side of a triangle parallel to another side bisects the third side (Using basic proportionality theorem). (AS₂)
Solution:
In ∆ABC, P is the mid-point of AB.
PQ is drawn parallel to BC, intersecting AC in Q.
By Basic Proportionality theorem,

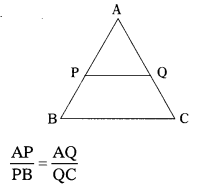
Since P is the mid-point of AB, we have
AP = PB
∴ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{\mathrm{AP}}{\mathrm{PB}}\)
⇒ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) \(\frac{\mathrm{AP}}{\mathrm{AP}}\) (∵ PB = AP)
⇒ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{1}{1}\)
⇒ AQ = QC
Since AQ = QC, Q bisects AC.

Question 5.
Prove that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem). (AS₂)
Solution:
In ∆ABC, D and E are the mid-points of the sides AB and AC respectively.

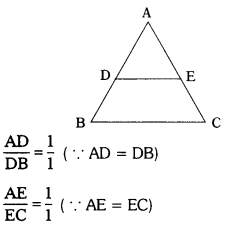
In ∆ABC, DE divides the sides.
AB and AC in the same ratio.
∴ DE||BC (Basic Proportionality Theorem)

Question 6.
In the given figure, DE || OQ and DF || OR. Show that EF || QR. (AS₂)

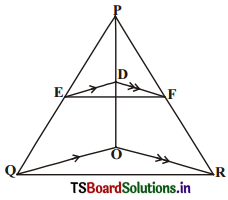
Solution:
In the given figure,
DE || OQ and DF || OR
In ∆PQO, DE || OQ
∴ \(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PD}}{\mathrm{DO}}\) (Basic Proportionality Theorem) ………….. (1)
Similarly in ∆PRO, DF || OR.
∴ \(\frac{\mathrm{PF}}{\mathrm{FR}}\) = \(\frac{\mathrm{PD}}{\mathrm{DO}}\) (Basic Proportionality Theorem) ………….. (2)
From (1) & (2), we have
\(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PF}}{\mathrm{FR}}\)
Now, in ∆PQR, we get that \(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF || QR (By converse of basic proportionality theorem).

Question 7.
In the adjacent figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR. (AS₂)

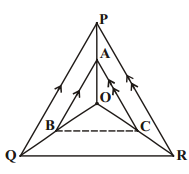
Solution:
In ∆ OPQ, A and B are the points on
OP and OQ such that AB || PQ.
So, in ∆ OPQ, AB || PQ.
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}\) = \(\frac{\mathrm{OB}}{\mathrm{BQ}}\) (Basic proportionality theorem) …………… (1)
In ∆ OPR, A and C are the points on OP and OR such that AC || PR.
So, in ∆ OPR, AC || PR.
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}\) = \(\frac{\mathrm{OC}}{\mathrm{CR}}\) (Basic proportionality theorem) …………… (2)
From (1) & (2), we get \(\frac{\mathrm{OB}}{\mathrm{BQ}}\) = \(\frac{\mathrm{OC}}{\mathrm{CR}}\)
Now, in ∆ OQR, we get that \(\frac{\mathrm{OB}}{\mathrm{BQ}}\) = \(\frac{\mathrm{OC}}{\mathrm{CR}}\)
Therefore, BC || QR (Converse of the Basic proportionality theorem).

Question 8.
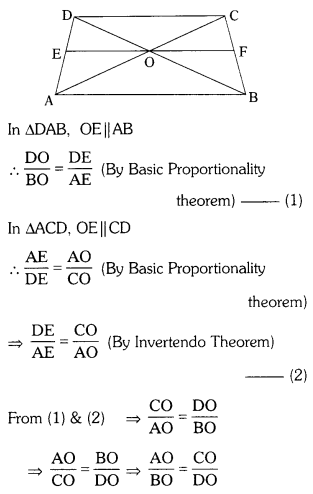
ABCD is a trapezium in which AB ||DC and its diagonals intersect each other at point ‘O’. Show that \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\) (AS₂)
Solution:
ABCD is a trapezium. AB || DC.
The diagonals AC and BD intersect in ‘O’.
Draw a line through ‘O’ parallel to AB, meeting AD in E and BC in F.

Question 9.
Draw a line segment of length 7.2 cm and divide it in the ratio 5:3. Measure the two parts. (AS₃, AS₅)
Solution:

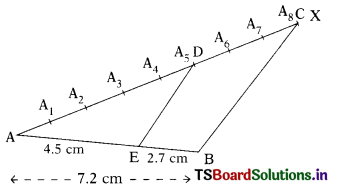
Construction :
Draw a line segment AB = 7.2 cm. Make an angle BAX. Mark A₁, A₂, A₃, A₄, A₅, A₆, A₇ on AX such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈. Mark D on AX such that AD = 5 equal parts and DC = 3 equal parts. Join BC. From D, draw DE || BC. E divides AB in the ratio 5:3. The parts are measured. AE = 4.2 cm on and EB = 2.7 cm.