TS 10th Class Maths Solutions Chapter 6 Progressions Ex 6.4

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions Ex 6.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions Exercise 6.4

Question 1.
In which of the following situations, does the list of numbers involved in form a G.P. ?

i) Salary of Sharmila, when her salary is Rs. 5,00,000 for the first year and expected to receive yearly increase of 10%.
Solution:
Given : Sharmila’s yearly salary = Rs. 5,00,000
Rate of annual increment = 10%

Here, a = a₁ = 5,00,000

Every term starting from the second can be obtained by multiplying its preceding term by a fixed number \(\frac{11}{10}\).
∴ r = common ratio = \(\frac{11}{10}\)
Hence the situation forms a G.R

ii) Number of bricks needed to make each step, if the stair case has total 30 steps. Bottom step needs 100 bricks and each successive step needs 2 bricks less than the previous step.
Solution:
Given : Bricks needed for the bottom step = 100.
Each successive step needs 2 bricks less than the previous step.
∴ Second step from the bottom needs = 100 – 2 = 98 bricks.
Third step from the bottom needs = 98 – 2 = 96 bricks
Fourth step from the bottom needs = 96 – 2 = 94 bricks.
Here the numbers are
100, 98, 96, 94, ………….
Clearly this is an A.P. but not G.R

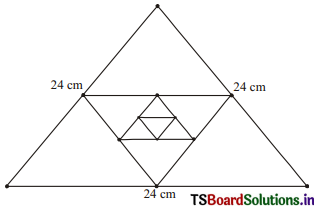
iii) Perimeter of the each triangle, when the mid-points of sides of an equilateral triangle whose side is 24 cm are joined to form another triangle, whose mid-points in turn are joined to form still another triangle and the process continues indefinitely.

Solution:
Perimeter of the 1^st equilateral triangle = 3 × 24 = 72 cm
Perimeter of the 2^nd equilateral triangle = 3 × 12 = 36 cm
Perimeter of the 3^rd equilateral triangle = 3 × 6 = 18 cm
Successive terms are obtained by dividing with 2 the preceding term except first term.
∴ The above situation is a G.P.

Question 2.
Write three terms of the G.P. when the first term ‘a’ and the common ratio ‘r’ are given.

i) a = 4; r = 3.
Solution:
The terms are a, ar, ar², ar³.
∴ 4, 4 × 3, 4 × 3², 4 × 3³
∴ 4, 12, 36, 108,…………

ii) a = \(\sqrt{5}\); r = \(\frac{1}{5}\)
Solution:
The terms of a G.P are:
a, ar, ar², ar³,……….

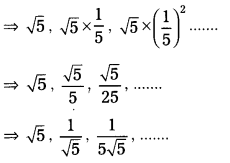
iii) a = 81; r = \(-\frac{1}{3}\).
Solution:
The terms of a G.P are:
a, ar, ar²,…………
⇒ 81, 81 × \(\left(\frac{-1}{3}\right)\), 81 × \(\left(\frac{-1}{3}\right)^2\)
⇒ 81, -27, 9,…………

iv) a = \(\frac{1}{64}\), r = 2.
Solution:
Given: a = \(\frac{1}{64}\) ; r = 2
a₁ = a = \(\frac{1}{64}\)
a₂ = ar = \(\frac{1}{64}\) × 2 = \(\frac{1}{32}\)
a₃ = ar² = \(\frac{1}{64}\) × 2² = \(\frac{1}{64}\) × 4 = \(\frac{1}{16}\)
∴ The G.P. is \(\frac{1}{16}\), \(\frac{1}{32}\), \(\frac{1}{16}\),………….

Question 3.
Which of the following are G.P.? If they are G.P, write three more terms.

i) 4, 8, 16,………….
Solution:
Given : 4, 8, 16,………….
where, a₁ = 4; a₂ = 8; a₃ = 16,………….
\(\frac{a_2}{a_1}\) = \(\frac{8}{4}\) = 2
\(\frac{\mathrm{a}_3}{\mathrm{a}_2}\) = \(\frac{16}{8}\) = 2
∴ r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = 2
Hence 4,8,16,……… is a G.P
where a = 4 and r = 2
a⁴ = a. r³ = 4 × 2³ = 4 × 8 = 32
a⁵ = a.r⁴ = 4 × 2⁴ = 4 × 16 = 64
a⁶ = a. r⁵ = 4 × 2⁵ = 4 × 32 = 128

ii) \(\frac{1}{3}\), \(\frac{-1}{6}\), \(\frac{1}{12}\)………, (x ≠ 0)
Solution:
Given: t₁= \(\frac{1}{3}\); t₂ = \(\frac{-1}{6}\): t₃ = \(\frac{1}{12}\),………….

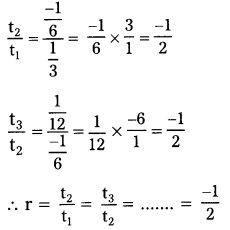
Hence the ratio is common between any two successive terms.
∴ \(\frac{1}{3}\), \(\frac{-1}{6}\), \(\frac{1}{12}\),………. is a G.P.

iii) 5, 55, 555,………….
Solution:
Given: t₁ = 5, t₂ = 55, t₃ = 555
\(\frac{\mathrm{t}_2}{\mathrm{t}_1}\) = \(\frac{55}{5}\) = 11
\(\frac{\mathrm{t}_3}{\mathrm{t}_2}\) = \(\frac{555}{55}\) = \(\frac{111}{11}\)
∴ \(\frac{t_2}{t_1}\) ≠ \(\frac{t_3}{t_2}\)

iv) -2, -6, -18,…………..
Solution:
Given : t₁ = -2; t₂ = -6; t₃ = -18
\(\frac{\mathrm{t}_2}{\mathrm{t}_1}\) = \(\frac{-6}{-2}\) = 3; \(\frac{t_3}{t_2}\) = \(\frac{-18}{-6}\) = 3
∴ r = \(\frac{t_2}{t_1}\) = \(\frac{t_3}{t_2}\) = …….. = 3
∴ -2, -6, -18,……….. is a G.P.
where a = -2 and r = 3
a_n =a.r^n-1
a₄ = ar³ = (-2) × 3³ = -2 × 27 = -54
a₅ = ar⁴ = (-2) × 3⁴ = – 2 × 81 = -162
a₆ = a.r⁵ = (-2) × 3⁵ = -2 × 243 = -486

v) \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), …………..
Solution:
Given: t₁ = \(\frac{1}{2}\), t₂ = \(\frac{1}{4}\), t₃ = \(\frac{1}{6}\)
\(\frac{t_2}{t_1}\) = \(\frac{\frac{1}{4}}{\frac{1}{2}}\) = \(\frac{1}{4}\) × \(\frac{2}{1}\) = \(\frac{1}{2}\)
\(\frac{t_3}{t_2}\) = \(\frac{\frac{1}{6}}{\frac{1}{4}}\) = \(\frac{1}{6}\) × \(\frac{4}{1}\) = \(\frac{2}{3}\)
∴ \(\frac{\mathrm{t}_2}{\mathrm{t}_1}\) ≠ \(\frac{t_3}{t_2}\)
i.e., \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\),………… is not a G.P.

vi) 3, -3², 3³,…………
Solution:
Given : t₁ = 3; t₂ = -3², t₃ = 3³,….
\(\frac{t_2}{t_1}\) = \(\frac{-3^2}{3}\) = -3
\(\frac{\mathrm{t}_3}{\mathrm{t}_2}\) = \(\frac{3^3}{-3^2}\) = -3
∴ r = \(\frac{t_2}{t_1}\) = \(\frac{t_3}{t_2}\) = …….. = -3
i.e., every term is obtained by multiplying its preceding term by a fixed number -3.
3, -3², 3³, ……… forms a G.P
where a = 3; r = -3
aⁿ = a.r^n-1
∴ a₄ = 3 × (-3)^4-1 = 3 × (-3)³ = -81
a₅ = 3 × (-3)⁴ = 3 × 81 = 243
a₆ = 3 × (-3)⁵ = 3 × (-243) = -729

vii) x, 1, \(\frac{1}{x}\),……… (x ≠ 0)
Solution:
Given:

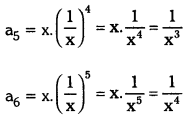
viii) \(\frac{1}{\sqrt{2}}\), -2, \(\frac{8}{\sqrt{2}}\),………..
Solution:
Given :

Given terms are not in G.P.

ix) 0.4, 0.04, 0.004,………
Solution:
Given : t₁ = 0.4; t₂ = 0.04; t₃ = 0.004,…………..

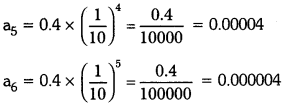
Question 4.
Find x so that x, x + 2, x + 6 are consecutive terms of a geometric progression.
Solution:
Given x, x + 2 and x + 6 are in G.P but read it as x, x + 2 and x + 6.
∴ r = \(\frac{t_2}{t_1}\) = \(\frac{t_3}{t_2}\)
⇒ \(\frac{x+2}{x}\) = \(\frac{x+3}{x+2}\)
⇒ (x + 2)² = x(x + 6)
⇒ x² + 4x + 4 = x² + 6x
⇒ 4x – 6x = -4 ⇒ -2x = -4
∴ x = 2