TS 10th Class Maths Solutions Chapter 8 Similar Triangles Ex 8.4

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.4

Question 1.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals. (AS₂)
Solution:
ABCD is a rhombus. Let its diagonals AC and BD meet at ‘O’.

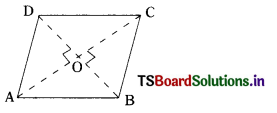
In ∆AOD, ∠AOD = 90°
∴ By Pythagoras theorem,
AD² = OA² + OD² …………… (1)
In ∆COD, ∠COD = 90°
∴ CD² = OC² + OD² …………… (2)
In ∆ AOB, ∠AOB = 90°
∴ AB² = OA² + OB² ……………… (3)
In ∆BOC, ∠BOC = 90°
∴ BC² = OB² + OC² ……………… (4)
Adding (1), (2), (3) & (4), we get
AD² + CD² + AB² + BC² = OA² + OD² + OC² + OD² + OA² + OB² + OB² + OC²
= OA² + OA² + OC² + OC² + OB² + OB² + OD² + OD²
= OA² + OA² + OA² + OA² + OB² + OB² + OB² + OB² (∵ OC = OA & OD = OB)
= 4OA² + 4OB²
= (2OA² + 2OB²) (∵ 2OA = AC & 2OB = BD)

Question 2.
ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively.
Prove that AE² + CD² = AC² + DE². (AS₂)

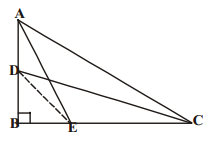
Solution:
In ∆ABE, ∠B = 90°
By Pythagoras Theorem,
AE² = AB² + BE² …………… (1)
In ∆CBD, ∠CBD = 90°
By Pythagoras Theorem,
CD² = BD² + BC² ……………. (2)
Adding (1) & (2), we get AE² + CD² = AB² + BE² + BD² + BC²
= (AB² + BC²) + (BE² + BD²)
= AC² + DE² (∵ In ∆ABC, ∠B = 90°)
(∴ AB² + BC² = AC² and In ∆DBE, ∠B = 90° ∴ BD² + BE² = DE²)

Question 3.
Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude. (AS₂)
Solution:
ABC is an equilateral triangle,

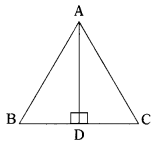
(∵ AD ⊥ BC)
(i.e„) AB = BC = CA, AD ⊥ BC
In ∆^les ADB and ADC
∠ADB = ∠ADC = 90°
Hyp. AB = Hyp. AC
AD is common.
∴ ∆ ADB = ∆ADC
∴ BD = DC
In ∆ADB, ∠ADB = 90°
By Pythagoras Theorem,
AB² = AD² + BD²
= AD² + \(\left(\frac{\mathrm{BC}}{2}\right)^2\) (∵ BD = CD)
= AD² + \(\frac{\mathrm{BC}^2}{4}\) = \(\frac{4 \mathrm{AD}^2+\mathrm{BC}^2}{4}\)
= \(\frac{4 \mathrm{AD}^2+\mathrm{AB}^2}{4}\) (∵ BC = AB)
⇒ 4AB² = 4AD² + AB²
⇒ 4AB² – AB² = 4AD²
⇒ 3AB² = 4AD²

Question 4.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥QR. Show that PM² = QM . MR (AS₂)
Solution:
∆PRM and ∆PQM are right angled triangles.

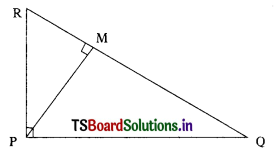
∴ PR² = PM² + RM² ……………. (1)
and PQ² = PM² + QM² …………… (2)
Adding (1) & (2), we get
PR² + PQ² = PM² + RM² + PM² + QM²
⇒ QR² = 2PM² + RM² + QM²
(∵ In ∆PQR, ∠P = 90° ∴ QR² = PR² + PQ²)
⇒ (QM + MR)² = 2PM² + RM² + QM²
⇒ QM² + RM² + 2QM. MR = 2PM² + RM² + QM²
⇒ 2QM. MR = 2PM²
⇒ PM² = QM. MR

Question 5.
ABD is a triangle right angled at A and AC ⊥ BD. Show that (AS₂)
(i) AB² = BC. BD
(ii) AC² = BC . DC
(iii) AD² = BD . CD

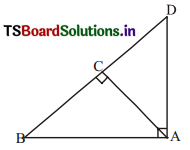
Solution:
(i) In ∆^les BAD and BCA,
∠BAD = ∠BCA = 90°
∠B is common.
∴ ∆BAD ~ ∆BCA

Hence, their corresponding sides are in proportion.
⇒ \(\frac{\mathrm{BD}}{\mathrm{AB}}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ AB² = BC . BD ……………. (1)

(ii) In ∆^les ACB and DCA,
∠ACB = ∠DCA = 90°
∠A is common.
∴ ∆ ACB ~ ∆DCA

Hence, their corresponding sides are in pro-portion.
⇒ \(\frac{\mathrm{AC}}{\mathrm{DC}}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ AC² = BC . DC ……………. (2)

iii) In ∆^les DAB and DCA,
∠DAB = ∠DCA = 90°
∠D is common.
∴ ∆DAB ~ ∆DCA

Hence, their corresponding sides are in proportion.
⇒ \(\frac{\mathrm{BD}}{\mathrm{AD}}\) = \(\frac{\mathrm{AD}}{\mathrm{CD}}\)
⇒ AD² = BD . CD ……………. (3)

Question 6.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC². (AS₂)
Solution:
In ∆ABC, ∠ACB = 90°

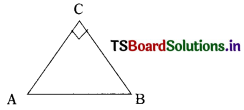
∴ AB is the hypotenuse, since it is an isosceles triangle, AC = BC
By Pythagoras Theorem,
AB² = AC² + BC²
= AC² + (AC)² (∵ BC = AC)
= AC² + AC² = 2AC²

Question 7.
‘O’ is any point in the interior of a triangle ABC. OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
ii) AF² + BD² + CE² = AE² + CD² + BF². (AS₂)

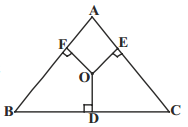
Solution:
In ∆ABC, OD, OE and OF are drawn perpendicular to BC, CA and AB respectively. Join OB, OC and OA.
i) In ∆AFO, ∠AFO = 90°
∴ By Pythagoras Theorem,
OA² = AF² + OF² …………….. (1)
In ABDO, ∠BDO = 90°
∴ OB² = OD² + BD² ………………. (2)
In ACEO, ∠CEO = 90°
∴ OC² = OE² + CE² ……………….. (3)

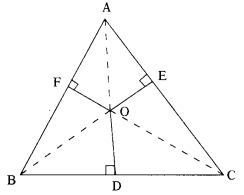
Adding (1), (2) & (3), we get
OA² + OB² + OC² = AF² + OF² + OD² + BD² + OE² + CE²
⇒ OA² + OB² + OC² – OD² – OE² – OF²
= AF² + BD² + CE² …………….. (4)

ii) From (4), we get
AF² + BD² + CE² = (OA² – OE²) + (OB² – OF²) + (OC² – OD²)
= AE² + BF² + CD² (∵ In the right triangle AEO,
∠AEO = 90° ∴ OA² = OE² + AE²
⇒ OA² – OE² = AE²
Similarly, in the right triangle OFB,
∠OFB = 90°; ∴ OB² = OF² + BF²
⇒ OB² – OF² = BF²
Lastly, in the right triangle ODC,
∠ODC = 90°,
OC² = OD² + CD²
⇒ O² – OD² = CD²

Question 8.
A wire attached to a vertical pole of height 18m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut ? (AS₄)
Solution:
In triangle ABC, ∠B = 90°
AB stands for the vertical pole AC represents the wire ‘B’ denotes ‘base’ and C denotes ‘stake’.

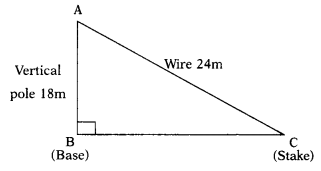
By Pythagoras Theorem,
AC² = AB² + BC²
⇒ BC² = AC² – AB²
= (24)² – (18)²
= 576 – 324 = 252
∴ BC = \(\sqrt{252}\)
= \(\sqrt{252}\) = \(\sqrt{2 2 3 3 7}\)
= \(\sqrt{2^2 \times 3^2}\) × 7
= 2 × 3 × \(\sqrt{7}\) = 6\(\sqrt{7}\) Therefore, the stake should be driven 6 \(\sqrt{7}\) meters for the base of the pole so that the wire will be taut.

Question 9.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance be¬tween the feet of the poles is 12m find the distance between their tops. (AS₄)
Solution:
AB and CD represent two poles of heights 11m and 6m respectively. BC represents the distance between their feet. BC = 12m
Draw DE || CB intersecting AB at E. Join AD.

ED = BC = 12m.
EB = DC = 6m
AE = AB – CD = 11 – 6 = 5m
In ∆AED, ∠AED = 90°
∴ By Pythagoras theorem,
AD² = AE² + DE²
= 5² + 12² = 25 + 144 = 169
∴ AD = \(\sqrt{169}\) = 13m
∴ The distance between the tops of the poles = 13 meters.

Question 10.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\) BC. Prove that 9AD² = 7 AB². (AS₂)
Solution:
ABC is an equilateral triangle.
∴ AB = BC = CA
D is a point on BC, such that
BD = \(\frac{1}{3}\) BC; Draw AE ⊥ BC.

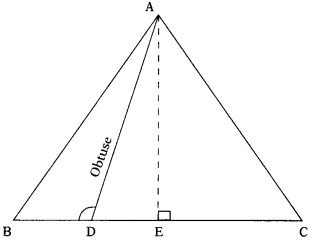
∴ E bisects BC.
⇒ BE = CE
In ∆ABD, ∠ADB is obtuse.
∴ AB² = AD² + BD² + 2 BD . DE
⇒ AD² = AB² – BD² – 2BD. DE

Question 11.
In the given figure, ABC Is a triangle right angled at B. D and E are points on BC trisect it. Prove that 8AE² = 3AC² + 5AD². (AS₂)

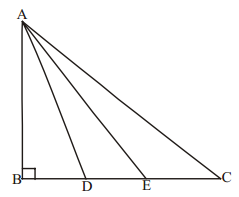
Solution:
In ∆ADC, ∠ADC is obtuse.
∠B = 90° and BD = DE = EC.
Let BD = DE = EC = x
AC² = AD² + DC² + 2 DC. DB
= AD² + (2x)² + 2. 2x. x
= AD² + 4x² + 4x²
= AD² + 8x² ………………… (1)
In ∆ABD, ∠B = 90°
∴ AD² = AB² + BD² (By Pythagoras Theorem)
⇒ AB² = AD² – BD² = AD² – x² …………. (2)
In ∆ABE = ∠B = 90°
∴ AE² = AB² + BE² = AB² + (2x)² = AB² + 4x²
∴ AB² = AE² – 4x² ……………. (3)
From (2) & (3), we get
AE² – 4x² = AD² – x²
AE² – 4x² = AD² – x² + 4x² = AD² + 3x²
8AE² = 8(AD² + 3x²)
= 8AD² + 24x² ………………. (4)
From (1),
3AC² + 5 AD²
= 3 (AD² + 8x²) + 5 AD²
= 3 AD² + 24x² + 5AD²
= 8AD² + 24x² ……………….. (5)
From (4) & (5), we have,
8AE² = 3AC² + 5 AD²

Question 12.
ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ∆ABE and ∆ACD.

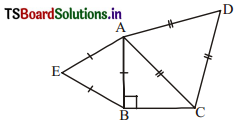
Solution:
In ∆ABC, ∠B = 90°
Let AB = BC = x

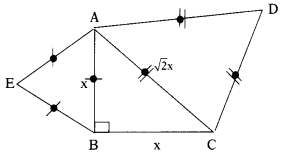
∴ By Pythagoras theorem,
AC² = AB² + BC² = x² + x² = 2x²
∴ AC = \(\sqrt{2 \mathrm{x}^2}\) = \(\sqrt{2}\)x
By problem ∆ACD ~ ∆ABE,
Therefore, \(\frac{\text { area of }(\triangle \mathrm{ABE})}{\text { area of }(\triangle \mathrm{ACD})}\) = \(\frac{\mathrm{AB}^2}{\mathrm{AC}^2}\)
= \(\frac{(x)^2}{(\sqrt{2} x)^2}\) (∵ AB = x and AC = \(\sqrt{2}\)x )
= \(\frac{x^2}{2 x^2}\) = \(\frac{1}{2}\)
Hence, the ratio between the areas of ∆ABE and ∆ACD = 1 : 2