TS 10th Class Maths Solutions Chapter 8 Similar Triangles Ex 8.3

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Ex 8.3 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Exercise 8.3

Question 1.
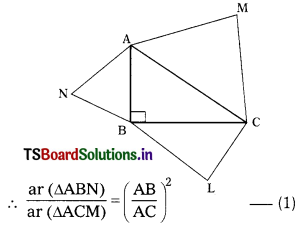
Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
Solution:
We have to prove that area of ∆ABN + area of ∆BCL = area of ∆ACM
∆ABN and ∆ACM are equilateral triangles.
In an equilateral triangles each angle is equal to 60°.
In ∆ABN, ∠A = ∠B = ∠N = 60°
In ∆ACM, ∠A = ∠C = ∠M = 60°
∴ ∆ABN ~ ∆ACM (A.A.A criterion)

Adding (1) & (2), we get

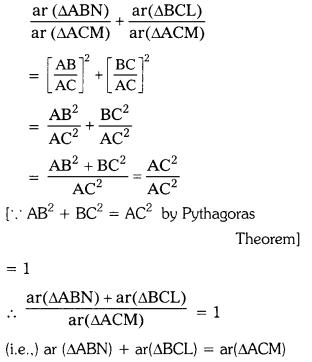
Question 2.
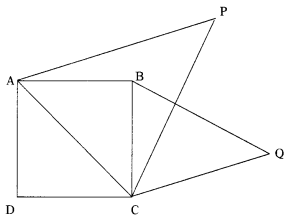
Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.
Solution:
We have to prove that ar (∆BQC) = \(\frac{1}{2}\) ar (∆APC)
∆APC ~ ∆BQC (∵ ∆APC and ∆BQC are equiangular)
∴ \(\frac{{ar}(\triangle \mathrm{APC})}{{ar}(\triangle \mathrm{BQC})}\) = \(\left(\frac{\mathrm{AC}}{\mathrm{BC}}\right)^2\)
(∵ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.)
= \(\frac{\mathrm{AC}^2}{\mathrm{BC}^2}\) = \(\frac{(\sqrt{2} \mathrm{BC})^2}{\mathrm{BC}^2}\)
[Since ABCD is a square, its diagonal.
AC = \(\sqrt{42}\) × side
= \(\sqrt{42}\) × BC]

= 2 \(\frac{\mathrm{BC}^2}{\mathrm{BC}^2}\) = 2
\(\frac{{ar}(\triangle \mathrm{APC})}{{ar}(\triangle \mathrm{BQC})}\) = \(\frac{2}{1}\)
2 ar (∆BQC) = ar(∆APC)
∴ ar(∆BQC) = \(\frac{1}{2}\) ar(∆APC)

Question 3.
D,E,F are mid points of sides BC, CA, AB of ∆ABC. Find the ratio of areas of ∆DEF and ∆ABC. (AS₁, AS₄)
Solution:
We have to find the ratio of area ∆DEF and area ∆ABC.
E E are the mid points of AB and AC respectively. In ∆ABC,
∴ FE || BC ⇒ FE|| BD

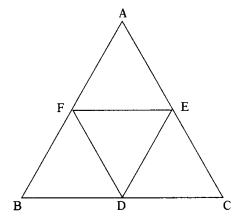
Similarly D, F are the mid points of BC and AB respectively.
In ∴ ∆ ABC.
DF || AC ⇒ DF || AE
Similarly DE || AB ⇒ DE || AF
FEDB is a parallelogram.
(∵ FB || ED and BD || FE)
∴ ∠FED = ∠B
(Opposite angles of a ▱^gm are equal)
FDEA is a parallelogram
(∵ FD || AE and DE || FA)
∴ ∠FDE = ∠A
(Opposite angles of a ▱^gm are equal)
In ∆^les ABC and DEE
∠FED = ∠B
∠FDE = ∠A
∴ ∠EFD = ∠C
∴ ∆ABC ~ ∆DEF
∴ \(\frac{{area}(\triangle \mathrm{DEF})}{{area}(\triangle \mathrm{ABC})}\) = \(\frac{\mathrm{DE}^2}{\mathrm{AB}^2}\) = \(\frac{\left[\frac{1}{2} \mathrm{AB}\right]^2}{\mathrm{AB}^2}\)
= \(\frac{\frac{1}{4} \mathrm{AB}^2}{\mathrm{AB}^2}\) = \(\frac{1}{4}\) (∵ DE = \(\frac{1}{2}\) AB)
∴ area (∆DEF) : area (∆ABC) = 1 : 4

Question 4.
In ∆ABC, XY || AC and XY divides the triangle into two parts of equal area. Find the ratio of \(\frac{\mathrm{A X}}{\mathrm{A B}}\). (AS₁, AS₄)
Solution:
In ∆ABC, XY || AC. We have to find the ratio \(\frac{\mathrm{A X}}{\mathrm{A B}}\)
Given that XY divides the triangle ABC into 2 parts of equal area.
In ∆ABC, since XY || AC, BA and BC are transversals.
∠BXY = ∠A (Corresponding angles)
∠BYX = ∠C (Corresponding angles)
∠B is common.
∆BXY ~ ∆BAC
area of ∆BXY = area of trapezium XYCA
area of ∆BXY + ar. of ∆BXY = area of trapezium XYCA + ar. ABXY
2 ar. ∆BXY = ar. ∆BAC
Since, ∆BXY ~ ∆BAC,

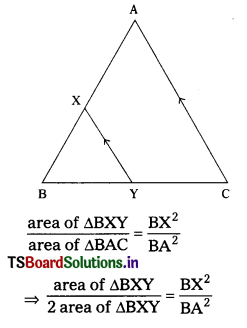
⇒ \(\frac{1}{2}\) = \(\left[\frac{\mathrm{BX}}{\mathrm{BA}}\right]^2\)
⇒ \(\frac{2}{1}\) = \(\frac{\mathrm{BA}^2}{\mathrm{BX}^2}\)
⇒ BA² = 2BX²
⇒ BA = \(\sqrt{2}\) . BX = \(\sqrt{2}\) (BA – AX)
⇒ (\(\sqrt{2}\) – 1)BA = \(\sqrt{2}\) AX
⇒ \(\frac{\mathrm{AX}}{\mathrm{AB}}\) = \(\frac{\sqrt{2}-1}{\sqrt{2}}\)

Question 5.
Prove that the ratio of areas of two simi¬lar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
∆ABC ~ ∆DEF
AP is the median drawn from A to BC.
DQ is the median drawn from D to EH
We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.

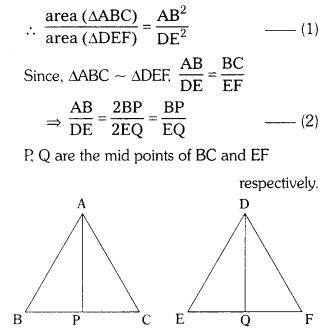
In ∆^les ∆PB and DQE, we have

Question 6.
∆ABC ~ ∆DEF, BC = 3 cm, EF = 4cm and area of ∆ABC = 54 cm². Determine the area of ∆DEF. (AS₁)
Solution:
∆ABC ~ ∆DEF
area of ∆ABC = 54 cm²
Given that BC = 3 cm and EF = 4 cm
We know that the areas of two similar triangles are in the ratio of the squares of the corresponding sides.

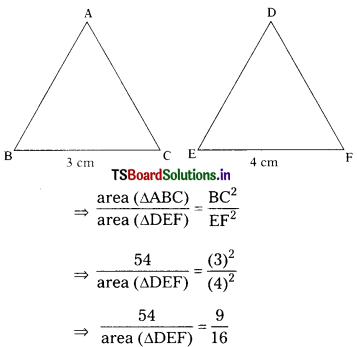
⇒ area (∆DEF) × 9 = 54 × 16
⇒ area (∆DEF) = \(\frac{54 \times 16}{9}\)
∴ area (∆DEF) = 96 cm²

Question 7.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm. and BP = 3 cm., AQ =1.5 cm., CQ = 4.5 cm. Prove that (area of ∆APQ) = \(\frac{1}{2}\) (area of ∆ABC). (AS₂)
Solution:
In ∆ABC,
AP = 1 cm, PB = 3 cm,
AQ = 1.5 cm, QC = 4.5 cm

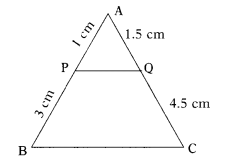
\(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{1}{3}\)
\(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{1.5}{4.5}\) = \(\frac{1}{3}\)
Since \(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = \(\frac{1.5}{4.5}\), PQ // BC.
Now in ∆^les ∆APQ and ABC
∠A = ∠A (Common)
∠APQ = ∠ABC (∵ PQ // BC, APB is a transversal.)
∴ ∠APQ = ∠ABC (Corresponding sides)
∴ ∠AQP = ∠ACB
Hence, ∆APQ ~ ∆ABC.
We know that the ratio of the areas of two similar triangles are equal to the ratio of the squares of any two corresponding sides.
AP and AB are corresponding sides.
AP = 1 cm,
AB = AP + PB = 1 + 3 = 4 cm
So, \(\frac{{area}(\Delta \mathrm{APB})}{{area}(\Delta \mathrm{ABC})}\) = \(\frac{(1)^2}{(4)^2}\)
\(\frac{{area}(\Delta \mathrm{APB})}{{area}(\Delta \mathrm{ABC})}\) = \(\frac{1}{16}\)
⇒ 16 × area (∆APB) = area (∆ABC)
⇒ area (∆APB) = \(\frac{1}{16}\) area (∆ABC)

Question 8.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. If the altitude of the bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle. (AS₁, AS₄)
Solution:
Areas of the two similar triangles are 81 cm² and 49 cm². Altitude of the bigger triangle = 4.5 cm
Let the corresponding altitude of the smaller triangle be x. We know that the areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.


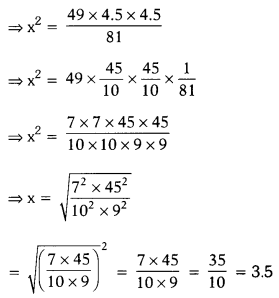
Length of the corresponding altitude of smaller triangle = 3.5 cm