TS 10th Class Maths Solutions Chapter 6 Progressions InText Questions

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions InText Questions

Try This

Question 1.
i) Which of these are arithmetic progressions and why ? (P.No. 128)

a) 2, 3, 5, 7, 8, 10, 15, …
Solution:
2, 3, 5, 7, 8, 10, 15, ……. is not an A.P
∵ a₂ – a₁ = 3 – 2 = 1
a₃ – a₂ = 3 – 2 = 1
a₄ – a₃ = 7 – 5 = 1
i.e., The difference between any two successive terms is not same throughout the series.
(or)
Every number is not formed by adding a fixed number to its preceding term.

b) 2, 5, 7, 10, 12, 15, ….
Solution:
The given list does not form an A.R, since each term is not obtained by adding a fixed number to its preceding term.

c) -1, – 3, – 5, -7
-1, – 3, – 5, – 7, … is an A.P.
∵ a₂ – a₁ = -3-(-1) = -3 + 1 = -2
a₃ – a₂ = -5 – (-3) = -5 + 3 = -2
a₄ – a₃ = -7 – (-5) = -7 + 3 = -2
Every number is formed by adding a fixed number to its preceding term.

ii) Write 3 more Arithmetic Progressions.
a) a = -7; d = – 3 and
A.P. is -7, -10, -13, -16, ….
b) a = 15; d = 4 and
A.P. is 15, 19, 23, 27, 31, ….
c) a = 100; d = 50 and
A.P. is 100, 150, 200, 250, ….

Think – Discuss

Question 1.
Think how each of the list given, form an A.P. Discuss with your friends. (Page No. 129)

a) Heights (in cm) of some students of a school standing in a queue in the morning assembly are 147,148,149,…., 157.
Solution:
The given list forms an A.P. since each term starting from the second is obtained by adding a fixed number +1 to its preceding term.

b) Minimum temperatures (in °C) recorded for a week, in the month of January in a city, arranged in ascending order are – 3.1, – 3.0, – 2.9, – 2.8, – 2.7, – 2.6, – 2.5
Solution:
The given list forms an A.R, since every term starting from the second is obtained by adding a fixed number +0.1 to its preceding term.

c) The balance money (in Rs.) after paying 5% of the total loan of Rs. 1000 every month is 950, 900, 850, 800, … , 50.
Solution:
The given list forms an A.P., since each term starting from the second is obtained by adding a fixed number (-50) to its preceding term.

d) Cash prizes (in Rs.) given by a school to the toppers of Classes I to XII are 200, 250, 300, 350, …., 750 respectively.
Solution:
The given list forms an A.P., since each term starting from the second is obtained by adding a fixed number 50 to its preceding term.

e) Total savings (in Rs.) after every month for 10 months when Rs. 50 are saved each month are 50, 100, 150, 200, 250, 300, 350, 400, 450, 500.
Solution:
The given list forms an A.P., since every term starting from the second term is obtained by adding a fixed number 50 to its preceding term.

Question 2.
Find the common difference of each of the above lists. Think when is it positive. (Page No. 129)
Solution:
Common difference d = a₂ – a₁
a) 148 -147 = 1
b) -3.0 – (-3.1) = 0.1
c) 900 – 950 = – 50
d) 250 – 200 = 50
e) 100 – 50 = 50
Common difference is positive when a₂ > a₁

Question 3.
Make a positive Arithmetic progression in which the common difference is a small positive quantity. (Page No. 129)
Solution:
a = 50; d = 0.5 then A.P is 50, 50.5, 51, 51.5, 52, …

Question 4.
Make an A.P. in which the common difference is negative. (Page No. 129)
Solution:
a = 100, d = 1000 then A.P. is 100, 1100, 2100, 3100, 4100, ….

Question 5.
Make an A.P. in which the common difference is negative. (Page No. 129)
Solution:
a = 80, d = -7 then A.P is 80, 73, 66, 59, 52,…….

Do This

Question 1.
Write three examples for finite A.P. and three for infinite A.P. (Page No. 130)
Solution:
Examples for finite A.P.
i) 3, 5, 7, 9, 11 where a = 3; d = 2.

ii) x, x + a, x + 2a, x + 3a, x + 4a, x + 5a
where a = x; d = a.

iii) \(\frac{1}{9}\), \(\frac{2}{9}\), \(\frac{3}{9}\), \(\frac{4}{9}\), \(\frac{5}{9}\), \(\frac{6}{9}\), \(\frac{7}{9}\)
where a = \(\frac{1}{9}\); d = \(\frac{1}{9}\).
Examples for infinite A.P

i) 10, 20, 30, 40,…
where a = 10, d = 10.
ii) 5.5, 6.6, 7,7, 8.8, 9.9,……..
where a = 5.5; d = 1.1.
iii) -100, -95, -90, -85,………
where a = -100, d = 5.

Question 2.
Take any Arithmetic Progression. (Page No. 131)
Solution:
4, 7, 10, 13, 16,……………

Question 3.
Add a fixed number to each and every term of A.P. Write the resulting numbers as a list. Check whether the resulting lists are AP. In each case. (Page No. 131)
Solution:
4, 7, 10, 13, 16, …
Adding 5’ to each term of the above A.P we get
4 + 5, 7 + 5, 10 + 5, 13 + 5, 16 + 5,……..
9, 12, 15, 18, 21,………
In the list obtained the first term
a₁ = 9; a₂ = 12, a₃ = 15,…………
Also a₂ – a₁ = 12 – 9 = 3
a₃ – a₂ = 15 – 12 = 3
a₄ – a₃ = 18 – 15 = 3
……………………
i.e., d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = …… = 3
∴ The resulting list forms an AP

Question 4.
Similarly subtract a fixed number from each and every term of A.P. Write the resulting numbers as a list. Check whether the resulting lists are A.P. in each case. (Page No. 131)
Solution:
4, 7, 10, 13, 16,………….
Subtracting ‘2’ from the each term of A.P. in given series, we get

In the list obtained, the first term
a₁ = 2, a₂ = 5, a₃ = 8, a₄ = 11, ……….
Also a₂ – a₁ = 5 – 2 = 3
a₃ – a₂ = 8 – 5 = 3
a₄ – a₃ = 11 – 8 = 3
…………………………….
i.e., d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ …… = 3
∴ The resulting list forms an A:P

Question 5.
Multiply and divide each term of A.P by a fixed number and write the resulting numbers as a list.
Check whether the resulting lists are A.P in each case. (Page No. 131)
Solution:
4, 7, 10, 13, 16,………….
Multiplying each term by 3. we get

In the list obtained, the first term
a₁ = 12 and a₂ = 21, a₃ = 30………
Also a₂ – a₁ = a₃ – a₂ = ……… = 9
∴ The resulting list also forms an A.P.
Now divide every term by 7, we get
\(\frac{4}{7}\), \(\frac{7}{7}\), \(\frac{10}{7}\), \(\frac{13}{7}\), \(\frac{16}{7}\),……….. is the resulting list.

Question 6.
Check whether the resulting lists are A.P in each case.
Solution:
The first term
a₁ = \(\frac{4}{7}\), a₂ = \(\frac{7}{7}\), a₃ = \(\frac{10}{7}\), a₄ = \(\frac{13}{7}\),………
Also, a₂ – a₁ = \(\frac{7}{7}\) – \(\frac{4}{7}\) = \(\frac{3}{7}\),
a₃ – a₂ = \(\frac{10}{7}\) – \(\frac{7}{7}\) = \(\frac{3}{7}\),
a₄ – a₃ = \(\frac{13}{7}\) – \(\frac{10}{7}\) = \(\frac{3}{7}\),
∴ d = a₂ – a₁= a₃ – a₂ = a₄ – a₃ = … = \(\frac{3}{7}\) and the above list forms an A.P

Question 7.
What is your conclusion? (Page No. 131)
Solution:
If a₁, a₂, a₃, … are in A.P, then
a₁ ± k, a₂ ± k, a₃ ± k, a₄ ± k. ….. are also inA.P
a₁k, a₂k, a₃k,………. are also in A.P
\(\frac{a_1}{\mathrm{k}}\), \(\frac{a_2}{\mathrm{k}}\), \(\frac{a_3}{\mathrm{k}}\) ,…….. are also in A.P.
i.e.. “If each term of an A.P is added/multiplied/divided by a fixed number,the resulting terms also form an A.P” and fixed term is subtraded from each term of an A.P, then the resulting terms also form an A.P

Do This

Question 1.
Find the sum of Indicated number of terms in each of the following A.Ps. (Page No. 143)

i) 16, 11, 6,……… 23 terms.
Solution:
Given: 16, 11, 6,……. S₂₃
t₁ = a = 16; t₂ = 11; t₃ = 6
d = t₂ – t₁ = 11 – 16 = -5
S_n = \(\frac{\mathrm{n}}{2}\)[2a + (n-1)d]
S₂₃ = \(\frac{23}{2}\)[2 × 16 + (23 – 1) × (-5)]
= \(\frac{23}{2}\)[32 + (22) × (-5)]
= \(\frac{23}{2}\)[32 – 110]
= \(\frac{23 \times(-78)}{2}\)
= -23 × 39 = -897

ii) -0.5, -1.0, -1.5,………. 10 terms.
Solution:
Given: -0.5, -1.0, -1.5, …….. S₁₀
a = -0.5
d = t₂ – t₁ = (-1.0) – (-0.5)
= -1.0 + 0.5 = -0.5
S_n = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d]
S₁₀ = \(\frac{10}{2}\) [ 2 × (-0.5) + (10 – 1)(-0.5)]
= 5[-1.0 + 9 × (-0.5)]
= 5[-1.0-4.5]
= 5 × (-5.5) = -27.5

iii) -1, \(\frac{1}{4}\), \(\frac{3}{2}\),……… 10 terms
Solution:
Given -1, \(\frac{1}{4}\), \(\frac{3}{2}\),……… S₁₀
a = -1

Do This

Question 1.
Find which of the following are not GP.? (Page No. 149)

Question 1.
6, 12, 24, 48,……..
Solution:
Given : 6, 12, 24, 48,……..
a₁ = a = 6; a₂ = 12; a₃ = 24
\(\frac{\mathrm{a}_2}{\mathrm{a}_1}\) = \(\frac{12}{6}\) = 2 ; \(\frac{a_3}{a_2}\) = \(\frac{24}{12}\) = 2 ;
\(\frac{a_4}{a_3}\) = \(\frac{48}{24}\) = 2
i.e., r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = \(\frac{a_4}{a_3}\) = …….. = 2
The given list is of the form
a, ar, ar², ar³,………..
∴ The given numbers are in G.P.

Question 2.
1, 4, 9, 16,………….
Solution:
Given: 1, 4, 9, 16,………
a₁ = a = 1
a₂ = 4; a₃ = 9, a₄ = 16

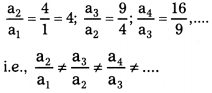
∴ The given numbers do not form a G.P.

Question 3.
1, -1, 1, -1,……….
Solution:

Question 4.
-4, -20, -100, -500,………
Solution:
Given, -4, -20, -100, -500,……….
a₁ = a = -4, a₂ = -20,
a₃ = -100, a₄ = -500,……….

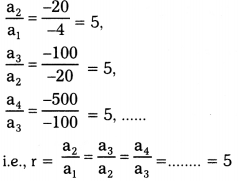
∴ The given list forms a G.P

Think – Discuss

Question 1.
Explain why each of the lists given is a G.P. (Page No. 149)

i) 1, 4, 16, 64, 256,…………
Here
a = 1 = a₁ ; a₂ = 4; a₃ = 16; a₄ = 64;….
\(\frac{a_2}{a_1}\) = \(\frac{4}{1}\) ; \(\frac{a_3}{a_2}\) = \(\frac{16}{4}\) ; \(\frac{a_4}{a_3}\) = \(\frac{64}{16}\) = 4
i.e., Common ratio r = 4.

ii) 550, 605, 665.5,………..
Solution:
The given series is in G.P Since every term can be obtained by multiplying its preceding term by a fixed number ‘1.1’.
(\(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = ……. = 1.1 = r)

iii) 256, 128, 64, 32,………….
Solution:
The given series forms a G.P Since every term, starting from the second can be obtained by multiplying its preceding term by a fixed number \(\frac{1}{2}\).
[∵ r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = ………. = \(\frac{1}{2}\)]

iv) 18, 16.2, 14.58, 13.122,……….
Solution:
The given list forms a G.P
Since each term, starting from the second can be obtained by multiplying its preceding term by a fixed number 0.9.
here r = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\) = \(\frac{a_4}{a_3}\) = …………. = 0.9

Question 2.
To know about a G.P. what is minimum information that we need ? (Page No. 149)
Solution:
To know whether a number pattern forms a G.P or not, we should check that the ratio between the successive terms is equal or not.