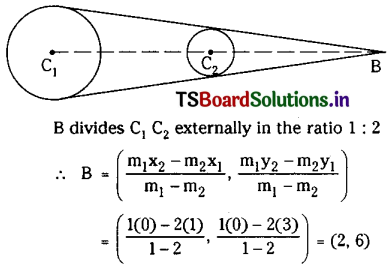
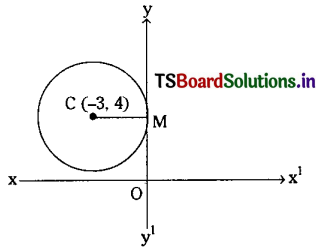
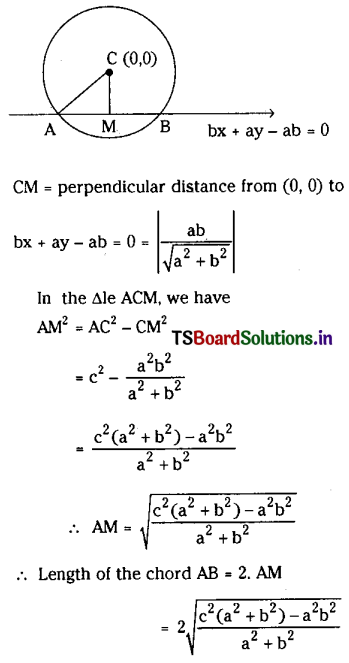
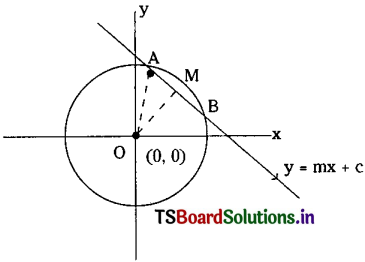
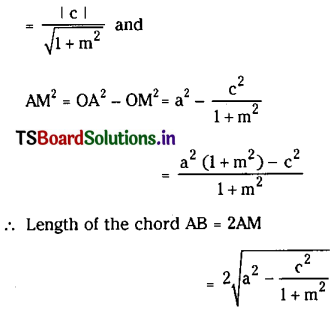
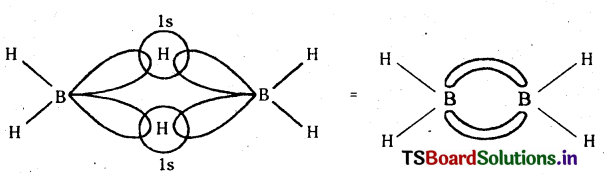
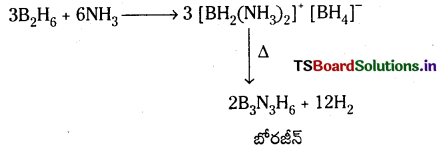
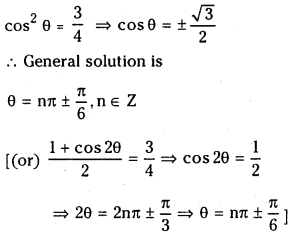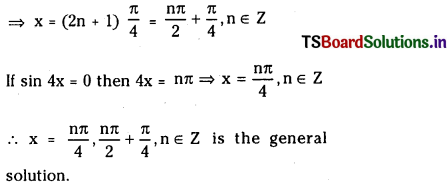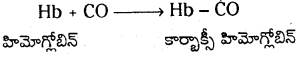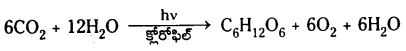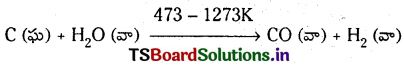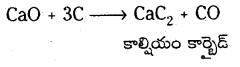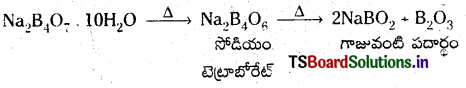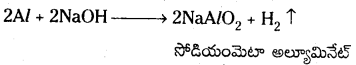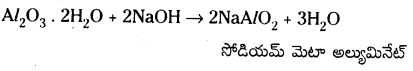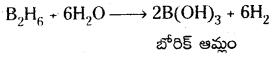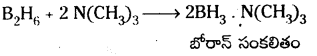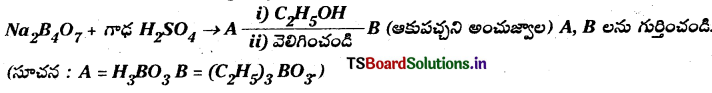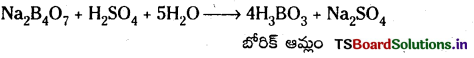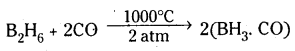Mahesh – Page 27 – TS Board Solutions

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b)

January 23, 2024January 21, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Exercise 2(b)

Question 1.
Find the equation of the radical axis of the following circles.
(i) x² + y² – 3x – 4y + 5 = 0, 3(x² + y²) – 7x + 8y – 11 = 0
Solution:
Let S ≡ x² + y² – 3x – 4y + 5 = 0 and S’ ≡ \(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}=0\) be the given circles.
The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ (x² + y² – 3x – 4y + 5) – (\(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}\)) = 0
⇒ -3x – 4y + 5 + \(\frac{7}{3} x-\frac{8}{3} y+\frac{11}{3}\) = 0
⇒ -9x – 12y + 15 + 7x – 8y + 11 = 0
⇒ -2x – 20y + 26 = 0
⇒ x + 10y – 13 = 0

(ii) x² + y² + 2x + 4y + 1 = 0, x² + y² + 4x + y = 0
Solution:
Let S ≡ x² + y² + 2x + 4y + 1 = 0 and S’ ≡ x² + y² + 4x + y = 0 be the given circles.
Then the radical axis of circles S = 0, S’ = 0 is S – S’ = 0.
⇒ (x² + y² + 2x + 4y + 1) – (x² + y² + 4x + y) = 0
⇒ -2x + 3y + 1 = 0
⇒ 2x – 3y – 1 = 0
∴ The equation of the radical axis of circles is 2x – 3y – 1 = 0.

(iii) x² + y² + 4x + 6y – 7 = 0, 4(x² + y²) + 8x + 12y – 9 = 0.
Solution:
Let S ≡ x² + y² + 4x + 6y – 7 = 0 and S’ ≡ x² + y² + 2x + 3y – \(\frac{9}{4}\) = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 2x + 3y – \(\frac{19}{4}\) = 0
⇒ 8x + 12y – 19 = 0

(iv) x² + y² – 2x – 4y – 1 = 0, x² + y² – 4x – 6y + 5 = 0
Solution:
Let S ≡ x² + y² – 2x – 4y – 1 = 0 and S’ ≡ x² + y² – 4x – 6y + 5 = 0
∴ The equation of radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ 2x + 2y – 6 = 0
⇒ x + y – 3 = 0

Question 2.
Find the equation of the common chord of the following pair of circles.
(i) x² + y² – 4x – 4y + 3 = 0, x² + y² – 5x – 6y + 4 = 0
Solution:
Let S ≡ x² + y² – 4x – 4y + 3 = 0 and S’ = x² + y² – 5x – 6y + 4 = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ x + 2y – 1 = 0

(ii) x² + y² + 2x + 3y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
Solution:
Denote S ≡ x² + y² + 2x + 3y + 1 = 0 and S’ ≡ x² + y² + 4x + 3y + 2 = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ -2x – 1 = 0
⇒ 2x + 1 = 0

(iii) (x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b)
Solution:
Denote S ≡ (x – a)² + (y – b)² = c²
⇒ x² + y² – 2ax – 2by + a² + b² – c² = 0 …….(1)
and S’ ≡ (x – b)² + (y – a)² = c²
⇒ x² + y² – 2bx – 2ay + b² + a² – c² = 0 ……..(2)
Radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 2bx – 2ax + 2ay – 2by = 0
⇒ 2x(b – a) + 2y(a – b) = 0
⇒ x – y = 0 (∵ a ≠ b)

II.

Question 1.
Find the equation of the common tangent of the following circles at their point of contact.
(i) x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0
Solution:
Denote S ≡ x² + y² + 10x – 2y + 22 = 0 and S’ ≡ x² + y² + 2x – 8y + 8 = 0.
The equation of the common tangent of the circles at their point of contact is the equation of the radical axis of S = 0 and S’ = 0 given by S – S’ = 0.
⇒ 8x + 6y + 14 = 0
⇒ 4x + 3y + 7 = 0

(ii) x² + y² – 8y – 4 = 0, x² + y² – 2x – 4y = 0
Solution:
Let S ≡ x² + y² – 8y – 4 = 0 and S’ ≡ x² + y² – 2x – 4y = 0
The equation of the common tangent at the point of contact of circles is the equation of the radical axis of the circles S = 0, S’ = 0 given by S – S’ = 0.
⇒ x² + y² – 8y – 4 – x² – y² + 2x + 4y = 0
⇒ 2x – 4y – 4 = 0
⇒ x – 2y – 2 = 0

Question 2.
Show that the circles x² + y² – 8x – 2y + 8 = 0 and x² + y² – 2x + 6y + 6 = 0 touch each other and find the point of contact.
Solution:
Let the equations of the given circles be denoted by S ≡ x² + y² – 8x – 2y + 8 = 0 and S’ = x² + y² – 2x + 6y + 6 = 0
Centres are C₁ = (4, 1) and C₂ = (1, -3)
and radii of circles are r₁ = \(\sqrt{16+1-8}\) = 3 and r₂ = \(\sqrt{1+9-6}\) = 2
∴ C₁C₂ = \(\sqrt{(4-1)^2+(1+3)^2}=\sqrt{9+16}\) = 5
Also r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the circles touch each other externally.
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) II Q2
The point of contact P divides C₁C₂ internally in the ratio of their radii i.e., 3 : 2.
∴ The point of contact

Question 3.
If the two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other, then show that fg’ = f’g.
Solution:
Let S = x² + y² + 2gx + 2fy = 0 and S’ = x² + y² + 2g’x + 2f’y = 0 be the given circles.
Centres of the circles are C₁ = (-g, -f) and C₂ = (-g, -f’)
Also r₁ = \(\sqrt{g^2+f^2}\) and r₂ = \(\sqrt{g^{\prime 2}+f^{\prime 2}}\)
Given that the two circles touch each other we have C₁C₂ = |r₁ ± r₂|
⇒ \(\sqrt{\left(g-g^{\prime}\right)^2+\left(f-f^{\prime}\right)^2}\) = \(\left|\sqrt{g^2+f^2} \pm \sqrt{g^{+2}+f^2}\right|\)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) II Q3

Question 4.
Find the radical centre of the following circles.
(i) x² + y² – 4x – 6y + 5 = 0, x² + y² – 2x – 4y – 1 = 0, x² + y² – 6x – 2y = 0
Solution:
Let S = x² + y² – 4x – 6y + 5 = 0, S₁ = x² + y² – 2x – 4y – 1 = 0 and S₂ = x² + y² – 6x – 2y = 0 be the given circles.
Radical axis of S = 0, S₁ = 0 is S – S₁ = 0
⇒ -2x – 2y + 6 = 0
⇒ x + y – 3 = 0 ……….(1)
Radical axis of S₁ = 0, S₂ = 0 is 4x – 2y – 1 = 0 ……….(2)
Solving (1) and (2), we get the coordinates 0f Radical centre of the circles S = 0, S₁ = 0, and S₂ = 0
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) II Q4(i)

(ii) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0
Solution:
Denote S = x² + y² + 4x – 7 = 0
S₁ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
and S₂ = x² + y² + y = 0
Radical axis of S = 0, S₁ = 0 is S – S₁ = 0.
⇒ \(\frac{5}{2} x-\frac{5}{2} y+\frac{5}{2}=0\)
⇒ x – y + 1 = 0 ………(1)
Radical axis of S₁ = 0, S₂ = 0 is S₁ – S₂ = 0.
⇒ \(\frac{3}{2} x+\frac{3}{2} y-\frac{9}{2}=0\)
⇒ x + y – 3 = 0 ……..(2)
Solving 2x – 2 = 0 ⇒ x = 1
and From (2), y = 2
∴ Radical centre = (1, 2)

III.

Question 1.
Show that the common chord of the circles x² + y² – 6x – 4y + 9 = 0 and x² + y² – 8x – 6y + 23 = 0 is the diameter of the second circle and also find its length.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q1
Let S = x² + y² – 6x – 4y + 9 = 0 and S’ = x² + y² – 8x – 6y + 23 = 0
Then the equation of the common chord of circles is S – S’ = 0 is 2x + 2y – 14 = 0
⇒ x + y – 7 = 0
The Centre of S’ = 0 is (4, 3)
∴ x + y – 7 = 4 + 3 – 7 = 0 and common chord of circles S = 0, S’ = 0 is the diameter of the second circle.
The length of the common chord = 2(the radius of the circle S’ = 0) = 2√2 units.
(or) C₁P = ⊥ distance from C₁(3, 2) to the common chord x + y – 7 = 0.
∴ C₁P = \(\left|\frac{3+2-7}{\sqrt{2}}\right|\) = √2
AC₁ = radius of S = 0
= \(\sqrt{9+4-9}\)
= 2
∴ AP = \(\sqrt{\mathrm{AC}_1^2-\mathrm{C}_1 \mathrm{P}^2}=\sqrt{4-2}=\sqrt{2}\)
∴ Length of the common chord AB = 2(AP) = 2√2.

Question 2.
Find the equation and length of the common chord of the following circles.
(i) x² + y² + 2x + 2y + 1 = 0, x² + y² + 4x + 3y + 2 = 0
Solution:
Let S = x² + y² + 2x + 2y + 1 = 0 and S₁ = x² + y² + 4x + 3y + 2 = 0
Then the equation of the common chord of S = 0, S₁ = 0 is S – S₁ = 0.
⇒ -2x – y – 1 = 0
⇒ 2x + y + 1 = 0
C₁ = Centre of S = 0 is (-1, 1) and r₁ = \(\sqrt{1+1-1}\) = 1
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q2(i)

(ii) x² + y² – 5x – 6y + 4 = 0, x² + y² – 2x – 2 = 0
Solution:
Denote S = x² + y² – 5x – 6y + 4 = 0 and S₁ = x² + y² – 2x – 2 = 0
Equation of common chord of S = 0, S₁ = 0 is S – S₂ = 0.
⇒ -3x – 6y + 6 = 0
⇒ x + 2y – 2 = 0
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q2(ii)

Question 3.
Prove that the radical axis of the circle x² + y² + 2gx + 2fy + c = 0 and x² + y² + 2g’x + 2f’y + c’ = 0 is the diameter of the latter circle (or the former bisector the circumference of the latter) if 2g'(g – g’) + 2f(f – f’) = c – c’.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 and S’ ≡ x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.
Centre of the circle S’ = 0 is C2 = (-g’, -f’)
The equation of the Radical axis of S = 0 and S’ = 0 is S – S’ = 0.
⇒ 2(g – g’)x + 2(f – f’)y + c – c’ = 0 …….(1)
Substituting the centre (-g’, -f’) of S’ = 0, we get
2(g – g’) (-g’) + 2(f – f’) (-f’) + c – c’ = 0
⇒ 2g'(g – g’) + 2f'(f – f’) = c – c’
The radical axis of the circles S = 0, S’ = 0 is the diameter of the circle S’ = 0 if 2g'(g – g’) + 2f(f – f’) = c – c’

Question 4.
Show that the circles x² + y² + 2ax + c = 0 and x² + y² + 2by + c = 0 touch each other if \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c}\)
Solution:
Let S = x² + y² + 2ax + c = 0 and S’ = x² + y² + 2by + c = 0 be the given circles.
Centre of S = 0 is C₁ (-a, 0) and radius of the circle S = 0 is \(\sqrt{a^2-c}\).
The equation of common tangent of circles S = 0, S’ = 0 is S – S’ = 0
⇒ 2ax – 2by = 0
⇒ ax – by = 0
Let L = ax – by = 0
The two circles S = 0 and S’ = 0 touch each other if the perpendicular distance from C₁ (-a, 0) to the common tangent L = 0 is equal to the radius of the circle S = 0.
∴ The perpendicular distance from C₁ (-a, 0)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q4

Question 5.
Show that the circles x² + y² – 2x = 0 and x² + y² + 6x + 6y + 2 = 0 touch each other. Find the coordinates of the point of contact. Is the point of contact external or Internal?
Solution:
Let S = x² + y² – 2x = 0 and S’ = x² + y² + 6x – 6y + 2 = 0 be the given circles.
Centre of S = 0 is C₁ = (1, 0),
and radius of S₁ = 0 is r₁ = √1 = 1.
Centre of S’ = 0 is C₂ = (-3, 3)
and radius of S’ = 0 is r₂ = \(\sqrt{9+9-2}\) = 4.
Distance between centres C₁C₂ = \(\sqrt{(1+3)^2+(0-3)^2}=\sqrt{16+9}\) = 5
and r₁ + r₂ = 1 + 4 = 5.
Since C₁C₂ = r₁ + r₂, the two circles touch externally at a point and the point of contact divides C₁C₂ internally in the ratio 1 : 4.
∴ Point of contact
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q5
∴ The point of contact is \(\left(\frac{1}{5}, \frac{3}{5}\right)\) and the two circles touch each other externally.

Question 6.
Find the equation of the circle which cuts the following circles orthogonally.
(i) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0
Solution:
Let S = x² + y² + 4x – 7 = 0
S’ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
and S” = x² + y² + y = 0 be the equations of the given circles.
Radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 5x – 5y – 5 = 0
⇒ x – y – 1 = 0 ………(1)
The radical axis of S’ = 0, S” = 0 is S’ – S” = 0.
⇒ \(\frac{3}{2} x+\frac{3}{2} y-\frac{9}{2}=0\)
⇒ x + y – 3 = 0 ………(2)
Solving (1) and (2), we get
the Radical centre of circles S = 0, S’ = 0 and S” = 0
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q6(i)
⇒ x = 2 and y = 1
∴ The radical centre of the given circles is (2, 1).
The length of the tangent drawn from (2, 1) to S = 0 is \(\sqrt{4+1+8-7}\) = √6
So by the property that a circle having radical centre as centre and length of the tangent to S = 0 as radius cuts every given circle orthogonally.
So the equation of a required circle with C(2, 1) as a radical centre and √6 as the radius is given by
(x – 2)² + (y + 1)² = (√6)²
⇒ x² + y² – 4x – 2y – 1 = 0

(ii) x² + y² + 2x + 4y + 1 = 0, 2x² + 2y² + 6x + 8y – 3 = 0, x² + y² – 2x + 6y – 3 = 0. (May ’12)
Solution:
Let S = x² + y² + 2x + 4y + 1 = 0
S’ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
and S” = x² + y² – 2x + 6y – 3 = 0 be the equations of the given circles.
Radical axis of centre S = 0, S’ = 0 is S – S’ = 0.
⇒ -x + \(\frac{5}{2}\) = 0
⇒ x = \(\frac{5}{2}\) ……..(1)
Radical axis of centre S’ = 0, S” = 0 is S’ – S” = 0
⇒ 5x – 2y + \(\frac{3}{2}\) = 0
⇒ 10x – 4y + 3 = 0 ………(2)
By solving (1) and (2), we get the Radical centre of the given circles.
Since x = \(\frac{5}{2}\) and from(2),
25 – 4y + 3 = 0
⇒ y = 7
∴ Radical centre = (\(\frac{5}{2}\), 7)
Length of the tangent from (\(\frac{5}{2}\), 7) to S = 0 is
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q6(ii)
Hence the circle with centre (\(\frac{5}{2}\), 7) and \(\sqrt{\frac{357}{4}}\) as radius cuts every circle of the given system orthogonally.
∴ The equation of required circle with centre (\(\frac{5}{2}\), 7) and \(\sqrt{\frac{357}{4}}\) as radius is
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q6(ii).1

(iii) x² + y² + 2x + 17y + 4 = 0, x² + y² + 7x + 6y + 11 = 0, x² + y² – x + 22y + 3 = 0
Solution:
Denote the given circles by
S = x² + y² + 2x + 17y + 4 = 0
S’ = x² + y² + 7x + 6y + 11 = 0
S” = x² + y² – x + 22y + 3 = 0
Radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ -5x + 11y – 7 = 0
⇒ 5x – 11y + 7 = 0 ………(1)
Radical axis of S’ = 0, S” = 0 is S’ – S” = 0
⇒ 8x – 16y + 8 = 0
⇒ x – 2y + 1 = 0 ……..(2)
Solving (1) and (2), we get the coordinates of the Radical centre of circles.
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) III Q6(iii)
∴ \(\frac{x}{-11+14}=\frac{y}{7-5}=\frac{1}{-10+11}\)
⇒ x = 3, y = 2
∴ Radical centre = (3, 2)
Length of the tangent from (3, 2) to the circle S = 0 is \(\sqrt{9+4+6+34+4}=\sqrt{57}\).
Since the circle with centre (3, 2) and radius √57 cuts every circle of the given system orthogonally,
the equation of the required circle is (x – 3)² + (y – 2)² = 57
⇒ x² + y² – 6x – 4y – 44 = 0.

(iv) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0.
Solution:
Denote the given circles by S = x² + y² + 4x + 2y + 1 = 0, S’ = x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0, and S” = x² + y² + 6x – 2y – 3 = 0
Radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ -y + \(\frac{5}{2}\) = 0
⇒ y = \(\frac{5}{2}\) ……..(1)
The radical axis of S’ = 0, S” = 0 is S’ – S” = 0.
⇒ -2x + 5y + \(\frac{3}{2}\) = 0
⇒ -4x + 10y + 3 = 0
⇒ 4x – 10y – 3 = 0 ………(2)
Solving (1) and (2), we get the Radical centre of circles.
∴ From (2), 4x – 25 – 3 = 0
⇒ x = 7
∴ Radical centre = (7, \(\frac{5}{2}\))
Length of the tangent from (7, \(\frac{5}{2}\)) to S = 0 is = \(\sqrt{49+\frac{25}{4}+28+5+1}=\sqrt{\frac{357}{4}}\)
∴ The equation of the required circle with centre (7, \(\frac{5}{2}\)) and as radius which cuts every circle of the system orthogonally is given by
(x – 7)² + \(\left(y-\frac{5}{2}\right)^2=\frac{357}{4}\)
⇒ x² + y² – 14x – 5y + 49 + \(\frac{25}{4}-\frac{357}{4}\) = 0
⇒ x² + y² – 14x – 5y – 34 = 0.

TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f)

January 23, 2024January 21, 2024 by Mahesh

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(f)

Question 1.
If A, B, C are angles in a triangle, then prove that
(i) sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C
Answer:
sin 2A – sin 2K + sin 2C,
Given A + B + C = 180°
= 2 cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) sin\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + 2 sin C cos C
= 2 cos (A – B) sin (A – B) + 2 sin C cos C
= – 2 cos C sin (A – B) + 2 sin C cos C
(∵ A + B + C = 180° ⇒ cos(A + B) cos(180 – C) = – cos C and sin (A + B) = sin C)
= 2 cos C [sin C – sin (A – B)
= 2 cos C [sin(A + B) – sin(A – B)]
= 2 cos C[2 cos A sin B]
= 4 cos A sin B cos C = R. H. S

(ii) cos 2A – cos 2B + cos 2C = 1 – 4 sin A cos B sin C
Answer:
cos 2A – cos2B + cos 2C
= 2 sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) sin\(\left(\frac{2 \mathrm{~B}-2 \mathrm{~A}}{2}\right)\) + cos 2C
= 2 sin (A + B) sin (B – A) + cos 2C
= 2 sin C sin(B – A + 1 – 2 sin² C
= 1 + 2 sin C sin(B – A) – 2 sin² C
= 1 + 2sinC [sin (B – A) – sin C]
(∵ A + B + C = 180° = sin(A + B) sin C)
= 1 + 2 sin C[sin (B – A) – sin(A + B)]
= 1 – 2 sin C [sin (A – B) + sin (A + B)]
= 1 – 2 sin C[2 sin A cos B]
= 1 – 4 sin A cos B sin C = R.H.S

Question 2.
If A, B, C are angles in a triangle, then prove that
(i) sin A + sin B – sin C = 4 sin \(\frac{\mathrm{A}}{2}\) sin \(\frac{\mathrm{B}}{2}\) cos \(\frac{\mathrm{C}}{2}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 1

(ii) cos A + cos B – cos C = – 1 + 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\) (March 2006)
Answer:
LH.S = cos A + cos B – cos C
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 2

Question 3.
If A, B, C are angles in a triangle, then prove that
(i) sin²A + sin²B – sin²C = 2 sin A sin B cos C
Answer:
Given A + B+ C = 180°
We have L.H. S = sin² A + sin²B – sin² C
= sin²A+ sin (B + C) sin (B – C)
= sin² A + sin A sin (B – C)
= sin A [sin A + sin (B – C)]
= sin A[sin (B + C) + sin (B – C)]
= sin A[2 sin B cos C] = 2 sin A sin B cos C = R.H.S

(ii) cos²A + cos² B – cos² C = 1 – 2 sin A sin B cos C
Answer:
L.H.S = cos² A + cos² B – cos² C
= cos² A + 1 – sin² B – cos² C
(∵ A + B + C = 180° = cos (A + B) = – cos C)
= 1 – cos² C + cos² A – sin² B
= 1 -. cos² C + cos (A + B) cos (A – B)
= 1 – cos² C – cos C cos (A – B)
= 1 – cos C [ cos C + cos (A – B)]
= 1 – cos C ( cos (A – B) – cos (A + B)]
= 1 – cos C[2 sin A sin B]
= 1 – 2 sin A sin B cos C = R.H.S

Question 4.
If A + B + C = π, then prove that
(i) cos² \(\frac{A}{2}\) + cos² \(\frac{B}{2}\) + cos² \(\frac{C}{2}\) = 2(1 + sin \(\frac{A}{2}\) + sin \(\frac{B}{2}\) sin \(\frac{C}{2}\) ) (Mar. 2012) (March 2015-A.P&T.S)
Answer:
Given A + B + C = π
We have B + C = π – A and
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 3

(ii) cos² \(\frac{A}{2}\) + cos² \(\frac{B}{2}\) +- cos² \(\frac{C}{2}\) = 2 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\) ) (June 2010)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 4

Question 5.
In triangle ABC, prove that
(i) cos \(\frac{A}{2}\) + cos \(\frac{B}{2}\) + cos \(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\) (Mar 2010, Jun 2007)
Answer:
In ∆ABC, A + B + C = 180°
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 5

(ii) cos \(\frac{A}{2}\) + cos \(\frac{B}{2}\) – cos \(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi+\mathrm{A}}{4}\right)\) cos\(\left(\frac{\pi+\mathrm{B}}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\) (Mar 2005)
Answer:
In ∆ABC, A + B + C = 180°
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 6

(iii) sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) – sin\(\frac{C}{2}\) = – 1 + 4 cos\(\left(\frac{\pi+A}{4}\right)\) cos\(\left(\frac{\pi+B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\)
Answer:
In ∆ABC, A + B + C = 180° ……………………. (1)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 7

Question 6.
If A + B + C = \(\frac{\pi}{2}\), then prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C
Answer:
LH.S = cos 2A + cos 2B cos 2C
= 2 cos \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + 1 – 2 sin² C
= 2 sin C cos (A – B) + 1 – 2 sin 2C
= 1 + 2 sin C [cos (A – B) – sin C]
(∵ A + B = \(\frac{\pi}{2}\) – C ⇒ cos (A + B) = cos (\(\frac{\pi}{2}\) – C) = sin C)
= 1 + 2 sin C[cos (A – B) – sin C]
= 1 + 2 sin C[cos (A – B) – cos(A + B)]
= 1 + 4 sin A sin B sin C = RHS.

Question 7.
If A + B + C = \(\frac{3 \pi}{2}\), then prove that
(i) cos² A + cos²B – cos² C = – 3 cos A cos B sin C
Answer:
L.H.S = cos²A + cos² B – cos² C
= cos² A + 1 – sin² B – cos² C
= (cos² A – sin² B) + (1 – cos²C)
= (cos² A – sin² B) + sin² C
= cos (A + B) cos (A – B) + sin²C
= – sin C cos (A – B) + sin² C
= sin C [sin C – cos (A – B)]
= sin C (- cos (A + B) – cos (A – B)]
= – sin C [cos (A + B) + cos (A – B)]
= – 2 cos A cos B sin C
(Given A + B + C = \(\frac{3 \pi}{2}\)
cos (A + B) = cos (270 – c) = – sin C)

(ii) sin 2A + sin 2B – sin 2C = – 4 sin A sin B cos C
Answer:
A + B + C = \(\frac{3 \pi}{2}\)
LH.S = sin 2A + sin 2B – sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) – sin 2C
= 2 sin (A + B) cos (A – B) – 2 sin C cos C
= – 2 cos C cos (A – B) – 2 sin C cos C
= – 2 cos C (cos (A – B) + sin C]
= – 2 cos C[cos (A – B) – cos(A + B)]
= – 2 cos C [ 2 sin A sin B]
= – 4 sin A sin B cos C R.H.S
(∵ A + B = 270 – C
⇒ cos(A + B) = cos(270 – C) = – sin C)

Question 8.
If A + B + C = 0 then prove that
(i) sin 2A + sin 2B – sin 2C = – 4 sin A sin B sin C
Answer:
Given A + B + C = O
∴ cos(B + C) = cos A and sin (B + C) = – sin A
L.H.S = sin 2A + sin 2B + sin 2C
= 2 sin (A+B) cos (A – B) + 2 sin C cos C
= – 2 sin C cos (A – B) + 2 sin C cosC
= 2 sin C [cos C – cos(A – B)]
= 2 sin C [cos (A + B) – cos(A – B)]
= – 4 sin C sin A sin B
= R.H.S

(ii) sin A + sin B – sin C = – 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)
Answer:
sin A + sin B – sin C
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 8

Question 9.
If A + B + C + D = 2π, then prove that
(i) sin A – sin B + sin C – sin D
= – 4 cos \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{A+C}{2}\right)\) cos \(\left(\frac{A+D}{2}\right)\)
Answer:
sin A – sin B + sin C – sin D
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 9

(ii) cos 2A + cos 2B + cos 2C + cos 2D = 4 cos (A + B) cos (A + C) cos (A +D)
Answer:
A + B + C + D = 360°
⇒ C + D = 360° – (A + B)
L.H.S = 2 cos (A + B) cos (A – B) + 2 cos (C + D) cos (C – D)
= 2 cos (A + B) cos (A – B) + 2 cos [360 – (A + B)] cos (C – D)
= 2 cos (A + B) cos (A – B) + 2 cos (A + B) cos (C – D)
= 2 cos (A + B) [cos (A – B) + cos (C – D)]
= 2 cos (A + B)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 10
= 4 cos (A + B) cos [- 180 + (A + C)] cos [- 180 + (A + D)]
= 4 cos (A + B) cos (A + C) cos (A + D)

Question 10.
If A + B + C = 2S, then prove that
(i) sin (S – A) + sin (S – B) + sin C = 4 cos \(\left(\frac{S-A}{2}\right)\) cos \(\left(\frac{S-B}{2}\right)\) sin \(\frac{C}{2}\) (Jun 2008)
Answer:
Given A + B + C = 2S
LHS = sin(s – A) + sin (s – B) + sin C
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 11

(ii) cos (s – A) + cos (S – B) + cos C = – 1 + 4 cos \(\left(\frac{S-A}{2}\right)\) cos \(\left(\frac{S-B}{2}\right)\) cos \(\frac{C}{2}\)
Answer:
Given A + B + C = 2S
L.H.S
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) 12

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e)

January 22, 2024January 20, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(e) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(e)

Question 1.
Discuss the relative position of the following pair of circles.
(i) x² + y² – 4x – 6y – 12 = 0, x² + y² + 6x + 18y + 26 = 0
Solution:
Let S ≡ x² + y² – 4x – 6y – 12 = 0 ……..(1) and S’ ≡ x² + y² + 6x + 18y + 26 = 0 ……..(2) be the given circles.
The Centre of the circle (1) is C₁ = (2, 3)
Centre of circle (2) is C₂ = (-3, -9)
Radius of circle (1) is \(\sqrt{4+9+12}\) = 5 = r₁
Radius of circle (2) is \(\sqrt{9+81-26}\) = 8 = r₂
Now C₁C₂ = \(\sqrt{(2+3)^2+(3+9)^2}\) = 13
and r₁ + r₂ = 5 + 8 = 13
Since C₁C₂ = r₁ + r₂, the two circles touched each other externally.

(ii) x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0
Solution:
Taking S ≡ x² + y² + 6x + 6y + 14 = 0 ……….(1) and S’ ≡ x² + y² – 2x – 4y – 4 = 0 ………(2)
The Centre of the circle (1) is C₁1 = (-3, -3)
and the Centre of the circle (2) is C₂ = (1, 2)
Radius of circle (1) is r₁ = \(\sqrt{9+9-14}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{1+4+4}\) = 3
Now C₁C₂ = \(\sqrt{(1+3)^2+(2+3)^2}\) = √41
r₁ + r₂ = 5
Since C₁C₂ > r₁ + r₂, each circle lies on the exterior of the other circle.

(iii) (x – 2)² + (y + 1)² = 9, (x + 1)² + (y – 3)² = 4
Solution:
The equation of the given circles are
(x – 2)² + (y + 1)² = 9 ………(1)
(x + 1)² + (y – 3)² = 4 ……….(2)
Centre of circle (1) is C₁ = (2, -1)
The Centre of the circle (2) is C₂ = (-1, 3)
The radius of the circle (1) is r₁ = 3
The radius of the circle (2) is r₂ = 2
C₁C₂ = \(\sqrt{(2+1)^2+(-1-3)^2}\) = 5
and r₁ + r₂ = 3 + 2 = 5
∴ Since C₁C₂ = r₁ + r₂, the two circles touch each other externally.

(iv) x² + y² – 2x + 4y – 4 = 0, x² + y² + 4x – 6y – 3 = 0
Solution:
Given equations of circles are
x² + y² – 2x + 4y – 4 = 0 ……….(1)
x² + y² + 4x – 6y – 3 = 0 ……….(2)
Centre of circle (1) is C₁ = (1, -2)
The Centre of the circle (2) is C₂ = (-2, 3)
Radius of circle (1) is r₁ = \(\sqrt{1+4+4}\) = 3
Radius of circle (2) is r₂ = \(\sqrt{4+9+3}\) = 4
Distance between centres C₁C₂ = \(\sqrt{(1+2)^2+(-2-3)^2}=\sqrt{9+25}=\sqrt{34}\)
r₁ + r₂ = 3 + 4 = 7 and |r₁ – r₂| = |3 – 4| = 1
∴ |r₁ – r₂| < C₁C₂ < r₁ + r₂
∴ The two given circles (1) and (2) intersect each other in two points.

Question 2.
Find the number of possible common tangents that exist for the following pairs of circles.
(i) x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0
Solution:
The given equations of circles are
x² + y² + 6x + 6y + 14 = 0 ………(1)
and x² + y² – 2x – 4y – 4 = 0 ……..(2)
Centre of circle (1) is C₁ = (-3, -3)
The Centre of the circle (2) is C₂ = (1, 2)
Radius of circle (1) is r₁ = \(\sqrt{9+9-14}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{1+4+4}\) = 3
C₁C₂ = \(\sqrt{(-3-1)^2+(-3-2)^2}=\sqrt{16+25}\) = √41
and r₁ + r₂ = 2 + 3 = 5
Since C₁C₂ > r₁ + r₂ the given circles do not intersect each other.
The number of possible common tangents that can be drawn to the above circles is ‘4’.

(ii) x² + y² – 4x – 2y + 1 = 0, x² + y² – 6x – 4y + 4 = 0
Solution:
The given equations of circles are
x² + y² – 4x – 2y + 1 = 0 ………(1)
and x² + y² – 6x – 4y + 4 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (2, 1)
The Centre of the circle (2) is C₂ = (3, 2)
Radius of circle (1) is r₁ = \(\sqrt{4+1-1}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{9+4-4}\) = 3
C₁C₂ = \(\sqrt{(2-3)^2+(1-2)^2}=\sqrt{1+1}=\sqrt{2}\)
and r₁ + r₂ = 2 + 3 = 5
∴ |r₁ – r₂| = |2 – 3| = 1
∴ |r₁ – r₂| < C₁C₂ < r₁ + r₂
∴ The two given circles intersect each other in two points.
The number of possible common tangents that can be drawn to the circles is ‘2’.

(iii) x² + y² – 4x + 2y – 4 = 0, x² + y² + 2x – 6y + 6 = 0
Solution:
The given equations of circles are
x² + y² – 4x + 2y – 4 = 0 ……….(1)
and x² + y² + 2x – 6y + 6 = 0 …………(2)
Centre of circle (1) is C₁ = (2, -1)
The Centre of the circle (2) is C₂ = (-1, 3)
Radius of circle (1) is r₁ = \(\sqrt{4+1+4}\) = 3
Radius of circle (2) is r₂ = \(\sqrt{1+9-6}\) = 2
C₁C₂ = \(\sqrt{(2+1)^2+(-1-3)^2}=\sqrt{9+16}\) = 5
and r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the two circles touch externally and the number of possible common tangents is ‘3’.

(iv) x² + y² = 4, x² + y² – 6x – 8y + 16 = 0
Solution:
The equations of given circles are x² + y² = 4 ………(1) and x² + y² – 6x – 8y + 16 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (0, 0)
The Centre of the circle (2) is C₂ = (3, 4)
The radius of the circle (1) is r₁ = 2
Radius of circle (2) is r₂ = \(\sqrt{9+16-16}\) = 3
C₁C₂ = \(\sqrt{9+16}\) = 5 = r₁ + r₂
Hence the two circles touch externally and the number of possible common tangents is ‘3’.’

(v) x² + y² + 4x – 6y – 3 = 0, x² + y² + 4x – 2y + 4 = 0
Solution:
The equations of circles are
x² + y² + 4x – 6y – 3 = 0 ……….(1)
and x² + y² + 4x – 2y + 4 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (-2, 3)
The Centre of the circle (2) is C₂ = (-2, 1)
Also radius of circle are r1 = \(\sqrt{4+9+3}\) = 4
Radius of circle (2) are r2 = \(\sqrt{4+1-4}\) = 1
Now C₁C₂ = \(\sqrt{(-2+2)^2+(3-1)^2}\) = 4
and |r₁ – r₂| = |4 – 1| = 3
∴ C₁C₂ < |r₁ + r₂|, one circle lies completely inside the other circle.
∴ The number of common tangents that can be drawn to the circles S = 0 and S’ = 0 is zero.

Question 3.
Find the internal centre of similitude of the circles x² + y² + 6x – 2y + 1 = 0 and x² + y² – 2x – 6y + 9 = 0.
Solution:
Equations of given circles are
x² + y² + 6x – 2y + 1 = 0 ……….(1)
x² + y² – 2x – 6y + 9 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (-3, 1)
The Centre of the circle (2) is C₂ = (1, 3)
Also radius of circle (1) is r₁ = \(\sqrt{9+1-1}\) = 3
radius of circle (2) is r₂ = \(\sqrt{1+9-9}\) = 1
Now C₁C₂ = \(\sqrt{(-3-1)^2+(1-3)^2}=\sqrt{16+4}\) = √20
and r₁ + r₂ = 3 + 1 = 4
Since C₁C₂ > r₁ + r₂, the two circles do not touch or do not intersect each other but each circle lies in the exterior of the other.
∴ Number of common tangents = 4
Both internal and external centres of similitude exist.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) I Q3
Let A be the internal centre of similitude and r₁ : r₂ = 3 : 1.
∴ A divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio 3 : 1 internally.

∴ The internal centre of similitude is (0, \(\frac{5}{2}\))

Question 4.
Find the external centre of similitude for the circles x² + y² – 2x – 6y + 9 = 0, x² + y² = 4.
Solution:
The equations of given circles are x² + y² – 2x – 6y + 9 = 0 ……..(1) and x² + y² = 4 ……..(2)
Centre of circles are C₁ = (1, 3) and C₂ = (0, 0)
Radius of circles are r₁ = \(\sqrt{1+9-9}\) = 1 and r₂ = √4 = 2
Now C₁C₂ = \(\sqrt{1+9}=\sqrt{10}\) and r₁ + r₂ = 1 + 2 = 3
Since C₁C₂ > r₁ + r₂, each circle lies in the exterior of the other circle, and the number of common tangents = 4
∴ Both internal and external centres of similitudes do exist in this case.
C₁ = (1, 3) = (x₁, y₁) and C₂ = (0, 0) = (x₂, y₂)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) I Q4
∴ The external centre of the similitude of the circle is (2, 6).

II.

Question 1.
(i) Show that the circles x² + y² – 6x – 2y + 1 = 0, x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. (Mar. ’11, ’10, ’09)
Solution:
Let S = x² + y² – 6x – 2y + 1 = 0 and S’ = -x² + y² + 2x – 8y + 13 = 0 be the given circles.
The centre of circles are C₁ = (3, 1) and C₂ = (-1, 4)
Radius of circles are r₁ = \(\sqrt{9+1-1}\) = 3 and r₂ = \(\sqrt{1+16-13}\) = 2
Distance between centres C₁C₂ = \(\sqrt{(3+1)^2+(1-4)^2}=\sqrt{16+9}\) = 5 and r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the two circles touch externally at a point.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) II Q1(i)
Let P be the point of contact of circles such that r₁ : r₂ = 3 : 2.
Since P divides C₁, C₂ internally in the ratio 3 : 2,
the coordinates of the point of contact

The equation of common tangent is S – S’ = 0
⇒ x² + y² – 6x – 2y + 1 – x² – y² – 2x + 8y + 13 = 0
⇒ -8x + 6y – 12 = 0
⇒ 4x – 3y + 6 = 0
∴ The equation of the common tangent at the point of contact is 4x – 3y + 6 = 0.

(ii) Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact.
Solution:
Given equations of circles are S = x² + y² – 6x – 9y + 13 = 0 and S’ = x² + y² – 2x – 16y = 0
Centre of circles are C₁ = (3, \(\frac{9}{2}\)) and C₂ = (1, 8)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) II Q1(ii)
The point P divides C₁C₂ externally in the ratio of their radius \(\frac{\sqrt{65}}{2}\) : √65 = 1 : 2

The equation of the common tangent at P(5, 1) to the circles S = 0 and S’ = 0 is S – S’ = 0.
⇒ x² + y² – 6x – 9y + 13 – x² – y² + 2x + 16y = 0
⇒ -4x + 7y – 13 = 0
⇒ 4x – 7y + 13 = 0
∴ The equation of the required common tangent is 4x – 7y + 13 = 0.

Question 2.
Find the equation of the circle which touches the circle x² + y² – 2x – 4y – 20 = 0 externally at (5, 5) with radius ‘5’.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) II Q2
Let C₁ = (h, k) be the centre and r1 be the radius of the required circle.
Given r₁ = 5
Equation of the given circle is x² + y² – 2x – 4y – 20 = 0 ……….(1)
Centre of the circle C₂ = (1, 2) and radius r₂ = \(\sqrt{1+4+20}\) = 5
∴ r₁ : r₂ = 5 : 5 = 1 : 1
Point P(5, 5) divides C₁C₂ in the ratio 1 : 1 internally.
∴ \(\left(\frac{\mathrm{h}+1}{2}, \frac{\mathrm{k}+2}{2}\right)\) = (5, 5)
⇒ \(\frac{\mathrm{h}+1}{2}\) = 5 and \(\frac{\mathrm{k}+2}{2}\) = 5
⇒ h = 9 and k = 18
∴ C1 = (h, k) = (9, 8)
∴ The equation of a required circle with centre (9, 8) and radius ‘5’ is (x – 9)² + (y – 8)² = 25
⇒ x² + y² – 18x – 16y + 120 = 0

Question 3.
Find the direct common tangents of the circles x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0. (New Model Paper)
Solution:
Let S = x² + y² + 22x – 4y – 100 = 0 ……….(1) and S’ = x² + y² – 22x + 4y + 100 = 0 …….(2) be the given circles.
Then centres of the circles are C₁ = (-11, +2) and C₂ = (11, -2)
The radius of the circles are
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) II Q3
and r₁ + r₂ = 15 + 5 = 20
Since C₁C₂ > r₁ + r₂, the two circles are such that each lies on the exterior of the other.
Hence both internal and external centre of similitude exists.

Now r₁ : r₂ = 15 : 5 = 3 : 1
Point P divides C₁, C₂ externally in the ratio of radii 3 : 1.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) II Q3.2
The equation of direct common tangent passing through (22, -4) having slope ‘m’ is y + 4 = m(x – 22)
⇒ mx – y – 4 – 22m = 0 …….(1)
Since the line is tangent to S’ = 0.
Perpendicular distance from C₂ = (11, -2) to the line (1) = radius of the circle S’ = 0
∴ \(\left|\frac{m(11)+2-4-22 m}{\sqrt{m^2+1}}\right|\) = 5
⇒ \(\left|\frac{-(11 m+2)}{\sqrt{m^2+1}}\right|\) = 5
⇒ (11m + 2)² = 25(m² + 1)
⇒ 121m² + 44m + 4 = 25m² + 25
⇒ 96m² + 44m – 21 = 0
⇒ 96m² + 72m – 28 m – 21 = 0
⇒ 24m(4m + 3) – 7(4m + 3) = 0
⇒ (24m – 7) (4m + 3) = 0
⇒ m = \(\frac{-3}{4}\) or m = \(\frac{7}{24}\)
∴ Equations of direct common tangents from (1) are y + 4 = \(\frac{-3}{4}\)(x – 22)
⇒ 4y + 16 = -3x + 66
⇒ 3x + 4y – 50 = 0
and y + 4 = \(\frac{7}{24}\)(x – 22)
⇒ 24y + 96 = 7x – 154
⇒ 7x – 24y – 250 = 0
∴ The equations of direct common tangents are given by 3x + 4y – 50 = 0 and 7x – 24y – 250 = 0.

Question 4.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x – 6y + 4 = 0.
Solution:
Let S = x² + y2 – 4x – 10y + 28 = 0 ………(1)
S’ = x² + y2 + 4x – 6y + 4 = 0 ……….(2)
be the given circles.
Centres of the circles are C₁ = (2, 5) and C₂ = (-2, 3)
Also, the radius of circles are r₁ = \(\sqrt{4+25-28}\) = 1 and r₂ = \(\sqrt{4+9-4}\) = 3
Also C₁C₂ = \(\sqrt{(2+2)^2+(5-3)^2}\) = √20 = 2√5 and r₁ + r₂ = 4
Since C₁C₂ > r₁ + r₂, we have each circle lying in the exterior of other circles.
Hence we get 2 direct common tangents and 2 transverse common tangents that can be drawn.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) II Q4
Point P divides C₁C₂ internally in the ratio r₁ : r₂ = 1 : 3.
Let P be the internal centre of similitude.

Let the equation of transverse common tangent be y – \(\frac{9}{2}\) = m(x – 1) ……(1)
⇒ 2y – 9 = 2mx – 2m
⇒ 2mx – 2y + (9 – 2m) = 0 ……….(2)
Since line (2) is a tangent to the circle S = 0, the perpendicular distance from C₁ (2, 5) to line (2) is equal to the radius of the circle S = 0.
∴ \(\left|\frac{2 m(2)-2(5)+9-2 m}{\sqrt{4 m^2+4}}\right|\) = 1
⇒ |2m – 1| = \(2 \sqrt{m^2+1}\)
⇒ 4m² – 4m + 1 = 4(m² + 1)
⇒ 4m² – 4m + 1 – 4m² – 4 = 0
⇒ -4m – 3 = 0
⇒ m = \(\frac{-3}{4}\)
∴ Equation of tangent is y – \(\frac{9}{2}\) = \(\frac{-3}{4}\)(x – 1)
⇒ \(\frac{2 y-9}{2}=-\frac{3}{4}(x-1)\)
⇒ 2(2y – 9) = -3(x – 1)
⇒ 4y – 18 = -3x + 3
⇒ 3x + 4y – 21 = 0
Since the m² term is canceled, the slope of one of the transverse common tangents is not defined.
One transverse common tangent is passing through P(1, \(\frac{9}{2}\)) and parallel to y-axis.
∴ The equation of other transverse common tangents is x = 1.
∴ The equations of transverse common tangents are x = 1 and 3x + 4y – 21 = 0.

Question 5.
Find the pair of tangents from (4, 10) to the circle x² + y² = 25.
Solution:
Let P(x₁, y₁) be the given point.
The equation to the pair of tangents drawn from P(4, 10) to S = 0 is \(\mathrm{S}_1^2=\mathrm{SS}_{11}\).
Given S = x² + y² – 25 = 0
(xx₁ + yy₁ – 25)² = (x² + y² – 25) (\(x_1^2+y_1^2\) – 25)
⇒ (4x + 10y – 25)² = (x² + y² – 25) (16 + 100 – 25)
⇒ (4x + 10y – 25)² = (x² + y² – 25) (91)
⇒ 16x² + 100y² + 625 + 80xy – 500y – 200x = 91x² + 91y² – 2275
⇒ 75x² – 9y² – 80xy + 200x + 500y – 2900 = 0

Question 6.
Find the pair of tangents drawn from (0, 0) to x² + y² + 10x + 10y + 40 = 0.
Solution:
Let P(x₁, y₁) be the given point.
The equation to the pair of tangents drawn from P(0, 0) to S = 0 is \(\mathrm{S}_1^2=\mathrm{SS}_{11}\).
Given S = x² + y² + 10x + 10y + 40 = 0
∴ The equation to the pair of tangents from (0, 0) to S = 0 is [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]² = (x² + y² + 2gx + 2fy + c) (\(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c)
⇒ (5x + 5y + 40)² = (x² + y² + 10x + 10y + 40) (40)
⇒ 25x² + 25y² + 1600 + 50xy + 400xy + 400x = 40(x² + y² + 10x + 10y + 40)
⇒ 15x² + 15y² – 50xy = 0
⇒ 3x² + 3y² – 10xy = 0

III.

Question 1.
Find the equation of the circle which touches x² + y² – 4x + 6y – 12 = 0 at (-1, 1) internally with a radius of ‘2’.
Solution:
The given circle is x² + y² – 4x + 6y – 12 = 0
The centre of the circle is (2, -3) and radius = \(\sqrt{4+9+12}\) = 5
Let the centre of the required circle be (h, k), and given that 2 is the radius with the point of contact of circles internally as (-1, 1).
Suppose (x₁, y₁) = (2, -3), (x₂, y₂) = (h, k), r₁ = 5, r₂ = 2
point of contact (x, y) = (-1, 1)
using the formula for the external division since two circles touch internally.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) III Q1
⇒ (5x – 1)² + (5y – 3)² = 100
⇒ 25x² + 25y² – 10x – 30y – 90 = 0
⇒ 5x² + 5y² – 2x – 6y – 18 = 0

Question 2.
Find all common tangents of the following pairs of circles.
(i) x² + y² = 9 and x² + y² – 16x + 2y + 49 = 0
Solution:
Let S = x² + y² – 9 = 0 and S’ = x² + y² – 16x + 2y + 49 = 0 be the given circles.
Centre of the circle S = 0 is C₁ (0, 0) and radius = 3
Centre of the circle S’ = 0 is C₂ (8, -1) and radius r2 = \(\sqrt{64+1-49}\) = 4
r₁ + r₂ = 3 + 4 = 7 and C₁C₂ = \(\sqrt{64+1}=\sqrt{65}\) > 7
Since C₁C₂ > r₁ + r₂ we get each circle lies completely in the exterior of the other.
∴ Two direct and two transverse common tangents can be drawn to S = 0 and S’ = 0.
r₁ : r₂ = 3 : 4
Let A be the internal centre of similitude and A divides C₁C₂ in the ratio 3 : 4 internally
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) III Q2(i)
⇒ 64x² + y² + 441 – 16xy + 42y – 336x = 16(x² + y² – 9)
⇒ 48x² – I6xy – 15y² + 42y – 336x + 585 = 0
⇒ 48x² – 36xy + 20xy – 15y² + 42y – 336x + 585 = 0
⇒ 12x(4x – 3y) + 5y(4x – 3y) + 42y – 336x + 585 = 0
⇒ (12x + 5y)(4x – 3y) – 336x + 42y + 585 = 0
Let 48x² – 16xy – 15y² + 42y – 336x + 585 = (12x + 5y + l) (4x – 3y + m)
= 48x² – 36xy + 12mx + 20xy – 15y² + 5ym + 4lx + 3ly + lm
= 48x² – 16xy – 15y² + (4l + 12m)x + (-3l + 5m)y + lm
Equating coefficients of x, y, and the constant term
4l + 12m = -336
⇒ l + 3m = -84 ………(1)
-3l + 5m = 42
⇒ 3l – 5m = -42 ……..(2)
and lm = 585 …….(3)
From (1), 5l + 15m = -420
From (2), 9l – 15m = -126
∴ 14l = -546
⇒ l = -39
From (1), -39 + 3m = -84
⇒ 3m = -45
⇒ m = -15
∴ 48x² – 16xy – 15y² + 42y – 336x + 585 = (12x + 5y – 39) (4x – 3y – 15)
∴ The transverse common tangents are 12x + 5y – 39 = 0 and 4x – 3y – 15 = 0
Let B be the external centre of the similitude of circles.
∴ B divides C1C2 in the ratio 3 : 4 externally
∴ B = \(\left(\frac{3(8)-4(0)}{3-4}, \frac{3(-1)-4(0)}{3-4}\right)\) = (-24, 3)
The equation is the pair of direct common tangents to the circle S = 0 from (-24, 3) is \(S_1^2=S S_{11}\)
⇒ [x(-24) + y(3) – 9]² = (x² + y² – 9) (576 + 9 – 9)
⇒ (-24x + 3y – 9)² = (576) (x² + y2 – 9)
⇒ 9(-8x + y – 3)² = 9 × 64 (x² + y2 – 9)
⇒ (-8x + y – 3)² = 64(x² + y2 – 9)
⇒ 64x² + y² + 9 – 16xy – 6y + 48x = 64x² + 64y² – 576
⇒ 63y² + 16xy – 48x + 6y – 585 = 0
⇒ y(63y + 16x) – 48x + 6y – 585 = 0
∴ 63y² + 16xy – 48x + 6y – 585 = (y + l) (63y + 16x + m)
Equating coefficients of x, y, and constants
16l = 48 ……..(4)
63l + m = 6 ………(5)
lm = -585 ……….(6)
∴ l = -3 and from (6), m = 195
∴ 63y² + 16xy – 48x + 6y – 585 = (y – 3) (63y + 16x + 195)
∴ The equations of direct common tangents to the circles S = 0, S’ = 0 are y – 3 = 0, 63y + 16x + 195 = 0.
Hence equations of all common tangents to the circles S = 0 and S’ = 0 are 4x – 3y – 15 = 0, 12x + 5y – 39 = 0 and y – 3 = 0, 16x + 63y + 195 = 0.

(ii) x² + y² + 4x + 2y – 4 = 0 and x² + y² – 4x – 2y + 4 = 0
Solution:
Let S = x² + y² + 4x + 2y – 4 = 0 and S’ = x² + y² – 4x – 2y + 4 = 0
Centre of S = 0 is C₁ (-2, 1) and the radius is r₁ = \(\sqrt{4+1+4}\) = 3
Centre of S’ = 0 is C₂ (2, 1) and the radius r₂ = \(\sqrt{4+1-4}\) = 1
Also C₁C₂ = \(\sqrt{(2+2)^2+(1+1)^2}=\sqrt{16+4}\) = √20 = 2√5 and r₁ + r₂ = 3 + 1 = 4
Since C₁C₂ > r₁ + r₂, each circle lies in the exterior of the other circle.
∴ Two direct and two transverse common tangents can be drawn to the circles S = 0 and S’ = 0.
Let A, B be the internal and external centres of similitudes of circles S = 0 and S’ = 0
A divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ = 3 : 1 internally
∴ A = \(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)\)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) III Q2(ii)

⇒ -(2x + y – 1)² = (x² + y² + 4x + 2y – 4)
⇒ (2x + y – 1)² = (x² + y² + 4x + 2y – 4)
⇒ 4x² + y² + 1 + 4xy – 2y – 4x = x² + y² + 4x + 2y – 4
⇒ 3x² + 4xy – 8x – 4y + 5 = 0
⇒ x(3x + 4y) – 8x – 4y + 5 = 0
⇒ 3x² + 4xy – 8x – 4y + 5 = (x + l) (3x + 4y + m)
Comparing the coefficients of x, y, and constants
3l + m = -8 ………(1)
4l = -4 ……….(2)
lm = 5 ……….(3)
∴ From (2), l = -1 and From (3), m = -5
∴ 3x² + 4xy – 8x – 4y + 5 = (x – 1) (3x + 4y – 5)
The equations of transverse common tangents are x – 1 = 0, 3x + 4y – 5 = 0.
The equation of pair of direct common tangents to the circle S = 0 is \(\mathrm{s}_1^2=\mathrm{S} \mathrm{S}_{11}\).
⇒ [x(4) + y(2) + 2(x + 4) + 1(y + 2) – 4]² = (x² + y² + 4x + – 2y – 4) (16 + 4 + 16 + 4 – 4)
⇒ (6x + 3y + 6)² = (x² + y² + 4x + 2y – 4)(36)
⇒ 9(2x + y + 2)² = 36(x² + y² + 4x + 2y – 4)
⇒ (2x + y + 2)² = 4(x² + y² + 4x + 2y – 4)
⇒ 4x² + y² + 4 + 4xy + 4y + 4x = 4x² + 4y² + 16x + 8y – 16
⇒ 3y² – 4xy + 8x + 4y – 20 = 0
⇒ y(3y – 4x) + 8x + 4y – 20 = 0
∴ 3y² – 4xy + 8x + 4y – 20 = (y + l) (3y – 4x + m)
Comparing coefficients of x, y, and constants we get
-4l = 8 ………(4)
3l + m = 4 ………(5)
lm = -20 ………(6)
From (4), l = -2 and from (6), m = 10
∴ 3y² – 4xy + 8x + 4y – 20 = (y – 2) (3y – 4x + 10)
Hence the equations of direct common tangents are y – 2 = 0, 3y – 4x + 10 = 0.
∴ The equations of all common tangents to the circles S = 0, S’ = 0 are x – 1 = 0, 3x + 4y – 5 = 0 and y – 2 = 0, 4x – 3y – 10 = 0

Question 3.
Find the pair of tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0.
Solution:
Let S ≡ x² + y² – 6x + 4y – 2 = 0 be the given circle.
The equation of pair of tangents drawn from (3, 2) to the circle S = 0 is \(S_1^2=S . S_{11}\)
⇒ [x(3) + y(2) – 3(x + 3) + 2(y + 2) – 2]² = (x² + y² – 6x + 4y – 2) (3² + 2² – 18 + 8 – 2)
⇒ (4y – 7)² = 1 . (x² + y² – 6x + 4y – 2)
⇒ 16y² – 56y + 49 = x² + y² – 6x + 4y – 2
⇒ x² – 15y² – 6x + 60y – 51 = 0

Question 4.
Find the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 and also find the angle between them.
Solution:
Denote S ≡ x² + y² – 2x + 4y – 11 = 0
The equation of pair of tangents from (1, 3) to the circle S = 0 is by the formula \(S_1^2=S . S_{11}\)
⇒ [x(1) + y(3) – (x + 1) + 2(y + 3) – 11]² = (x² + y² – 2x + 4y – 11) (1² + 3² – 2 + 12 – 11)
⇒ (5y – 6)² = (x² + y² – 2x + 4y – 11) (9)
⇒ 25y² – 60y + 36 = 9x² + 9y² – 18x + 36y – 99
⇒ 9x² – 16y² – 18x + 96y – 135 = 0
If θ is the angle between the above pair of tangents to S = 0, then
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) III Q4
(or) θ = \(\cos ^{-1}\left(\frac{7}{25}\right)\) is the angle between pair of tangents to S = 0.

Question 5.
Find the pair of tangents from the origin to the circle x² + y² + 2gx + 2fy + c = 0 and hence deduce a condition for these tangents to the perpendicular.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 be the given circle.
Then the equation of the pair of tangents drawn from (0, 0) to S = 0 is by the formula \(S_1^2=S . S_{11}\)
⇒ [x(0) + y(0) + g(x + 0) + f(y + 0) + c]² = (x² + y² + 2gx + 2fy + c) (c)
⇒ (gx + fy + c)² = cx² + cy² + 2gcx + 2fcy + c²
⇒ (g²x² + f²y² + c² + 2fgxy + 2fcy + 2cgx) = cx² + cy² + 2gcx + 2fcy + c²
⇒ x²(g² – c) + y²(f² – c) + 2fgxy = 0
Given that pair of tangents represented by this equation are perpendicular we have
coefficient of x² + coefficient of y² = 0
⇒ g² – c + f² – c = 0
⇒ g² + f² = 2c

Question 6.
From a point on the circle x² + y² + 2gx + 2fy + c = 0 two tangents are drawn to the circle x² + y² + 2gx + 2fy + c sin²α + (g² + f²) cos²α = 0 (0 < α < π/2). Prove that the angle between them is 2α.
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0 and S’ = x² + y² + 2gx + 2fy + c sin²α + (g² + f²) cos²α = 0 be the given circles.
Let P(x₁, y₁) be any point on S = 0 then
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e) III Q6
Let θ be the angle between the tangents drawn from P(x₁, y₁) to S’ = 0 then

= \(\frac{\left(g^2+f^2-c\right)\left(\cos ^2 \alpha-\sin ^2 \alpha\right)}{\left(g^2+f^2-c\right)\left(\cos ^2 \alpha+\sin ^2 \alpha\right)}\)
= cos 2α
∴ cos θ = cos 2α ⇒ θ = 2α
∴ The angle between the tangents drawn from P(x1, y1) to the circle S’ = 0 is 2α.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d)

January 22, 2024January 20, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(d)

Question 1.
Find the condition that the tangents are drawn from (0, 0) to S ≡ x² + y² + 2gx + 2fy + c = 0 be perpendicular to each other.
Solution:
If the angle between the tangents drawn from P(x₁, y₁) to S = 0 is θ then
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) I Q1

Question 2.
Find the chord of contact of (0, 5) with respect to the circle x² + y² – 5x + 4y – 2 = 0.
Solution:
Comparing with x² + y² + 2gx + 2fy + c = 0,
we get g = \(-\frac{5}{2}\), f = 2, c = -2
∴ Equation of chord of contact of (x1, y1) w.r.t S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
∴ The equation of chord of contact of (0, 5) w.r.t. x² + y² – 5x + 4y – 2 = 0 is x(0) + y(5) + \(\left(\frac{-5}{2}\right)\) (x + 0) + 2(y + 5) – 2 = 0
⇒ 5y – \(\frac{5 x}{2}\) + 2y + 10 – 2 = 0
⇒ 5y – \(\frac{5 x}{2}\) + 2y + 8 = 0
⇒ 10y – 5x + 4y + 16 = 0
⇒ -5x + 14y + 16 = 0
⇒ 5x – 14y – 16 = 0

Question 3.
Find the chord of contact of (1, 1) to the circle x² + y² = 9.
Solution:
Equation of chord of contact of (x₁, y₁) w.r.t x² + y² = a² is xx₁ + yy₁ – a² = 0.
∴ The equation of chord of contact of (1, 1) w.r.t x² + y² = 9 is x(1) + y(1) – 9 = 0
⇒ x + y – 9 = 0

Question 4.
Find the polar of (1, 2) with respect to x² + y² = 7.
Solution:
Equation of polar of (x₁, y₁) with respect to x² + y² = a² is xx₁ + yy₁ – 9 = 0.
∴ The equation of polar of (1, 2) with respect to x² + y² = 7 is x(1) + y(2) – 7 = 0
⇒ x + 2y – 7 = 0

Question 5.
Find the polar of (3, -1) with respect to the circle 2x² + 2y² = 11.
Solution:
Given equation of circle is x² + y² = \(\frac{11}{2}\)
∴ Equation of polar of (x₁, y₁) w.r.t x² + y² = a² is xx₁ + yy₁ – a² = 0.
⇒ x(3) + y(-1) – \(\frac{11}{2}\) = 0
⇒ 6x – 2y – 11 = 0

Question 6.
Find the polar of (1, -2) with respect to x² + y² – 10x – 10y + 25 = 0.
Solution:
Polar of (x₁, y₁) w.r.t x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
⇒ -4x – 7y + 30 = 0
⇒ 4x + 7y – 30 = 0

Question 7.
Find the pole of ax + by + c = 0 (c ≠ 0) w.r.t x² + y² = r²
Solution:
Let (x₁, y₁) be the pole of ax + by + c = 0 ……(1) w.r.t. x² + y² = r²; then the equation of polar is xx₁ + yy₁ – r² = 0 ……….(2)
∴ From (1) and (2)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) I Q7

Question 8.
Find the pole of 3x + 4y – 45 = 0 w.r.t x² + y² – 6x – 8y + 5 = 0
Solution:
Let (x₁, y₁) be the pole of 3x + 4y – 45 = 0 ………(1)
Then the equation of polar of (x₁, y₁) w.r.t the circle x² + y² – 6x – 8y + 5 = 0 is xx₁ + yy₁ – 3(x + x1) – 4(y + y1) + 5 = 0
⇒ x(x₁ – 3) + y(y₁ – 4) – (3x₁ + 4y₁ – 5) = 0 ……….(2)
∴ From (1) and (2)
\(\frac{x_1-3}{3}=\frac{y_1-4}{4}=\frac{-\left(3 x_1+4 y_1-5\right)}{-45}\)
⇒ \(\frac{x_1-3}{3}=\frac{y_1-4}{4}\)
⇒ 4x₁ – 12 = 3y₁ – 12
⇒ 4x₁ – 3y₁ = 0 ……….(3)
\(\frac{y_1-4}{4}=\frac{3 x_1+4 y_1-5}{45}\)
⇒ 45y₁ – 180 = 12x₁ + 16y₁ – 20
⇒ 12x₁ – 29y₁ + 160 = 0 ………(4)
Solving (3) and (4) we get
12x₁ – 9y₁ = 0
12x₁ – 29y₁ = -160
∴ 20y₁ = 160
⇒ y₁ = 8
and from (3)
4x₁ = 24
⇒ x₁ = 6
∴ Pole of 3x + 4y – 45 = 0 w.r.t x² + y² – 6x – 8y + 5 = 0 is (6, 8).

Question 9.
Find the pole of x – 2y + 22 = 0 w.r.t x² + y² – 5x + 8y + 6 = 0.
Solution:
Let (x₁, y₁) be the pole of the line x – 2y + 22 = 0 ………(1)
Then the equation of polar of (x₁, y₁) w.r.t circle x² + y² – 5x + 8y + 6 = 0 ………(2) is
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) I Q9
⇒ 22y₁ + 88 = 5x₁ – 8y₁ – 12
⇒ 5x₁ – 30y₁ – 100 = 0
⇒ x₁ – 6y₁ – 20 = 0 ………(5)
∴ 2x₁ – 12y₁ – 40 = 0 and 2x₁ + y₁ – 1 = 0
solving -13y₁ – 39 = 0 ⇒ y₁ = -3
and from (4), 2x₁ – 3 – 1 = 0 ⇒ x₁ = 2
pole of x – 2y + 22 = 0 w.r.t. x² + y² – 5x + 8y + 6 = 0 is (2, -3).

Question 10.
Show that the points (-6, 1) and (2, 3) are conjugate points w.r.t the circle x² + y² – 2x + 2y + 1 = 0.
Solution:
Let P(-6, 1) and Q(2, 3) be the given points.
Two points P(x₁, y₁) and Q(x₂, y₂) one said to be conjugate
⇔ S₁₂ = 0
⇔ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
∴ S₁₂ = (-6)(2) + (1)(3) – 1(-6 + 2) + 1(1 + 3) + 1
= -12 + 3 + 4 + 4 + 1
= 0
∴ Hence the points P and Q are conjugate w.r.t. the given circle.

Question 11.
Show that the points (4, 2) and (3, -5) are conjugate points w.r.t the circle x² + y² – 3x – 5y + 1 = 0.
Solution:
Let P(x₁, y₁) = (4, 2) and Q(x₂, y₂) = (3, -5)
Now S₁₂ = x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
= (4)(3) + (2)(-5) – \(\frac{3}{2}\)(4 + 3) – \(\frac{5}{2}\)(2 – 5) + 1
= 12 – 10 – \(\frac{21}{2}+\frac{15}{2}\) + 1 = 0
= 24 – 20 – 21 + 15 + 2
= 0
Hence the points P and Q are conjugate w.r.t. the given circle.

Question 12.
Find the value of k if kx + 3y – 1 = 0, 2x + y + 5 = 0 are conjugate lines w.r.t the x² + y² – 2x – 4y – 4 = 0.
Solution:
Two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 are said to be conjugate w.r.t. x² + y² + 2gx + 2fy + c = 0.
If r²(l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
Here g = -1, f = -2,
r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{1+4+4}\) = 3
l₁ = k, m₁ = 3, n₁ = -1, l₂ = 2, m₂2 = 1, n₂ = 5
∴ r²(l₁l₂ + m₁m₂) = 9(2k + 3)
and (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = (-k – 6 + 1) (-2 – 2 – 5) = (-k – 5) (-9)
∴ 9(2k + 3) = 9(k + 5)
⇒ 2k + 3 = k + 5
⇒ k – 2 = 0
⇒ k = 2

Question 13.
Find the value of k if x + y – 5 = 0, 2x + ky – 8 = 0 are conjugate w.r.t the circle x² + y² – 2x – 2y – 1 = 0.
Solution:
Comparing the given equation of circle with x² + y² + 2gx + 2fy + c = 0,
we have g = -1, f = -1, c = -1 and
radius = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{1+1+1}=\sqrt{3}\)
Condition for two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 to be conjugate w.r.t. S = 0
r² (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
Given that the equations of lines are x + y – 5 = 0 and 2x + ky – 8 = 0
l₁ = 1, m₁ = 1, n₁ = -5, l₂ = 2, m₂ = k, n₂ = -8
∴ r²(l₁l₂ + m₁m₂) = 3(2 + k) and (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = (-1 – 1 + 5) (-2 – k + 8)
∴ 3(2 + k) = 3(6 – k) = 18 – 3k
⇒ 6 + 3k = 18 – 3k
⇒ 6k = 12
⇒ k = 2

Question 14.
Find the value of k if the points (1, 3) and (2, k) are conjugate w.r.t the circle x² + y² = 35.
Solution:
The condition for two points P(x₁, y₁) and Q(x₂, y₂) to be conjugate w.r.t x² + y² = a² is x₁x₂ + y₁y₂ – a² = 0
Given P(x₁, y₁) = (1, 3) and Q(x₂, y₂) = (2, k) and a² = 35.
∴ x₁x₂ + y₁y₂ – a² = 2 + 3k – 35
⇒ 3k – 33 = 0
⇒ k = 11

Question 15.
Find the value of k if the points (4, 2), (k, -3) are conjugate points w.r.t the circle x² + y² – 5x + 8y + 6 = 0.
Solution:
Two points P(x₁, y₁) and Q(x₂, y₂) are said to be conjugate w.r.t the circle S = 0 if S₁₂ = 0.
i.e., x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
Given P(x₁, y₁) = (4, 2) and Q(x₂, y₂) = (k, -3)
Then S₁₂ = 4k – 6 – \(\frac{5}{2}\)(4 + k) + 4(2 – 3) + 6 = 0
⇒ 4k – 6 – \(\frac{5}{2}\)(4 + k) – 4 + 6 = 0
⇒ 4k – \(\frac{5}{2}\)(4 + k) – 4 = 0
⇒ 4k – 10 – \(\frac{5k}{2}\) – 4 = 0
⇒ 8k – 20 – 5k – 8 = 0
⇒ 3k – 28 = 0
⇒ k = \(\frac{28}{3}\)

II.

Question 1.
Find the angle between the tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0. (Mar. ’12)
Solution:
If θ is the acute angle between the tangents drawn from P(3, 2) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\) where r is the radius of the circle.
Where S₁₁ = \(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c
= 9 + 4 – 6(3) + 4(2) – 2
= 1
and r = radius of the given circle = \(\sqrt{9+4+2}=\sqrt{15}\)
∴ cos θ = \(\left|\frac{1-15}{1+15}\right|=\left|\frac{-14}{16}\right|=\frac{7}{8}\)
∴ θ = \({Cos}^{-1} \cdot\left(\frac{7}{8}\right)\)
∴ The angle between tangents drawn from (3, 2) to the given circle is \({Cos}^{-1} \cdot\left(\frac{7}{8}\right)\).

Question 2.
Find the angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0.
Solution:
If θ is the acute angle between the tangents drawn from P(3, 2) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\) where r is the radius of the circle.
S₁₁ = \(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c
= 1 + 9 – 2 + 12 – 11
= 9
and r = radius of the given circle (r) = \(\sqrt{1+4+11}\) = 4
∴ cos θ = \(\left|\frac{9-16}{9+16}\right|=\left|\frac{7}{25}\right|\)
∴ θ = \({Cos}^{-1}\left(\frac{7}{25}\right)\)
∴ The angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 is \({Cos}^{-1}\left(\frac{7}{25}\right)\)

Question 3.
Find the angle between the pair of tangents drawn from (0, 0) to the circle x² + y² – 14x + 2y + 25 = 0.
Solution:
If θ is the angle between the tangents drawn from O(0, 0) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\)
where S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2\) + 2gx₁ + 2fy₁ + c
= 0 + 0 + 0 + 0 + 25
= 25
and r = \(\sqrt{49+1-25}\) = 5
∴ cos θ = \(\left|\frac{25-25}{25+5}\right|\) = 0
∴ θ = \(\frac{\pi}{2}\)
∴ The angle between the pair of tangents drawn from (0, 0) to the given circle is \(\frac{\pi}{2}\).

Question 4.
Find the locus of P if the tangents drawn from P to x² + y² = a² include an angle α.
Solution:
The centre of the circle x² + y² = a² is C = (0, 0) and radius = a
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) II Q4

Question 5.
Find the locus of P if the tangents drawn from P to x² + y² = a² are perpendicular to each other.
Solution:
Equation of the given circle is x² + y² = a² and radius = a
Let P(x₁, y₁) be any point on the locus.
Since the tangents drawn from P(x₁, y₁) to the circle are perpendicular to each other,
the angle between tangents is \(\frac{\pi}{2}\)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) II Q5

Question 6.
Find the slope of the polar of (1, 3) with respect to the circle x² + y² – 4x – 4y – 4 = 0. Also, find the distance from the centre to it.
Solution:
Equation of polar of the point P(x₁, y₁) w.r.t circle S ≡ x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
∴ Polar of (1, 3) w.r.t. circle x² + y² – 4x – 4y – 4 = 0 is x(1) + y(3) – 2(x + 1) – 2(y + 3) – 4 = 0
⇒ -x + y – 12 = 0
⇒ x – y + 12 = 0
∴ The slope of the polar is ‘1’
Also, the distance from the centre (2, 2) to the polar of (1, 3) i.e., x – y + 12 = 0 is \(\left|\frac{2-2+12}{\sqrt{1+1}}\right|=\frac{12}{\sqrt{2}}=6 \sqrt{2}\)

Question 7.
If ax + by + c = 0 is a polar of (1, 1) w.r.t the circle x² + y² – 2x + 2y + 1 = 0 and H.C.F of a, b, c is equal to one then find a² + b² + c².
Solution:
Equation of polar of (1, 1) w.r.t the circle x² + y² – 2x + 2y + 1 = 0 is x(1) + y(1) – 1(x + 1) + 1(y + 1) + 1 = 0
⇒ 2y + 1 = 0 ……….(1)
Given that polar of P(1, 1) is ax + by + c = 0 ………(2)
since (1) and (2) represent the same line
\(\frac{\mathrm{a}}{0}=\frac{\mathrm{b}}{2}=\frac{\mathrm{c}}{1}=\mathrm{k}\)
⇒ a = 0, b = 2k, c = k
Given that H.C.F of a, b, c is ‘1’ we have k = 1
∴ a = 0, b = 2, c = 1
∴ a² + b² + c² = 0 + 4 + 1 = 5

III.

Question 1.
Find the coordinates of the point of intersection of tangents at the points where x + 4y – 14 = 0 meets the circle x² + y² – 2x + 3y – 5 = 0.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) III Q1
Let P(x₁, y₁) be the point of intersection of tangents drawn to the circle x² + y² – 2x + 3y – 5 = 0 …………(1) and given that x + 4y – 14 = 0 ………..(2) meets the circle at points A, B.
∴ Equation of chord of contact of (x₁, y₁) w.r.t circle (1) is xx₁ + yy₁ – (x + x₁) + \(\frac{3}{2}\)(y + y₁) – 5 = 0
⇒ \(x\left(x_1-1\right)+y\left(y_1+\frac{3}{2}\right)-\left(x_1-\frac{3}{2} y_1+5\right)=0\) …….(3)
Since (2) and (3) represent the same chord of contact
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) III Q1.1

Question 2.
If the polar of the points on the circle x² + y² = a² w.r.t the circle x² + y² = b2 touches the circle x² + y² = c² then prove that a, b, c are in geometrical progression.
Solution:
Given equations of circles
x² + y² = a² …….(1)
x² + y² = b² …….(2)
x² + y² = c² ……(3)
Let P(x₁, y₁) be any point on (1) then
\(x_1^2+y_1^2\) = a² ………(4)
The equation of polar of P(x₁, y₁) w.r.t circle (2) is xx₁ + yy₁ – b² = 0 ……..(5)
The Centre of (3) is (0, 0), and the radius = c.
Given that line (5) is polar of P w.r.t the circle (2) which touches the circle (3).
∴ The perpendicular distance from C(0, 0) of circle (3) to the line (5) = radius of circle (3)
∴ \(\frac{1-b^2 \text { । }}{\sqrt{x_1^2+y_1^2}}\) = c
⇒ \(\frac{\mathrm{b}^2}{\sqrt{\mathrm{a}^2}}\) = c
⇒ b² = ac
⇒ a, b, c are in geometric progression.

Question 3.
Tangents are drawn to the circle x² + y² = 16 from the point P(3, 5). Find the area of the triangle formed by these tangents and the chord of contact of P.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) III Q3
The given equation of a circle is x² + y² = 16
Centre C = (0, 0) and radius = 4
The equation of chord of contact of (3, 5) w.r.t. circle x² + y² = 16 is xx₁ + yy₁ – 16 = 0
⇒ 3x + 5y – 16 = 0
PL is the perpendicular distance from the point P(3, 5) to the chord AB.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) III Q3.1

∴ Area of the triangle formed by the tangents and the chord of P = \(\frac{108 \sqrt{2}}{17}\) square units.

Question 4.
Find the locus of the point whose polar with respect to the circles x² + y² – 4x – 4y – 8 = 0 and x² + y² – 2x + 6y – 2 = 0 are mutually perpendicular.
Solution:
Let P(x₁, y₁) be the locus of the point whose polars w.r.t the given circles x² + y² – 4x – 4y – 8 = 0 ……(1) and x² + y² – 2x + 6y – 2 = 0 ……(2) are mutually perpendicular.
Polar of P(x₁, y₁) w.r.t circle (2) is xx₁ + yy₁ – (x + x₁) + 3(y + y₁) – 2 = 0
⇒ x(x₁ – 1) + y(y₁ – 3) – (x₁ – 3y₁ + 2) = 0 ………(3)
Polar of P(x₁, y₁) w.r.t circle (1) is xx₁ + yy₁ – 2(x + x₁) – 2(y + y₁) – 8 = 0
⇒ x(x₁ – 2) + y(y₁ – 2) – (2x₁ + 2y₁ + 8) = 0 ………(4)
Slope of (3) is \(-\left(\frac{x_1-1}{y_1+3}\right)\)
and slope of (4) is \(\left(\frac{x_1-2}{y_1-2}\right)\)
If (3) and (4) are mutually perpendicular then
\(\left(\frac{x_1-1}{y_1+3}\right)\left(\frac{x_1-2}{y_1-2}\right)\) = -1
⇒ \(\left(x_1^2-3 x_1+2\right)=-\left(y_1^2+y_1-6\right)\)
⇒ \(x_1^2+y_1^2-3 x_1+y_1-4=0\)
∴ Locus of P(x₁, y₁) is x² + y² – 3x + y – 4 = 0.

Question 5.
Find the locus of the foot of the perpendicular drawn from the origin to any chord of the circle S ≡ x² + y² + 2gx + 2fy + c = 0 which subtends a right angle at the origin.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) III Q5
Any chord of the circle may be taken as lx + my = 1 ………(1)
Given equation of circle is x² + y² + 2gx + 2fy + c = 0 ………(2)
Chord (1) subtends a right angle at the origin.
Hence the lines joining the origin to the points of intersection of (1) and (2) are obtained by homogenizing equation (2) with equation (1).
From (1), lx + my = 1
and from (2), x² + y² + (2gx + 2fy)(1) + c(1)² = 0
⇒ x² + y² + (2gx + 2fy) (lx + my) + c(lx + my)² = 0
⇒ x² + y² + (2glx² + 2fy²m + 2flm + 2gmxy) + c(l²x² + 2lmxy + m²y²) = 0
⇒ (1 + 2gl + cl²) x² + (1 + 2fm + cm²)y² + xy(2fl + 2gm + 2lmc) = 0
This is a homogenizing second-degree equation that represents pair of lines OA and OB passing through the origin. If these lines are perpendicular then
the coefficient of x² + coefficient of y² = 0.
⇒ 1 + 2gl + 1 + cl² + 2fm + cm² = 0
⇒ c(l² + m²) + 2(gl + fm) + 2 = 0 ……….(3)
From (1), the equation of the line perpendicular to the chord is mx – ly = 0 ………..(4)
Solving lx + my = 1 …..(1) and mx – ly = 0 ………(4)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d) III Q5.1
To find the locus of the foot of the perpendiculars we have to eliminate ‘l’ and ‘m’.
Substituting these values of l and m in (3), we get

⇒ c + 2(gx + fy) + 2(x2 + y2) = 0
⇒ 2(x² + y²) + 2(gx + fy) + c = 0
∴ Locus of the foot of the perpendiculars drawn from the origin to any chord of circle S ≡ x² + y² + 2gx + 2fy + c = 0 which subtends a right angle at the origin is 2(x² + y²) + 2(gx + fy) + c = 0.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a)

January 22, 2024January 20, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Exercise 2(a)

Question 1.
Find k if the following pairs of circles are orthogonal.
(i) x² + y² + 2by – k = 0, x² + y² + 2ax + 8 = 0.
Solution:
The given equations of circles are x² + y² + 2by – k = 0 ……….(1) and x² + y² + 2ax + 8 = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 0, f = b, c = -k, g’ = a, f’ = 0, c’ = 8
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 0 + 0 = 8 – k
⇒ k = 8

(ii) x² + y² – 6x – 8y + 12 = 0, x² + y² – 4x + 6y + k = 0
Solution:
The given equations of circles are x² + y² – 6x – 8y + 12 = 0 …….(1) and x² + y² – 4x + 6y + k = 0 ……….(2)
Comparing with S = 0 and S’ = 0
We get g = -3, f = -4, c = 12 and g’ = -2, f’ = 3, c’ = k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 2(6 – 12) = 12 + k
⇒ -12 = 12 + k
⇒ k = -24

(iii) x² + y² – 5x – 14y – 34 = 0, x² + y² + 2x + 4y + k = 0
Solution:
The given equations of circles are x² + y² – 5x – 14y – 34 = 0 ……..(1) and x² + y² + 2x + 4y + k = 0 ……….(2)
Comparing with S = 0 and S’ = 0
We get g = \(\frac{-5}{2}\), f = -7, c = -34 and g’ = 1, f = 3, c’ = k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 2[\(\frac{-5}{2}\)(1) + (-7)(2)] = k – 34
⇒ -5 – 28 = k – 34
⇒ k = 1

(iv) x² + y² + 4x + 8 = 0, x² + y² – 16y + k = 0
Solution:
The given equations of circles are x² + y² + 4x + 8 = 0 ………(1) and x² + y² – 16y + k = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 2, f = 0, c = + 8 and g’ = 0, f’ = -8, c’ = +k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 0 = 8 + k
⇒ k = -8

Question 2.
Find the angle between the circles given by the equations
(i) x² + y² – 12x – 6y + 41 = 0, x² + y² + 4x + 6y – 59 = 0
Solution:
The given equations of circles are
x² + y² – 12x – 6y + 41 = 0 ………(i)
and x² + y² + 4x + 6y – 59 = 0 ……..(ii)
Comparing with S = 0 and S’ = 0 We get
g = -6, f = -3, c = 41
g’ = 2, f’ = 3, c’ = -59
Also, centres of circles (1) and (2) are C₁ = (6, 3) and C₂ = (-2, -3)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) I Q2(i)

(ii) x² + y² + 6x – 10y – 135 = 0, x² + y² – 4x + 14y – 116 = 0
Solution:
The given equations of circles are
x² + y² + 6x – 10y – 135 = 0 ………(1)
and x² + y² – 4x + 14y – 116 = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 3, f = -5, c = -135 and g’ = -2, f’ = 7, c’ = -116
Also, centres of circles (1) and (2) are C₁ = (-3, 5) and C₂ = (2, -7)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) I Q2(ii)

Question 3.
Show that the angle between the circles x² + y² = a², x² + y² = ax + ay is \(\frac{3 \pi}{4}\).
Solution:
Let S = x² + y² – a² = 0 and S’ = x² + y² – ax + ay = 0 be the given of circles.
C₁ = (0, 0) and C₂ = \(\left(\frac{\mathrm{a}}{2}, \frac{\mathrm{a}}{2}\right)\) are the centres of circles.
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) I Q3

Question 4.
Show that the circles given by the following equations intersect each other orthogonally.
(i) x² + y² – 2x – 2y – 7 = 0, 3x² + 3y² – 8x + 29y = 0
Solution:
Equations of given circles are
x² + y² – 2x – 2y – 7 = 0 ………(1)
and \(x^2+y^2-\frac{8}{3} x+\frac{29}{3} y=0\) ……….(2)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) I Q4(i)
c + c’ = -7 + 0 = 7
∴ 2(gg’ + ff’) = c + c’, hence circles (1) and (2) intersect orthogonally.

(ii) x² + y² + 4x – 2y – 11 = 0, x² + y² – 4x – 8y + 11 = 0
Solution:
Equations of given circles are
x² + y² + 4x – 2y – 11 = 0 ………(1)
and x² + y² – 4x – 8y + 11 = 0 ………(2)
g = 2, f = -1, c = -11 and g’ = -2, f’ = -4, c = 11
∴ 2(gg’ + ff’) = 2(-4 + 4) = 0 and c + c’ = -11 + 11 = 0
Since 2(gg’ + ff’) = c + c’, the two circles intersect orthogonally.

(iii) x² + y² – 2x + 4y + 4 = 0, x² + y² + 3x + 4y + 1 = 0
Solution:
Equations of given circles are
x² + y² – 2x + 4y + 4 = 0 ………(1)
and x² + y² + 3x + 4y + 1 = 0 ……….(2)
Centres of circles are C₁ = (1, -2) and C₂ = (\(\frac{-3}{2}\), -2)
Also g = -1, f = 2, c = 4
g’ = \(\frac{3}{2}\), f’ = 2, c’ = 1
∴ 2(gg’ + ff’) = 2(\(\frac{-3}{2}\) + 4) = 5
c + c’ = 4 + 1 = 5
Since 2(gg’ + ff’) = c + c’, we have the two circles intersect orthogonally with each other.

(iv) x² + y² – 2lx + g = 0, x² + y² + 2my – g = 0
Solution:
Equations of given circles are
x² + y² – 2lx + g = 0 ……..(1)
and x² + y² + 2my – g = 0 ……….(2)
g = -l, f = 0, c = g and g’ = -0, f’ = m, c’ = -g
∴ 2(gg’ + ff’) = 2[(0) + (0)] = 0
c + c’ = g – g = 0
Since 2(gg’ + ff’) = c + c’, the two circles intersect each other orthogonally.

II.

Question 1.
Find the equation of the circle which passes through the origin and intersects the circle given below orthogonally.
(i) x² + y² – 4x – 6y + 10 = 0, x² + y² + 12y + 6 = 0.
Solution:
Equations of given circles are
x² + y² – 4x – 6y + 10 = 0 ……..(1)
and x² + y² + 12y + 6 = 0 ………(2)
Let the equation of the circle passing through the origin be
x² + y² + 2gx + 2fy = 0 ………(3)
If (1) intersects (3) orthogonally then
2(-2) (g) + 2(3)(f) = 10
⇒ -4g + 6f = 10
⇒ 2g – 3f = -5 ……….(4)
If (2) intersects (3) orthogonally then
2g(0) + 2f(6) = 6
⇒ 12f = 6
⇒ f = \(\frac{1}{2}\) …….(5)
∴ From (4),
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) II Q1(i)

(ii) x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0
Solution:
Equations of given circles are
x² + y² – 4x – 6y – 3 = 0 ……..(1)
and x² + y² – 8y + 12 = 0 ……(2)
Let the equation of the required circle passing through the origin be
x² + y² + 2gx + 2fy = 0 ……..(3)
If (1) and (3) are orthogonal then
2g(-2) – 2f (- 3) = -3
⇒ 4g + 6f = 3
If (2) and (3) are orthogonal then
2g(0) + 2f(- 4) = 12
⇒ -8f = 12
⇒ f = \(\frac{-12}{8}=\frac{-3}{2}\) ………(5)
∴ From (4),
4g + 6(\(\frac{-3}{2}\)) = -3
⇒ 4g – 9 = -3
⇒ 4g = 6
⇒ g = \(\frac{3}{2}\) …….(6)
∴ From (3), the Equation of the required circle is x² + y² + 6x – 3y = 0.

Question 2.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally.
Solution:
Equations of given circles are
x² + y² – 6x + 3y + 5 = 0 ……..(1)
and x² + y² – x – 7y = 0 …….(2)
Let S ≡ x² + y² + 2gx + 2fy + c = 0 ………(3) be the required circle.
Let S’ = 0 …….(1) and S” = 0 ……..(2) be the given circles.
Given that (3) passes through (0, -3) we have
0 + 9 – 6f + c = 0
⇒ 9 – 6f + c = 0 ……(4)
If (1) and (3) are orthogonal then
2g(-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f = c + 5 ……..(5)
If (2) and (3) are orthogonal then
\(2 g\left(-\frac{1}{2}\right)+2 f\left(-\frac{7}{2}\right)=c\)
⇒ -g – 7f = c
⇒ g + 7f + c = 0
From (5)
6g – 3f + c = -5
⇒ -5g + 10f = 5
⇒ g – 2f = -1 ………(7)
Also from (4), 9 – 6f + c = 0
and from (5), 6g – 3f + c = -5
∴ -6g – 3f + 9 = 5
⇒ -6g – 3f + 4 = 0
⇒ 6g + 3f – 4 = 0
From (7) and (8),
6g – 12f = -6
⇒ 15f – 10 = 0
⇒ f = \(\frac{10}{15}\)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) II Q2

Question 3.
Find the equation of the circle passing through the origin and having its center on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let the equation of the circle passing through the origin be x² + y² + 2gx + 2fy = 0 ……..(1)
Given that the centre (-g, -f) lies on the line x + y = 4
⇒ -g – f = 4
⇒ g + f = -4 ……….(2)
If (1) intersects x² + y² – 4x + 2y + 4 = 0 orthogonally then
2g (-2) + 2f(1) = 4
⇒ -2g + f = 2
⇒ 2g – f = -2 ………(3)
From (2) and (3)
3g = -6
⇒ g = -2
2(-2) – f = -2
⇒ -f = 2
⇒ f = -2
∴ The equation of the required circle from (1) is x² + y² – 4x – 4y = 0.

Question 4.
Find the equation of the circle which passes through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ……..(1)
If this passes through the points (2, 0) and (0, 2) then
4 + 4g + c = 0 ………(2)
and 4 + 4f + c = 0 ………(3)
From (2) and (3),
g = f …….(4)
Also (1) intersects the given circle x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 orthogonally then
\(2 g\left(\frac{5}{4}\right)+2 f\left(\frac{-3}{2}\right)\) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = c + 2
⇒ 5g – 6f = 2c + 4
Since g = f, we have
5f – 6f = 2c + 4
⇒ -f = 2c + 4
⇒ f + 2c + 4 = 0
From (3)
4f + c + 4 = 0
-3f + c = 0
⇒ c = 3f
From (5)
f + 6f + 4 = 0
⇒ 7f + 4 = 0
⇒ f = \(\frac{-4}{7}\)
and c = 3f = \(\frac{-12}{7}\), Also g = \(\frac{-4}{7}\)
∴ The equation of the required circle from (1) is \(x^2+y^2-\frac{8}{7} x-\frac{8}{7} y-\frac{12}{7}=0\)
⇒ 7(x² + y²) – 8x – 8y – 12 = 0.

Question 5.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having centre at (2, 3).
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ………(1)
Since the centre is given to be (2, 3) we have
-g = 2 and -f = 3
⇒ g = -2 and f = -3
Since (1) cuts x² + y² – 4x + 2y – 7 = 0 orthogonally we have
2g(-2) + 2f(1) = c – 7
⇒ -4(-2) – 6 = c – 7
⇒ 2 = c – 7
⇒ c = 9
∴ The equation of the required circle from (1) is x² + y² – 4x – 6y + 9 = 0.

III.

Question 1.
Find the equation of the circle which intersects the circle x² + y² – 6x + 4y – 3 = 0 orthogonally and passes through the point (3, 0) and touches Y-axis.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since this passes through point (3, 0) we have
9 + 6g + c = 0 ……..(2)
If (1) touches Y-axis then \(\sqrt{\mathfrak{f}^2-c}\) = 0
⇒ c = f² ……..(3)
If (1) intersects x² + y² – 6x + 4y – 3 = 0 orthogonally then
2g(-3) + 2f(2) = c – 3
⇒ -6g + 4f = c – 3 ………(3)
Also from (2), 6g = -c – 9
Solving, 4f = -12
⇒ f = -3
From (3)
c = f²
⇒ c = 9
From (2)
9 + 6g + 9 = 0
⇒ g = -3
∴ The equation of the required circle from (1) is x² + y² – 6x – 6y + 9 = 0.

Question 2.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 = 0 and x² + y² – 10x – 4y + 21 = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7.
Solution:
Equations are given circles are
x² + y² – 4x – 6y + 11 = 0 ……..(1)
and x² + y² – 10x – 4y + 21 = 0 ………(2)
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……..(3)
If this cuts (1) and (2) orthogonally then
2g(-2) + 2f(-3) = c + 11
⇒ 4g + 6g = – c – 11 …….(3)
and if (1) and (3) are orthogonal then
2g(-5) + 2f(-2) = c + 21
⇒ -10g – 4f = c + 21
⇒ 10g + 4f = -c – 21 ………..(4)
From (3) and (4)
-6g + 2f = 10
⇒ 6g – 2f = -10
⇒ 3g – f = -5 ………(5)
Since the centre of circle (1) (-g, -f) lies on the diameter 2x + 3y = 7, we have
2(-g) + 3(-f) = 7
⇒ 2g + 3f = -7 ……..(6)
Solving (5) and (6)
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) III Q2
∴ From (3)
(-8) – 6 = -c – 11
⇒ -14 = -c – 11
⇒ c = 3
∴ The equation of a required circle is x² + y² – 4x – 2y + 3 = 0.

Question 3.
If P, Q are conjugate points w.r.t. a circle S ≡ x² + y² + 2gx + 2fy + c = 0 then prove that the circle on PQ as diameter cuts the circle S = 0 orthogonally.
Solution:
Given S ≡ x² + y² + 2gx + 2fy + c = 0 ………(1)
Let P(x₁, y₁) and Q(x₂, y₂) be the given points.
The polar of P(x₁, y₁) w.r.t. a circle S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0.
Since P, Q are conjugate points w.r.t. S = 0
⇒ x₁x₂ + y₁y₂ + g(x₂ + x₁) + f(y₂ + y₁) + c = 0
∴ -g(x₁ + x₂) – f(y₁ + y₂) = x₁x₂ + y₁y₂ + c ……(2)
The equation of the circle having \(\overline{\mathrm{PQ}}\) as diameter is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ x² – x(x₁ + x₂) + y² – y(y₁ + y₂) + (x₁x₂ + y₁y₂) = 0 …….(3)
Using conditions between (1) and (3) orthogonally
2gg’ + 2ff’ = \(2 \mathrm{~g}\left[\left(\frac{-\mathrm{x}_1+\mathrm{x}_2}{2}\right)\right]+2 \mathrm{f}\left[\left(\frac{-\mathrm{y}_1+\mathrm{y}_2}{2}\right)\right]\)
= -g(x₁ + x₂) – f(y₁ + y₂)
= x₁x₂ + y₁y₂ + c [∵ From (2)]
= c’ + c When c’ = x₁x₂ + y₁y₂ from (3)
∴ The circle (3) cuts the circle S = 0 orthogonally.

Question 4.
If the equation of two circles whose radii are a, a’ are S = 0 and S’ = 0, then show that the circles \(\frac{\mathbf{S}}{\mathbf{a}}+\frac{\mathbf{S}^{\prime}}{\mathbf{a}^{\prime}}=0\) and \(\frac{S}{a}-\frac{S^{\prime}}{a^{\prime}}=0\) intersect orthogonally.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 and S’ ≡ x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) III Q4

Question 5.
Find the equation of the circle which intersects each of the following circles orthogonally.
(i) x² + y² + 2x + 4y + 1 = 0, x² + y² – 2x + 6y – 3 = 0, 2(x² + y²) + 6x + 8y – 3 = 0 (May ’12)
Solution:
Let the circle x² + y² + 2gx + 2fy + c = 0 …….(1) cuts each of the circles
x² + y² + 2x + 4y + 1 = 0 …….(2)
x² + y² – 2x + 6y – 3 = 0 ………(3)
and x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0 ………(4) orthogonally.
Then (1) and (2) are orthogonal.
⇒ 2g(1) + 2f(2) = c + 1 …….(4)
(1) and (3) are orthogonal
⇒ 2g(-1) + 2f(3) = c – 3 ……..(5)
(1) and (4) are orthogonal
⇒ 2g(\(\frac{3}{2}\)) + 2f(2) = c – \(\frac{3}{2}\) …….(6)
From (4) and (5),
2g + 4f = c + 1 and -2g + 6f = c – 3
4g – 2f = 4
⇒ 2g – f = 2 ………(7)
From (5) and (6)
-2g + 6f = c – 3
and 3g + 4f = c – \(\frac{3}{2}\)
⇒ -5g + 2f = \(-\frac{3}{2}\) …….(8)
From (7),
2g – f = 2 and -10g + 4f = -3 from (8)
Solving
TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) III Q5(i)
From (4),
2g + 4f = c + 1
⇒ -5 – 28 = c + 1
⇒ c = -34
∴ The equation of required circle (1) cutting each of the circles (2), (3), and (4) is x² + y² – 5x – 14y – 34 = 0.

(ii) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0
Solution:
Equations of given circles are
x² + y² + 4x + 2y + 1 = 0 ………(1)
x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ……..(2)
and x² + y² + 6x – 2y – 3 = 0 ………(3)
Let the equation of the circle that cuts (1), (2), and (3) orthogonally be
x² + y² + 2gx + 2fy + c = 0 ……..(4)
Since (1) and (4) are orthogonal
2g(2) + 2f(1) = c + 1 ……(4)
⇒ 4g + 2f = c + 1 ………(5)
Since (2) and (4) are orthogonal
and from (2), x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0
2g(2) + 2f(\(\frac{3}{2}\)) = c – \(\frac{3}{2}\)
⇒ 4g + 3f = c – \(\frac{3}{2}\) …….(6)
Since (3) and (4) are orthogonal
2g(3) + 2f(-1) = c – 3 ………(6)
⇒ 6g – 2f = c – 3 …….(7)
From (5) and (6),
-f = \(\frac{5}{2}\)
⇒ f = \(\frac{-5}{2}\)
From (6) and (7),
-2g + 5f = \(\frac{3}{2}\)
⇒ 2g – \(\frac{25}{2}\) = \(\frac{3}{2}\)
⇒ -2g = 14
⇒ g = -7
∴ From (5),
4g + 2f = c + 1
⇒ -28 – 5 = c + 1
⇒ c = -34
∴ The equation of the required circle from (4) which cuts (1), (2), and (3) orthogonally is given by x² + y² – 14x – 5y – 34 = 0.

Question 6.
If the straight line 2x + 3y = 1 intersects the circle x² + y² = 4 at points A and B, then find the equation of the circle having AB as diameter.
Solution:
Given that the line 2x + 3y – 1 = 0 intersects the circle x² + y² – 4 = 0 at points A and B then
the equation of the circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0
⇒ x² + y² – 4 + λ(2x + 3y – 1) = 0
⇒ x² + y² + 2λx + 3λy – (4 + λ) = 0 ………(1)
Centre of the circle C’ = \(\left(-\lambda-\frac{3 \lambda}{2}\right)\)
Given that the circle x² + y² – 4 = 0 has the line 2x + 3y – 1 = 0 as the diameter, the centre C’ lies on line 2x + 3y = 1.
∴ 2(-λ) + 3\(\left(-\frac{3}{2} \lambda\right)\) – 1 = 0
⇒ -4λ – 9λ – 2 = 0
⇒ λ = \(\frac{-2}{13}\)
∴ From (1), Equation of required circle is x² + y² – 4 – \(\frac{2}{13}\)(2x + 3y – 1) = 0
⇒ 13(x² + y²) – 52 – 4x – 6y + 2 = 0
⇒ 13(x² + y²) – 4x – 6y – 50 = 0

Question 7.
If x + y = 3 is the equation of chord AB of the circle x² + y² – 2x + 4y – 8 = 0, find the equation of the circle having AB as diameter.
Solution:
Let S ≡ x² + y² – 2x + 4y – 8 = 0 be the circle.
Let L ≡ x + y – 3 = 0 be the given line.
Given that L = 0 intersects the circle S = 0 at A, B.
The equation of the circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0 where λ is a constant.
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0
⇒ x² + y² + (λ – 2)x + y(λ + 4) – (8 + 3λ) = 0 …….(1)
Centre of the circle = \(\left[-\left(\frac{\lambda-2}{2}\right),-\left(\frac{\lambda+4}{2}\right)\right]\)
Given that the line L = 0 is the diameter of the circle (1).
Centre \(\left(\frac{2-\lambda}{2},-\frac{\lambda-4}{2}\right)\) lies on the line x + y – 3 = 0.
∴ \(\frac{2-\lambda}{2}+\left[-\left(\frac{\lambda+4}{2}\right)\right]-3=0\)
⇒ -λ + 2 – λ – 4 – 6 = 0
⇒ – 2λ – 8 = 0
⇒ 2λ = -8
⇒ λ = -4
∴ The equation of the required circle from (1) is x² + y² + (-4 – 2)x + (-4 + 4)y – 8 – 3(-4) = 0
⇒ x² + y² – 6x + 4 = 0

Question 8.
Find the equation of the circle passing through the intersection of the circles x² + y² = 2ax and x² + y² = 2by and having its centre on the line \(\frac{x}{a}-\frac{y}{b}=2\).
Solution:
Let S = x² + y² – 2ax = 0 and S’ = x² + y² – 2by be the given circles.
Given line is \(\frac{x}{a}-\frac{y}{b}=2\)
⇒ bx – ay = 2ab
⇒ bx – ay – 2ab = 0 …….(1)
The equation of the radical axis of circles S = 0 and S’ = 0 is S – S’ = 0.
⇒ x² + y² – 2ax – (x² + y² – 2by) = 0
⇒ ax – by = 0
Let L = ax – by = 0 ……….(2)
The equation of the circle passing through the points of intersection of S = 0 and L = 0 is S + λL = 0.
⇒ x² + y² – 2ax + λ(ax – by) = 0 — (3)
⇒ x² + y² + x(λa – 2a) – λby = 0
Centre of the circle (3) is \(\left(\frac{2 a-\lambda a}{2}, \frac{\lambda b}{2}\right)\)
Given that centre lies on (1)
∴ \(\mathrm{b}\left(\frac{2 \mathrm{a}-\lambda \mathrm{a}}{2}\right)-\mathrm{a} \frac{\lambda \mathrm{b}}{2}-2 \mathrm{ab}=0\)
⇒ 2ab – abλ – abλ – 4ab = 0
⇒ -2abλ – 2ab = 0
⇒ λ = -1
∴ From (3), the equation of the required circle is x² + y² – 3ax + by = 0.

TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a)

January 22, 2024January 20, 2024 by Mahesh

Students must practice these TS Intermediate Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Equations Solutions Exercise 7(a)

I.
Question 1.
Find the principal solutions of the angles in the equations. (V.S.A)
(i) 2 cos² θ = 1
Answer:
cos² θ = \(\frac{1}{2}\)
⇒ principal values are θ = 45°,135° (∵ cos θ = ±\(\frac{1}{\sqrt{2}}\))

(ii) √sec θ + 2 = 0
Answer:
sec θ = \(\frac{-2}{\sqrt{3}}\), cos θ = – \(\frac{\sqrt{3}}{2}\)
∴ Principal solution is θ = 150°.

(iii) √3 tan²θ = 1
Answer:
tan²θ = \(\frac{1}{3}\) ⇒ tan θ = ± \(\frac{1}{\sqrt{3}}\)
∴ θ = ± \(\frac{\pi}{6}\)

Question 2.
Solve the following equations. (VSA)
(i) cos 2θ = \(\frac{\sqrt{5}+1}{4}\), θ ∈ [0, 2π]
Answer:
cos 2θ = \(\frac{\sqrt{5}+1}{4}\) = cos 36° = cos \(\left(\frac{\pi}{5}\right)\)
and \(\frac{\pi}{5}\) ∈ [0, 2π] ∴ 2θ = \(\frac{\pi}{5}\) ⇒ θ = \(\frac{\pi}{10}\)
is the principal solution.
and 2θ = 2nπ ± \(\frac{\pi}{5}\) where n ∈ Z is the general solution
∴ θ = nπ ± \(\frac{\pi}{10}\)
Values of θ in [0, 2π] are \(\left\{\frac{\pi}{10}, \frac{9 \pi}{10}, \frac{11 \pi}{10}, \frac{19 \pi}{10}\right\}\)
for n = 0, n = 1 and n = 2.

(ii) tan²θ = 1, θ ∈ [- π, π]
Answer:
tan θ = ± 1 + tan \(\left(\pm \frac{\pi}{4}\right)\)
The principal solutions are θ = ± \(\frac{\pi}{4}\)
and general solution is θ = nπ ± \(\frac{\pi}{4}\), n ∈ Z
For n = – 1, 0, 1 we have \(\left\{-\frac{3 \pi}{4}, \frac{-\pi}{4}, \frac{\pi}{4}, \frac{3 \pi}{4}\right\}\) is
the solution set [or the given equation in [-π, π].

(iii) sin 3θ = \(\frac{\sqrt{3}}{2}\), θ ∈ [- π, π]
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 1

(iv) cos² θ = \(\frac{3}{4}\), θ ∈ [0, π]
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 2
For values of n = 0, 1 we have solution set for the given equation in [0, π] is \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

(v) 2 sin² θ = sin θ, θ ∈ (0, π)
Answer:
2 sin² θ = sin θ
⇒ sin θ (2 sin θ – 1) = 0
⇒ sin θ = 0 or sin θ = \(\frac{1}{2}\)
When sin θ = 0 we have θ = nπ
and sin θ = \(\frac{1}{2}\) ⇒ θ = nπ + (- 1)ⁿ \(\frac{\pi}{6}\)
Since θ ∈ (0, π), solution set is \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

Question 3.
Find general solutions of the following equations. (V.S.A)
(i) sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = – \(\frac{1}{2}\)
Answer:
sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = – \(\frac{1}{2}\)
⇒ θ has in II quadrant.
∴ The principal value of θ is π – \(\frac{\pi}{3}\) = \(\frac{2 \pi}{3}\)
∴ The general solution is
θ = 2nπ + \(\frac{2 \pi}{3}\), n ∈ Z

(ii) tan x = – \(\frac{1}{\sqrt{3}}\), sec x = \(\frac{2}{\sqrt{3}}\)
Answer:
Given tan x = – \(\frac{1}{\sqrt{3}}\) and sec x = \(\frac{2}{\sqrt{3}}\)
⇒ x lies in IV quadrant.
∴ The principal values of x are \(\frac{-\pi}{6}\) or 2π – \(\frac{\pi}{6}\) = \(\frac{11 \pi}{6}\)
n ∈ Z (or) x = 2nπ – \(\frac{\pi}{6}\), n ∈ Z

(iii) cosec θ = – 2, cot θ = – √3
Answer:
cosec θ = – 2, cot θ = – √3
⇒ θ lies in IV quadrant.
The principal value of θ is
θ = 2π – \(\frac{\pi}{6}\) = \(\frac{11\pi}{6}\) or θ = – \(\frac{\pi}{6}\)
∴ General solution of θ is θ = 2nπ + \(\frac{11\pi}{6}\)
or θ = 2nπ – \(\frac{\pi}{6}\)

Question 4.
(i) If sin (270° – x) = cos 292° then find x in (0, 360°) (V.S.A)
Answer:
sin (270° – x) = cos 292°
= sin (270° – x) = cos (270° + 22°) sin 22°
270° – x = 22° ⇒ x = 270° – 22 = 248°

(ii) If x < 90°and sin (x + 28°) = cos(3x – 78°) then find x.
Answer:
Given sin (x + 28°) = cos (3x – 78°)
= sin [90° – (3x – 78°)]
∴ x + 28° = 90 – (3x – 78°)
⇒ 3x + x = 168° – 28° = 140°
⇒ 4x = 140° ⇒ x = 35°

Question 5.
Find the general solutions of the following equations.
(i) 2 sin² θ 3 cos θ
Answer:
Given 2 sin²θ = 3 cos θ
⇒ 2(1 – cos²θ) = 3 cos θ
⇒ 2 cos² θ + 3 cos θ – 2 = 0
⇒ 2 cos² θ + 4 cos θ – cos θ – 2 = θ
⇒ 2 cos θ(cos θ + 2) – 1 (cos θ + 2) = θ
⇒ (2cos θ – 1) (cos θ + 2) = 0
⇒ cos θ = \(\frac{1}{2}\) or cos θ = – 2 (not admissible)
⇒ cos θ = \(\frac{1}{2}\) ⇒ principal solution is α = – \(\frac{\pi}{3}\)
∴ General solution is θ = 2nπ ± α
= 2nπ ± \(\frac{\pi}{3}\)

(ii) sin² θ – cos θ = \(\frac{1}{4}\)
Answer:
sin² θ – cos θ = \(\frac{1}{4}\)
⇒ 1 – cos² θ – cos θ = 1
⇒ 4 – 4 cos² θ – 4 cos θ = 1
⇒ 4 cos² θ + 4 cos θ – 3 = 0
⇒ 4cos² θ + 6 cos θ – 2 cos θ – 3 = 0
⇒ 2 cos θ(2 cos θ + 3) – 1(2 cos θ + 3) = 0
⇒ (2 cos θ – 1)(2 cos θ + 3)= 0
⇒ cos θ = \(\frac{1}{2}\) or cos θ = \(\frac{-3}{2}\) (not admissible)
If cos θ = \(\frac{1}{2}\) then the principal value α = \(\frac{\pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ z

(iii) 5 cos² θ + 7 sin² θ = 6
Sol.
Given 5 cos² θ + 7 sin² θ = 6
Dividing by cos² θ we get,
⇒ 5 + 7 tan² θ = 6 sec² θ
⇒ 5 + 7 tan² θ = 6(1 + tan² θ)
⇒ tan² θ – 1 = 0 ⇒ tan² θ = 1
= tan θ = ±1
∴ θ = nπ ± \(\frac{\pi}{4}\), n ∈ Z is the general solution.

(iv) 3 sin⁴ x + cos⁴ x = 1
Answer:
3 sin⁴ x + cos⁴ x = 1
⇒ 3(sin² x)² + cos⁴ = 1
⇒ 3(1 – cos² x)² + cos⁴ x = 1
⇒ 4 cos⁴ x – 6 cos² x + 2 = 0
⇒ 2 cos⁴ x – 3 cos² x + 1 = 0
⇒ 2 cos⁴ x – 2 cos² x – cos² x + 1 = 0
⇒ 2 cos² x (cos²x – 1) – 1(cos² x – 1) = 0
⇒ (2cos² x – 1) (cos² x – 1) = 0

Case (i): 2 cos² x – 1 = 0
⇒ cos² x = \(\frac{1}{2}\) ⇒ cos x = ± \(\frac{1}{\sqrt{2}}\)
General solution is
x = 2nπ ± \(\frac{\pi}{4}\), n ∈ Z if cos x = \(\frac{1}{\sqrt{2}}\) and
x = 2nπ ± \(\frac{3 \pi}{4}\), n ∈ Z for cos x = – \(\frac{1}{\sqrt{2}}\)

Case(ii): cos²x – 1 = 0
⇒ cos²x = 1
cos x = ±1
If cos x = 1 then x = 2nπ, n ∈ Z and
If cos x = – 1 then x = 2nπ ± π, n ∈ Z
∴ General solution is x = 2nπ ± \(\frac{3 \pi}{4}\), n ∈ Z
x = 2nπ ± π, x = 2nπ, and x = 2nπ ± π

II.
Question 1.
Solve the following equations and write general solutions. (SA)
(i) 2 sin² θ – 4 = 5 cos θ
Answer:
2 sin2 θ – 4 = 5 cos θ
⇒ 2(1 – cos² θ) – 5 cos θ – 4 = 0
⇒ 2 cos² θ + 5 cos θ + 4 – 2 = 0
⇒ 2 cos² θ + 5 cos θ + 2 = 0
⇒ 2 cos² θ + 4 cos θ + cos θ + 2 = 0
⇒ 2 cos θ (cos θ + 2) + 1(cos θ + 2) = 0
⇒ (cos θ + 2) (2 cos θ + 1) = 0
cos θ + 2 = 0 is not admissible.
Consider 2 cos θ + 1 = 0 ⇒ cos θ = –\(\frac{1}{2}\), the
principal solution is α = \(\frac{2 \pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z

(ii) 2 + √3 sec x – 4 cos x = 2√3
Answer:
2 + \(\frac{\sqrt{3}}{\cos x}\) – 4 cos x = 2√3
⇒ 2 cos x + √3 – 4 cos² x = 2√3 cos x
⇒ 4 cos² x – 2 cos x + 2√3 cos x – √3 = 0
⇒ 2 cos x(2 cos x + √3) – 1(2 cos x + √3) = 0
⇒ (2 cos x – 1) (2 cos x + √3) = 0

Case (i): If 2 cos x – 1 = 0 then cos x = \(\frac{1}{2}\) and the principal solution is α = \(\frac{\pi}{3}\)
∴ General solution is x = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z

Case (ii): 2 cos x + √3 = 0 cos x = – \(\frac{\sqrt{3}}{2}\)
∴ The principal solution is α = 150° = \(\frac{5 \pi}{6}\)
∴ The general solution is
x = 2nπ ± \(\frac{5 \pi}{6}\), n ∈ Z

(iii) 2 cos² θ + 11 sin θ = 7
Answer:
Given equation is 2 cos² θ + 11 sin θ = 7
⇒ 2 (1 – sin² θ) + 11 sin θ = 7
⇒ – 2 sin² θ + 11 sin θ = 5
⇒ 2 sin² θ – 11 sin θ + 5 = 0
⇒ 2 sin² θ – 10 sin θ – sin θ + 5 = 0
⇒ 2 sin² θ (sin θ – 5) – 1(sin θ – 5) = 0
⇒ (2 sin θ – 1) (sin θ – 5) = 0
If sin θ – 5 = 0 then sin θ = 5 is not admissible.
If 2 sin θ – 1 = 0 ⇒ Sin θ = \(\frac{1}{2}\) and the principal solution is α = \(\frac{\pi}{6}\)
∴ General solution is θ = nπ + (- 1)ⁿ \(\frac{\pi}{6}\), n ∈ z

(iv) 6 tan² x – 2 cos² x = cos 2x
Answer:
Given 6 tan² x – 2 cos² x = cos 2x
⇒ 6(sec² x – 1) – 2 cos² x = 2 cos² x – 1
⇒ 6\(\left(\frac{1}{\cos ^2 x}-1\right)\) – 2 cos² x = 2 cos² x – 1
⇒ \(\frac{6}{\cos ^2 x}\) – 4 cos² x – 5 = 0
⇒ 6 – 4 cos⁴ x – 5 cos² x = 0
⇒ 4 cos⁴ x + 5 cos² x – 6 = 0
⇒ 4 cos⁴ x + 8 cos² x – 3 cos² x – 6 = 0
⇒ 4 cos⁴ x (cos² x + 2) – 3(cos⁴ x + 2) = o
⇒ (4 cos² x – 3) (cos²x + 2) = o
If cos² x + 2 = 0 then solution is admissible
and if 4 cos² x – 3 = 0 ⇒ cos²x = \(\frac{3}{4}\)
⇒ cos x = ± \(\frac{\sqrt{3}}{2}\)
and the general solution is x = nπ ± \(\frac{\pi}{6}\), n ∈ Z

(v) 4 cos² θ + √3 = 2(√3 + 1) cos θ
Answer:
4 cos² θ – 2(√3 + 1) cos θ + √3 = 0
⇒ 4 cos² 0 – 2√3 cos θ – 2 cos θ + √3 = 0
⇒ 2 cos θ(2 cos θ – √3) – 1 (2 cos θ – √3) = 0
⇒ (2 cos θ – 1) (2 cos θ – √3) = 0
If cos θ = \(\frac{1}{2}\) then θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
If 2 cos θ – √3 = 0 then cos θ = \(\frac{\sqrt{3}}{2}\)
Hence the general solution in this case is
θ = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z

(vi) 1 + sin 2x = (sin 3x – cos 3x)²
Answer:
1 + sin 2x = sin² 3x. cos² 3x – 2 sin 3x cos 3x
= 1 – sin 6x
⇒ sin 6x + sin 2x = 0
⇒ 2 sin\(\left(\frac{6 x+2 x}{2}\right)\) cos\(\left(\frac{6 x-2 x}{2}\right)\) = 0
⇒ sin 4x cos 2x = 0
If cos 2x = 0 then 2x = (2n + 1) \(\frac{\pi}{2}\)
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 3

(vii) 2 sin² x + sin² 2x = 2
Answer:
2 sin² x + (2 sin x cos x)² = 2
⇒ sin² x + 2 sin² x cos² x – 1 = 0
⇒ 2 sin² x cos² x – (1 – sin² x) = o
⇒ 2 sin² x cos² x – cos² x = 0
⇒ cos² x (2 sin² x – 1) = o

Case (i): cos² x = 0 ⇒ cos x = 0
⇒ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z is the general solution.

Case (ii): 2 sin²x – 1 = 0 ⇒ sin²x = \(\frac{1}{2}\)
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 4

Question 2.
Solve the following equations. (S.A)
(i) √3 sin θ – cos θ = √2 (May 2014)
Answer:
Given √3 sin θ – cos θ = √2
Divide both sides by √3 + 1 = 2
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 5

(ii) cot x + cosec x = √3
Answer:
\(\frac{\cos x}{\sin x}+\frac{1}{\sin x}\) = √3
⇒ cos x + 1 = √3 sin x
⇒ √3 sin x – cos x – 1= 0
Divide both sides by √3 + 1 = 2,
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 6

(iii) sin x + √3 cos x = √2 (March 2010)
Answer:
Given sin x + √3 cos x = √2
Divide both sides by √1 + 3 = 2, we get
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 7

Question 3.
Solve the following equations. (S.A)
(i) tan θ + sec θ = √3, 0 ≤ θ ≤ 2π
Answer:
Given tan θ + sec θ = √3
⇒ \(\frac{\sin \theta}{\cos \theta}+\frac{1}{\cos \theta}\) = √3
⇒ sin θ + 1 = √3 cos θ
⇒ √3 cos θ – sin θ = 1
Divide both sides by √3 + 1 = 2, we get
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 8
We find that \(\frac{\pi}{6}\) is the only solution in (0, 2π)
Since θ = \(\frac{3 \pi}{2}\) is not admissible since tan θ is not defined for odd multiples of \(\frac{\pi}{2}\).
Also \(\frac{13 \pi}{6}\) ∉ (0, 2π)

(ii) cos 3x + cos 2x = sin \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\), 0 ≤ x ≤ 2π.
Answer:
Given cos 3x + cos 2x = sin \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\)
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 9

Case (i) cos \(\frac{x}{2}\) = 0 ⇒ \(\frac{x}{2}\) = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
x = (2n + 1)π, n ∈ Z
Put n = 0, we get {π} is the solution in [0, 2π]

Case (ii):
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 10

(iii) cot² x – (√3 + 1) cot x + √3 = 0; 0 < x < \(\frac{\pi}{2}\). (Mar. ‘14, ’12)
Answer:
Given cot² x – (√3 + 1) cot x + √3 = o
⇒ cot² x – √3 cot x – cot x + √3 = 0
⇒ cot x (cot x – √3) – 1 (cot x – √3) = 0
⇒(cot x – 1) (cot x – √3) = 0

Case (i) cot x – 1 = 0 = cot x = 1;
Principal solution is α = \(\frac{\pi}{4}\)
∴ General solution is x = nπ + \(\frac{\pi}{4}\), n ∈ Z

Case(ii): cot x – √3 = 0 ⇒ cot x = √3
Principal solution is α = \(\frac{\pi}{6}\)
∴ General solution is x = nπ + \(\frac{\pi}{6}\), n ∈ Z
For n = 0, we get x = \(\frac{\pi}{4}\) and x = \(\frac{\pi}{6}\) and they belong to \(\left(0, \frac{\pi}{2}\right)\)
∴ Solutions are \(\left\{\frac{\pi}{6}, \frac{\pi}{4}\right\}\)

(iv) sec x cos 5x + 1 = 0. 0 < x < 2π.
Answer:
Given sec x cos 5x + 1 = 0. 0 < x < 2π.
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 11

Case (i):
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 12

III.
Question 1.
(i) Solve sin x + sin 2x + sin 3x = cos x + cos 2x + cos 3x (E.Q)
Answer:
(sin 3x + sin x) + sin 2x = (cos 3x + cos x) + cos 2x
⇒ 2 sin 2x cos x + sin 2x = 2 cos 2x cos x + cos 2x
⇒ sin 2x (2 cos x + 1) = cos 2x (2cos x + 1)
⇒ (2 cos x + 1) (sin 2x – cos 2x) = 0

Case (i):2 cos x + 1 = 0 ⇒ cos x = – \(\frac{1}{2}\)
Principal solution is α = \(\frac{2 \pi}{3}\)
∴ General solution is x = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z

Case (ii): sin 2x – cos 2x = 0 ⇒ tan 2x = 1
Principal solution is α = \(\frac{\pi}{4}\);
∴ General solution is 2x = nπ ± \(\frac{\pi}{4}\)
⇒ x = \(\frac{\mathrm{n} \pi}{2}+\frac{\pi}{8}\), n ∈ Z
∴ General solution is
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 13

(ii) If x + y = \(\frac{2 \pi}{3}\), and sin x + sin y = \(\frac{3}{2}\) find x and y.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 14
Given x + y = 120° ………………. (2)
Solving x = 90°, y = 30°

(iii) If sin 3x + sin x + 2 cos x = sin 2x + 2 cos 2x, find the general solution.
Answer:
Given sin 3x + sin x + 2 cos x = sin 2x + 2 cos 2x
⇒ 2 sin 2x cos x + 2 cos x = 2 sin x cos x + 2 cos² x
⇒ 2 cos x(sin 2x + 1) = 2 cos x(sin x + cos x)
⇒ 2 cos x[sin 2x + 1 – sin x – cos x] = 0
⇒ cos x = 0 or sin 2x + 1 – sin x – cos x = 0
⇒ cos x = 0 or (sin 2x – sin x) + (1 – cos x) = 0
⇒ cos x = 0 (or) 2 cos \(\frac{3 x}{2}\) sin \(\frac{x}{2}\) + 2 sin²\(\frac{x}{2}\) = 0
⇒ cos x = 0 or 2 sin \(\frac{x}{2}\) (cos \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\)) = 0
⇒ cos x = 0 or sin \(\frac{x}{2}\) = 0 or cos \(\frac{3 x}{2}\) + sin \(\frac{x}{2}\) = 0

Case (i): cos x = 0 ⇒ x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z

Case (ii): sin \(\frac{x}{2}\) = 0 ⇒ \(\frac{x}{2}\) = nπ ⇒ 2nπ, n ∈ Z

Case (iii):
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 15

(iv) Solve cos 3x – cos 4x = cos 5x – cos 6x
Answer:
Given cos 3x – cos 4x = cos 5x – cos 6x
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 16

Question 2.
Solve the following equations. (E.Q)
(i) cos 2θ + cos 8θ = cos 5θ
Answer:
Given cos 2θ + cos 8θ = cos 5θ
⇒ 2 cos 5θ cos 3θ = cos 5θ
⇒ cos 5θ (2 cos 3θ – 1) = 0

Case (i): cos 5θ = 0 ⇒ 5θ = (2n + 1)\(\frac{\pi}{2}\)
⇒ θ = (2n + 1)\(\frac{\pi}{10}\), n ∈ Z

Case (ii): 2 cos 3θ – 1 = 0
⇒ cos 3θ = \(\frac{1}{2}\)
Principal solution is α = \(\frac{\pi}{3}\)
∴ General solution is 3θ = 2nπ ± \(\frac{\pi}{3}\)
⇒ θ = \(\frac{2 n \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z
∴ General solutions are

(ii) cos θ – cos 7θ = sin 4θ
Answer:
2 sin\(\left(\frac{\theta+7 \theta}{2}\right)\) sin\(\left(\frac{7 \theta-\theta}{2}\right)\) = sin 4θ
⇒ 2sin 4θ sin 3θ = sin 4θ
⇒ sin 4θ (2 sin 3θ – 1) = θ

Case (i): sin 4θ = 0 ⇒ 4θ = nπθ ⇒ \(\frac{\mathrm{n} \pi}{4}\), n ∈ Z

Case (ii): 2 sin 3θ – 1 = 0
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 18

(iii) sin θ + sin 5θ = sin 3θ, 0 < θ < π
Answer:
Given sin θ + sin 5θ = sin 3θ
⇒ 2 sin \(\left(\frac{\theta+5 \theta}{2}\right)\) cos \(\left(\frac{\theta-5 \theta}{2}\right)\) = sin 3θ
⇒ 2 sin 3θ cos 2θ = sin 3θ
⇒ sin 3θ (2 cos 2θ – 1) = 0
⇒ sin 3θ = 0 or 2 cos 2θ – 1 = 0

Case (i): sin 3θ = 0 and the general solution is given by 3θ = nπ ⇒ θ = \(\frac{\mathrm{n} \pi}{3}\), n ∈ Z

Case (ii): 2 cos 2θ – 1 = 0
⇒ cos 2θ = \(\frac{1}{2}\) and the principal solution is α = \(\frac{\pi}{3}\)
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 19

Question 3.
(i) If tan pθ = cot qθ and p ≠ – q, show that the solutions are in A.P. with common difference \(\frac{\pi}{\mathbf{p}+\mathbf{q}}\). (E.Q)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 20
The solutions form an arithmetical progression with \(\frac{2 \pi}{2(p+q)}=\frac{\pi}{p+q}\) as common difference.

(ii) Show that the solutions of cos pθ = sin qθ form two series each of which is an A.P.
Find also the common difference of each A.P. (p ≠ ±q)
Answer:
cos pθ = sin qθ ⇒ cos pθ – sin qθ = 0
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 21

(iii) Find the number of solutions of the equation tan x + sec x = 2 cos x; cos x ≠ 0, lying in the interval (0, π).
Answer:
Given tan x + sec x = 2 cos x
⇒ \(\frac{\sin x}{\cos x}+\frac{1}{\cos x}\) = 2 cos x
⇒ 1 + sin x = 2 cos 2x
⇒ 1 + sin x = 2 (1 – sin² x)
⇒ 2 sin² x + sin x – 1 = 0
⇒ 2 sin² x + 2 sin x – sin x – 1 = 0
⇒ 2 sin x(sin x + 1) – 1 (sin x + 1) = 0
⇒ (2 sin x – 1) (sin x + 1) = 0

Case (i): 2 sin x – 1 = 0 ⇒ sin x = \(\frac{1}{2}\),
Principal solution is α = \(\frac{\pi}{6}\); and
general solution is x = nπ + (- 1)ⁿ \(\frac{\pi}{6}\)
solutions in (0, π) are \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

Case (ii) sin x + 1 ⇒ sin x = – 1
⇒ x = – \(\frac{\pi}{2}\) (or) \(\frac{3 \pi}{2}\)
∴ Number of solutions in (0, π) for the given equation is two.

(iv) Solve sin 3α = 4 sin α sin(x + α) sin(x – α) where α ≠ nπ, n ∈ Z.
Answer:
Given
sin 3α = 4 sin α sin(x + α)sin(x – α)
= 4 sin α(sin² x – sin² α)
= 3 sin α – 4 sin³ α
= 4 sin α (sin²x – sin²α)
⇒ 3 sin α = 4 sin α sin² x
⇒ sin α (3 – 4 sin² x) = 0
⇒ 3 – 4 sin² x = 0 ⇒ sin²x = \(\frac{3}{4}\)
⇒ sin x = ±\(\frac{\sqrt{3}}{2}\)
∴ General solution is
x = nπ + (- 1)ⁿ (±\(\frac{\pi}{3}\)), n ∈ Z.
Since the principal solution is α = ±\(\frac{\pi}{3}\)

Question 4.
(i) If tan (π cos θ) = cot (π sin θ), then prove that cos \(\left(\theta-\frac{\pi}{4}\right)\) = ± \(\frac{1}{2 \sqrt{2}}\) (E.Q.)
Answer:
Given that tan (π cos θ) = cot (π sin θ) = tan (\(\frac{\pi}{2}\) – π sin θ)
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 22

(ii) Find the average of θ if cos θ + sin θ is positive.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 23

Question 5.
If α, β are the solutions of the equation a cos θ + b sin θ = c, where a, b, c ∈ R and If a² + b² >0, cos α ≠ cos β and sin α ≠ sin β then show that (E.Q)
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α . cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Answer:
Given a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ a² cos² θ = c² – 2bc sin θ + b² sin² θ
⇒ a² (1 – sin²θ) = c² – 2bc sin θ + b² sin² θ
⇒ (a² + b²)sin²θ – 2bc sin θ + (c² – a²) = 0
This is a quadratic in sin θ and let the roots be sin α and sin β. Then
sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Also b sin θ = c – a cos θ
⇒ b² sin² θ = c² – 2ac cos θ + a² cos² θ
⇒ b² (1 – cos² θ) = c² – 2ac cos θ + a² cos² θ
⇒ (b² + a²)cos² θ – 2ac cos θ + (c² – b²) = 0
This is a quadratic in cos θ and let cos α, cos β be the roots. Then
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 24

Question 6.
(i) Find the common roots of the equations cos 2x + sin 2x cot x and 2 cos² x + cos² 2x = 1. (E.Q)
Answer:
Let tan x = A and given that
cos 2x + sin 2x = cot x
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 25
⇒ (1 – A² + 2A)A = (1 + A²)
⇒ A – A³ + 2A² = A² + 1
⇒ A³ – A² – A + 1 = 0
∴ A = 1 satisfy the equation.
By synthetic division

∴ A³ – A² – A + 1 = 0
⇒ (A – 1)(A³ – 1) = 0
⇒ A = 1, A = – 1
When A = ±1 then tan x = ±1.
⇒ x = nπ ± \(\frac{\pi}{4}\) ……………….. (1)
Also given 2 cos² x + cos² 2x = 1
⇒ (2 cos² x – 1) + cos² 2x = 0
⇒ cos 2x(1 + cos 2x) = 0
⇒ cos 2x = 0 (or) cos 2x = – 1

Case (i): When cos 2x = 0 then
2x = (2n + 1) \(\frac{\pi}{2}\)
⇒ x = (2n + 1)\(\frac{\pi}{4}\), n ∈ Z ……………….. (2)
From (1) and (2) we have
(2n + 1)\(\frac{\pi}{4}\), n ∈ Z is the common root for the given two trigonometric equations.

(ii) Solve the equation
\(\sqrt{6-\cos x+7 \sin ^2 x}\) + cos x = 0
Answer:
Given
\(\sqrt{6-\cos x+7 \sin ^2 x}\) + cos x = 0
∴ 6 – cos x + 7 sin² x = cos²x
⇒ 7(1 – cos²x – cos x + 6 = cos²x
⇒ 8 cos x + cos x – 13 = 0
∴ cos x = \(\frac{-1 \pm \sqrt{1+4(8)(13)}}{16}\)
= \(\frac{-1 \pm \sqrt{417}}{16}\)
The solution is not possible since – 1 ≤ cos x ≤ 1

(iiii) It |tan x| = tan x + \(\frac{1}{\cos x}\) and x ∈ [0, 2π], find the value of x.
Answer:
|tan x| = tan x if x lies either in 1 or in III quadrants.
∴ tan x = tan sec x
⇒ sec x = 0 since sec x ∉ (- 1, 1)
Also |tan x| = – tan x If x lies in either II or IV quadrants.
∴ – tan x = tan x + sec x
⇒ – 2 tan x = sec x
TS Inter 1st Year Maths 1A Solutions Chapter 7 Trigonometric Equations Ex 7(a) 27

TS Inter 1st Year Chemistry Study Material Chapter 12 పర్యావరణ రసాయన శాస్త్రం

January 20, 2024January 18, 2024 by Mahesh

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 12th Lesson పర్యావరణ రసాయన శాస్త్రం Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 12th Lesson పర్యావరణ రసాయన శాస్త్రం

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాతావరణం, జీవావరణం పదాలను వర్ణించండి.
జవాబు:
వాతావరణం : భూగోళాన్ని చుట్టుకొని ఉండే వాయుస్థితిలోని రక్షక పొరను వాతావరణం అంటారు. వాతావరణంలో అధికభాగం నైట్రోజన్ మరియు ఆక్సిజన్ స్వల్ప పరిమాణంలో కార్బన్ డై ఆక్సైడు, నీటిఆవిరి ఉంటాయి. దీనిలో నాలుగు ఖండాలు ఉన్నాయి. ఇవి భూఉపరితలం నుంచి 500 కి.మీ. ఎత్తు వరకు వ్యాపించి ఉన్నాయి. ఇవి ట్రోపోవరణం, స్ట్రాటోవరణం, మిసోవరణం, థెర్మోవరణం.
జీవావరణం : జీవరాశులు అన్నీ అంటే మొక్కలు, జంతువులు, మానవులను ఉమ్మడిగా జీవావరణం అంటారు.

ప్రశ్న 2.
శిలావరణం, జలావరణం పదాలను వివరించండి.
జవాబు:
శిలావరణం : ఖనిజాలు, మట్టి (భూసారం)తో నిండి ఉన్న ఘనస్థితి భూమి బాహ్య పొరను శిలావరణం అంటాం. భూ ఉపరితలంలో శిలావరణం 5వ వంతు ఉంటుంది. భూమి లోపలి పొరలలో ఖనిజాలు ఉంటాయి. మరింత లోతుగా సహజ వాయువు మరియు చమురు నిక్షేపాలు ఉంటాయి. ఇవన్నీ మరియు కొండలు, పర్వతాలు కూడా శిలావరణంగానే పరిగణించబడతాయి.

జలావరణం : అన్ని రకాల సహజ నీటివనరులు, జలావరణంగా పరిగణించబడతాయి. మహాసముద్రాలు, సముద్రాలు, నదులు, జలాశయాలు, నీటి కాలువలు, రిజర్వాయర్లు, పోలార్ ప్రాంతంలోని మంచు శిఖరాలు, భూగర్భ జలాలు, అనే అన్ని రకాల నీటి వనరులు ఈ ఆవరణ పరిధిలోకే వస్తాయి.

ప్రశ్న 3.
భూకాలుష్యం నిర్వచించండి.
జవాబు:
భూమి అనేది అనేక సహజపదార్థాలు పోగుపడిన ఒక పొర. దీనిలో ఖనిజాలు మరియు మట్టి ఉంటాయి. ఈ పొర పరిశ్రమల వల్ల వచ్చే వృధా పదార్థాలతోను, నగరాలలో వచ్చే వ్యర్థ పదార్థాలతోను, వ్యవసాయదారులు ఉపయోగించే క్రిమినాశకాలు, చీడల నాశకాలు మరియు జీవసంబంధ కారకాలతో కలుషితం అవుతుంది. దీనినే భూమి కాలుష్యం
అంటారు.
క్రిమిసంహారక మందులు, ఆర్గానోఫాస్ఫేట్లు, పెస్టిసైడ్లు, హెర్బిసైడ్లు, ఫంగిసైడ్లు, రొడెంటిసైడ్లు మొదలగు రసాయనాలు కూడా మట్టిని కాలుష్యానికి గురిచేస్తాయి.

ప్రశ్న 4.
రసాయన ఆక్సిజన్ అవసరం (COD) అంటే ఏమిటి ?
జవాబు:
రసాయనిక ఆక్సిజన్ అవసరం (COD) : కలుషిత నీటిలో కరిగి ఉన్న కర్బన రసాయన పదార్థాలను ఆక్సీకరణం చెందించడానికి అవసరమయ్యే ఆక్సిజన్ పరిమాణాన్ని రసాయనిక ఆక్సిజన్ అవసరం అంటాం. నీటిలో ఉండే కర్బన రసాయన పదార్థాల పరిమాణాన్ని తెలిపే ముఖ్య సూచిక ఇది. కర్బన రసాయన పదార్థాలను (50%) ఆమ్లీకృత (H₂SO₄ పొటాషియం డైక్రోమేటు ద్రావణం ద్వారా ఆక్సీకరణం చేసి COD ని నిర్ణయిస్తారు.

ప్రశ్న 5.
జీవరసాయన ఆక్సిజన్ అవసరం (BOD) అంటే ఏమిటి ?
జవాబు:
నీటిలో ఉండే కొన్ని ప్రత్యేక సూక్ష్మజీవులు 20°C వద్ద 5 రోజుల కాలంలో ఉపయోగించుకొనే ఆక్సిజన్ పరిమాణాన్ని జీవరసాయన ఆక్సిజన్ అవసరం అంటారు. శుద్ధనీటి BOD విలువ సుమారు 5pm. 17 ppm కంటే ఎక్కువ BOD విలువ గరిష్ఠ కాలుష్యాన్ని తెలుపుతుంది.

ప్రశ్న 6.
ట్రోపోవరణం, స్ట్రాటోవరణం అంటే ఏమిటి ?
జవాబు:
ట్రోపోవరణం : మానవులు, వారితో సహజీవనం చేసే ఇతర జీవులు మనుగడ సాగించే వాతావరణంలోని మిక్కిలి కింది ప్రదేశాన్ని ట్రోపోవరణం అంటారు. సముద్రమట్టం నుంచి 10 కి.మీ. ఎత్తు వరకు ఇది వ్యాప్తిచెంది ఉంటుంది.
స్ట్రాటోవరణం : ట్రోపోవరణంకు పైభాగంలో స్ట్రాటోవరణం ఉంటుంది. సముద్రమట్టం నుంచి 10-50 కి.మీ. ఎత్తులో స్ట్రాటోవరణం ఉంటుంది. సూర్యుని నుంచి వెలువడే హానికరమైన అతినీలలోహిత కిరణాలను భూ ఉపరితలాన్ని చేరకుండా స్ట్రాటోవరణంలోని ఓజోన్ పొర అడ్డుకుంటుంది.

ప్రశ్న 7.
ట్రోపోవరణంలో ఉండే ప్రధాన కణస్థితి కాలుష్యాలను పేర్కొనండి.
జవాబు:
కణస్థితి కాలుష్యాలు : ఇవి దుమ్ము, పలచని పొగమంచు, ధూమాలు, పొగ, స్మాగ్ మొదలైనవి.

ప్రశ్న 8.
కాలుష్య గాలిలో ఉండే నాలుగు వాయుస్థితి కాలుష్యాలను పేర్కొనండి.
జవాబు:

సల్ఫర్ యొక్క ఆక్సైడ్లు SO₂ మరియు SO,₂
నైట్రోజన్ యొక్క ఆక్సైడ్లు NO₂
కార్బన్ యొక్క ఆక్సైడ్లు CO మరియు CO₂
హైడ్రోకార్బన్లు.

ప్రశ్న 9.
గ్రీన్హౌస్ ఫలితం ……, …… వాయువుల ద్వారా కలుగుతుంది.
జవాబు:
గ్రీన్ హౌస్ ఫలితం కార్బన్ డై ఆక్సైడ్ మరియు మీథేన్, ఓజోన్, నీటి ఆవిరి వాయువుల వల్ల కలుగుతుంది.

ప్రశ్న10.
ఆక్సైడ్లు ఆమ్ల వర్షానికి కారణంగా ఉన్నాయి ? దీని pH విలువ ఎంత ? (March 2013)
జవాబు:
SO₂, NO₂ లు ఆమ్ల వర్షాన్ని కలుగజేస్తాయి. SO₂, NO₂ లు ఆక్సీకరణం చెంది నీటితో చర్య జరిపిన తరువాత ఆమ్ల వర్షానికి ప్రధాన కారకాలుగా పనిచేస్తాయి.
2SO₂(వా) + O₂ (వా) + 2H₂O(ద్ర) → 2H₂SO₄ (జల)
4NO₂(వా) + O₂ (వా) + 2H₂O(ద్ర) → 4HNO₃ (జల)
వర్షపు నీరు pH విలువ 5.6 కంటే దిగువకు పడిపోతే దానిని ఆమ్ల వర్షం అంటారు.

ప్రశ్న11.
ఆమ్ల వర్షం కలిగించే రెండు చెడు ప్రభావాలను తెలపండి.
జవాబు:

నేలలోని pH విలువ తగ్గి, భూసారం క్షీణించిపోతుంది.
కట్టడాల జీవితకాలం అనూహ్యంగా తగ్గిపోతుంది.
చలువరాళ్ళతో కట్టిన తాజ్మహల్ గాజులా ఉండే నునుపు స్వభావం ఆమ్ల వర్ష ప్రభావానికి లోనవుతున్నది.

ప్రశ్న12.
పొగ, పలుచని పొగ అంటే ఏమిటి ?
జవాబు:
కర్బన ద్రవ్యాలు దహనం చెందినప్పుడు ఏర్పడిన ఘనస్థితి కణాలను లేదా ఘనద్రవస్థితి మిశ్రమ కణాలను పొగ అనవచ్చు. సిగరెట్ పొగ, శిలాజ జాతి ఇంధనాలు, చెత్తా చెదారం, ఎండిన ఆకులు, తైలాలు మండినప్పుడు ఏర్పడు పొగలు వీటికి ఉదాహరణలు.

పలుచని పొగ : పిచికారీ ద్రవాలలోని కణాల ద్వారాను, గాలిలోని బాష్పాలు ద్రవీకరణం చెందడం ద్వారాను మిస్ట్లు (పలచని పొగమంచులు) ఏర్పడతాయి. ఉదాహరణకు సల్ఫ్యూరిక్ ఆమ్లం ఏర్పరిచే పొగమంచు, కలుపు మొక్కల నాశకాలు, క్రిమినాశకాలు వాటి లక్ష్యాల గురితప్పి గాలిలో ప్రయాణించేటప్పుడు పలుచని పొగలను (మిస్ట్) ఏర్పరుస్తాయి.

ప్రశ్న13.
సంప్రదాయక స్మాగ్ అంటే ఏమిటి ? దాని రసాయన స్వభావం ఏమిటి ? (ఆక్సీకరణ / క్షయీకరణ)
జవాబు:
స్మోక్ (పొగ), ఫాగ్ (మంచు) పదాల నుంచి స్మాగ్ అనే పదం వచ్చింది. శీతల (ఆర్ద్ర) శీతోష్ణస్థితులలో చోటుచేసుకుంటుంది. ఇది పొగ, మంచు, సల్ఫర్ డై ఆక్సైడ్ మిశ్రమం. రసాయనికంగా ఇది క్షయీకరణ స్వభావం ఉన్న మిశ్రమం. కాబట్టి దీనిని క్షయీకరణ సామర్థ్య స్మాగ్ అంటాం.

ప్రశ్న14.
కాంతి రసాయన స్మాగ్ ని సాధారణ అనుఘటకాలను తెలపండి.
జవాబు:
ఇది వేడి, తడిలేని సౌర శీతోష్ణస్థితిలో ఏర్పడుతుంది. ఆటోమొబైల్లు (రవాణా వాహనాలు), కర్మాగారాల నుంచి వెలువడే అసంతృప్త హైడ్రోకార్బన్లు, నైట్రోజన్ ఆక్సెడ్ పై సూర్యకాంతి చర్యలో కాంతి రసాయన స్మాగ్ ఏర్పడుతుంది. కాంతిరసాయన స్మాగ్ ఆక్సీకరణ కారకాలు అధిక గాఢతలలో ఉంటాయి. ఈ కారణంగా దీనిని ఆక్సీకరణ సామర్థ్యం గల స్మాగ్ అంటాం. దీనిలో ఫార్మాల్ డిహైడ్, ఎక్రోలిన్, పెరాక్సీ ఎసిటైల్ నైట్రేటు వంటి పదార్థాలు ఉంటాయి.

ప్రశ్న15.
PAN అంటే ఏమిటి ? దీని ప్రభావం ఏమిటి ?
జవాబు:
PAN అనగా పేరాక్సీ ఎసిటైల్ నైట్రేట్. ఇది కాంతి రసాయన స్మాగ్లో ఉంటుంది. దీని ప్రభావం వల్ల కంటి ప్రకోపాలు కలుగుతాయి. లోహాలు, రాళ్ళు, నిర్మాణ వస్తువులు, రబ్బరు, రంగు పూయబడిన ఉపరితలాల క్షీణతను ఇది కలిగిస్తుంది.

ప్రశ్న16.
స్ట్రాటోవరణంలో ఓజోను ఎలా ఏర్పడుతుంది ?
జవాబు:
స్ట్రాటోవరణంలో డై ఆక్సిజన్ (O₂) అణువులపై UV వికిరణాల చర్య ద్వారా ఏర్పడిన క్రియాజన్యమే ఓజోను. అణు ఆక్సిజన్ ను, UV వికిరణాలు, స్వేచ్ఛా స్థితిలో ఉండే ఆక్సిజన్ పరమాణువులు (0) గా వియోగిస్తాయి. ఈ ఆక్సిజన్ పరమాణువులు అణు ఆక్సిజన్తో సంకలనం చెంది ఓజోన్ ను ఏర్పరుస్తాయి.
TS Inter 1st Year Chemistry Study Material Chapter 12 పర్యావరణ రసాయన శాస్త్రం 8

ప్రశ్న17.
CF₂ Cl₂ ద్వారా ఓజోను తరుగుదల ప్రాప్తించే చర్యలో ఇమిడి ఉండే అంతర్గత రసాయన సమీకరణాలు తెలపండి.
జవాబు:
స్ట్రాటోవరణంలోకి చేరిన క్లోరో ఫ్లోరోకార్బన్ సమ్మేళనాలు UV వికిరణాలచే వియోగం చెందించబడి క్లోరిన్ స్వేచ్ఛా ప్రాతిపదికను విడుదల చేస్తాయి.
TS Inter 1st Year Chemistry Study Material Chapter 12 పర్యావరణ రసాయన శాస్త్రం 9

ప్రశ్న18.
ఓజోను రంధ్రం అంటే ఏమిటి ? దీనిని తొలిసారిగా ఎక్కడ గమనించారు ?
జవాబు:
స్ట్రాటోవరణంలోని ఓజోన్ పొర తరుగుదలను ఓజోన్ రంధ్రం అంటారు. దీనిని అంటార్కిటికాలోని దక్షిణ ధ్రువప్రాంతంలో మొదటిసారిగా కనుగొన్నారు.

ప్రశ్న19.
చల్లని శుద్ధ నీటిలో కరిగి ఉండే ఆక్సిజన్ పరిమాణం తెలపండి.
జవాబు:
చల్లని శుద్ధనీటిలో కరిగి ఉండే ఆక్సిజన్ పరిమాణం 4-6 మి.గ్రా/లీ.

ప్రశ్న20.
శుద్ధ నీరు, కలుషిత నీరు వీటి BOD విలువలను తెలపండి.
జవాబు:
శుద్ధనీటి BOD విలువ సుమారు 5 ppm. పురపాలక మురుగు నీటి BOD 100 – 4000 ppm విలువ కలిగి ఉంటుంది. 17 ppm కంటే ఎక్కువ BOD విలువ గరిష్ఠ కాలుష్యాన్ని తెలుపుతుంది.

ప్రశ్న21.
నీటిని కాలుష్యానికి గురిచేసే మూడు పారిశ్రామిక రసాయన పదార్థాలను తెలపండి.
జవాబు:

పాలిక్లోరినేటెడ్ బైఫినైల్, డిటర్జెంట్లు మరియు ఎరువులు.
పరిశ్రమల నుంచి లోహవ్యర్థాలు కూడా నీటిలో చేరవచ్చు.
అవి కాడ్మియం, మెర్క్యురీ, నికెల్ మొదలైన భారలోహ అయాన్లు.

ప్రశ్న22.
నీటి కాలుష్యానికి కారణమైన వ్యవసాయరంగ రసాయన పదార్థాలను తెలపండి.
జవాబు:

ఫాస్ఫేటును కలిగిన ఎరువులు
కలుపు మొక్కల నాశనులు
మలాథియాన్ వంటి పురుగుమందులు
ఎలుకల నివారణకు వాడే ఫాస్ఫైడ్లు.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న23.
భూవాతావరణంలోని భిన్న భాగాలను తెలపండి.
జవాబు:
వాతావరణాన్ని నాలుగు భాగాలుగా విభజించారు. అవి :

1) ట్రోపో ఆవరణం (0-11 కి.మీ)
2) స్ట్రాటో ఆవరణం (11-50 కి.మీ.)
3) మిసో ఆవరణం (50-85 కి.మీ.)
4) థెర్మో ఆవరణం (85-500 కి.మీ.)

1) ట్రోపో ఆవరణం : ఇది భూ ఉపరితలానికి అతి దగ్గరగా ఉంటుంది. వాతావరణ ద్రవ్యరాశిలో సుమారు 70% ఇది కలిగి ఉంటుంది.
2) స్ట్రాటో ఆవరణం : ఈ ఆవరణం ఓజోన్ పొరను కలిగి ఉంటుంది. సూర్యుని నుంచి వచ్చే అతినీలలోహిత కాంతిని ఇది శోషించుకుంటుంది. తద్వారా భూమిపై అతినీలలోహిత కిరణాలు పడకుండా చేస్తుంది.
3) మిసో ఆవరణం : ఈ ఆవరణం అల్ప మొత్తంలో O₃ ను కలిగి ఉంటుంది.
4) థెర్మో ఆవరణం : ఈ ఆవరణంలో అల్ప సాంద్రతలు, అల్పపీడనాలు ఉంటాయి. O₂, NO మొదలయిన వాయువులు ఈ ఆవరణంలో ఉంటాయి.

ప్రశ్న 24.
సింక్, COD, BOD, TLV పదాలను వివరించండి. (March 2013)
జవాబు:
సింక్ : చాలా కాలం నిలిచి ఉండే కాలుష్యాన్ని తనలో నిలుపుకొని దానితో అన్యోన్య చర్య జరిపే మాధ్యమాన్ని సింక్ అంటారు. ఉదా : వాతావరణ కార్బన్ డై ఆక్సైడుకు సముద్రాలు సింక్లుగా ఉంటాయి.
COD (Chemical Oxygen Demand] : కలుషిత నీటిలో కరిగి ఉన్న కర్బన రసాయన పదార్థాలను ఆక్సీకరణం చెందించడానికి అవసరమయ్యే ఆక్సిజన్ పరిమాణాన్ని రసాయనిక ఆక్సిజన్ అవసరం అంటారు.
BOD (Biochemical Oxygen Demand] : నీటిలో ఉండే కొన్ని ప్రత్యేక సూక్ష్మజీవులు, ) 20°C వద్ద అయిదురోజుల కాలవ్యవధిలో ఉపయోగించుకొనే ఆక్సిజన్ పరిమాణాన్ని జీవరసాయన ఆక్సిజన్ అవసరం అంటారు. శుద్ధనీటి BOD విలువ సుమారు 5 ppm.

ఆరంభ అవధి విలువ : TLV (Threshold Limit Value)
ఆరోగ్యవంతుడైన పారిశ్రామిక కార్మికుడు తన ఎనిమిది గంటల పనికాలంలో వాతావరణంలోని విష స్వభావ కాలుష్యానికి గురైనప్పటికి, తాను ఎటువంటి హానికర ప్రభావానికి గురికాకుండా ఉండటానికి ఆమోదించబడిన విష కాలుష్య కనిష్ఠ పరిమాణాన్ని ఆరంభ అవధి విలువ అంటారు.

ప్రశ్న 25.
గాలిలో చోటు చేసుకొని ఉన్న వాయుస్థితి కాలుష్యాలను తెలిపి, అవి ఎలా ఏర్పడతాయో వివరించండి.
జవాబు:
1) సల్ఫర్ ఆక్సైడులు : SO₂, SO₃
2) నైట్రోజన్ ఆక్సెడులు : NO, NO₂
3) హైడ్రోకార్బన్లు
4) కార్బన్ ఆక్సైడులు : CO, CO₂

1) సల్ఫర్ ఆక్సైడులు : సల్ఫర్ అనుఘటకంగా గల శిలాజ జాతి ఇంధనాలు మండినప్పుడు సల్ఫర్ ఆక్సైడ్లు ఏర్పడతాయి. వీటిలో సర్వ సాధారణంగా ఉండే రసాయన పదార్థం సల్ఫర్ డై ఆక్సైడ్ వాయుస్థితిలో ఉంటుంది.
S + O₂ → SO₂ (వా)
సల్ఫర్ డై ఆక్సైడ్ ఆక్సీకరణం చెంది సల్ఫర్ ట్రై ఆక్సైడ్గా ఆక్సీకరణం చెందుతుంది.
2SO₂ (వా) + O₂ (వా) → 2SO₃ (వా)

2) నైట్రోజన్ ఆక్సైడులు : ఎత్తైన ప్రదేశాలలో మెరుపులు సంభవించినప్పుడు గాలిలోని N₂, O₂ లు చర్యనొంది NO ఏర్పడుతుంది.
N₂ + O₂ → 2NO (వా)
2NO (వా) + O₂ → 2NO₂ (వా)

3) హైడ్రోకార్బన్లు : ఆటోమొబైల్లో వాడే ఇంధనాలు అసంపూర్ణంగా మండినప్పుడు ఇవి ఏర్పడతాయి.

4) కార్బన్ మొనాక్సైడ్ : కార్బన్ అసంపూర్ణ దహనచర్యకు గురైనప్పుడు కార్బన్ మోనాక్సైడ్ (CO) ఏర్పడుతుంది. పూర్తిగా దహనం చెందినప్పుడు కార్బన్ డైఆక్సైడ్ (CO₂) ఏర్పడుతుంది.
C (ఘ) + \(\frac{1}{2}\)O₂ (వా) → CO (వా)
C (ఘ) + O₂ (వా) → CO₂ (వా)

ప్రశ్న 26.
గ్రీన్ హౌస్ ఫలితం అంటే ఏమిటి ? ఇది ఎలా కలుగుతుంది ?
జవాబు:
కార్బన్ డై ఆక్సైడ్, క్లోరోఫ్లోరో కార్బన్లు, నైట్రిక్ ఆక్సైడ్ మరియు నీటిఆవిరులు పరారుణకాంతిని శోషించుకొని మరల భూమిపైకి ఉద్గారం చేస్తాయి. ఈ క్రియ వల్ల భూమి ఉపరితలం వేడెక్కుతుంది. ఈ దృగ్విషయాన్ని భూమి వేడెక్కడం లేదా భౌగోళిక తాపనం అంటారు. ఈ తాపనానికి కారణమయ్యే వాయువులను హరితగృహ వాయువులు అంటారు.

హరితగృహ ప్రభావం యొక్క దుష్ప్రభావాలు :

వాతావరణంలో 1°C ఉష్ణోగ్రత పెరిగితే, ధ్రువ ప్రాంతాలలోని మంచు శిఖరాలు కరిగి సముద్రపు నీటిమట్టం పెరుగుతుంది. దీనివల్ల అనేక తీరప్రాంతాలు ముంపునకు గురయ్యే అవకాశం అధికంగా ఉన్నది.
భూగోళం వేడెక్కడం వలన సముద్రాలు, నదులు, సరస్సులలోని నీటి బాష్పీభవనం రేటు కూడా పెరుగుతుంది. దీని కారణంగా అకాల వర్షాలు, తుపానులు వచ్చే అవకాశం ఉన్నది.
ఉపరితల నీరు వేగంగా బాష్పీభవనం చెందటం వల్ల వ్యవసాయరంగం కూడా దుష్ప్రభావానికి గురి అవుతుంది. వ్యవసాయరంగానికి నీటికొరత అధికమవుతుంది.
చెట్లను, అడవులను పెంచటం, CFC తయారీని నిలుపుచేయటం మొదలగు చర్యల వల్ల భౌగోళిక తాపనాన్ని నివారించవచ్చు.

ప్రశ్న 27.
ఆమ్ల వర్షం ఏర్పడే విధానాన్ని తెలుపుతూ దానిలోని అంతర్గత రసాయన సమీకరణాలను వివరించండి.
జవాబు:
నైట్రోజన్ మరియు సల్ఫర్ యొక్క ఆక్సెడ్లు (రవాణా మరియు పారిశ్రామికరంగాల నుండి విడుదల చేయబడినవి) వాతావరణంలోకి చేరుతాయి. అంతేకాక ఇవి నీటిలో కరిగి HNO₃ మరియు H₂SO₄ లను తయారుచేస్తాయి. ఈ ఆమ్లాలు నీటిలో కరిగి ఆమ్ల వర్షాలుగా భూమిని చేరుతాయి.
2SO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 2H₂SO₄ (జల)
4NO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 4HNO₃ (జల)

ప్రశ్న 28.
ఆమ్ల వర్షం ద్వారా కలిగే చెడు ప్రభావాలను వివరించండి.
జవాబు:
ఆమ్లవర్షం వల్ల కలిగే చెడు ప్రభావాలు :

నేలలో pH విలువ తగ్గి, భూసారం క్షీణించిపోతుంది.
కట్టడాల జీవితకాలం అనూహ్యంగా తగ్గిపోతుంది.
చలువరాళ్ళతో కట్టిన తాజ్మహల్ యొక్క గాజులా ఉండే నునుపు స్వభావం ఆమ్లవర్ష ప్రభావానికి లోనవుతున్నది.

ప్రశ్న 29.
కాంతి రసాయన స్మాగ్ ఎలా ఏర్పడుతుంది ? ఇది కలుగజేసే చెడు ప్రభావాలు ఏమిటి ?
జవాబు:
కాంతి రసాయన స్మాగ్ ఏర్పడటం : శిలాజ జాతి ఇంధనాలు మండినప్పుడు భిన్న రకాల కాలుష్యాలు భూగోళ ట్రోపోవరణంలోకి ఉద్గారించబడతాయి. ఉద్గారించబడిన కాలుష్యాలలో హైడ్రోకార్బన్లు (మండనటువంటి ఇంధనాలు), నైట్రిక్ ఆక్సైడ్ (NO) లు రెండూ కాలుష్యాలుగా ఉన్నాయి. ఈ కాలుష్యాల గాఢతలు అధిక స్థాయిలకు చేరినప్పుడు అవి సౌరకాంతితో పరస్పర చర్యలో పాల్గొని, ఒక గొలుసు చర్యను జరుపుతాయి. ఈ గొలుసు చర్యలో NO నైట్రోజన్ ఆక్సైడ్గా (NO₂) మారుతుంది. ఈ NO₂ తిరిగి సౌరకాంతి నుంచి శక్తిని గ్రహించి నైట్రిక్ ఆక్సైడ్గాను, స్వేచ్ఛాస్థితిలో ఉండే ఆక్సిజన్గాను విడిపోతుంది.

ఆక్సిజన్ పరమాణువులు రసాయనికంగా చాలా చురుకైనవి. ఇవి గాలిలోని O₂తో సంకలనం చెంది ఓజోన్ ను ఏర్పరుస్తాయి.
O (వా) + O₂ (వా) ⇌ O₃ (వా)

NO, ఓజోన్ తో చర్య జరిపి NO₂ ను తిరిగి ఏర్పరుస్తుంది. NO₂ బ్రౌన్ రంగు వాయువు. ఇది సరైన అధిక గాఢతల వద్ద “మసకత్వం” (chaze) ఏర్పడటానికి దారితీస్తుంది.
NO (వా) + O₃ (వా) → NO₂ (వా) + O₂ (వా)

ఓజోన్ విషవాయువు. NO₂, O₃ లు రెండూ బలమైన ఆక్సీకరణులు. ఇవి కాలుష్య గాలిలో మండే చర్యకు గురి కాకుండా మిగిలి ఉన్న హైడ్రోకార్బన్లతో చర్యజరిపి, ఫార్మాల్డిహైడ్, ఎక్రోలీన్, పెరాక్సీ ఎసిటైల్ నైట్రేట్ (PAN) వంటి రసాయన పదార్థాలను ఏర్పరుస్తాయి. దీనినే కాంతి రసాయన స్మాగ్ అంటారు.

ప్రశ్న 30.
వాతావరణంలో ఓజోన్ పొర తరుగుదల ఎలా ఏర్పడుతుంది ? ఈ ఓజోన్ పొర తరుగుదల వల్ల ప్రాప్తించే హానికరమైన ప్రభావాలను పేర్కొనండి.
జవాబు:
స్ట్రాటోవరణంలో ఉండే ఓజోను సూర్యుని నుంచి వెలువడే అపాయకరమైన అతినీలలోహిత కిరణాల నుంచి మనల్ని రక్షిస్తుంది. దీనిని ఓజోన్ పొర అంటారు. క్లోరోఫ్లోరో కార్బన్లు వాతావరణంలోనికి విడుదల కావడం ఓజోన్ పొర తరుగుదలకు ముఖ్యకారణం.

స్ట్రాటోవరణంలోని UV వికిరణాలచే CFC లు వియోగం చెందించబడి, క్లోరిన్ స్వేచ్ఛాప్రాతిపదికను విడుదల చేస్తాయి.

క్లోరిన్ స్వేచ్ఛా ప్రాతిపదిక స్ట్రాటోవరణంలోని ఓజోన్తో చర్యజరిపి, క్లోరిన్ మోనాక్సైడ్ ప్రాతిపదికలను అణు ఆక్సిజన్ ను విడుదలచేస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 12 పర్యావరణ రసాయన శాస్త్రం 3

క్లోరిన్ మోనాక్సైడ్ ప్రాతిపదిక, పరమాణు స్థితిలో ఉండే ఆక్సిజన్తో చర్యజరిపి అధిక సంఖ్యలో క్లోరిన్ ప్రాతిపదికలను ఏర్పరుస్తుంది.

క్లోరిన్ ప్రాతిపదికలు నిరంతరంగా ఏర్పడి ఓజోను అణువు వియోగచర్యను జరుపుతాయి. కాబట్టి క్లోరిన్ ప్రాతిపదికలను నిరంతరంగా ఉత్పత్తి చేసి, స్ట్రాటోవరణంలోకి చేర్చడానికి CFC లు రవాణా కారకాలుగా పనిచేస్తాయి. ఇవి ఓజోన్ పొరను నాశనం చేస్తాయి. ఒక CFC అణువు, సుమారు ఒక లక్ష O₃ అణువులను నాశనం చేస్తుంది.

ఓజోన్ పొర తరుగుదల ప్రభావాలు :

UV కిరణాలు అధిక పరిమాణంలో ట్రోపోవరణంలోకి చేరతాయి.
UV కిరణాల వల్ల చర్మం వడిలిపోతుంది.
కంటిలో శుక్లాలు ఏర్పడతాయి.
చర్మంపై బొబ్బలు వస్తాయి.
చర్మక్యాన్సర్ వస్తుంది.
చేపల ఉత్పత్తికి నష్టం కలుగుతుంది.

ప్రశ్న 31.
నీటి కాలుష్యానికి కారణమైన పారిశ్రామిక వ్యర్థాలను పేర్కొనండి. త్రాగేనీటి అంతర్జాతీయ ప్రమాణాలను పేర్కొనండి.
జవాబు:

పారిశ్రామిక రసాయన పదార్థాలను పాలిక్లోరినేటెడ్ బై ఫినైల్ను ఉపయోగించే పరిశ్రమల నుండి వెలువడే వ్యర్థాల వల్ల నీటికాలుష్యం జరుగుతుంది.
ఎరువుల పరిశ్రమల నుండి వెలువడే ఫాస్ఫేటులు నీటిలోకి చేరితే ఆల్గేల అభివృద్ధి జరుగుతుంది. అవి నీటిలోని ఆక్సిజన్ గాఢతను తగ్గించేస్తాయి.
చాలా నీటివనరులను పెట్రోలియం ఉత్పన్నాలు కాలుష్యానికి గురిచేస్తున్నాయి.
పేపరు మరియు బట్టల మిల్లుల నుండి వెలువడే వ్యర్థాల వల్ల నీటికాలుష్యం జరుగుతుంది.
ఆమ్లాలు, క్షారాలు, డిటర్జెంట్లు, ప్రేలుడు పదార్థాలు, అద్దకాలు, చీడ నాశినులు, ఎరువులు, సిలికోనులు, ప్లాస్టిక్ లు తయారుచేసే పరిశ్రమల నుండి వెలువడే వ్యర్థాలు నీటికాలుష్యానికి కారణభూతాలవుతున్నాయి.

త్రాగునీటి అంతర్జాతీయ ప్రమాణాలు :

ఫ్లోరైడ్ : 1 ppm నైట్రేటు – 50 ppm
సల్ఫేటు : < 500 ppm లెడ్ – 50 ppb

ప్రశ్న 32.
పర్యావరణ కాలుష్యాన్ని నివారించడానికి అవలంబించే హరిత రసాయనశాస్త్రంలోని ప్రణాళికలను సవివరంగా తెలపండి.
జవాబు:
రసాయనశాస్త్రం మరియు ఇతర శాస్త్ర విభాగాలను ఉపయోగించి వాటి అవగాహన, సూత్రాలతో సాధ్యమైనంతవరకు పర్యావరణంలో కాలుష్యం రాకుండా చూడడం గురించి చెప్పేదే హరిత రసాయనశాస్త్రం.
పరిశ్రమలలో వ్యర్థ పదార్థాలు ఏర్పడకుండా లేదా అతికొద్ది మాత్రంలో ఏర్పడే చర్యలను హరిత రసాయన చర్యలు అంటారు. ఈ దిశగా ఆలోచించి హరిత రసాయనశాస్త్రానికి కొన్ని సూత్రాలను ఏర్పరిచారు. అవి :

వ్యర్థ అనుజనిత పదార్థాల పరిమాణాన్ని కనిష్ఠ స్థాయికి తగ్గించాలి.
విషరహిత, ప్రమాదరహిత క్రియాజనకాలను ఎన్నుకోవాలి.
అత్యధిక దిగుబడి వచ్చే విధంగా చర్యాపరిస్థితులను స్థిరీకరించాలి.
కాలుష్యరహిత మరియు సురక్షితమైన ద్రావణిని ఉపయోగించాలి.
వీలైనచోట సాధారణ వేడిచేసే పద్ధతులు బదులు మైక్రోతరంగాలతో గాని, అతిధ్వనులతో గాని వేడిచేయాలి. ఎందుకంటే ఆ పద్ధతిలో రసాయన చర్యలు హరిత చర్యలుగా జరపబడతాయి.

దైనందిన జీవితంలో హరిత రసాయనశాస్త్రం :

వస్త్రాల నిర్జల శుద్ధిక్రియ (Dry Cleaning) : నిర్జల పద్ధతిలో వస్త్రాలను శుభ్రంచేసే ప్రక్రియలో టెట్రాక్లోరో ఈథేన్ ను (Cl₂ C = CCl₂) ఉపయోగించేవారు. ఈ పదార్ధం భూగర్భజలాలను మలినం చేస్తుంది. అంతేకాక క్యాన్సర్ కారకం. దీనికి బదులు ప్రస్తుతం ద్రవరూపంలో ఉన్న కార్బన్ డై ఆక్సైడ్కు డిటర్జెంటును కలిపి ఏర్పడిన మిశ్రమం ద్వారా శుభ్రంచేసే ప్రక్రియను జరుపుతున్నారు.
వస్త్రాలను వివర్ణం చేయడానికి, లాండ్రి ప్రక్రియలలో హైడ్రోజన్పరాక్సైడ్ను (H₂O₂) వాడుతున్నారు.
కాగితాలను వివర్ణం చేయడం : కాగితాలను వివర్ణం చేయడానికి పూర్వం క్లోరిన్ వాయువును ఉపయోగించేవారు. ఈ రోజుల్లో హైడ్రోజన్ పెరాక్సైడును, హైడ్రోజన్ పెరాక్సైడ్ వివర్ణ సామర్థ్యాన్ని పెంచే ఉత్ప్రేరకాన్ని దానితో కలిపి వాడుతున్నారు. ‘
రసాయన పదార్థాల సంశ్లేషణం : 90% దక్షతతో జలమాధ్యమంలో అయానిక ఉత్ప్రేరకం సమక్షంలో ఈథేన్ ను ఏక అంచె ఆక్సీకరణం చర్యకు గురిచేసి ఇథనాల్ (ఎసిటాల్డిహైడ్, (CH₃CHO) ను తయారుచేస్తున్నారు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 33.
పర్యావరణ కాలుష్యం అంటే ఏమిటి ? ఈ కాలుష్యం ఎన్ని రకాలు ?
జవాబు:
మొక్కలు, జంతువులు, మానవులపై హానికరమైన ప్రభావం ప్రదర్శిస్తూ పరిసరాలలో చోటుచేసుకొని ఉండే, అవాంఛనీయ మార్పులు ప్రదర్శించే ప్రభావాన్నే పర్యావరణ కాలుష్యం అంటారు.
పారిశ్రామికీకరణ కారణంగాను, జనాభా పెరుగుదల కారణంగాను ఎన్నో వ్యర్థ పదార్థాలు పర్యావరణంలోనికి ప్రవేశించుటవలన పర్యావరణం కాలుష్యం అవుతోంది.

పర్యావరణ కాలుష్యానికి కారణాలు :

జనాభా పెరుగుదల, సహజ వనరుల తరుగుదల
పారిశ్రామికీకరణ
అడవులను నరికివేయుట
పట్టణీకరణ

కాలుష్య రకాలు :

వాయు కాలుష్యం
జల కాలుష్యం
భూమి కాలుష్యం
ధ్వని కాలుష్యం
రేడియోధార్మిక కాలుష్యం

వాయు కాలుష్యం :

సల్ఫర్ ఆక్సైడులు : సల్ఫర్ అనుఘటకంగా గల శిలాజ జాతి ఇంధనాలు మండినప్పుడు సల్ఫర్ ఆక్సైడ్లు ఏర్పడతాయి.

SO₂ వాయుస్థితిలో ఉంటుంది. శ్వాసకోశ వ్యాధులు, కళ్ల వెంబడి నీరు కారడం, కళ్లు ఎర్రబడటం వంటివి, సల్ఫర్ డైఆక్సైడ్ కళ్లకు కలిగించిన ప్రకోపనం ద్వారా వస్తుంది.

S (ఘ) + O₂ (వా) → SO₂ (వా) ;
2 SO₂ (వా) + O₂ (వా) → SO₃ (వా)
SO₂ (వా) + O₃ (వా) → SO₃ (వా) + O₂ (వా)
SO₂ (వా) + H₂O₂ (ద్ర) → H₂SO₄ (ద్ర)

నైట్రోజన్ ఆక్సైడ్లు : రవాణా వాహనాలలో శిలాజ జాతి ఇంధనాలు మండించినప్పుడు, నైట్రిక్ ఆక్సైడ్ ఏర్పడుతుంది.

N₂ (వా) + O₂ (వా) → 2NO (వా)
NO తక్షణమే ఆక్సిజన్తో చర్య జరిపి NO₂ ను ఏర్పరుస్తుంది.
స్ట్రాటో ఆవరణంలో నైట్రిక్ ఆక్సైడ్ ఓజోన్ తో చర్య జరిపినపుడు NO₂ ఏర్పడుతుంది.
2NO (వా) + O₃ (వా) → NO₂ (వా) + O₂ (వా)
2NO (వా) + O₂ (వా) → 2NO₂ (వా)
అధిక పరిమాణాలలో ఉండే NO₂ మొక్కల ఆకులను పాడుచేసి, కిరణజన్య సంయోగక్రియ రేటును తగ్గిస్తుంది.

కార్బన్ మోనాక్సైడ్ : కార్బన్ అసంపూర్ణ దహనచర్యకు గురైనప్పుడు CO ఏర్పడుతుంది. ఆటోమొబైల్ల నుంచి వెలువడే బహిష్కృతాల ద్వారా ఇది గాలిలోకి చేరుకుంటుంది. ఇది రక్తంలోని హీమోగ్లోబిన్ తో బంధించబడి కార్బాక్సీ హీమోగ్లోబిన్ ను ఏర్పరుస్తుంది. రక్తం యొక్క ఆక్సిజన్ రవాణా సామర్ధ్యం విపరీతంగా తగ్గిపోతుంది.

కార్బన్ డై ఆక్సైడ్ : అడవులను నరికివేయడం, శిలాజ జాతి ఇంధనాలను మండించడం మొదలైన చర్యల ద్వారా వాతావరణంలో CO₂స్థాయి పెరిగి, వాతావరణ సమతుల్యత లోపిస్తుంది. గాలిలో పెరిగిన CO₂ పరిమాణం కారణంగా భూగోళం వేడెక్కడం జరుగుతుంది.

నీటి కాలుష్యం : మానవ కార్యకలాపాల ద్వారా నీటి కాలుష్యం ఏర్పడుతుంది. భిన్నమార్గాల ద్వారా నీటి కాలుష్యం ఉపరితల నీటి వనరులను, భూగర్భ నీటివనరులను చేరుతుంది. COD, BOD విలువల ద్వారా నీటి కాలుష్య పరిమాణాన్ని నిర్ణయించవచ్చు.

ప్రశ్న 34.
కింది వాటిని వివరంగా తెలపండి.
(a) భూగోళం వేడెక్కడం
(b) ఓజోను తరుగుదల
(c) ఆమ్ల వర్షం
(d) యూట్రోఫికేషన్
జవాబు:
(a) భూగోళం వేడెక్కడం కార్బన్ డై ఆక్సైడ్, క్లోరోఫ్లోరో కార్బన్లు, నైట్రిక్ ఆక్సైడ్ మరియు నీటిఆవిరులు పరారుణ కాంతిని శోషించుకొని మరల భూమిపైకి ఉద్గారం చేస్తాయి. ఈ క్రియ వల్ల భూమి ఉపరితలం వేడెక్కుతుంది. ఈ దృగ్విషయాన్ని భూమి వేడెక్కడం లేదా భౌగోళిక తాపనం అంటారు. ఈ తాపనానికి కారణమయ్యే వాయువులను హరిత గృహ వాయువులు అంటారు.

హరిత గృహ ప్రభావం యొక్క దుష్ప్రభావాలు :

వాతావరణంలో 1°C ఉష్ణోగ్రత పెరిగితే, ధ్రువ ప్రాంతాలలోని మంచు శిఖరాలు కరిగి, సముద్రపు నీటి మట్టం పెరుగుతుంది. దీనివల్ల అనేక తీర ప్రాంతాలు ముంపునకు గురయ్యే అవకాశం అధికంగా ఉన్నది.
భూగోళం వేడెక్కడం వలన సముద్రాలు, నదులు, సరస్సులలోని నీటి బాష్పీభవనం రేటు కూడా పెరుగుతుంది. దీని కారణంగా అకాల వర్షాలు, తుపానులు వచ్చే అవకాశం ఉన్నది.
ఉపరితల నీరు వేగంగా బాష్పీభవనం చెందటం వల్ల వ్యవసాయరంగం కూడా దుష్ప్రభావానికి గురవుతుంది. వ్యవసాయ రంగానికి నీటి కొరత అధికమౌతుంది.
చెట్లను, అడవులను పెంచటం, CFC తయారీని నిలుపుచేయటం మొ॥గు చర్యల వల్ల భౌగోళిక తాపనాన్ని నివారించవచ్చు.

(b) ఓజోను తరుగుదల : క్లోరోఫ్లోరో కార్బన్లు త్వరితంగా వాతావరణంలోని పైపొరను చేరుకొని, అక్కడి UV వికిరణాన్ని శోషించుకొని, విఘటనం చెంది క్లోరిన్ పరమాణువులను ఇస్తాయి.

స్వేచ్ఛా స్థితిలోని Cl^* పరమాణువు ఓజోన్ ను విఘటనం చెందించి O₂ ను ఇస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 12 పర్యావరణ రసాయన శాస్త్రం 7
దీనివల్ల ఓజోన్ సాంద్రతలో క్షీణత కనిపిస్తుంది. ఈ క్షీణత కారణంగా ఓజోన్ పొరకు రంధ్రాలు ఏర్పడతాయి. ఈ రంధ్రాల ద్వారా అతినీలలోహిత కిరణాలు భూమిని చేరి, మానవులకు అనేక సమస్యలను సృష్టిస్తున్నాయి. కంటిలో శుక్లాలు, చర్మ క్యాన్సర్ వంటి అనారోగ్యాలను కలుగచేస్తాయి.

(c) ఆమ్ల వర్షం : నైట్రోజన్ మరియు సల్ఫర్ యొక్క ఆక్సైడ్లు (రవాణా మరియు పారిశ్రామిక రంగాల నుండి విడుదల చేయబడినవి) వాతావరణంలోకి చేరుతాయి. అంతేకాక ఇవి నీటిలో కరిగి HNO₃ మరియు H₂SO₄లను తయారు చేస్తాయి. ఈ ఆమ్లాలు నీటిలో కరిగి, ఆమ్ల వర్షాలుగా భూమిని చేరుతాయి.
2SO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 2H₂SO₄ (జల)
4NO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 4HNO₃ (జల)

ఆమ్ల వర్ష ప్రభావాలు :

నేలలోని pH విలువ తగ్గి, భూసారం క్షీణించిపోతుంది.
కట్టడాల జీవితకాలం అనూహ్యంగా తగ్గిపోతుంది.
చలువ రాళ్ళతో కట్టిన తాజ్మహల్ గాజులా ఉండే నునుపు స్వభావం ఆమ్ల వర్ష ప్రభావానికి లోనవుతున్నది.

(d) యూట్రోఫికేషన్ : నీటి వనరులైన సరస్సులు, చెరువులలోకి వ్యవసాయ, పారిశ్రామిక రంగాల నుంచి వచ్చిన కర్బన రసాయన పదార్థాలు చేరితే ఆ నీటికి పోషక గుణం పెరుగుతుంది. ఇది విపరీతంగా ఆల్గే పెరుగుదలకు దోహదం చేస్తుంది. ఇలా పోషక గుణం పెరిగిన సరస్సును “యూట్రోఫిక్ సరస్సు” అనీ, ఈ దృగ్విషయాన్ని “యూట్రోఫికేషన్” అని అంటారు.

ప్రశ్న 35.
హరిత రసాయనశాస్త్రం పర్యావరణ కాలుష్యాన్ని నివారిస్తుంది. వివరించండి.
జవాబు:
పర్యావరణానికి ఏ మాత్రం హాని కలుగకుండా రసాయన పదార్థాలను సంశ్లేషించుటనే హరిత రసాయనశాస్త్రం అంటారు.
పాల్.టి. అనస్టాస్ కృషి ఫలితంగా రసాయనశాస్త్రానికి సంబంధించి కొన్ని ప్రాథమిక నియమాలు ఏర్పరచబడినాయి. ఈ నియమాలను పాటిస్తే కాలుష్యాన్ని నివారించవచ్చు.

వ్యర్థ పదార్థాలను నివారించాలి లేదా కనిష్ఠ స్థాయికి తగ్గించాలి.
రసాయన సంశ్లేషణను వ్యర్థ అనుజనిత పదార్థం ఏర్పడని విధంగా సూత్రీకరించాలి. లేదా అట్టి పదార్థం కనిష్ఠ స్థాయిలో ఏర్పడే విధంగా సూత్రీకరించాలి.
క్రియాజనకాలను, కారకాలను గరిష్ఠ స్థాయిలో ఉత్పన్నాలుగా మార్చాలి.
ఉదా : డీల్స్ – ఆల్డర్ చర్య.
ఆరోగ్యానికి హానికర లేదా ప్రమాదకర ఉత్పన్నాలను నిరోధించాలి.
తక్కువశక్తితో (వేడి . మొ॥) మరియు తక్కువ సమయంలో సంశ్లేషణ పూర్తి అయ్యే విధంగా రసాయన చర్యను ఎన్నుకోవాలి.
సంశ్లేషణలో బాష్పశీల మరియు కర్బన ద్రావణులను వీలైనంత వరకు నివారించాలి. ఎందుకంటే ఇట్టి ద్రావణులు తక్కువ ఉష్ణోగ్రత వద్ద ఆవిరై వాతావరణాన్ని కలుషితం చేస్తాయి. బెంజీన్ వంటి కొన్ని ద్రావణులైతే క్యాన్సర్ కారకాలు. అందుకే నీటిలో జరిపే చర్యలు చాలా క్షేమకరం.

కొన్నిసార్లు అసలు ద్రావణమే లేకుండా ఘనస్థితిలో రసాయనచర్యలు జరపగలిగి ఉంటాయి. ఆ విధమైన సంశ్లేషణత హరిత సంశ్లేషణత అవుతుంది.
ఈ నియమాలను పాటిస్తే కాలుష్యం నివారించబడుతుంది.

అదనపు ప్రశ్నలు

ప్రశ్న 1.
నీటిలో ఫ్లోరైడ్ ఉండటం వల్ల ఏం జరుగుతుంది ?
జవాబు:
త్రాగేనీటిలో ఫ్లోరైడ్ గాఢత 2 ppm మించకుండా ఉంటే అది హానికరం కాదు. అదే గాఢత 2 ppm దాటితే ఆరోగ్యానికి హానికరం. ఒకవేళ ఫ్లోరైడ్ గాఢత అధికంగా కలిగిన నీటిని త్రాగితే అందులోని F^– అయానులు మన శరీరంలోని ఎముకలు, దంతాలలోని కాల్షియంతో చర్య జరిపి కాల్షియం ఫ్లోరైడులను తయారుచేస్తాయి.
Ca + F₂ → CaF₂
ఈ చర్య వలన దంతాలు పసుపు వర్ణంలోకి మారతాయి. అంతేకాక శరీరంలోని ఎముకలు బలహీనపడతాయి.

ప్రశ్న 2.
నీటిలో ఫ్లోరైడులను తొలగించే నల్గొండ పద్ధతిని వ్రాయండి.
జవాబు:
నల్గొండ పద్ధతి : ఈ పద్ధతిలో విరంజనచూర్ణం, సున్నం, పటిక ఇదే క్రమంలో నీటిలో కలిపి ఆ నీటిని కొంతకాలం నిలవ ఉంచుతారు. నీటిలోని ఫ్లోరైడ్ అయాన్లు కాల్షియం అమోనియం ఫ్లోరైడ్ అని సంక్లిష్టంగా అవక్షేపం చెందుతాయి. దీనిని వడపోస్తారు. ఏర్పడ్డ శుద్ధ నీటిని అవసరాలకు ఉపయోగిస్తారు.

ప్రశ్న 3.
పారిశ్రామిక వ్యర్థాలు గురించి వ్రాయండి.
జవాబు:
పారిశ్రామిక ఘనస్థితి వ్యర్థపదార్థాలను జీవవిచ్ఛిన్నశీలత గల పదార్థాలుగాను, జీవ విచ్ఛిన్నశీలతలేని వ్యర్థపదార్థాలుగాను వర్గీకరిస్తారు.
పత్తిమిల్లులు, ఆహారపదార్థాలను తయారుచేసే యూనిట్లు, కాగితపు మిల్లులు జీవవిచ్ఛిన్నశీలత గల వ్యర్థపదార్థాలను ఉత్పన్నం చేస్తాయి.

విద్యుత్ను ఉత్పత్తి చేయడంలో ఫ్లై బూడిదను విడుదల చేసే యంత్రాగారాలు, బ్లాస్ట్ బల్బు నుంచి వెలువడే లోహమలం, జీవవిచ్ఛిన్నశీలత లేని వ్యర్థపదార్థం.
జీవవిచ్ఛిన్నశీలతలేని పారిశ్రామిక ఘనస్థితి వ్యర్థపదార్థాలను సరైన క్రమమైన పద్ధతుల ద్వారా పరిష్కరించకపోతే అవి పర్యావరణానికి ప్రమాదాన్ని కల్గిస్తాయి.

ప్రశ్న 4.
కొన్ని సేంద్రియ కాలుష్య కారకాలు తెలపండి.
జవాబు:
మలాథియాన్, DDT, క్లోరోఫినాక్స్ వర్ణసమ్మేళనాలు, ఫినైల్ మెర్క్యురీ ఎసిటేట్ మొ||నవి..

ప్రశ్న 5.
పర్యావరణాన్ని కాలుష్యం నుంచి ఎలా కాపాడుకోవచ్చు ?
జవాబు:
పర్యావరణం కలుషితం కాకుండా ఉండాలంటే ఈ క్రింది జాగ్రత్తలు తీసుకోవాలి.

వ్యర్థ పదార్థాల నిర్వహణ.
క్రిమిసంహారక మందులు, తెగుళ్ళ మందులు తయారుచేసే పరిశ్రమలలో వెలువడే వ్యర్థ పదార్థాలను జీవ పతనం చెందించాలి.
హరిత రసాయనశాస్త్రాన్ని విస్తరింపచేయటం.
అడవులను పెంచాలి.
సంప్రదాయ ఇంధనాలకు బదులుగా సంప్రదాయేతర ఇంధనాల ఉత్పత్తిని, వాడుకను ఎక్కువ చేయాలి. సౌరశక్తిని నిలువచేసే విధానాలపై దృష్టి సారించాలి.
ప్లాస్టిక్లను జీవపతనం చెందించాలి.
అధిక జనాభాను అరికట్టాలి.
మామూలు రసాయన పద్ధతులకు బదులుగా జీవసాంకేతిక పద్ధతులను పరిశ్రమలలో ఉపయోగించాలి.
ప్రజలకు పర్యావరణ కాలుష్యం వల్ల జరిగే నష్టాలను తెలియజేయడం, పర్యావరణాన్ని పరిశుభ్రంగా ఉంచాల్సిన అవసరం తెలియజేయడం.

TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbolic Functions Ex 9(a)

January 19, 2024January 17, 2024 by Mahesh

Students must practice these TS Intermediate Maths 1A Solutions Chapter 9 Hyperbolic Functions Ex 9(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Hyperbolic Functions Solutions Exercise 9(a)

I.
Question 1.
If sinh x = \(\frac{3}{4}\) find cosh (2x) and sinh (2x). (May 2014, Mar.’14, ’12)
Answer:
Given sinh x = \(\frac{3}{4}\)
and we have cosh² x – sinh² x = 1
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 1

Question 2.
If sinhx = 3, then show that
x = log_e(3 + √10) (Board New Model Paper).
Answer:
Given sin hx = 3
⇒ x = sinh^-1 3 = log_e (3 + \(\sqrt{3^2+1}\))
= log_e (3 + √10)
(∵ sinh x = log (x + \(\sqrt{x^2+1}\)) ∀ x ∈ R)

Question 3.
Prove that
(i) tanh (x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh x \tanh y}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 2

(ii) coth (x – y) = \(\frac{{coth} x \cdot {coth} y-1}{{coth} y-{coth} x}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 3

Question 4.
Prove that
(i) (cosh x – sinh x)ⁿ
= cosh (nx) – sinh (nx) for any n ∈R.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 4

(ii) (cosh x + sinh x)ⁿ = cosh (nx) + sinh (nx) for any n ∈ R.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 5

Question 5.
Prove that
\(\frac{\tanh x}{{sech} x-1}+\frac{\tanh x}{{sech} x+1}\) = -2cosechx for x ≠ 0.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 6

Question 6.
Prove that \(\frac{\cosh x}{1-\tanh x}+\frac{\sinh x}{1-{coth} x}\) = sinhx + coshx for x ≠ 0.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 7

Question 7.
For any x ∈ R, prove that cosh⁴ x – sinh⁴ x = cosh 2x.
Answer:
cosh⁴ x – sinh⁴ x
= (cosh² x)² – (sinh² x)²
= (cosh² x + sinh² x) (cosh² x – sinh² x)
= cosh 2x (1) = cosh 2x

Question 8.
If u = log_e \(\left\{\tan \left(\frac{\pi}{4}+\frac{\theta}{2}\right)\right\}\) and if cos θ > 0 then prove that cosh u = sec θ
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 9 Hyperbola Ex 9(a) 8

TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్

January 19, 2024January 17, 2024 by Mahesh

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 11th Lesson P బ్లాక్ మూలకాలు – 14వ గ్రూప్ Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 11th Lesson P బ్లాక్ మూలకాలు – 14వ గ్రూప్

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
గ్రూపు 14 మూలకాల ఆక్సీకరణ స్థితులలో మార్పును చర్చించండి.
జవాబు:
14వ గ్రూపు మూలకాల బాహ్యతమ కర్పరంలో 4 ఎలక్ట్రానులు ఉన్నాయి. ఈ మూలకాలు కనబరచే సాధారణ ఆక్సీకరణ స్థితులు +4, + 2. కార్బన్ ఋణ ఆక్సీకరణ స్థితుల్ని కూడా చూపుతుంది.
+ 4 ఆక్సీకరణ స్థితిలో ఉన్న సమ్మేళనాలు సమయోజనీయ స్వభావం కలవిగా ఉంటాయి. భారతర మూలకాలలో +2 ఆక్సీకరణ స్థితిని చూపే ప్రవృత్తి పెరిగే క్రమం Ge < Sn < Pb. కార్బన్, సిలికాన్లు తరచుగా +4 ఆక్సీకరణ స్థితిని చూపుతాయి. జెర్మేనియం స్థిర సమ్మేళనాలను +4 స్థితిలో ఏర్పరుస్తుంది. టిన్ రెండు (+2, +4) ఆక్సీకరణ. స్థితులలోను సమ్మేళనాలను ఏర్పరుస్తుంది. లెడ్ సమ్మేళనాలు +2 స్థితిలో స్థిరమైనది.

ప్రశ్న 2.
క్రింది సమ్మేళనాలు నీటితో ఎలా ప్రవర్తిస్తాయి.
a) BCl₃
b) CCl₄
జవాబు:
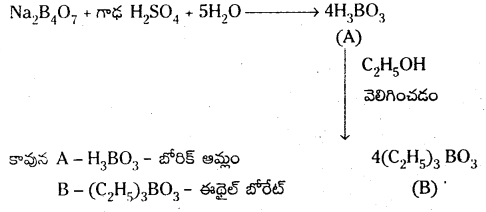
a) BCl₃ నీటితో చర్య పొంది H₃BO₃ ను ఏర్పరుస్తుంది.
BCl₃ + 3 H₂O → H₃BO₃ + 3HCl
b) CCl₄ నీటితో చర్య పొందదు. నీటిలో కరుగదు. వేరే ప్రావస్థగా వుంటుంది.

ప్రశ్న 3.
BCl₃, SiCl₄ ఎలక్ట్రాన్ కొరత ఉన్న సమ్మేళనాలా ? వివరించండి.
జవాబు:
BCl₃ లో బోరాన్ బాహ్య కర్పరంలో ఎలక్ట్రాన్ అష్టకం లేదు. కనుక అది ఎలక్ట్రాన్ కొరత గల సమ్మేళనం.
SiCl₄ లోని Si కు బాహ్య కర్పరంలో ఎలక్ట్రాన్ అష్టకం ఉన్నది. అది ఎలక్ట్రాన్ కొరత గల సమ్మేళనం కాదు.

ప్రశ్న 4.
క్రింది వాటిలో కార్బన్ సంకరీకరణాన్ని సూచించండి.
a) C\(\mathrm{O}_3^{-2}\)
b) వజ్రం
c) గ్రాఫైట్
d) పుల్లరీన్
జవాబు:
a) C\(\mathrm{O}_3^{-2}\) : …….. sp² సంకరీకరణం
b) వజ్రం : ………… sp³ సంకరీకరణం
c) గ్రాఫైట్ : ……… sp² సంకరీకరణం
d) పుల్లరీన్ : …….. sp² సంకరీకరణం

ప్రశ్న 5.
CO ఎందుకు విషపూరితమైనది ? (March 2013)
జవాబు:
CO విషపూరితమైనది. అది రక్తంలోని హిమోగ్లోబిన్ తో కలిసి స్థిరమైన సంక్లిష్టం ఏర్పరుస్తుంది. అందువల్ల హీమోగ్లోబిన్
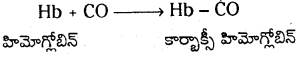
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 1
కార్బాక్సీ హిమోగ్లోబిన్ ఆక్సీహిమోగ్లోబిన్ కన్నా 300 రెట్లు అధిక స్థిరమైనది.

ప్రశ్న 6.
రూపాంతర (allotropy) అంటే ఏమిటి ? స్పటిక రూపంలోని కార్బన్ భిన్న రూపాంతరాలను తెలపండి. (March 2013)
జవాబు:
ఒకే మూలకం భిన్న భౌతిక రూపాలలో లభించుటను రూపాంతరత అంటారు.
కార్బన్ మూడు స్ఫటిక రూపాంతరాలలో లభిస్తోంది. అవి వజ్రం, గ్రాఫైట్, ఫుల్లరిన్.

ప్రశ్న 7.
కింది ఆక్సెడులను తటస్థ, ఆమ్ల, క్షార, ద్విస్వభావం గల వాటిగా వర్గీకరించండి.
a) CO
b) B₂O₃
c) SiO₂
d) CO₂
e) Al₂O₃
f) PbO₂
g) Tl₂O₃
జవాబు:
a) CO – తటస్థ
b) B₂O₃ – ఆమ్ల
c) SiO₂ – ఆమ్ల
d) CO₂ – ఆమ్ల
e) Al₂O₃ – ద్విస్వభావ
f) PbO₂ – ద్విస్వభావ
g) Tl₂O₃ – క్షార
e) Al₂O₃ – ద్విస్వభావ
f) PbO₂ – ద్విస్వభావ
g) Tl₂O₃ – క్షార

ప్రశ్న 8.
మనిషి (కృత్రిమంగా) తయారుచేసిన ఏవైనా రెండు సిలికేట్ల పేర్లు రాయండి.
జవాబు:

గాజు
సిమెంట

ప్రశ్న 9.
గ్రూపు 14 మూలకాల బాహ్య ఎలక్ట్రాన్ విన్యాసాన్ని రాయండి.
జవాబు:
గ్రూపు 14 మూలకాలు కార్బన్ (C); సిలికాన్ (Si); జెర్మేనియం (Ge); టిన్ (Sn) మరియు లెడ్ (Pb).
వాటి ఎలక్ట్రాన్ విన్యాసాలు :
కార్బన్ : 1s²2s²2p² (Z = 6)
సిలికాన్ : 1s²2s²2p⁶3s²3p² (Z = 14)
జెర్మేనియం : 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p² (Z = 32)
టిన్ : 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰5s²5p² (Z = 50)
లెడ్ : 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰4f¹⁴5s²5p⁶5d¹⁰6s²6p² (Z = 82)
గ్రూపు 14 మూలకాల సాధారణ ఎలక్ట్రాన్ విన్యాసం ns²np².

ప్రశ్న 10.
గ్రాఫైట్ కందెనలాగా ఎట్లా పనిచేస్తుంది ?
జవాబు:
గ్రాఫైట్ ద్వి జ్యామితీయ పొరల నిర్మాణం కలిగి ఉంటుంది. అంతేగాక ఈ పొరలు ఒకదానిపై ఒకటి జారుతూ ఉంటాయి. అందుకనే గ్రాఫైట్ కందెనగా పనిచేస్తుంది.

ప్రశ్న 11.
గ్రాఫైట్ మంచి వాహకం – వివరించండి.
జవాబు:
గ్రాఫైట్ ప్రతి కార్బన్ పరమాణువు వద్ద సంకరీకరణంలో పాల్గొనని p – ఆర్బిటాల్లో ఎలక్ట్రాన్ ఉంది. దీనినే స్వేచ్ఛా ఎలక్ట్రాన్ అంటారు. ఒక్కొక్క కార్బన్ పరమాణువు మూడు ఆసన్న కార్బన్ sp² సంకర ఆర్బిటాల్లను ఉపయోగించుకొని మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. నాలుగవ ఎలక్ట్రాన్ π బంధాన్ని ఏర్పరుస్తుంది. ఈ ఎలక్ట్రాన్లు మొత్తం పొర అస్థానీకృతం అవుతాయి. ఈ ఎలక్ట్రానులు చలనంలో ఉంటాయి. అందువల్ల గ్రాఫైట్ మంచి విద్యుద్వాహకం.

ప్రశ్న 12.
సిలికా నిర్మాణాన్ని వివరించండి.
జవాబు:
సిలికాన్ డై ఆక్సైడును సిలికా అంటారు. సిలికాన్ డై ఆక్సైడ్ సమయోజనీయ, త్రిమితీయ అల్లిక గల ఘనం. ఇందులో సిలికాన్ పరమాణువు సమయోజనీయ బంధంతో టెట్రా హెడ్రల్ రీతిలో నాలుగు ఆక్సిజన్ పరమాణువులతో కలిసి ఉంటుంది. ప్రతి ఆక్సిజన్ పరమాణువు ఇంకొక సిలికాన్ పరమాణువుతో సమయోజనీయ బంధంతో ఉంటుంది. మొత్తం స్ఫటికాన్ని బృహత్ అణువుగా భావించవచ్చు.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 2

ప్రశ్న 13.
“సంశ్లేషణ వాయువు” అంటే ఏమిటి ?
జవాబు:
వేడిగానున్న కోక్ మీదకు నీటి ఆవిరిని పంపడం ద్వారా వ్యాపార పద్ధతిలో CO, H₂ ల మిశ్రమాన్ని తయారుచేస్తారు. ఏర్పడిన CO, H₂ ల మిశ్రమాన్ని సంశ్లేషణ వాయువు అంటారు.

ప్రశ్న 14.
“ప్రొడ్యూసర్ వాయువు” అంటే ఏమిటి ?
జవాబు:
CO, N₂ ల మిశ్రమాన్ని ప్రొడ్యూసర్ గ్యాస్ అంటారు. దీని సంఘటనం CO = 33%, N₂ = 64%, CO₂ మరియు
H₂ = 2.5%

ప్రశ్న 15.
వజ్రానికి అధిక ద్రవీభవన ఉష్ణోగ్రత ఉంటుంది. వివరించండి.
జవాబు:
వజ్రం త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. ప్రతి కార్బన్ sp³ సంకరీకరణం చెందుతుంది. ప్రతి కార్బన్ నాలుగు ఇతర కార్బన్ పరమాణువులతో sp³ సంకర ఆర్బిటాళ్ళతో బంధాలను ఏర్పరుస్తుంది. ఈ నిర్మాణం ప్రాదేశికంగా వ్యాపించి కార్బన్ పరమాణువులతో దృఢమైన త్రిమితీయ అల్లికను ఏర్పరుస్తుంది. ఇలా వ్యాపించి ఉన్న సమయోజనీయ బంధాలను విచ్ఛిన్నం చేయడం చాలా శక్తితో కూడుకున్న పని. అందువల్ల వజ్రానికి అధిక ద్రవీభవన ఉష్ణోగ్రత ఉంటుంది.

ప్రశ్న 16.
కిరణజన్య సంయోగ క్రియలో CO₂ పాత్ర ఏమిటి ?
జవాబు:
కిరణజన్య సంయోగక్రియ ద్వారా పచ్చటి చెట్లు వాతావరణంలోని కార్బన్ డై ఆక్సైడ్ను గ్లూకోజ్ వంటి కార్బోహైడ్రేటులుగా మారుస్తాయి.
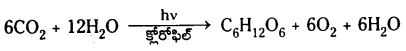
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 3

ప్రశ్న 17.
హరిత గృహ ప్రభావాన్ని ఏ విధంగా CO₂ పెంచుతుంది ?
జవాబు:
శిలాజ ఇంధనాల దహనం పెరగడం, సిమెంట్ను ఉత్పత్తి చేయడానికి ఇటీవలి కాలంలో లైమ్ స్టోన్ వినియోగం బాగా పెరగడం వల్ల వాతావరణంలో CO₂ భాగం పెరుగుతోంది. దీనివల్ల హరితగృహ ఫలితం పెరుగుతోంది.

ప్రశ్న 18.
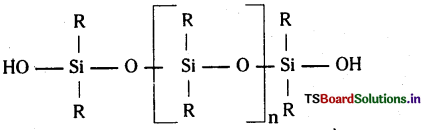
సిలికోన్లు అంటే ఏమిటి ?
జవాబు:
సిలికోన్లు ఆర్గానో సిలికాన్ సమ్మేళనాలు. వీటిలో సిలికాన్ కు ఆక్సిజన్, కార్బన్లు బలంగా బంధింపబడి ఉంటాయి.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 4

ప్రశ్న 19.
సిలికోన్ల ఉపయోగాలు వ్రాయండి.
జవాబు:
సిలికోన్ల ఉపయోగాలు :

వాటర్ ఫ్రూఫ్ బట్టలు, కాగితాలను తయారుచేయడానికి వాడతారు.
సిలికోన్ రబ్బరు ఉత్తమ విద్యున్నిరోధకం. అందువల్ల ఎలక్ట్రికల్ మోటార్లలో ఉపయోగిస్తారు.
వీటికి రసాయన జడత్వం ఉన్నది. అందువలన అధిక ఉష్ణోగ్రతలను తట్టుకుంటాయి. ఈ కారణంగా వాటిని పెయింట్లలోనూ, పింగాణీలలోనూ ఉపయోగిస్తారు.
ద్రవ సిలికోన్ల స్నిగ్ధత ఉష్ణోగ్రతతో మారదు. -40°C వద్ద కూడ ఇవి గడ్డ కట్టవు. అందువలన వీటిని విమానాలలో కందెనగా వాడతారు.
సిలికోన్ నూనెలు అధిక స్థిరత్వం కలిగి ఉంటాయి. వేడిచేసినా కూడా ఆవిరి చెందవు. అందువలన వాటిని అధిక ఉష్ణోగ్రతల వద్ద ఆయిల్ బాథ్ మరియు అధిక శూన్యత పంపులలోనూ వాడతారు.

ఈ విధంగా ఆధునిక యుగంలో సిలికోన్లను అన్ని రంగాలలో వాడతారు.

ప్రశ్న 20.
తగరం (టిన్) మీద నీటి ప్రభావం ఏమిటి ?
జవాబు:
టిన్ నీటి ఆవిరిని వియోగం చెందించి డై ఆక్సైడు, డై హైడ్రోజన్లను ఏర్పరుస్తుంది.

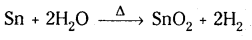
ప్రశ్న 21.
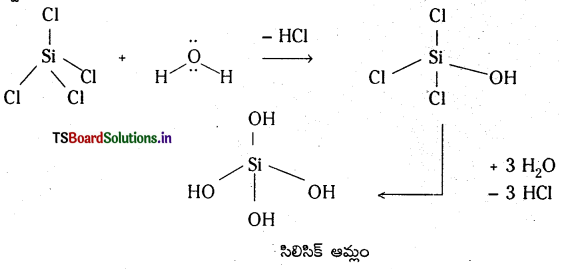
SiCl₄ గురించి వ్రాయండి.
జవాబు:
సిలికాన్ టెట్రా క్లోరైడును సిలికాన్పై క్లోరిన్ చర్యవల్ల ఏర్పడుతుంది.
Si + 2Cl₂ – SiCl₄
SiCl₄ బాష్పశీలి ద్రవం. నీటి అణువు ఇచ్చే ఒంటరి ఎలక్ట్రాన్ జంటను Si లోని d ఆర్బిటాల్ స్వీకరించి Si(OH)₄ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 6

ప్రశ్న 22.
CO₂ వాయువు కానీ SiO₂ ఘనపదార్థం – వివరించండి.
జవాబు:
సిలికాన్ డై ఆక్సైడ్ త్రిమితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. ప్రతి సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో చతుర్ముఖీయంగా నాలుగు సమయోజనీయ బంధాలతో బంధింపబడి ఉంటుంది. అందువలన SiO₂ ఘనపదార్థంగా ఉంటుంది.

CO₂ రేఖీయ అణువు. ఈ అణువులు విడివిడిగా ఉంటాయి. ఈ అణువుల మధ్య వాన్ డర్వాల్ బలాలు ఉంటాయి. అందువలన CO₂ వాయువుగా ఉంటుంది.

ప్రశ్న 23.
ZSM – 5 ఉపయోగం వ్రాయండి.
జవాబు:
జియొలైట్లను ఉత్ప్రేరకాలుగా వాడతారు. ZSM-5 అనే జియోలైట్ను ఆల్కహాల్లను నేరుగా గాసోలిన్ మార్చడానికి ఉపయోగిస్తారు.

ప్రశ్న 24.
పొడి మంచు ఉపయోగం ఏమిటి ?
జవాబు:
ఘన CO₂ ను పొడి మంచు అంటారు. ఐస్క్రీమ్, అతిశీతలమైన ఆహారపదార్థాల కోసం ప్రశీతకంగా ఉ పయోగిస్తున్నారు. బరువైనదీ, దహనానికి దోహదపడేదీ కనుక దీనిని మంటలను ఆర్పడానికి వాడతారు.

ప్రశ్న 25.
జలవాయువు (Water gas) ను ఎలా తయారుచేస్తారు ?
జవాబు:
వేడిగా నున్న కోక్ మీదకు నీటి ఆవిరిని పంపుట ద్వారా వ్యాపార పద్ధతిలో జలవాయువును తయారుచేస్తారు.
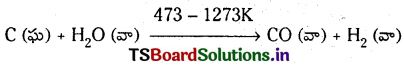
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 7

ప్రశ్న 26.
ప్రొడ్యూసర్ వాయువును ఎలా తయారుచేస్తారు ?
జవాబు:
కొలిమిని కోక్తో నింపి, దాని అడుగు భాగం నుండి వేడి గాలిని పంపుతారు. మొదట CO₂ వాయువు ఏర్పడుతుంది.
CO₂ కోల్ బెడ్ మీదుగా ప్రయాణించి CO గా క్షయకరణం చెందుతుంది.
CO, N₂ ల మిశ్రమం బయటకు వస్తుంది.
C + O₂ → CO₂
C + O₂ → 2CO

ప్రశ్న 27.
గ్రాఫైట్లో C − C బంధ దూరం, వజ్రంలో C – C బంధ దూరం కంటే తక్కువ – వివరించండి.
జవాబు:
గ్రాఫైట్ కార్బన్ C – C బంధ దూరం 141.5 pm గ్రాఫైట్లో కార్బన్ sp² సంకరీకరణం చెంది ఉంటుంది. అందువల్ల మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. నాల్గవ ఎలక్ట్రాన్ 7 బంధాన్ని ఏర్పరుస్తుంది. ద్విబంధ స్వభావం వల్ల C – C బంధ దూరం తక్కువ.
వజ్రంలో కార్బన్ sp³ ఆర్బిటాళ్ళతో C – C ఏకబంధాలను మాత్రమే ఏర్పరుస్తుంది. అందువల్ల C – C బంధ దూరం 154 pm.

ప్రశ్న 28.
వజ్రాన్ని అమూల్యమైన రాయిగా వాడతారు – వివరించండి.
జవాబు:
వజ్రానికి వక్రీభవన గుణకం గరిష్ఠంగా 2.45 ఉన్నది. కాంతి పతనమైనపుడు అధిక వక్రీభవన గుణకం వల్ల సంపూర్ణాంతర పరావర్తనం జరుగుతుంది. అందువల్ల వజ్రం కాంతి పడినపుడు ప్రకాశిస్తుంది. అందువల్ల వజ్రాన్ని అమూల్య రాయిగా వాడతారు.

ప్రశ్న 29.
కార్బన్ సంయోజకత నాలుగు కంటే ఎక్కువ ఎప్పుడూ చూపించదు. కానీ ఆ కుటుంబంలో మిగతా మూలకాలు
సంయోజకత ఆరు వరకు చూపిస్తాయి – వివరించండి.
జవాబు:
కార్బన్ బాహ్య కర్పరం 2వ కర్పరం. దీనిలో d ఆర్బిటాళ్ళు ఉండవు. అందువల్ల బాహ్య కర్పరంలో నాలుగు ఎలక్ట్రానులను ఉపయోగించుకొని నాలుగు బంధాలను మాత్రమే ఏర్పరుస్తుంది. కావున కార్బన్ సంయోజకత నాలుగుకు మించదు. మిగిలిన 14వ గ్రూపు మూలకాలు బాహ్య స్థాయిలో ఖాళీ d ఆర్బిటాళ్ళు అందుబాటులో ఉన్నాయి. అందువల్ల అవి ఎలక్ట్రాన్ జంటలను స్వీకరించగలవు. అధిక సమన్వయ సంఖ్యను చూపించగలవు.

ప్రశ్న 30.
ప్రొడ్యూసర్ వాయువు, జల వాయువు కంటె తక్కువ సామర్థ్యం గల ఇంధనం – వివరించండి.
జవాబు:
ప్రొడ్యూసర్ వాయువులో 33% CO మరియు 65% N₂ ఉన్నాయి. నైట్రోజన్ దహనశీలి కాదు. అందువల్ల దాని కెలోరిఫిక్ విలువ 5439 కి.జౌ./మీ³.
జలవాయువులో CO మరియు H₂ లు దహనశీలి వాయువులు. అందువల్ల జలవాయువులో దహనం చెందగల వాయువుల శాతం ఎక్కువ. దాని కెలోరిఫిక్ విలువ 13,000 కి.జౌ./మీ³.

ప్రశ్న 31.
Si\(F_6^{-2}\) తెలుసు కాని SiC\(l_6^{-2}\) తెలియదు వివరించండి.
జవాబు:

Si⁺ అయాన్ సైజు పరిమితి వల్ల దాని చుట్టూ ఆరు పెద్ద క్లోరైడు అయాన్లకు సరిపడినంత చోటు లేకపోవుట.
క్లోరైడు అయాన్ ఒంటరి జంట, si⁴⁺ ల మధ్య అన్యోన్య చర్య బలహీనమైనది.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 32.
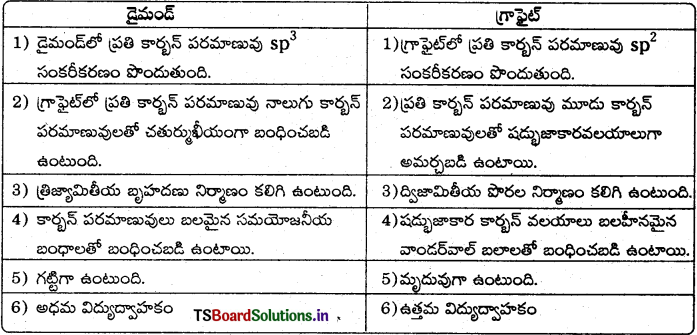
నిర్మాణాల ఆధారంగా వజ్రం, గ్రాఫైట్ల ధర్మాలలో తేడాలను వివరించండి.
జవాబు:
గ్రాఫైట్ :

1) గ్రాఫైట్ మృదువుగా వుండి, జారుడు స్వభావం కలిగి ఉంటుంది. కందెనగా ఉపయోగించవచ్చు.
కారణం : గ్రాఫైట్ ని ప్రంతి కార్బన్ (0 సంకరీకరణం చగ్రాఫైట్ పొరల నిర్మాణం కలిగి ఉండి, ఆ పొరలు ఒకదానిపై ఒకటి బలహీన వాండర్ వాల్ బలాలచే బంధించబడి ఉంటాయి. అందువల్లనే, ఒత్తిడి కలుగచేసినపుడు ఆ పొరలు ఒకదానిపై ఒకటి జారుతాయి. అందువలననే గ్రాఫైట్ మృదువుగా ఉంటుంది. కందెనగా ఉపయోగిస్తారు.

2) గ్రాఫైట్ ఉత్తమ ఉష్ణ వాహకం.
కారణం : గ్రాఫైట్లో స్వేచ్ఛా ఎలక్ట్రాన్ ఉంది. అది π బంధాన్ని ఏర్పరుస్తుంది. ఈ ఎలక్ట్రానులు మొత్తం పొర అంతా అస్థానీకృతం అవుతాయి. ఈ ఎలక్ట్రానులు చలనంలో ఉంటాయి. అందువల్ల గ్రాఫైట్ మంచి విద్యుద్వాహకం.

వజ్రం :

1) వజ్రం కఠినంగా ఉండి అరగదీసే రాయిగా పనిచేస్తుంది.
కారణం : వజ్రంలోని ప్రతి కార్బన్ sp³ సంకరీకరణం చెంది వుంటుంది. ప్రతి కార్బన్ నాలుగు ఇతర కార్బన్లతో sp³ – sp³ అతిపాతాల ద్వారా బలమైన బంధాలను ఏర్పరచడం వల్ల త్రిమితీయ బృహదణు నిర్మాణాన్ని పొందుతుంది. ఈ బంధాలను ఛేదించుట కష్టం. అందువల్ల వజ్రం కఠినం.

2) వజ్రం ఉష్ణ వాహకం కాదు.
కారణం : వజ్రంలోని కార్బన్ల వద్ద స్వేచ్ఛా ఎలక్ట్రానులు లేవు.
డైమండ్ మరియు గ్రాఫైట్ మధ్య భేదాలు :
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 8

ప్రశ్న 33.
క్రింది వాటిని వివరించండి.
a) PbCl₂, Cl₂ తో చర్య జరిగి, PbCl₄ ఇస్తుంది
b) PbCl₄ ఉష్ణ అస్థిర పదార్ధం
c) లెడ్ PbI₄ ను ఏర్పరచదు
జవాబు:
a) PbCl₂ లో Pb + 2 ఆక్సీకరణ స్థితిలో ఉన్నది. Cl₂ బలమైన ఆక్సీకారిణి. అందువల్ల అది Pb⁺² ను Pb⁺⁴ గా
ఆక్సీకరణం చేస్తుంది. కనుక PbCl₂ ను Cl₂, PbCl₄ గా ఆక్సీకరణం చేస్తుంది.

b) జడ ఎలక్ట్రాన్ జంట ప్రభావం కారణంగా Pb⁺⁺, Pb⁺⁺⁺⁺ కన్నా స్థిరమైనది. అంటే PbCl₂, PbCl₄ కన్నా స్థిరమైనది. అందువల్ల వేడి చేసినపుడు PbCl₄ ను వేడి చేస్తే Cl₂ ను కోల్పోయి PbCl₂ గా మారుతుంది.
c) Pb⁺⁴ జడ ఎలక్ట్రాన్ జంట ప్రభావం కారణంగా అస్థిరం. అందువల్ల Pb⁺⁴ మంచి ఆక్సీకారిణి. I^– మంచి క్షయకారిణి. అందువల్ల Pb⁺⁴ ను Pb⁺² గా క్షయీకరిస్తుంది. అందువల్ల PbI₄ ఏర్పడదు.

ప్రశ్న 34.
క్రింది వాటిని వివరించండి.
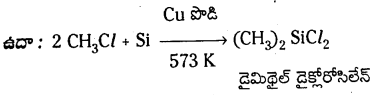
a) సిలికాన్ను మిథైల్ క్లోరైడ్తో కాపర్ సమక్షంలో అత్యధిక ఉష్ణోగ్రత వద్ద వేడి చేయబడింది.
b) SiO₂ ను HF తో చర్య జరపడం
c) గ్రాఫైట్ కందెనగా పనిచేస్తుంది
d) వజ్రం అపఘర్షకంగా ఉంటుంది.
జవాబు:
a) 573K వద్ద కాపర్ ఉత్ప్రేరకం సమక్షంలో మిథైల్ క్లోరైడ్ను సిలికాన్ పైకి పంపితే అనేక రకాలైన మిథైల్ ప్రతిక్షేపిత క్లోరో సైలేనులు, Me SiCl₃, Me₂, SiCl₂, Me₃, SiCl చాలా తక్కువ పరిమాణంలో Me₄ Si ఏర్పడతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 9

b) SiO_n ను HF తో చర్య జరపడం
SiO₂ + 4HF → SiF₄ + 2H₂O
సిలికా HF లో కరిగి Silicon టెట్రా ఫ్లోరైడ్ను ఏర్పరుస్తుంది.

c) గ్రాఫైట్ ద్విజ్యామితీయ పొరల నిర్మాణం కలిగి ఉంటుంది. అంతేగాక, ఈ పొరలు ఒకదానిపై ఒకటి జారుతూ ఉంటాయి. అందుకనే గ్రాఫైట్ కందెనగా పనిచేస్తుంది.

d) వజ్రం త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. దీనిలో ప్రతి కార్బన్ పరమాణువు నాలుగు వేరు వేరు కార్బన్లతో బలమైన ఏకబంధాలతో బంధింపబడి ఉంటుంది. అందువల్ల వజ్రం కఠిన పదార్థం. అందువల్ల అపఘర్షకంగా ఉంటుంది.

ప్రశ్న 35.
మీరేమి అర్ధం చేసుకొన్నారు :
a) రూపాంతరత
b) జడజంట ప్రభావం
c) శృంఖలత్వం (catination)
జవాబు:
a) రూపాంతరత : ఒకే మూలకం రెండు లేక అంతకన్నా ఎక్కువ భౌతిక రూపాలలో లభించడాన్ని రూపాంతరత అంటారు.
డైమండ్, గ్రాఫైట్లు, కార్బన్ స్ఫాటిక రూపాంతరాలు. కోక్, కోల్, అస్ఫాటిక రూపాంతరాలు.

b) జడజంట ప్రభావం : బాహ్య కర్పరంలో ns² ఎలక్ట్రాన్ జంట. బంధాలు ఏర్పరచడంలో పాల్గొనకపోవడాన్ని జడజంట ప్రభావం అంటారు. ఈ ప్రభావం కారణంగా తక్కువ విలువ గల ఆక్సీకరణ స్థితి అధిక ఆక్సీకరణ స్థితి కన్నా స్థిరమైనదిగా ఉంటుంది. ఒక గ్రూపు మూలకాలలో పైనుండి క్రిందకు, అల్ప ఆక్సీకరణ స్థితి స్థిరత్వం
పెరుగుతుంది.
13వ గ్రూపు మూలకాలలో +3 సాధారణ ఆక్సీకరణ స్థితి కాగా Tl లో +1 స్థితి స్థిరమైనది. అదే విధంగా 14వ గ్రూపు మూలకాలలో +4 సాధారణ ఆక్సీకరణ స్థితి కాగా Pb లో +2 స్థితి స్థిరమైనది.

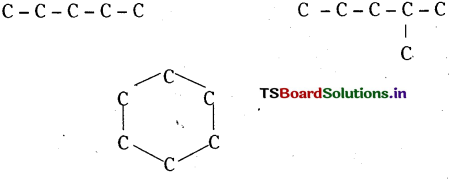
c) శృంఖలత్వం :
ఏదేని మూలక పరమాణువులు తమలో తాము గొలుసుకట్టుగా ఏర్పడే స్వభావాన్ని శృంఖలత్వం అంటారు. ఈ ధర్మం కార్బన్కు అధికం. అందువల్ల కార్బన్ గొలుసులు, వలయాలు ఏర్పడతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 10

ప్రశ్న 36.
సిలికోన్ల తయారీలో RSiCl₃ ప్రారంభ పదార్థంగా వాడితే తయారైన క్రియాజన్యాల నిర్మాణాలను రాయండి.
జవాబు:
R SiCl₃ + 3H₂O → R Si (OH)₃
జలవిశ్లేషణ ఉత్పన్నం సంఘననం చెందితే త్రిజ్యామితీయ సిలికోన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 11

ప్రశ్న 37.
జియొలైట్ల మీద సంక్షిప్తంగా రాయండి.
జవాబు:
అల్యూమినియం సిలికేటులను జియొలైట్లు అంటారు. త్రిమితీయంగా అల్లిక గల సిలికాన్ డై ఆక్సైడ్లో కొన్ని సిలికాన్ పరమాణువులను అల్యూమినియం పరమాణువులు స్థానభ్రంశం చేస్తే అల్యూమినియం సిలికేట్లు ఏర్పడతాయి. దీనికి రుణావేశం ఉంటుంది. Na⁺, K⁺ లేదా Ca⁺⁺ కేటయాన్లు రుణావేశాన్ని తుల్యం చేస్తాయి.

ఉదా : ఫెల్డ్స్పర్ జియొలైటులు. పెట్రో కెమికల్ పరిశ్రమల్లో హైడ్రోకార్బన్లను భంజనం చేయడానికి, వాటి సాదృశీకరణ చర్యలకు జియొలైట్లను ఉత్ప్రేరకాలుగా విస్తృతంగా వాడతారు. ఉదా : ZSM-5 ఆల్కహాల్లను నేరుగా గాసోలీన్ గా మార్చడానికి ఉపయోగిస్తారు. కఠినజలం కఠినత్వాన్ని తగ్గించడానికి ఆర్ద్ర జియొలైట్లను అయాన్ వినిమయాలుగా ఉపయోగిస్తారు.

ప్రశ్న 38.
సిలికేట్ల మీద సంక్షిప్తంగా వ్రాయండి.
జవాబు:
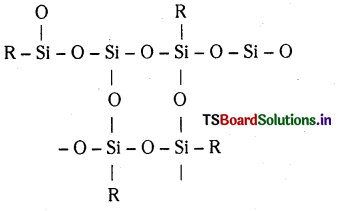
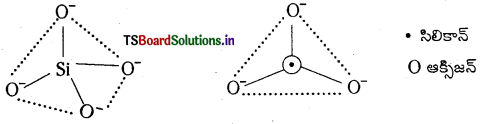
సిలికేట్ల మూల నిర్మాణాత్మక యూనిట్ Si\(\mathrm{O}_4^{4-}\). ఇందులో సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో టెట్రాహెడ్రల్ రీతిలో బంధంలో కలిసి ఉంటాయి. సిలికేట్లలో ఆక్సిజన్ పరమాణువులను ఇతర యూనిట్లతో పంచుకోవడం ద్వారా శృంఖల, వలయ, షీట్ లేదా త్రిమితీయ నిర్మాణాలు ఏర్పడవచ్చు.

సిలికేట్ యూనిట్లలో రుణావేశం ధనావేశం గల లోహ అయానులతో తటస్థీకరించబడుతుంది. ఒకవేళ, యూనిట్ యొక్క నాలుగు మూలలు ఇతర టెట్రాహెడ్రల్ యూనిట్లతో పంచుకుంటే త్రిమితీయ అల్లిక నిర్మాణాన్ని పొందుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 12

ప్రశ్న 39.
సిలికోన్లు అంటే ఏమిటి ? అవి ఏ విధంగా పొందుతారు ?
జవాబు:

సిలికోన్లు ఆర్గానో సిలికాన్ తరగతికి చెందిన అణుపుంజాలు.
సిలికోన్లలో అనేక పర్యాయాలు పునరావృతమయ్యే R₂SiO – యూనిట్ ఉంది.
సిలికోన్ల తయారీకి ఆల్కైల్ లేదా ఎరైల్ ప్రతిక్షేపిత సిలికాన్ క్లోరైడులు R_n SiCl_(4-n) ప్రారంభ పదార్థాలు. ఇందులో R ఆల్కైల్ లేదా ఎరైల్ సమూహం.
573 K వద్ద కాపర్ ఉత్ప్రేరకం సమక్షంలో మిథైల్ క్లోరైడును సిలికాన్ పైకి పంపితే అనేక రకాలైన మిథైల్ ప్రతిక్షేపిత క్లోరో సినులు ఏర్పడతాయి.
డైమిథైల్ క్లోరో సిలేన్ (CH₃)₂ SiCl₂ జలవిశ్లేషణం చెందగా ఏర్పడిన ఉత్పన్నాలు సంఘననం చెంది పొడవైన గొలుసుల అణుపుంజాలు ఇస్తాయి.

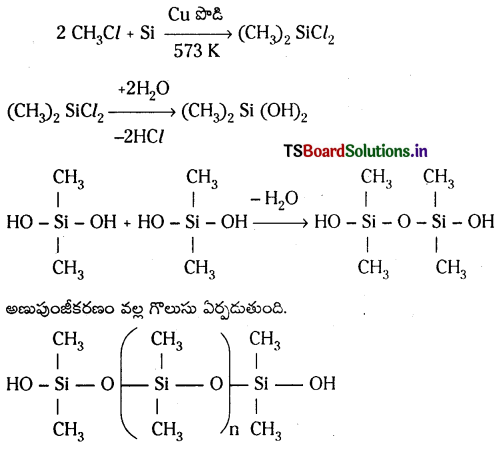
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 13
అణుపుంజీకరణం వల్ల గొలుసు ఏర్పడుతుంది.

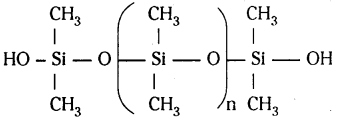
ఉపయోగాలు :

వీటిని సీల్ వేసే పదార్థాలుగా, గ్రీజులుగా, విద్యుత్ బంధకాలుగాను
బట్టలపై జలనిరోధకంగా ఉపయోగిస్తారు.
శస్త్ర చికిత్స సంబంధమైన, సౌందర్య సాధన ద్రవ్యాల తయారీ పరిశ్రమలలో వాడతారు.

ప్రశ్న 40.
ఫుల్లరీన్ మీద సంక్షిప్తంగా వ్రాయండి.
జవాబు:
ఫుల్లరీన్ కార్బన్ స్ఫాటిక రూపాంతరం
తయారుచేయుట : జడవాయువులైన హీలియం లేదా ఆర్గాన్ల సమక్షంలో గ్రాఫైట్ను విద్యుచ్ఛాపంతో వేడి చేసిన ఫుల్లరీన్ తయారవుతుంది.

బాష్పీభవనం చెందిన C_n చిన్న అణువులు ఘనీభవించడం వల్ల వచ్చిన మసిలాంటి పదార్థంలో ముఖ్యంగా C₆₀ తక్కువ పరిమాణంలో C₇₀ ఉంటాయి. కార్బన్ పరమాణువులు 350 ఆ పైన ఫుల్లరిన్లు లేశమాత్రం ఉంటాయి.

ఫుల్లరీన్లు పంజరాన్ని పోలిన అణువులు. C₆₀ అణువుకు సాకర్ బంతిని పోలిన నిర్మాణం ఉండటం వల్ల దీనిని బక్ మినిష్టర్ ఫుల్లరీన్ అంటారు. దీనిలో ఆరు కార్బన్లున్న వలయాలు ఇరవై, ఐదు కార్బన్లున్న వలయాలు పన్నెండు ఉంటాయి. ఆరు కార్బన్ల వలయం ఆరు కార్బన్ల వలయం లేదా అయిదు కార్బన్ల వలయంతో సంలీనం చెందుతాయి. కానీ అయిదు కార్బన్ల వలయాలు ఆరు కార్బన్ల వలయాలతో మాత్రమే సంలీనం చెందుతాయి. అన్ని కార్బన్లు sp² సంకరీకరణం చెంది ఉంటాయి.

ప్రతి కార్బన్ ఆసన్న కార్బన్లతో మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. మిగిలిన ఎలక్ట్రాన్ అణు ఆర్బిటాల్ తో అస్థానీకృతమయి అణువుకు ఎరోమాటిక్ స్వభావం చేకూరుస్తుంది. ఈ బంతి ఆకృతి గల అణువుకు 60 శీర్షాలు ఉన్నాయి. ప్రతి శీర్షంను ఒక కార్బన్ పరమాణువు ఆక్రమించి ఉంటుంది. ఈ కార్బన్లకు ఏక, ద్విబంధాలు రెండు ఉండి C – C బంధ దూరాలు 143.5 pm, 138.3 pm లు ఉంటాయి.

ప్రశ్న 41.
SiO₂ నీటిలో ఎందుకు కరగదు ?
జవాబు:
సిలికాన్ డై ఆక్సెడ్ సమయోజనీయ, త్రిమితీయ అల్లిక గల ఘనం. ఇందులో సిలికాన్ పరమాణువు సమయోజనీయ బంధంతో టెట్రాహెడ్రల్ రీతిలో నాలుగు ఆక్సిజన్ పరమాణువులతో కలిసి ఉంటుంది.
సాధారణ స్థితిలో సిలికా దాదాపు చర్యాశీలత లేనిది. ఎందుకంటే Si – O బంధ ఎంథాల్పీ చాలా ఎక్కువ. అందువల్లనే అది నీటిలో కరగదు.

ప్రశ్న 42.
వజ్రం కఠినంగా ఎందుకు వుంటుంది ?
జవాబు:
డైమండ్ ప్రతి కార్బన్ sp³ సంకరీకరణం చెందుతుంది. ప్రతి కార్బన్ నాలుగు ఇతర కార్బన్ పరమాణువులతో sp³ సంకర ఆర్బిటాల్లను టెట్రా హెడ్రల్ రీతిలో ఉపయోగించుకొని బంధాలను ఏర్పరుస్తుంది. ఈ నిర్మాణం ప్రాదేశికంగా వ్యాపించి కార్బన్ పరమాణువులతో దృఢమైన త్రిమితీయ అల్లికను ఏర్పరుస్తుంది. ఇలా వ్యాపించి వున్న సమయోజనీయ బంధాలను విచ్ఛిన్నం చేయడం చాలా శక్తితో కూడుకున్న పని. అందువల్ల డైమండ్ (వజ్రం) కఠినమైనది.
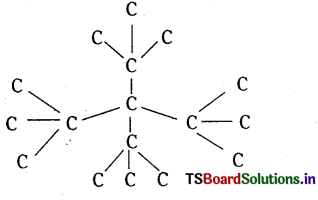
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 15

ప్రశ్న 43.
కింది వాటిని వేడి చేసినపుడు ఏమి జరుగుతుంది ?
a) CaCO₃
b) CaCO₃, SiO₂
c) CaCO₃ అధికంగా కోక్
జవాబు:
a) కాల్షియం కార్బొనేటు విఘటనం చెంది CO₂ విడుదలవుతుంది.
CaCO₃ (ఘ) → CaO (ఘ) + CO₂ (వా)

b) CaCO₃ మరియు SiO₂
CaCO₃ విఘటనం చెందినపుడు ఏర్పడిన CaO తో SiO₂ చర్యపొంది కాల్షియం సిలికేటు ఏర్పడుతుంది.
CaCO₃ → CaO + CO₂
CaO + SiO₂ → CaSiO₃

c) CaCO₃ విఘటనం వల్ల ఏర్పడిన CaO తో కోక్ చర్య పొందుతుంది. కాల్షియం కార్బైడ్ ఏర్పడుతుంది.
CaCO₃ → CaO + CO₂
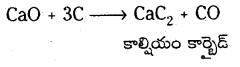
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 16

ప్రశ్న 44.
Na₂CO₃ ద్రావణాన్ని CO₂ వాయువులో సంతృప్తం చేస్తే అవలంబనం అవుతుంది. ఎందువల్ల ?
జవాబు:
నీటిలో సోడియం బైకార్బొనేటు అల్పద్రావణీయత గలది. స్వల్పంగా కరుగుతుంది. దీనికి బై కార్బొనేటు అయాన్లు హైడ్రోజన్ బంధాల వల్ల పొలిమరీకరణం చెంది ఉంటుంది. Na₂CO₃ ద్రావణంలోని CO₂ ను పంపితే అల్ప ద్రావణీయత కల సోడియం బై కార్బొనేటు ఏర్పడుతుంది. అందువల్ల NaHCO₃ అవలంబనం చెందుతుంది.
Na₂CO₃ + H₂O + CO₂ → 2 NaHCO₃

ప్రశ్న 45.
ఈ క్రింది చర్యలలో ఏమి జరుగుతుంది ?
a) తడిసున్నం ద్వారా CO₂ను పంపడం
b) CaC₂ ను N₂ తో వేడిచేయడం
జవాబు:
a) తడిసున్నంలోనికి CO₂ ను పంపితే నీటిలో కరగని CaCO₃ ఏర్పడుతుంది. ద్రావణం పాలవలె మారుతుంది.
Ca(OH)₂ + CO₂ → CaCO₃ + H₂O + CO₂
CO₂ అధికంగా పంపితే కాల్షియం బైకార్బొనేటు ఏర్పడుతుంది. అందువల్ల CaCO₃ కరుగుతుంది.
CaCO₃ + H₂O + CO₂ → Ca(HCO₃)₂
Ca(HCO₃)₂ నీటిలో కరుగుతుంది.

b) వేడి చేసిన CaC₂ మీదికి నైట్రోజన్ వాయువును పంపితే కాల్షియం సైనమైడ్ మరియు గ్రాఫైట్ల మిశ్రమం ఏర్పడుతుంది.
CaC₂ + N₂ → Ca CN₂ + C
కాల్షియం సైనమైడ్, గ్రాఫైట్ల మిశ్రమాన్ని నైట్రోలిమ్ అంటారు.

ప్రశ్న 46.
గ్రూపు 14 లో కార్బన్ అసంగత స్వభావాన్ని గురించి వ్రాయండి.
జవాబు:
ఒక గ్రూపులోని మొదటి మూలకం మిగిలిన మూలకాల కంటే భిన్న ధర్మాలను చూపుతుంది. కార్బన్ కూడా గ్రూపులోని మిగిలిన మూలకాలతో పోలిస్తే భిన్నంగా ప్రవర్తిస్తుంది. దీనికి కారణం కార్బన్కు గల తక్కువ పరిమాణం, అధిక ఋణ విద్యుదాత్మకత, అధిక అయనీకరణ ఎంథాల్పీ, d – ఆర్బిటాళ్ళు లేకపోవటం.

కార్బన్ ప్రకృతిలో స్వేచ్ఛా స్థితిలో లభిస్తుంది. మిగతా మూలకాలు ప్రకృతిలో స్వేచ్ఛా స్థితిలో దాదాపుగా దొరకవు.
కార్బన్లో అందుబాటులో ఉండే d – ఆర్బిటాళ్ళు ఉండవు. మిగతా మూలకాలలో d – ఆర్బిటాళ్ళు అందుబాటులో ఉంటాయి.
కార్బన్ అలోహం. దీని పరమాణు సైజు చాలా చిన్నది. అందువలన ఇది అధిక కోవలంటే స్వభావం ఉన్న సమ్మేళనాలను ఇస్తుంది.
కార్బన్ కెటనేషన్ అనే విశిష్ట లక్షణం చూపిస్తుంది. ఈ లక్షణం కొంతవరకు సిలికాన్లో ఉంటుంది.
కార్బన్ తన పరమాణువుల మధ్య బహు బంధాలను ఏర్పరచగలదు. అలాగే ఇతర మూలకాలతో కూడా బహు బంధాలను ఏర్పరచగలదు.
కార్బన్ యొక్క హైడ్రైడ్లను హైడ్రోకార్బన్లు అంటారు. మిగిలిన మూలకాలు కూడా హైడ్రైడ్లను ఇస్తాయి. ఈ హైడ్రైడ్ స్థిరత్వం క్రమంగా తగ్గుతుంది.
కార్బన్ క్షయకరణ సామర్థ్యం చాలా ఎక్కువ. మిగిలిన మూలకాల క్షయకరణ సామర్థ్యం తక్కువ.
కార్బన్ – హాలోజన్ సమ్మేళనాలు జల విశ్లేషణం చెందవు. కాని మిగతా మూలకాలు టెట్రాహాలైడ్లు తేలిగ్గా జలవిశేషణం చెందుతాయి.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 47.
సిలికోన్లు అంటే ఏమిటి ? వాటిని ఏ విధంగా తయారుచేస్తారు ? ఉదాహరణ ఇవ్వండి.
జవాబు:
సిలికోన్లు ఆర్గానో సిలికాన్ సమ్మేళనాలు. వీటిలో సిలికాన్కు ఆక్సిజన్, కార్బన్లు బలంగా బంధింపబడి ఉంటాయి. వీటి నిర్మాణాత్మక ఫార్ములా క్రింది విధంగా ఉంటుంది.
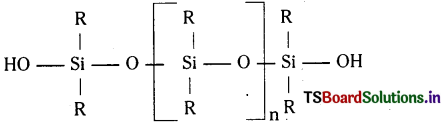
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 17
573 K వద్ద కాపర్ ఉత్ప్రేరకం సమక్షంలో మిథైల్ క్లోరైడును సిలికాన్ పైకి పంపితే అనేక రకాలైన మిథైల్ ప్రతిక్షేపిత క్లోరోసిలేనులు, ఏర్పడతాయి.

డై మిథైల్ డైక్లోరోసిలేన్ (CH₃)₂ SiCl₂ జల విశ్లేషణ చెందగా ఏర్పడిన ఉత్పన్నాలు సంఘనన అణుపుంజీకరణం చెంది పొడవైన గొలుసుల అణుపుంజాలు ఇస్తాయి.
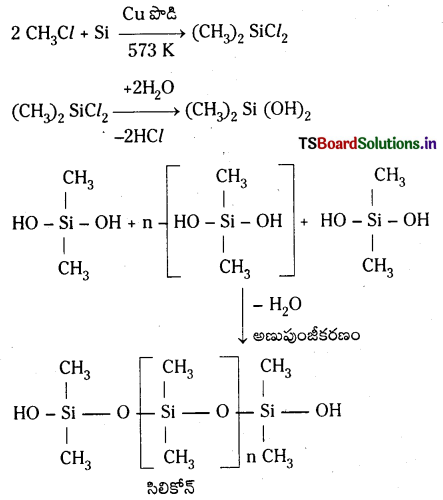
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 18
పొలిమర్ శృంఖలం పొడవును (CH₃)₃ SiCl ను కలిపి నియంత్రించవచ్చు.

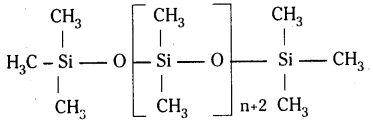
ధర్మాలు :

అధ్రువ ఆల్కెల్ సమూహాలతో చుట్టుకొన్న సిలికోన్లు జలవికర్షణ స్వభావం ఉన్నవి.
వీటికి అధిక ఉష్ణ స్థిరత్వం కలదు. ఆక్సీకరణం, ఇతర రసాయన చర్యలను నిరోధిస్తాయి.

ఉపయోగాలు :

సిలికోన్ రబ్బర్లు తయారీలో వాడతారు.
వాటర్ ఫ్రూఫ్ బట్టలు, కాగితాలు తయారుచేయడానికి వాడతారు.
విమానాలలో కందెనలుగాను, గ్రీజు తయారీలోను వాడతారు.
వీటికి రసాయన జడత్వం ఉన్నది. అందువలన అధిక ఉష్ణోగ్రతలను తట్టుకొంటాయి. కనుక పెయింటులలోను, పింగాణీలలోను ఉపయోగిస్తారు.
సీలు వేసే పదార్థాలుగా
విద్యుత్ బంధకాలుగా ఉపయోగిస్తారు.
-40°C వద్ద కూడా గడ్డ కట్టవు. అందువలన విమానాలలో కందెనగా ఉపయోగిస్తారు.

ప్రశ్న 48.
సిలికా నిర్మాణాన్ని వివరించండి. అది
a) NaOH
b) HF తో ఏ విధంగా చర్య జరుపుతుంది ?
జవాబు:
సిలికాన్ డై ఆక్సైడ్ను సాధారణంగా సిలికా అంటారు. ఇది అనేక స్ఫాటిక రూపాలలో దొరుకుతుంది. క్వార్ట్జ్, క్రిస్టో బలైట్, ట్రిడిమైట్లు సిలికా యొక్క కొన్ని స్ఫటికాకారాలు. సిలికాన్ ఆక్సైడ్ సమయోజనీయ, త్రిమితీయ అల్లికగన ఘనం.

సిలికాన్ నిర్మాణం : సిలికాలో ప్రతి సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో ఏక సమయోజనీయ బంధంతో చతుర్ముఖీయంగా అమర్చబడి ఉంటుంది. ప్రతి ఆక్సిజన్ పరమాణువు రెండు సిలికాన్ పరమాణువుల మధ్య బంధింపబడి ఉంటుంది. ఈ విధంగా SiO₂ బలమైన త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. సాధారణ స్థితిలో సిలికా దాదాపు చర్యాశీలత లేనిది. ఎందుకంటే Si – O బంధ ఎంథాల్ఫీ చాలా ఎక్కువ.

a) NaOH తో చర్య జరిపి సోడియం సిలికేటును ఏర్పరుస్తుంది.
SiO₂ + 2 NaOH → Na₂ SiO₃ + H₂O

b) HF తో చర్య జరిపి SiF₄ ను ఏర్పరుస్తుంది.
SiO₂ + 4 HF → SiF₄ + 2H₂O

ప్రశ్న 49.
కార్బన్ రూపాంతరాలపై వివరణ వ్రాయండి.
జవాబు:
కార్బన్ భిన్న రూపాలలో లభిస్తుంది. అవి స్పటిక, అస్ఫాటిక రూపాలు.

స్ఫాటిక రూపాలు : డైమండ్, గ్రాఫైట్, ఫుల్లరీన్
అస్ఫాటిక రూపాలు : కోక్, కోల్ మొదలైనవి.

డైమండ్ మరియు గ్రాఫైట్లు కార్బన్ యొక్క స్ఫటిక రూపాంతరాలు. డైమండ్ త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది.
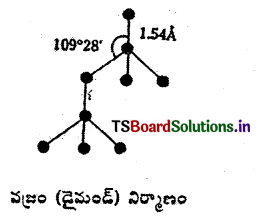
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 20
వజ్రం (డైమండ్) నిర్మాణం : వజ్రంలో ప్రతికార్బన్ పరమాణువు sp³ సంకరీకరణాన్ని పొందుతుంది. దానివలన ప్రతి కార్బన్ పరమాణువు మీద నాలుగు sp³ సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. ప్రతి కార్బన్ పరమాణువులోని నాలుగు sp³ సంకర ఆర్బిటాళ్ళు నాలుగు ఇతర కార్బన్ పరమాణువులతో బంధాలను ఏర్పరచుకుంటాయి. ప్రతి కార్బన్ పరమాణువు చతుర్ముఖీయ సౌష్ఠవాన్ని కలిగి ఉంటుంది. ఈ విధంగా కార్బన్ పరమాణువులు ఒకదానితో ఒకటి బంధింపబడి ఉండటం వలన పెద్ద అణువు ఏర్పడుతుంది.

దీనిలో C – C బంధదూరం 1.54 Ä, బంఢకోణం 190°28′

ఉపయోగాలు :

ఆభరణాలలో విలువైన రాళ్ళుగా ఉపయోగిస్తారు.
పాలరాయిని కోయడానికి ఉపయోగిస్తారు.
టంగ్స్టన్ వంటి లోహాల నుండి అతి సన్నని తీగను తీయుటకు వాడతారు.

గ్రాఫైట్ నిర్మాణము : గ్రాఫైట్ ద్విజ్యామితీయ పొరల నిర్మాణాన్ని కల్గి ఉంటుంది. ఈ నిర్మాణం కార్బన్ పరమాణువులతో కూడిన షడ్భుజాకార వలయాలను కల్గి ఉంటుంది. గ్రాఫైట్లో ప్రతి కార్బన్ పరమాణువు sp² సంకరీకరణాన్ని పొంది, మూడు ఇతర కార్బన్ పరమాణువులతో షడ్భుజాకార వలయాలుగా బంధించబడి ఉంటాయి. ఇటువంటి అనేక వలయాలు కలిసి ఒకే తలంలో ఉంటాయి. ఒంటరి ఎలక్ట్రాలు గల p ఆర్బిటాల్ ఈ తలానికి లంబంగా ఉంటుంది. ఈ p ఆర్బిటాళ్ళు ఒకదానితో ఒకటి కలిసిపోయి షడ్భుజాకార తలానికి పైన, క్రింద విస్తరించి ఉంటాయి. ఈ వలయాకారాలు ఒకదానిపై ఒకటి బలహీనమైన వాండర్వాల్ బలాలచే బంధించబడి ఉంటాయి. దీనిలో C – C బంధదూరం 1.42 రెండు వలయాల మధ్య దూరం 3.4 .
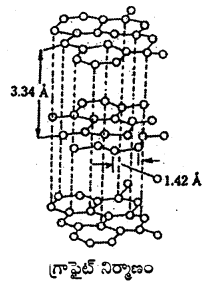
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 21

ఉపయోగాలు :

కందెనగా ఉపయోగిస్తారు.
లెడ్ పెన్సిళ్ళ తయారీలో ఉపయోగిస్తారు.
గ్రాఫైట్ ఉత్తమ విద్యుద్వాహకము. అందువల్ల ఎలక్ట్రోడ్ల తయారీలో ఉపయోగిస్తారు.

ఫుల్లరీన్ : ఫుల్లరీన్ కార్బన్ స్పాటిక రూపాంతరం

తయారుచేయుట : జడవాయువులైన హీలియం లేదా ఆర్గాన్ల సమక్షంలో గ్రాఫైట్ను విద్యుచ్ఛాపంతో వేడి చేసిన ఫుల్లరీన్ తయారవుతుంది.

బాష్పీభవనం చెందిన C_n చిన్న అణువులు ఘనీభవించడం వల్ల వచ్చిన మసిలాంటి పదార్థంలో ముఖ్యంగా C₆₀, తక్కువ పరిమాణంలో C₇₀ ఉంటాయి. కార్బన్ పరమాణువులు 350 ఆ పైన పుల్లరిన్లు లేశమాత్రం ఉంటాయి.
ఫుల్లరీన్లు పంజరాన్ని పోలిన అణువులు. C₆₀ అణువుకు సాకర్ బంతిని పోలిన నిర్మాణం ఉండటం వల్ల దీనిని బక్ మినిష్టర్ ఫుల్లరీన్ అంటారు. దీనిలో ఆరు కార్బన్లున్న వలయాలు ఇరవై, ఐదు కార్బన్లున్న వలయాలు పన్నెండు ఉంటాయి. .ఆరు కార్బన్ల వలయం ఆరు కార్బన్ల వలయం లేదా అయిదు కార్బన్ల వలయంతో సంలీనం చెందుతాయి. కానీ అయిదు కార్బన్ల వలయాలు ఆరు కార్బన్ల వలయాలతో మాత్రమే సంలీనం చెందుతాయి. అన్ని కార్బన్లు sp² సంకరీకరణం చెంది ఉంటాయి.

ప్రతి కార్బన్ ఆసన్న కార్బన్లతో మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. మిగిలిన ఎలక్ట్రాన్ ఆర్బిటాల్లతో అస్థానీకృతమయి అణువుకు ఎరోమాటిక్ స్వభావం చేకూరుస్తుంది. ఈ బంతి ఆకృతి గల అణువుకు 60 శీర్షాలు ఉన్నాయి. ప్రతి శీర్షంను ఒక కార్బన్ పరమాణువు ఆక్రమించి ఉంటుంది. ఈ కార్బన్లకు ఏక, ద్విబంధాలు రెండు ఉండి C – C బంధ దూరాలు 143.5 pm, 138.3 pm లు ఉంటాయి.

అస్ఫాటిక రూపాంతరాలు :

కోల్ : భూమిలో కొన్ని శతాబ్దాల క్రితం మట్టితో కప్పబడిపోయిన వృక్ష సంబంధమైన పదార్థాలు ఆక్సిజన్ సమక్షంలో అధిక పీడనం, ఉష్ణోగ్రతల వద్ద కృశించిపోయినపుడు కోల్ ఏర్పడుతుంది. కోల్లో కార్బన్, హైడ్రోజన్, ఆక్సిజన్, నైట్రోజన్ ఉంటాయి. 60% కార్బన్ ఉన్న కోలన్ను పీట్ అని 70% కార్బన్ ఉన్న కోల్న లిగ్నైట్ అని, 78% బిట్యూ మినస్ అని, 83% సెమి బిట్యూమినస్ కోల్, 90% కార్బన్ ఉన్నదాన్ని ఆంధ్ర సైట్ అని అంటారు.

కోక్ : కోల్న ఆక్సిజన్ లేని వాతావరణంలో విధ్వంసక స్వేదనం చర్యకు గురి చేసినపుడు భాష్పశీలి పదార్థాలయిన కోల్స్, అమ్మోనియా, బెంజీన్ లు ఏర్పడతాయి. మిగిలిన అవశేషాన్నే కోక్ అంటారు.

ఉపయోగాలు :

కోల్ను ఇంధనంగా వాడతారు.
కృత్రిమ పెట్రోలు తయారీలో వాడతారు.
కోకను స్టీలు పరిశ్రమలో క్షయకారిణిగా వాడతారు.
గ్రాఫైట్ను, వాటర్ సన్ను తయారుచేయడానికి వాడతారు.

ప్రశ్న 50.
కిందివాటిపై వివరణ వ్రాయండి.
ఎ) సిలికేట్లు
బి) జియోలైట్లు
సి) పుల్లరీన్లు
జవాబు:
ఎ) సిలికేట్లు : సిలికేట్ల మూల నిర్మాణాత్మక యూనిట్ Si\(\mathrm{O}_4^{4-}\). ఇందులో సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో టెట్రాహెడ్రల్ రీతిలో బంధంలో కలిసి ఉంటాయి. సిలికేట్లలో ఆక్సిజన్ పరమాణువులను ఇతర యూనిట్లతో పంచుకోవడం ద్వారా శృంఖల, వలయ, షీట్ లేదా త్రిమితీయ నిర్మాణాలు ఏర్పడవచ్చు.

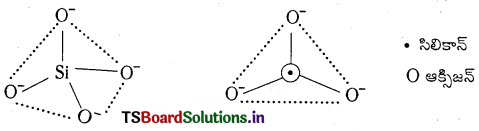
బి) జియోలైట్లు : అల్యూమినియం సిలికేటులను జియొలైట్లు అంటారు. త్రిమితీయంగా అల్లిక గల సిలికాన్ డై ఆక్సైడ్ కొన్ని సిలికాన్ పరమాణువులను అల్యూమినియం పరమాణువులు స్థానభ్రంశం చేస్తే అల్యూమినియం సిలికేట్లు ఏర్పడతాయి. దీనికి రుణావేశం ఉంటుంది. Na⁺, K⁺ లేదా Ca⁺⁺ కేటయాన్లు రుణావేశాన్ని తుల్యం చేస్తాయి.
ఉదా : ఫెల్డ్ స్పార్ జియొలైటులు. పెట్రో కెమికల్ పరిశ్రమల్లో హైడ్రోకార్బన్లను భంజనం చేయడానికి, వాటి సాదృశీకరణ చర్యలకు జియొలైట్లను ఉత్ప్రేరకాలుగా విస్తృతంగా వాడతారు. ఉదా : ZSM – 5 ఆల్కహాల్లను నేరుగా గాసోలీన్ మార్చడానికి ఉపయోగిస్తారు. కఠినజలం కఠినత్వాన్ని తగ్గించడానికి ఆర్ద్ర జియొలైట్లను అయాన్ వినిమయాలుగా ఉపయోగిస్తారు.

సి) ఫుల్లరీన్లు : ఫుల్లరీన్ కార్బన్ స్పాటిక రూపాంతరం
తయారుచేయుట : జడవాయువులైన హీలియం లేదా ఆర్గాన్ల సమక్షంలో గ్రాఫైట్ను విద్యుచ్ఛాపంతో వేడి చేసిన ఫుల్లరీన్ తయారవుతుంది.

బాష్పీభవనం చెందిన C_n చిన్న అణువులు ఘనీభవించడం వల్ల వచ్చిన మసిలాంటి పదార్థంలో ముఖ్యంగా C₆₀. తక్కువ పరిమాణంలో C₇₀ ఉంటాయి. కార్బన్ పరమాణువులు 350 ఆ పైన పుల్లరిన్లు లేశమాత్రం ఉంటాయి.

ఫుల్లరీన్ లు పంజరాన్ని పోలిన అణువులు. C₆₀ అణువుకు సాకర్ బంతిని పోలిన నిర్మాణం ఉండటం వల్ల దీనిని బక్ మినిష్టర్ ఫుల్లరీన్ అంటారు. దీనిలో ఆరు కార్బన్లున్న వలయాలు ఇరవై, ఐదు కార్బన్లున్న వలయాలు పన్నెండు ఉంటాయి. ఆరు కార్బన్ల వలయం. ఆరు కార్బన్ల వలయం లేదా అయిదు కార్బన్ల వలయంతో సంలీనం చెందుతాయి. కానీ అయిదు కార్బన్ల వలయాలు ఆరు కార్బన్ల వలయాలతో మాత్రమే సంలీనం చెందుతాయి. అన్ని కార్బన్లు sp² సంకరీకరణం చెంది ఉంటాయి.

ప్రతి కార్బన్ ఆసన్న కార్బన్లతో మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. మిగిలిన ఎలక్ట్రాన్ అణు ఆర్బిటాల్లతో అస్థానీకృతమయి అణువుకు ఎరోమాటిక్ స్వభావం చేకూరుస్తుంది. ఈ బంతి ఆకృతి గల అణువుకు 60 శీర్షాలు ఉన్నాయి. ప్రతి శీర్షంను ఒక కార్బన్ పరమాణువు ఆక్రమించి ఉంటుంది. ఈ కార్బన్లకు ఏక, ద్విబంధాలు రెండు ఉండి C – C బంధ దూరాలు 143.5 pm, 138.3 pm లు ఉంటాయి.

అదనపు పశ్నలు

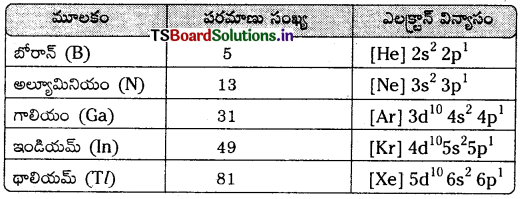
ప్రశ్న 1.
14వ గ్రూపు మూలకాలలో
1) అధిక ఆమ్ల డై ఆక్సెడును ఏర్పరచేది
2) సాధారణంగా +2 ఆక్సీకరణ స్థితిలో ఏర్పడేది.
3) అర్థవాహక ఉపకరణాలలో ఉపయోగపడేది
జవాబు:
1) కార్బన్
2) లెడ్
3) సిలికాన్, జెర్మేనియం

ప్రశ్న 2.
డైమండ్ సమయోజనీయ స్వభావం కలది. అయినప్పటికి అధిక ద్రవీభవన ఉష్ణోగ్రత ఎందుకు ?
జవాబు:
ధృఢమైన C – C బంధాల అల్లికతో ఉన్న త్రిమితీయ నిర్మాణం డైమండ్కు ఉంటుంది. దృఢమైన C – C బంధాలను విచ్ఛిన్నం చేయడానికి చాలా శక్తి కావాలి. అందువల్ల దీని ద్రవీభవన ఉష్ణోగ్రత చాలా అధికం.

ప్రశ్న 3.
కార్బన్ మోనాక్సైడ్ నిర్మాణం వ్రాయండి.
జవాబు:
CO అణువులో ఒక సిగ్మా, రెండు π బంధాలు కార్బన్ ఆక్సిజన్ల మధ్య గలవు. :C ≡ O: కార్బన్ పై ఒంటరి ఎలక్ట్రాన్ ఉండుటవలన CO అణువు ఎలక్ట్రాన్ జంట దాతగా పనిచేస్తుంది.

ప్రశ్న 4.
IV A గ్రూపులో రూపాంతరతను చూపించని మూలకం ఏది ?
జవాబు:
లెడ్

ప్రశ్న 5.
కార్బన్ మోనాక్సైడ్ యొక్క అనువర్తనాలను రాయండి.
జవాబు:

వాటర్స్, ప్రొడ్యూసర్గాస్, కోల్గాస్ల వంటి వాయు ఇంధనాలలో CO ముఖ్యమైన అనుఘటకం.
అనేక లోహ ఆక్సైడ్లను క్షయకరణం చెందించి లోహాలుగా మారుస్తుంది.
మాండ్ పద్ధతిలో Ni నిష్కర్షణలో CO ని లైగాండ్గా వాడతారు.

ప్రశ్న 6.
కార్బన్ డై ఆక్సైడ్ యొక్క అనువర్తనాలను రాయండి.
జవాబు:

ఘనస్థితిలో ఉన్న CO₂ ను డ్రై ఐస్ అంటారు. దీనిని ప్రశీతకంగా వాడతారు.
ప్రయోగశాలలో శీతలీకరణిగా వాడతారు.
యూరియాను తయారుచేయడానికి, జడవాతావరణాన్ని ఏర్పరచడానికి, క్షారాలను తటస్థీకరించడానికి వాడతారు.
అగ్నిమాపక యంత్రాలలో వాడతారు.

ప్రశ్న 7.
CO₂, SiO₂ ధర్మాలలో భేదాలు వ్రాయండి.
జవాబు:
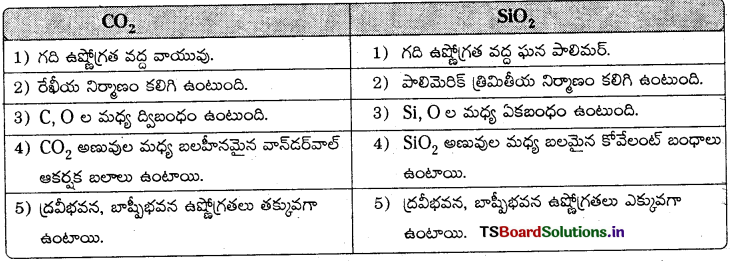
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 23

ప్రశ్న 8.
కార్బన్, సిలికాన్ల మధ్య గల పోలికలను రాయండి.
జవాబు:
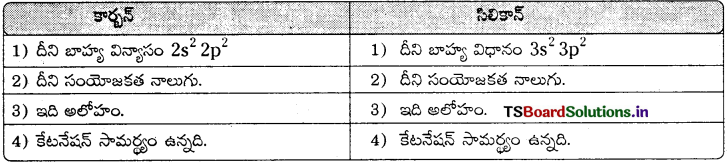
TS Inter 1st Year Chemistry Study Material Chapter 11 P బ్లాక్ మూలకాలు – 14వ గ్రూప్ 24

ప్రశ్న 9.
పెన్సిళ్ళ తయారీలో కార్బన్ యొక్క ఏ రూపాంతరాన్ని వాడతారు ?
జవాబు:
గ్రాఫైట్ను పెన్సిళ్ళ తయారీలో వాడతారు.

ప్రశ్న 10.
లెడ్ యొక్క స్థిర ఆక్సీకరణ స్థితి ఏది ? కారణం ఏమిటి ?
జవాబు:
లెడ్ యొక్క స్థిర ఆక్సీకరణ స్థితి + 2 (జడ ఎలక్ట్రాన్ +4 ఆక్సీకరణ స్థితి అస్థిరమైనది. జంట ప్రభావం వల్ల చూపదు)

ప్రశ్న 11.
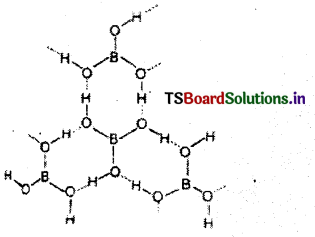
కార్బొరండం అనగా ఏమి ? ఇది ఎలా ఏర్పడుతుంది ?
జవాబు:
సిలికాన్ కార్బెడు కార్బొరండం అంటారు. విద్యుత్ కొలిమిలో సిలికాన్, కార్బన్లను కలిపి వేడి చేయడం ద్వారా దీనిని తయారుచేస్తారు.

ప్రశ్న 12.
గ్రాఫైట్లో రెండు పొరల మధ్య దూరం ఎంత ? కారణం ఏమిటి ?
జవాబు:
గ్రాఫైట్లో రెండు పొరల మధ్య దూరం 3.35. గ్రాఫైట్ పొరల మధ్య బలహీన వాన్ డర్ వాల్ బలాలు ఉండటం వల్ల పొరల మధ్య దూరం ఎక్కువగా ఉంటుంది.

ప్రశ్న 13.
CO₂మరియు SiO₂ లలో ఉండే సంకరీకరణాలు ఏమిటి ?
జవాబు:
CO₂ లో sp సంకరీకరణం ఉంటుంది. SiO₂ లో sp³ సంకరీకరణం ఉంటుంది.

ప్రశ్న 14.
డైమండ్ కఠినంగా ఉండగా గ్రాఫైట్ మృదువుగా ఉంటుంది. ఎందువలన ?
జవాబు:
డైమండ్కు బృహదణు నిర్మాణం ఉంటుంది. అందువలన అది కఠినంగా ఉంటుంది. గ్రాఫైట్లో పొరల నిర్మాణం ఉంటుంది. అందువలన అది మృదువుగా ఉంటుంది.

ప్రశ్న 15.
సిలికా ఫార్ములా SiO₂ గా ఎందుకు ఉంటుంది ?
జవాబు:
Si సిలికా నిర్మాణంలో ప్రతి టెట్రాహెడ్రన్ మూలమీద ఉన్న ఆక్సిజన్ను రెండు సిలికాన్ పరమాణువులు పంచుకుంటాయి. ప్రతి సిలికాన్ పరమాణువు శీర్షం వద్ద ఆక్సిజన్లో అర్ధ భాగాన్ని మాత్రమే ప్రదానం చేస్తుంది అన్నమాట. అందువలననే సిలికా ఫార్ములా SiO₂ అవుతుంది.

ప్రశ్న 16.
క్వార్ట్జ్ అంటే ఏమిటి ?
జవాబు:
పరిశుద్ధ సిలికాను క్వార్ట్జ్ అంటారు.

ప్రశ్న 17.
ఆర్థో సిలికేట్స్, పైరో సిలికేట్స్ మరియు చైన్ సిలికేట్స్లోలో గల యూనిట్లను తెలపండి.
జవాబు:
ఆర్థో సిలికేట్లు : Si\(\mathrm{O}_4^{-4}\) యూనిట్లు
పైరో సిలికేట్లు : SiO^-6 యూనిట్లు
చైన్ సిలికేట్లు : \(\mathrm{O}_3^{-4}\) యూనిట్లు

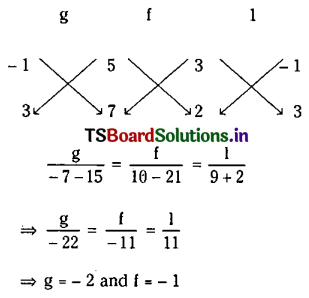
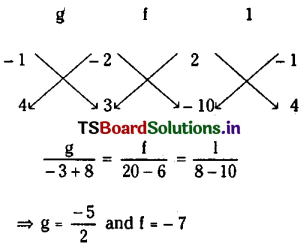
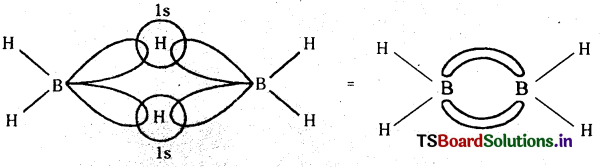
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c)

January 19, 2024January 17, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(c)

Question 1.
Find the equation of the tangent at P of the circle S = 0 where P and S are given by
(i) P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Solution:
P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Comparing the equation x² + y² – 6x + 4y – 12 =0 with the general equation we have
2g = -6, 2f = 4 and c = -12
g = -3, f = 2, c = -12
∴Equation of tangent at P(x₁, y₁) to the circle S = 0 is given by xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(7) + y(-5) – 3(x + 7) + 2(y – 5) – 12 = 0
⇒ 4x – 3y – 43 = 0

(ii) P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Solution:
P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Comparing the equation x² + y² – 6x + 4y – 12 = 0 with the general equation S = 0, we get
2g = -6, 2f = 4 and c = -12
g = -3, f = 2, c = -12
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-1) + y(1) – 3(x – 1) + 2(y + 1) – 12 = 0
⇒ -4x + 3y – 7 = 0
⇒ 4x – 3y + 7 = 0

(iii) P = (-6, -9), S ≡ x² + y² + 4x + 6y – 39
Solution:
Given P = (-6, -9) = (x₁, y₁) and S ≡ x² + y² + 4x + 6y – 39 = 0
Also 2g = 4, 2f = 6 and c = -39
g = 2, f = 3, c = -39
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-6) + y(-9) + 2(x – 6) + 3(y – 9) – 39 = 0
⇒ -4x – 6y – 78 = 0
⇒ 2x + 3y + 39 = 0

(iv) P = (3, 4), S ≡ x² + y² – 4x – 6y + 11
Solution:
Given P = (3, 4) = (x₁, y₁) and S ≡ x² + y² – 4x – 6y + 11 = 0
2g = -4, 2f = -6 and c = 11
g = -2, f = -3, c = 11
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ 3x + 4y – 2(x + 3) – 3(y + 4) + 11 = 0
⇒ x + y – 7 = 0

Question 2.
Find the equation of normal at P of the circle S = 0 where P and S are given by
(i) P = (3, -4), S ≡ x² + y² + x + y – 24
Solution:
P = (3, -4) = (x₁, y₁) and S ≡ x² + y² + x + y – 24 = 0
we have g = \(\frac{1}{2}\), f = \(\frac{1}{2}\), c = -24
∴ Equation of normal at (x₁, y₁) is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 3) (-4 + \(\frac{1}{2}\)) – (y + 4) (3 + \(\frac{1}{2}\)) = 0
⇒ (x – 3) + (-7) – (y + 4) (7) = 0
⇒ -7x – 7y – 7 = 0
⇒ x + y + 1 = 0

(ii) P = (3, 5), S ≡ x² + y² – 10x – 2y + 6
Solution:
P = (3, 5) = (x₁, y₁) and S ≡ x² + y² – 10x – 2y + 6 = 0
2g = -10, 2f = -2, c = 6
g = -5, f = -1
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 3) (5 – 1) – (y – 5) (3 – 5) = 0
⇒ 4(x – 3) + 2(y – 5) = 0
⇒ 4x + 2y – 22 = 0
⇒ 2x + y – 11 = 0

(iii) P = (1, 3), S ≡ 3(x² + y²) – 19x – 29y + 76
Solution:
P = (1, 3) = (x₁, y₁) and S ≡ \(x^2+y^2-\frac{19}{3} x-\frac{29}{3} y+\frac{76}{3}=0\)
\(2 g=-\frac{19}{3}, 2 f=-\frac{29}{3}, c=\frac{76}{3}\)
\(g=-\frac{19}{6}, f=-\frac{29}{3}\)
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 1) (3 – \(\frac{29}{6}\)) – (y – 3) (1 – \(\frac{19}{6}\)) = 0
⇒ (x – 1) (\(\frac{-11}{6}\)) – (y – 3) (\(\frac{-13}{6}\)) = 0
⇒ -11(x – 1) + 13(y – 3) = 0
⇒ -11x + 13y – 28 = 0
⇒ 11x – 13y + 28 = 0

(iv) P = (1, 2), S ≡ x² + y² – 22x – 4y + 25
Solution:
P = (1, 2) = (x₁, y₁) and S ≡ x² + y² – 22x – 4y + 25 = 0
2g = -22, 2f = -4 and c = 25
g = -11, f = -2
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 1) (2 – 2) – (y – 2) (1 – 11) = 0
⇒ -(y – 2) (-10) = 0
⇒ y – 2 = 0
⇒ y = 2

II.

Question 1.
Find the length of the chord intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3. (May. ’11)
Solution:
Given equation of circle is x² + y² – x + 3y – 22 = 0
comparing with general equation S = 0, we get
2g = -1, 2f = 3 and c = -22
g = \(-\frac{1}{2}\), f = \(\frac{3}{2}\)
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) II Q1
Given line is y = x – 3 and L = x – y – 3 = 0.
AB is the chord intercepted by the line L = 0 on the circle.
CM = Perpendicular distance from C\(\left(\frac{1}{2},-\frac{3}{2}\right)\) to x – y – 3 = 0.

∴ AM = √24
and the length of the chord AB = 2 AM
= 2√24
= 4√6 units

Question 2.
Find the length of the chord intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0.
Solution:
The Centre of the given circle is C(4, 1)
and radius = \(\sqrt{16+1+8}\) = 5
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) II Q2
AB is the chord intercepted by the line x + y + 1 = 0 on the circle.
CM = Perpendicular distance from C(4, 1) to x + y + 1 = 0.
∴ CM = \(\left|\frac{4+1+1}{\sqrt{1^2+1^2}}\right|=\frac{6}{\sqrt{2}}\) = 3√2
In the ∆ACM, we have AM² = AC² – CM²
= 25 – 18
= 7
∴ AM = √7
∴ Length of the chord AB = 2 AM = 2√7 units.

Question 3.
Find the length of the chord formed by x² + y² = a² on the line x cos α + y sin α = p.
Solution:
Centre of the circle x² + y² = a² is C(0, 0) and radius = ‘a’
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) II Q3
CM = Perpendicular distance from the centre C(0, 0) to the line x cos α + y sin α = p.
∴ CM = \(\left|\frac{0(\cos \alpha)+0(\sin \alpha)-p}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\right|\) = p
In the ∆ACM, we have AM² = AC² – CM² = a² – p²
∴ AM = \(\sqrt{a^2-p^2}\)
and length of the chord AB = 2.AM = 2\(\sqrt{a^2-p^2}\)

Question 4.
Find the equation of the circle with centre (2, 3) and touch the line 3x – 4y + 1 = 0.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) II Q4
If a given line touches the circle, then the perpendicular distance from the centre to the line is equal to the radius of the circle.
∴ Radius = perpendicular distance from C(2, 3) to the line 3x – 4y + 1 = 0.
∴ Radius = \(\left|\frac{3(2)-4(3)+1}{\sqrt{9+16}}\right|=\left|\frac{-5}{5}\right|\) = 1
∴ The equation of a circle with radius ‘1’ and centre (2, 3) is given by (x – 2)² + (y – 3)² = 12
∴ x² + y² – 4x – 6y + 12 = 0

Question 5.
Find the equation of the circle with centre (-3, 4) and touching y-axis.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) II Q5
Equation of y-axis is x = 0 and given that the centre C = (-3, 4)
CM = perpendicular distance from C to y = axis
i.e., x = 0,
= |-3|
= 3
∴ The equation of a circle with centre (-3, 4) and radius ‘3’ is given by (x + 3)² + (y – 4)² = 9
x² + y² + 6x – 8y + 16 = 0

Question 6.
Find the equations of tangents to the circle x² + y² – 8x – 2y + 12 = 0 at the points whose ordinates are 1.
Solution:
Let P(x₁, y₁) be a point on the circle x² + y² – 8x – 2y + 12 = 0
given that ordinates of points is ‘1’ i.e., y₁ = 1
∴ \(x_1^2\) + 1 – 8x₁ – 2 + 12 – 0
\(x_1^2\) – 8x₁ + 11 = 0 which is a quadratic equation.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) II Q6
∴ Points on the circle are P = (4 + √5, 1) and Q = (4 – √5, 1)
Equation of tangent at P(4 + √5, 1) is by the formula xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(4 + √5) + y – 4(x + 4 + √5) – 1(y + 1) + 12 = 0
⇒ 4x + √5x + y – 4x – 16 – 4√5 – y – 1 + 12 = 0
⇒ √5x – 4√5 – 5 = 0
⇒ x – 4 – √5 = 0
⇒ x = 4 + √5
Similarly the equation of tangent at Q(4 – √5, 1) is
x(4 – √5) + y – 4(x + 4 – √5) – 1(y + 1) + 12 = 0
⇒ 4x – √5x + y – 4x – 16 + 4√5 – y – 1 + 12 = 0
⇒ -√5x + 4√5 – 5 = 0
⇒ x – 4 + √5 = 0
⇒ x = 4 – √5
∴ The equation of tangents of the given circle at the points when ordinates are ‘1’ are given by x = 4 + √5, x = 4 – √5

Question 7.
Find the equations of the tangents of the circle x² + y² – 10 = 0 at the points whose abscissae are 1.
Solution:
Let P(x1, y1) be a point on the circle x² + y² – 10 = 0
given that abscissae are ‘1’
i.e., x₁ = 1
1 + \(y_1^2\) – 10 = 0
y₁ = ±3
Hence the points on the circle are P(1, 3), Q(1, -3).
Equation of tangent at the point P(1, 3) on the circle x² + y² – 10 = 0 is xx₁ + yy₁ – 10 = 0
x + 3y – 10 = 0
Similarly equation of tangent at the point Q(1, -3) on the circle x² + y² – 10 = 0 is xx₁ + yy₁ – 10 = 0
x – 3y – 10 = 0

III.

Question 1.
If x² + y² = c² and \(\frac{x}{a}+\frac{y}{b}=1\) intersect at A and B then find \(\overline{\mathbf{A B}}\). Hence deduce the condition that the line touches the circle.
Solution:
Given x² + y² = c² ……..(1)
and \(\frac{x}{a}+\frac{y}{b}=1\)
⇒ bx + ay – ab = 0 ……….(2)
Centre of the circle C = (0, 0) and the radius of the circle CA = ‘c’.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q1
If the line touches the circle that is if the line becomes a tangent to the circle, then the perpendicular distance from (0, 0) to the given line is equal to the radius of the circle.

Question 2.
The line y = mx + c and the circle x² + y² = a² intersect at A and B and if AB = 2λ then show that c² = (1 + m²) (a² – λ²).
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q2
Centre of the circle C = (0, 0).
The line y = mx + c intersects the circle at A and B.
OM = Perpendicular distance from (0, 0) to mx – y + c = 0

Question 3.
Find the equation of the circle with centre (-2, 3) cutting a chord of length 2 units on 3x + 4y + 4 = 0. (Mar. ’11)
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q3
Given the length of the chord AB = 2 units
∴ AM = 1 unit
CM = Perpendicular distance from the centre (-2, 3) to the line 3x + 4y + 4 = 0.
= \(\left|\frac{3(-2)+4(3)+4}{\sqrt{3^2+4^2}}\right|=\left|\frac{-6+12+4}{5}\right|=\frac{10}{5}=2\)
In the ΔACM, we have
AC² = AM² + CM²
= 1 + 4
= 5
∴ The equation of a circle with centre (-2, 3) and radius √5 units is (x + 2)² + (y – 3)² = 5
⇒ x² + 4x + 4 + y² – 6y + 9 = 5
⇒ x² + y² + 4x – 6y + 8 = 0

Question 4.
Find the equation of the tangent and normal at (3, 2) of the circle x² + y² – x – 3y – 4 = 0.
Solution:
Let S = x² + y² – x – 3y – 4 = 0 be the given circle, comparing with the general equation.
2g = -1, 2f = 3 and c = -4
∴ Equation of tangent at (x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 3x + 2y – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 6x + 4y – x – 3 – 3y – 6 – 8 = 0
⇒ 5x + y – 17 = 0
Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁)(x₁ + g) = 0
⇒ (x – 3) (2 – \(\frac{3}{2}\)) – (y – 2) (3 – \(\frac{1}{2}\)) = 0
⇒ (x – 3) (\(\frac{1}{2}\)) – (y – 2) (\(\frac{5}{2}\)) = 0
⇒ x – 3 – 5y + 10 = 0
⇒ x – 5y + 7 = 0

Question 5.
Find the equation of the tangent and normal at (1, 1) of the circle 2x² + 2y² – 2x – 5y + 3 = 0.
Solution:
Given equation of circle is x² + y² – x – \(\frac{5}{2}\)y + \(\frac{3}{2}\) = 0
2g = -1, 2f = \(-\frac{5}{2}\) and c = \(\frac{3}{2}\)
The point (1, 1) = (x₁, y₁)
The equation of the tangent at (x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q5

Question 6.
Prove that the tangent at (3, -2) of the circle x² + y² = 13 touches the circle x² + y² + 2x – 10y – 26 = 0 and find its point of contact
Solution:
The equation of tangent at (3, -2) to the circle x² + y² = 13 is x(3) + y(-2) – 13 = 0
3x – 2y – 13 = 0 ………..(1) [∵ By the formula, xx₁ + yy₁ – a2 = 0]
To show that (1) touches the circle x² + y² + 2x – 10y – 26 = 0.
We have to show that the perpendicular distance from the centre of the circle (-1, 5) to the line 3x- 2y – 13 = 0 is equal to the radius of the circle which is \(\sqrt{1+25+26}=\sqrt{52}\).
∴ The perpendicular distance from (-1, 5) to the line 3x – 2y – 13 = 0 is \(\left|\frac{3(-1)-2(5)-13}{\sqrt{9+4}}\right|\)
= \(\left|\frac{-26}{\sqrt{13}}\right|\)
= 2√13
= √52
Hence the tangent 3x – 2y – 13 = 0 touches the circle x² + y² + 2x – 10y – 26 = 0
Let P(h, k) be the point of contact between the tangent and the circle.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q6
Then P(h, k) will be the foot of the perpendicular drawn from C(-1, 5) to 3x – 2y – 13 = 0.
So by the formula

∴ The point of contact of the line (1) to the circle x² + y² + 2x – 10y – 26 = 0 is (5, 1).

Question 7.
Show that the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0 and also finds its point of contact. (New Model Paper and June ’10)
Solution:
Let S = x² + y² – 4x – 8y + 7 = 0 and S’ = x² + y² + 4x + 6y = 0,
comparing S = 0 with x² + y² + 2gx + 2fy + c = 0
we have 2g = -4, 2f = -8, c = 7
g = -2, f = -4, c = 7
Equation of tangent at (-1, 2) to the circle S = 0 is xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
⇒ x(-1) + y(2) + (-2)(x – 1) – 4(y + 2) + 7 = 0
⇒ -x + 2y – 2x + 2 – 4y – 8 + 7 = 0
⇒ -3x – 2y + 1 = 0
⇒ 3x + 2y – 1 = 0 ……….(1)
Centre of the circle S’ = x² + y² + 4x + 6y = 0 is (-2, -3)
If (1) touches S’ = 0, then the perpendicular distance from (-2, -3) to the line 3x + 2y -1 = 0 is equal to the radius of the circle.
Radius = \(\sqrt{4+9}=\sqrt{13}\)
Perpendicular distance from (-2, -3) to 3x + 2y – 1 = 0 is equal to \(\left|\frac{3(-2)+2(-3)-1}{\sqrt{9+4}}\right|=\left|\frac{-6-6-1}{\sqrt{13}}\right|=\sqrt{13}\)
Hence tangent at (-1, 2) to the circle S = 0 touches the circle S’ = 0.
Let P(h, k) be the point of contact of (1) and S’ = 0.
Then P(h, k) will be the foot of the perpendicular drawn from the centre (-2, -3) to the line 3x + 2y – 1 = 0.
By the formula
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q7
∴ The point of contact = (1, -1)

Question 8.
Find the equations of tangents to the circle x² + y² – 4x + 6y – 12 = 0 which are parallel to x + y – 8 = 0.
Solution:
Let S = x² + y² – 4x + 6y – 12 = 0 and comparing with x² + y² + 2gx + 2fy + c = 0 we get
g = -2, f = 3, c = -12
Centre of the circle = (2, -3)
and radius = \(\sqrt{4+9+12}\) = 5
The equation of any line parallel to x + y – 8 = 0 is of the form x + y + k = 0.
So the perpendicular distance from (2, -3) to x + y + k = 0 is equal to the radius.
∴ \(\left|\frac{2-3+k}{\sqrt{2}}\right|\) = 5
⇒ \(\left|\frac{k-1}{\sqrt{2}}\right|\) = 5
⇒ k – 1 = ±5√2
⇒ k = 1 ± 5√2
The equations of tangents to the circle S = 0 which are parallel to the line x + y – 8 = 0 are x + y + (1 ± 5√2) = 0.

Question 9.
Find the equations of the circle x² + y² + 2x – 2y – 3 = 0 which are perpendicular to 3x – y + 4 = 0.
Solution:
Centre of the circle x² + y² + 2x – 2y – 3 = 0 is (-1, 1) and radius = \(\sqrt{1+1+3}=\sqrt{5}\)
Equation of any line perpendicular to 3x – y + 4 = 0 is x + 3y + k = 0
If this is a tangent to the above circle then the perpendicular distance from (-1, 1) to the line x + 3y + k = 0 is equal to radius √5.
∴ \(\left|\frac{-1+3+\mathbf{k}}{\sqrt{1+9}}\right|\) = √5
⇒ \(\left|\frac{k+2}{\sqrt{10}}\right|\) = √5
⇒ k + 2 = ±5√2
⇒ k = -2 ± 5√2
∴ Equations of required tangents is x + 3y – 2 ± 5√2 = 0.

Question 10.
Find the equation of the tangents to the circle x² + y² – 4x – 6y + 3 = 0 which makes an angle of 45° with the X-axis.
Solution:
Centre of the circle x² + y² – 4x – 6y + 3 = 0 is (2, 3)
and radius = \(\sqrt{4+9-3}=\sqrt{10}\)
Since the tangents make an angle of 45° with X-axis we have
m = tan 45° = 1.
∴ The equation of tangent will be y = x + c
x – y + c = 0 ……….(1)
The perpendicular distance from (2, 3) to x – y + c = 0is equal to the radius of circle
∴ \(\left|\frac{2-3+c}{\sqrt{1+1}}\right|\) = √10
⇒ \(\left|\frac{c-1}{\sqrt{2}}\right|\) = √10
⇒ c – 1 = ±2√5
⇒ c = 1 ± 2√5
∴ Equations of required tangents are x – y + (1 ± 2√5) = 0

Question 11.
Find the equation of the circle passing through (-1, 0) and touching the line x + y – 7 = 0 at (3, 4).
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q11
Let the circle passes through P(-1, 0) and touching the line x + y – 7 = 0 …….(1)
at Q(3, 4), suppose centre of the circle be C = (h, k)
Then PC = PQ
⇒ PC² = PQ²
⇒ (h + 1)² + k² = (h – 3)² + (k – 4)²
⇒ h² + 2h + 1 + k² = h² – 6h + 9 + k² – 8k + 16
⇒ 8h + 8k – 24 = 0
⇒ h + k – 3 = 0 ……..(2)
Slope of the line x + y – 7 = 0 is -1
and slope of CQ is = \(\frac{\mathrm{k}-4}{\mathrm{~h}-3}\)
Since CQ is perpendicular to the line x + y – 7 = 0
we have a product of slopes = -1
∴ (\(\frac{\mathrm{k}-4}{\mathrm{~h}-3}\)) (-1) = (-1)
⇒ k – 4 = h – 3
⇒ h – k + 1 = 0 ……….(3)
Solving (2) and (3)
2h – 2 = 0
⇒ h = 1
and -k + 2 = 0
⇒ k = 2
∴ Centre of the circle C(h, k) = C(1, 2)
and radius PC = \(\sqrt{(1+1)^2+(2-0)^2}\) = √8
Hence equation of a circle with centre (1, 2) and radius √8 is given by (x – 1)² + (y – 2)² = 8
⇒ x² – 2x + 1 + y² – 4y + 4 = 8
⇒ x² + y² – 2x – 4y – 3 = 0

Question 12.
Find the equation of the circle passing through (1, -1) touching the lines 4x + 3y + 5 = 0 and 3x – 4y – 10 = 0.
Solution:
Given lines are
4x + 3y + 5 = 0 ……..(1)
3x – 4y – 10 = 0 ………(2)
Since the circle touches the given lines which are perpendicular, centre of the circle lies on the bisectors of angles between the given lines.
The bisectors of angles between the given lines are
\(\frac{4 x+3 y+5}{\sqrt{16+9}} \pm \frac{3 x-4 y-10}{\sqrt{16+9}}=0\)
⇒ (4x + 3y + 5) ± (3x – 4y – 10) = 0
⇒ 4x + 3y + 5 + 3x – 4y – 10 = 0
⇒ 7x – y – 5 = 0 ……….(3)
or
4x + 3y + 5 – 3x + 4y + 10 = 0
⇒ x + 7y + 15 = 0 ………(4)
From (3) we have y = 7x – 5
and from (4), x = -(7y + 15)
If the centre lies on y = 7x – 5 then the centre will be of the form (k, 7k – 5).
∴ The perpendicular distance from (k, 7k – 5) to the line (1) is equal to the radius of the circle.
∴ \(\left|\frac{4 k+3(7 k-5)+5}{\sqrt{16+9}}\right|=\sqrt{(k-1)^2+(7 k-5+1)^2}\)
⇒ \(\frac{|4 k+21 \mathrm{k}-10|}{5}=\sqrt{(\mathrm{k}-1)^2+(7 \mathrm{k}-4)^2}\)
⇒ \(\frac{|25 k-10|}{5}=\sqrt{k^2-2 k+1+49 k^2-56 k+16}\)
⇒ |5k – 2| = \(\sqrt{50 k^2-58 k+17}\)
⇒ (5k – 2)² = 50k² – 58k + 17
⇒ 25k² – 20k + 4 = 50k² – 58k + 17
⇒ 25k² – 38k + 13 = 0
⇒ 25k² – 25k – 13k + 13 = 0
⇒ 25k(k – 1) – 13(k – 1) = 0
⇒ k = 1 or k = \(\frac{13}{25}\)
when k = 1, centre of the circle is [1, 7(1) – 5] = (1, 2)
and radius of the centre = \(\sqrt{(1-1)^2+(2+1)^2}\) = 3
∴ Equation of required circle is (x – 1)² + (y – 2)² = 3²
⇒ x² + y² – 2x – 4y – 4 = 0
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q12

Question 13.
Show that x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0 and find its point of contact. (May ’09)
Solution:
The equation of the given circle is x² + y² – 3x + 7y + 14 = 0 ………(1)
If the line x + y + 1 = 0 ……..(2) touches the circle (1)
then the perpendicular distance from the centre of the circle C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0 is equal to the radius of the circle.
Radius of the given circle = \(\sqrt{\frac{9}{4}+\frac{49}{4}-14}=\sqrt{\frac{2}{4}}=\frac{1}{\sqrt{2}}\)
Perpendicular distance from C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0 is \(\left|\frac{\frac{3}{2}-\frac{7}{2}+1}{\sqrt{1^2+1^2}}\right|=\left|-\frac{1}{\sqrt{2}}\right|=\frac{1}{\sqrt{2}}\)
Hence circle (1) touches line (2).
Let P(h, k) be the point of contact between the circle (1) and line (2).
Then P(h, k) will be the foot of the perpendicular drawn from C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0.
∴ By the formula
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c) III Q13
∴ The point of contact of the given line with the circle (1) is (2, -3).

TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్

January 19, 2024January 17, 2024 by Mahesh

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 10th Lesson P బ్లాక్ మూలకాలు – 13వ గ్రూప్ Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 10th Lesson P బ్లాక్ మూలకాలు – 13వ గ్రూప్

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బోరాన్, థాలియం ఆక్సిడేషన్ స్థితుల మార్పు విధానాన్ని చర్చించండి.
జవాబు:
IIIA గ్రూపు మూలకాల బాహ్య ఎలక్ట్రాన్ విన్యాసం ns² np¹. ఈ విన్యాసం వలన ఈ మూలకాలన్ని +3 ఆక్సిడేషన్ స్థితిని కనపరుస్తాయి. B, Al మినహా మిగిలిన అన్ని మూలకాలు +1 ఆక్సిడేషన్ స్థితిని చూపిస్తాయి. +3 ఆక్సీకరణ స్థితి యొక్క స్థిరత్వం B నుంచి Tl కు తగ్గుతుంది. +1 ఆక్సీకరణ స్థితి యొక్క స్థిరత్వం జడ ఎలక్ట్రాన్ జంట ప్రభావం వలన పై నుంచి క్రిందకు పెరుగుతుంది.

ప్రశ్న 2.
Tl Cl₃ అధిక స్థిరత్వాన్ని ఎట్లా వివరిస్తారు ?
జవాబు:
TlCl₃ అస్థిరమైనది జడ ఎలక్ట్రాన్ జంట ప్రభావం వలన Tl⁺³ అయాన్ అస్థిరమైనది. థాలియం +1 ఆక్సీకరణ స్థితిలో స్థిరంగా ఉంటుంది. కావున TlCl స్థిరమైనది.

ప్రశ్న 3.
BF₃ లూయీ ఆమ్లంగా ఎందుకు ప్రవర్తిస్తుంది ?
జవాబు:

BF₃ ఎలక్ట్రాన్ కొరత గల సమ్మేళనం.
అష్టక విన్యాసం పొందటం కోసం ఇది ఎలక్ట్రాన్ జంటను స్వీకరిస్తుంది.
ఎలక్ట్రాన్ జంటల స్వీకర్తలను లూయీ ఆమ్లాలు అంటారు.
కావున BF₃ లూయీ ఆమ్లంగా ప్రవర్తిస్తుంది.

ప్రశ్న 4.
బోరిక్ ఆమ్లం ప్రోటాన్ ఇచ్చే ఆమ్లమా ? వివరించండి.
జవాబు:

బోరిక్ ఆమ్లం ప్రోటాన్ ఇచ్చే ఆమ్లము కాదు. కాని ఇది లూయీ ఆమ్లంగా ప్రవర్తిస్తుంది.
ఇది ఎలక్ట్రాన్ జంటను హైడ్రాక్సిల్ అయాన్ నుంచి స్వీకరించి లూయీ ఆమ్లంగా పనిచేస్తుంది.
B(OH)₃ + 2HOH → [B(OH)₄]^– + H₃\(\mathrm{O}^{+}\)

ప్రశ్న 5.
బోరిక్ ఆమ్లాన్ని వేడిచేస్తే ఏమవుతుంది ?
జవాబు:
బోరిక్ ఆమ్లాన్ని 370K కంటే ఎక్కువ ఉష్ణోగ్రతకు వేడిచేస్తే మెటాబోరికామ్లం (HBO₂) ఏర్పడుతుంది. దీనిని ఇంకా వేడిచేస్తే బోరిక్ ఆక్సైడ్ (B₂O₃) ఏర్పడుతుంది.

ప్రశ్న 6.
BF₃, B\(H_4^{-}\) ల ఆకారాలను వర్ణించండి. ఈ కణాలలో బోరాన్ సంకరకరణం రాయండి.
జవాబు:

BF₃ అణువు ఆకారం సమతల త్రిభుజాకారం. దీనిలో బోరాన్ sp² సంకరీకరణం జరుపుకుంటుంది.
B\(\mathrm{H}_4^{-}\) అణువు ఆకారం టెట్రాహెడ్రల్. దీనిలో బోరాన్ sp³ సంకరీకరణం జరుపుకుంటుంది.

ప్రశ్న 7.
Ga పరమాణు వ్యాసార్ధం Al కంటే ఎందుకు తక్కువ ఉంటుంది ? వివరించండి.
జవాబు:

గాలియంలో ఉపాంత్యకర్పరంలో పది 3d – ఎలక్ట్రాన్లు ఉంటాయి.
ఈ ఎలక్ట్రాన్ల వలన పరిరక్షక ప్రభావం తక్కువగా ఉంటుంది. కావున ‘Ga’ లో కేంద్రక ఆవేశం పెరుగును.
కావున Ga యొక్క పరమాణు వ్యాసార్ధం Al కంటే తక్కువగా ఉంటుంది.

ప్రశ్న 8.
జడజంట ప్రభావాన్ని వివరించండి.
జవాబు:
బాహ్యస్థాయి (ns) లోని ఎలక్ట్రాన్లను విడగొట్టి బంధంలో పాల్గొనకుండా చేసే ప్రభావాన్ని జడ ఎలక్ట్రాన్ జంట ప్రభావం అంటారు.

ప్రశ్న 9.
ఈ క్రింది సమీకరణాలను తుల్యంచేసి రాయండి.
a) BF₃ + LiH →
b) B₂H₆ + H₂O →
c) NaH + B₂H₆
d)

e)

జవాబు:
a) 2BF₃ + 6LiH → B₂H₆ + 6LiF
b) B₂H₆ + 6H₂O → 2 H₃BO₃ + 6H₂
c) 2NaH + B₂H₆ → 2 NaBH₄
d)

e)
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 5

ప్రశ్న 10.
బోరిక్ ఆమ్లం బహ్వణుకగా ఎందుకు ఉంటుంది ?
జవాబు:
బోరిక్ ఆమ్లం పొరలవంటి జాలక నిర్మాణాన్ని కలిగి ఉంటుంది. ఈ నిర్మాణంలో BO₃ యూనిట్లు హైడ్రోజన్ బంధాలతో కలుపబడి బహ్వణుక (పాలిమర్) అణువుగా ఏర్పడుతుంది.

ప్రశ్న 11.
డైబోరేన్, బోరజీన్లలో బోరాన్ సంకరకరణం ఏమిటి ?
జవాబు:

డై బోరేన్లో బోరాన్ sp³ సంకరీకరణం జరుపుకుంటుంది.
బోరజీన్లో బోరాన్ sp² సంకరీకరణం జరుపుకుంటుంది.

ప్రశ్న 12.
13 గ్రూప్ మూలకాల ఎలక్ట్రాన్ విన్యాసాన్ని రాయండి.
జవాబు:
13 గ్రూపు మూలకాల ఎలక్ట్రాన్ విన్యాసం
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 6

ప్రశ్న 13.
బోరజీన్ సాంకేతికాన్ని రాయండి. దాని సాధారణ నామం ఏమిటి?
జవాబు:

బోరజీనన్ను B₃N₃H₆ అనే ఫార్ములాతో సూచిస్తారు.
దీని నిర్మాణం బెంజీన్ నిర్మాణాన్ని పోలి ఉండటం వలన దీనిని ఇనార్గానిక్ బెంజీన్ అని అంటారు.

ప్రశ్న 14.
(a) బోరాక్స్
(b) కోలిమనైట్ సాంకేతికాలు ఇవ్వండి.
జవాబు:
a) బోరాక్స్ ఫార్ములా Na₂B₄O₇. 10H₂O
b) కోలిమనైట్ ఫార్ములా Ca₂B₆O₁₁ . 5H₂O

ప్రశ్న 15.
అల్యూమినియం ఉపయోగాలు రెండు రాయండి.
జవాబు:

అల్యూమినియమ్న మిశ్రమ లోహాల తయారీలో ఉపయోగిస్తారు.
విమాన విడిభాగాల తయారీలో ఉపయోగిస్తారు.
పైపులు, ట్యూబులు, రాడ్లు, తీగలు వంటి వాటి తయారీలో ఉపయోగిస్తారు.
నిర్మాణాలలో, రవాణా పరిశ్రమల్లో కూడా దీనిని ఉపయోగిస్తారు.

ప్రశ్న 16.
కింది చర్యల్లో ఏమి జరుగుతుంది ?
(a) LiAlH₄, BCl₃ మిశ్రమాన్ని అనార్ద్ర ఈథర్లో వెచ్చబెట్టినప్పుడు
b) బోరాక్స్న H₂SO₄ తో వేడిచేసినప్పుడు
జవాబు:
a) LiAlH₄, BCl₃ మిశ్రమాన్ని అనార్ద్ర ఈథర్ వెచ్చబెట్టినపుడు డైబోరేన్ ఏర్పడుతుంది.

b) బోరాక్స్ను H₂SO₄ తో వేడిచేసినపుడు బోరిక్ ఆమ్లం ఏర్పడును.
Na₂B₄O₇ + H₂SO₄ + 5H₂O → Na₂SO₄ + 4H₃BO₃

ప్రశ్న 17.
ఆర్థోబోరిక్ ఆమ్ల నిర్మాణాన్ని గీయండి.
జవాబు:
ఆర్థోబోరిక్ ఆమ్లం నిర్మాణం :
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 8

ప్రశ్న 18.
AlCl₃ ద్విఅణుక నిర్మాణాన్ని రాయండి.
జవాబు:
AlCl₃ ద్విఅణుక నిర్మాణం :
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 9

ప్రశ్న 19.
లోహ బోరైడ్లను (¹⁰B) రక్షణ కవచాలుగా వాడతారు. ఎందుకు ?
జవాబు:
లోహ బోరైడ్లకు (¹⁰B) న్యూట్రాన్లను శోషించుకొనే సామర్థ్యం కలదు. కావున వీనిని న్యూక్లియర్ పరిశ్రమలలో రక్షణ కవచాలుగా వాడతారు.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 20.
అల్యూమినియంకు ద్విస్వభావికం ఉన్నదని రుజువు చేసే చర్యలు రాయండి.
జవాబు:
అల్యూమినియం ఆమ్ల మరియు క్షారద్రావణాలలో కరుగుతుంది. కావున దీనికి ద్విస్వభావికం కలదు.

విలీన ఆమ్లాలలో Al కరిగి H₂ వాయువును విడుదల చేస్తుంది.
2 Al + 6 HCl → 2 AlCl₃ + 3H₂↑
క్షారాలలో Al కరిగి H2 వాయువును విడుదలచేస్తుంది.
2 Al + 2NaOH + 6H₂O → 2 Na⁺ [Al (OH)₄]^– + 3H₂

ప్రశ్న 21.
ఎలక్ట్రాన్ కొరత గల సమ్మేళనాలంటే ఏమిటి ? BCl₃ ఎలక్ట్రాన్ కొరత గల సమ్మేళనమా ? వివరించండి.
జవాబు:

అష్టక విన్యాసాన్ని పొందని కేంద్రక పరమాణువులు కలిగి ఉన్న అణువులను ఎలక్ట్రాన్ కొరత గల అణువులు అంటారు.
BCl₃ ఎలక్ట్రాన్ కొరత గల సమ్మేళనం. దీనిలో కేంద్రకం B చుట్టూ 6 ఎలక్ట్రాన్లు మాత్రమే ఉంటాయి.
BCl₃ అణువులోని కేంద్రక బోరాన్ పరమాణువు అష్టక విన్యాసాన్ని పొందలేదు.

ప్రశ్న 22.
BF₃, B\(F_4^{-}\) లో B – F బంధ దూరాలు వరసగా 130 pm, 143 pm ఎందుకు వేరువేరుగా ఉన్నాయో కారణాలు సూచించండి.
జవాబు:
BF₃ లో B పరమాణువు sp² సంకరీకరణం జరుపుకుంటుంది. ఇది సమతల త్రిభుజాకృతిని కలిగి ఉంటుంది. BF₃ లో బోరాన్ పరమాణువు ఫ్లోరిన్ నుంచి ఒక ఎలక్ట్రాన్ జంటను స్వీకరించి దానితో బాక్ బంధంలో పాల్గొంటుంది. కావున B – F బంధము కొంత ద్విబంధ స్వభావాన్ని కలిగి ఉంటుంది.

కాని B\(F_4^{-}\) లో B పరమాణువు sp³ సంకరీకరణం జరుపుకుంటుంది. ఇది టెట్రెహెడ్రల్ ఆకృతిని కలిగి ఉంటుంది. బోరాన్కు ఫ్లోరిన్కు మధ్య బాక్ బంధం ఉండదు.
కావున BF₃ లో బంధ దూరం 130PPM ఉంటే B\(F_4^{-}\) లో 143 PPM ఉంటుంది.

ప్రశ్న 23.
B – Cl బంధానికి బంధ భ్రామకం ఉంది కాని BCl₃ అణువుకు ద్విధ్రువ భ్రామకం సున్నా ఉంటుంది. వివరించండి.
జవాబు:
B – Cl బంధం దృవణ బంధం కావున బంధ భ్రామకం ఉంటుంది. కాని BCl₃ అణువు సౌష్టవ నిర్మాణాన్ని కలిగి ఉంటుంది. మూడు B – Cl బంధ బ్రామకాలు వ్యతిరేక దిశలలో పనిచేయటం వలన మొత్తం ద్విద్రువ భ్రామకం సున్నాగా ఉంటుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 10

ప్రశ్న 24.
బోరిక్ ఆమ్లం నిర్మాణాన్ని వివరించండి.
జవాబు:

బోరిక్ ఆమ్లం పొరలవంటి జాలక నిర్మాణాన్ని కలిగి ఉంటుంది.
ఈ నిర్మాణంలో BO₃ యూనిట్లు హైడ్రోజన్ బంధాలతో కలపబడి ఉంటాయి.
కావున బోరిక్ ఆమ్లం బాహ్వణుక అణువుగా ఉంటుంది.

ఆర్థోబోరిక్ ఆమ్లం నిర్మాణం :
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 11

ప్రశ్న 25.
ఏమి జరుగుతుంది :
a) బోరాక్స్న ప్రబలంగా వేడిచేస్తే,
b) బోరిక్ ఆమ్లాన్ని నీటికి కలిపితే,
c) అల్యూమినియాన్ని సజల NaOH తో వేడిచేస్తే
d) అమ్మోనియాతో BF₃ చర్య జరిపినప్పుడు
e) అర్థ అల్యూమినాను సజల NaOH ద్రావణంతో చర్య జరిపినప్పుడు
జవాబు:
a) బోరాక్స్న ప్రబలంగా వేడిచేస్తే చివరగా గాజువంటి పదార్థం ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 12

b) బోరిక్ ఆమ్లంనకు నీటిని కలిపితే బోరిక్ ఆమ్లం నీటి నుంచి OH అయాన్లను స్వీకరిస్తుంది.
B(OH)₃ + 2H₂O → [B(OH)₄]^– + H₃O⁺

c) Al ను సజల NaOH తో వేడిచేస్తే సోడియం మెటా అల్యూమినేట్తో పాటు H₂ వాయువు విడుదలవుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 13

d) BF₃, ని NH₃ లో చర్య జరిపినపుడు NH₃ ఎలక్ట్రాన్ జంటను BF₃ కి దానం చేస్తుంది. రెండింటి మధ్య సమన్వయ సమయోజనీయ బంధం ఏర్పడుతుంది.
BF₃ + NH₃ → [BF₃ ← NH₃] లేదా [BF₃ . NH₃]

e) ఆర్ద్ర అల్యూమినాను సజల NaOH ద్రావణంతో చర్య జరిపితే సోడియం మెటా అల్యూమినేట్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 14

ప్రశ్న 26.
కారణాలు తెలపండి :
సోడియమ్ మెటా అల్యుమినేట్
a) అల్యూమినియం పాత్రలలో గాఢ HNO₃ రవాణా చేయవచ్చు.
b) సజల NaOH, అల్యూమినియం ముక్కల మిశ్రమాన్ని మురుగు కాలువను తెరవడానికి వాడతారు.
c) అల్యూమినియం మిశ్రమలోహాన్ని విమానాలను తయారుచేయడానికి వాడతారు.
d) అల్యూమినియం పాత్రలను రాత్రంతా నీళ్ళలో పెట్టకూడదు.
e) అల్యూమినియం తీగలను ప్రసార కేబుల్ తయారీకి వాడతారు.
జవాబు:
a) Al మరియు గాఢ HNO₃ కి మధ్య చర్యారాహిత్యం కలదు. అందువలన అల్యూమినియం పాత్రలలో గాఢ HNO₃ని రవాణా చేయవచ్చు.

b) సజల NaOH అల్యూమినియమ్ చర్య జరిపి H₂ వాయువును విడుదలచేస్తుంది. ఈ వాయు పీడనం వలన మురుగు కాలువలు తెరచుకుంటాయి. కావున సజల NaOH, Al మిశ్రమాన్ని మురుగు కాలువను తెరవటానికి వాడతారు.

c) Al తేలికయిన, బలమైన లోహం. గాలిలో క్షయం చెందదు. కావున దీనిని విమాన విడిభాగాలను తయారుచేయటానికి వాడతారు.

d) అల్యూమినియమ్ పాత్రలను రాత్రంతా నీటిలో పెట్టకూడదు. నీటిలోని లవణాలు పాత్ర ఉపరితలంపై ఉన్న ఆక్సైడ్ పొరతో చర్య జరిపి అల్యూమినియమ్ యొక్క చర్యాశీలతను పెంచుతాయి. దీనివలన Al నీటితో చర్య జరుపుతుంది.

e) అల్యూమినియమ్ తీగలను ప్రసార కేబుల్ తయారీకి వాడతారు. దీనికి కారణం దాని యొక్క మంచి విద్యుద్వాహకత.

ప్రశ్న 27.
Ga, ln, Tl లలో రుణవిద్యుదాత్మకత భేదం ఎందుకు ఎక్కువగా మారదో వివరించండి.
జవాబు:
Ga మరియు ln లలో d ఎలక్ట్రాన్ల వలన పరిరక్షక ప్రభావం తక్కువగా ఉంటుంది. అలాగే Tl లో ‘d’ మరియు ‘f’ ఎలక్ట్రాన్ల వలన పరిరక్షక ప్రభావం తక్కువగా ఉంటుంది. కావున Ga, ln, Tl ల యొక్క పరమాణు పరిమాణంలో పెద్దగా మార్పు ఉండదు. కాని కేంద్రక ఆవేశం మాత్రము పెరుగుతుంది. కావున ఈ మూడు మూలకాల ఋణవిద్యుదాత్మకత విలువలలో భేదం ఎక్కువగా మారదు.

ప్రశ్న 28.
సరైన ఉదాహరణతో బోరాక్స్ పూస పరీక్షను వివరించండి. (March 2013)
జవాబు:
బోరాక్సిని వేడిచేస్తే మొదట నీటి అణువులను కోల్పోయి ఉబ్బి పరిమాణంలో పెద్దదవుతుంది. ఇంకా వేడిచేస్తే అది పారదర్శక ద్రవంగా మారి ఘనీభవనం చెంది గాజులాంటి పదార్థంగా మారుతుంది. దీనిలో సోడియం బొరేట్ మరియు B₂O₃ ఉంటాయి. ఈ B₂O₃ను లోహ ఆక్సైడ్ తో కలిపి వేడి చేస్తే లోహ మెటాబొరేట్లు ఏర్పడతాయి. ఈ మెటాబొరేట్లు ప్రత్యేకమైన రంగును కలిగి ఉంటాయి. వచ్చిన రంగును బట్టి లవణంలోని కేటయాను గుర్తించవచ్చును.

Na₂B₄O₇ + CoO → 2NaBO₂ + Co (BO₂)

ఆక్సీకరణ, క్షయకరణ జ్వాలలో వేడి చేసినపుడు ఒక్కొక్క లోహం ఒక్కొక్క రంగుగల మెటాబోరేట్లను ఏర్పరుస్తుంది. దీనిని బోరాన్ పూస పరీక్ష అంటారు.

ప్రశ్న 29.
డైబోరేన్ నిర్మాణాన్ని వివరించండి.
జవాబు:
డైబోరేన్ నిర్మాణము :

డైబోరేన్లో రెండు సమతల BH₂ గ్రూపులు ఉంటాయి. ఈ రెండు BH₂ గ్రూపులను కలుపుతూ రెండు H పరమాణువులు ఉంటాయి. రెండు బోరాన్ పరమాణువులకు అతకబడి ఉన్న నాలుగు H లను అంత్య హైడ్రోజన్లు అని, BH₂ గ్రూపులను కలిపే రెండు H పరమాణువులను వారధి (బ్రిడ్జ్) H పరమాణువులని అంటారు.
B₂H₆ లో రెండు బోరాన్ పరమాణువులు sp³ సంకరీకరణం జరుపుకొని నాలుగు sp³ సంకర ఆర్బిటాళ్ళను ఏర్పరుస్తాయి. నాలుగు sp³ సంకర ఆర్బిటాళ్లలో ఒక ఆర్బిటాల్లో ఎలక్ట్రాన్ ఉండదు.
ప్రతి బోరాన్లోని రెండు బంధ ఎలక్ట్రాన్లు గల sp³ సంకర ఆర్బిటాల్స్లో రెండు హైడ్రోజన్ల యొక్క s ఆర్బిటాల్స్తో అతిపాతం చెంది సహజమైన B-H బంధాలు (2 – కేంద్రక 2 – ఎలక్ట్రాన్లు) ఏర్పడతాయి.
ఒక బోరాన్లోని బంధ ఎలక్ట్రాన్ గల sp³ సంకర ఆర్బిటాల్, వేరొక బోరాన్లోని ఖాళీ sp³ సంకర ఆర్బిటాల్ మరియు H యొక్క 1s ఆర్బిటాల్తో అతిపాతం చెంది B-H-B (బిడ్జ్ బంధాన్ని ఏర్పరుస్తాయి. ఈ విధంగా B₂H₆ లో రెండు B-H-B బ్రిడ్జ్ బంధాలు ఏర్పడతాయి. ఈ బంధాలనే బనానా బంధాలు అని లేదా 3-కేంద్రక-2-ఎలక్ట్రాన్ బంధాలని అంటారు.

ప్రశ్న 30.
ఆమ్లాలతో అల్యూమినియం చర్యలను వివరించండి.
జవాబు:

అల్యూమినియమ్ విలీన లేదా గాఢ HCl లో కరిగి H₂ వాయువును విడుదలచేస్తుంది.
2Al + 6HCl → 2AlCl₃ + 3H₂ ↑
అల్యూమినియమ్ విలీన H₂SO₄ లో H₂ ను విడుదలచేస్తుంది.
2Al + 3H₂SO₄ → Al₂ (SO₄)₃ + 3H₂ ↑
అల్యూమినియమ్ గాఢ H₂SO₄ లో కరిగి SO₄ ను ఇస్తుంది.
2Al + 6H₂SO₄ → Al₂(SO₄)₃ + 3SO₂ + 6H₂O
అతి విలీన HNO₃ని అల్యూమినియమ్ NH₄NO₃ గా క్షయకరణం చేస్తుంది.
8Al + 30HNO₃ → 8Al (NO₃)₃ + 3NH₄NO₃ + 9H₂O
గాఢ HNO₃ తో Al క్రియారహితం అవుతుంది. లోహపు ఉపరితలంపై పలుచని ఆక్సైడ్ పొర ఏర్పడటం వలన క్రియారాహిత్యం వస్తుంది.

ప్రశ్న 31.
గ్రూపు 13లో బోరాన్ అసంగత ప్రవర్తనను సంక్షిప్తంగా రాయండి.
జవాబు:
బోరాన్ పరమాణు సైజు చిన్నది కావటం, అయొనైజేషన్ పొటెన్షియల్ ఎక్కువగా ఉండటం వలన మిగిలిన మూలకాలతో అసంగత ప్రవర్తనను చూపిస్తుంది. ఉదా :

బోరాన్ అలోహం, Al ద్వంద్వ స్వభావం గల లోహం Ga, ln, Tl లు లోహాలు.
బోరాన్ ఎల్లప్పుడు కోవలంట్ సమ్మేళనాలను ఇస్తుంది. కాని మిగిలిన మూలకాలు అయానిక సమ్మేళనాలను ఇస్తాయి.
బోరాన్కు సిలికాన్తో కర్ణ సంబంధం ఉంటుంది. మిగిలిన మూలకాలు ఈ కర్ణ సంబంధాన్ని చూపవు.
ఆమ్లాల నుండి బోరాన్ H₂ ను స్థానభ్రంశం చేయదు. కాని మిగిలిన మూలకాలు H₂ స్థానభ్రంశం చెందిస్తాయి. బోరాన్ ఆక్సైడ్ ఆమ్ల ఆక్సెడ్. కాని మిగిలిన మూలకాల ఆక్సైడ్లు ద్విస్వభావ ఆక్సైడ్లుగా గాని క్షార ఆక్సైడ్లుగా గాని ఉంటాయి.
సరళ బోరేట్లు, సిలికేటులు తేలికగా పాలిమరీకరణం చెంది పాలీ ఆమ్లాలను ఇస్తాయి. మిగిలిన మూలకాలు పాలిమర్ ఆమ్లాలను ఇవ్వవు.
బోరాన్ అత్యధిక కో వేలన్సీ 4. ఇతర మూలకాల అత్యధిక కోవలన్సీ 6.
స్థిరమైన కోవలంట్ హైడ్రేడ్లను ఇస్తుంది. మిగిలిన మూలకాలు స్థిరమైన హైడ్రైడ్లను ఇవ్వవు.

ప్రశ్న 32.
అల్యూమినియం సజల HNO₃ తో చర్య జరుపుతుంది కాని గాఢ HNO₃ తో చర్య జరపదు. వివరించండి.
జవాబు:
విలీన HNO₃ తో అల్యూమినియమ్ చర్యజరిపి HNO₃ ని NH₄ NO₃ గా క్షయకరణం చేస్తుంది.
8Al + 3OHNO₃ → 8Al(NO₃)₃ + 3NH₄NO₃ + 9H₂O

కాని గాఢ HNO₃ కి అల్యూమినియమ్ను కలిపినపుడు లోహపు తలంపై పలుచని ఆక్సైడ్పొర ఏర్పడుతుంది.. ఈ. ఆక్సైడ్ పొర రక్షిత పొరగా పనిచేసి Al ని HNO₃ తో చర్య జరగకుండా అడ్డుకుంటుంది. కావున గాఢ HNO₃ తో Al క్రియారహితం అవుతుంది.

ప్రశ్న 33.
డైబోరేన్ ను తయారుచేసే రెండు పద్ధతులు రాయండి.
జవాబు:
డైబోరేన్ [B₂H₆] ను తయారుచేయు పద్ధతులు :
బోరాన్ ట్రై ఫ్లోరైడు లిథియమ్ అల్యూమినియమ్ హైడ్రైడ్తో డైఈథైల్ ఈథర్లో చర్య జరిపి డైబోరేన్ను తయారుచేస్తారు.
4BF₃ + 3LiAlH₄ → 2B₂H₆ + 3LiF + 3AlF₃

ప్రయోగశాలలో సోడియం బోరోహైడ్రైడు, అయోడిన్ ఆక్సీకరణం చేసి డైబోరేన న్ను తయారుచేస్తారు.
2NaBH₄ + I₂ → B₂H₆ + 2Nal + H₂
పారిశ్రామికంగా డైబోరేన్ న్ను ఉత్పత్తి చేయడానికి BF₃ ని సోడియం హైడ్రైడ్తో చర్య జరిపిస్తారు.

ప్రశ్న 34.
డైబోరేన్ ఈ కింది వాటితో ఏ విధంగా చర్య జరుపుతుంది ?
a) H₂O
b) CO
c) N(CH₃)₃
జవాబు:
a) డైబోరేన్ నీటితో చర్య : డైబోరేన్ నీటిలో జలవిశ్లేషణ చెంది బోరిక్ ఆమ్లాన్ని ఇస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 17

b) డైబోరేన్ CO తో చర్య : డైబోరేన్ 1000°C ఉష్ణోగ్రత మరియు 2 atm పీడనం వద్ద CO తో చర్య జరిపి బోరేన్ కార్బోనైల్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 18

c) డైబోరేన్ N(CH₃)₃ తో చర్య : డైబోరేన్ N(CH₃)₃ తో చర్య జరిపి బోరాన్ సంకలితాన్ని ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 19

ప్రశ్న 35.
Al₂O₃ ద్విస్వభావం కలదని సరైన చర్యలతో వివరించండి.
బోరాన్ సంకలితం
జవాబు:
Al₂O₃ కు ద్విస్వభావం కలదు. ఇది ఆమ్లాలతో మరియు క్షారాలతో చర్య జరిపి లవణాలను ఏర్పరుస్తుంది.
ఆమ్లాలతో చర్య : ‘Al₂O₃ ఆమ్లాలతో ఈ క్రింది విధంగా చర్య జరుపుతుంది.
Al₂O₃ +6HCl → 2AlCl₃ + H₂O
క్షారాలతో చర్య : Al₂O₃ క్షారాలతో ఈ క్రింది విధంగా చర్య జరుపుతుంది.
Al₂O₃ + 2NaOH → NaAlO₂ + H₂O

ప్రశ్న 36.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 20
జవాబు:

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 37.
బోరాక్స్న, బోరిక్ ఆమ్లాన్ని ఎలా తయారుచేస్తారు ? వాటిమీద ఉష్ణం చర్యను వివరించండి.
జవాబు:
బోరాక్స్ తయారీ : బోరిక్ ఆమ్లంను వేడిచేయగా టెట్రాబోరిక్ ఆమ్లం ఏర్పడుతుంది. దీనిని NaOH తో చర్య జరపగా బోరాక్స్ ఏర్పడును.

బోరాకున్ను అధికంగా వేడిచేస్తే గాజులాంటి పదార్థంగా మారుతుంది. దీనినే బోరాక్స్ పూస అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 23
బోరిక్ ఆమ్లం తయారీ : బోరాక్స్ను గాఢ H₂SO₄ తో చర్య జరిపినపుడు బోరిక్ ఆమ్లం ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 24
బోరిక్ ఆమ్లంను వేడిచేయగా మెటాబోరికామ్లం ఏర్పడుతుంది. దీనిని ఇంకా వేడిచేస్తే బోరిక్ ఆక్సైడ్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 25

ప్రశ్న 38.
డైబోరేన్ ను ఎలా తయారుచేస్తారు ? దాని నిర్మాణాన్ని వివరించండి.
జవాబు:
డైబోరేన్ [B₂H₆] ను తయారుచేయు పద్ధతులు :

బోరాన్ ట్రై ఫ్లోరైడ్ను లిథియమ్ అల్యూమినియమ్ హైడ్రైడ్తో డైఈథైల్ ఈథర్లో చర్య జరిపి డైబోరేన్ ను తయారుచేస్తారు.
4BF₃ + 3LiAlH₄ → 2B₂H₆ + 3LiF + 3AlF₃
ప్రయోగశాలలో సోడియం బోరోహైడ్రైడ్న, అయోడిన్తో ఆక్సీకరణం చేసి డైబోరేన్ తయారుచేస్తారు.
2NaBH₄ + I₂ → B₂H₆ + 2Nal + H₂
పారిశ్రామికంగా డైబోరేన్ ను ఉత్పత్తి చేయడానికి BF₃ ని సోడియం హైడ్రైడ్తో చర్య జరిపిస్తారు.

డైబోరేన్ నిర్మాణము :

డైబోరేన్లో రెండు సమతల BH₂ గ్రూపులు ఉంటాయి. ఈ రెండు BH₂ గ్రూపులను కలుపుతూ రెండు H పరమాణువులు ఉంటాయి. రెండు బోరాన్ పరమాణువులకు అతకబడి ఉన్న నాలుగు H లను అంత్య హైడ్రోజన్లు అని, BH₂ గ్రూపులను కలిపే రెండు H పరమాణువులను వారధి (బ్రిడ్జ్) H పరమాణువులని అంటారు.
B₂H₆ లో రెండు బోరాన్ పరమాణువులు sp³ సంకరీకరణం జరుపుకొని నాలుగు sp³ సంకర ఆర్బిటాళ్ళను ఏర్పరుస్తాయి. నాలుగు sp³ సంకర ఆర్బిటాళ్లలో ఒక ఆర్బిటాల్లో ఎలక్ట్రాన్ ఉండదు.
ప్రతి బోరాన్లోని రెండు బంధ. ఎలక్ట్రాన్లు గల sp³ సంకర ఆర్బిటాల్స్తో రెండు హైడ్రోజన్ల యొక్క s – ఆర్బిటాల్స్తో అతిపాతం చెంది సహజమైన B – H బంధాలు (2 – కేంద్రక 2 – ఎలక్ట్రాన్లు) ఏర్పడతాయి.
ఒక బోరాన్లోని బంధ ఎలక్ట్రాన్ గల sp³ సంకర ఆర్బిటాల్, వేరొక బోరాన్లోని ఖాళీ sp³ సంకర ఆర్బిటాల్ మరియు H యొక్క 1s ఆర్బిటాల్తో అతిపాతం చెంది B-H-B బ్రిడ్జ్ బంధాన్ని ఏర్పరుస్తాయి. ఈ విధంగా B₂H₆ లో రెండు B-H-B బ్రిడ్జ్ బంధాలు ఏర్పడతాయి. ఈ బంధాలనే బనానా బంధాలు అని లేదా 3-కేంద్రక-2-ఎలక్ట్రాన్ బంధాలని అంటారు.

ప్రశ్న 39.
డైబోరేన్ను తయారుచేసే ఏవైనా రెండు పద్ధతులు రాయండి. అది ఈ కింది వాటితో ఏ విధంగా చర్య జరుపుతుంది?
a) కార్బన్ మోనాక్సైడ్
b) అమ్మోనియా
జవాబు:
డైబోరేన్ [B₂H₆] ను తయారుచేయు పద్ధతులు :

బోరాన్ ట్రై ఫ్లోరైడ్ను లిథియమ్ అల్యూమినియమ్ హైడ్రైడ్ డైఈథైల్ ఈథర్లో చర్య జరిపి డైబోరేన్ను తయారుచేస్తారు.
4BF₃ + 3LiAlH₄ → 2B₂H₆ + 3LiF + 3AlF₃
ప్రయోగశాలలో సోడియం బోరోహైడ్రైడ్న, అయోడిన్తో ఆక్సీకరణం చేసి డైబోరేన్ ను తయారుచేస్తారు.
2NaBH₄ + I₂ → B₂HË₆ + 2Nal + H₂
పారిశ్రామికంగా డైబోరేన్ను ఉత్పత్తి చేయడానికి BF₃ ని సోడియం హైడ్రైడ్తో చర్య జరిపిస్తారు.

a) డైబోరేన్ కార్బన్ మోనాక్సైడ్తో చర్య : డైబోరేన్ 1000°C ఉష్ణోగ్రత మరియు 22atm పీడనం వద్ద CO తో చర్య జరిపి బోరేన్ కార్బనైల్ అనే బోరాన్ సంకలితాన్ని ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 29

b) డైబోరేన్ అమ్మోనియాతో చర్య డైబోరేన్ అమ్మోనియాతో చర్యనొంది మొదట B₆H₆. 2NH₃ ని ఇస్తుంది. దీనినే
(BH₂(NH₃)₂)⁺ B\(\mathrm{H}_4^{-}\) గా కూడా వ్రాయవచ్చు. దీనిని ఇంకా వేడిచేస్తే బోరజీన్ ఏర్పడుతుంది. బోరజీన్కు బెంజీన్ వంటి వలయ నిర్మాణం ఉంటుంది. కావున దీనిని ఇనార్గానిక్ బెంజీన్ అని కూడా అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 10 P బ్లాక్ మూలకాలు – 13వ గ్రూప్ 30