TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(a)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 2 System of Circles Ex 2(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Exercise 2(a)

I.

Question 1.
Find k if the following pairs of circles are orthogonal.
(i) x² + y² + 2by – k = 0, x² + y² + 2ax + 8 = 0.
Solution:
The given equations of circles are x² + y² + 2by – k = 0 ……….(1) and x² + y² + 2ax + 8 = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 0, f = b, c = -k, g’ = a, f’ = 0, c’ = 8
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 0 + 0 = 8 – k
⇒ k = 8

(ii) x² + y² – 6x – 8y + 12 = 0, x² + y² – 4x + 6y + k = 0
Solution:
The given equations of circles are x² + y² – 6x – 8y + 12 = 0 …….(1) and x² + y² – 4x + 6y + k = 0 ……….(2)
Comparing with S = 0 and S’ = 0
We get g = -3, f = -4, c = 12 and g’ = -2, f’ = 3, c’ = k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 2(6 – 12) = 12 + k
⇒ -12 = 12 + k
⇒ k = -24

(iii) x² + y² – 5x – 14y – 34 = 0, x² + y² + 2x + 4y + k = 0
Solution:
The given equations of circles are x² + y² – 5x – 14y – 34 = 0 ……..(1) and x² + y² + 2x + 4y + k = 0 ……….(2)
Comparing with S = 0 and S’ = 0
We get g = \(\frac{-5}{2}\), f = -7, c = -34 and g’ = 1, f = 3, c’ = k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 2[\(\frac{-5}{2}\)(1) + (-7)(2)] = k – 34
⇒ -5 – 28 = k – 34
⇒ k = 1

(iv) x² + y² + 4x + 8 = 0, x² + y² – 16y + k = 0
Solution:
The given equations of circles are x² + y² + 4x + 8 = 0 ………(1) and x² + y² – 16y + k = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 2, f = 0, c = + 8 and g’ = 0, f’ = -8, c’ = +k
Condition for the orthogonality is 2(gg’ + ff’) = c + c’
⇒ 0 = 8 + k
⇒ k = -8

Question 2.
Find the angle between the circles given by the equations
(i) x² + y² – 12x – 6y + 41 = 0, x² + y² + 4x + 6y – 59 = 0
Solution:
The given equations of circles are
x² + y² – 12x – 6y + 41 = 0 ………(i)
and x² + y² + 4x + 6y – 59 = 0 ……..(ii)
Comparing with S = 0 and S’ = 0 We get
g = -6, f = -3, c = 41
g’ = 2, f’ = 3, c’ = -59
Also, centres of circles (1) and (2) are C₁ = (6, 3) and C₂ = (-2, -3)

(ii) x² + y² + 6x – 10y – 135 = 0, x² + y² – 4x + 14y – 116 = 0
Solution:
The given equations of circles are
x² + y² + 6x – 10y – 135 = 0 ………(1)
and x² + y² – 4x + 14y – 116 = 0 ………(2)
Comparing with S = 0 and S’ = 0
We get g = 3, f = -5, c = -135 and g’ = -2, f’ = 7, c’ = -116
Also, centres of circles (1) and (2) are C₁ = (-3, 5) and C₂ = (2, -7)

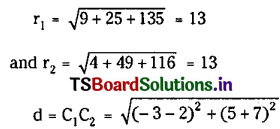
Question 3.
Show that the angle between the circles x² + y² = a², x² + y² = ax + ay is \(\frac{3 \pi}{4}\).
Solution:
Let S = x² + y² – a² = 0 and S’ = x² + y² – ax + ay = 0 be the given of circles.
C₁ = (0, 0) and C₂ = \(\left(\frac{\mathrm{a}}{2}, \frac{\mathrm{a}}{2}\right)\) are the centres of circles.

Question 4.
Show that the circles given by the following equations intersect each other orthogonally.
(i) x² + y² – 2x – 2y – 7 = 0, 3x² + 3y² – 8x + 29y = 0
Solution:
Equations of given circles are
x² + y² – 2x – 2y – 7 = 0 ………(1)
and \(x^2+y^2-\frac{8}{3} x+\frac{29}{3} y=0\) ……….(2)

c + c’ = -7 + 0 = 7
∴ 2(gg’ + ff’) = c + c’, hence circles (1) and (2) intersect orthogonally.

(ii) x² + y² + 4x – 2y – 11 = 0, x² + y² – 4x – 8y + 11 = 0
Solution:
Equations of given circles are
x² + y² + 4x – 2y – 11 = 0 ………(1)
and x² + y² – 4x – 8y + 11 = 0 ………(2)
g = 2, f = -1, c = -11 and g’ = -2, f’ = -4, c = 11
∴ 2(gg’ + ff’) = 2(-4 + 4) = 0 and c + c’ = -11 + 11 = 0
Since 2(gg’ + ff’) = c + c’, the two circles intersect orthogonally.

(iii) x² + y² – 2x + 4y + 4 = 0, x² + y² + 3x + 4y + 1 = 0
Solution:
Equations of given circles are
x² + y² – 2x + 4y + 4 = 0 ………(1)
and x² + y² + 3x + 4y + 1 = 0 ……….(2)
Centres of circles are C₁ = (1, -2) and C₂ = (\(\frac{-3}{2}\), -2)
Also g = -1, f = 2, c = 4
g’ = \(\frac{3}{2}\), f’ = 2, c’ = 1
∴ 2(gg’ + ff’) = 2(\(\frac{-3}{2}\) + 4) = 5
c + c’ = 4 + 1 = 5
Since 2(gg’ + ff’) = c + c’, we have the two circles intersect orthogonally with each other.

(iv) x² + y² – 2lx + g = 0, x² + y² + 2my – g = 0
Solution:
Equations of given circles are
x² + y² – 2lx + g = 0 ……..(1)
and x² + y² + 2my – g = 0 ……….(2)
g = -l, f = 0, c = g and g’ = -0, f’ = m, c’ = -g
∴ 2(gg’ + ff’) = 2[(0) + (0)] = 0
c + c’ = g – g = 0
Since 2(gg’ + ff’) = c + c’, the two circles intersect each other orthogonally.

II.

Question 1.
Find the equation of the circle which passes through the origin and intersects the circle given below orthogonally.
(i) x² + y² – 4x – 6y + 10 = 0, x² + y² + 12y + 6 = 0.
Solution:
Equations of given circles are
x² + y² – 4x – 6y + 10 = 0 ……..(1)
and x² + y² + 12y + 6 = 0 ………(2)
Let the equation of the circle passing through the origin be
x² + y² + 2gx + 2fy = 0 ………(3)
If (1) intersects (3) orthogonally then
2(-2) (g) + 2(3)(f) = 10
⇒ -4g + 6f = 10
⇒ 2g – 3f = -5 ……….(4)
If (2) intersects (3) orthogonally then
2g(0) + 2f(6) = 6
⇒ 12f = 6
⇒ f = \(\frac{1}{2}\) …….(5)
∴ From (4),

(ii) x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0
Solution:
Equations of given circles are
x² + y² – 4x – 6y – 3 = 0 ……..(1)
and x² + y² – 8y + 12 = 0 ……(2)
Let the equation of the required circle passing through the origin be
x² + y² + 2gx + 2fy = 0 ……..(3)
If (1) and (3) are orthogonal then
2g(-2) – 2f (- 3) = -3
⇒ 4g + 6f = 3
If (2) and (3) are orthogonal then
2g(0) + 2f(- 4) = 12
⇒ -8f = 12
⇒ f = \(\frac{-12}{8}=\frac{-3}{2}\) ………(5)
∴ From (4),
4g + 6(\(\frac{-3}{2}\)) = -3
⇒ 4g – 9 = -3
⇒ 4g = 6
⇒ g = \(\frac{3}{2}\) …….(6)
∴ From (3), the Equation of the required circle is x² + y² + 6x – 3y = 0.

Question 2.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally.
Solution:
Equations of given circles are
x² + y² – 6x + 3y + 5 = 0 ……..(1)
and x² + y² – x – 7y = 0 …….(2)
Let S ≡ x² + y² + 2gx + 2fy + c = 0 ………(3) be the required circle.
Let S’ = 0 …….(1) and S” = 0 ……..(2) be the given circles.
Given that (3) passes through (0, -3) we have
0 + 9 – 6f + c = 0
⇒ 9 – 6f + c = 0 ……(4)
If (1) and (3) are orthogonal then
2g(-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f = c + 5 ……..(5)
If (2) and (3) are orthogonal then
\(2 g\left(-\frac{1}{2}\right)+2 f\left(-\frac{7}{2}\right)=c\)
⇒ -g – 7f = c
⇒ g + 7f + c = 0
From (5)
6g – 3f + c = -5
⇒ -5g + 10f = 5
⇒ g – 2f = -1 ………(7)
Also from (4), 9 – 6f + c = 0
and from (5), 6g – 3f + c = -5
∴ -6g – 3f + 9 = 5
⇒ -6g – 3f + 4 = 0
⇒ 6g + 3f – 4 = 0
From (7) and (8),
6g – 12f = -6
⇒ 15f – 10 = 0
⇒ f = \(\frac{10}{15}\)

Question 3.
Find the equation of the circle passing through the origin and having its center on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let the equation of the circle passing through the origin be x² + y² + 2gx + 2fy = 0 ……..(1)
Given that the centre (-g, -f) lies on the line x + y = 4
⇒ -g – f = 4
⇒ g + f = -4 ……….(2)
If (1) intersects x² + y² – 4x + 2y + 4 = 0 orthogonally then
2g (-2) + 2f(1) = 4
⇒ -2g + f = 2
⇒ 2g – f = -2 ………(3)
From (2) and (3)
3g = -6
⇒ g = -2
2(-2) – f = -2
⇒ -f = 2
⇒ f = -2
∴ The equation of the required circle from (1) is x² + y² – 4x – 4y = 0.

Question 4.
Find the equation of the circle which passes through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ……..(1)
If this passes through the points (2, 0) and (0, 2) then
4 + 4g + c = 0 ………(2)
and 4 + 4f + c = 0 ………(3)
From (2) and (3),
g = f …….(4)
Also (1) intersects the given circle x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 orthogonally then
\(2 g\left(\frac{5}{4}\right)+2 f\left(\frac{-3}{2}\right)\) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = c + 2
⇒ 5g – 6f = 2c + 4
Since g = f, we have
5f – 6f = 2c + 4
⇒ -f = 2c + 4
⇒ f + 2c + 4 = 0
From (3)
4f + c + 4 = 0
-3f + c = 0
⇒ c = 3f
From (5)
f + 6f + 4 = 0
⇒ 7f + 4 = 0
⇒ f = \(\frac{-4}{7}\)
and c = 3f = \(\frac{-12}{7}\), Also g = \(\frac{-4}{7}\)
∴ The equation of the required circle from (1) is \(x^2+y^2-\frac{8}{7} x-\frac{8}{7} y-\frac{12}{7}=0\)
⇒ 7(x² + y²) – 8x – 8y – 12 = 0.

Question 5.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having centre at (2, 3).
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ………(1)
Since the centre is given to be (2, 3) we have
-g = 2 and -f = 3
⇒ g = -2 and f = -3
Since (1) cuts x² + y² – 4x + 2y – 7 = 0 orthogonally we have
2g(-2) + 2f(1) = c – 7
⇒ -4(-2) – 6 = c – 7
⇒ 2 = c – 7
⇒ c = 9
∴ The equation of the required circle from (1) is x² + y² – 4x – 6y + 9 = 0.

III.

Question 1.
Find the equation of the circle which intersects the circle x² + y² – 6x + 4y – 3 = 0 orthogonally and passes through the point (3, 0) and touches Y-axis.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since this passes through point (3, 0) we have
9 + 6g + c = 0 ……..(2)
If (1) touches Y-axis then \(\sqrt{\mathfrak{f}^2-c}\) = 0
⇒ c = f² ……..(3)
If (1) intersects x² + y² – 6x + 4y – 3 = 0 orthogonally then
2g(-3) + 2f(2) = c – 3
⇒ -6g + 4f = c – 3 ………(3)
Also from (2), 6g = -c – 9
Solving, 4f = -12
⇒ f = -3
From (3)
c = f²
⇒ c = 9
From (2)
9 + 6g + 9 = 0
⇒ g = -3
∴ The equation of the required circle from (1) is x² + y² – 6x – 6y + 9 = 0.

Question 2.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 = 0 and x² + y² – 10x – 4y + 21 = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7.
Solution:
Equations are given circles are
x² + y² – 4x – 6y + 11 = 0 ……..(1)
and x² + y² – 10x – 4y + 21 = 0 ………(2)
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……..(3)
If this cuts (1) and (2) orthogonally then
2g(-2) + 2f(-3) = c + 11
⇒ 4g + 6g = – c – 11 …….(3)
and if (1) and (3) are orthogonal then
2g(-5) + 2f(-2) = c + 21
⇒ -10g – 4f = c + 21
⇒ 10g + 4f = -c – 21 ………..(4)
From (3) and (4)
-6g + 2f = 10
⇒ 6g – 2f = -10
⇒ 3g – f = -5 ………(5)
Since the centre of circle (1) (-g, -f) lies on the diameter 2x + 3y = 7, we have
2(-g) + 3(-f) = 7
⇒ 2g + 3f = -7 ……..(6)
Solving (5) and (6)

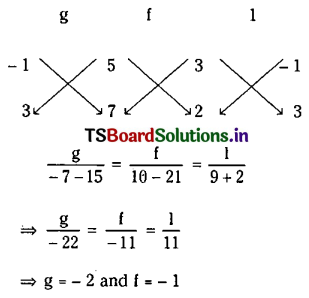
∴ From (3)
(-8) – 6 = -c – 11
⇒ -14 = -c – 11
⇒ c = 3
∴ The equation of a required circle is x² + y² – 4x – 2y + 3 = 0.

Question 3.
If P, Q are conjugate points w.r.t. a circle S ≡ x² + y² + 2gx + 2fy + c = 0 then prove that the circle on PQ as diameter cuts the circle S = 0 orthogonally.
Solution:
Given S ≡ x² + y² + 2gx + 2fy + c = 0 ………(1)
Let P(x₁, y₁) and Q(x₂, y₂) be the given points.
The polar of P(x₁, y₁) w.r.t. a circle S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0.
Since P, Q are conjugate points w.r.t. S = 0
⇒ x₁x₂ + y₁y₂ + g(x₂ + x₁) + f(y₂ + y₁) + c = 0
∴ -g(x₁ + x₂) – f(y₁ + y₂) = x₁x₂ + y₁y₂ + c ……(2)
The equation of the circle having \(\overline{\mathrm{PQ}}\) as diameter is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ x² – x(x₁ + x₂) + y² – y(y₁ + y₂) + (x₁x₂ + y₁y₂) = 0 …….(3)
Using conditions between (1) and (3) orthogonally
2gg’ + 2ff’ = \(2 \mathrm{~g}\left[\left(\frac{-\mathrm{x}_1+\mathrm{x}_2}{2}\right)\right]+2 \mathrm{f}\left[\left(\frac{-\mathrm{y}_1+\mathrm{y}_2}{2}\right)\right]\)
= -g(x₁ + x₂) – f(y₁ + y₂)
= x₁x₂ + y₁y₂ + c [∵ From (2)]
= c’ + c When c’ = x₁x₂ + y₁y₂ from (3)
∴ The circle (3) cuts the circle S = 0 orthogonally.

Question 4.
If the equation of two circles whose radii are a, a’ are S = 0 and S’ = 0, then show that the circles \(\frac{\mathbf{S}}{\mathbf{a}}+\frac{\mathbf{S}^{\prime}}{\mathbf{a}^{\prime}}=0\) and \(\frac{S}{a}-\frac{S^{\prime}}{a^{\prime}}=0\) intersect orthogonally.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 and S’ ≡ x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.

Question 5.
Find the equation of the circle which intersects each of the following circles orthogonally.
(i) x² + y² + 2x + 4y + 1 = 0, x² + y² – 2x + 6y – 3 = 0, 2(x² + y²) + 6x + 8y – 3 = 0 (May ’12)
Solution:
Let the circle x² + y² + 2gx + 2fy + c = 0 …….(1) cuts each of the circles
x² + y² + 2x + 4y + 1 = 0 …….(2)
x² + y² – 2x + 6y – 3 = 0 ………(3)
and x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0 ………(4) orthogonally.
Then (1) and (2) are orthogonal.
⇒ 2g(1) + 2f(2) = c + 1 …….(4)
(1) and (3) are orthogonal
⇒ 2g(-1) + 2f(3) = c – 3 ……..(5)
(1) and (4) are orthogonal
⇒ 2g(\(\frac{3}{2}\)) + 2f(2) = c – \(\frac{3}{2}\) …….(6)
From (4) and (5),
2g + 4f = c + 1 and -2g + 6f = c – 3
4g – 2f = 4
⇒ 2g – f = 2 ………(7)
From (5) and (6)
-2g + 6f = c – 3
and 3g + 4f = c – \(\frac{3}{2}\)
⇒ -5g + 2f = \(-\frac{3}{2}\) …….(8)
From (7),
2g – f = 2 and -10g + 4f = -3 from (8)
Solving

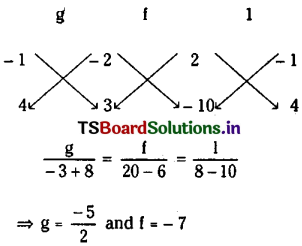
From (4),
2g + 4f = c + 1
⇒ -5 – 28 = c + 1
⇒ c = -34
∴ The equation of required circle (1) cutting each of the circles (2), (3), and (4) is x² + y² – 5x – 14y – 34 = 0.

(ii) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0
Solution:
Equations of given circles are
x² + y² + 4x + 2y + 1 = 0 ………(1)
x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ……..(2)
and x² + y² + 6x – 2y – 3 = 0 ………(3)
Let the equation of the circle that cuts (1), (2), and (3) orthogonally be
x² + y² + 2gx + 2fy + c = 0 ……..(4)
Since (1) and (4) are orthogonal
2g(2) + 2f(1) = c + 1 ……(4)
⇒ 4g + 2f = c + 1 ………(5)
Since (2) and (4) are orthogonal
and from (2), x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0
2g(2) + 2f(\(\frac{3}{2}\)) = c – \(\frac{3}{2}\)
⇒ 4g + 3f = c – \(\frac{3}{2}\) …….(6)
Since (3) and (4) are orthogonal
2g(3) + 2f(-1) = c – 3 ………(6)
⇒ 6g – 2f = c – 3 …….(7)
From (5) and (6),
-f = \(\frac{5}{2}\)
⇒ f = \(\frac{-5}{2}\)
From (6) and (7),
-2g + 5f = \(\frac{3}{2}\)
⇒ 2g – \(\frac{25}{2}\) = \(\frac{3}{2}\)
⇒ -2g = 14
⇒ g = -7
∴ From (5),
4g + 2f = c + 1
⇒ -28 – 5 = c + 1
⇒ c = -34
∴ The equation of the required circle from (4) which cuts (1), (2), and (3) orthogonally is given by x² + y² – 14x – 5y – 34 = 0.

Question 6.
If the straight line 2x + 3y = 1 intersects the circle x² + y² = 4 at points A and B, then find the equation of the circle having AB as diameter.
Solution:
Given that the line 2x + 3y – 1 = 0 intersects the circle x² + y² – 4 = 0 at points A and B then
the equation of the circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0
⇒ x² + y² – 4 + λ(2x + 3y – 1) = 0
⇒ x² + y² + 2λx + 3λy – (4 + λ) = 0 ………(1)
Centre of the circle C’ = \(\left(-\lambda-\frac{3 \lambda}{2}\right)\)
Given that the circle x² + y² – 4 = 0 has the line 2x + 3y – 1 = 0 as the diameter, the centre C’ lies on line 2x + 3y = 1.
∴ 2(-λ) + 3\(\left(-\frac{3}{2} \lambda\right)\) – 1 = 0
⇒ -4λ – 9λ – 2 = 0
⇒ λ = \(\frac{-2}{13}\)
∴ From (1), Equation of required circle is x² + y² – 4 – \(\frac{2}{13}\)(2x + 3y – 1) = 0
⇒ 13(x² + y²) – 52 – 4x – 6y + 2 = 0
⇒ 13(x² + y²) – 4x – 6y – 50 = 0

Question 7.
If x + y = 3 is the equation of chord AB of the circle x² + y² – 2x + 4y – 8 = 0, find the equation of the circle having AB as diameter.
Solution:
Let S ≡ x² + y² – 2x + 4y – 8 = 0 be the circle.
Let L ≡ x + y – 3 = 0 be the given line.
Given that L = 0 intersects the circle S = 0 at A, B.
The equation of the circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0 where λ is a constant.
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0
⇒ x² + y² + (λ – 2)x + y(λ + 4) – (8 + 3λ) = 0 …….(1)
Centre of the circle = \(\left[-\left(\frac{\lambda-2}{2}\right),-\left(\frac{\lambda+4}{2}\right)\right]\)
Given that the line L = 0 is the diameter of the circle (1).
Centre \(\left(\frac{2-\lambda}{2},-\frac{\lambda-4}{2}\right)\) lies on the line x + y – 3 = 0.
∴ \(\frac{2-\lambda}{2}+\left[-\left(\frac{\lambda+4}{2}\right)\right]-3=0\)
⇒ -λ + 2 – λ – 4 – 6 = 0
⇒ – 2λ – 8 = 0
⇒ 2λ = -8
⇒ λ = -4
∴ The equation of the required circle from (1) is x² + y² + (-4 – 2)x + (-4 + 4)y – 8 – 3(-4) = 0
⇒ x² + y² – 6x + 4 = 0

Question 8.
Find the equation of the circle passing through the intersection of the circles x² + y² = 2ax and x² + y² = 2by and having its centre on the line \(\frac{x}{a}-\frac{y}{b}=2\).
Solution:
Let S = x² + y² – 2ax = 0 and S’ = x² + y² – 2by be the given circles.
Given line is \(\frac{x}{a}-\frac{y}{b}=2\)
⇒ bx – ay = 2ab
⇒ bx – ay – 2ab = 0 …….(1)
The equation of the radical axis of circles S = 0 and S’ = 0 is S – S’ = 0.
⇒ x² + y² – 2ax – (x² + y² – 2by) = 0
⇒ ax – by = 0
Let L = ax – by = 0 ……….(2)
The equation of the circle passing through the points of intersection of S = 0 and L = 0 is S + λL = 0.
⇒ x² + y² – 2ax + λ(ax – by) = 0 — (3)
⇒ x² + y² + x(λa – 2a) – λby = 0
Centre of the circle (3) is \(\left(\frac{2 a-\lambda a}{2}, \frac{\lambda b}{2}\right)\)
Given that centre lies on (1)
∴ \(\mathrm{b}\left(\frac{2 \mathrm{a}-\lambda \mathrm{a}}{2}\right)-\mathrm{a} \frac{\lambda \mathrm{b}}{2}-2 \mathrm{ab}=0\)
⇒ 2ab – abλ – abλ – 4ab = 0
⇒ -2abλ – 2ab = 0
⇒ λ = -1
∴ From (3), the equation of the required circle is x² + y² – 3ax + by = 0.