TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(d)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(d)

I.

Question 1.
Find the condition that the tangents are drawn from (0, 0) to S ≡ x² + y² + 2gx + 2fy + c = 0 be perpendicular to each other.
Solution:
If the angle between the tangents drawn from P(x₁, y₁) to S = 0 is θ then

Question 2.
Find the chord of contact of (0, 5) with respect to the circle x² + y² – 5x + 4y – 2 = 0.
Solution:
Comparing with x² + y² + 2gx + 2fy + c = 0,
we get g = \(-\frac{5}{2}\), f = 2, c = -2
∴ Equation of chord of contact of (x1, y1) w.r.t S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
∴ The equation of chord of contact of (0, 5) w.r.t. x² + y² – 5x + 4y – 2 = 0 is x(0) + y(5) + \(\left(\frac{-5}{2}\right)\) (x + 0) + 2(y + 5) – 2 = 0
⇒ 5y – \(\frac{5 x}{2}\) + 2y + 10 – 2 = 0
⇒ 5y – \(\frac{5 x}{2}\) + 2y + 8 = 0
⇒ 10y – 5x + 4y + 16 = 0
⇒ -5x + 14y + 16 = 0
⇒ 5x – 14y – 16 = 0

Question 3.
Find the chord of contact of (1, 1) to the circle x² + y² = 9.
Solution:
Equation of chord of contact of (x₁, y₁) w.r.t x² + y² = a² is xx₁ + yy₁ – a² = 0.
∴ The equation of chord of contact of (1, 1) w.r.t x² + y² = 9 is x(1) + y(1) – 9 = 0
⇒ x + y – 9 = 0

Question 4.
Find the polar of (1, 2) with respect to x² + y² = 7.
Solution:
Equation of polar of (x₁, y₁) with respect to x² + y² = a² is xx₁ + yy₁ – 9 = 0.
∴ The equation of polar of (1, 2) with respect to x² + y² = 7 is x(1) + y(2) – 7 = 0
⇒ x + 2y – 7 = 0

Question 5.
Find the polar of (3, -1) with respect to the circle 2x² + 2y² = 11.
Solution:
Given equation of circle is x² + y² = \(\frac{11}{2}\)
∴ Equation of polar of (x₁, y₁) w.r.t x² + y² = a² is xx₁ + yy₁ – a² = 0.
⇒ x(3) + y(-1) – \(\frac{11}{2}\) = 0
⇒ 6x – 2y – 11 = 0

Question 6.
Find the polar of (1, -2) with respect to x² + y² – 10x – 10y + 25 = 0.
Solution:
Polar of (x₁, y₁) w.r.t x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
⇒ -4x – 7y + 30 = 0
⇒ 4x + 7y – 30 = 0

Question 7.
Find the pole of ax + by + c = 0 (c ≠ 0) w.r.t x² + y² = r²
Solution:
Let (x₁, y₁) be the pole of ax + by + c = 0 ……(1) w.r.t. x² + y² = r²; then the equation of polar is xx₁ + yy₁ – r² = 0 ……….(2)
∴ From (1) and (2)

Question 8.
Find the pole of 3x + 4y – 45 = 0 w.r.t x² + y² – 6x – 8y + 5 = 0
Solution:
Let (x₁, y₁) be the pole of 3x + 4y – 45 = 0 ………(1)
Then the equation of polar of (x₁, y₁) w.r.t the circle x² + y² – 6x – 8y + 5 = 0 is xx₁ + yy₁ – 3(x + x1) – 4(y + y1) + 5 = 0
⇒ x(x₁ – 3) + y(y₁ – 4) – (3x₁ + 4y₁ – 5) = 0 ……….(2)
∴ From (1) and (2)
\(\frac{x_1-3}{3}=\frac{y_1-4}{4}=\frac{-\left(3 x_1+4 y_1-5\right)}{-45}\)
⇒ \(\frac{x_1-3}{3}=\frac{y_1-4}{4}\)
⇒ 4x₁ – 12 = 3y₁ – 12
⇒ 4x₁ – 3y₁ = 0 ……….(3)
\(\frac{y_1-4}{4}=\frac{3 x_1+4 y_1-5}{45}\)
⇒ 45y₁ – 180 = 12x₁ + 16y₁ – 20
⇒ 12x₁ – 29y₁ + 160 = 0 ………(4)
Solving (3) and (4) we get
12x₁ – 9y₁ = 0
12x₁ – 29y₁ = -160
∴ 20y₁ = 160
⇒ y₁ = 8
and from (3)
4x₁ = 24
⇒ x₁ = 6
∴ Pole of 3x + 4y – 45 = 0 w.r.t x² + y² – 6x – 8y + 5 = 0 is (6, 8).

Question 9.
Find the pole of x – 2y + 22 = 0 w.r.t x² + y² – 5x + 8y + 6 = 0.
Solution:
Let (x₁, y₁) be the pole of the line x – 2y + 22 = 0 ………(1)
Then the equation of polar of (x₁, y₁) w.r.t circle x² + y² – 5x + 8y + 6 = 0 ………(2) is

⇒ 22y₁ + 88 = 5x₁ – 8y₁ – 12
⇒ 5x₁ – 30y₁ – 100 = 0
⇒ x₁ – 6y₁ – 20 = 0 ………(5)
∴ 2x₁ – 12y₁ – 40 = 0 and 2x₁ + y₁ – 1 = 0
solving -13y₁ – 39 = 0 ⇒ y₁ = -3
and from (4), 2x₁ – 3 – 1 = 0 ⇒ x₁ = 2
pole of x – 2y + 22 = 0 w.r.t. x² + y² – 5x + 8y + 6 = 0 is (2, -3).

Question 10.
Show that the points (-6, 1) and (2, 3) are conjugate points w.r.t the circle x² + y² – 2x + 2y + 1 = 0.
Solution:
Let P(-6, 1) and Q(2, 3) be the given points.
Two points P(x₁, y₁) and Q(x₂, y₂) one said to be conjugate
⇔ S₁₂ = 0
⇔ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
∴ S₁₂ = (-6)(2) + (1)(3) – 1(-6 + 2) + 1(1 + 3) + 1
= -12 + 3 + 4 + 4 + 1
= 0
∴ Hence the points P and Q are conjugate w.r.t. the given circle.

Question 11.
Show that the points (4, 2) and (3, -5) are conjugate points w.r.t the circle x² + y² – 3x – 5y + 1 = 0.
Solution:
Let P(x₁, y₁) = (4, 2) and Q(x₂, y₂) = (3, -5)
Now S₁₂ = x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
= (4)(3) + (2)(-5) – \(\frac{3}{2}\)(4 + 3) – \(\frac{5}{2}\)(2 – 5) + 1
= 12 – 10 – \(\frac{21}{2}+\frac{15}{2}\) + 1 = 0
= 24 – 20 – 21 + 15 + 2
= 0
Hence the points P and Q are conjugate w.r.t. the given circle.

Question 12.
Find the value of k if kx + 3y – 1 = 0, 2x + y + 5 = 0 are conjugate lines w.r.t the x² + y² – 2x – 4y – 4 = 0.
Solution:
Two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 are said to be conjugate w.r.t. x² + y² + 2gx + 2fy + c = 0.
If r²(l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
Here g = -1, f = -2,
r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{1+4+4}\) = 3
l₁ = k, m₁ = 3, n₁ = -1, l₂ = 2, m₂2 = 1, n₂ = 5
∴ r²(l₁l₂ + m₁m₂) = 9(2k + 3)
and (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = (-k – 6 + 1) (-2 – 2 – 5) = (-k – 5) (-9)
∴ 9(2k + 3) = 9(k + 5)
⇒ 2k + 3 = k + 5
⇒ k – 2 = 0
⇒ k = 2

Question 13.
Find the value of k if x + y – 5 = 0, 2x + ky – 8 = 0 are conjugate w.r.t the circle x² + y² – 2x – 2y – 1 = 0.
Solution:
Comparing the given equation of circle with x² + y² + 2gx + 2fy + c = 0,
we have g = -1, f = -1, c = -1 and
radius = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{1+1+1}=\sqrt{3}\)
Condition for two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 to be conjugate w.r.t. S = 0
r² (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
Given that the equations of lines are x + y – 5 = 0 and 2x + ky – 8 = 0
l₁ = 1, m₁ = 1, n₁ = -5, l₂ = 2, m₂ = k, n₂ = -8
∴ r²(l₁l₂ + m₁m₂) = 3(2 + k) and (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = (-1 – 1 + 5) (-2 – k + 8)
∴ 3(2 + k) = 3(6 – k) = 18 – 3k
⇒ 6 + 3k = 18 – 3k
⇒ 6k = 12
⇒ k = 2

Question 14.
Find the value of k if the points (1, 3) and (2, k) are conjugate w.r.t the circle x² + y² = 35.
Solution:
The condition for two points P(x₁, y₁) and Q(x₂, y₂) to be conjugate w.r.t x² + y² = a² is x₁x₂ + y₁y₂ – a² = 0
Given P(x₁, y₁) = (1, 3) and Q(x₂, y₂) = (2, k) and a² = 35.
∴ x₁x₂ + y₁y₂ – a² = 2 + 3k – 35
⇒ 3k – 33 = 0
⇒ k = 11

Question 15.
Find the value of k if the points (4, 2), (k, -3) are conjugate points w.r.t the circle x² + y² – 5x + 8y + 6 = 0.
Solution:
Two points P(x₁, y₁) and Q(x₂, y₂) are said to be conjugate w.r.t the circle S = 0 if S₁₂ = 0.
i.e., x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
Given P(x₁, y₁) = (4, 2) and Q(x₂, y₂) = (k, -3)
Then S₁₂ = 4k – 6 – \(\frac{5}{2}\)(4 + k) + 4(2 – 3) + 6 = 0
⇒ 4k – 6 – \(\frac{5}{2}\)(4 + k) – 4 + 6 = 0
⇒ 4k – \(\frac{5}{2}\)(4 + k) – 4 = 0
⇒ 4k – 10 – \(\frac{5k}{2}\) – 4 = 0
⇒ 8k – 20 – 5k – 8 = 0
⇒ 3k – 28 = 0
⇒ k = \(\frac{28}{3}\)

II.

Question 1.
Find the angle between the tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0. (Mar. ’12)
Solution:
If θ is the acute angle between the tangents drawn from P(3, 2) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\) where r is the radius of the circle.
Where S₁₁ = \(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c
= 9 + 4 – 6(3) + 4(2) – 2
= 1
and r = radius of the given circle = \(\sqrt{9+4+2}=\sqrt{15}\)
∴ cos θ = \(\left|\frac{1-15}{1+15}\right|=\left|\frac{-14}{16}\right|=\frac{7}{8}\)
∴ θ = \({Cos}^{-1} \cdot\left(\frac{7}{8}\right)\)
∴ The angle between tangents drawn from (3, 2) to the given circle is \({Cos}^{-1} \cdot\left(\frac{7}{8}\right)\).

Question 2.
Find the angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0.
Solution:
If θ is the acute angle between the tangents drawn from P(3, 2) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\) where r is the radius of the circle.
S₁₁ = \(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c
= 1 + 9 – 2 + 12 – 11
= 9
and r = radius of the given circle (r) = \(\sqrt{1+4+11}\) = 4
∴ cos θ = \(\left|\frac{9-16}{9+16}\right|=\left|\frac{7}{25}\right|\)
∴ θ = \({Cos}^{-1}\left(\frac{7}{25}\right)\)
∴ The angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 is \({Cos}^{-1}\left(\frac{7}{25}\right)\)

Question 3.
Find the angle between the pair of tangents drawn from (0, 0) to the circle x² + y² – 14x + 2y + 25 = 0.
Solution:
If θ is the angle between the tangents drawn from O(0, 0) to the circle S = 0 then
cos θ = \(\left|\frac{s_{11}-r^2}{s_{11}+r^2}\right|\)
where S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2\) + 2gx₁ + 2fy₁ + c
= 0 + 0 + 0 + 0 + 25
= 25
and r = \(\sqrt{49+1-25}\) = 5
∴ cos θ = \(\left|\frac{25-25}{25+5}\right|\) = 0
∴ θ = \(\frac{\pi}{2}\)
∴ The angle between the pair of tangents drawn from (0, 0) to the given circle is \(\frac{\pi}{2}\).

Question 4.
Find the locus of P if the tangents drawn from P to x² + y² = a² include an angle α.
Solution:
The centre of the circle x² + y² = a² is C = (0, 0) and radius = a

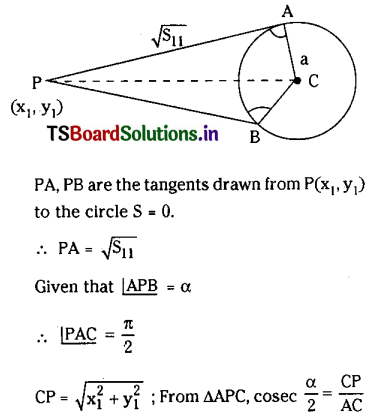
Question 5.
Find the locus of P if the tangents drawn from P to x² + y² = a² are perpendicular to each other.
Solution:
Equation of the given circle is x² + y² = a² and radius = a
Let P(x₁, y₁) be any point on the locus.
Since the tangents drawn from P(x₁, y₁) to the circle are perpendicular to each other,
the angle between tangents is \(\frac{\pi}{2}\)

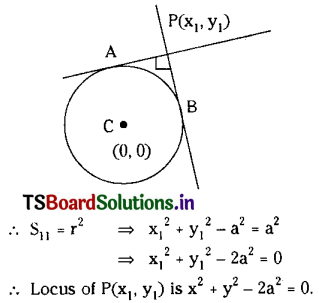
Question 6.
Find the slope of the polar of (1, 3) with respect to the circle x² + y² – 4x – 4y – 4 = 0. Also, find the distance from the centre to it.
Solution:
Equation of polar of the point P(x₁, y₁) w.r.t circle S ≡ x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
∴ Polar of (1, 3) w.r.t. circle x² + y² – 4x – 4y – 4 = 0 is x(1) + y(3) – 2(x + 1) – 2(y + 3) – 4 = 0
⇒ -x + y – 12 = 0
⇒ x – y + 12 = 0
∴ The slope of the polar is ‘1’
Also, the distance from the centre (2, 2) to the polar of (1, 3) i.e., x – y + 12 = 0 is \(\left|\frac{2-2+12}{\sqrt{1+1}}\right|=\frac{12}{\sqrt{2}}=6 \sqrt{2}\)

Question 7.
If ax + by + c = 0 is a polar of (1, 1) w.r.t the circle x² + y² – 2x + 2y + 1 = 0 and H.C.F of a, b, c is equal to one then find a² + b² + c².
Solution:
Equation of polar of (1, 1) w.r.t the circle x² + y² – 2x + 2y + 1 = 0 is x(1) + y(1) – 1(x + 1) + 1(y + 1) + 1 = 0
⇒ 2y + 1 = 0 ……….(1)
Given that polar of P(1, 1) is ax + by + c = 0 ………(2)
since (1) and (2) represent the same line
\(\frac{\mathrm{a}}{0}=\frac{\mathrm{b}}{2}=\frac{\mathrm{c}}{1}=\mathrm{k}\)
⇒ a = 0, b = 2k, c = k
Given that H.C.F of a, b, c is ‘1’ we have k = 1
∴ a = 0, b = 2, c = 1
∴ a² + b² + c² = 0 + 4 + 1 = 5

III.

Question 1.
Find the coordinates of the point of intersection of tangents at the points where x + 4y – 14 = 0 meets the circle x² + y² – 2x + 3y – 5 = 0.
Solution:

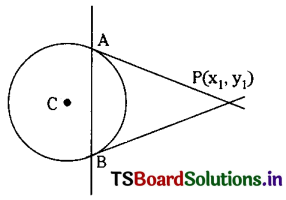
Let P(x₁, y₁) be the point of intersection of tangents drawn to the circle x² + y² – 2x + 3y – 5 = 0 …………(1) and given that x + 4y – 14 = 0 ………..(2) meets the circle at points A, B.
∴ Equation of chord of contact of (x₁, y₁) w.r.t circle (1) is xx₁ + yy₁ – (x + x₁) + \(\frac{3}{2}\)(y + y₁) – 5 = 0
⇒ \(x\left(x_1-1\right)+y\left(y_1+\frac{3}{2}\right)-\left(x_1-\frac{3}{2} y_1+5\right)=0\) …….(3)
Since (2) and (3) represent the same chord of contact

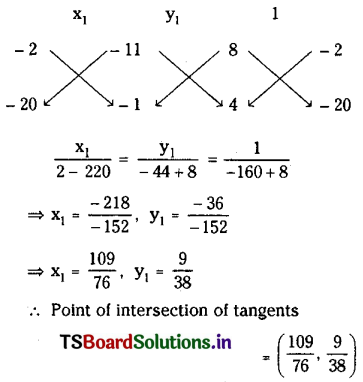
Question 2.
If the polar of the points on the circle x² + y² = a² w.r.t the circle x² + y² = b2 touches the circle x² + y² = c² then prove that a, b, c are in geometrical progression.
Solution:
Given equations of circles
x² + y² = a² …….(1)
x² + y² = b² …….(2)
x² + y² = c² ……(3)
Let P(x₁, y₁) be any point on (1) then
\(x_1^2+y_1^2\) = a² ………(4)
The equation of polar of P(x₁, y₁) w.r.t circle (2) is xx₁ + yy₁ – b² = 0 ……..(5)
The Centre of (3) is (0, 0), and the radius = c.
Given that line (5) is polar of P w.r.t the circle (2) which touches the circle (3).
∴ The perpendicular distance from C(0, 0) of circle (3) to the line (5) = radius of circle (3)
∴ \(\frac{1-b^2 \text { । }}{\sqrt{x_1^2+y_1^2}}\) = c
⇒ \(\frac{\mathrm{b}^2}{\sqrt{\mathrm{a}^2}}\) = c
⇒ b² = ac
⇒ a, b, c are in geometric progression.

Question 3.
Tangents are drawn to the circle x² + y² = 16 from the point P(3, 5). Find the area of the triangle formed by these tangents and the chord of contact of P.
Solution:

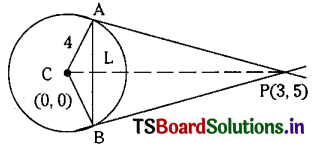
The given equation of a circle is x² + y² = 16
Centre C = (0, 0) and radius = 4
The equation of chord of contact of (3, 5) w.r.t. circle x² + y² = 16 is xx₁ + yy₁ – 16 = 0
⇒ 3x + 5y – 16 = 0
PL is the perpendicular distance from the point P(3, 5) to the chord AB.


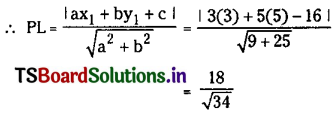
∴ Area of the triangle formed by the tangents and the chord of P = \(\frac{108 \sqrt{2}}{17}\) square units.

Question 4.
Find the locus of the point whose polar with respect to the circles x² + y² – 4x – 4y – 8 = 0 and x² + y² – 2x + 6y – 2 = 0 are mutually perpendicular.
Solution:
Let P(x₁, y₁) be the locus of the point whose polars w.r.t the given circles x² + y² – 4x – 4y – 8 = 0 ……(1) and x² + y² – 2x + 6y – 2 = 0 ……(2) are mutually perpendicular.
Polar of P(x₁, y₁) w.r.t circle (2) is xx₁ + yy₁ – (x + x₁) + 3(y + y₁) – 2 = 0
⇒ x(x₁ – 1) + y(y₁ – 3) – (x₁ – 3y₁ + 2) = 0 ………(3)
Polar of P(x₁, y₁) w.r.t circle (1) is xx₁ + yy₁ – 2(x + x₁) – 2(y + y₁) – 8 = 0
⇒ x(x₁ – 2) + y(y₁ – 2) – (2x₁ + 2y₁ + 8) = 0 ………(4)
Slope of (3) is \(-\left(\frac{x_1-1}{y_1+3}\right)\)
and slope of (4) is \(\left(\frac{x_1-2}{y_1-2}\right)\)
If (3) and (4) are mutually perpendicular then
\(\left(\frac{x_1-1}{y_1+3}\right)\left(\frac{x_1-2}{y_1-2}\right)\) = -1
⇒ \(\left(x_1^2-3 x_1+2\right)=-\left(y_1^2+y_1-6\right)\)
⇒ \(x_1^2+y_1^2-3 x_1+y_1-4=0\)
∴ Locus of P(x₁, y₁) is x² + y² – 3x + y – 4 = 0.

Question 5.
Find the locus of the foot of the perpendicular drawn from the origin to any chord of the circle S ≡ x² + y² + 2gx + 2fy + c = 0 which subtends a right angle at the origin.
Solution:

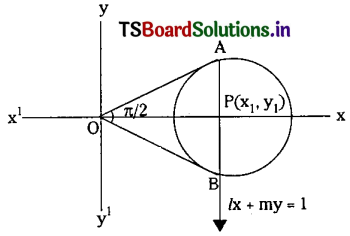
Any chord of the circle may be taken as lx + my = 1 ………(1)
Given equation of circle is x² + y² + 2gx + 2fy + c = 0 ………(2)
Chord (1) subtends a right angle at the origin.
Hence the lines joining the origin to the points of intersection of (1) and (2) are obtained by homogenizing equation (2) with equation (1).
From (1), lx + my = 1
and from (2), x² + y² + (2gx + 2fy)(1) + c(1)² = 0
⇒ x² + y² + (2gx + 2fy) (lx + my) + c(lx + my)² = 0
⇒ x² + y² + (2glx² + 2fy²m + 2flm + 2gmxy) + c(l²x² + 2lmxy + m²y²) = 0
⇒ (1 + 2gl + cl²) x² + (1 + 2fm + cm²)y² + xy(2fl + 2gm + 2lmc) = 0
This is a homogenizing second-degree equation that represents pair of lines OA and OB passing through the origin. If these lines are perpendicular then
the coefficient of x² + coefficient of y² = 0.
⇒ 1 + 2gl + 1 + cl² + 2fm + cm² = 0
⇒ c(l² + m²) + 2(gl + fm) + 2 = 0 ……….(3)
From (1), the equation of the line perpendicular to the chord is mx – ly = 0 ………..(4)
Solving lx + my = 1 …..(1) and mx – ly = 0 ………(4)

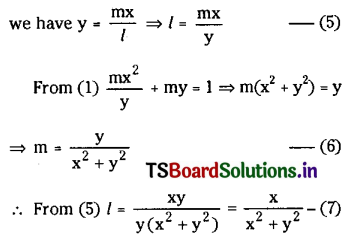
To find the locus of the foot of the perpendiculars we have to eliminate ‘l’ and ‘m’.
Substituting these values of l and m in (3), we get

⇒ c + 2(gx + fy) + 2(x2 + y2) = 0
⇒ 2(x² + y²) + 2(gx + fy) + c = 0
∴ Locus of the foot of the perpendiculars drawn from the origin to any chord of circle S ≡ x² + y² + 2gx + 2fy + c = 0 which subtends a right angle at the origin is 2(x² + y²) + 2(gx + fy) + c = 0.