TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(f) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(f)

Question 1.
If A, B, C are angles in a triangle, then prove that
(i) sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C
Answer:
sin 2A – sin 2K + sin 2C,
Given A + B + C = 180°
= 2 cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) sin\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + 2 sin C cos C
= 2 cos (A – B) sin (A – B) + 2 sin C cos C
= – 2 cos C sin (A – B) + 2 sin C cos C
(∵ A + B + C = 180° ⇒ cos(A + B) cos(180 – C) = – cos C and sin (A + B) = sin C)
= 2 cos C [sin C – sin (A – B)
= 2 cos C [sin(A + B) – sin(A – B)]
= 2 cos C[2 cos A sin B]
= 4 cos A sin B cos C = R. H. S

(ii) cos 2A – cos 2B + cos 2C = 1 – 4 sin A cos B sin C
Answer:
cos 2A – cos2B + cos 2C
= 2 sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) sin\(\left(\frac{2 \mathrm{~B}-2 \mathrm{~A}}{2}\right)\) + cos 2C
= 2 sin (A + B) sin (B – A) + cos 2C
= 2 sin C sin(B – A + 1 – 2 sin² C
= 1 + 2 sin C sin(B – A) – 2 sin² C
= 1 + 2sinC [sin (B – A) – sin C]
(∵ A + B + C = 180° = sin(A + B) sin C)
= 1 + 2 sin C[sin (B – A) – sin(A + B)]
= 1 – 2 sin C [sin (A – B) + sin (A + B)]
= 1 – 2 sin C[2 sin A cos B]
= 1 – 4 sin A cos B sin C = R.H.S

Question 2.
If A, B, C are angles in a triangle, then prove that
(i) sin A + sin B – sin C = 4 sin \(\frac{\mathrm{A}}{2}\) sin \(\frac{\mathrm{B}}{2}\) cos \(\frac{\mathrm{C}}{2}\)
Answer:

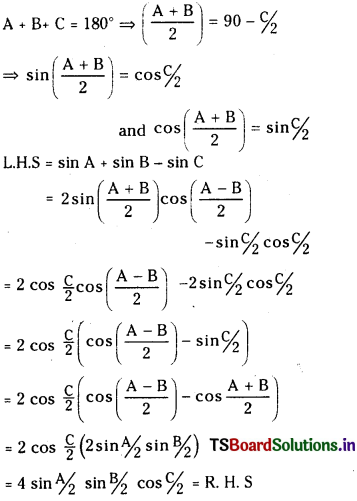
(ii) cos A + cos B – cos C = – 1 + 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\) (March 2006)
Answer:
LH.S = cos A + cos B – cos C

Question 3.
If A, B, C are angles in a triangle, then prove that
(i) sin²A + sin²B – sin²C = 2 sin A sin B cos C
Answer:
Given A + B+ C = 180°
We have L.H. S = sin² A + sin²B – sin² C
= sin²A+ sin (B + C) sin (B – C)
= sin² A + sin A sin (B – C)
= sin A [sin A + sin (B – C)]
= sin A[sin (B + C) + sin (B – C)]
= sin A[2 sin B cos C] = 2 sin A sin B cos C = R.H.S

(ii) cos²A + cos² B – cos² C = 1 – 2 sin A sin B cos C
Answer:
L.H.S = cos² A + cos² B – cos² C
= cos² A + 1 – sin² B – cos² C
(∵ A + B + C = 180° = cos (A + B) = – cos C)
= 1 – cos² C + cos² A – sin² B
= 1 -. cos² C + cos (A + B) cos (A – B)
= 1 – cos² C – cos C cos (A – B)
= 1 – cos C [ cos C + cos (A – B)]
= 1 – cos C ( cos (A – B) – cos (A + B)]
= 1 – cos C[2 sin A sin B]
= 1 – 2 sin A sin B cos C = R.H.S

Question 4.
If A + B + C = π, then prove that
(i) cos² \(\frac{A}{2}\) + cos² \(\frac{B}{2}\) + cos² \(\frac{C}{2}\) = 2(1 + sin \(\frac{A}{2}\) + sin \(\frac{B}{2}\) sin \(\frac{C}{2}\) ) (Mar. 2012) (March 2015-A.P&T.S)
Answer:
Given A + B + C = π
We have B + C = π – A and

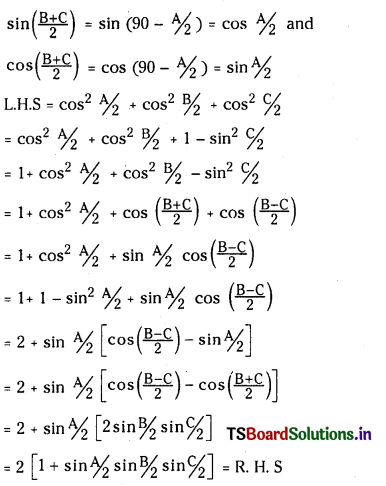
(ii) cos² \(\frac{A}{2}\) + cos² \(\frac{B}{2}\) +- cos² \(\frac{C}{2}\) = 2 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\) ) (June 2010)
Answer:

Question 5.
In triangle ABC, prove that
(i) cos \(\frac{A}{2}\) + cos \(\frac{B}{2}\) + cos \(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\) (Mar 2010, Jun 2007)
Answer:
In ∆ABC, A + B + C = 180°

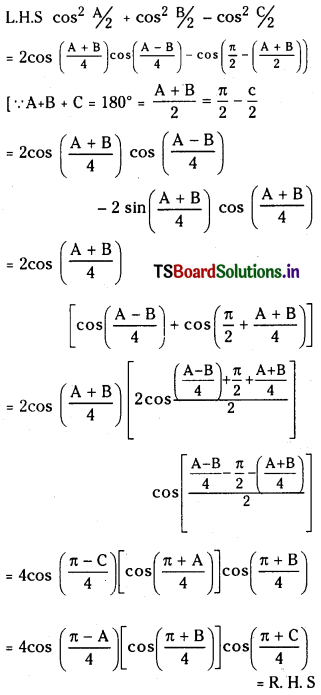
(ii) cos \(\frac{A}{2}\) + cos \(\frac{B}{2}\) – cos \(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi+\mathrm{A}}{4}\right)\) cos\(\left(\frac{\pi+\mathrm{B}}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\) (Mar 2005)
Answer:
In ∆ABC, A + B + C = 180°

(iii) sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) – sin\(\frac{C}{2}\) = – 1 + 4 cos\(\left(\frac{\pi+A}{4}\right)\) cos\(\left(\frac{\pi+B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\)
Answer:
In ∆ABC, A + B + C = 180° ……………………. (1)

Question 6.
If A + B + C = \(\frac{\pi}{2}\), then prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C
Answer:
LH.S = cos 2A + cos 2B cos 2C
= 2 cos \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + 1 – 2 sin² C
= 2 sin C cos (A – B) + 1 – 2 sin 2C
= 1 + 2 sin C [cos (A – B) – sin C]
(∵ A + B = \(\frac{\pi}{2}\) – C ⇒ cos (A + B) = cos (\(\frac{\pi}{2}\) – C) = sin C)
= 1 + 2 sin C[cos (A – B) – sin C]
= 1 + 2 sin C[cos (A – B) – cos(A + B)]
= 1 + 4 sin A sin B sin C = RHS.

Question 7.
If A + B + C = \(\frac{3 \pi}{2}\), then prove that
(i) cos² A + cos²B – cos² C = – 3 cos A cos B sin C
Answer:
L.H.S = cos²A + cos² B – cos² C
= cos² A + 1 – sin² B – cos² C
= (cos² A – sin² B) + (1 – cos²C)
= (cos² A – sin² B) + sin² C
= cos (A + B) cos (A – B) + sin²C
= – sin C cos (A – B) + sin² C
= sin C [sin C – cos (A – B)]
= sin C (- cos (A + B) – cos (A – B)]
= – sin C [cos (A + B) + cos (A – B)]
= – 2 cos A cos B sin C
(Given A + B + C = \(\frac{3 \pi}{2}\)
cos (A + B) = cos (270 – c) = – sin C)

(ii) sin 2A + sin 2B – sin 2C = – 4 sin A sin B cos C
Answer:
A + B + C = \(\frac{3 \pi}{2}\)
LH.S = sin 2A + sin 2B – sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) – sin 2C
= 2 sin (A + B) cos (A – B) – 2 sin C cos C
= – 2 cos C cos (A – B) – 2 sin C cos C
= – 2 cos C (cos (A – B) + sin C]
= – 2 cos C[cos (A – B) – cos(A + B)]
= – 2 cos C [ 2 sin A sin B]
= – 4 sin A sin B cos C R.H.S
(∵ A + B = 270 – C
⇒ cos(A + B) = cos(270 – C) = – sin C)

Question 8.
If A + B + C = 0 then prove that
(i) sin 2A + sin 2B – sin 2C = – 4 sin A sin B sin C
Answer:
Given A + B + C = O
∴ cos(B + C) = cos A and sin (B + C) = – sin A
L.H.S = sin 2A + sin 2B + sin 2C
= 2 sin (A+B) cos (A – B) + 2 sin C cos C
= – 2 sin C cos (A – B) + 2 sin C cosC
= 2 sin C [cos C – cos(A – B)]
= 2 sin C [cos (A + B) – cos(A – B)]
= – 4 sin C sin A sin B
= R.H.S

(ii) sin A + sin B – sin C = – 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)
Answer:
sin A + sin B – sin C

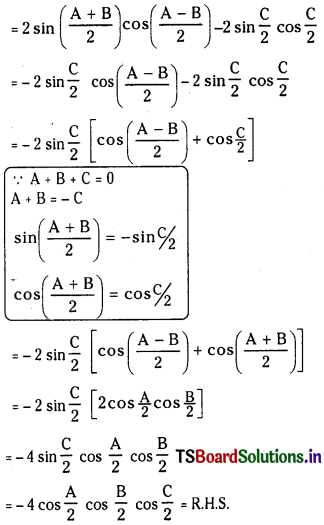
Question 9.
If A + B + C + D = 2π, then prove that
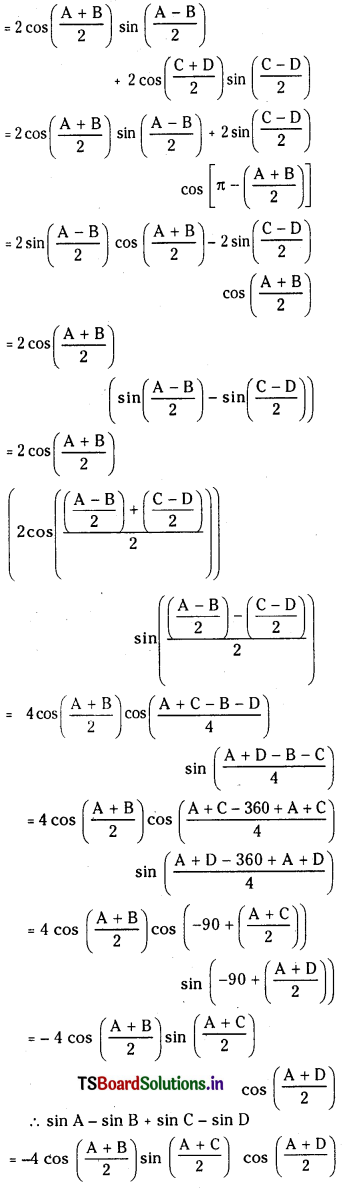
(i) sin A – sin B + sin C – sin D
= – 4 cos \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{A+C}{2}\right)\) cos \(\left(\frac{A+D}{2}\right)\)
Answer:
sin A – sin B + sin C – sin D

(ii) cos 2A + cos 2B + cos 2C + cos 2D = 4 cos (A + B) cos (A + C) cos (A +D)
Answer:
A + B + C + D = 360°
⇒ C + D = 360° – (A + B)
L.H.S = 2 cos (A + B) cos (A – B) + 2 cos (C + D) cos (C – D)
= 2 cos (A + B) cos (A – B) + 2 cos [360 – (A + B)] cos (C – D)
= 2 cos (A + B) cos (A – B) + 2 cos (A + B) cos (C – D)
= 2 cos (A + B) [cos (A – B) + cos (C – D)]
= 2 cos (A + B)

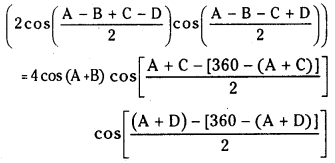
= 4 cos (A + B) cos [- 180 + (A + C)] cos [- 180 + (A + D)]
= 4 cos (A + B) cos (A + C) cos (A + D)

Question 10.
If A + B + C = 2S, then prove that
(i) sin (S – A) + sin (S – B) + sin C = 4 cos \(\left(\frac{S-A}{2}\right)\) cos \(\left(\frac{S-B}{2}\right)\) sin \(\frac{C}{2}\) (Jun 2008)
Answer:
Given A + B + C = 2S
LHS = sin(s – A) + sin (s – B) + sin C

(ii) cos (s – A) + cos (S – B) + cos C = – 1 + 4 cos \(\left(\frac{S-A}{2}\right)\) cos \(\left(\frac{S-B}{2}\right)\) cos \(\frac{C}{2}\)
Answer:
Given A + B + C = 2S
L.H.S