TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Ex 2(b)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 2 System of Circles Ex 2(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 2 System of Circles Exercise 2(b)

I.

Question 1.
Find the equation of the radical axis of the following circles.
(i) x² + y² – 3x – 4y + 5 = 0, 3(x² + y²) – 7x + 8y – 11 = 0
Solution:
Let S ≡ x² + y² – 3x – 4y + 5 = 0 and S’ ≡ \(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}=0\) be the given circles.
The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ (x² + y² – 3x – 4y + 5) – (\(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}\)) = 0
⇒ -3x – 4y + 5 + \(\frac{7}{3} x-\frac{8}{3} y+\frac{11}{3}\) = 0
⇒ -9x – 12y + 15 + 7x – 8y + 11 = 0
⇒ -2x – 20y + 26 = 0
⇒ x + 10y – 13 = 0

(ii) x² + y² + 2x + 4y + 1 = 0, x² + y² + 4x + y = 0
Solution:
Let S ≡ x² + y² + 2x + 4y + 1 = 0 and S’ ≡ x² + y² + 4x + y = 0 be the given circles.
Then the radical axis of circles S = 0, S’ = 0 is S – S’ = 0.
⇒ (x² + y² + 2x + 4y + 1) – (x² + y² + 4x + y) = 0
⇒ -2x + 3y + 1 = 0
⇒ 2x – 3y – 1 = 0
∴ The equation of the radical axis of circles is 2x – 3y – 1 = 0.

(iii) x² + y² + 4x + 6y – 7 = 0, 4(x² + y²) + 8x + 12y – 9 = 0.
Solution:
Let S ≡ x² + y² + 4x + 6y – 7 = 0 and S’ ≡ x² + y² + 2x + 3y – \(\frac{9}{4}\) = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 2x + 3y – \(\frac{19}{4}\) = 0
⇒ 8x + 12y – 19 = 0

(iv) x² + y² – 2x – 4y – 1 = 0, x² + y² – 4x – 6y + 5 = 0
Solution:
Let S ≡ x² + y² – 2x – 4y – 1 = 0 and S’ ≡ x² + y² – 4x – 6y + 5 = 0
∴ The equation of radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ 2x + 2y – 6 = 0
⇒ x + y – 3 = 0

Question 2.
Find the equation of the common chord of the following pair of circles.
(i) x² + y² – 4x – 4y + 3 = 0, x² + y² – 5x – 6y + 4 = 0
Solution:
Let S ≡ x² + y² – 4x – 4y + 3 = 0 and S’ = x² + y² – 5x – 6y + 4 = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ x + 2y – 1 = 0

(ii) x² + y² + 2x + 3y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
Solution:
Denote S ≡ x² + y² + 2x + 3y + 1 = 0 and S’ ≡ x² + y² + 4x + 3y + 2 = 0
∴ The equation of the radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ -2x – 1 = 0
⇒ 2x + 1 = 0

(iii) (x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b)
Solution:
Denote S ≡ (x – a)² + (y – b)² = c²
⇒ x² + y² – 2ax – 2by + a² + b² – c² = 0 …….(1)
and S’ ≡ (x – b)² + (y – a)² = c²
⇒ x² + y² – 2bx – 2ay + b² + a² – c² = 0 ……..(2)
Radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 2bx – 2ax + 2ay – 2by = 0
⇒ 2x(b – a) + 2y(a – b) = 0
⇒ x – y = 0 (∵ a ≠ b)

II.

Question 1.
Find the equation of the common tangent of the following circles at their point of contact.
(i) x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0
Solution:
Denote S ≡ x² + y² + 10x – 2y + 22 = 0 and S’ ≡ x² + y² + 2x – 8y + 8 = 0.
The equation of the common tangent of the circles at their point of contact is the equation of the radical axis of S = 0 and S’ = 0 given by S – S’ = 0.
⇒ 8x + 6y + 14 = 0
⇒ 4x + 3y + 7 = 0

(ii) x² + y² – 8y – 4 = 0, x² + y² – 2x – 4y = 0
Solution:
Let S ≡ x² + y² – 8y – 4 = 0 and S’ ≡ x² + y² – 2x – 4y = 0
The equation of the common tangent at the point of contact of circles is the equation of the radical axis of the circles S = 0, S’ = 0 given by S – S’ = 0.
⇒ x² + y² – 8y – 4 – x² – y² + 2x + 4y = 0
⇒ 2x – 4y – 4 = 0
⇒ x – 2y – 2 = 0

Question 2.
Show that the circles x² + y² – 8x – 2y + 8 = 0 and x² + y² – 2x + 6y + 6 = 0 touch each other and find the point of contact.
Solution:
Let the equations of the given circles be denoted by S ≡ x² + y² – 8x – 2y + 8 = 0 and S’ = x² + y² – 2x + 6y + 6 = 0
Centres are C₁ = (4, 1) and C₂ = (1, -3)
and radii of circles are r₁ = \(\sqrt{16+1-8}\) = 3 and r₂ = \(\sqrt{1+9-6}\) = 2
∴ C₁C₂ = \(\sqrt{(4-1)^2+(1+3)^2}=\sqrt{9+16}\) = 5
Also r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the circles touch each other externally.

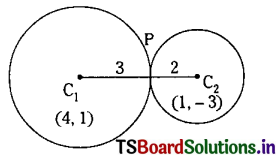
The point of contact P divides C₁C₂ internally in the ratio of their radii i.e., 3 : 2.
∴ The point of contact

Question 3.
If the two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other, then show that fg’ = f’g.
Solution:
Let S = x² + y² + 2gx + 2fy = 0 and S’ = x² + y² + 2g’x + 2f’y = 0 be the given circles.
Centres of the circles are C₁ = (-g, -f) and C₂ = (-g, -f’)
Also r₁ = \(\sqrt{g^2+f^2}\) and r₂ = \(\sqrt{g^{\prime 2}+f^{\prime 2}}\)
Given that the two circles touch each other we have C₁C₂ = |r₁ ± r₂|
⇒ \(\sqrt{\left(g-g^{\prime}\right)^2+\left(f-f^{\prime}\right)^2}\) = \(\left|\sqrt{g^2+f^2} \pm \sqrt{g^{+2}+f^2}\right|\)

Question 4.
Find the radical centre of the following circles.
(i) x² + y² – 4x – 6y + 5 = 0, x² + y² – 2x – 4y – 1 = 0, x² + y² – 6x – 2y = 0
Solution:
Let S = x² + y² – 4x – 6y + 5 = 0, S₁ = x² + y² – 2x – 4y – 1 = 0 and S₂ = x² + y² – 6x – 2y = 0 be the given circles.
Radical axis of S = 0, S₁ = 0 is S – S₁ = 0
⇒ -2x – 2y + 6 = 0
⇒ x + y – 3 = 0 ……….(1)
Radical axis of S₁ = 0, S₂ = 0 is 4x – 2y – 1 = 0 ……….(2)
Solving (1) and (2), we get the coordinates 0f Radical centre of the circles S = 0, S₁ = 0, and S₂ = 0

(ii) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0
Solution:
Denote S = x² + y² + 4x – 7 = 0
S₁ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
and S₂ = x² + y² + y = 0
Radical axis of S = 0, S₁ = 0 is S – S₁ = 0.
⇒ \(\frac{5}{2} x-\frac{5}{2} y+\frac{5}{2}=0\)
⇒ x – y + 1 = 0 ………(1)
Radical axis of S₁ = 0, S₂ = 0 is S₁ – S₂ = 0.
⇒ \(\frac{3}{2} x+\frac{3}{2} y-\frac{9}{2}=0\)
⇒ x + y – 3 = 0 ……..(2)
Solving 2x – 2 = 0 ⇒ x = 1
and From (2), y = 2
∴ Radical centre = (1, 2)

III.

Question 1.
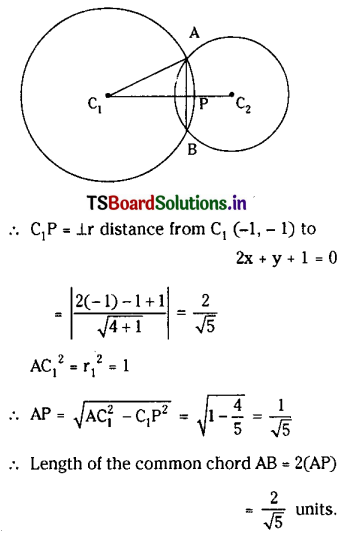
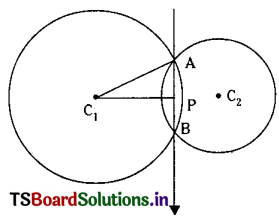
Show that the common chord of the circles x² + y² – 6x – 4y + 9 = 0 and x² + y² – 8x – 6y + 23 = 0 is the diameter of the second circle and also find its length.
Solution:

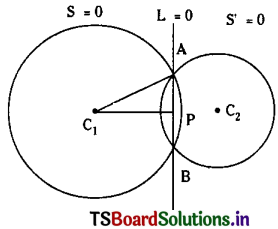
Let S = x² + y² – 6x – 4y + 9 = 0 and S’ = x² + y² – 8x – 6y + 23 = 0
Then the equation of the common chord of circles is S – S’ = 0 is 2x + 2y – 14 = 0
⇒ x + y – 7 = 0
The Centre of S’ = 0 is (4, 3)
∴ x + y – 7 = 4 + 3 – 7 = 0 and common chord of circles S = 0, S’ = 0 is the diameter of the second circle.
The length of the common chord = 2(the radius of the circle S’ = 0) = 2√2 units.
(or) C₁P = ⊥ distance from C₁(3, 2) to the common chord x + y – 7 = 0.
∴ C₁P = \(\left|\frac{3+2-7}{\sqrt{2}}\right|\) = √2
AC₁ = radius of S = 0
= \(\sqrt{9+4-9}\)
= 2
∴ AP = \(\sqrt{\mathrm{AC}_1^2-\mathrm{C}_1 \mathrm{P}^2}=\sqrt{4-2}=\sqrt{2}\)
∴ Length of the common chord AB = 2(AP) = 2√2.

Question 2.
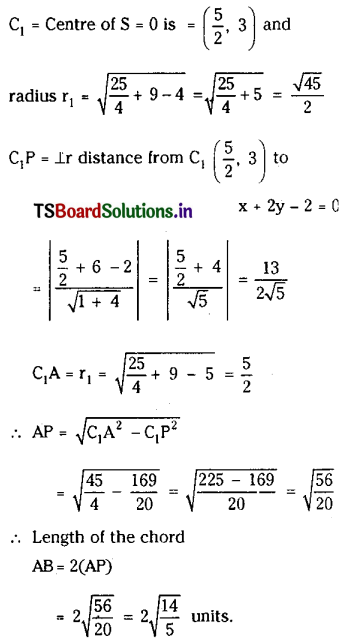
Find the equation and length of the common chord of the following circles.
(i) x² + y² + 2x + 2y + 1 = 0, x² + y² + 4x + 3y + 2 = 0
Solution:
Let S = x² + y² + 2x + 2y + 1 = 0 and S₁ = x² + y² + 4x + 3y + 2 = 0
Then the equation of the common chord of S = 0, S₁ = 0 is S – S₁ = 0.
⇒ -2x – y – 1 = 0
⇒ 2x + y + 1 = 0
C₁ = Centre of S = 0 is (-1, 1) and r₁ = \(\sqrt{1+1-1}\) = 1

(ii) x² + y² – 5x – 6y + 4 = 0, x² + y² – 2x – 2 = 0
Solution:
Denote S = x² + y² – 5x – 6y + 4 = 0 and S₁ = x² + y² – 2x – 2 = 0
Equation of common chord of S = 0, S₁ = 0 is S – S₂ = 0.
⇒ -3x – 6y + 6 = 0
⇒ x + 2y – 2 = 0

Question 3.
Prove that the radical axis of the circle x² + y² + 2gx + 2fy + c = 0 and x² + y² + 2g’x + 2f’y + c’ = 0 is the diameter of the latter circle (or the former bisector the circumference of the latter) if 2g'(g – g’) + 2f(f – f’) = c – c’.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 and S’ ≡ x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.
Centre of the circle S’ = 0 is C2 = (-g’, -f’)
The equation of the Radical axis of S = 0 and S’ = 0 is S – S’ = 0.
⇒ 2(g – g’)x + 2(f – f’)y + c – c’ = 0 …….(1)
Substituting the centre (-g’, -f’) of S’ = 0, we get
2(g – g’) (-g’) + 2(f – f’) (-f’) + c – c’ = 0
⇒ 2g'(g – g’) + 2f'(f – f’) = c – c’
The radical axis of the circles S = 0, S’ = 0 is the diameter of the circle S’ = 0 if 2g'(g – g’) + 2f(f – f’) = c – c’

Question 4.
Show that the circles x² + y² + 2ax + c = 0 and x² + y² + 2by + c = 0 touch each other if \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c}\)
Solution:
Let S = x² + y² + 2ax + c = 0 and S’ = x² + y² + 2by + c = 0 be the given circles.
Centre of S = 0 is C₁ (-a, 0) and radius of the circle S = 0 is \(\sqrt{a^2-c}\).
The equation of common tangent of circles S = 0, S’ = 0 is S – S’ = 0
⇒ 2ax – 2by = 0
⇒ ax – by = 0
Let L = ax – by = 0
The two circles S = 0 and S’ = 0 touch each other if the perpendicular distance from C₁ (-a, 0) to the common tangent L = 0 is equal to the radius of the circle S = 0.
∴ The perpendicular distance from C₁ (-a, 0)

Question 5.
Show that the circles x² + y² – 2x = 0 and x² + y² + 6x + 6y + 2 = 0 touch each other. Find the coordinates of the point of contact. Is the point of contact external or Internal?
Solution:
Let S = x² + y² – 2x = 0 and S’ = x² + y² + 6x – 6y + 2 = 0 be the given circles.
Centre of S = 0 is C₁ = (1, 0),
and radius of S₁ = 0 is r₁ = √1 = 1.
Centre of S’ = 0 is C₂ = (-3, 3)
and radius of S’ = 0 is r₂ = \(\sqrt{9+9-2}\) = 4.
Distance between centres C₁C₂ = \(\sqrt{(1+3)^2+(0-3)^2}=\sqrt{16+9}\) = 5
and r₁ + r₂ = 1 + 4 = 5.
Since C₁C₂ = r₁ + r₂, the two circles touch externally at a point and the point of contact divides C₁C₂ internally in the ratio 1 : 4.
∴ Point of contact

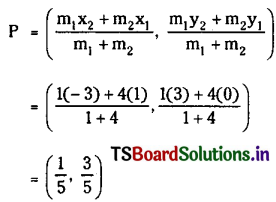
∴ The point of contact is \(\left(\frac{1}{5}, \frac{3}{5}\right)\) and the two circles touch each other externally.

Question 6.
Find the equation of the circle which cuts the following circles orthogonally.
(i) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0
Solution:
Let S = x² + y² + 4x – 7 = 0
S’ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
and S” = x² + y² + y = 0 be the equations of the given circles.
Radical axis of S = 0, S’ = 0 is S – S’ = 0.
⇒ 5x – 5y – 5 = 0
⇒ x – y – 1 = 0 ………(1)
The radical axis of S’ = 0, S” = 0 is S’ – S” = 0.
⇒ \(\frac{3}{2} x+\frac{3}{2} y-\frac{9}{2}=0\)
⇒ x + y – 3 = 0 ………(2)
Solving (1) and (2), we get
the Radical centre of circles S = 0, S’ = 0 and S” = 0

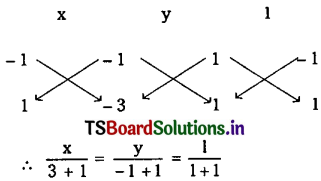
⇒ x = 2 and y = 1
∴ The radical centre of the given circles is (2, 1).
The length of the tangent drawn from (2, 1) to S = 0 is \(\sqrt{4+1+8-7}\) = √6
So by the property that a circle having radical centre as centre and length of the tangent to S = 0 as radius cuts every given circle orthogonally.
So the equation of a required circle with C(2, 1) as a radical centre and √6 as the radius is given by
(x – 2)² + (y + 1)² = (√6)²
⇒ x² + y² – 4x – 2y – 1 = 0

(ii) x² + y² + 2x + 4y + 1 = 0, 2x² + 2y² + 6x + 8y – 3 = 0, x² + y² – 2x + 6y – 3 = 0. (May ’12)
Solution:
Let S = x² + y² + 2x + 4y + 1 = 0
S’ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
and S” = x² + y² – 2x + 6y – 3 = 0 be the equations of the given circles.
Radical axis of centre S = 0, S’ = 0 is S – S’ = 0.
⇒ -x + \(\frac{5}{2}\) = 0
⇒ x = \(\frac{5}{2}\) ……..(1)
Radical axis of centre S’ = 0, S” = 0 is S’ – S” = 0
⇒ 5x – 2y + \(\frac{3}{2}\) = 0
⇒ 10x – 4y + 3 = 0 ………(2)
By solving (1) and (2), we get the Radical centre of the given circles.
Since x = \(\frac{5}{2}\) and from(2),
25 – 4y + 3 = 0
⇒ y = 7
∴ Radical centre = (\(\frac{5}{2}\), 7)
Length of the tangent from (\(\frac{5}{2}\), 7) to S = 0 is

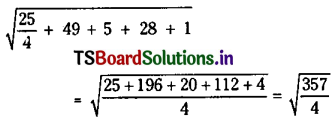
Hence the circle with centre (\(\frac{5}{2}\), 7) and \(\sqrt{\frac{357}{4}}\) as radius cuts every circle of the given system orthogonally.
∴ The equation of required circle with centre (\(\frac{5}{2}\), 7) and \(\sqrt{\frac{357}{4}}\) as radius is

(iii) x² + y² + 2x + 17y + 4 = 0, x² + y² + 7x + 6y + 11 = 0, x² + y² – x + 22y + 3 = 0
Solution:
Denote the given circles by
S = x² + y² + 2x + 17y + 4 = 0
S’ = x² + y² + 7x + 6y + 11 = 0
S” = x² + y² – x + 22y + 3 = 0
Radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ -5x + 11y – 7 = 0
⇒ 5x – 11y + 7 = 0 ………(1)
Radical axis of S’ = 0, S” = 0 is S’ – S” = 0
⇒ 8x – 16y + 8 = 0
⇒ x – 2y + 1 = 0 ……..(2)
Solving (1) and (2), we get the coordinates of the Radical centre of circles.

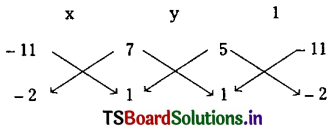
∴ \(\frac{x}{-11+14}=\frac{y}{7-5}=\frac{1}{-10+11}\)
⇒ x = 3, y = 2
∴ Radical centre = (3, 2)
Length of the tangent from (3, 2) to the circle S = 0 is \(\sqrt{9+4+6+34+4}=\sqrt{57}\).
Since the circle with centre (3, 2) and radius √57 cuts every circle of the given system orthogonally,
the equation of the required circle is (x – 3)² + (y – 2)² = 57
⇒ x² + y² – 6x – 4y – 44 = 0.

(iv) x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0.
Solution:
Denote the given circles by S = x² + y² + 4x + 2y + 1 = 0, S’ = x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0, and S” = x² + y² + 6x – 2y – 3 = 0
Radical axis of S = 0, S’ = 0 is S – S’ = 0
⇒ -y + \(\frac{5}{2}\) = 0
⇒ y = \(\frac{5}{2}\) ……..(1)
The radical axis of S’ = 0, S” = 0 is S’ – S” = 0.
⇒ -2x + 5y + \(\frac{3}{2}\) = 0
⇒ -4x + 10y + 3 = 0
⇒ 4x – 10y – 3 = 0 ………(2)
Solving (1) and (2), we get the Radical centre of circles.
∴ From (2), 4x – 25 – 3 = 0
⇒ x = 7
∴ Radical centre = (7, \(\frac{5}{2}\))
Length of the tangent from (7, \(\frac{5}{2}\)) to S = 0 is = \(\sqrt{49+\frac{25}{4}+28+5+1}=\sqrt{\frac{357}{4}}\)
∴ The equation of the required circle with centre (7, \(\frac{5}{2}\)) and as radius which cuts every circle of the system orthogonally is given by
(x – 7)² + \(\left(y-\frac{5}{2}\right)^2=\frac{357}{4}\)
⇒ x² + y² – 14x – 5y + 49 + \(\frac{25}{4}-\frac{357}{4}\) = 0
⇒ x² + y² – 14x – 5y – 34 = 0.